Pedestrian Detection with Lidar Point Clouds Based on Single Template Matching
Abstract
:1. Introduction
1.1. Training-Based Methods
1.2. Foreground and Background Segmentation Methods
1.3. KDE-Based Method
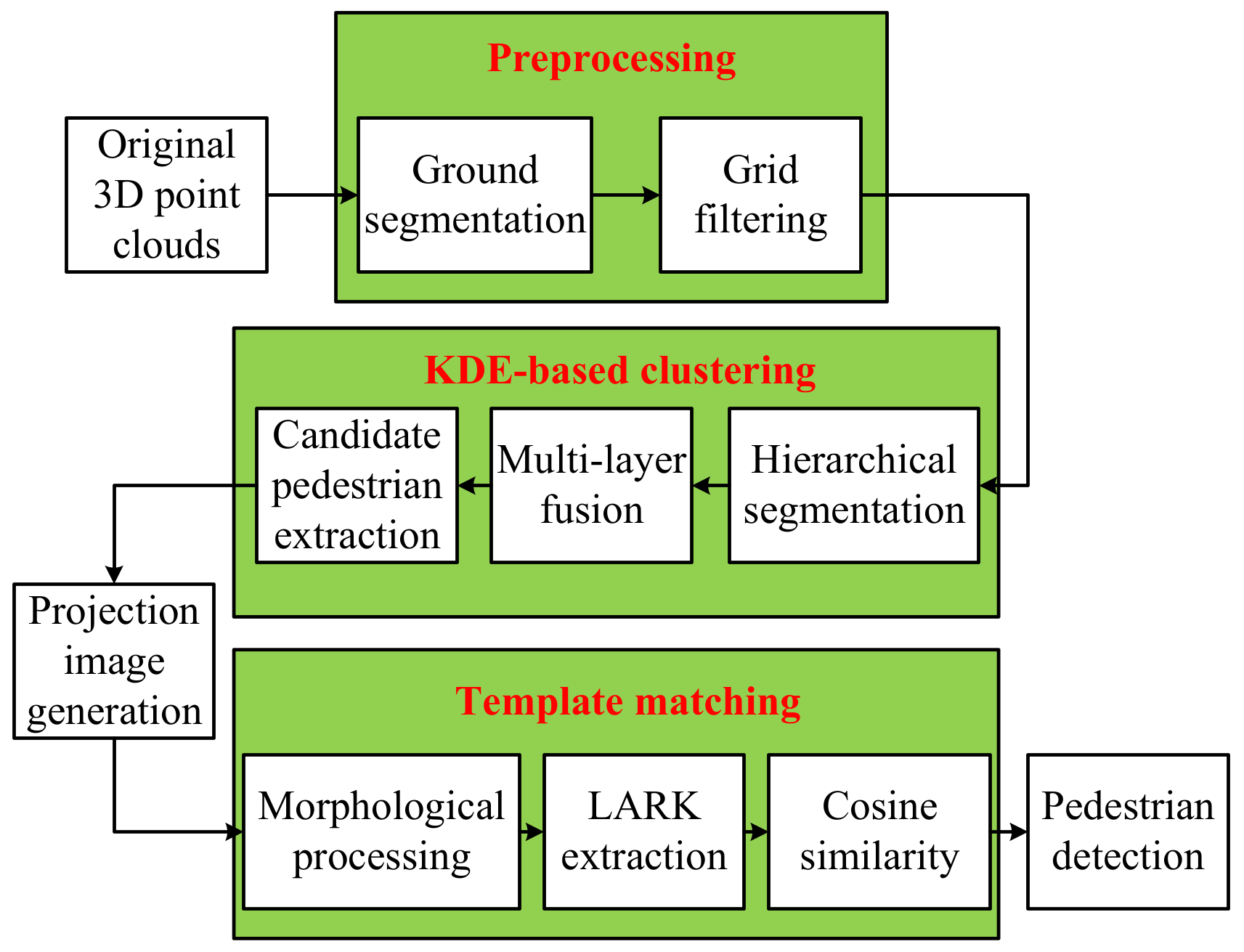
2. Materials and Methods
- Point-cloud preprocessing. This process includes ground segmentation and grid filtering, which is mainly utilized to reduce the number of point clouds and improve the efficiency of the algorithm.
- Pedestrian clustering based on KDE, which is employed to extract candidate pedestrians from point clouds with size limitation.
- Template matching. Three-dimensional point clouds are projected onto the 2D plane, from which contour features are extracted. Cosine Similarity between the features of the template and the projection image is calculated for pedestrian detection.
2.1. Preprocessing
- Generally, points that are returned by a human are dense. If the point number contained in a grid cell is smaller than a preset value, these points may come from the measurement noise, mis-segmented ground points and other interference objects. Therefore, these points are filtered out.
- If the height difference of the point clouds in a grid cell that can be calculated with and is small and the average height of the point clouds is small, these points may come from roads or low obstacles and are filtered out.
- If the height difference of the point clouds in a grid cell is large or the maximum height is big, these points are likely to come from tall buildings and are therefore filtered out.
2.2. Clustering Based on KDE
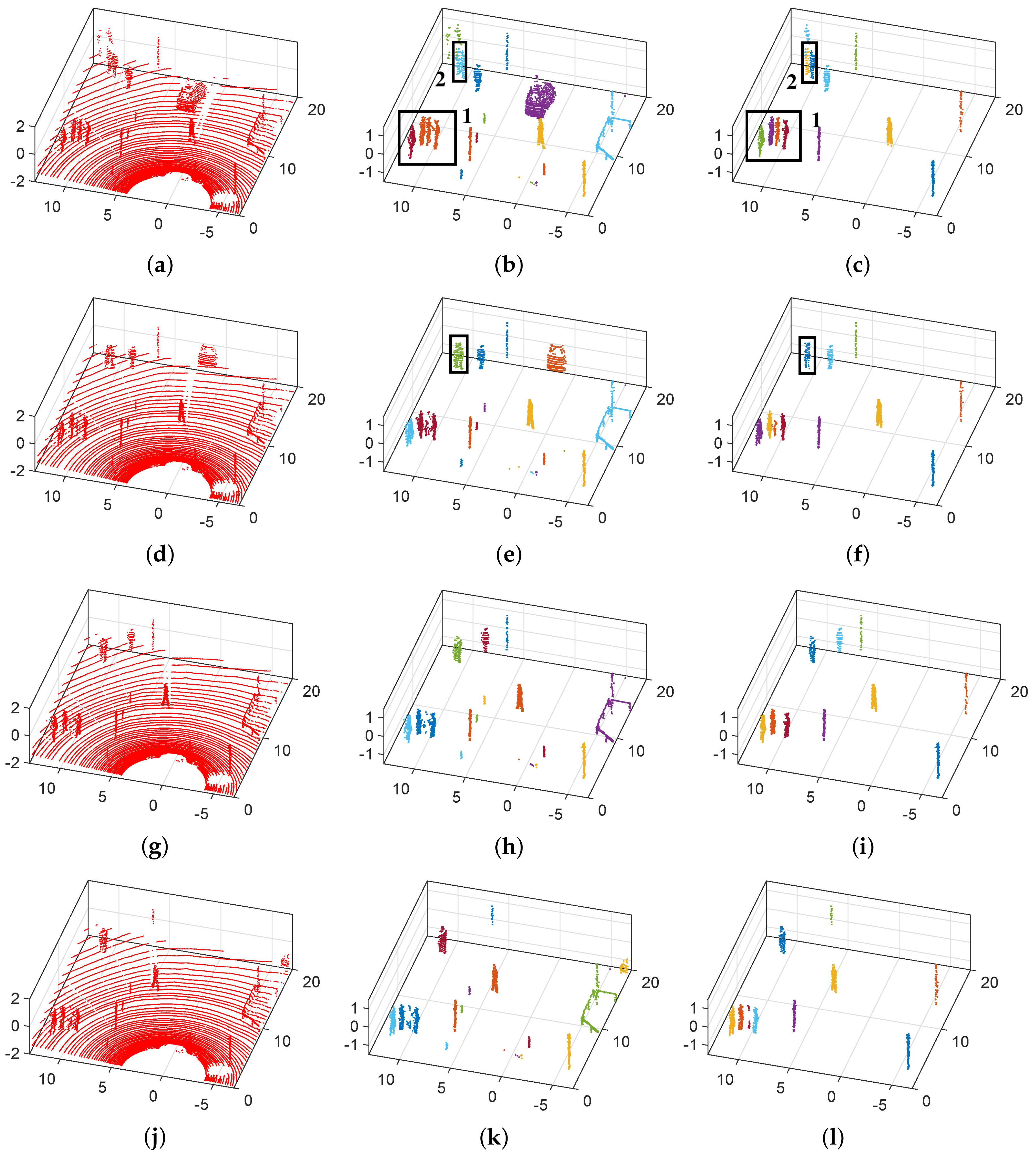
2.2.1. Hierarchical Segmentation
| Algorithm 1 Hierarchical segmentation. |
Input:, , , ;
|
2.2.2. Multilayer Fusion
2.3. Template Matching
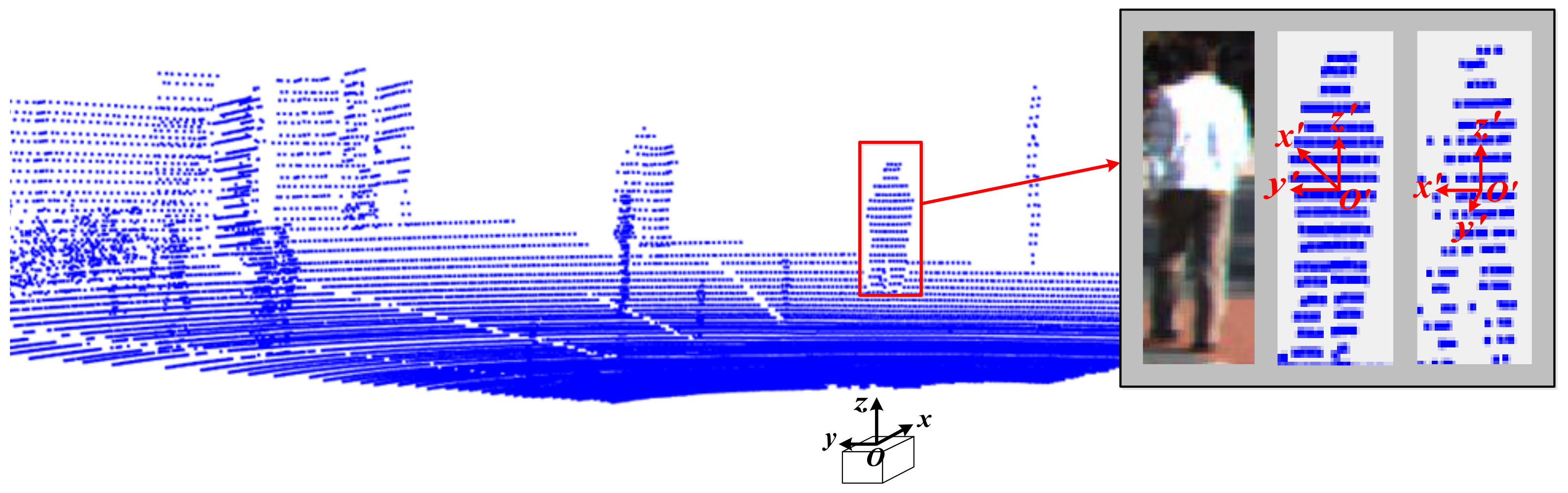
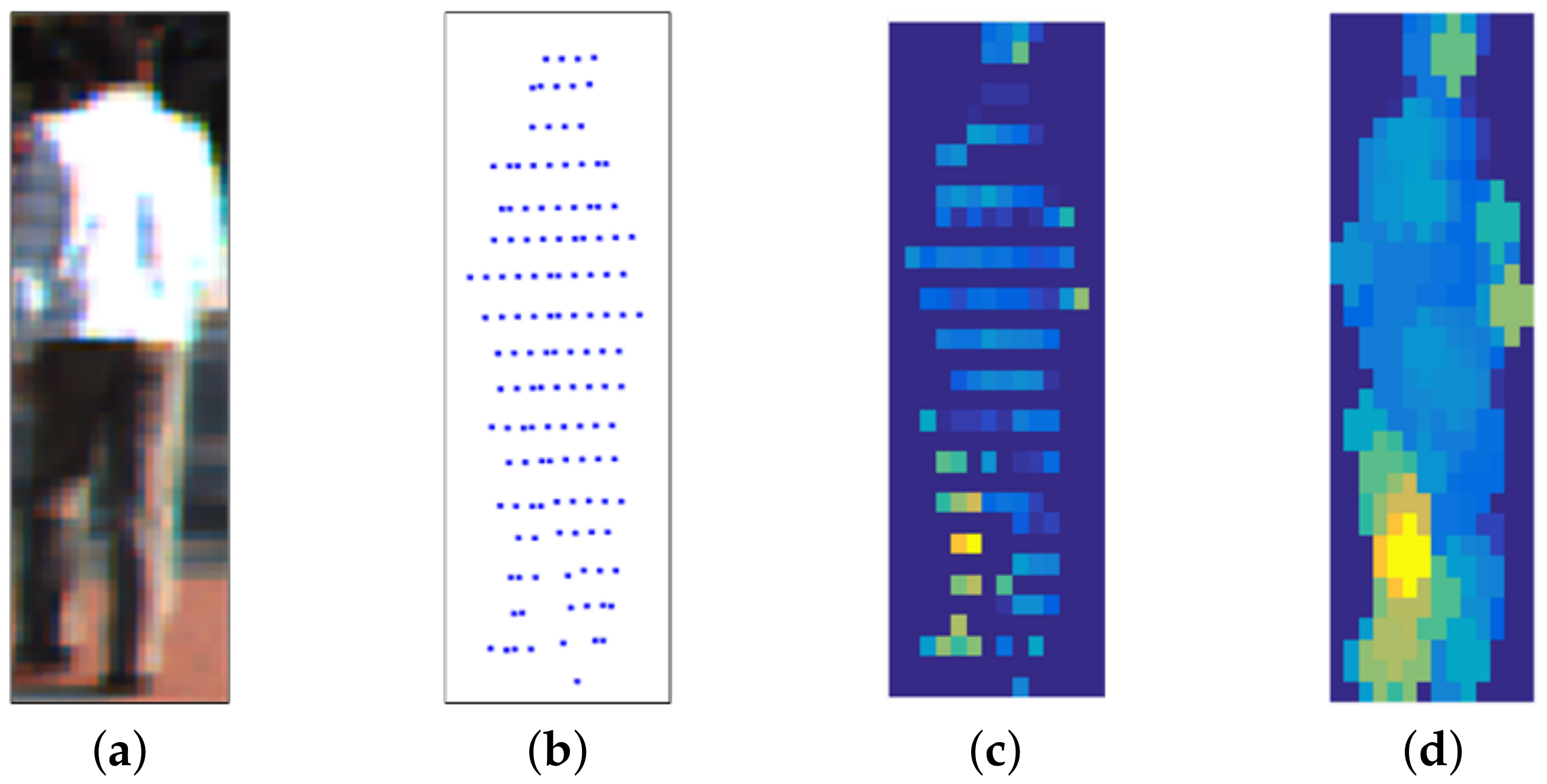
2.3.1. Projection-Image Generation
2.3.2. Feature Extraction
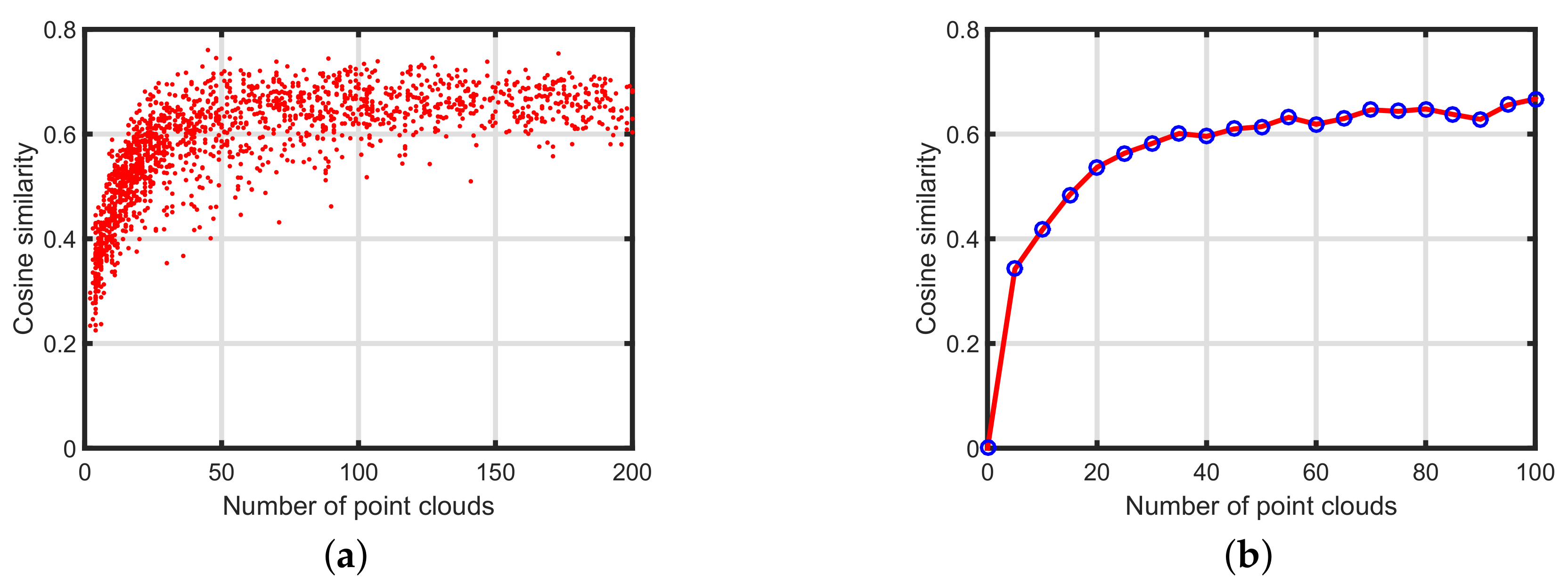
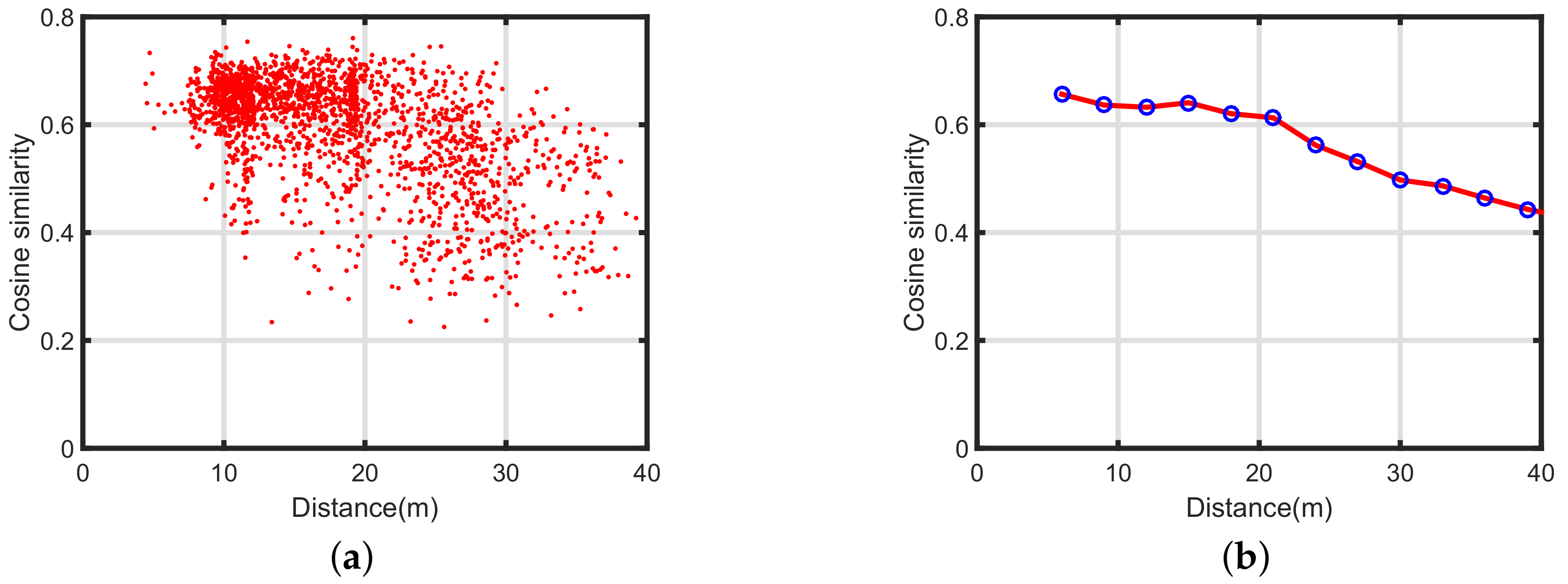
2.3.3. Cosine Similarity
2.4. Pedestrian Detection
| Algorithm 2 Pedestrian-detection method based on single template. |
Input:, , , ;
|
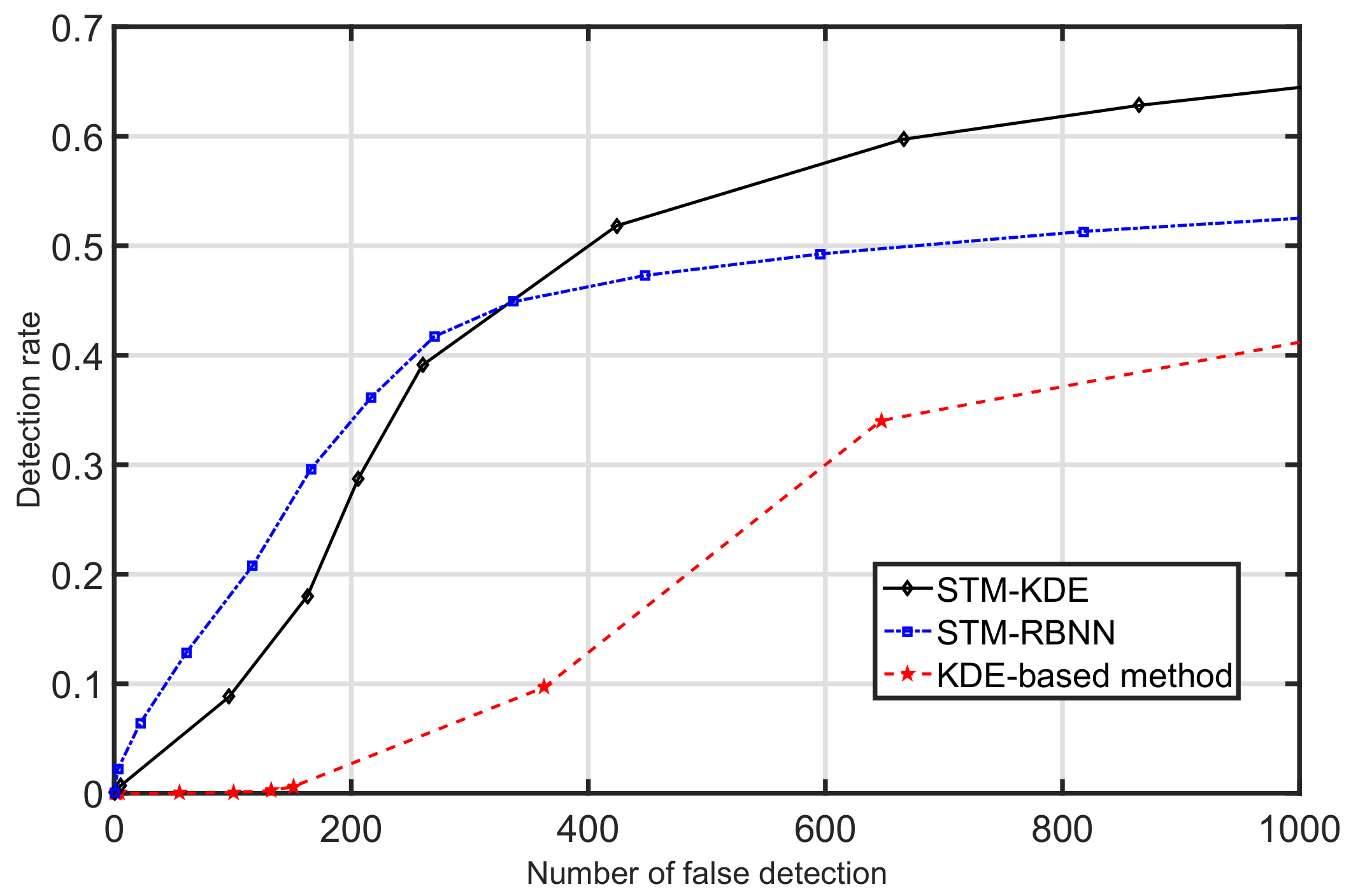
2.5. Comparing with Existing Methods
2.6. Computation Complexity
3. Results
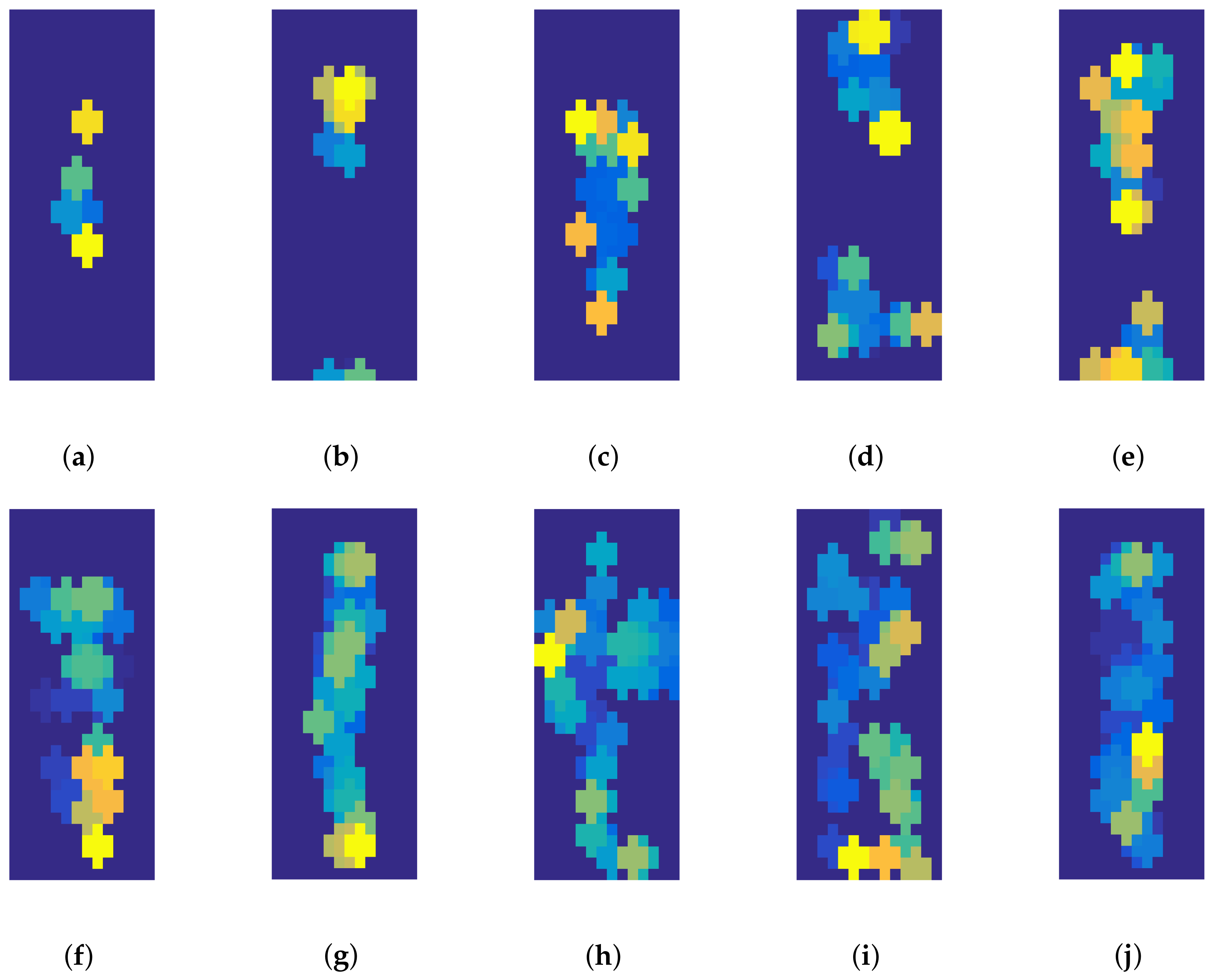
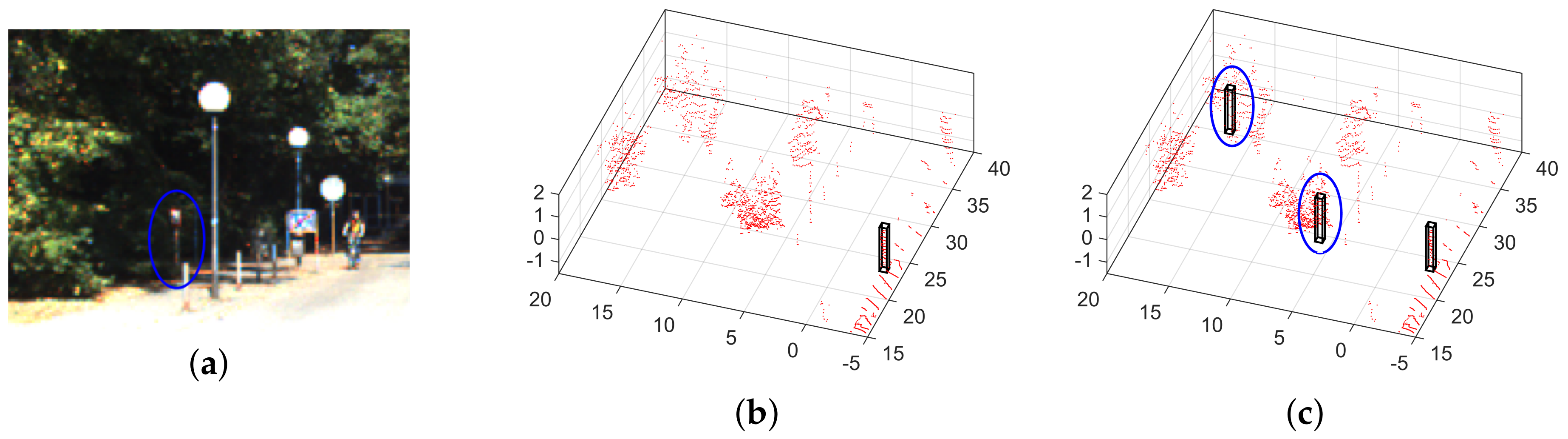
3.1. Clustering
3.2. Template Matching
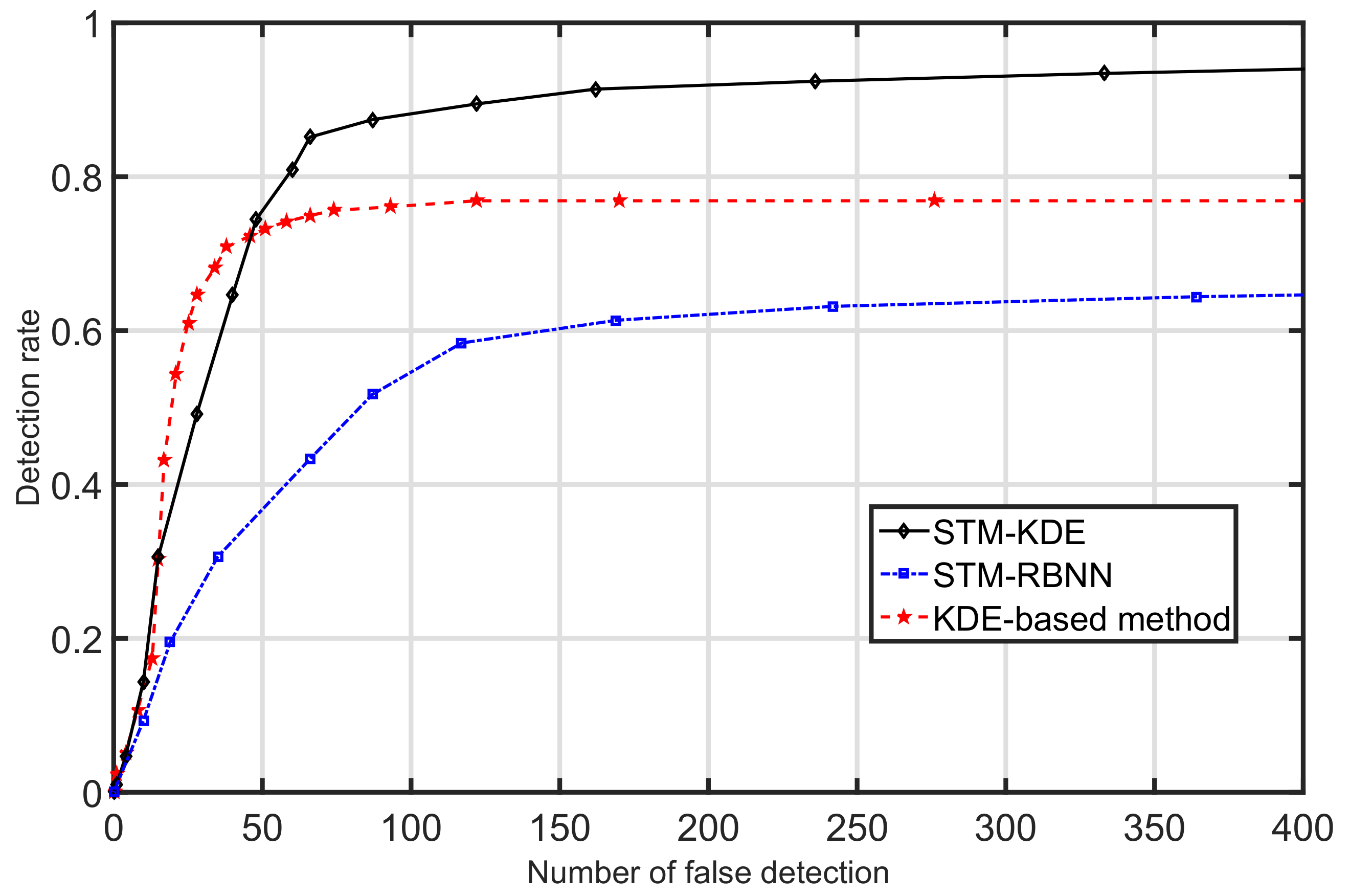
3.3. Pedestrian Detection
3.4. Operation Time
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ren, R.; Fu, H.; Wu, M. Large-Scale Outdoor SLAM Based on 2D Lidar. Electronics 2019, 8, 613. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Ouyang, W.; Zeng, X.; Wang, X. Single-Pedestrian Detection Aided by Two-Pedestrian Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1875–1889. [Google Scholar] [CrossRef] [PubMed]
- Hurney, P.; Waldron, P.; Morgan, F.; Jones, E.; Glavin, M. Review of Pedestrian Detection Techniques in Automotive Far-Infrared Video. IET Intell. Transp. Syst. 2015, 9, 824–832. [Google Scholar] [CrossRef]
- Inan, T.; Halici, U. 3-D Face Recognition with Local Shape Descriptors. IEEE Trans. Inf. Forensics Secur. 2012, 7, 577–587. [Google Scholar] [CrossRef]
- Wang, R.; Xu, Y.; Sotelo, M.A.; Ma, Y.; Sarkodie-Gyan, T.; Li, Z.; Li, W. A Robust Registration Method for Autonomous Driving Pose Estimation in Urban Dynamic Environment Using LiDAR. Electronics 2019, 8, 43. [Google Scholar] [CrossRef]
- Goodin, C.; Carruth, D.; Doude, M.; Hudson, C. Predicting the Influence of Rain on LIDAR in ADAS. Electronics 2019, 8, 89. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, H.; Wu, J.; Zheng, Y.; Liu, H. Trajectory Tracking and Prediction of Pedestrian’s Crossing Intention Using Roadside LiDAR. IET Intell. Transp. Syst. 2019, 13, 789–795. [Google Scholar] [CrossRef]
- Arras, K.O.; Mozos, O.M.; Burgard, W. Using Boosted Features for the Detection of People in 2D Range Data. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3402–3407. [Google Scholar]
- Premebida, C.; Ludwig, O.; Nunes, U. Exploiting LIDAR-based Features on Pedestrian Detection in Urban Scenarios. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; pp. 1–6. [Google Scholar]
- Kim, B.; Choi, B.; Yoo, M.; Kim, H.; Kim, E. Robust Object Segmentation Using A Multi-layer Laser Scanner. Sensors 2014, 14, 20400–20418. [Google Scholar] [CrossRef]
- Kim, B.; Choi, B.; Park, S.; Kim, H.; Kim, E. Pedestrian/Vehicle Detection Using a 2.5-D Multi-Layer Laser Scanner. IEEE Sens. J. 2016, 16, 400–408. [Google Scholar] [CrossRef]
- Tang, H.L.; Chien, S.C.; Cheng, W.H.; Chen, Y.Y.; Hua, K.L. Multi-cue Pedestrian Detection from 3D Point Cloud Data. In Proceedings of the 2017 IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017; pp. 1279–1284. [Google Scholar]
- Li, K.; Wang, X.; Xu, Y.; Wang, J. Density Enhancement-Based Long-Range Pedestrian Detection Using 3-D Range Data. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1368–1380. [Google Scholar] [CrossRef]
- Stauffer, C.; Grimson, W.E.L. Learning Patterns of Activity Using Real-time Tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 747–757. [Google Scholar] [CrossRef]
- Benedek, C.; Gálai, B.; Nagy, B.; Jankó, Z. Lidar-Based Gait Analysis and Activity Recognition in a 4D Surveillance System. IEEE Trans. Circuits Syst. Video Technol. 2016, 28, 101–113. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Zha, H.; Zhao, H.; Shibasaki, R. Laser-Based Detection and Tracking of Multiple People in Crowds. Comput. Vis. Image Underst. 2007, 106, 300–312. [Google Scholar] [CrossRef]
- Gidel, S.; Checchin, P.; Blanc, C.; Chateau, T.; Trassoudaine, L. Pedestrian Detection and Tracking in an Urban Environment Using a Multilayer Laser Scanner. IEEE Trans. Intell. Transp. Syst. 2010, 11, 579–588. [Google Scholar] [CrossRef]
- Liu, K.; Wang, W.; Tharmarasa, R.; Wang, J. Dynamic Vehicle Detection With Sparse Point Clouds Based on PE-CPD. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1964–1977. [Google Scholar] [CrossRef]
- Börcs, A.; Nagy, B.; Benedek, C. Instant Object Detection in LiDAR Point Clouds. IEEE Geosci. Remote Sens. Lett. 2017, 14, 992–996. [Google Scholar] [CrossRef]
- Liu, K.; Wang, W.; Tharmarasa, R.; Wang, J.; Zuo, Y. Ground Surface Filtering of 3D Point Clouds Based on Hybrid Regression Technique. IEEE Access 2019, 7, 23270–23284. [Google Scholar] [CrossRef]
- Giorgini, M.; Barbieri, F.; Aleotti, J. Ground Segmentation from Large-Scale Terrestrial Laser Scanner Data of Industrial Environments. IEEE Robot. Autom. Lett. 2017, 2, 1948–1955. [Google Scholar] [CrossRef]
- Wei, P.; Cagle, L.; Reza, T.; Ball, J.; Gafford, J. LiDAR and Camera Detection Fusion in a Real-Time Industrial Multi-Sensor Collision Avoidance System. Electronics 2018, 7, 84. [Google Scholar] [CrossRef]
- Jun, W.; Wu, T.; Zheng, Z. LIDAR and Vision Based Pedestrian Detection and Tracking System. In Proceedings of the 2015 IEEE International Conference on Progress in Informatics and Computing (PIC), Nanjing, China, 18–20 December 2015; pp. 118–122. [Google Scholar]
- Klasing, K.; Wollherr, D.; Buss, M. A Clustering Method for Efficient Segmentation of 3D Laser Data. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 4043–4048. [Google Scholar]
- Chavez-Garcia, R.O.; Aycard, O. Multiple sensor fusion and classification for moving object detection and tracking. IEEE Trans. Intell. Transp. Syst. 2015, 17, 525–534. [Google Scholar] [CrossRef]
- Cheng, Y. Mean Shift, Mode Seeking, and Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Navarro-Serment, L.E.; Mertz, C.; Hebert, M. Pedestrian Detection and Tracking Using Three-dimensional Ladar Data. Int. J. Robot. Res. 2010, 29, 1516–1528. [Google Scholar] [CrossRef]
- Seo, H.J.; Milanfar, P. Training-Free, Generic Object Detection Using Locally Adaptive Regression Kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1688–1704. [Google Scholar] [PubMed]
- Wang, Y.; Wang, W. Face Detection Using Skin Color and Locally Adaptive Regression Kernels. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–8. [Google Scholar]
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel Regression for Image Processing and Reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, D.; Lu, H.; Bo, C. Visual Tracking via Weighted Local Cosine Similarity. IEEE Trans. Cybern. 2015, 45, 1838–1850. [Google Scholar] [CrossRef] [PubMed]
- Pirlo, G.; Impedovo, D. Cosine Similarity for Analysis and Verification of Static Signatures. IET Biom. 2013, 2, 151–158. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision Meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]

| Algorithm | Datasets | Total Number | Truely Detected | False Alarms | Precision | Recall | Score |
|---|---|---|---|---|---|---|---|
| KDE-based method | 0016 | 852 | 579 | 23 | 96.2% | 68.0% | 0.80 |
| 0047 | 30 | 22 | 11 | 66.7% | 73.3% | 0.70 | |
| Total | 882 | 601 | 34 | 94.6% | 68.1% | 0.79 | |
| STM-RBNN | 0016 | 852 | 427 | 77 | 84.7% | 50.1% | 0.63 |
| 0047 | 30 | 29 | 10 | 74.4% | 96.7% | 0.84 | |
| Total | 882 | 456 | 87 | 84.0% | 51.7% | 0.64 | |
| STM-KDE | 0016 | 852 | 629 | 34 | 94.9% | 73.8% | 0.83 |
| 0047 | 30 | 28 | 14 | 66.7% | 93.3% | 0.78 | |
| Total | 882 | 657 | 48 | 93.2% | 74.5% | 0.83 |
| Algorithm | Datasets | Total Number | Truely Detected | False Alarms | Precision | Recall | Score |
|---|---|---|---|---|---|---|---|
| KDE-based method | 0016 | 1591 | 890 | 27 | 97.1% | 55.9% | 0.71 |
| 0047 | 100 | 90 | 33 | 73.2% | 90.0% | 0.81 | |
| Total | 1691 | 980 | 60 | 94.2% | 58.0% | 0.72 | |
| STM-RBNN | 0016 | 1591 | 711 | 27 | 96.3% | 44.7% | 0.61 |
| 0047 | 100 | 97 | 18 | 84.3% | 97.0% | 0.90 | |
| Total | 1691 | 808 | 45 | 94.7% | 47.8% | 0.64 | |
| STM-KDE | 0016 | 1591 | 945 | 38 | 96.1% | 59.4% | 0.73 |
| 0047 | 100 | 97 | 23 | 80.8% | 97.0% | 0.88 | |
| Total | 1691 | 1042 | 61 | 94.4% | 61.6% | 0.75 |
| Algorithm | Datasets | Total Number | Truely Detected | False Alarms | Precision | Recall | Score |
|---|---|---|---|---|---|---|---|
| KDE-based method | 0016 | 2174 | 962 | 1106 | 46.5% | 44.3% | 0.45 |
| 0047 | 118 | 97 | 59 | 62.2% | 82.2% | 0.71 | |
| Total | 2292 | 1059 | 1165 | 47.6% | 46.2% | 0.47 | |
| STM-RBNN | 0016 | 2174 | 731 | 196 | 78.9% | 33.6% | 0.47 |
| 0047 | 118 | 98 | 21 | 82.4% | 83.1% | 0.83 | |
| Total | 2292 | 829 | 217 | 79.3% | 36.2% | 0.50 | |
| STM-KDE | 0016 | 2174 | 965 | 313 | 75.5% | 44.3% | 0.56 |
| 0047 | 118 | 102 | 26 | 79.7% | 86.4% | 0.83 | |
| Total | 2292 | 1067 | 339 | 75.9% | 46.6% | 0.58 |
| Total Time | Time/ Frame | Read Data | Preprocessing | Scan Layer Mark | Cluster | Template Match | Cluster Number | Detection/ Cluster |
|---|---|---|---|---|---|---|---|---|
| 28.4 s | 916 ms | 248 ms | 1791 ms | 242 ms | 11231 ms | 11831 ms | 583 | 48 ms |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Wang, W.; Wang, J. Pedestrian Detection with Lidar Point Clouds Based on Single Template Matching. Electronics 2019, 8, 780. https://doi.org/10.3390/electronics8070780
Liu K, Wang W, Wang J. Pedestrian Detection with Lidar Point Clouds Based on Single Template Matching. Electronics. 2019; 8(7):780. https://doi.org/10.3390/electronics8070780
Chicago/Turabian StyleLiu, Kaiqi, Wenguang Wang, and Jun Wang. 2019. "Pedestrian Detection with Lidar Point Clouds Based on Single Template Matching" Electronics 8, no. 7: 780. https://doi.org/10.3390/electronics8070780
APA StyleLiu, K., Wang, W., & Wang, J. (2019). Pedestrian Detection with Lidar Point Clouds Based on Single Template Matching. Electronics, 8(7), 780. https://doi.org/10.3390/electronics8070780




