Analysis of Counting Bloom Filters Used for Count Thresholding
Abstract
:1. Introduction
2. Previous Bloom Filter (BF) and Counting Bloom Filter (CBF) Analysis
3. Proposed Analysis and Results
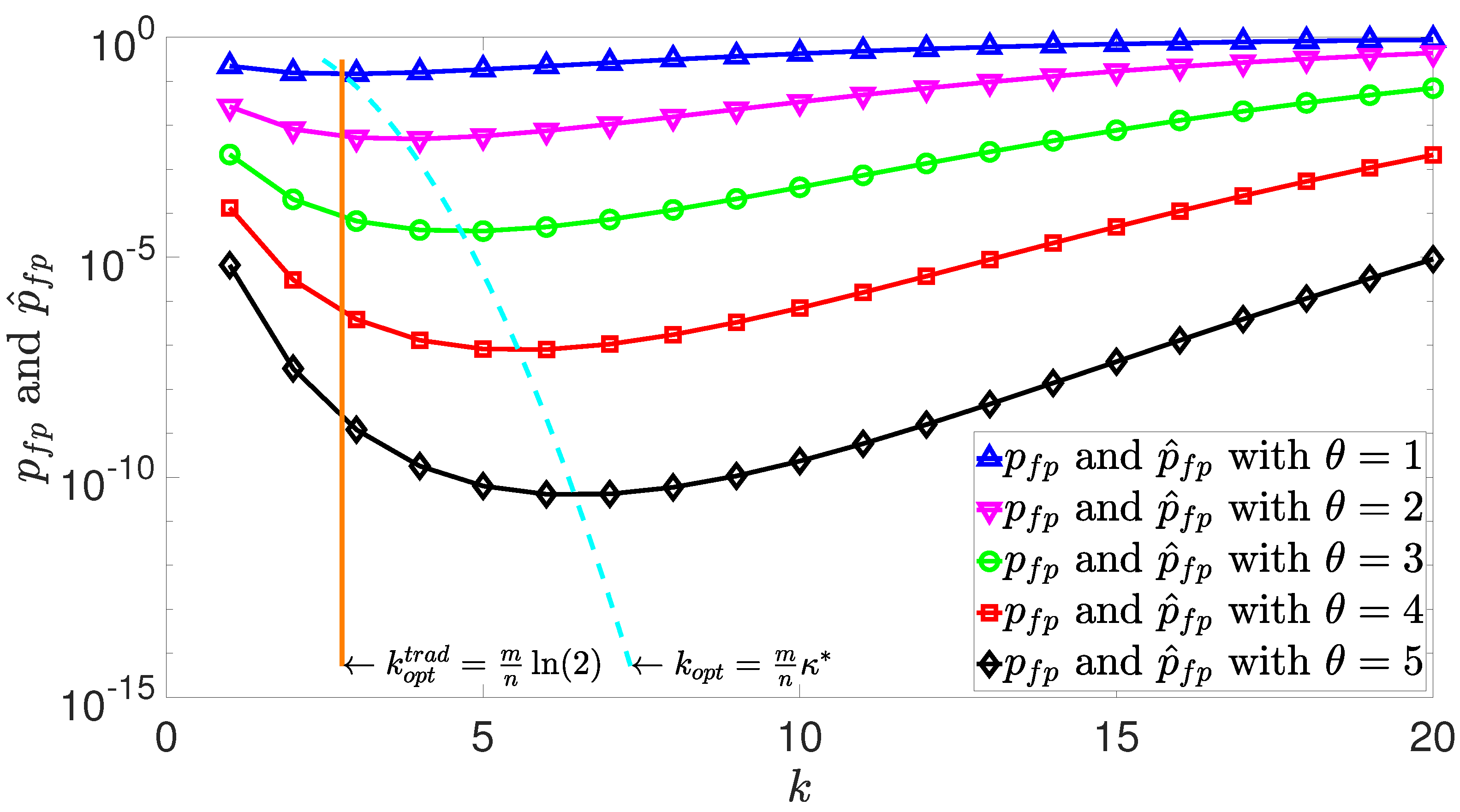
3.1. False Positive Probability
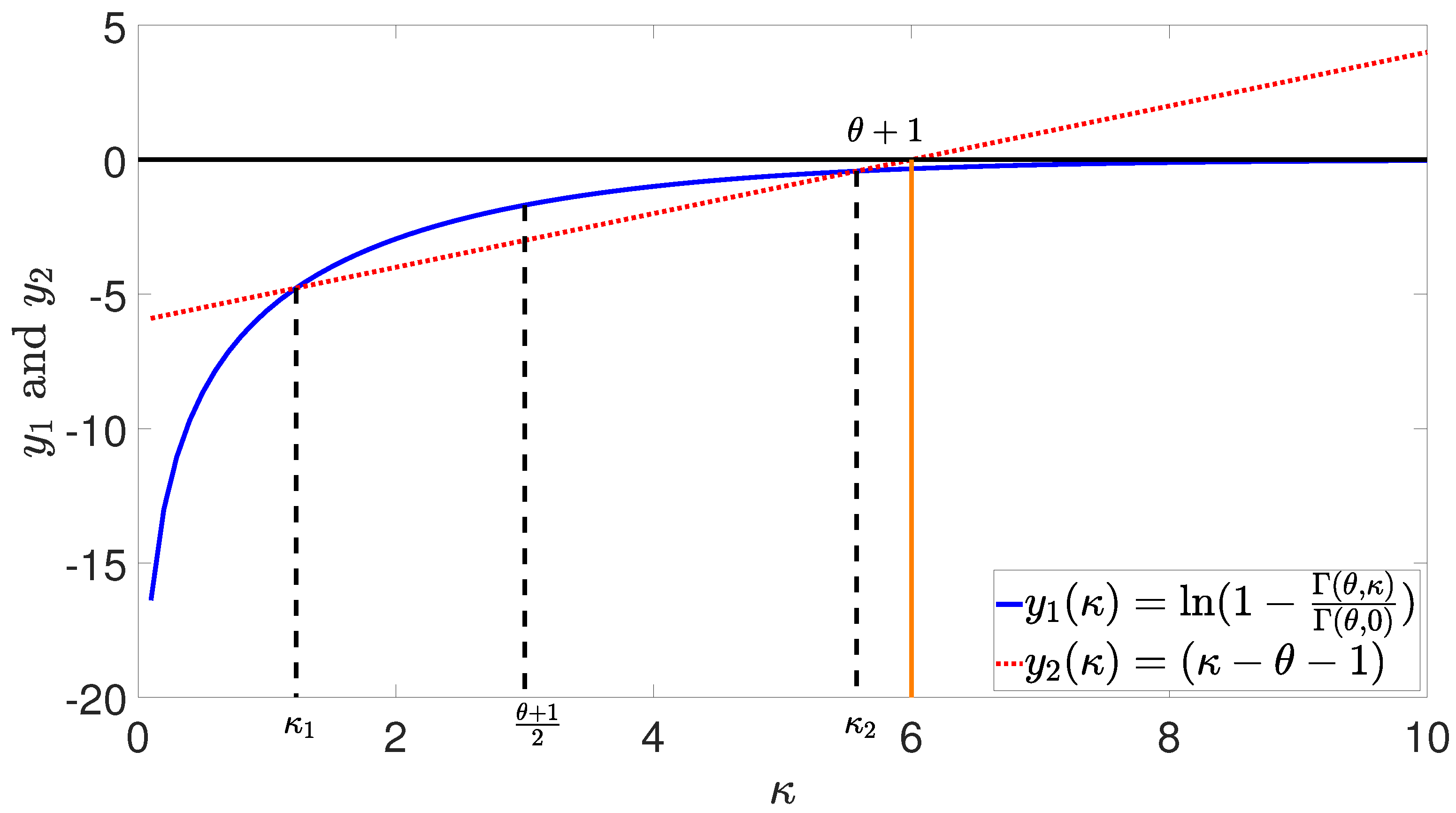
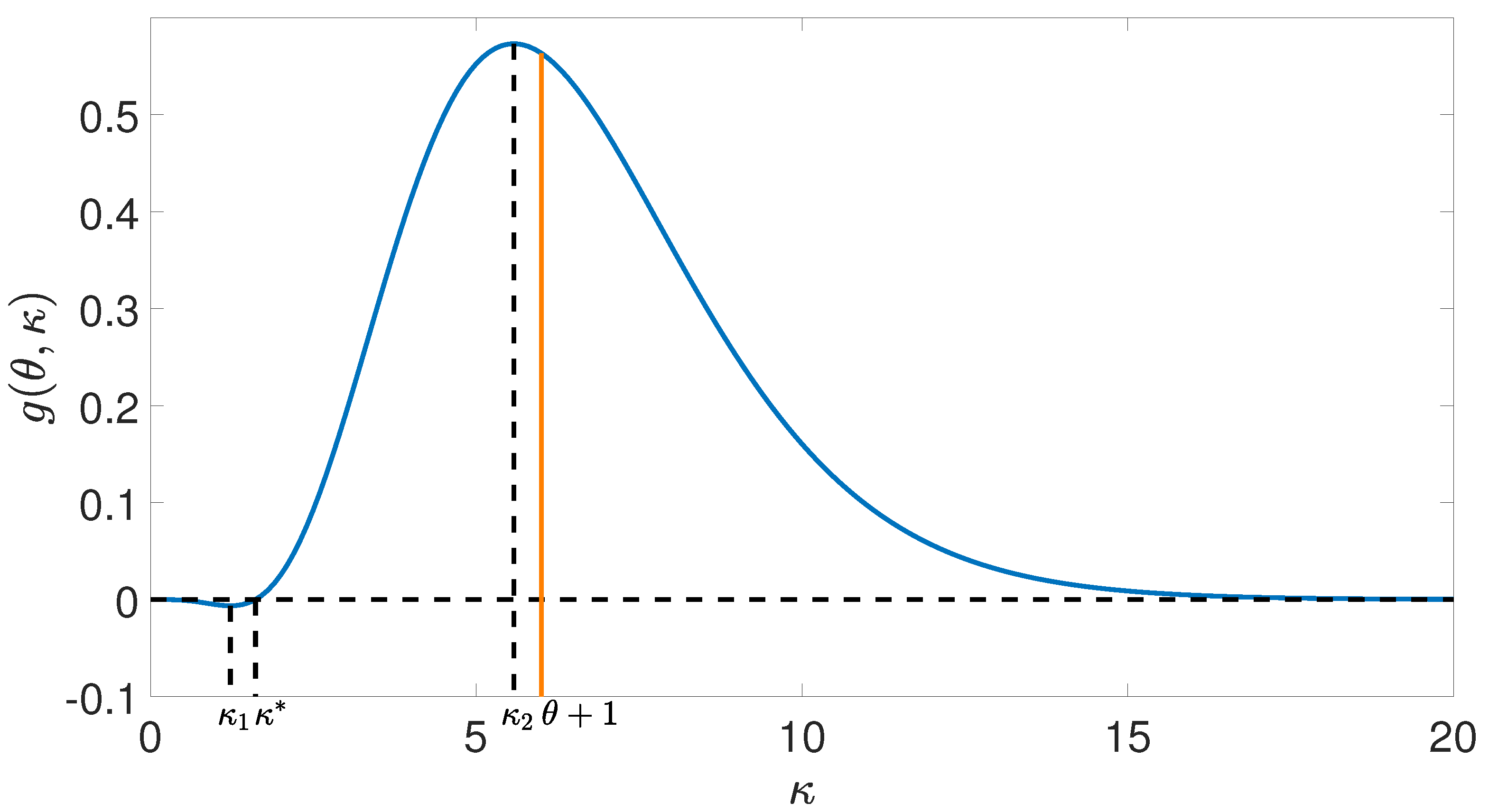
3.2. Uniqueness of Optimal Number of Hash Functions
3.3. Procedure for Determining the Optimal Number of Hash Functions
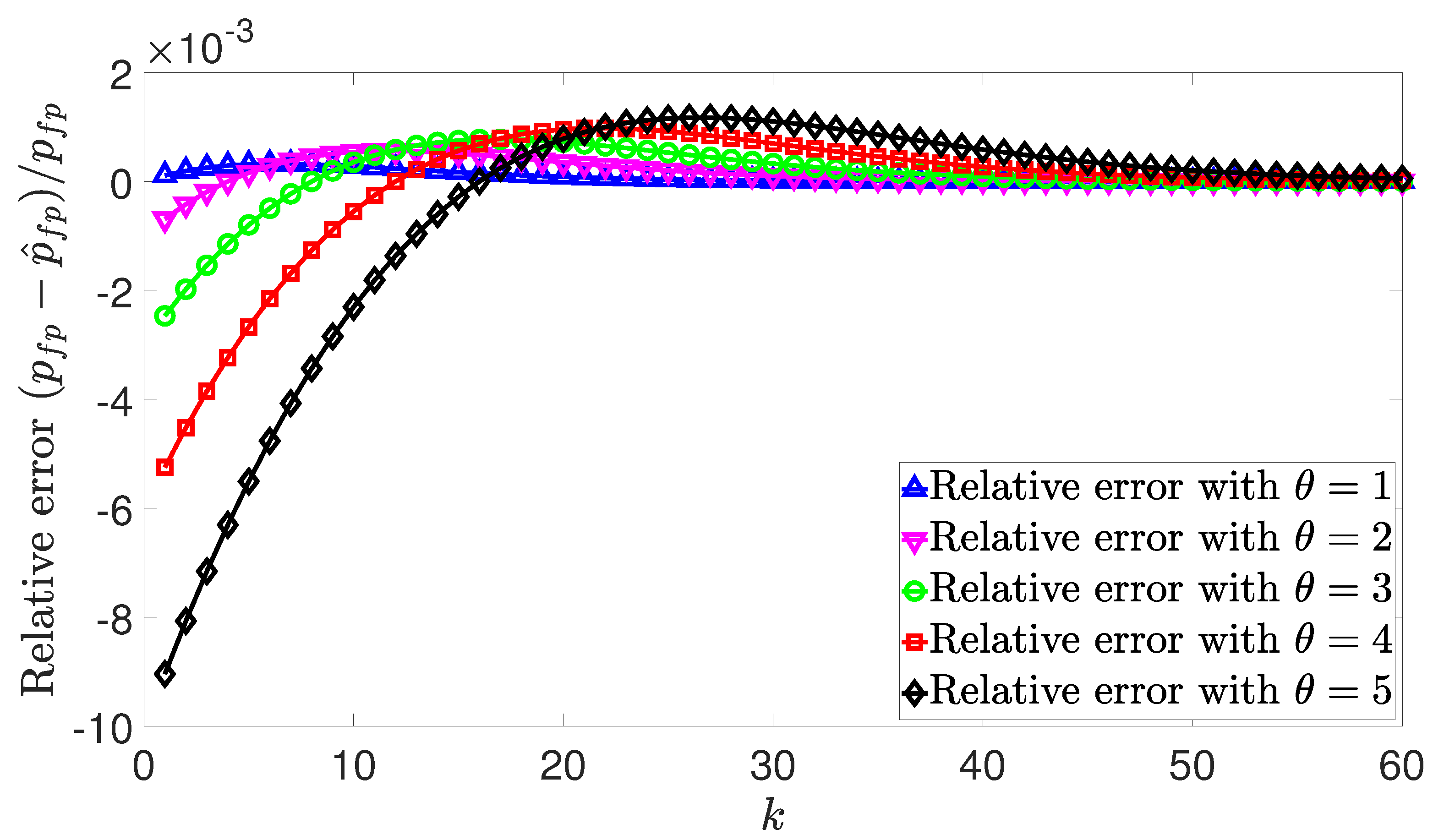
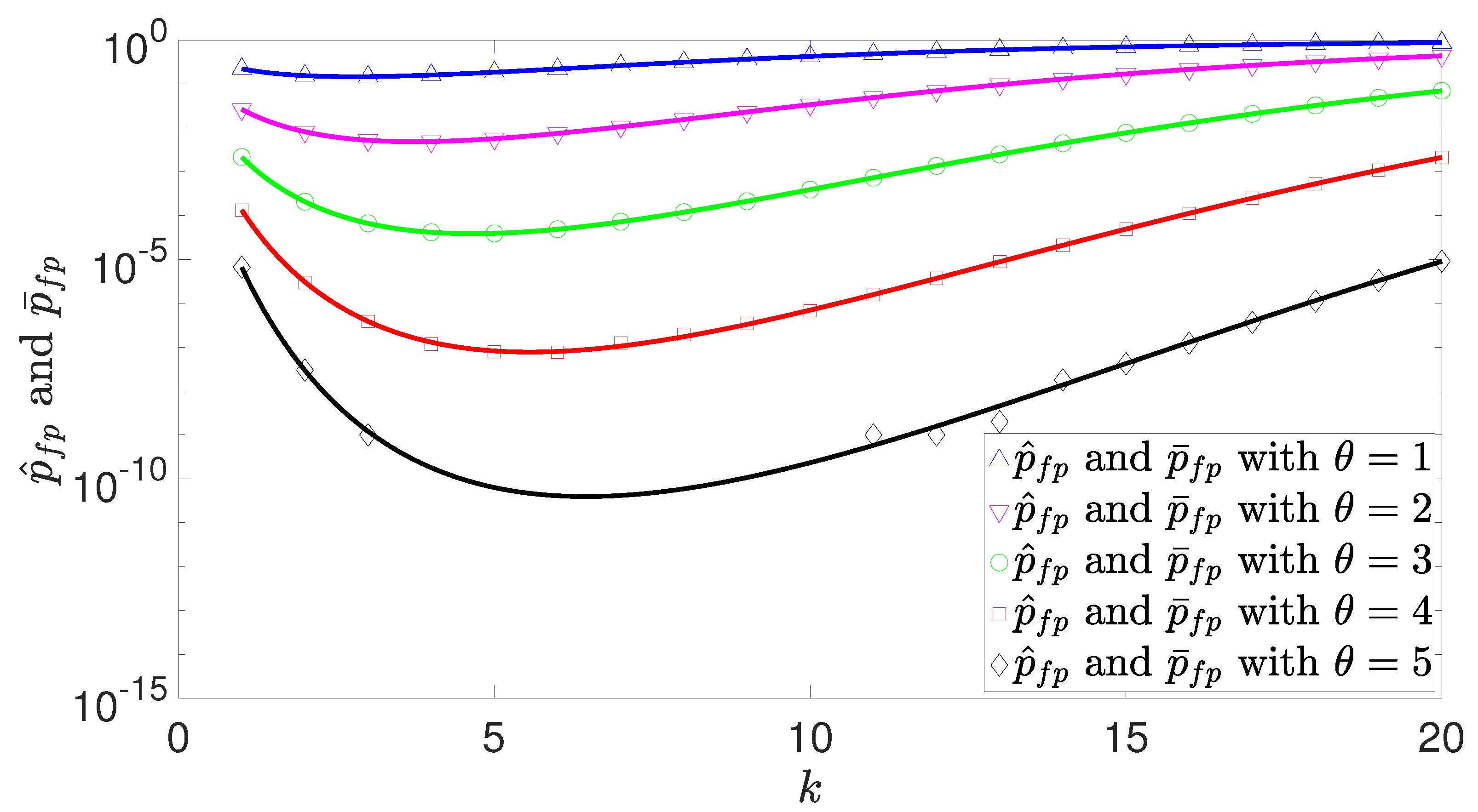
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BF | Bloom filter |
| CBF | Counting bloom filter |
| pmf | Probability mass function |
| cmf | Cumulative mass function |
References
- Bloom, B.H. Space/time trade-offs in hash coding with allowable errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Guo, D.; Liu, Y.; Li, X.; Yang, P. False negative problem of counting bloom filter. IEEE Trans. Knowl. Data Eng. 2010, 22, 651–664. [Google Scholar]
- Ghosh, M.; Ozer, E.; Ford, S.; Biles, S.; Lee, H.H.S. Way Guard: A segmented counting Bloom filter approach to reducing energy for set-associative caches. In Proceedings of the International Symposium on Low Power Electronics and Design (ISPLED), San Fancisco, CA, USA, 19–21 August 2009; pp. 165–170. [Google Scholar]
- Yun, J.; Lee, S.; Yoo, S. Dynamic wear leveling for phase-change memories with endurance variations. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 1604–1615. [Google Scholar] [CrossRef]
- Maggs, B.M.; Sitaraman, R.K. Algorithmic nuggets in content delivery. ACM SIGCOMM Comput. Commun. Rev. 2015, 45, 52–66. [Google Scholar] [CrossRef]
- Lu, Y.; Montanari, A.; Prabhakar, B.; Dharmapurikar, S.; Kabbani, A. Counter braids: A novel counter architecture for per-flow measurement. ACM SIGMETRICS Perform. Eval. Rev. 2008, 36, 121–132. [Google Scholar] [CrossRef]
- Bonomi, F.; Mitzenmacher, M.; Panigrah, R.; Singh, S.; Varghese, G. Beyond bloom filters: From approximate membership checks to approximate state machines. In Proceedings of the ACM SIGCOMM 2006 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Pisa, Italy, 11–15 September 2006; Volume 36, pp. 315–326. [Google Scholar]
- Dharmapurikar, S.; Krishnamurthy, P.; Taylor, D.E. Longest prefix matching using bloom filters. In Proceedings of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Karlsruhe, Germany, 25–29 August 2003; pp. 201–212. [Google Scholar]
- Song, H.; Hao, F.; Kodialam, M.; Lakshman, T. Ipv6 lookups using distributed and load balanced bloom filters for 100gbps core router line cards. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2518–2526. [Google Scholar]
- Ficara, D.; Di Pietro, A.; Giordano, S.; Procissi, G.; Vitucci, F. Enhancing counting Bloom filters through Huffman-coded multilayer structures. IEEE/ACM Trans. Netw. (TON) 2010, 18, 1977–1987. [Google Scholar] [CrossRef]
- Fan, L.; Cao, P.; Almeida, J.; Broder, A.Z. Summary cache: A scalable wide-area web cache sharing protocol. IEEE/ACM Trans. Netw. (TON) 2000, 8, 281–293. [Google Scholar] [CrossRef]
- Chazelle, B.; Kilian, J.; Rubinfeld, R.; Tal, A. The Bloomier filter: An efficient data structure for static support lookup tables. In Proceedings of the Fifteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics, New Orleans, LA, USA, 11–14 January 2004; pp. 30–39. [Google Scholar]
- Moraru, I.; Andersen, D.G. Exact pattern matching with feed-forward bloom filters. J. Exp. Algorithm. (JEA) 2012, 17, 3–4. [Google Scholar] [CrossRef]
- Ho, J.T.L.; Lemieux, G.G. PERG: A scalable FPGA-based pattern-matching engine with consolidated bloomier filters. In Proceedings of the 2008 IEEE International Conference on Field-Programmable Technology, Taipei, Taiwan; 2008; pp. 73–80. [Google Scholar]
- Melsted, P.; Pritchard, J.K. Efficient counting of k-mers in DNA sequences using a bloom filter. BMC Bioinform. 2011, 12, 333. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Fan, J.; Shi, L.; Liu, B. A novel router-based scheme to mitigate SYN flooding DDoS attacks. IEEE INFOCOM (Student Poster). 2007. Available online: https://pdfs.semanticscholar.org/fdae/7b20d220a1c23f9f6c0f8464574f78ef55c0.pdf (accessed on 11 July 2019).
- Tarkoma, S.; Rothenberg, C.E.; Lagerspetz, E. Theory and Practice of Bloom Filters for Distributed Systems. IEEE Commun. Surv. Tutor. 2012, 14, 131–155. [Google Scholar] [CrossRef]
- Broder, A.; Mitzenmacher, M. Network Applications of Bloom Filters: A Survey. Int. Math. 2003, 1, 485–509. [Google Scholar] [CrossRef]
- Mitzenmacher, M.; Upfal, E. Probability and Computing: Randomized Algorithms and Probabilistic Analysis; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; Tata McGraw-Hill Education: Pennsylvania Plaza, NY, USA, 2002; pp. 55–57. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables Applied Mathematics Series; National Bureau of Standards: Gaithersburg, MD, USA, 1964; pp. 260–265.
- Klar, B. Bounds on tail probabilities of discrete distributions. Probab. Eng. Inf. Sci. 2000, 14, 161–171. [Google Scholar] [CrossRef]
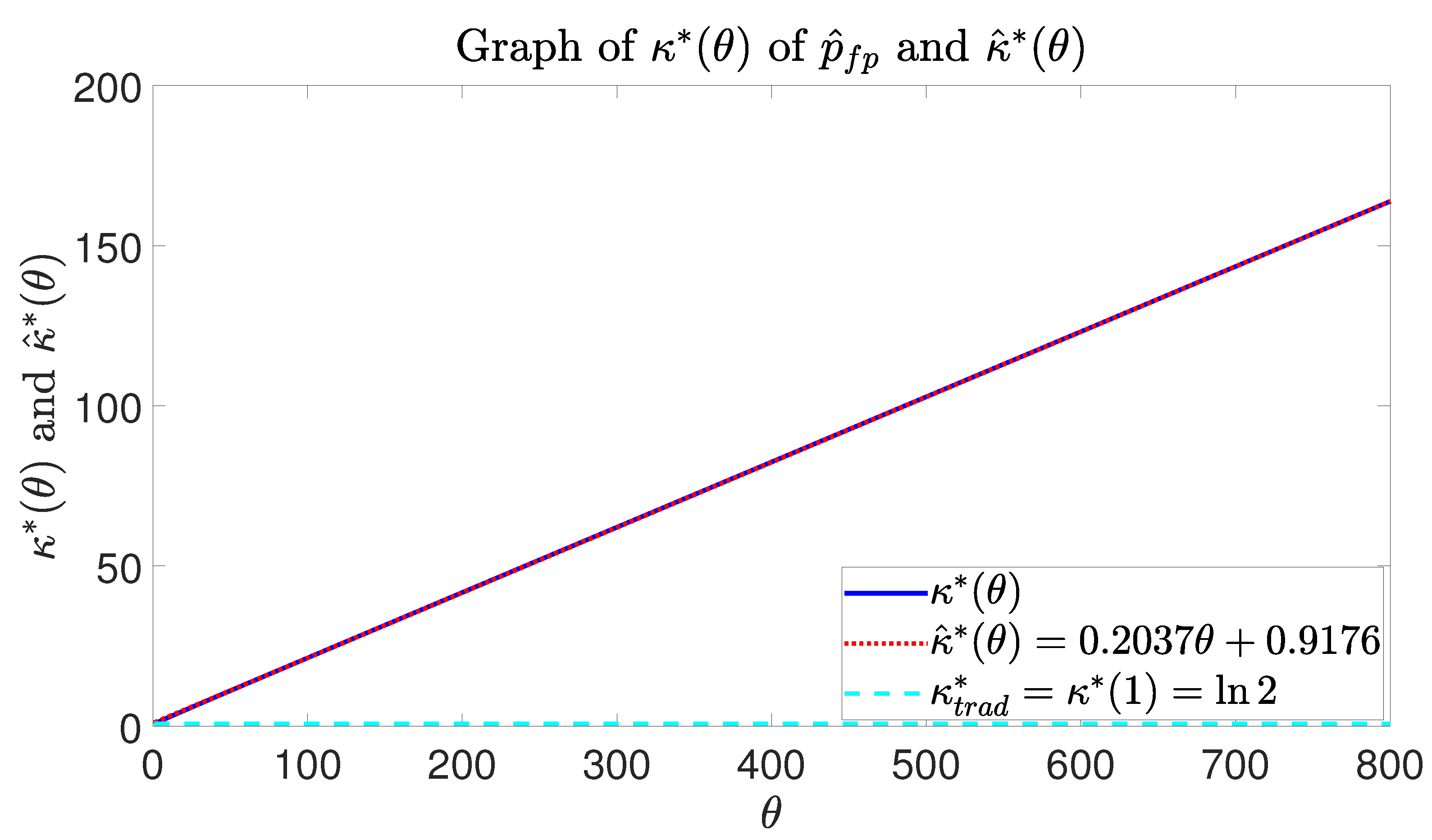
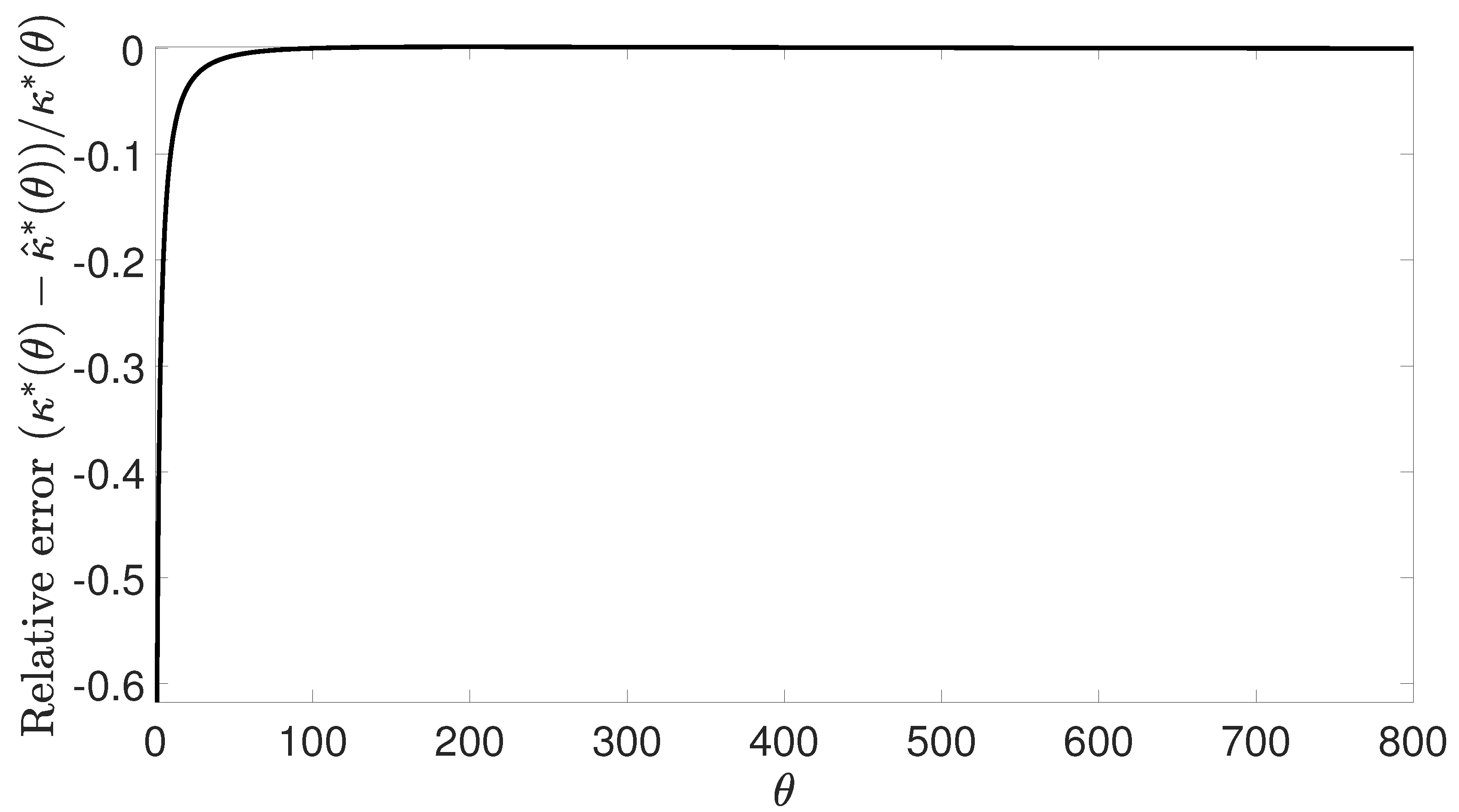
| 1 | 0.6931 | 1.1213 | −0.6177 | 11 | 2.9099 | 3.1583 | −0.0854 | 21 | 5.0183 | 5.1953 | −0.0353 |
| 2 | 0.9326 | 1.3250 | −0.4207 | 12 | 3.1228 | 3.3620 | −0.0766 | 22 | 5.2274 | 5.3990 | −0.0328 |
| 3 | 1.1635 | 1.5287 | −0.3139 | 13 | 3.3351 | 3.5657 | −0.0691 | 23 | 5.4362 | 5.6027 | −0.0306 |
| 4 | 1.3893 | 1.7324 | −0.2469 | 14 | 3.5469 | 3.7694 | −0.0627 | 24 | 5.6448 | 5.8064 | −0.0286 |
| 5 | 1.6117 | 1.9361 | −0.2013 | 15 | 3.7582 | 3.9731 | −0.0572 | 25 | 5.8533 | 6.0101 | −0.0268 |
| 6 | 1.8317 | 2.1398 | −0.1682 | 16 | 3.9690 | 4.1768 | −0.0524 | 26 | 6.0616 | 6.2138 | −0.0251 |
| 7 | 2.0498 | 2.3435 | −0.1433 | 17 | 4.1795 | 4.3805 | −0.0481 | 27 | 6.2697 | 6.4175 | −0.0236 |
| 8 | 2.2664 | 2.5472 | −0.1239 | 18 | 4.3896 | 4.5842 | −0.0443 | 28 | 6.4776 | 6.6212 | −0.0222 |
| 9 | 2.4818 | 2.7509 | −0.1084 | 19 | 4.5995 | 4.7879 | −0.0410 | 29 | 6.6854 | 6.8249 | −0.0209 |
| 10 | 2.6963 | 2.9546 | −0.0958 | 20 | 4.8090 | 4.9916 | −0.0380 | 30 | 6.8931 | 7.0286 | −0.0197 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Jeong, Y.; Lee, Y.; Lee, S. Analysis of Counting Bloom Filters Used for Count Thresholding. Electronics 2019, 8, 779. https://doi.org/10.3390/electronics8070779
Kim K, Jeong Y, Lee Y, Lee S. Analysis of Counting Bloom Filters Used for Count Thresholding. Electronics. 2019; 8(7):779. https://doi.org/10.3390/electronics8070779
Chicago/Turabian StyleKim, Kibeom, Yongjo Jeong, Youngjoo Lee, and Sunggu Lee. 2019. "Analysis of Counting Bloom Filters Used for Count Thresholding" Electronics 8, no. 7: 779. https://doi.org/10.3390/electronics8070779
APA StyleKim, K., Jeong, Y., Lee, Y., & Lee, S. (2019). Analysis of Counting Bloom Filters Used for Count Thresholding. Electronics, 8(7), 779. https://doi.org/10.3390/electronics8070779







