An Energy Efficient Task Scheduling Strategy in a Cloud Computing System and its Performance Evaluation using a Two-Dimensional Continuous Time Markov Chain Model
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions
- (1)
- We provide additional analyses for our proposed task scheduling strategy, and present the two forms of the state transition based on the relationship between the number of VMs in the system and the waking-up threshold.
- (2)
- We evaluate the system performance of the energy efficient task scheduling strategy with a two-dimensional continuous-time Markov chain (CTMC).
- (3)
- We provide new system experiments with analysis and simulation to investigate the proposed strategy. We also make a comparison between our proposed strategy and conventional strategies.
- (4)
- By considering both the average sojourn time of tasks and the energy conservation level of the system, we establish a cost function to make a compromise between the performance degradation and the energy efficiency.
- (5)
- By dynamically adjusting the crossover probability and the mutation probability, and initializing the individuals with chaotic equations, we present an improved genetic algorithm to jointly optimize the system parameters with the proposed strategy.
2. Descriptions of a Task Scheduling Strategy and Establishment of the System Model
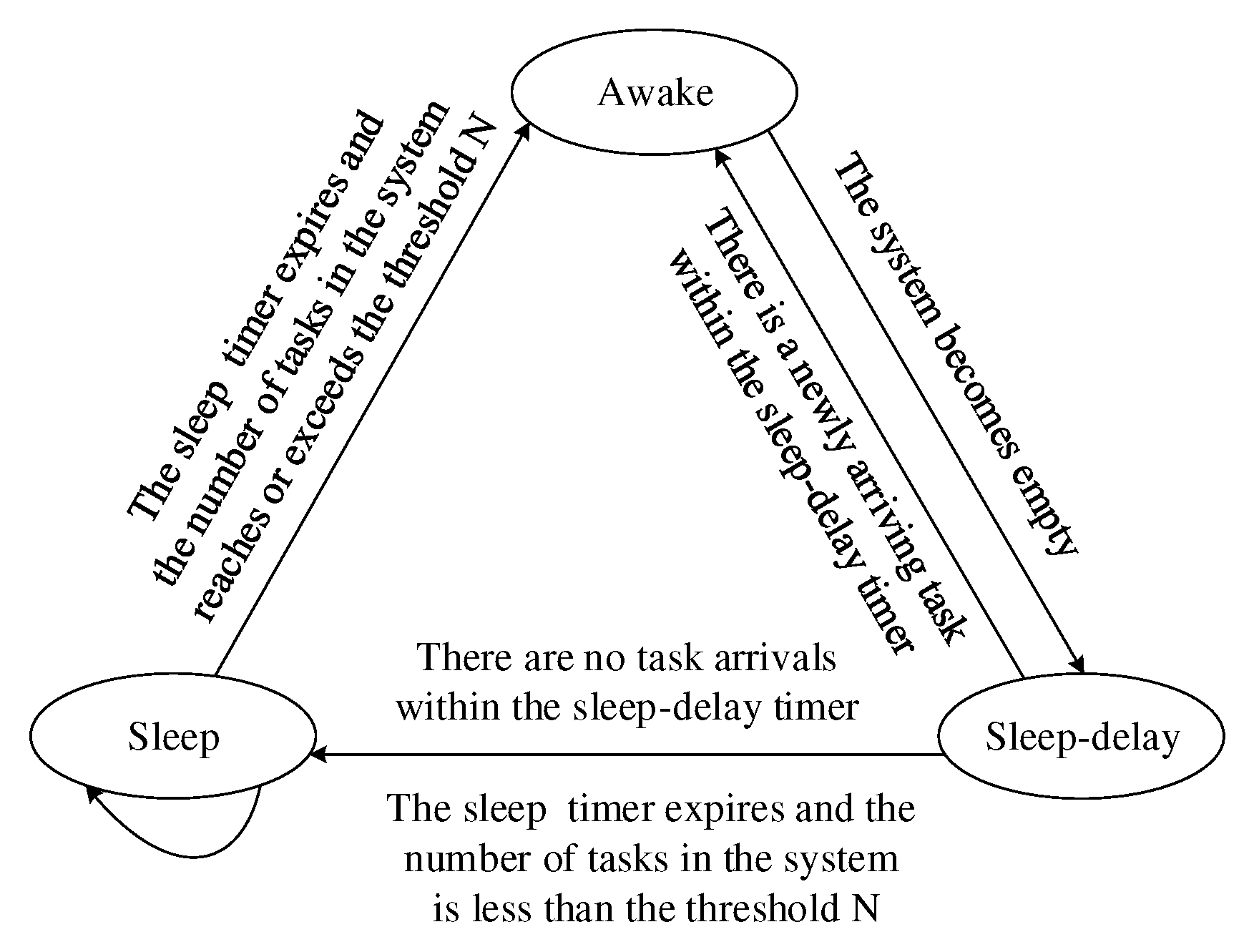
2.1. Description of Task Scheduling Strategy
- Awake State: During the awake state, there is at least one VM busy with task processing. The tasks in the system receive service in accordance with a first-come first-served (FCFS) policy.
- Sleep-delay State: To extend the awake period and improve the response performance, once all the tasks in the system are completely executed, a sleep-delay timer with a random time length will be started, and all the VMs will remain active within the constraint of the sleep-delay timer. We call this state the sleep-delay state. A new task arriving at the system during the sleep-delay period will receive service promptly. At the epoch when the sleep-delay timer expires, if there are no tasks queueing in the system buffer, the PM will switch into sleep state.
- Sleep State: A sleep timer with a random time length will also be started as soon as the PM enters the sleep state. In the sleep state, the power of some accessories, with the exception of the memory, will be cut off, and the tasks in the system will not be served. All the tasks arriving at the system during the sleep state have to wait in the system buffer. When the sleep timer expires, if there are fewer tasks waiting in the system buffer than the threshold N, another sleep period will be started. The time duration of this sleep period is controlled by a new sleep timer. Otherwise, the PM will switch to the awake state, and all the VMs in the PM will wake up and prepare to serve all the tasks queueing in the system buffer.
2.2. Establishment of System Model
3. Model Analysis in the Steady State
3.1. State Transition
- (1)
- When the initial level x is 0, the sub-matrices and are given as follows:
- (2)
- When the initial level x is 1, the sub-matrices , and are given as follows:
- (3)
- When the initial level x ranges from 2 to , the sub-matrices , and are given as follows:
- (4)
- When the initial level x ranges from N to , the sub-matrices , and are given as follows:
- (1)
- When the initial level x is 0, the sub-matrices and are the same as those given in Case I.
- (2)
- When the initial level x is 1, the sub-matrices , and are the same as those given in Case I, too.
- (3)
- When the initial level x ranges from 2 to , the sub-matrices , and can be given as follows:
- (4)
- When the initial level x ranges from N to , the sub-matrices , and are given as follows:
3.2. Steady-State Probability Distribution
4. Performance Measures and Genetic Algorithm
4.1. Energy Model
4.2. Genetic Algorithm
| Algorithm 1 Improved genetic algorithm to obtain and . |
|
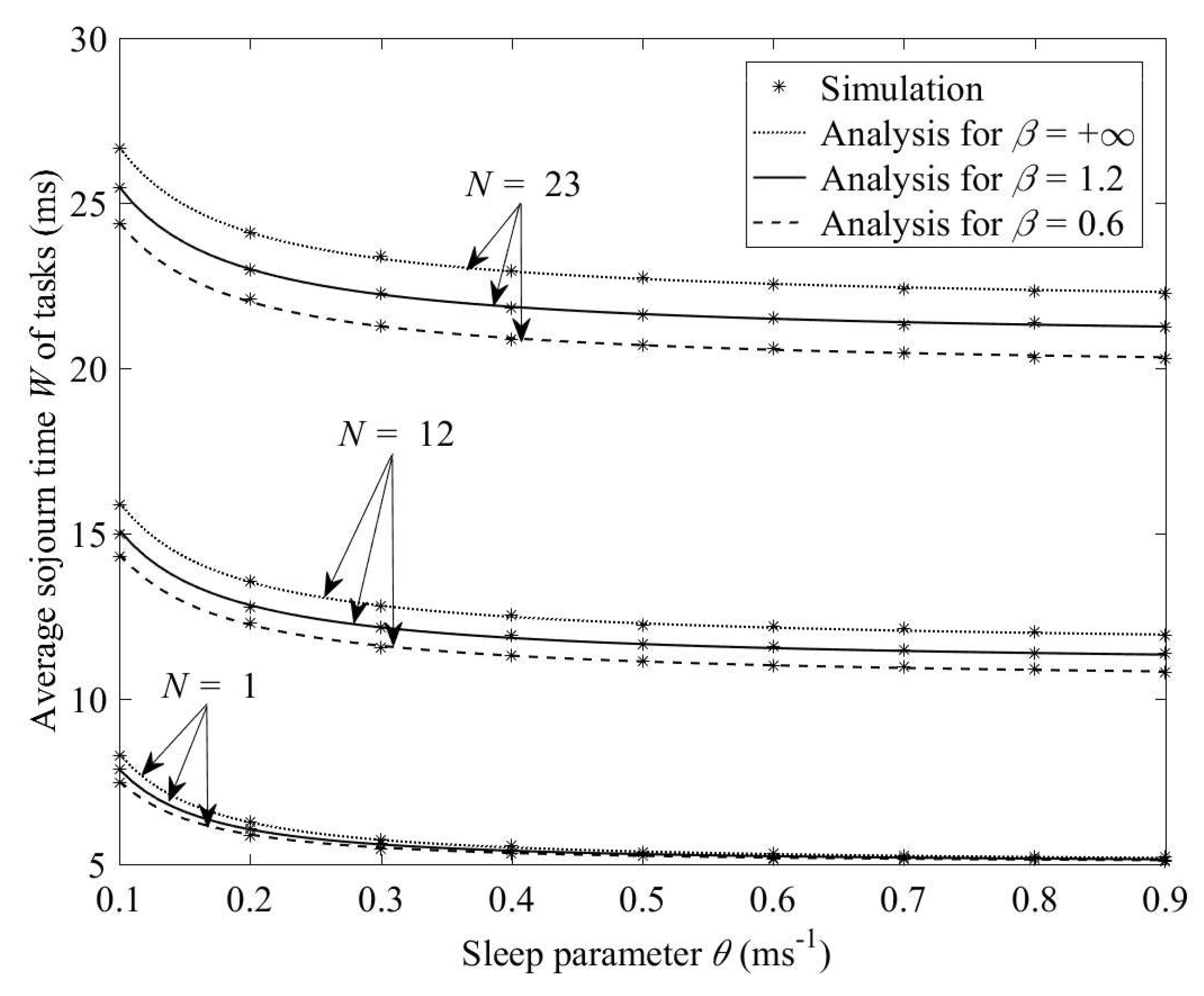
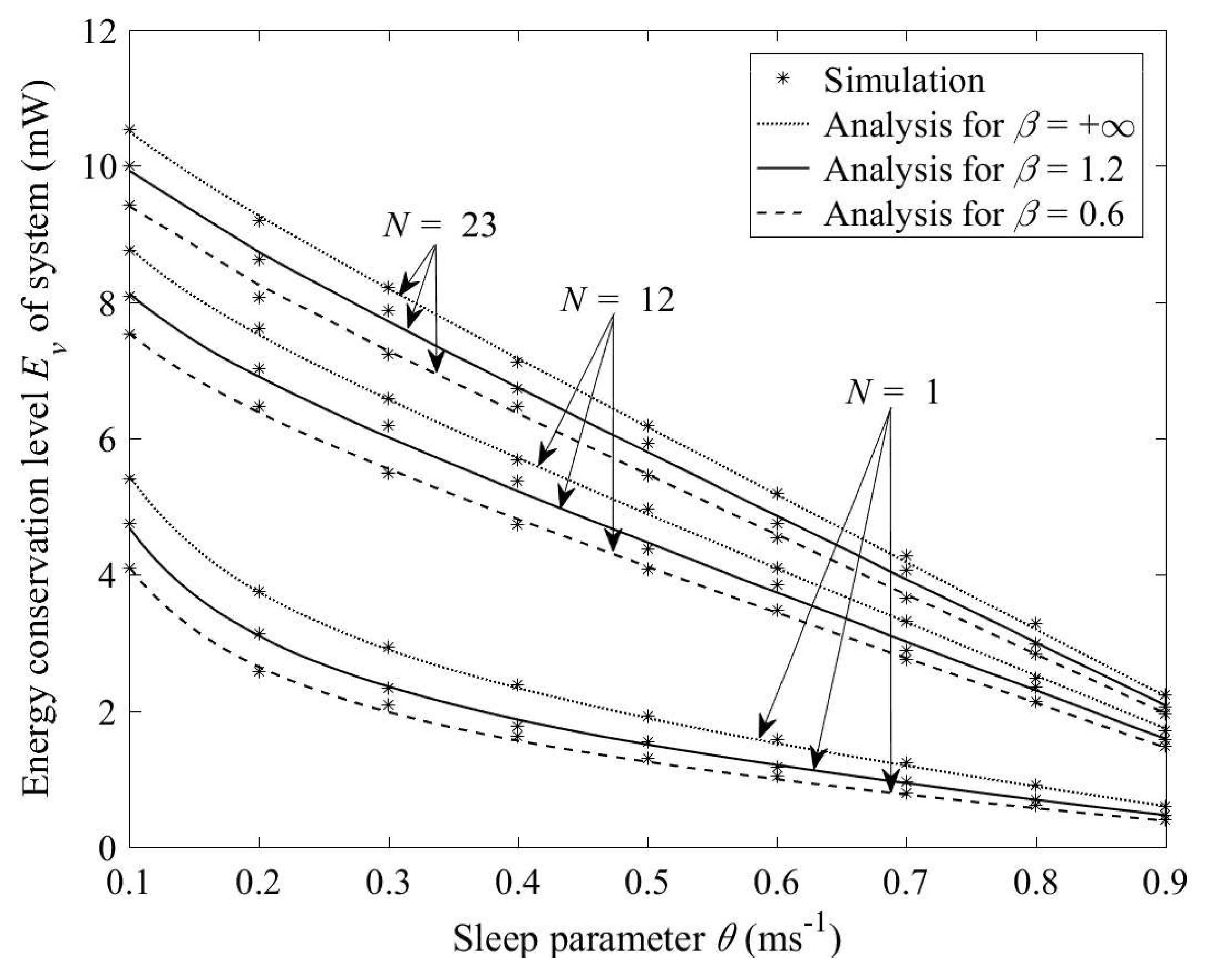
5. Statistical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Olokunde, T.; Misra, S.; Adewumi, A. Quality Model for Evaluating Platform as a Service in Cloud Computing. In Proceedings of the International Conference on Information and Software Technologies (2017), Da Nang, Vietnam, 16–19 April 2017; pp. 280–291. [Google Scholar]
- Mondal, S.; Das, G.; Wong, E. An Analytical Cost-Optimal Cloudlet Placement Framework over Fiber-Wireless Networks with Quasi-Convex Latency Constraint. Electronics 2019, 8, 404. [Google Scholar] [CrossRef]
- Fatima, A.; Javaid, N.; Butt, A.; Sultana, T.; Hussain, W.; Bilal, M.; Aqeel, M.; Hashmi, R.; Akbar, M.; Ilahi, M. An Enhanced Multi-Objective Gray Wolf Optimization for Virtual Machine Placement in Cloud Data Centers. Electronics 2019, 8, 218. [Google Scholar] [CrossRef]
- Madni, S.; Latiff, M.; Coulibaly, Y. Recent Advancements in Resource Allocation Techniques for Cloud Computing Environment: A Systematic Review. Clust. Comput. 2017, 20, 2489–2533. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, J.; Guan, H. Intelligent Cloud Resource Management with Deep Reinforcement Learning. IEEE Cloud Comput. 2017, 4, 60–69. [Google Scholar] [CrossRef]
- Abdullahi, M.; Ngadi, M.; Abdulhamid, S. Symbiotic Organism Search Optimization Based Task Scheduling in Cloud Computing Environment. Future Gener. Comput. Syst. 2016, 56, 640–650. [Google Scholar] [CrossRef]
- Ullah, A.; Li, J.; Shen, Y.; Hussain, A. A Control Theoretical View of Cloud Elasticity: Taxonomy, Survey and Challenges. Clust. Comput. 2018, 21, 1735–1764. [Google Scholar] [CrossRef]
- Dechouniotis, D.; Leontiou, N.; Athanasopoulos, N.; Christakidis, A.; Denazis, S. A Control-Theoretic Approach Towards Joint Admission Control and Resource Allocation of Cloud Computing Services. Int. J. Netw. Manag. 2015, 25, 159–180. [Google Scholar] [CrossRef]
- Abdulhamid, S.; Latiff, M.; Bashir, M. On-Demand Grid Provisioning using Cloud Infrastructures and Related Virtualization Tools: A Survey and Taxonomy. Int. J. Adv. Stud. Comput. Sci. Eng. 2014, 3, 49–59. [Google Scholar]
- Li, X.; Garraghan, P.; Jiang, X.; Wu, Z.; Xu, J. Holistic Virtual Machine Scheduling in Cloud Datacenters Towards Minimizing Total Energy. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1317–1331. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Siu, S.; Song, W.; Guan, S. Adaptive Incremental Genetic Algorithm for Task Scheduling in Cloud Environments. Symmetry 2018, 10, 168. [Google Scholar] [CrossRef]
- Zakarya, M.; Gillam, L. Energy Efficient Computing, Clusters, Grids and Clouds: A Taxonomy and Survey. Sustain. Comput. Inform. Syst. 2017, 14, 13–33. [Google Scholar] [CrossRef]
- You, C.; Huang, K.; Chae, H. Energy Efficient Mobile Cloud Computing Powered by Wireless Energy Transfer. IEEE J. Sel. Areas Commun. 2016, 2, 1757–1771. [Google Scholar] [CrossRef]
- Hashem, L.; Yaqoob, L.; Mokhtar, S.; Gani, A.; Khan, S. The Rise of “Big Data” on Cloud Computing: Review and Open Research Issues. Inf. Syst. 2015, 47, 98–115. [Google Scholar] [CrossRef]
- Yang, B.; Tan, F.; Dai, Y.; Guo, S. Performance Evaluation of Cloud Service Considering Fault Recovery. In Proceedings of the IEEE International Conference on Cloud Computing, Beijing, China, 1–4 December 2009; Springer: Berlin, Germany, 2009; Volume 5931, pp. 571–576. [Google Scholar]
- Fellera, E.; Ramakrishnan, L.; Morin, C. Performance and Energy Efficiency of Big Data Applications in Cloud Environments: A Hadoop Case Study. J. Parallel Distrib. Comput. 2015, 79–80, 80–89. [Google Scholar] [CrossRef]
- Xia, Y.; Zhou, M.; Luo, X.; Pang, S.; Zhu, Q. A Stochastic Approach to Analysis of Energy-Aware DVS-Enabled Cloud Datacenters. IEEE Trans. Syst. Man Cybern. 2015, 45, 73–83. [Google Scholar]
- Cheng, C.; Li, J.; Wang, Y. An Energy-Saving Task Scheduling Strategy Based on Vacation Queueing Theory in Cloud Computing. Tsinghua Sci. Technol. 2015, 20, 28–39. [Google Scholar] [CrossRef]
- Chen, Y.; Chang, M.; Liang, W.; Lee, C. Performance and Energy Efficient Dynamic Voltage and Frequency Scaling Scheme for Multicore Embedded System. In Proceedings of the IEEE 6th International Conference on Consumer and Electronics (2016), Las Vegas, NV, USA, 27–30 January 2016; pp. 58–59. [Google Scholar]
- Shen, Y.; Bao, Z.; Qin, X.; Shen, J. Adaptive Task Scheduling Strategy in Cloud: When Energy Consumption Meets Performance Guarantee. World Wide Web 2017, 20, 155–173. [Google Scholar] [CrossRef]
- Khosravi, A.; Andrew, L.; Buyya, R. Dynamic VM Placement Method for Minimizing Energy and Carbon Cost in Geographically Distributed Cloud Data Centers. IEEE Trans. Sustain. Comput. 2017, 2, 183–196. [Google Scholar] [CrossRef]
- Kempa, W. Time-Dependent Analysis of Transmission Process in a Wireless Sensor Network with Energy Efficient Mechanism Based on Threshold Waking up. In Proceedings of the IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (2015), Stockholm, Sweden, 28 June–1 July 2015; pp. 26–30. [Google Scholar]
- Mcbay, C.; Parr, G.; Mcclean, G. Energy Efficient in Data Center Servers using Optimal Scheduling to Ensure QoS. In Proceedings of the 7th International Conference on Cloud Computing, GRIDs, and Virtualization (2016), Rome, Italy, 20–24 March 2016; pp. 56–60. [Google Scholar]
- Lawanyashri, M.; Balusamy, B.; Subha, S. Threshold-Based Workload Control for an Under-Utilized Virtual Machine in Cloud Computing. Int. J. Intell. Eng. Syst. 2016, 9, 234–241. [Google Scholar] [CrossRef]
- Singh, D.; Devgan, M. Task Scheduling with Multilayer Hybrid Energy Efficient Approach in Green Cloud Computing. Int. J. Sci. Res. Dev. 2016, 4, 814–818. [Google Scholar]
- Madni, S.; Abd, L.; Abdullahi, M.; Abdulhamid, S.; Usman, M. Performance Comparison of Heuristic Algorithms for Task Scheduling in IaaS Cloud Computing Environment. PLoS ONE 2017, 12, e0176321. [Google Scholar] [CrossRef] [PubMed]
- Qiu, M.; Ming, Z.; Li, J.; Gai, K.; Zong, Z. Phase-Change Memory Optimization for Green Cloud with Genetic Algorithm. IEEE Trans. Comput. 2015, 6, 3528–3540. [Google Scholar] [CrossRef]
- Huang, S.; Jiau, M.; Lin, C. A Genetic-Algorithm-Based Approach to Solve Carpool Service Problems in Cloud Computing. IEEE Trans. Intell. Transp. Syst. 2015, 16, 352–364. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, J.; Zhang, Y. A Novel Fuzzy Multiobjective Model using Adaptive Genetic Algorithm Based on Cloud Theory for Service Restoration of Shipboard Power Systems. IEEE Trans. Power Syst. 2012, 27, 612–620. [Google Scholar] [CrossRef]
- Jin, S.; Wang, X.; Yue, W. A Task Scheduling Strategy with a Sleep-Delay Timer and a Waking-Up Threshold in Cloud Computing. In Proceedings of the 13th International Conference on Queueing Theory and Network Applications (2018), Tsukuba, Japan, 25–27 July 2018; pp. 1115–1123. [Google Scholar]
- Mevada, A.; Patel, H.; Patel, N. Enhanced Energy Efficient Virtual Machine Placement Policy for Load Balancing in Cloud Environment. Int. J. Curr. Res. Rev. 2017, 9, 50–53. [Google Scholar]
- Khoshkholghi, M.; Derahman, M.; Abdullah, A.; Subramaniam, S.; Othman, M. Energy-Efficient Algorithms for Dynamic Virtual Machine Consolidation in Cloud Data Centers. IEEE Access 2017, 5, 10709–10722. [Google Scholar] [CrossRef]
- Dzheparov, F.; Shestopal, V. Asymptotically Exactly Solvable Models of Processes in Stochastically Homogeneous Disordered Lattice Media. Theor. Math. Phys. 2003, 135, 549–565. [Google Scholar]
- Zhao, Y.; Jin, S.; Yue, W. Performance Analysis of Cognitive Radio Networks for Secondary Users with Slotted Central Control. Telecommun. Syst. 2017, 66, 689–699. [Google Scholar] [CrossRef]
- He, H.; Yuan, D.; Hou, Y.; Xu, J. Preconditioned Gauss-Seidel Iterative Method for Linear Systems. Int. Forum Inf. Technol. Appl. 2009, 1, 382–385. [Google Scholar]
- Yue, D.; Yu, J.; Yue, W. A Markovian Queue with two Heterogeneous Servers and Multiple Vacations. J. Ind. Manag. Optim. 2009, 5, 453–465. [Google Scholar] [CrossRef]
- Honnappa, H.; Jain, R.; Ward, A. A Queueing Model with Independent Arrivals, and its Fluid and Diffusion Limits. Queueing Syst. 2015, 80, 71–103. [Google Scholar] [CrossRef][Green Version]
- Nguyen, T.; Gribaudo, M.; Pernici, B. Characterizing Energy per Job in Cloud Applications. Electronics 2015, 6, 90–114. [Google Scholar]
- Chen, Y.; Xie, G.; Li, R. Reducing Energy Consumption with Cost Budget using Available Budget Preassignment in Heterogeneous Cloud Computing Systems. IEEE Access 2018, 6, 20572–20583. [Google Scholar] [CrossRef]
- Peiravi, A.; Mashhadi, H.; Javadi, S. An Optimal Energy-Efficient Clustering Method in Wireless Sensor Networks using Multi-Objective Genetic Slgorithm. Int. J. Commun. Syst. 2013, 26, 114–126. [Google Scholar] [CrossRef]
- Hussain, S.; Matin, A.; Islam, O. Genetic Slgorithm for Energy Efficient Clusters in Wireless Sensor Networks. In Proceedings of the 4th International Conference on Information Technology (2007), Las Vegas, NV, USA, 2–4 April 2007; pp. 147–154. [Google Scholar]
- Gandomi, A.; Yang, X. Chaotic Bat Algorithm. J. Comput. Sci. 2014, 5, 224–232. [Google Scholar] [CrossRef]
- Rajagopal, M.; Jayarajan, P.; Dhasarathan, V.; Sivasankaran, V.; Udaiyakumar, R. Performance Analysis of Contention Based Priority Queuing Model using N-Policy Model for Cluster Based Sensor Networks. In Proceedings of the 7th IEEE International Conference on Communication and Signal Processing (2018), Pune, India, 23–24 November 2018; pp. 229–233. [Google Scholar]
- Jin, S.; Han, L.; Yue, W. Performance Evaluation for the Power Saving Class Type III with a Sleep-Delay in IEEE 802.16e. In Proceedings of the 4th International Conference on Queueing Theory and Network Applications (2009), Singapore, 29–31 July 2009; pp. 1–6. [Google Scholar]
- Jin, S.; Hao, S.; Yue, W. Energy-Efficient Strategy with a Speed Switch and a Multiple-Sleep Mode in Cloud Data Centers. In Proceedings of the 12th International Conference on Queueing Theory and Network Applications (2017), Qinhuangdao, China, 21–23 August 2017; pp. 143–154. [Google Scholar]
- Chen, H.; Zhu, X.; Guo, H.; Qin, X.; Wu, J. Towards Energy-Efficient Scheduling for Real-Time Tasks under Uncertain Cloud Computing Environment. J. Syst. Softw. 2015, 99, 20–35. [Google Scholar] [CrossRef]
- Stavrinides, G.; Karatza, H. An Energy-Efficient, QoS-Aware and Cost-Effective Scheduling Approach for Real-Time Workflow Applications in Cloud Computing Systems utilizing DVFS and Approximate Computations. Future Gener. Comput. Syst. 2019, 96, 216–226. [Google Scholar] [CrossRef]
- Tantalaki, N.; Souravlas, S.; Roumeliotis, M. A Review on Big Data Real-Time Stream Processing and its Scheduling Techniques. Int. J. Parallel Emerg. Distrib. Syst. 2019, 1–31. [Google Scholar] [CrossRef]
- Kao, B.; Garcia-Molina, H. Scheduling soft real-time jobs over dual non-real-time servers. IEEE Trans. Parallel Distrib. Syst. 1996, 7, 56–68. [Google Scholar] [CrossRef]
- Štefanič, P.; Cigale, M.; Jones, A.; Knight, L.; Taylor, I.; Istrate, C. SWITCH Workbench: A Novel Approach for the Development and Deployment of Time-Critical Microservice-Based Cloud-Native Applications. Future Gener. Comput. Syst. 2019, 99, 197–212. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| Total number k of VMs in the system | 20 |
| Task arrival rate | (tasks/ms) |
| Service rate | (tasks/ms) |
| Energy consumption level of a busy VM | 20 (mW) |
| Energy consumption level of a sleeping VM | 2 (mW) |
| Energy consumption level of each switching | 12 (mJ) |
| Energy consumption level of each listening | 4 (mJ) |
| Service Rate | Optimal Combination | System Cost F |
|---|---|---|
| 0.07 | (6, 0.1468, 7.9699) | 4.2246 |
| 0.10 | (6, 0.1269, 9.8577) | 2.7236 |
| 0.13 | (5, 0.1481, 8.5751) | 1.7222 |
| 0.16 | (4, 0.2306, 6.9526) | 0.9801 |
| 0.19 | (4, 0.1357, 6.1439) | 0.4045 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Wang, X.; Jin, S.; Yue, W.; Takahashi, Y. An Energy Efficient Task Scheduling Strategy in a Cloud Computing System and its Performance Evaluation using a Two-Dimensional Continuous Time Markov Chain Model. Electronics 2019, 8, 775. https://doi.org/10.3390/electronics8070775
Zhao W, Wang X, Jin S, Yue W, Takahashi Y. An Energy Efficient Task Scheduling Strategy in a Cloud Computing System and its Performance Evaluation using a Two-Dimensional Continuous Time Markov Chain Model. Electronics. 2019; 8(7):775. https://doi.org/10.3390/electronics8070775
Chicago/Turabian StyleZhao, Wenjuan, Xiushuang Wang, Shunfu Jin, Wuyi Yue, and Yutaka Takahashi. 2019. "An Energy Efficient Task Scheduling Strategy in a Cloud Computing System and its Performance Evaluation using a Two-Dimensional Continuous Time Markov Chain Model" Electronics 8, no. 7: 775. https://doi.org/10.3390/electronics8070775
APA StyleZhao, W., Wang, X., Jin, S., Yue, W., & Takahashi, Y. (2019). An Energy Efficient Task Scheduling Strategy in a Cloud Computing System and its Performance Evaluation using a Two-Dimensional Continuous Time Markov Chain Model. Electronics, 8(7), 775. https://doi.org/10.3390/electronics8070775





