Micro-Motion Dynamics and Shape Parameters Estimation Based on an Infrared Signature Model of Spatial Targets
Abstract
1. Introduction
2. Infrared Signature Model
2.1. Emitted Radiation Analysis
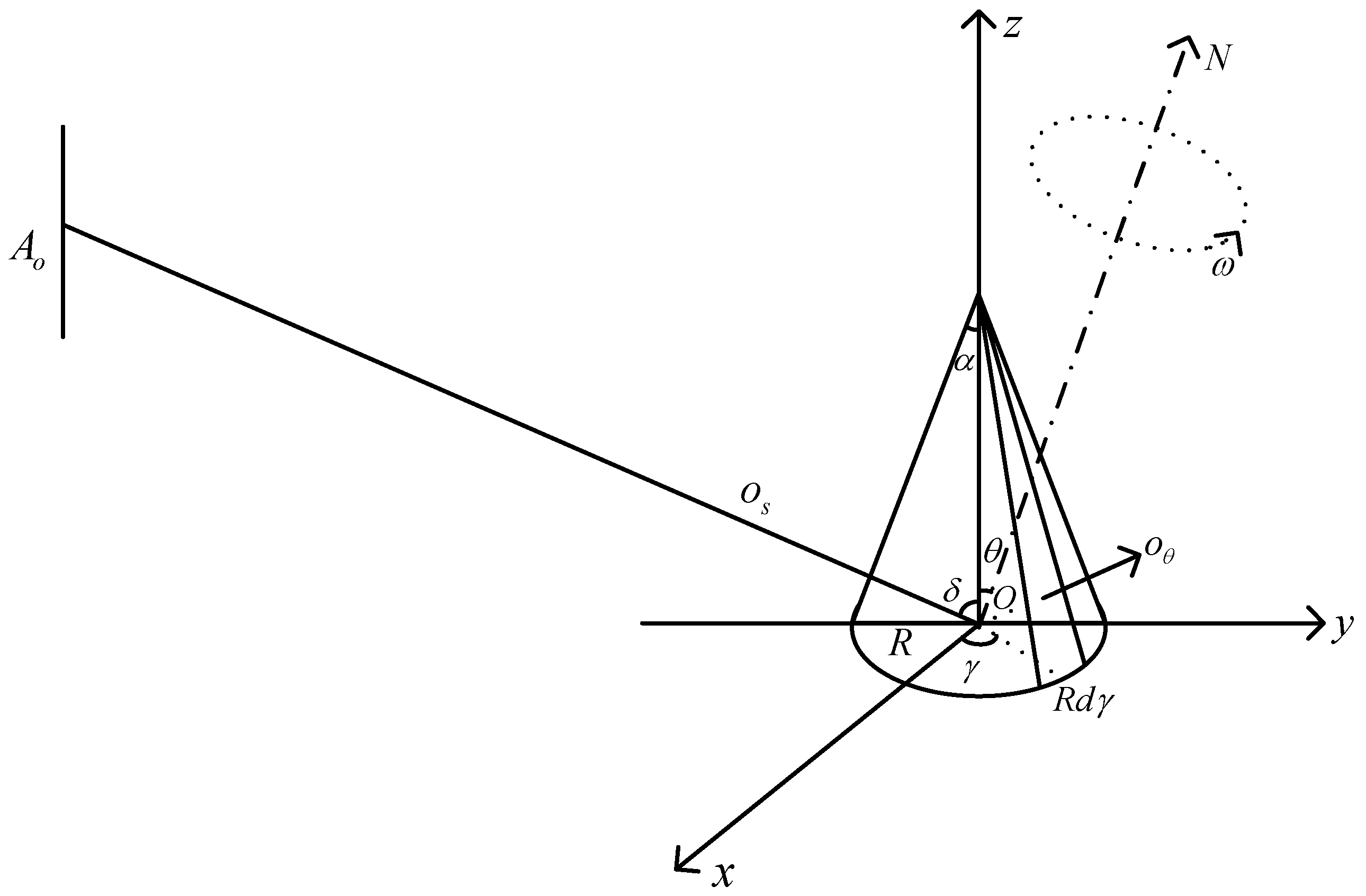
2.2. Target Geometry Model
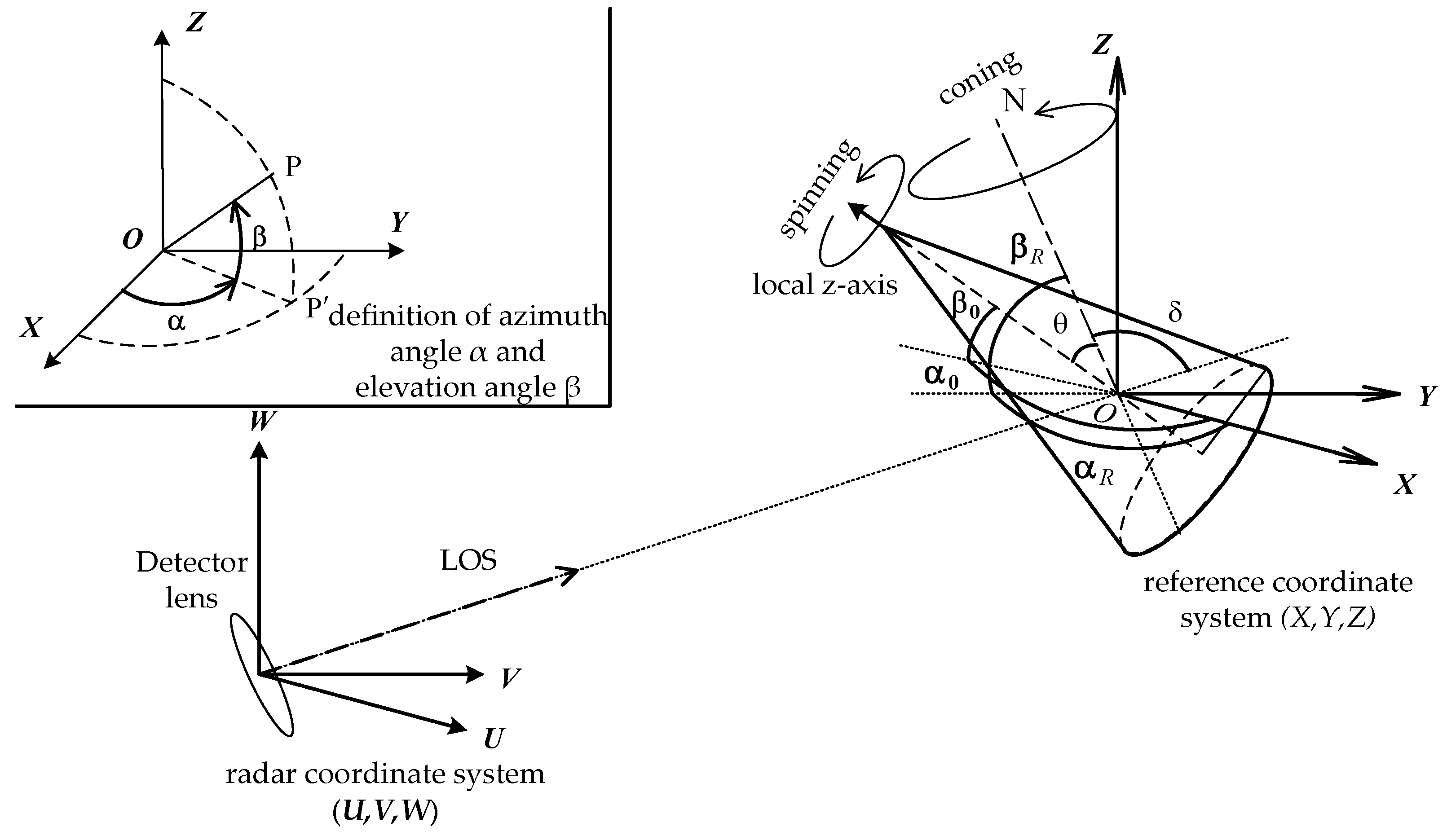
2.3. Attitude Motion Model
2.4. Infrared Signature Model Simulation
3. Shape Parameters Estimation Algorithm
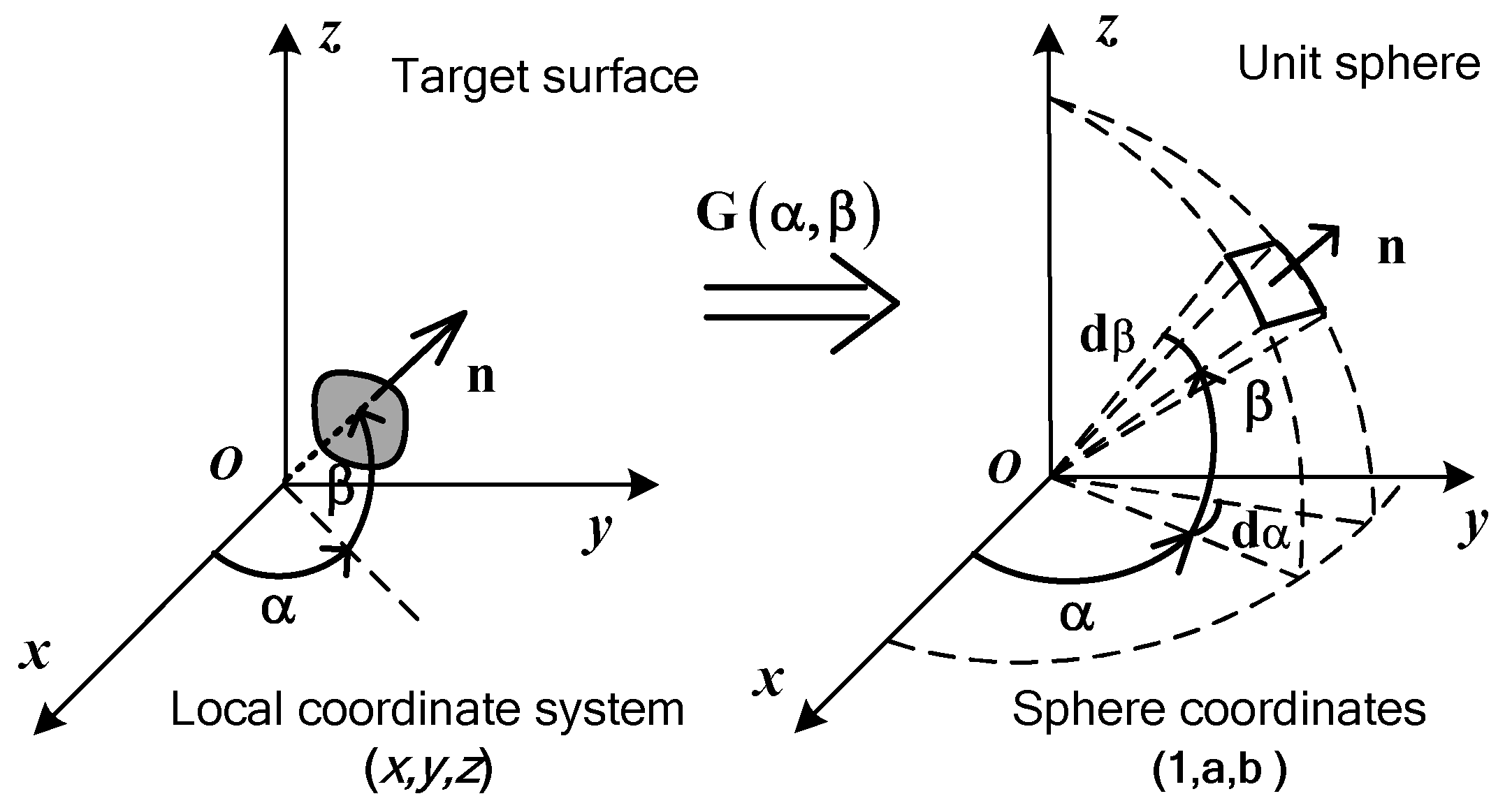
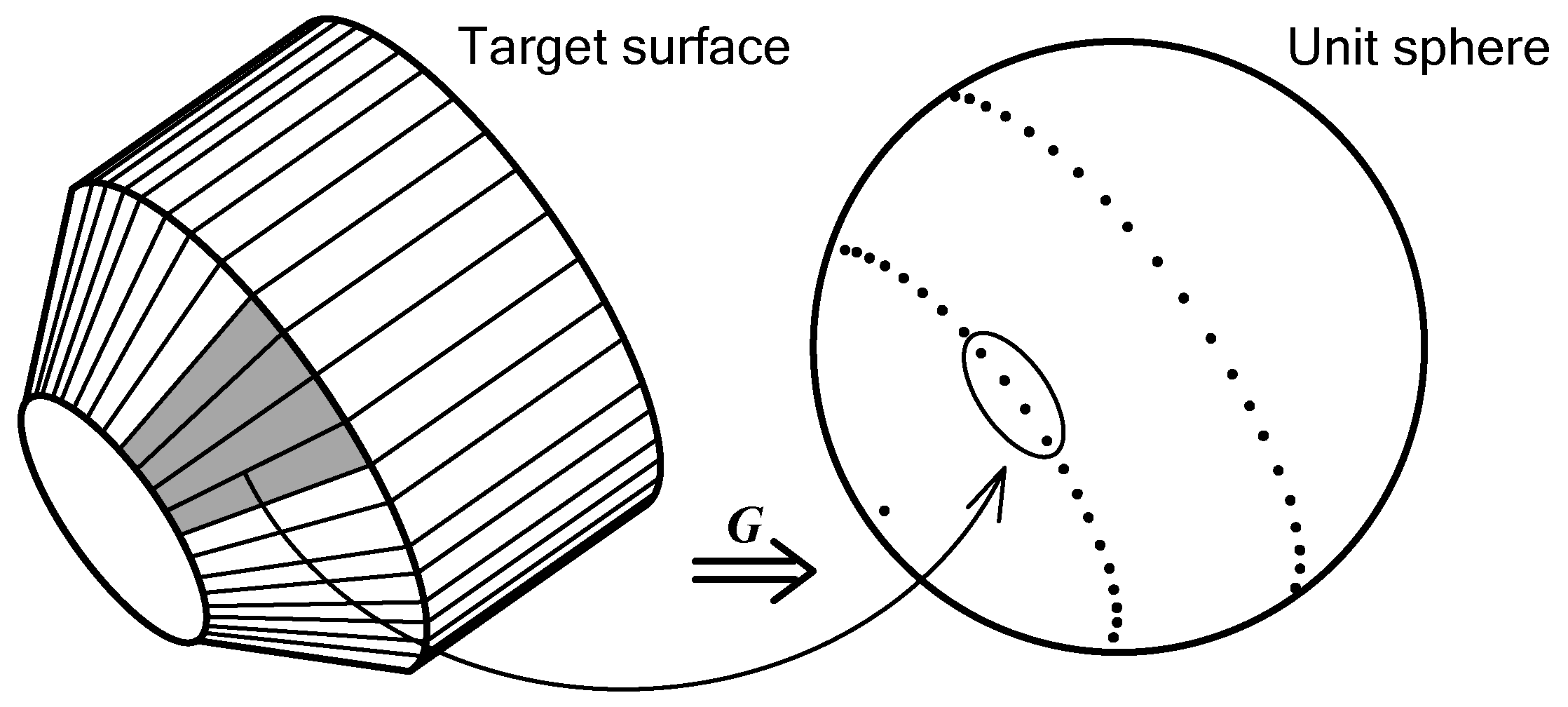
3.1. Gaussian Image Representation
3.2. Shape Discrete Description and Estimation
3.3. Space Target Shape Estimation Experiment
4. Shape and Micro-Motion Parameters’ Joint Estimation
4.1. Problem Description
4.2. Joint Estimation Algorithm and Experiment
4.2.1. Minimum Spacing Selection in the Grid Method
| Algorithm 1 Diagram of our estimation. |
| Input: projection area of spatial target dataset, line of sight vector nLOS. |
| Output: estimation of micro-motion parameters , , , , and shape parameters . |
| Step 1 Initialization |
| (1) determine the range of values for ; (2) confirm the value space of θ, β, ω, φ, and divide the grid area and try to ensure that there is no more than one minimum value in each block; (3) randomly select the initial value of the variable in each block θ0, β0, ω0, φ00. |
| Step2 Search for a minimum value in a single grid to get , , , and the objective function value χ2. |
| Step 3 Select the minimum χ2 corresponding to , , , in all grid areas as the final output. |
4.2.2. Estimation Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Resch, C.L. Neural network for exo-atmospheric target discrimination. Proc. SPIE Int. Soc. Opt. Eng. 1998, 3371, 119–128. [Google Scholar]
- Zhu, D.; Shen, W.; Cai, G.; Ke, W. Numerical simulation and experimental study of factors influencing the optical characteristics of a spatial target. Appl. Therm. Eng. 2013, 50, 749–762. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Wang, F. Infrared imaging characteristics of space-based targets based on bidirectional reflection distribution function. Infrared Phys. Technol. 2012, 55, 368–375. [Google Scholar] [CrossRef]
- Kaasalainen, M.; Torppa, J. Optimization methods for asteroid lightcurve inversion—I. shape determination. Icarus 2001, 153, 24–36. [Google Scholar] [CrossRef]
- Deng, Q.; Lu, H.; Xiao, S.; Wu, Y. Analysis of infrared signatures of exo-atmosphere micro-motion objects based on inertial parameters. Infrared Phys. Technol. 2018, 88, 32–40. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Lu, H.; Zhao, B. Ballistic targets micro-motion and geometrical shape parameters estimation from sparse decomposition representation of infrared signatures. Appl. Opt. 2017, 56, 1276–1285. [Google Scholar] [CrossRef]
- Bohren, C.; Clothiaux, E.; Johnson, N. Fundamentals of Atmospheric Radiation. Am. J. Phys. 2007, 75, 671. [Google Scholar]
- Zhang, W.; Li, K.; Jiang, W. Parameter estimation of radar targets with macro-motion and micro-motion based on circular correlation coefficients. IEEE Signal Process. Lett. 2015, 22, 633–637. [Google Scholar] [CrossRef]
- Calef, B.; Africano, J.; Birge, B.; Halla, D.; Kervin, P. Photometric signature inversion. Proc. SPIE 2016, 6307, 63070E. [Google Scholar]
- Qiu, C.; Zhang, Z.; Lu, H.; Zhang, K. Infrared modeling and imaging simulation of midcourse ballistic targets based on strap-down platform. J. Syst. Eng. Electron 2014, 25, 776–785. [Google Scholar] [CrossRef]
- Aumeunier, M.H.; Travere, J.M.; Reichle, R. Simulation of the infrared views of the upper port VIS/IR imaging system of ITER. IEEE Trans. Plasma Sci. 2014, 40, 753–760. [Google Scholar] [CrossRef]
- Liu, Z. Research on Techniques of Detection and Discrimination of Point Target in IR Image. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2005. [Google Scholar]
- Alam, M.S.; Bhuiyan, S.M. Trends in correlation-based pattern recognition and tracking in forward-looking infrared imagery. Sensors 2014, 14, 13437–13475. [Google Scholar] [CrossRef]
- Shi, L.; Cai, G.; Zhu, D. The simulation to infrared signatures of spacecraft. Astronautics 2009, 30, 229–234. [Google Scholar]
- Andrew, M.; Sessler, J.M.C.; Dietz, B. Countermeasures: A Technical Evaluation of the Operational Effectiveness of the Planned US National Missile Defense System. April 2000. Available online: http://www.ucsusa.org/sites/default/files/legacy/assets/documents/nwgs/cm_all.pdf (accessed on 16 October 2016).
- Gardner, R.J.; Milanfar, P. Reconstruction of convex bodies from brightness functions. Discret. Comput. Geom. 2003, 29, 279–303. [Google Scholar] [CrossRef][Green Version]
- Horn, B. Extended Gaussian Images. In Proceedings of the IEEE International Conference, New York, NY, USA, 8–11 October 1984; Volume 72, pp. 1671–1686. [Google Scholar]
- Linares, R.; Jah, M.; Crassidis, J.L.; Christopher, K.N. Space object shape characterization and tracking using light curve and angles data. J. Guid. Control. Dyn. 2014, 37, 13–26. [Google Scholar] [CrossRef]
- Lei, P.; Sun, J.; Wang, J.; Hong, W. Micromotion parameter estimation of free rigid targets based on radar micro-Doppler. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3776–3786. [Google Scholar] [CrossRef]
- Holzinger, M.J.; Alfriend, K.T.; Wetterer, C.J.; Luu, K.K.; Sabol, C.; Hamada, K. Photometric attitude estimation for agile space objects with shape uncertainty. J. Guid. Control. Dyn. 2014, 37, 921–932. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Chen, S.; Lu, H.; Zhao, B. Micro-motion dynamics analysis of ballistic targets based on infrared detection. J. Syst. Eng. Electron. 2017, 28, 472–480. [Google Scholar]
- Liu, J.; Wu, Y.; Lu, H.; Zhao, B. Micromotion dynamics and geometrical shape parameters estimation of exoatmospheric infrared targets. Opt. Eng. 2016, 55, 113103. [Google Scholar] [CrossRef]
- Li, K.; Liu, Y.; Huo, K.; Jiang, W. Estimation of micro-motion parameters based on cyclostationary analysis. IET Signal Process. 2010, 4, 218–223. [Google Scholar] [CrossRef]
- Zhao, B.; Lu, H.; Chen, S. Convolutional neural networks for time series classification. J. Syst. Eng. Electron. 2017, 28, 169. [Google Scholar] [CrossRef]
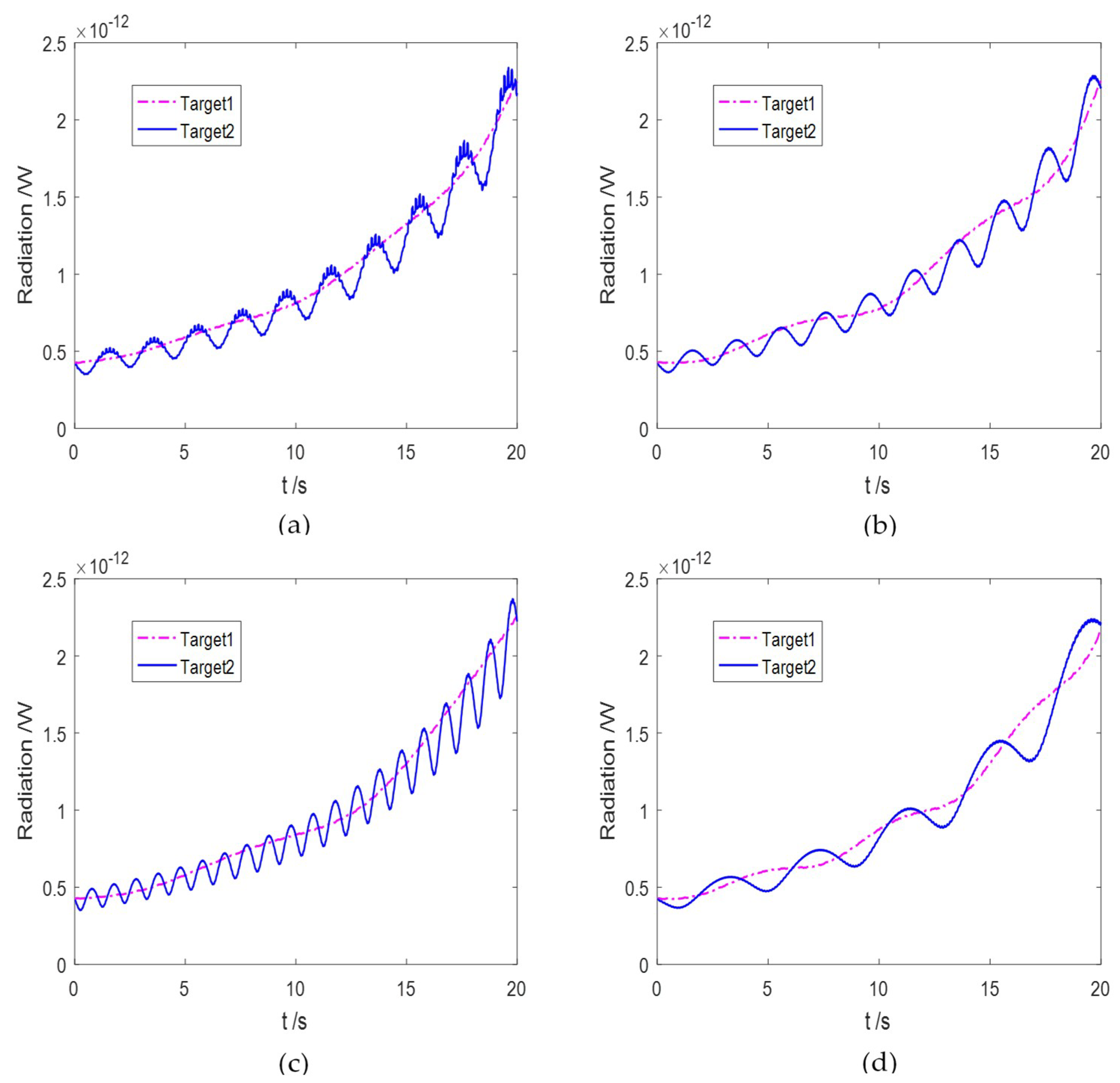
| Tests Index | Test 1 | Test 2 | Test 3 | Test 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Targets index | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| Precession angle (θp) | 2° | 10° | 4° | 8° | 3° | 9° | 3° | 9° |
| Precession period (Tp) | 8 s | 2 s | 8 s | 2 s | 10 s | 1 s | 6 s | 4 s |
| Partition | 200 | |||||||
| Initial temperature(T0) | 330 K | |||||||
| Emissivity (ε) | 0.45 | |||||||
| Waveband (λ1–λ2) | 7–9 μm | |||||||
| Initial distance (Rs) | 250 km | |||||||
| Radius (R) | 0.25 m | |||||||
| Height (H) | 1.5 m | |||||||
| Shape Parameters | Micro-Motion Parameters | 3D Models | Observed Signatures |
|---|---|---|---|
| Flat-base cone: hcone = 1.134 m, r = 0.2 m. | Precession: α0 = 0.0 π, β0 = 0.5 π, ω = 1.0π |  | 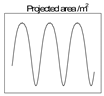 |
| Cone-cylinder: hcone = 1.134 m, hcylinde = 1.0 m, r = 0.2 m. |  | 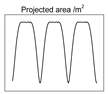 | |
| Cylinder: hcylinder = 1.0 m, r = 0.2 m | Tumbling: α0 = 0.1π, β0 = 0.2π, ω = 1.0π |  | 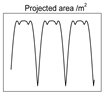 |
| Ball-base cone: hcone = 1.134 m, r = 0.2 m. | 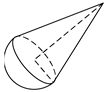 | 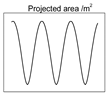 | |
| Equal curvature arc: r = 0.20 m, h = 0.35 m, θ = 45°. | 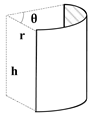 | 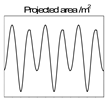 | |
| Non-equal curvature arc: r1 = 0.375 m, r2 = 0.5 m, h = 0.125 m, θ = 80°. | 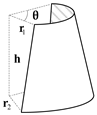 | 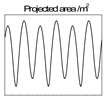 | |
| Circular ring: r = 0.20 m, h = 0.20 m. | 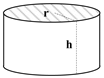 |  |
| SNR (dB) | 0 | 10 | 20 | 30 |
|---|---|---|---|---|
| Sectional view | 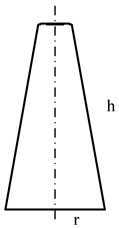 | 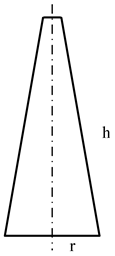 |  | 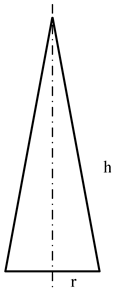 |
| Size parameters (m) | r = 1.0411 | r = 1.0129 | r = 1.0039 | r = 1.0010 |
| h = 3.9321 | h = 4.6337 | h = 5.0655 | h = 5.3214 |
| (rad) | 0.250π | 0.275π | 0.325π | 0.350π |
|---|---|---|---|---|
| Sectional view | 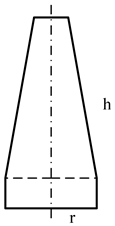 | 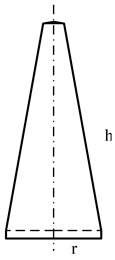 |  |  |
| Size parameters (m) | r = 0.9582 | r = 0.9939 | r = 0.9831 | r = 0.9144 |
| h = 4.0977 | h = 4.6027 | h = 4.9493 | h = 4.4621 |
| 0.98π | 0.99π | 1.01π | 1.02π | |
|---|---|---|---|---|
| Sectional view | 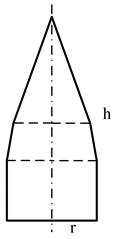 | 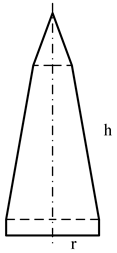 | 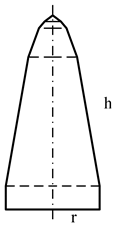 | 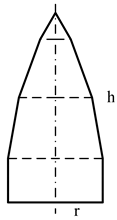 |
| Size parameters (m) | r = 0.9550 | r = 0.9833 | r = 0.9936 | r = 0.9976 |
| h = 4.2982 | h = 4.7170 | h = 4.1035 | h = 4.0024 |
| SNR (dB) | 30 | 20 | 10 | 0 |
|---|---|---|---|---|
| Δθπ rad | 0.004 | 0.000 | 0.020 | 0.036 |
| Δβπ rad | 0.007 | 0.009 | 0.012 | 0.034 |
| Δφ0π rad | 0.001 | 0.002 | 0.008 | 0.033 |
| Δωπ rad/s | 0.000 | 0.000 | 0.000 | 0.001 |
| Sectional view | 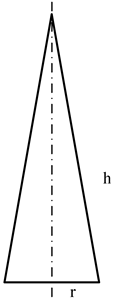 | 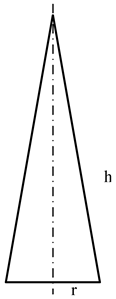 |  |  |
| Size parameters (m) | r = 0.9993 | r = 0.9987 | r = 0.9957 | r = 0.9714 |
| h = 5.6681 | h = 5.6654 | h = 5.5210 | h = 4.1017 | |
| χ2 | 0.170 | 1.671 | 16.625 | 169.009 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Lu, H.; Zhao, B.; Liu, J.; Zhao, M. Micro-Motion Dynamics and Shape Parameters Estimation Based on an Infrared Signature Model of Spatial Targets. Electronics 2019, 8, 755. https://doi.org/10.3390/electronics8070755
Wu D, Lu H, Zhao B, Liu J, Zhao M. Micro-Motion Dynamics and Shape Parameters Estimation Based on an Infrared Signature Model of Spatial Targets. Electronics. 2019; 8(7):755. https://doi.org/10.3390/electronics8070755
Chicago/Turabian StyleWu, Dongya, Huanzhang Lu, Bendong Zhao, Junliang Liu, and Ming Zhao. 2019. "Micro-Motion Dynamics and Shape Parameters Estimation Based on an Infrared Signature Model of Spatial Targets" Electronics 8, no. 7: 755. https://doi.org/10.3390/electronics8070755
APA StyleWu, D., Lu, H., Zhao, B., Liu, J., & Zhao, M. (2019). Micro-Motion Dynamics and Shape Parameters Estimation Based on an Infrared Signature Model of Spatial Targets. Electronics, 8(7), 755. https://doi.org/10.3390/electronics8070755




