Construction of Residue Number System Using Hardware Efficient Diagonal Function
Abstract
:1. Introduction
2. Materials and Methods
2.1. Background on RNS
| Algorithm 1. Magnitude comparison using DF [22]. |
| Input:, , , ; Variable:, ; Calculations: ; ; for do ; ; end for; if then return (""); else if then return (""); else if then return (""); else if then return (""); else return (""); end if; end if; end if; end if; |
2.2. Construction Methods of RNS with Hardware Efficient DF
- Among the RNS moduli , , …, there is an even one, and the others are odd. Then among , , …, there is an odd one, and the others are even and therefore is odd.
- All RNS moduli , , …, are odd. Then all , , …, are odd and parity of is the same as the parity of the number of moduli .
2.2.1. RNS with Even Module
- Choose a composite .
- Compute .
- Consider the possible cases.
- If then , , were for . , where , , .
- If then , , where , , and is order of 2 modulo .
- If then , , where , , and is order of 2 modulo .
- , , .
- , .
- , , .
- , .
- , , etc.
- , , .
- , , , .
- , , .
- , .
- , , etc.
2.2.2. RNS with Odd Moduli
- .
- and are odd.
- .
- is odd.
- is prime and not equal to 2.
- is a primitive root modulo .
- gives ,
- gives , ,
- gives , , .
- is prime.
- 2 is a primitive root modulo
- ;.
- and are odd
- , , .
- .
- is odd, is prime and 2 is a primitive root modulo 443.
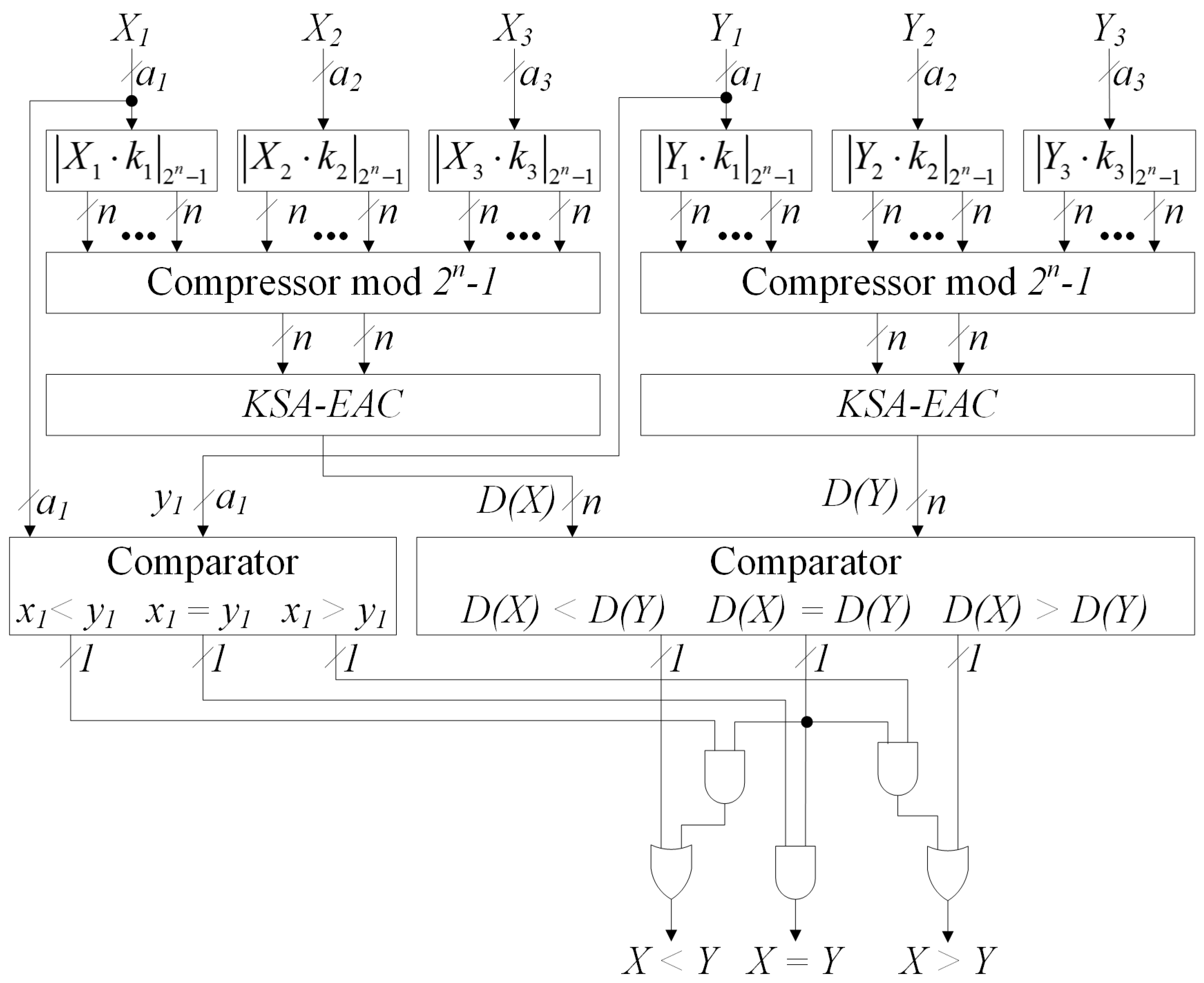
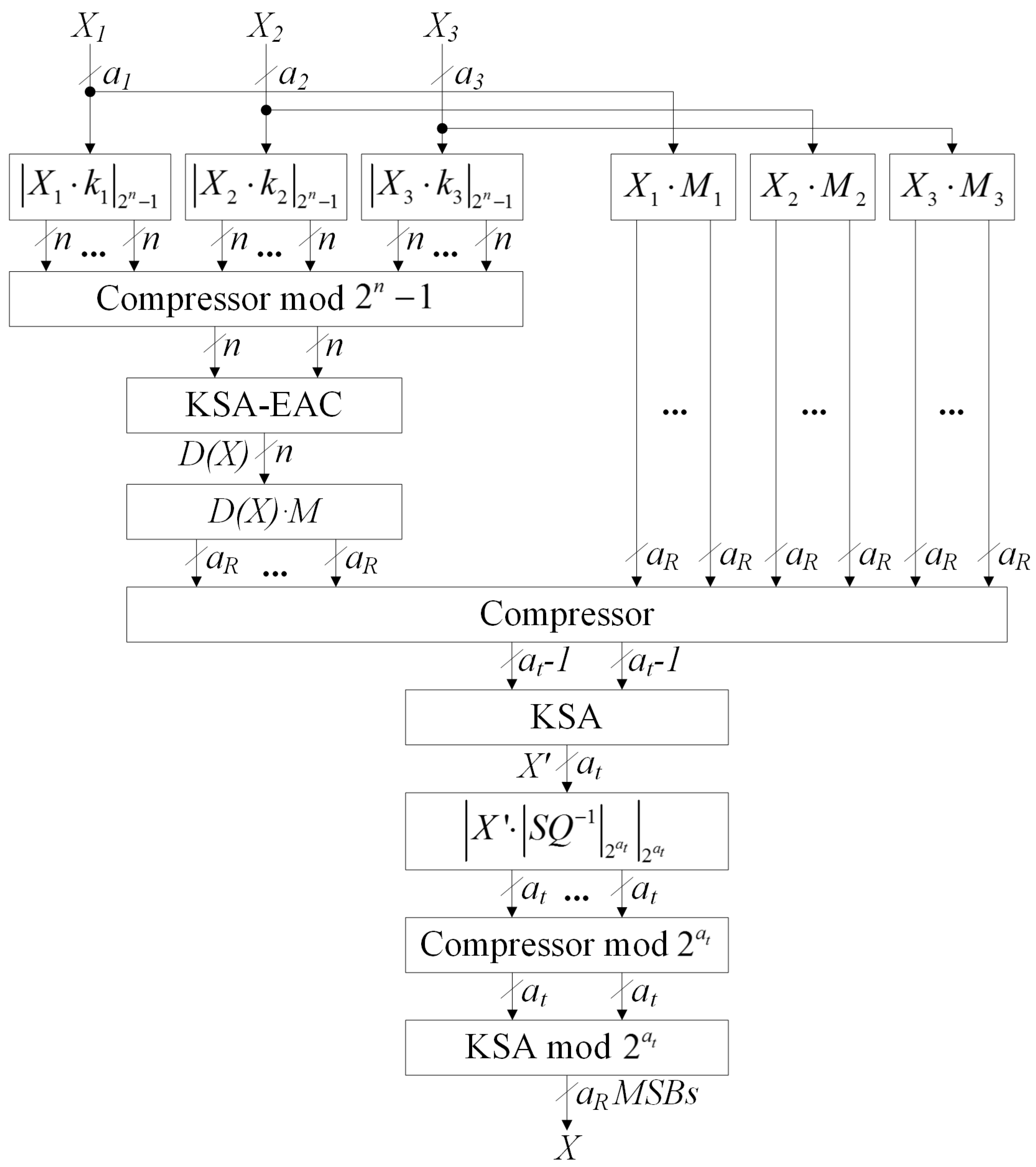
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Akkal, M.; Siy, P. A new mixed radix conversion algorithm MRC-II. J. Syst. Archit. 2007, 53, 577–586. [Google Scholar] [CrossRef]
- Ramirez, J.; Garcia, A.; Lopez-Buedo, S.; Lloris, A. RNS-enabled digital signal processor design. Electron. Lett. 2002, 38, 266–268. [Google Scholar] [CrossRef]
- Chang, C.; Molahosseini, A.S.; Zarandi, A.A.E.; Tay, T.F. Residue number systems: A new paradigm to datapath optimization for low-power and high-performance digital signal processing applications. IEEE Circuits Syst. Mag. 2015, 15, 26–44. [Google Scholar] [CrossRef]
- Kaplun, D.; Butusov, D.; Ostrovskii, V.; Veligosha, A.; Gulvanskii, V. Optimization of the FIR filter structure in finite residue field algebra. Electronics 2018, 7, 372. [Google Scholar] [CrossRef]
- Esmaeildoust, M.; Schinianakis, D.; Javashi, H.; Stouraitis, T.; Navi, K. Efficient RNS implementation of elliptic curve point multiplication GF(p). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 21, 1545–1549. [Google Scholar] [CrossRef]
- Bajard, J.-C.; Imbert, L. A full RNS implementation of RSA. IEEE Trans. Comput. 2004, 53, 769–774. [Google Scholar] [CrossRef]
- Sousa, L.; Antao, S.; Martins, P. Combining residue arithmetic to design efficient cryptographic circuits and systems. IEEE Circuits Syst. Mag. 2016, 16, 6–32. [Google Scholar] [CrossRef]
- Chervyakov, N.I.; Lyakhov, P.A.; Babenko, M.G. Digital filtering of images in a residue number system using finite-field wavelets. Autom. Control Comput. Sci. 2014, 48, 180–189. [Google Scholar] [CrossRef]
- Kar, A.; Sur, K.; Godara, S.; Basak, S.; Mukherjee, D.; Sukla, A.S.; Das, R.; Choudhury, R. Security in cloud storage: An enhanced technique of data storage in cloud using RNS. In Proceedings of the IEEE 7th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 20–22 October 2016; pp. 1–4. [Google Scholar]
- Navi, K.; Esmaeildoust, M.; Molahosseini, A.S. A general reverse converter architecture with low complexity and high performance. IEICE Trans. Inf. Syst. 2011, 94, 264–273. [Google Scholar] [CrossRef]
- Milanezi Junior, J.; da Costa, J.P.C.L.; Römer, F.; Miranda, R.K.; Marinho, M.A.M.; Del Galdo, G. M-estimator based Chinese remainder theorem with few remainders using a kroenecker product based mapping vector. Digit. Signal Process. 2019, 87, 60–74. [Google Scholar] [CrossRef]
- Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Gerardi, L.; Re, M.; Campolo, G.; Cascone, D. A new electric encoder position estimator based on the Chinese Remainder Theorem for the CMG performance improvements. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), New York, NY, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Chervyakov, N.I.; Lyakhov, P.A.; Valueva, M.V. Increasing of convolutional neural network performance using residue number system. In Proceedings of the 2017 IEEE International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), New York, NY, USA, 18–22 September 2017; pp. 135–140. [Google Scholar]
- Cardarilli, G.C.; Del Re, A.; Nannarelli, A.; Re, M. Impact of RNS coding overhead on FIR filters performance. In Proceedings of the 2007 Conference Record of the Forty-First Asilomar Conference on Signals, Systems and Computers, New York, NY, USA, 4–7 November 2007; pp. 1426–1429. [Google Scholar]
- Chang, C.; Lee, W.; Liu, Y.; Goi, B.; Phan, R.C.-W. Signature gateway: Offloading signature generation to IoT gateway accelerated by GPU. IEEE Internet Things J. 2019, 6, 4448–4461. [Google Scholar] [CrossRef]
- Chervyakov, N.I.; Babenko, M.G.; Lyakhov, P.A.; Lavrinenko, I.N. An approximate method for comparing modular numbers and its application to the division of numbers in residue number systems. Cybern. Syst. Anal. 2014, 50, 977–984. [Google Scholar] [CrossRef]
- Selvam, R.; Tyagi, A. Power side channel resistance of RNS secure logic. In Proceedings of the 2018 31st International Conference on VLSI Design and 2018 17th International Conference on Embedded Systems (VLSID), New York, NY, USA, 6–10 January 2018; pp. 143–148. [Google Scholar]
- Mohan, P.V.A. Residue Number Systems: Theory and Applications; Birkhauser: Basel, Switzerland, 2016; ISBN 9783319413853. [Google Scholar]
- Gonnella, J. The application of core functions to residue number system. IEEE Trans. Signal Process. 1991, 39, 69–75. [Google Scholar] [CrossRef]
- Akushskii, I.J.; Burcev, V.M.; Pak, I.T. A new positional characteristic of nonpositional codes and its applications. Coding Theory Optim. Complex Syst. 1977, 8–16. [Google Scholar]
- Matos, R.; Paludo, R.; Chervyakov, N.; Lyakhov, P.A.; Pettenghi, H. Efficient implementation of modular multiplication by constants applied to RNS reverse converters. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Dimauro, G.; Impedovo, S.; Pirlo, G. A new technique for fast number comparison in the residue number system. IEEE Trans. Comput. 1993, 42, 608–612. [Google Scholar] [CrossRef]
- Dimauro, G.; Impedovo, S.; Pirlo, G.; Salzo, A. RNS architectures for the implementation of the ‘diagonal function’. Inf. Process. Lett. 2000, 73, 189–198. [Google Scholar] [CrossRef]
- Mohan, P.V.A. RNS to binary conversion using diagonal function and pirlo and impedovo monotonic function. Circuits Syst. Signal Process. 2015, 35, 1–14. [Google Scholar] [CrossRef]
- Piestrak, S.J. A note on RNS architectures for the implementation of the diagonal function. Inf. Process. Lett. 2015, 115, 453–457. [Google Scholar] [CrossRef]
- Kalampoukas, L.; Nikolos, D.; Efstathiou, C.; Vergos, H.T.; Kalamatianos, J. High-speed parallel-prefix modulo 2n − 1 Adders. IEEE Trans. Comput. 2000, 49, 673–680. [Google Scholar] [CrossRef]
- Efstathiou, C.; Vergos, H.T.; Nikolos, D. Fast parallel-prefix Modulo 2n + 1 Adders. IEEE Trans. Comput. 2004, 53, 1211–1216. [Google Scholar] [CrossRef]
- Vergos, H.T.; Dimitrakopoulos, G. On Modulo 2n + 1 Adder design. IEEE Trans. Comput. 2012, 61, 173–186. [Google Scholar] [CrossRef]
- Chaves, R.; Sousa, L. Improving residue number system multiplication with more balanced moduli sets and enhanced modular arithmetic structures. IET Comput. Digit. Tech. 2007, 1, 472. [Google Scholar] [CrossRef]
- Jaberipur, G.; Nejati, S. Balanced minimal latency RNS addition for moduli set {2n − 1, 2n, 2n + 1}. In Proceedings of the 18th International Conference on Systems, Signals and Image Processing, Sarajevo, Bosnia and Herzegovina, 16–18 June 2011; pp. 1–7. [Google Scholar]
- Hiasat, A. Efficient RNS Scalers for the extended three-moduli set {2n − 1, 2n+p, 2n + 1}. IEEE Trans. Comput. 2017, 66, 1253–1260. [Google Scholar] [CrossRef]
- Patronik, P.; Piestrak, S.J. Design of reverse converters for the new RNS moduli set {2n + 1, 2n − 1, 2n, 2n−1 + 1} (n odd). IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 3436–3449. [Google Scholar] [CrossRef]
- Hiasat, A. A reverse converter and sign detectors for an extended RNS five-moduli set. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 111–121. [Google Scholar] [CrossRef]
- Mohan, P.V.A.; Premkumar, A.B. RNS-to-Binary converters for two four-moduli sets {2n + 1, 2n − 1, 2n, 2n−1 − 1} and {2n + 1, 2n − 1, 2n, 2n+1 + 1}. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 1245–1254. [Google Scholar] [CrossRef]
- Kumar, S.; Chang, C.-H.; Tay, T.F. New algorithm for signed integer comparison in {2n+k, 2n − 1, 2n + 1, 2n±1 − 1} and its efficient hardware implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1481–1493. [Google Scholar] [CrossRef]
- Kumar, S.; Chang, C.-H. A scaling-assisted signed integer comparator for the balanced five-moduli set RNS {2n − 1, 2n, 2n + 1, 2n+1 − 1, 2n−1 − 1}. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 3521–3533. [Google Scholar] [CrossRef]
- Skavantzos, A.; Abdallah, M.; Stouraitis, T.; Schinianakis, D. Design of a balanced 8-modulus RNS. In Proceedings of the 2009 16th IEEE International Conference on Electronics, Circuits and Systems (ICECS 2009), New York, NY, USA, 13–16 December 2009; pp. 61–64. [Google Scholar]
- Vayalil, N.C.; Paul, M.; Kong, Y. A residue number system hardware design of fast-search variable-motion-estimation accelerator for HEVC/H.265. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 572–581. [Google Scholar] [CrossRef]
- Cheng, S.W. A high-speed magnitude comparator with small transistor count. In Proceedings of the 10th IEEE International Conference on Electronics, Circuits and Systems, 2003 (ICECS 2003), New York, NY, USA, 14–17 December 2003; pp. 1168–1171. [Google Scholar]
- Chervyakov, N.I.; Lyakhov, P.A.; Kalita, D.I.; Shulzhenko, K.S. Effect of RNS dynamic range on grayscale images filtering. In Proceedings of the XV International Symposium Problems of Redundancy in Information and Control Systems (REDUNDANCY), St. Petersburg, Russia, 26–29 September 2016; pp. 33–37. [Google Scholar]
- Molahosseini, A.S.; Sorouri, S.; Zarandi, A.A.E. Research challenges in next-generation residue number system architectures. In Proceedings of the IEEE 7th International Conference on Computer Science & Education (ICCSE), Melbourne, VIC, Australia, 14–17 July 2012; pp. 1658–1661. [Google Scholar]
- Parhami, B. Computer Arithmetic: Algorithms and Hardware Designs; Oxford University Press: Oxford, UK, 2010; ISBN 9780195328486. [Google Scholar]
| Number of Modules | Moduli Set | Condition | References |
|---|---|---|---|
| 3 | [29,30] | ||
| [31] | |||
| odd, | [32] | ||
| 4 | even | [33] | |
| odd | [32] | ||
| odd | [34] | ||
| even, | [35] | ||
| 5 | even | [36] | |
| odd, | [33] | ||
| 8 | , | [37] |
| Moduli Set | Known Methods | Proposed Method | ||
|---|---|---|---|---|
| CRT [18] | CRTf [21] | |||
| Delay, ns | 10.961 | 7.680 | 9.749 | |
| 16.110 | 11.123 | 11.830 | ||
| 15.363 | 12.611 | 11.991 | ||
| LUTs | 135 | 169 | 110 | |
| 543 | 329 | 273 | ||
| 1,141 | 863 | 549 | ||
| A·D | 1479 | 1297 | 1072 | |
| 8747 | 3659 | 3229 | ||
| 17529 | 10883 | 6583 | ||
| Power, W | 4.061 | 5.757 | 4.581 | |
| 21.751 | 13.929 | 11.840 | ||
| 40.950 | 47.128 | 24.733 | ||
| Moduli Set | Known Methods | Proposed Method | ||
|---|---|---|---|---|
| CRT [18] | CRTf [21] | |||
| Delay, ns | 8.181 | 8.157 | 10.085 | |
| 15.493 | 13.351 | 13.531 | ||
| 21.228 | 16.814 | 17.600 | ||
| LUTs | 63 | 59 | 105 | |
| 289 | 358 | 285 | ||
| 997 | 920 | 1,049 | ||
| A·D | 515 | 481 | 1,058 | |
| 4,477 | 4,779 | 3,856 | ||
| 21,164 | 15,468 | 18,462 | ||
| Power, W | 5.946 | 5.504 | 11.733 | |
| 22.226 | 39.154 | 26.789 | ||
| 65.901 | 106.867 | 117.797 | ||
| Moduli Set | Ref. | Magnitude Comparison | Reverse Conversion | |||||
|---|---|---|---|---|---|---|---|---|
| Delay, ns | LUTs | A·D | Delay, ns | LUTs | A·D | |||
| [29,30] | 12.953 | 272 | 3,523 | 13.486 | 169 | 2,279 | ||
| , | [31] | 11.533 | 150 | 1,729 | 11.246 | 91 | 1,023 | |
| , | Proposed | 9.749 | 110 | 1,072 | 10.085 | 105 | 1,058 | |
| [29,30] | 14.964 | 275 | 4,115 | 15.855 | 263 | 4,169 | ||
| [34] | 16.710 | 427 | 7,135 | 20.217 | 447 | 9,036 | ||
| Proposed | 11.830 | 273 | 3,229 | 13.531 | 285 | 3,856 | ||
| , | [35] | 16.669 | 303 | 5,050 | 24.163 | 572 | 13,821 | |
| , | [35] | 24.962 | 1,767 | 44,107 | 30.831 | 1,496 | 46,123 | |
| Proposed | 11.991 | 549 | 6,583 | 17.600 | 1,049 | 18,462 | ||
| Type and Number of RNS Moduli | Form of SQ | |||
|---|---|---|---|---|
| one even module | exist | not exist | exist | |
| all moduli are odd | 3 moduli | exist | not exist | not exist |
| 4 moduli | not exist | exist | not exist | |
| 5 moduli | not exist | not exist | exist | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valueva, M.; Valuev, G.; Semyonova, N.; Lyakhov, P.; Chervyakov, N.; Kaplun, D.; Bogaevskiy, D. Construction of Residue Number System Using Hardware Efficient Diagonal Function. Electronics 2019, 8, 694. https://doi.org/10.3390/electronics8060694
Valueva M, Valuev G, Semyonova N, Lyakhov P, Chervyakov N, Kaplun D, Bogaevskiy D. Construction of Residue Number System Using Hardware Efficient Diagonal Function. Electronics. 2019; 8(6):694. https://doi.org/10.3390/electronics8060694
Chicago/Turabian StyleValueva, Maria, Georgii Valuev, Nataliya Semyonova, Pavel Lyakhov, Nikolay Chervyakov, Dmitry Kaplun, and Danil Bogaevskiy. 2019. "Construction of Residue Number System Using Hardware Efficient Diagonal Function" Electronics 8, no. 6: 694. https://doi.org/10.3390/electronics8060694
APA StyleValueva, M., Valuev, G., Semyonova, N., Lyakhov, P., Chervyakov, N., Kaplun, D., & Bogaevskiy, D. (2019). Construction of Residue Number System Using Hardware Efficient Diagonal Function. Electronics, 8(6), 694. https://doi.org/10.3390/electronics8060694







