Abstract
The residue number system (RNS) is a non-positional number system that allows one to perform addition and multiplication operations fast and in parallel. However, because the RNS is a non-positional number system, magnitude comparison of numbers in RNS form is impossible, so a division operation and an operation of reverse conversion into a positional form containing magnitude comparison operations are impossible too. Therefore, RNS has disadvantages in that some operations in RNS, such as reverse conversion into positional form, magnitude comparison, and division of numbers are problematic. One of the approaches to solve this problem is using the diagonal function (DF). In this paper, we propose a method of RNS construction with a convenient form of DF, which leads to the calculations modulo , or and allows us to design efficient hardware implementations. We constructed a hardware simulation of magnitude comparison and reverse conversion into a positional form using RNS with different moduli sets constructed by our proposed method, and used different approaches to perform magnitude comparison and reverse conversion: DF, Chinese remainder theorem (CRT) and CRT with fractional values (CRTf). Hardware modeling was performed on Xilinx Artix 7 xc7a200tfbg484-2 in Vivado 2016.3 and the strategy of synthesis was highly area optimized. The hardware simulation of magnitude comparison shows that, for three moduli, the proposed method allows us to reduce hardware resources by 5.98–49.72% in comparison with known methods. For the four moduli, the proposed method reduces delay by 4.92–21.95% and hardware costs by twice as much by comparison to known methods. A comparison of simulation results from the proposed moduli sets and balanced moduli sets shows that the use of these proposed moduli sets allows up to twice the reduction in circuit delay, although, in several cases, it requires more hardware resources than balanced moduli sets.
1. Introduction
The residue number system (RNS) is a non-positional number system that allows large length numbers to be presented as numbers in independent bits of a small length, which enables computations and the organizing of their parallelisms to be sped up. RNS has several advantages, such as the possibility of faster addition and multiplication compared to all other number systems. Moreover, the use of short numbers in RNS computations can significantly reduce the power consumption of digital devices [1]. It is useful in the synthesis of RNS computational devices with parallel structure, such as field-programmable gate array (FPGA) and application-specific integrated circuit (ASIC). All these attractive features increase interest to RNS in the areas where large amounts of computation are needed. The applications of RNS are digital signal processing [2,3,4], cryptography [5,6,7], digital image processing [8], cloud computing [9], Internet of Things [10] and others. In [11], the authors propose a technique to estimate real-valued numbers by means of the Chinese remainder theorem (CRT), employing for this goal a Kroenecker based M-Estimation, to improve robustness. A new method based on the Chinese remainder theorem (CRT) is proposed for absolute position computation in [12]. This has advantages in terms of hardware and flexibility because it does not use memory. The authors of [13] offer to use RNS to improve the performance of the convolutional neural network developed for pattern recognition tasks. Reference [14] describes the method of construction for finite impulse response filers using RNS.
However, the limitations of RNS include some operations such as reverse conversion into positional form, magnitude comparison and division of numbers in RNS [15,16]. These limitations exist because RNS is a non-positional number system, and magnitude comparison of numbers in RNS form is impossible, so the division operation consists of a magnitude comparison operation that is also a problematic operation. Improving the efficiency of the comparison operation in RNS is something that can be used in the development of new approaches to the implementation of other problematic operations in RNS, such as subtraction-based division and the detection of dynamic range overflow. Dynamic range overflow detectors in RNS are widely applied in the design of fault-tolerant systems and secure communication channels [17].
The state-of-the-art in the described problem is as follows. The most common approaches to performing non-modular RNS operations are based on mixed radix conversion (MRC) and the Chinese remainder theorem (CRT) [1,18]. Another class of approaches to perform magnitude comparison in RNS, which is based on the core functions defined from the RNS to the integer [19], was first proposed Akushskii et al. [20]. Recently new alternatives have been developed for the implementation of the non-modular RNS operations problem. These approaches are the use of CRT with fractional values (CRTf) [21] and diagonal function (DF) [22,23]. References [24] and [25] demonstrate that the use of DF has a significant drawback in the necessity to perform modulo sum of quotients (SQ) operations. The authors of these papers show that DF usually does not provide advantages in comparison with MRC and CRT. Therefore, in this paper, we will discuss the issue of constructing RNS with a convenient form of DF, which leads to the calculations modulo , or since the numbers of this form have very effective methods of hardware implementation, as designed in [26,27,28]. How balanced the moduli set is plays an important role in this method. Table 1 shows samples of known moduli sets.

Table 1.
Known balanced moduli sets.
The proposed approach to the construction of RNS can be effective in those applications in which the comparison operation is a significant part of the calculations. One of the examples of such an application is the motion estimation on video, estimated by using high-efficiency video coding (HEVC/H.265) [38]. Another example of a such application is customized signal processing units. For example, the sorting network uses a large number of comparators and is one of the key elements in electronic finance data management systems, digital computers and communication systems [39]. Due to the excessive number of magnitude comparisons required in sorting a large pool of data, the speed of the magnitude comparator determines the overall delay of the sorting process [35].
The rest of the paper is organized as follows. Section 2 discusses RNS issues, represented numbers, and arithmetic operations in RNS. The Section 3 presents the construction of RNS with a convenient form of DF and the results of the hardware simulation of magnitude comparison and reverse conversion into the positional form using CRT, CRTf, and DF. Section 4 discusses the methods of RNS construction presented in this paper and hardware simulation results. The conclusion of the paper is reported in Section 5.
2. Materials and Methods
2.1. Background on RNS
Numbers in RNS are represented in the form of relatively prime numbers which are called moduli , , for . Any integer number can be uniquely represented in RNS as a tuple , where . Operations of addition, subtraction, and multiplication in RNS are defined by the formulas showing the carry-free parallel nature of RNS:
The reverse conversion of a number from residues is based on CRT
where , and means a multiplicative inverse of modulo .
The DF is defined as
where is called the “diagonal modulus” of the RNS and . The principles of applying the DF for reverse conversion and numbers comparison are thoroughly shown in [24] and [25]. Reverse conversion using DF can be implemented by the formula
In [25], magnitude comparison is presented using DF. The work uses the magnitude comparison Algorithm 1 of X and Y, presented in [22], which relies on the following properties of the DF.
| Algorithm 1. Magnitude comparison using DF [22]. |
| Input:, , , ; Variable:, ; Calculations: ; ; for do ; ; end for; if then return (""); else if then return (""); else if then return (""); else if then return (""); else return (""); end if; end if; end if; end if; |
It is obvious that the main obstacle to the development of very-large-scale integration (VLSI) architectures based on the DF is the necessity to perform modulo SQ operations. Below, we show how to construct RNS with a convenient form of DF that leads to modulo , or computations.
2.2. Construction Methods of RNS with Hardware Efficient DF
The choice of the optimal moduli set is a very important question in RNS theory since it has an impact on performance and the quality of operations. In [26,27,28], authors perform high-speed architectures of modulo adders. The use of moduli , or allows for there to be an increase in computation performance. In addition, the choice of enough RNS dynamic range is a very important question too. In [40], authors considered the influence of the RNS dynamic range on the quality of image filtering. Therefore, it is necessary to choose optimal moduli sets, so we propose the method of RNS construction with a convenient form of DF.
Let us consider two possible cases.
- Among the RNS moduli , , …, there is an even one, and the others are odd. Then among , , …, there is an odd one, and the others are even and therefore is odd.
- All RNS moduli , , …, are odd. Then all , , …, are odd and parity of is the same as the parity of the number of moduli .
2.2.1. RNS with Even Module
One can suppose that , , …, are odd and is even. We will choose , , …, in such a way to satisfy or . We denote and , thus . If is odd then is even and therefore or . If is even then is odd and .
If then three cases are possible
Hence
We choose in a way that is a composite number and for . Since among the numbers, there are composite numbers much more than prime numbers, then the choice of is obviously possible. Therefore
Hence, since and we have
Suppose that or . We have
Hence
Congruence (21) is solvable due to the fact that . If is an order of 2 modulo , then , where . Hence . From this, if it is necessary to find , where is even and then proceed as follows.
- Choose a composite .
- Compute .
- Consider the possible cases.
- If then , , were for . , where , , .
- If then , , where , , and is order of 2 modulo .
- If then , , where , , and is order of 2 modulo .
Example 1.
Suppose that , . Then , . , . , , , . Examining a power of two, we have
- , , .
- , .
- , , .
- , .
- , , etc.
Thus, we obtained the following RNS: , , , , , .
Note. For the case one needs to take . The conclusions obtained are the same as for .
Example 2.
Suppose that , . Then
- , , .
- , , , .
- , , .
- , .
- , , etc.
Thus we obtained the following RNS:, , , .
2.2.2. RNS with Odd Moduli
We only consider the most important practical cases, for example, when RNS contains three, four or five moduli [41].
Case 1. RNS with three moduli. In analogy with the above notations , , and . One can verify that . Let us see whether it is possible for the odd and to choose such an odd , such that . If then . It is clear that . If , then the right part of equality
divisible by , and left part of Equality (22) is not divisible by . This means that for the satisfy Equality (22) it is necessary that
Under Condition (23) we have
where . If one of the numbers or is even, then (24) is impossible. Thus, for the validity of (24), it is necessary that both numbers and are odd.
Suppose that both conditions are performed.
- .
- and are odd.
Let us write (24) as a congruence
If is prime and 2 is a primitive root modulo then Congruence (25) will have solutions concerning by . Suppose that is the smallest non-negative solution of Congruence (25). Then
And therefore . Hence . This means that
According to the RNS definition, the number must be relatively prime with and .
If the number is prime and 2 is not a primitive root modulo then Congruence (25) may have no solutions. In addition, Congruence (25) may have no solutions if is a composite number. Thus, to construct RNS with three odd moduli and , four conditions must be fulfilled.
- .
- is odd.
- is prime and not equal to 2.
- is a primitive root modulo .
Note that these conditions are not sufficient, since the numbers found by Formula (27) may not be relatively prime with or .
Example 3.
Suppose that , . Then , is odd, is prime, 2 is a primitive root modulo 5.
From the equality , we obtain a congruence which implies , or , .
Testing of the value gives the following result:
- gives ,
- gives , ,
- gives , , .
So, we get the RNS with .
Case 2. RNS with 4 moduli. In this case, is even. Consider the problem: for , , choose in such a way as to . If we denote , then . It is clear that . From the equality follows
If is prime and 2 is a primitive root modulo then Congruence (28) has a solution on . Suppose that is the smallest non-negative solution of ongruence (28). Then , . It means that from which
Since then for any it will be obtained that the number is relatively prime with , and . If is a composite number, then Congruence (28) may have no solutions. If is prime and 2 is not a primitive root modulo then Congruence (28) may have no solutions too. In other words, to construct RNS with four odd moduli and , two conditions must be fulfilled.
- is prime.
- 2 is a primitive root modulo
Example 4.
Suppose that , , . In this case and is prime. Two is a primitive root modulo 131. From the equality follows congruence . The least nonnegative solution of this congruence is , therefore ,
Hence , For we have .
We received RNS with .
Case 3. RNS with 5 moduli. In analogy with the above notations, we denote and and . One can verify that . Let us see whether it is possible for the odd , , and choose such an odd that the .
If then . Similar to case 1, the equality
is possible if:
- ;.
- and are odd
Then or
If is prime and 2 is a primitive root modulo then Congruence (31) has solutions concerning modulo . Suppose that is the smallest nonnegative such a solution. Then and
Hence wherein should be chosen so that will be relatively prime with , , and .
Example 5.
Suppose that , , and . Then
- , , .
- .
- is odd, is prime and 2 is a primitive root modulo 443.
Hence, we can choose such an odd number as that the following . From the equality , we obtain , from which ,
Hence , where needs to be chosen such that .
The smallest where this condition is performed , therefore . We obtain RNS with .
The above methods for constructing RNS with a diagonal function of the , and forms allow us to develop efficient circuits for comparing numbers and reverse conversion. In the rest of this article, we demonstrate examples of such circuits and show the advantages of their technical characteristics in comparison with the known analogs.
3. Results
The goal of modeling is a comparison of the methods of implementing the numbers comparison operation and reverse RNS to binary conversion by the proposed methods, a method based on CRT [18] and a method based on CRTf [21]. We use , and moduli sets, because their DF has form and which are low-cost RNS [42]. Figure 1 shows the circuit for numbers comparison in RNS with DF of the form . The bit-widths of the RNS moduli are denoted as . Multipliers by constants modulo implement the generation of partial products modulo . A modulo compressor is implemented as in [21]. Kogge–Stone adder with end-around carry (KSA-EAC) uses for modulo addition, and it is implemented as in [27]. The circuit for numbers comparison in RNS with DF of the form has a similar structure to that presented in Figure 1, but it should have four inputs for compared numbers and , since in the theoretical part, we demonstrate that only RNS with four modules can have DF of the form . In addition, compressors and Kogge-Stone adders (KSAs) must implement modulo operations that are achieved by simply dropping the carrying of the most significant bit (MSB).
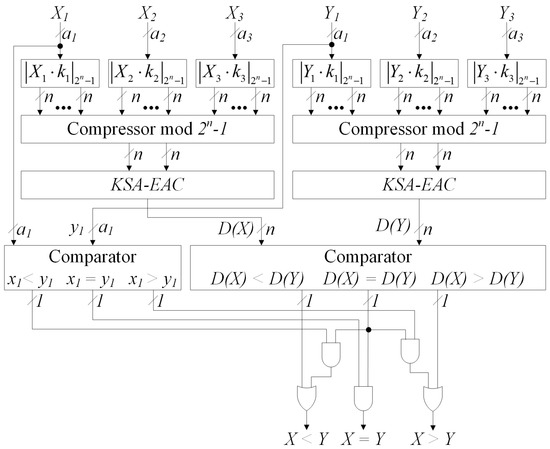
Figure 1.
Magnitude comparison circuit using the diagonal function (DF) of the form .
Figure 2 shows the reverse conversion circuit for RNS with the DF of the form . The bit-widths of the RNS moduli are denoted as . Multipliers by constants modulo , modulo compressor and KSA-EAC blocks are realized as in Figure 1. The rest of the blocks are implemented in standard binary form. The symbol denotes the bit-width of RNS range and symbol denotes the bit-width of the value . Division by is implemented as multiplication by multiplicative inverse modulo . The output of the circuit presented in Figure 2 is a group of most significant bits (MSBs) of the last KSA output. The reverse converter circuit for RNS with a DF of the form has a similar structure to that presented in Figure 2, with differences similar to the comparator described above.
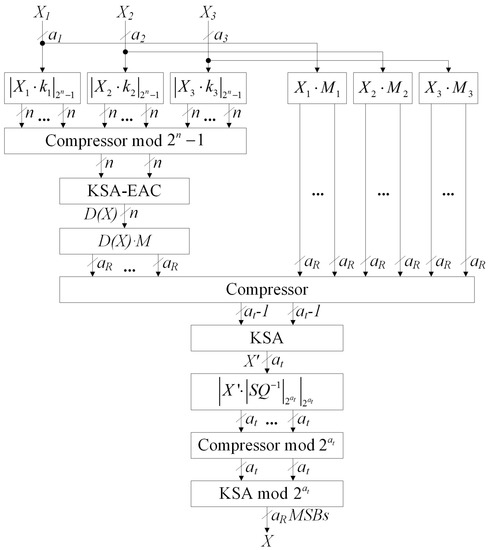
Figure 2.
Reverse conversion circuit for the residue number system (RNS) with a DF of the form .
Also, modeling was done to compare the proposed moduli sets with balanced RNS moduli sets. The following types of moduli sets were chosen for the simulation: [29,30], [31], [34], [35].
All simulated circuits were described in very high speed integrated circuit (VHSIC) hardware description language (VHDL). Hardware modeling was performed on Xilinx Artix 7 xc7a200tfbg484-2 in Vivado 2016.3 and the strategy of synthesis was highly area optimized. The modeling results are presented in Table 2, Table 3 and Table 4 and show time, hardware costs and the area·delay (A·D) metrics calculated as a product of delay by a number of look up tables (LUTs).

Table 2.
Modeling results of the circuit of magnitude comparison.

Table 3.
Modeling results of the circuit of reverse RNS to binary conversion.

Table 4.
Modeling results of magnitude comparison and reverse RNS to binary conversion for proposed and balanced moduli sets.
A simulation of magnitude comparison shows that for the moduli set, the method using CRTf works faster than the proposed method, and faster than the method using CRT. However, the proposed method uses fewer hardware resources than CRTf, and less than CRT. For , the circuit, based on CRTf, works faster than the circuit, which is based on the proposed method, and faster than the circuit which is based on CRT. Furthermore, the circuit, based on the proposed method, uses fewer hardware resources than CRTf method and less than CRT. For , the proposed method works faster than the method using CRTf, and faster than the method using CRT. Moreover, the proposed method uses fewer hardware resources than the method using CRTf, and two times fewer resources than the method using CRT. Thus, for the magnitude comparison operation, the proposed method reduces the consumption of hardware resources compared tp known methods. In addition, in the case of using the moduli set the proposed method also reduced the delay of the devices. Table 2 also demonstrates the advantages of the proposed method in A·D metrics and power consumption.
A simulation of reverse RNS to binary conversion shows that for the moduli set method using CRTf works faster than the proposed method, and faster than the method using CRT. Moreover, CRTf method uses fewer hardware resources than the proposed method and less than CRT. For , circuit, based on CRTf, works faster than the circuit based on the proposed method, and faster than circuit based on CRT. Furthermore, the circuit based on the proposed method uses fewer hardware resources than CRTf method and less than CRT. For , the method using CRTf works faster than the proposed method, and faster than the method using CRT. Moreover, it uses fewer hardware resources than the proposed method and fewer resources than the method using CRT. Therefore, the proposed method allows us to reduce hardware resources for the moduli set compared to known methods.
For the moduli set, the RNS dynamic range is equal to . Due to comparing the performance of the circuit using the proposed moduli set with a circuit using known common moduli sets, two balanced moduli sets were chosen: , [29,30] and , , [26], which are close to this dynamic range. Modeling of the magnitude comparison showed that the circuit using the proposed moduli set works faster than , moduli set and faster than , , moduli set. Moreover, the proposed moduli set uses times fewer hardware resources than , moduli set and less than , , moduli set. Hardware simulation of reverse RNS to binary conversion showed that using the proposed moduli set requires fewer time costs than the , moduli set and less than the , , moduli set. Although the proposed moduli set uses more hardware resources than , , moduli set, it uses less than the , moduli set.
For the proposed moduli set, the dynamic RNS range is equal to . For this dynamic range, two known balanced moduli sets were chosen:, [29,30] and , [34]. Modeling of magnitude comparison showed that circuit using proposed moduli set works faster than the , moduli set and faster than the , moduli set. In addition, the proposed moduli set uses fewer hardware resources than the , moduli set and less than the , moduli set. Hardware simulation of reverse RNS to binary conversion showed that using the proposed moduli set requires less time cost than the , moduli set and less than the , moduli set. Although the proposed moduli set uses more hardware resources than the , moduli set, it uses less than the , moduli set.
For the proposed moduli set, the dynamic range of RNS was equal to . For this dynamic range, two known balanced moduli sets were chosen: , , and , , [33]. Modeling of the magnitude comparison showed that the circuit using the proposed moduli set works faster than the , , moduli set and times faster than the , , moduli set. Although the proposed moduli set uses more hardware resources than the , , moduli set, it uses times less than the , , moduli set. Hardware simulation of reverse RNS to binary conversion showed that the using of the proposed moduli set requires fewer time costs than the , , moduli set and less than the , , moduli set. Although the proposed moduli set uses more hardware resources than the , , moduli set, it uses less than the , , moduli set.
Thus, in comparison to known balanced moduli sets, the proposed moduli sets reduce the delay of magnitude comparison and reverse conversion in devices. In case of operation magnitude comparison, using the proposed moduli sets, and , reduces the use of hardware resources in devices.
The experimentally obtained results showed that the approach developed in this paper allows us to improve two problem operations in the RNS: the comparison of numbers and reverse conversion. The proposed devices for such operations can be used in those applications of the RNS for which these operations are the most important, for example, in video processing systems, sorting networks, etc.
4. Discussion
The results obtained in Section 3 are summarized in Table 5. The main conclusion we can assume is that the RNS construction with all cases , , is principally possible. The cases and for RNS with one even module are easiest for practical implementation. All cases for RNS with all odd moduli are more complicated. However, among these cases, there is one particularly attractive option. As we have demonstrated, there is the possibility of RNS constructing with . This case requires the use of four odd RNS moduli.

Table 5.
The possibility of RNS constructing with a given sum of quotients (SQ) form.
According to the proposed construction method of RNS with a convenient form of DF, moduli sets with three and four moduli were chosen: , and . We performed the hardware simulation of magnitude comparison and reverse RNS to binary conversion using RNS with the presented moduli sets and using different approaches to perform the non-modulo comparison operation: the proposed method, method [18], and method [21]. The hardware simulation results of magnitude comparison show that, for three moduli, the use of the proposed method reduces hardware resources, and the use of method [21] reduces circuit delay. For four moduli, the proposed method reduces both time and hardware costs. The modeling of reverse RNS to binary conversion shows that method [21] works faster and requires fewer hardware resources than the others considered methods. Comparison of the simulation results of proposed moduli sets and balanced moduli sets shows that the use of the proposed moduli sets reduces circuit delay, although, in several cases, it required more hardware resources than balanced moduli sets.
5. Conclusions
The paper concerns the problem of RNS construction with convenient forms of DF. We propose several methods of RNS construction with SQ forms , and . The use of these forms of moduli allow for developing efficient methods of hardware implementation. We performed hardware implementation of magnitude comparison and reverse RNS to binary conversion using the proposed method, method [18] method [21]. A comparison of the implementation results shows that using the proposed method is effective for magnitude comparison operation, but for the reverse RNS to binary conversion operation, method [21] performs better modeling results than the proposed method and method [18]. In addition, according to the simulation results, the proposed moduli sets reduce circuit delay in comparison with balanced moduli sets, although, in several cases, require more hardware resources than balanced moduli sets.
The proposed method allows more efficient and problematic operations in RNS, such as sign detection, number comparison, and division, to be performed. It can be used in the development of video processing systems and customized signal processing units using RNS.
Author Contributions
Conceptualization, M.V.; Data curation, N.C.; Formal analysis, D.B.; Investigation, P.L., G.V. and D.K.; Methodology, N.S.; Project administration, P.L.; Resources, D.K. and D.B.; Software, P.L., G.V. and N.S.; Validation, M.V., N.C., P.L. and D.K.; Visualization, G.V., N.S., D.B.; Writing—original draft, M.V. and N.C.; Writing—review & editing, D.K., and P.L.
Funding
The research is supported by the grant of the Russian Science Foundation (Project No. 19-19-00566).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akkal, M.; Siy, P. A new mixed radix conversion algorithm MRC-II. J. Syst. Archit. 2007, 53, 577–586. [Google Scholar] [CrossRef]
- Ramirez, J.; Garcia, A.; Lopez-Buedo, S.; Lloris, A. RNS-enabled digital signal processor design. Electron. Lett. 2002, 38, 266–268. [Google Scholar] [CrossRef]
- Chang, C.; Molahosseini, A.S.; Zarandi, A.A.E.; Tay, T.F. Residue number systems: A new paradigm to datapath optimization for low-power and high-performance digital signal processing applications. IEEE Circuits Syst. Mag. 2015, 15, 26–44. [Google Scholar] [CrossRef]
- Kaplun, D.; Butusov, D.; Ostrovskii, V.; Veligosha, A.; Gulvanskii, V. Optimization of the FIR filter structure in finite residue field algebra. Electronics 2018, 7, 372. [Google Scholar] [CrossRef]
- Esmaeildoust, M.; Schinianakis, D.; Javashi, H.; Stouraitis, T.; Navi, K. Efficient RNS implementation of elliptic curve point multiplication GF(p). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 21, 1545–1549. [Google Scholar] [CrossRef]
- Bajard, J.-C.; Imbert, L. A full RNS implementation of RSA. IEEE Trans. Comput. 2004, 53, 769–774. [Google Scholar] [CrossRef]
- Sousa, L.; Antao, S.; Martins, P. Combining residue arithmetic to design efficient cryptographic circuits and systems. IEEE Circuits Syst. Mag. 2016, 16, 6–32. [Google Scholar] [CrossRef]
- Chervyakov, N.I.; Lyakhov, P.A.; Babenko, M.G. Digital filtering of images in a residue number system using finite-field wavelets. Autom. Control Comput. Sci. 2014, 48, 180–189. [Google Scholar] [CrossRef]
- Kar, A.; Sur, K.; Godara, S.; Basak, S.; Mukherjee, D.; Sukla, A.S.; Das, R.; Choudhury, R. Security in cloud storage: An enhanced technique of data storage in cloud using RNS. In Proceedings of the IEEE 7th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 20–22 October 2016; pp. 1–4. [Google Scholar]
- Navi, K.; Esmaeildoust, M.; Molahosseini, A.S. A general reverse converter architecture with low complexity and high performance. IEICE Trans. Inf. Syst. 2011, 94, 264–273. [Google Scholar] [CrossRef]
- Milanezi Junior, J.; da Costa, J.P.C.L.; Römer, F.; Miranda, R.K.; Marinho, M.A.M.; Del Galdo, G. M-estimator based Chinese remainder theorem with few remainders using a kroenecker product based mapping vector. Digit. Signal Process. 2019, 87, 60–74. [Google Scholar] [CrossRef]
- Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Gerardi, L.; Re, M.; Campolo, G.; Cascone, D. A new electric encoder position estimator based on the Chinese Remainder Theorem for the CMG performance improvements. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), New York, NY, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Chervyakov, N.I.; Lyakhov, P.A.; Valueva, M.V. Increasing of convolutional neural network performance using residue number system. In Proceedings of the 2017 IEEE International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), New York, NY, USA, 18–22 September 2017; pp. 135–140. [Google Scholar]
- Cardarilli, G.C.; Del Re, A.; Nannarelli, A.; Re, M. Impact of RNS coding overhead on FIR filters performance. In Proceedings of the 2007 Conference Record of the Forty-First Asilomar Conference on Signals, Systems and Computers, New York, NY, USA, 4–7 November 2007; pp. 1426–1429. [Google Scholar]
- Chang, C.; Lee, W.; Liu, Y.; Goi, B.; Phan, R.C.-W. Signature gateway: Offloading signature generation to IoT gateway accelerated by GPU. IEEE Internet Things J. 2019, 6, 4448–4461. [Google Scholar] [CrossRef]
- Chervyakov, N.I.; Babenko, M.G.; Lyakhov, P.A.; Lavrinenko, I.N. An approximate method for comparing modular numbers and its application to the division of numbers in residue number systems. Cybern. Syst. Anal. 2014, 50, 977–984. [Google Scholar] [CrossRef]
- Selvam, R.; Tyagi, A. Power side channel resistance of RNS secure logic. In Proceedings of the 2018 31st International Conference on VLSI Design and 2018 17th International Conference on Embedded Systems (VLSID), New York, NY, USA, 6–10 January 2018; pp. 143–148. [Google Scholar]
- Mohan, P.V.A. Residue Number Systems: Theory and Applications; Birkhauser: Basel, Switzerland, 2016; ISBN 9783319413853. [Google Scholar]
- Gonnella, J. The application of core functions to residue number system. IEEE Trans. Signal Process. 1991, 39, 69–75. [Google Scholar] [CrossRef]
- Akushskii, I.J.; Burcev, V.M.; Pak, I.T. A new positional characteristic of nonpositional codes and its applications. Coding Theory Optim. Complex Syst. 1977, 8–16. [Google Scholar]
- Matos, R.; Paludo, R.; Chervyakov, N.; Lyakhov, P.A.; Pettenghi, H. Efficient implementation of modular multiplication by constants applied to RNS reverse converters. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Dimauro, G.; Impedovo, S.; Pirlo, G. A new technique for fast number comparison in the residue number system. IEEE Trans. Comput. 1993, 42, 608–612. [Google Scholar] [CrossRef]
- Dimauro, G.; Impedovo, S.; Pirlo, G.; Salzo, A. RNS architectures for the implementation of the ‘diagonal function’. Inf. Process. Lett. 2000, 73, 189–198. [Google Scholar] [CrossRef]
- Mohan, P.V.A. RNS to binary conversion using diagonal function and pirlo and impedovo monotonic function. Circuits Syst. Signal Process. 2015, 35, 1–14. [Google Scholar] [CrossRef]
- Piestrak, S.J. A note on RNS architectures for the implementation of the diagonal function. Inf. Process. Lett. 2015, 115, 453–457. [Google Scholar] [CrossRef]
- Kalampoukas, L.; Nikolos, D.; Efstathiou, C.; Vergos, H.T.; Kalamatianos, J. High-speed parallel-prefix modulo 2n − 1 Adders. IEEE Trans. Comput. 2000, 49, 673–680. [Google Scholar] [CrossRef]
- Efstathiou, C.; Vergos, H.T.; Nikolos, D. Fast parallel-prefix Modulo 2n + 1 Adders. IEEE Trans. Comput. 2004, 53, 1211–1216. [Google Scholar] [CrossRef]
- Vergos, H.T.; Dimitrakopoulos, G. On Modulo 2n + 1 Adder design. IEEE Trans. Comput. 2012, 61, 173–186. [Google Scholar] [CrossRef]
- Chaves, R.; Sousa, L. Improving residue number system multiplication with more balanced moduli sets and enhanced modular arithmetic structures. IET Comput. Digit. Tech. 2007, 1, 472. [Google Scholar] [CrossRef]
- Jaberipur, G.; Nejati, S. Balanced minimal latency RNS addition for moduli set {2n − 1, 2n, 2n + 1}. In Proceedings of the 18th International Conference on Systems, Signals and Image Processing, Sarajevo, Bosnia and Herzegovina, 16–18 June 2011; pp. 1–7. [Google Scholar]
- Hiasat, A. Efficient RNS Scalers for the extended three-moduli set {2n − 1, 2n+p, 2n + 1}. IEEE Trans. Comput. 2017, 66, 1253–1260. [Google Scholar] [CrossRef]
- Patronik, P.; Piestrak, S.J. Design of reverse converters for the new RNS moduli set {2n + 1, 2n − 1, 2n, 2n−1 + 1} (n odd). IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 3436–3449. [Google Scholar] [CrossRef]
- Hiasat, A. A reverse converter and sign detectors for an extended RNS five-moduli set. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 111–121. [Google Scholar] [CrossRef]
- Mohan, P.V.A.; Premkumar, A.B. RNS-to-Binary converters for two four-moduli sets {2n + 1, 2n − 1, 2n, 2n−1 − 1} and {2n + 1, 2n − 1, 2n, 2n+1 + 1}. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 1245–1254. [Google Scholar] [CrossRef]
- Kumar, S.; Chang, C.-H.; Tay, T.F. New algorithm for signed integer comparison in {2n+k, 2n − 1, 2n + 1, 2n±1 − 1} and its efficient hardware implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1481–1493. [Google Scholar] [CrossRef]
- Kumar, S.; Chang, C.-H. A scaling-assisted signed integer comparator for the balanced five-moduli set RNS {2n − 1, 2n, 2n + 1, 2n+1 − 1, 2n−1 − 1}. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 3521–3533. [Google Scholar] [CrossRef]
- Skavantzos, A.; Abdallah, M.; Stouraitis, T.; Schinianakis, D. Design of a balanced 8-modulus RNS. In Proceedings of the 2009 16th IEEE International Conference on Electronics, Circuits and Systems (ICECS 2009), New York, NY, USA, 13–16 December 2009; pp. 61–64. [Google Scholar]
- Vayalil, N.C.; Paul, M.; Kong, Y. A residue number system hardware design of fast-search variable-motion-estimation accelerator for HEVC/H.265. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 572–581. [Google Scholar] [CrossRef]
- Cheng, S.W. A high-speed magnitude comparator with small transistor count. In Proceedings of the 10th IEEE International Conference on Electronics, Circuits and Systems, 2003 (ICECS 2003), New York, NY, USA, 14–17 December 2003; pp. 1168–1171. [Google Scholar]
- Chervyakov, N.I.; Lyakhov, P.A.; Kalita, D.I.; Shulzhenko, K.S. Effect of RNS dynamic range on grayscale images filtering. In Proceedings of the XV International Symposium Problems of Redundancy in Information and Control Systems (REDUNDANCY), St. Petersburg, Russia, 26–29 September 2016; pp. 33–37. [Google Scholar]
- Molahosseini, A.S.; Sorouri, S.; Zarandi, A.A.E. Research challenges in next-generation residue number system architectures. In Proceedings of the IEEE 7th International Conference on Computer Science & Education (ICCSE), Melbourne, VIC, Australia, 14–17 July 2012; pp. 1658–1661. [Google Scholar]
- Parhami, B. Computer Arithmetic: Algorithms and Hardware Designs; Oxford University Press: Oxford, UK, 2010; ISBN 9780195328486. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).