1. Introduction
Existing distribution systems are evolving towards smart distribution grids due to the emergence of distributed generation and the need for environmentally friendly, flexible, and reliable electric power. The smart distribution grid requires an appropriate bidirectional communication system. Thus, various communication technologies have been compared, including optical fiber, wireless, power-line communication (PLC), and so forth. Among them, PLC has the unique advantages of low cost and wide coverage, which makes it promising for use in constructing smart distribution grids [
1,
2,
3].
However, since power-line networks have been traditionally designed to provide channels for power transmission, they often have complex network structures and numerous branches, especially in medium-voltage (MV) distribution networks. These factors result in signal reflections at junctions and mismatched line ends, which directly influence the performance of MV-PLC. Hence, the calculations and analyses of the frequency response characteristics (FRCs) of MV distribution networks are fundamental for PLC because they help to optimize PLC equipment and network designs [
4,
5].
Generally, the methods to model the FRCs of distribution networks can be categorized as top–bottom and bottom–top methods. The former depends on exhausted measurements to obtain the multipath model for a certain scenario [
6,
7,
8]. This method is relatively simple but lacks the ability to predict the FRCs of distribution networks; thus, its applications are limited. The latter is based on two-conductor or multiconductor transmission line (MTL) theory. This method can predict channel characteristics and comprehensively evaluate the influences of network structures, line types, and signal coupling modes on PLC data transmission to improve the performance of PLC systems.
The most widespread bottom-top method is to calculate the channel transfer function based on the transmission matrix [
9,
10,
11]. In this method, the distribution network is divided into several substructures, and their transmission matrices are calculated. Then, the overall transmission matrix is obtained by the sequential multiplication of these divided transmission matrices. This method is suitable for radial distribution networks but cannot be applied to ring distribution networks. Set against that, there is a growing trend of using ring distribution networks due to the improving requirements of power reliability [
12,
13]. Moreover, for a large-scale distribution network with many nodes, this method needs the distribution network to be repartitioned each time to get the FRC of each node, which is highly inconvenient for the calculations.
Another popular alternative is using nodal analysis [
14,
15], in which the power-lines, loads, and junctions are all represented by the admittance matrices. This method can be applied to distribution networks of arbitrary topologies and is appropriate to address the FRCs of large-scale distribution networks. However, this method requires that the admittance matrix of each part of the distribution network has the same dimension, which is not always true. Although the power-lines studied in recent works are mostly three-phase power-lines containing three conductors, power-lines containing more conductors are ubiquitous. For example, the MV overhead power-lines may be of single-circuit-line or twin-circuit-line configuration, and the latter contains six conductors. Also, in underground cable systems, there are shields except for core conductors, and mutual inductances exist between them. Consequently, for a hybrid network containing power-lines of different total conductor numbers, it may be necessary to address the interconnections of the power-line channels with different total conductor numbers, which leads to the failure of the admittance-matrix-based method. In [
16,
17,
18], scattering-matrix-based methods were proposed to handle the interconnections of overhead power-lines with different configurations and the interconnections of underground cables with different inner conductors.
In this study, we focused on the FRCs of distribution networks with special consideration of the scenario where the single-circuit overhead lines and the underground cables join at junctions; simultaneously, the shields of underground cables are grounded at the junctions for safe operation. A traditional approximate method for this problem is to assume that the grounding points have zero potential and then eliminate the grounded conductors by matrix operations so that the FRCs can be obtained by the abovementioned common bottom–top methods [
19,
20]. However, such an assumption is distinct from realistic situations, where the grounding impedances are often nonzero. Moreover, several studies [
21,
22,
23,
24] have proved that the grounding of partial conductors will lead to resonance, which not only affects the frequency responses of grounded conductors but also that of ungrounded conductors. These effects are related to the grounding impedances. Further, this method cannot provide the FRCs of shields, which are of concern in studies on the natural modes [
25]. In fact, there are similar issues for indoor power-line channels. In [
26], the imperfect grounding conditions of indoor power-lines and their impacts on PLC were considered, and the grounded indoor power-line channel was modelled based on modal transformations and transmission matrices. This method helps with the further analysis of indoor PLC channel characteristics. However, for ring distribution networks and large-scale distribution networks, it is inappropriate because of the use of transmission matrices, which has been shown above. Therefore, an effective method to calculate the FRCs of various hybrid distribution networks should be developed considering imperfect grounding conditions and the interconnection of power-line channels with different total conductor numbers.
To this end, we devised a new method to calculate the FRCs of MV distribution networks based on the Baum-Liu-Tesche (BLT) equation originating in the electromagnetic compatibility (EMC) field. The power-line propagation and node scattering characteristics of the entire distribution network were analyzed to express the frequency responses of nodes with a simple binary function. The method can be applied to distribution networks of arbitrary topologies, and the overall scattering matrix allows it to address the interconnection of power-line channels with different total conductor numbers.
The remainder of this paper is organized as follows.
Section 2 presents the fundamental forms of the overall propagation matrix and overall scattering matrix for a two-node network with lumped excitation. In
Section 3, these overall matrix representations are extended to common MV hybrid distribution networks, and the binary function is set up to give the voltage-frequency responses of nodes. The numerical results of the FRCs under different network configurations and the validity of the proposed method are discussed in
Section 4. A conclusion is given in
Section 5.
2. BLT Equation with Lumped Excitation
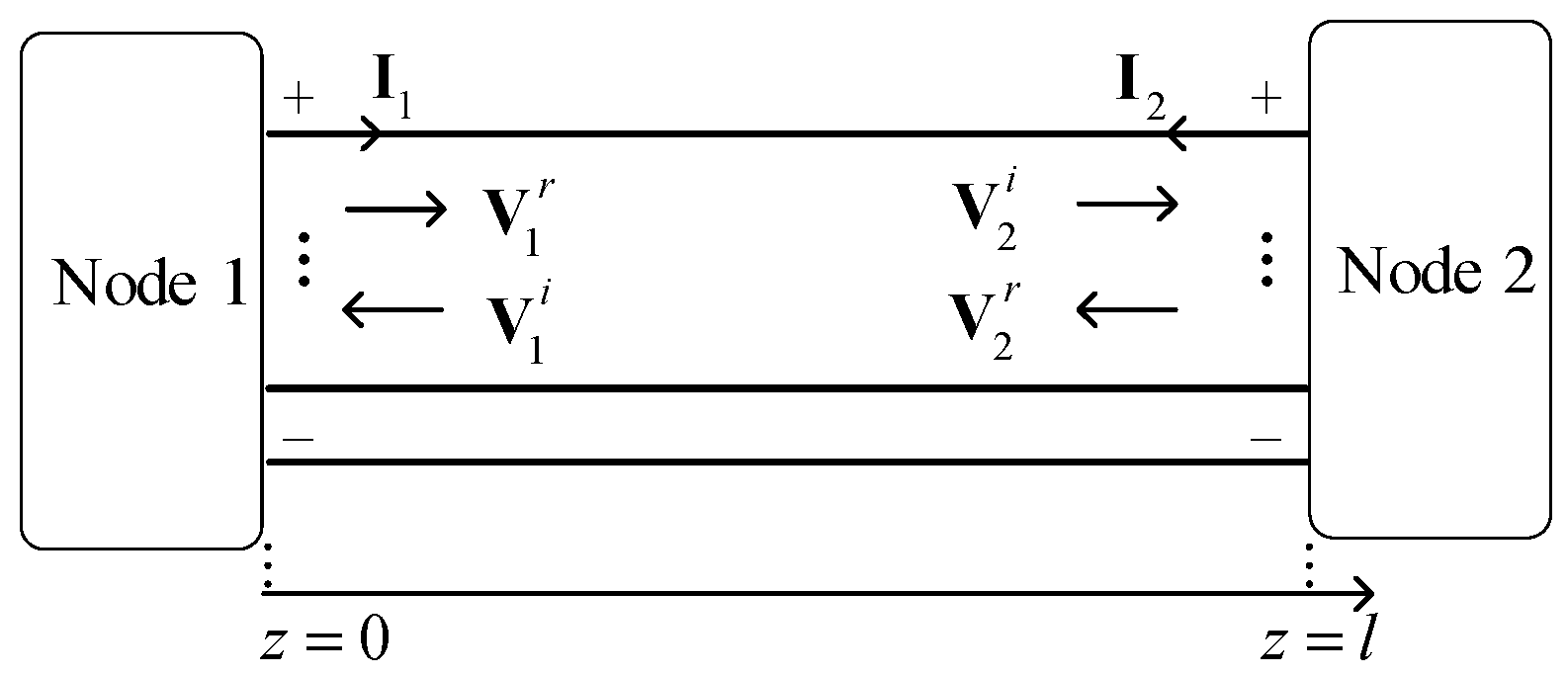
For MV-PLC networks, the lumped carrier signal sources are located at specific nodes of the MV distribution network, and the FRCs of other nodes need to be solved. In this paper, this kind of problem was solved based on the BLT equation. First, the simplest two-node transmission line network (
Figure 1) was studied, and the BLT equation with lumped excitation was given by combining MTL theory and the general boundary conditions.
There are
n + 1 transmission lines in
Figure 1, and
l denotes the lengths of the transmission lines. The bottom conductor refers to the ground, which has zero potential, and the other conductors are the power-lines. The positive directions of currents flow out from node 1 or 2. The per unit length (p.u.l.) impedance matrix and admittance matrix of the MTL are denoted by
Z and
Y, respectively.
According to MTL theory [
27], the
voltage phasor vector
V and
current phasor vector
I can be expressed as
where
z denotes the position at the conductors. The
matrices
and
denote the forward and backward modal voltage vectors, respectively. The
matrix
denotes the eigenvector matrix of
ZY and is called the modal transformation matrix. The
diagonal matrix
denotes the eigenvalue matrix of
ZY, and its
n diagonal elements are the propagation constants of
n modes. The
matrix
denotes the characteristic admittance matrix of the MTL and
.
In the following, the voltage vector at the coordinate
is represented as
, and the voltage vector at the coordinate
is represented as
.
and
can be decomposed into incident and reflected vectors according to Equation (1), such that
where
and
denote the incident vectors, and
and
denote the reflected vectors. These components have the following relationship:
where
and
denote the reflected and incident voltage vectors of two nodes, respectively.
denotes the transpose of a matrix.
denotes the propagation matrix of the MTL and is defined by
with entries
To solve the four voltage components in Equation (2), another set of equations representing the relationship between incident vectors and reflected vectors should be obtained through the boundary conditions.
Applying Kirchhoff’s law and the volt–ampere relationships, the boundary condition of node 1 can be expressed as
where
and
denote the coefficient matrices of the voltage and current vectors of node 1.
denotes the lumped source vector of node 1, which is either a voltage source vector or a current source vector.
Similar to the first equation of Equation (2), the current of node 1 can also be decomposed into two components, such that
Combining Equations (6) and (7),
can be expressed in terms of
as
where
denotes the scattering matrix of node 1, and
is the voltage source vector of node 1. They are determined through
The processes of Equations (7)–(10) are also applicable to node 2. Hence,
and
have the following relationship:
where
denotes the voltage source vector of two nodes.
denotes the node scattering matrix of the MTL network and is defined by
Combining Equations (3) and (11), the BLT equation describing the resulting voltage vector
can be put in the simple form
where
denotes the voltage vector of two nodes.
is the
identity matrix.
3. Frequency Responses of Distribution Networks
Equation (13) indicates that it is necessary to obtain the propagation matrix and scattering matrix of the entire network before establishing the function of the resulting voltage vector. However, as opposed to the situation depicted in
Figure 1, a typical MV distribution network has more nodes and more complex branches. The common topology of an MV distribution network includes the radial type, ring type, and mesh type.
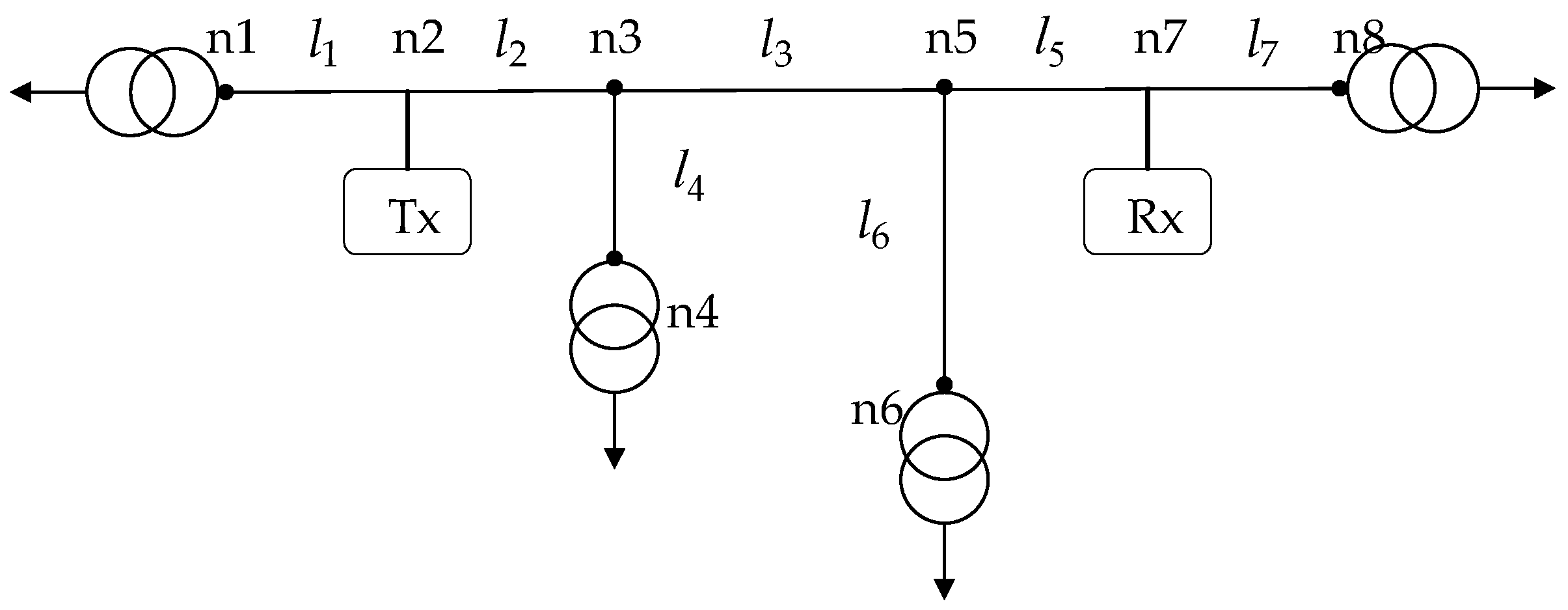
A simple radial MV distribution network is illustrated in
Figure 2. It can be found that multiple power-lines join at nodes 3 and 5. For this reason, the nodes are classified into the terminal node and the interconnection node [
27]. The former is only connected with one power-line, and the latter is connected with multiple power-lines. The power-line is hereinafter referred to as the tube.
For tube i () connected to node k (), the voltage and current vectors of the two ends are denoted by and , respectively; the corresponding voltage incident and reflected components are denoted by and , respectively; and the corresponding current components are denoted by and , respectively. Obviously, there are only two nodes connected with one tube i, and their corresponding subscripts are and . There may be tubes connected to node k, and their corresponding subscripts are , , …, . For terminal nodes, , and for interconnected nodes, .
3.1. Overall Tube Propagation Matrix
It can be found from Equations (4) and (5) that the propagation matrix of the entire network depends on the p.u.l. impedance and admittance matrices of the power-lines. So, before the overall tube propagation matrix, two type power-line geometries are given here, and the parameter matrices are discussed.
3.1.1. Parameter Matrices of MV Power-Lines
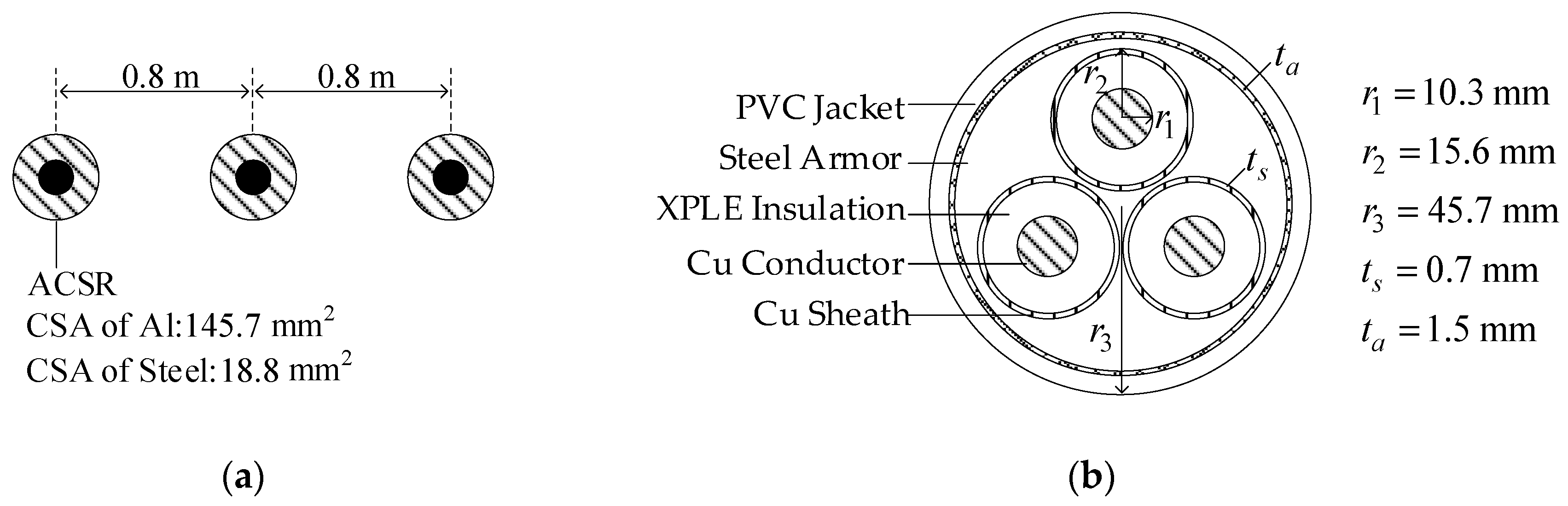
The configurations of the examined MV overhead line and underground cable are illustrated in
Figure 3. The overhead line is aluminum conductor steel reinforced (ACSR), located 10 m above the ground. Its cross-sectional areas (CSA) of Al and steel are annotated in
Figure 3a. The underground cable is a pipe-type cross-linked polyethylene (XPLE) insulated cable, buried 3 m deep below the ground. The radiuses
r and thicknesses
t are annotated in
Figure 3b.
For the overhead line, the p.u.l. impedance matrix
and admittance matrix
can be expressed in the form
where
denotes the self-impedance of a phase conductor,
and
denote the mutual impedances between two phase conductors,
denotes the self-admittance of a phase conductor, and
and
denote the mutual admittances between two phase conductors.
For the underground cable, the mode propagating via the steel armor and earth is negligible [
12], so the grounded armor was taken as the reference of voltage. Therefore, the underground cable is considered to be a system containing three subsystems. Each subsystem is composed of the core, the insulation, and the shield. The p.u.l. impedance matrix
and admittance matrix
can be expressed in the form
where
and
denote the impedance matrix and admittance matrix of a subsystem, respectively, and
and
denote the mutual impedance matrix and mutual admittance matrix of two subsystems, respectively. The impedances and admittances matrices in Equation (15) were analyzed in [
28,
29,
30]. Each conductor has its own self-impedance, and there are mutual impedances between any two conductors. The mutual admittances exist only between the directly adjacent conductors. Further, the aforementioned matrices can be expressed as
where
and
denote the self-impedances of the core and shield, respectively;
denotes the mutual impedance between the core and shield;
denotes the mutual impedance between two subsystems;
and
denote the self-admittances of the core and shield, respectively;
denotes the mutual admittance between the core and shield; and
denotes the mutual admittance between two subsystems.
The impedances and admittances in Equations (14), (16), and (17) can be obtained by the line constants routines and cable constants routines of the ATP-EMTP software (Version 6.0, NTNU/SINTFE, Trondheim, Norway, 2015), which was adopted in this study.
3.1.2. Overall Tube Propagation Matrix of Distribution Networks
The tube propagation characteristic of the entire distribution network is given by sorting Equation (3) in the ascending order of the tube number, in that the voltage vectors at both ends of a tube are at adjacent positions, as shown below:
where
where
and
denote the overall reflected and incident voltage vectors of all nodes sorted in the ascending order of the tube number, respectively. The square matrix
denotes the overall propagation matrix of the entire distribution network. Its order is
, where
and
denote the total number of overhead lines and underground cables in the distribution network, respectively.
is determined by the p.u.l. impedance and admittance matrices of the tubes, which vary with the frequency; thus,
is frequency dependent. The tube propagation matrix in Equation (18) establishes the relationship between the incident and reflected voltage components in the entire distribution network. However, it is insufficient to solve these components, and another set of equations representing the relationship between the incident and reflected components are essential, as shown below.
3.2. Overall Node Scattering Matrix
Similar to the procedures in Equations (6)–(12), the overall node scattering matrix of the entire network is introduced in the following through the boundary conditions. The overall node scattering matrix provides another set of equations between incident and reflected components.
In MV distribution networks, the boundary conditions of terminal or interconnection nodes can be obtained by the following processes (taking node
k as an example): Firstly, the total number of conductors connected with node
k is determined. Then, equations are listed to describe the relationships of voltage and current of each conductor, applying Kirchhoff’s law and the volt-ampere relationships. The total number of equations is equal to the number of conductors connected to node
k. Lastly, all of the equations are expressed in the matrix form as
It can be found that Equation (6) is the simplified form of Equation (22) when . Similarly, and denote the voltage and current vectors of node k. and denote the corresponding coefficient matrices, and denotes the lumped source vector of node k.
3.2.1. Boundary Conditions of Distribution Transformers
In MV distribution networks, distribution transformers often play the role of terminal nodes. The voltage vector
and the current vector
of the MV side of the distribution transformer have the following relationship:
where
denotes the input impedance matrix seen from the MV side of the distribution transformer. The current is positive when it flows out from the transformer and the potential of the ground is zero. Comparing Equations (22) and (23), it can be found that
,
, and
, where
is an identity matrix, and its order is identical to the total number of conductors connected to the distribution transformer.
3.2.2. Boundary Conditions of Power-Line Junctions
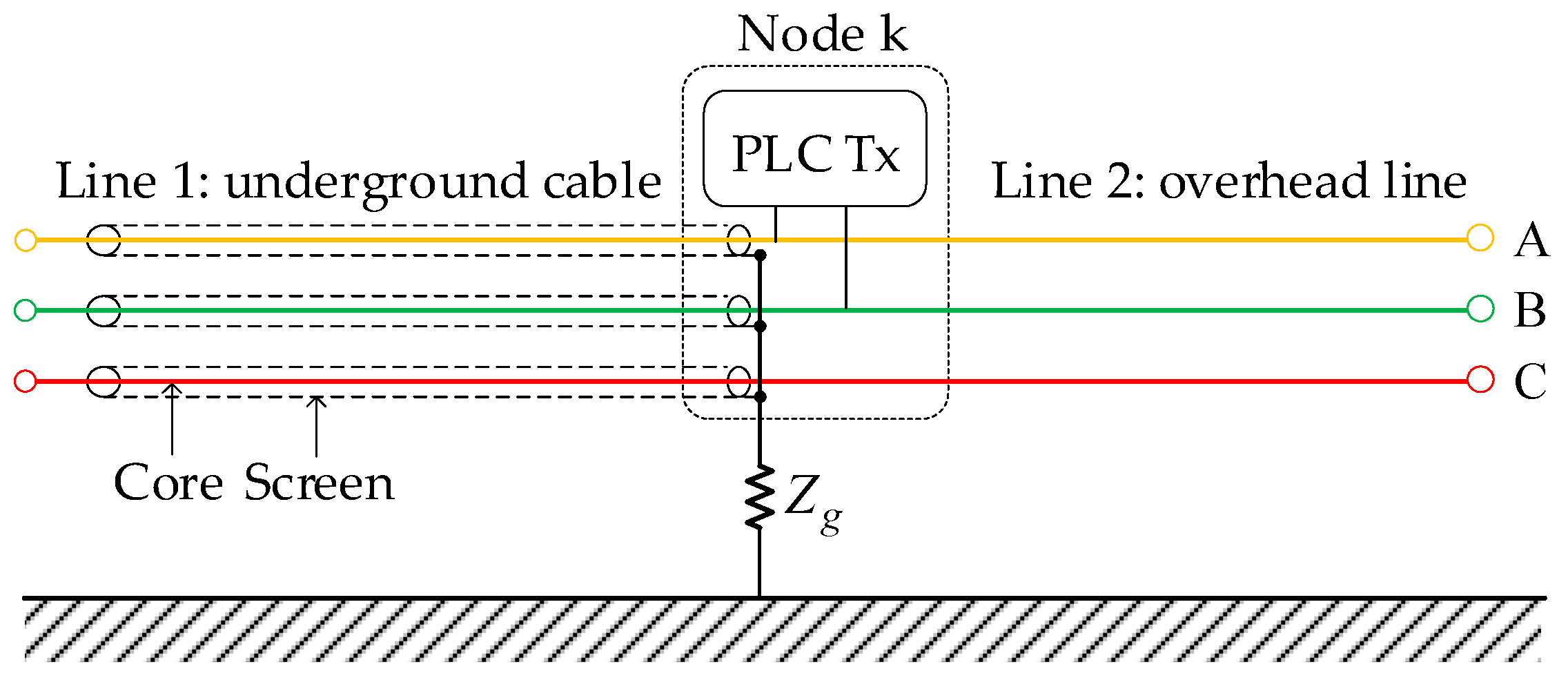
There are many junctions in MV distribution networks due to the branches, which worsen the channel characteristics of PLC. Here, a typical case is illustrated in
Figure 4, where the underground cable and overhead line join at node
k with a PLC transmitter (Tx). The coupling mode is A phase core to B phase core (PP) mode. The internal impedance and the equivalent voltage source of the transmitter are denoted by
and
.
The positive direction is the same as that defined in Equation (23), and the voltage and current relationships are
where
, and superscripts
and
are reminders of the core and shield of underground cables’
phase, respectively. The coefficient matrices describing the connection relationships of the interconnected node can be obtained from Equations (24) and (25). For example,
3.2.3. Overall Node Scattering Matrix of Distribution Networks
After obtaining the boundary conditions of node
k in the form of Equation (22), similar to the processes in Equations (6)–(8), the scattering matrix of node
k can be obtained to describe the relationships between the reflected and incident components:
where
where
and
denote the reflected and incident voltage vectors of node
k, respectively;
denotes the scattering matrix of node
k; and
denotes the voltage source vector of node
k. In Equations (32) and (33),
where
denotes the characteristic admittance matrix of tube
.
Since the node scattering matrix is related to the characteristic admittance matrices of the tubes connected to the node, which vary with the frequency, the node scattering matrix is frequency dependent. By sorting Equation (29) in the ascending order of the node number, the overall node scattering characteristics of the entire distribution network are given by
where
where
and
denote the overall reflected and incident voltage vectors of all nodes sorted by the node number, respectively. The square matrix
denotes the overall scattering matrix of all nodes in the distribution network. Its order is 6
Nol + 12
Nuc, the same as the order of the overall tube propagation matrix in Equation (18), owing to the fact that the differences in the orders of the node voltages do not affect their total number.
denotes the overall voltage source vector of the entire distribution network.
The overall node scattering matrix establishes a relationship between all of the reflected and incident voltage components in the distribution network and forms a complete description together with the aforementioned overall tube propagation matrix, uniquely determining all reflected and incident voltage components in the entire MV distribution network.
3.3. Frequency Response of Distribution Networks
Based on Equations (18) and (37), the FRCs of distribution networks can be obtained. However, the overall reflected and incident vectors in the two equations are not consistent. To facilitate the calculation, Equation (18) needs to be rearranged in the ascending order of the node number. Thus, Equation (18) is rewritten as
where
and
are the same as that in Equations (38) and (39).
denotes the overall propagation matrix of all nodes sorted by the node number. It can be built through the following principle: each row of
has only one submatrix
, of which the column coordinate is determined by the row coordinate of the other node connected to the same tube
i. For the distribution network depicted in
Figure 2, the specific form of Equation (41) is given in Equation (42). Taking the third row as an example, the corresponding reflected voltage vector is
, implying the tube number is 2, so there is a submatrix
in the third row of
. At the same time, another reflected voltage vector with the same tube number is
, which is located in the fourth row. Therefore, there is a submatrix
in the third row and the fourth column of
:
By sorting properly, the overall tube propagation matrix in Equation (41) and the overall node scattering matrix in Equation (37) correspond to the same overall voltage vectors. Therefore, under the lumped excitation, the voltage responses of all nodes in MV distribution networks have the same form as that in Equation (13):
where
denotes the resulting voltage vector of all nodes in the network. It is arranged in the ascending order of the node number.
is an identity matrix of the order
.
After determining the reference potential (the ground or one-phase conductor), the voltage of Tx (assumed as
) and the voltage to be calculated (assumed as
) can be obtained from Equation (43). So, the transfer function is
Then, it is easy to obtain the voltage amplitude-frequency response and phase-frequency response of each node in the distribution network.
4. Method Validation and Discussion
To validate the proposed method, the FRCs of the radial distribution network in
Figure 2 were investigated, where
. The power-line Sections 1–3, 5 and 7 were overhead lines, and the power-line Sections 4 and 6 were underground cable branches. Their configurations and parameters were the same as those depicted in
Figure 3, and their p.u.l. impedance matrices and admittance matrices were calculated using the ATP-EMTP software. The grounding impedances of the underground cables’ shields were resistances of 2 Ω. The input impedance matrices of the distribution transformers were obtained based on the measurement data in [
31]. Both the transmitter and receiver had internal impedances of 50 Ω, and they were coupled to the power-lines with PP mode (A phase core to B phase core coupling mode) or PG mode (A phase core to ground coupling mode). The transmitter was located at node 2.
In fact, there is an intuitive method to approximate transmission line networks. In the approximation method, long transmission lines are divided into electrically short line fragments at the frequencies of interest so that each fragment can be represented with lumped-π cells, and the whole transmission line network can be represented by the cascaded lumped-π cells [
15,
27]. The lumped-π cells are easy to implement through the resistances, inductances, and capacitances under laboratory conditions. Thus, this method was used to model the MV power-line networks and to validate the proposed method.
The FRCs of the distribution network in
Figure 2 were calculated and measured over the frequency of 10–500 kHz, which was sampled into 246 frequency points with a sample interval of 2 kHz. In measurements, the distribution network was modeled in the laboratory. Each power-line section was represented by 40 cascaded lumped-π cells, which were welded using lumped parameter components. The parameters of π circuits were calculated by the p.u.l. parameters and the cable lengths. The distribution transformers were modeled by the lumped electrical networks according to the measured impedance parameters in [
31]. The signal generator used was the AFG 1062 ( Tektronix, Johnston, OH, USA) arbitrary function generator, and the TBS 1152B (Tektronix, Johnston, OH, USA) was used to measure the signal voltages of nodes.
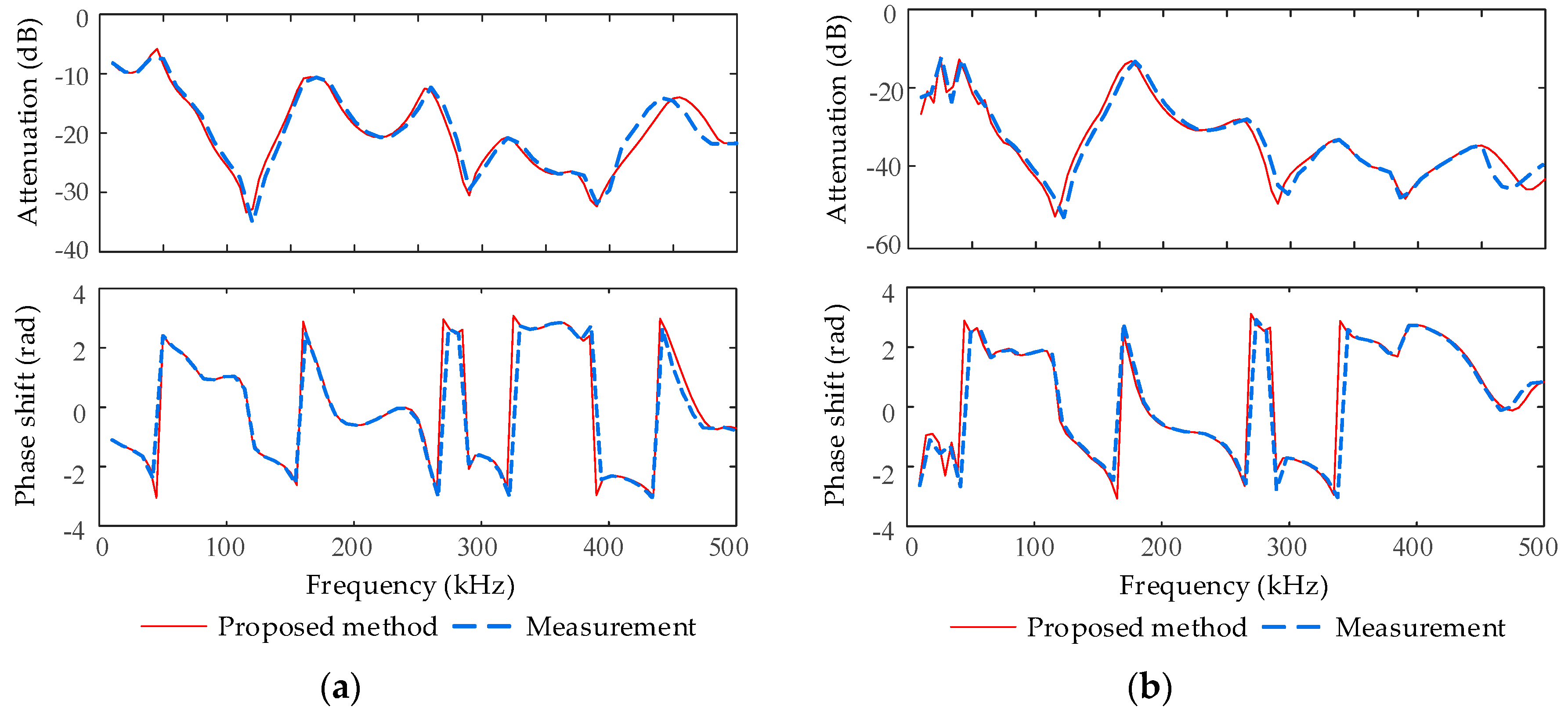
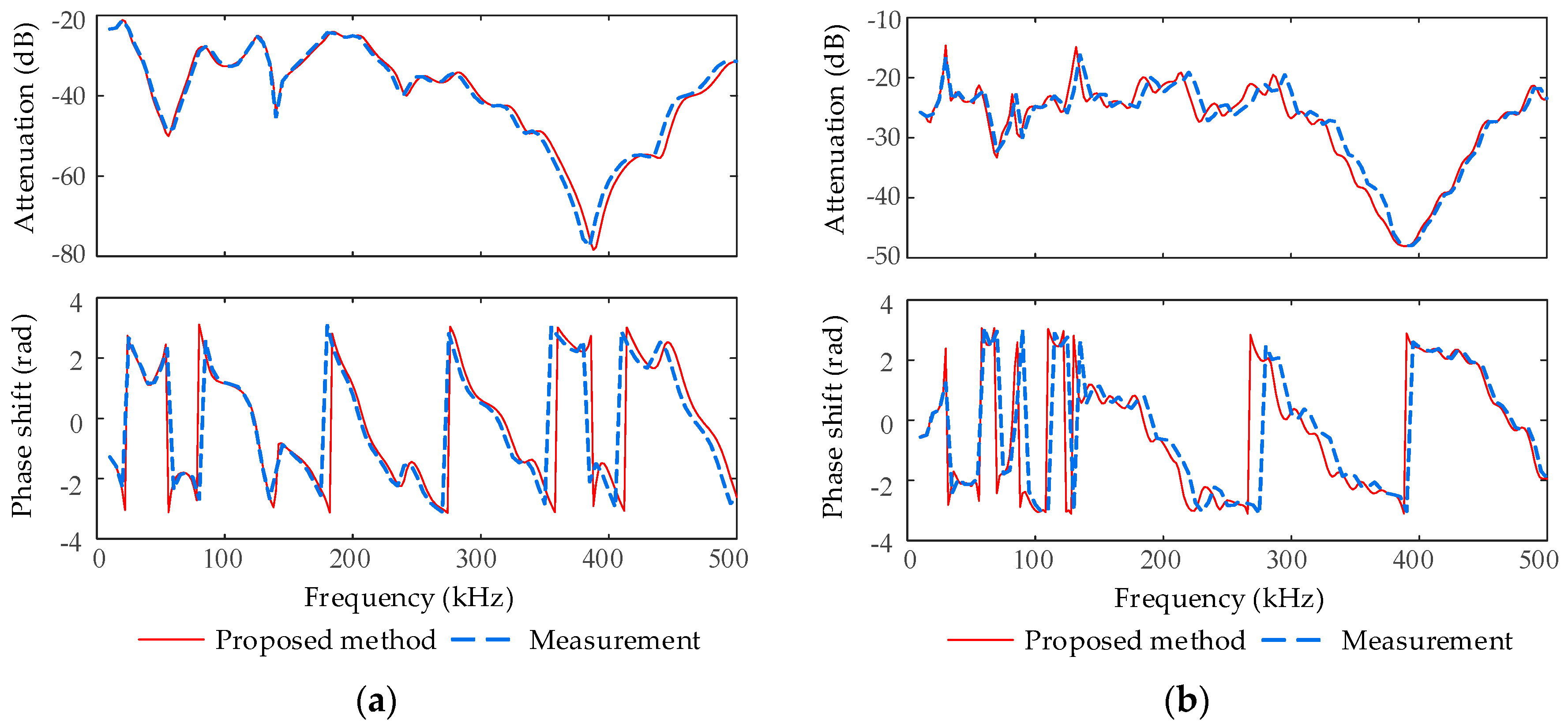
For node 7 in
Figure 2,
Figure 5 presents the calculated and measured results of FRCs. It can be observed that the FRCs predicted by the proposed method matched well with the measured results, which validated the proposed method.
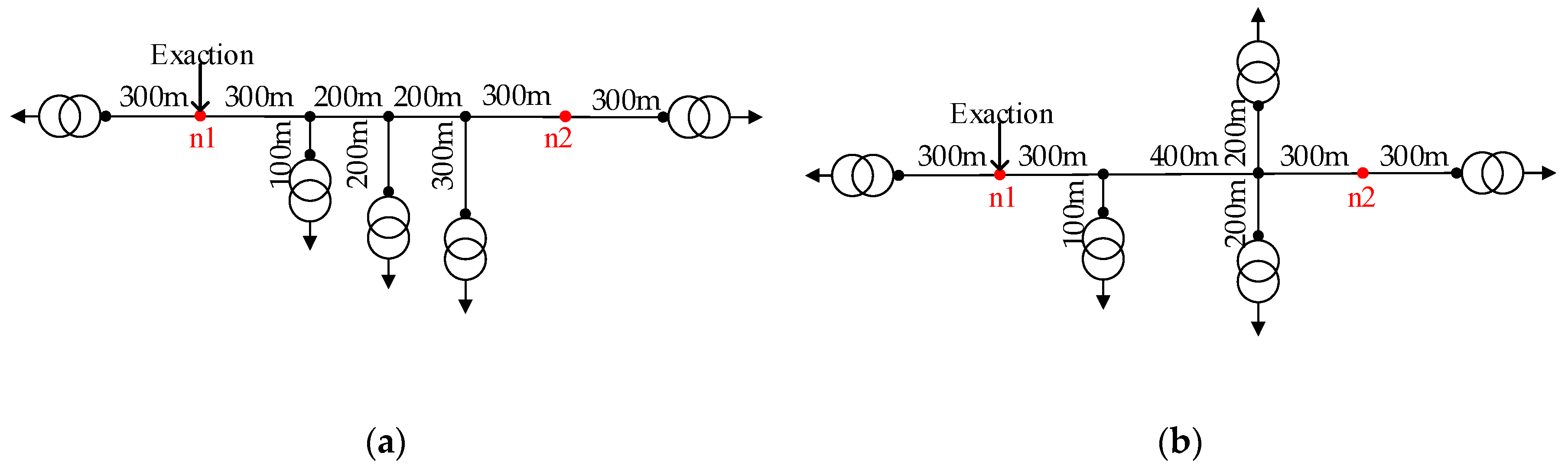
Figure 6 shows another two examples, where the transmitters were located at node 1 and the receivers were located at node 2. The transmitters and receivers were all coupled to the power-lines with PP coupling mode. The topologies shown in
Figure 2 and
Figure 6a were similar; the only difference was that the former had two underground cable branches, and the latter had three underground cable branches on the same trunk line of 400 m. The topologies shown in
Figure 2 and
Figure 6b were also similar; the only difference was that each junction shown in
Figure 2 had only one underground cable branch, and one of the junctions shown in
Figure 6b had two underground cable branches. Other configurations were the same as that of the first example in this section, and the same experimental measurements were carried out.
For node 2 in
Figure 6a,b,
Figure 7a,b shows the calculated and measured results of the FRCs, respectively. Contrasting
Figure 5a and
Figure 7, it is obvious that the additional underground cable branch influenced the FRCs of the distribution network to different degrees. However, the FRCs predicted by the proposed method still matched well with the measured results, which validated the proposed method again.
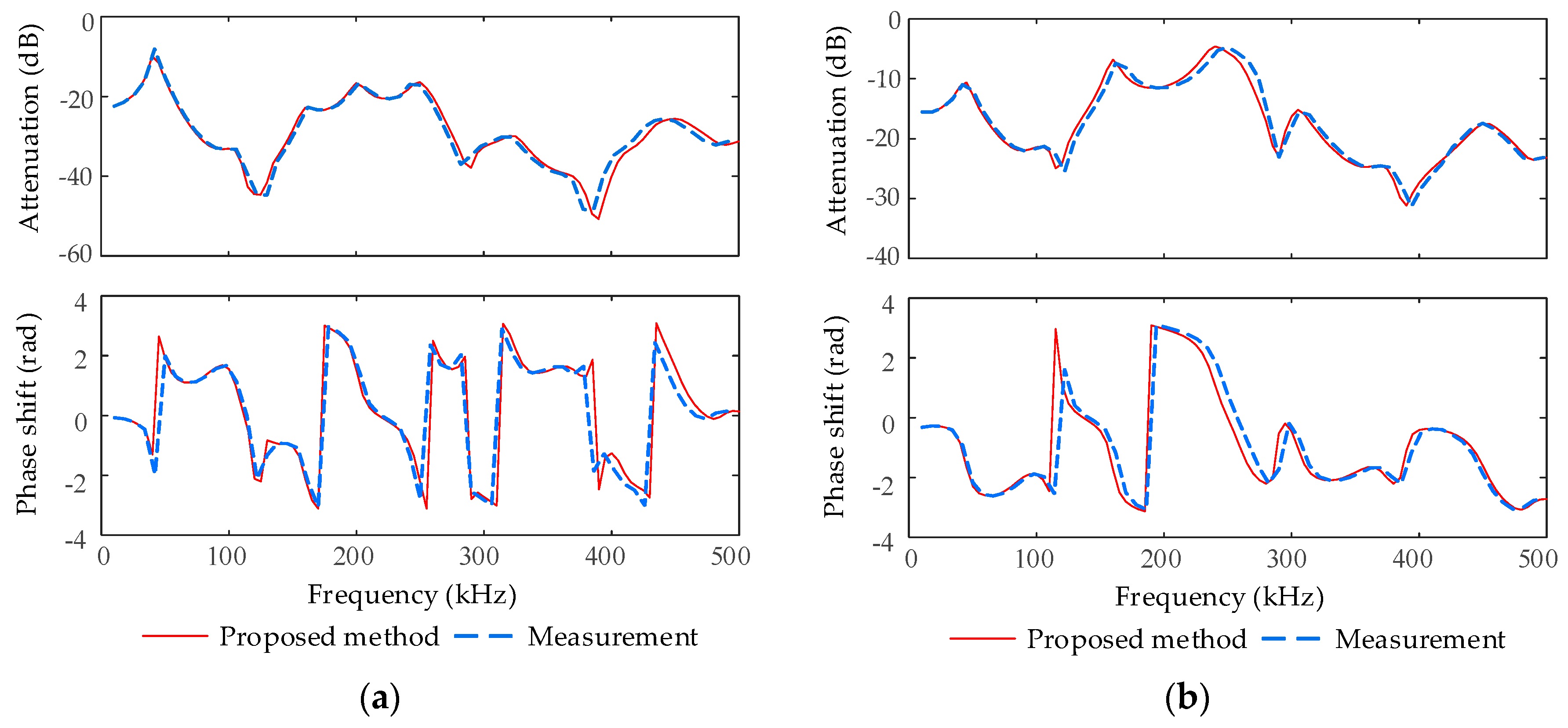
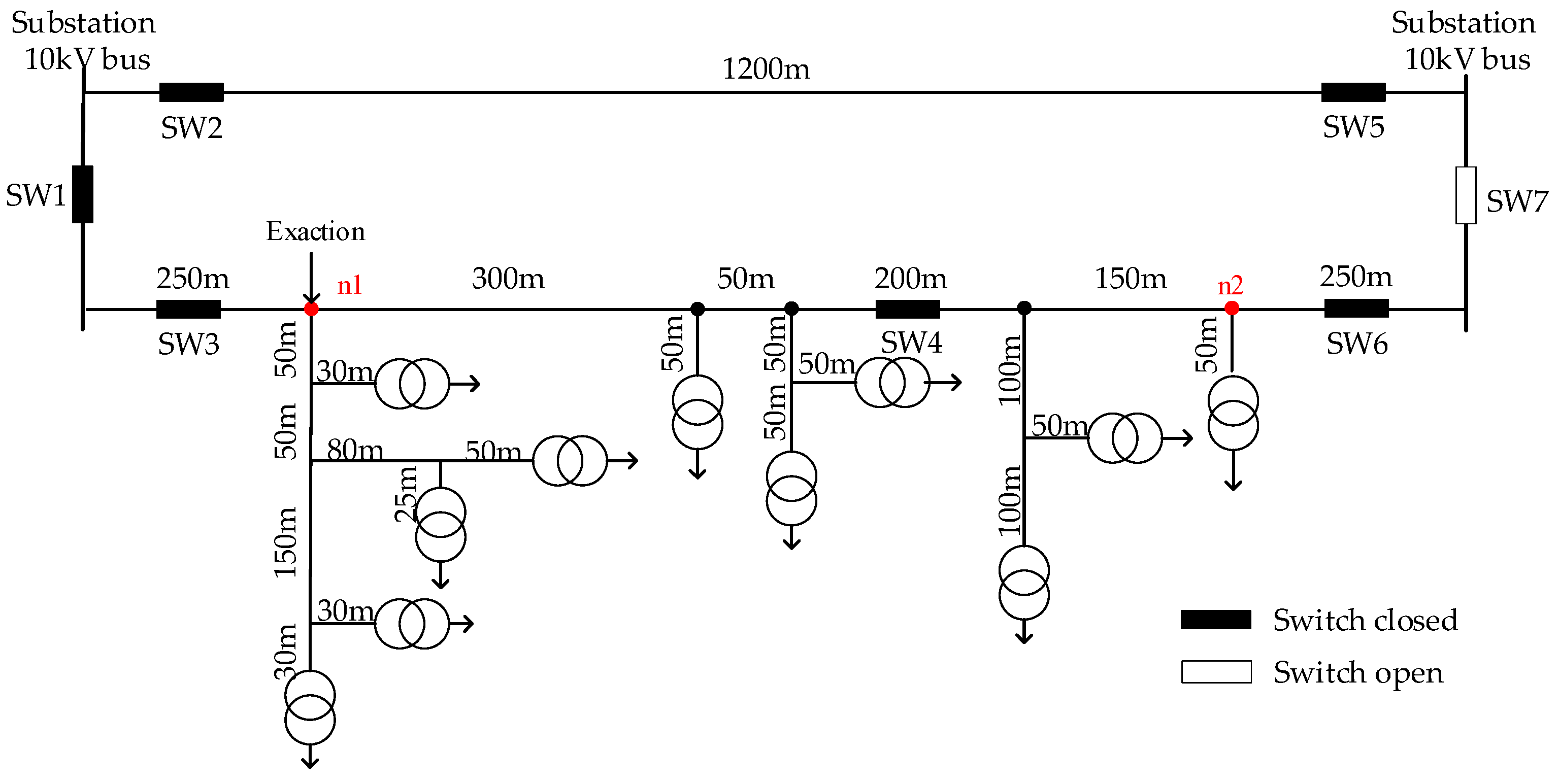
To further validate the proposed method, a ring distribution network with more branches was investigated. The topology and configurations of the ring distribution network are shown in
Figure 8. The two operation modes of the closed loop mode (all the switches were closed) and the open loop mode (only switch 7 was open; the others were closed) were considered. The horizontal power-lines were overhead lines, and the vertical power-lines were underground cables. The transmitter was located at node 1 with PP coupling mode. The rest of the configurations were consistent with the first example in this section. Similarly, the corresponding laboratory model was built, and each power-line section was represented by 60 cascaded π cells.
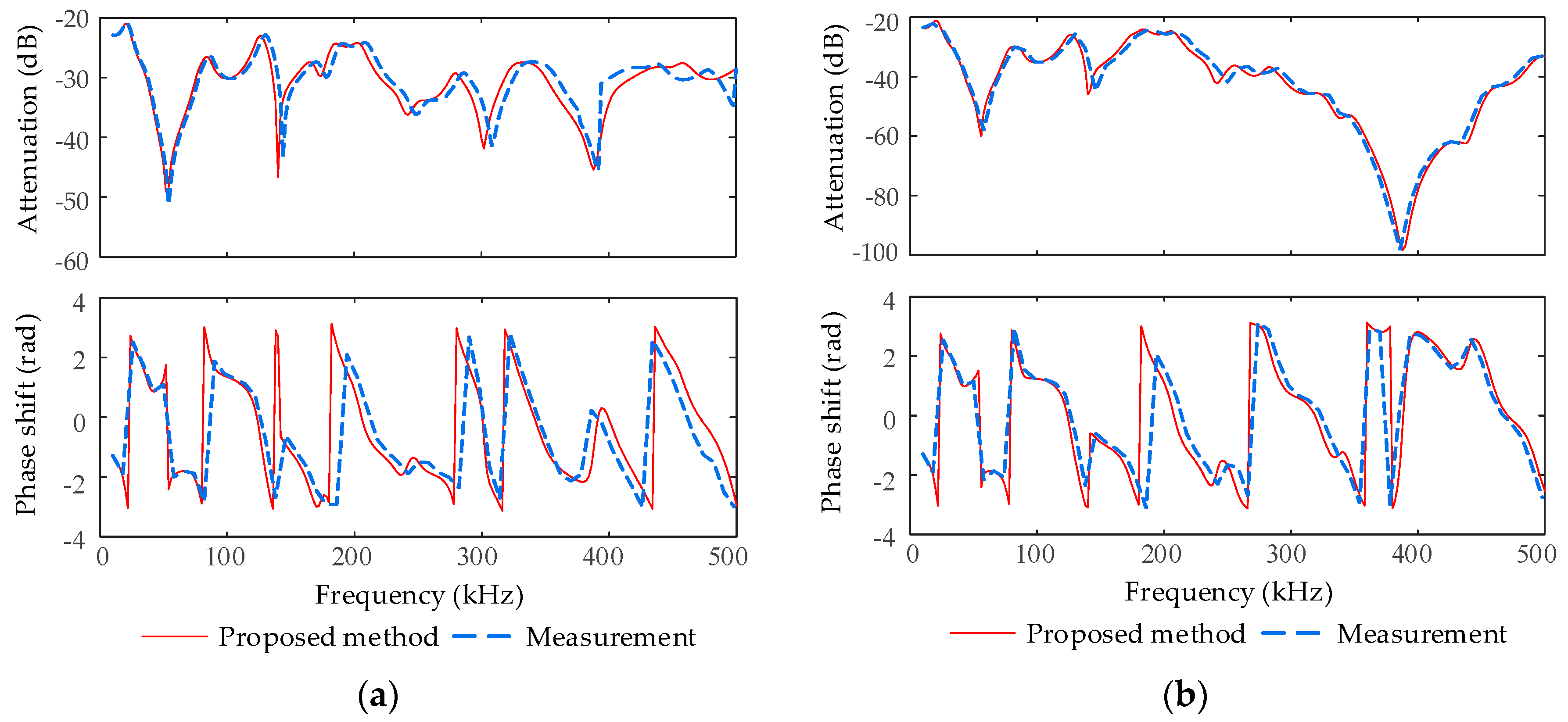
For node 2 in
Figure 8,
Figure 9 demonstrates the calculated and measured results of the FRCs under the closed loop and the open loop operation modes. Again, whether under closed loop or open loop mode, the FRCs obtained by the proposed method agreed well with the measured results. In addition, the signal attenuation under the closed loop mode was significantly lower than that under the open loop mode, owing to the additional transmission path of the unbranched power-line between switches 2 and 5 under the closed loop mode.
For node 2 in
Figure 8,
Figure 10 shows the calculated and measured FRCs under the open loop mode again, but the underground cables’ shields were grounded with different grounding impedances. As stated above, for the results in
Figure 9a, all the grounding impedances of underground cables’ shields were resistances of 2 Ω. This grounding condition is referred to as case 1. For the results in
Figure 10a, the corresponding grounding condition is referred to as case 2; that is, all the grounding impedances of the underground cables’ shields were 2 +
jω
L Ω, where
L = 5 μH [
32], and ω is the angular frequency of the carrier. For the results in
Figure 10b, the corresponding grounding condition is referred to as case 3; that is, all the underground cables’ shields were connected to ground perfectly (i.e., all grounding impedances were zero).
Figure 8 demonstrates that the calculation and measured results had good agreement, which validated the proposed method again. From
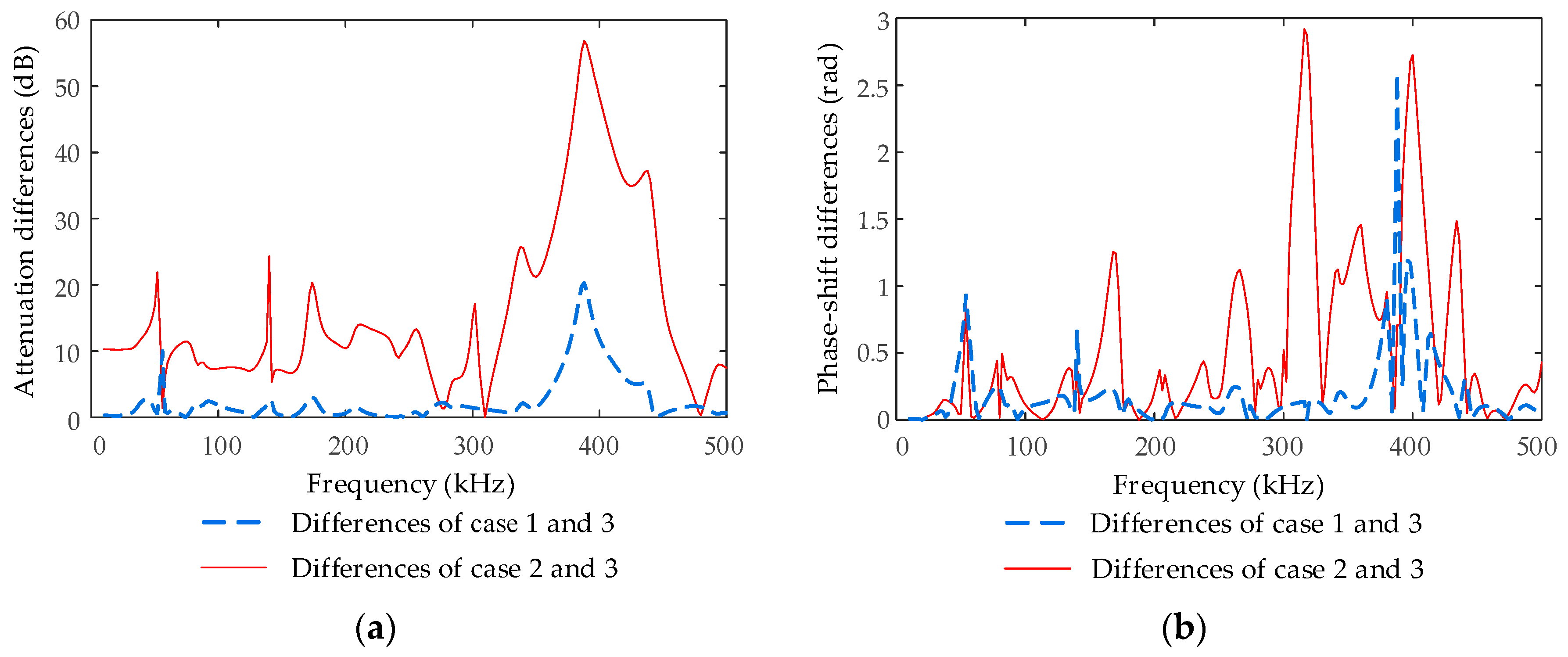
Figure 10 and
Figure 9a, it is clear that the FRCs were affected by the grounding conditions of the underground cables’ shields. The absolute values of the calculated attenuations and phase shifts under different grounding conditions were contrasted, and their absolute values of differences are shown in
Figure 11.
When the grounding inductances were considered, the amplitude attenuation (under case 2) was significantly lower than that under the other two situations. Relatively, the amplitude attenuation under perfect grounding conditions (case 3) showed the highest attenuation. On the other hand, the grounding inductances had apparent effects on the phase-frequency characteristics, and the effects of grounding resistance were slight. These conclusions are easy to understand due to the fact that the modulus values of grounding impedances directly decide the distribution proportions of signal power at the grounding points, and the inductive components have major effects on the phases. Simultaneously, these results indicate that the traditional approximate method that assumes all the grounding impedances are zero may cause considerable deviation compared with realistic situations.
According to the above calculation results, it can be seen that the proposed method can handle the interconnection of power-lines with different total conductor numbers. Further, the proposed method allows consideration of different grounding impedances in engineering practice, which are ignored in the traditional approximate method. The proposed method can also be used to solve the FRCs of simple radial networks or more complex ring networks. In fact, in the proposed method, the distribution networks are treated as the combinations of tubes and nodes, independent of the network topologies, so it is applicable to distribution networks of arbitrary topologies. For the reconstruction of distribution networks, the differences between the topologies before and after reconstruction are only local power-line connection relationships. The changes for the proposed method involve only adding or removing the local submatrices of the overall tube propagation matrix and updating the local submatrices of the overall node scattering matrix. Hence, the proposed method can adapt to the dynamic changes of the network topologies at a small cost.