Active Disturbance Rejection Control of Multi-Joint Industrial Robots Based on Dynamic Feedforward

Abstract

In this paper, the dynamics-based high-performance robot motion control technology has been mainly studied, and the overall structure is controlled via dynamics forward, given the nonlinearity, strong coupling and time-variability of robots. Considering the unavailability of precise robot model parameters and the uncertain disturbance in real operation, we put forward an active disturbance rejection control (ADRC) strategy based on dynamic feedforward, aiming to improve the control robustness and combining the simple structure, strong anti- disturbance ability, and no restriction from the control model of ADRC. Given the multi-joint coupling of robots, controlled decoupling is conducted by using dynamic characteristics. The ADRC cascade control structure and algorithm based on dynamic feedforward have been studied and the closed-loop stability of the system is investigated by analyzing the system dynamic linearization compensation and the anti-disturbance ability of the extended state observer. Experiments have shown the new strategy is more robust over uncertain disturbance than the conventional proportional-integral-derivative control strategy.

1. Introduction

Industrial robot systems are featured with nonlinearity, strong coupling and multivariate time-variability [1]. High-quality motion control refers to high-speed and high-precision motion control, that is the robot in the high-speed motion process, can have fast dynamics response, high tracking accuracy, smooth start and stop stage. Although the robot ontology parameters are fixed, the changing load and uncertain disturbances can affect the robustness of the control, and even significant mechanical vibration. Moreover, the control systems during high-speed motion are largely challenged by the severe multi-joint torque coupling, large inertia change and significant nonlinear effect. The attitude variation stable refers to the robot maintaining a smooth, non-jitter throughout the movement. The stability index needs to be determined by the actual requirements, such as in the air blade grinding process the trajectory error is required to be less than 0.05 mm. To keep the position and attitude variation stable and achieve high-quality motion control, researchers have to first solve the nonlinear time-variability due to the characteristics of robots. Namely, the control system should provide real-time control characteristics that match with the dynamics of robots and the multi-source disturbance characteristics, thereby achieving multi-joint nonlinear decoupling control.

The conventional proportional-integral-derivative (PID) controllers are structurally simple and achievable, but demand high power consumption for large-inertia changes and can ensure only local stability. The main reason is that this control strategy is usually applicable to linear stationary systems, and its conservative control parameters limit the gain bandwidth and thereby affect dynamic characteristics, leading to large delayed errors. Moreover, the large inertia variation may cause vibration in the system and destroy the stability. Thus, this strategy does not meet the requirement of robot systems for nonlinear time-variability. Later, nonlinear PID [2], blur PID [3] and neural network PID [4,5] controllers have been put forward and relatively outperform traditional PID controllers. These new strategies match with the nonlinear time-variability of robot systems by similarly optimizing the PID structure and improving its performance, but they are little dependent on the information of dynamics models and thus fail to meet the requirements of multi-joint high-quality motion control.

To promote further the motion performances of robots and solve the nonlinear time-variability and multi-source disturbance of robots, researchers have proposed finer nonlinear control algorithms, such as adaptive control, robust control and active disturbance rejection control (ADRC).

The adaptive control algorithms, which are structurally diverse, essentially extract the information of system states from closed-loop error feedback models, and regulate the control parameters via adaptive algorithms, so as to compensate the time-variability of the systems [6]. However, adaptive control has a strict requirement for real-time performance and is too complex to be realized, and its parameter mutations often destroy the overall stability; the parameter convergence is dependent on sufficient continual excitation, which is unachievable in real life. Thus, the system robustness of adaptive control should also be considered. For this reason, robust adaptive controlling algorithms have been put forward, which adopt the modified adaptive rate to make the system robust to the nonparametric uncertain disturbance in the models [7,8]. Typically, Hu et al. theoretically verified the two merits of comprehensive adaptive control and robust control of adaptive robust control [9,10]. However, adaptive robust control algorithms are yet based on the system feedback status, and control movement through the estimation of system characteristics, which raise the requirements for the amount and timeliness of state information. In fact, no enough state information can be acquired in advance at the initial stage, which leads to severe control lag and heavy following errors. Moreover, its structural complexity and diversity complicate practical applications.

ADRC [11], put forward in 1989, has been theoretically verified and continually improved [12,13,14,15]. ADRC mainly consists of an extended state observer (ESO), a tracking differentiator (TD) and error feedback control laws, and focuses on solving the uncertain external disturbance. ADRC controllers are structurally simple, efficient and excellent at anti-interference, and have been applied into industrial robot control [16,17]. The anti-disturbance core of ADRC controllers is dependent on ESO and largely affected by the unknown disturbance amplitude. If the whole dynamic characteristics of robots are estimated and compensated by regarding them as systematic disturbance, the fast convergence and systematic stability of ESO cannot be ensured, which limit the use of ADRC. The advanced control algorithms above have modestly improved the control performance of robots, but are unable to really describe the dynamic characteristics of robots and thus are limited in use. Nevertheless, along with the development of electronic technique and computer science recently, the controlling algorithms based on dynamic models have gained growing attention and are considered as the most efficient way to enhance the dynamic characteristics and tracking precision of robots. Their aims are to compensate according to the dynamic characteristics of robots and thereby simplify the complex robot system into a controllable system, such as decoupling it into a linear time-invariant system [18].

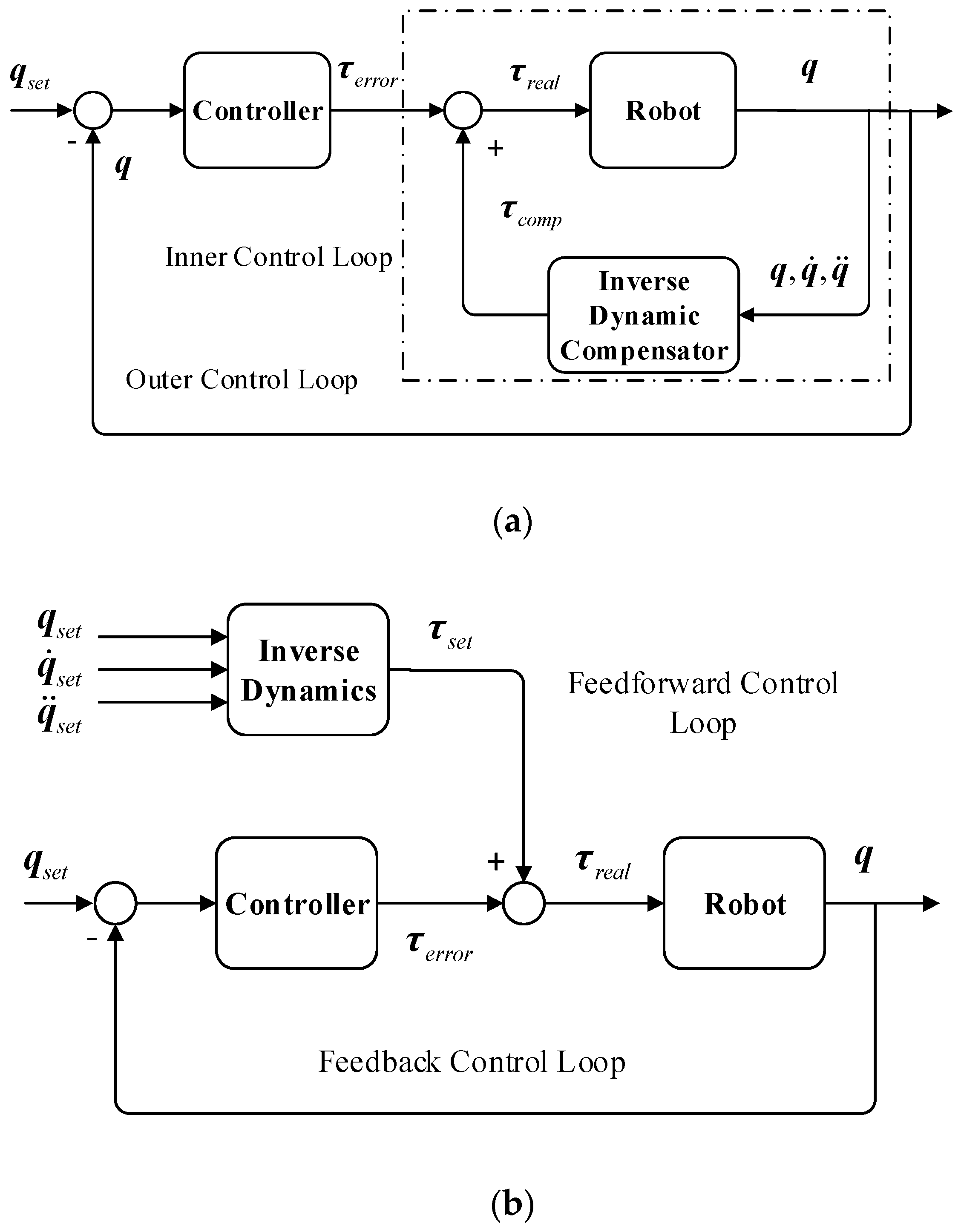
Generally, there are two schemes of model-based control: (1) Robot dynamic feedback compensation control (Figure 1a) and robot dynamic feedforward control (Figure 1b). For the first structure, when the dynamic model is precise enough, it can well solve the nonlinear time-variability of robots through feedback compensation, and reduces the power consumption in regulation, due to external feedback loop errors, improving the dynamic response and following the performance of controllers. However, it faces three difficulties. (1) No precise model parameters can be acquired, due to the load variation and sampling/computation errors. (2) This control structure raises the requirement for computation timeliness and has to overcome the time restraint of the torque loop control algorithm. (3) The real-time information of joint acceleration is needed, but in fact, the high-order differential signals are low-qualified, due to the magnifying effect of differential noise. Thus, model-based dynamic compensation control strategies are difficult to implement in practice.

Different from the first structure, the dynamic feedforward model inputs the expected joint movement order and offers the far-higher-quality signals than the sampled values. Moreover, despite the complexity of dynamic computation, the problem of dynamic feedforward timeliness can be solved through pre-storing or setting background programs, which are favorable for the implementation of control algorithms. Its ideas are to rapidly compensate the system characteristics through a precise dynamic model and thus to precisely control the movement. In fact, however, due to the diversity of model parameters and the severe effects of external loading and interference, the model parameters are hard to acquire precisely, which reduce the feedforward control performance. For this reason, an observer is usually used to pre-estimate and compensate for the uncertain disturbance, which would improve the robustness of feedforward controllers. The model uncertain disturbance observer is usually based on the construction of a system model, but a complicated robot system involves the computation of robot forward dynamics, which interfere with the timeliness of motion control. For this reason and regarding the simple structure, strong robustness and no constraint from the control model of ADRC, we put forward an ADRC strategy based on dynamic feedforward.

As for the nonlinearity and strong coupling time-variability of robots, we use dynamic feedforward compensation and uncertainty disturbance compensation into multi-joint control decoupling, or namely to regard the joints as independent control units. To reduce the order of disturbance observation and improve the observation precision, we study the ADRC cascade control structure and algorithm based on dynamic feedforward. We analyze the system dynamic linearization compensation and the anti-disturbance ability of ESO, and the stability of closed-loop systems. On this basis, the robot ADRC based on dynamic feedforward has been realized.

2. Robot System Decoupling Control

2.1. Analysis of System Disturbance Compensation

The basic ways of multi-joint decoupling control are to use dynamic feedforward compensation and uncertainty disturbance compensation. To solve disturbance via ADRC, we had to clarify the input, output, relative order number and disturbance compensation of the controlled system. According to the dynamic feedforward control structure, the current instruction is the input and the motor rolling angle is the output of the system. For the motor, the robot dynamic characteristics can be regarded as a result of the motor output torque ${\mathit{\tau }}_m$ overcoming friction torque ${\mathit{\tau }}_{mf}$ and inertia torque (in Figure 2):

$${\mathit{\tau }}_m={\mathit{J}}_m{\ddot{\mathit{q}}}_m+{\mathit{\tau }}_{ml}+{\mathit{\tau }}_{mf},$$

(1)

where

$${\mathit{J}}_m=\mathrm{diag}(J_{m1},J_{m2},\cdots ,J_{mn}),$$

(2)

is the rotary inertia of the motor shaft; ${\ddot{\mathit{q}}}_m$ is the angular acceleration of the motor shaft; ${\mathit{\tau }}_{ml}$ is the loaded torque vector of the motor to overcome the joint dynamic characteristics, including joint inertia torque, friction torque, gravity torque and joint loading. To build the relation between motor input current ${\mathit{I}}_q$ and output position ${\mathit{q}}_m$, firstly, we had the machinery transmission relation ${\eta }_i$ to express the gear kinematic relations at both ends:

$$\{\begin{array}{l}\mathit{\Lambda }=\mathrm{diag}(1/{\eta }_1,1/{\eta }_2,\cdots 1/{\eta }_n)\\ \mathit{q}=\mathit{\Lambda }{\mathit{q}}_m,\dot{\mathit{q}}=\mathit{\Lambda }{\dot{\mathit{q}}}_m,\ddot{\mathit{q}}=\mathit{\Lambda }{\ddot{\mathit{q}}}_m\\ {\mathit{\tau }}_{ml}=\mathit{\Lambda }\mathit{\tau }\end{array},$$

(3)

where $\mathit{q},\dot{\mathit{q}},\ddot{\mathit{q}}$ express the kinestate of robot joints, $\mathit{\tau }$ is the output torque vector at the joint end:

$$\mathit{\tau }=\mathit{M}(\mathit{q})\ddot{\mathit{q}}+\mathit{V}(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+\mathit{G}(\mathit{q})+\mathit{F}(\mathit{q},\dot{\mathit{q}})+{\mathit{\tau }}_{load},$$

(4)

where $\mathit{M}(\mathit{q})$ is the inertia matrix of Joints; $\mathit{V}(\mathit{q},\dot{\mathit{q}})$ is the centrifugal force and Coriolis force vectors; $\mathit{G}(\mathit{q})$, $\mathit{F}(\mathit{q},\dot{\mathit{q}})$ and ${\mathit{\tau }}_{load}$ are the gravitational torque, friction torque, joint loading torque vectors, respectively. Combining with the electromagnetic torque equation:

$${\mathit{\tau }}_m={\mathit{K}}_m{\mathit{I}}_q,$$

(5)

where ${\mathit{K}}_m=\mathrm{diag}(k_{m1},k_{m2},\cdots k_{mn})$ is the torque constant matrix, ${\mathit{I}}_q={[i_{q1},i_{q2},\cdots ,i_{qn}]}^T$ is the current order vector, we can determine the motor shaft motion equation:

$${\ddot{\mathit{q}}}_m={\mathit{J}}_m{}^{-1}({\mathit{K}}_m{\mathit{I}}_q-\mathit{\Lambda }\mathit{\tau }-{\mathit{\tau }}_{mf})$$

(6)

Let $\mathit{f}(\mathit{q},\dot{\mathit{q}},t)=-{\mathit{J}}_m{}^{-1}(\mathit{\Lambda }\mathit{\tau }+{\mathit{\tau }}_{mf})$, we have

$${\ddot{\mathit{q}}}_m={\mathit{J}}_m{}^{-1}{\mathit{K}}_m{\mathit{I}}_q+\mathit{f}(\mathit{q},\dot{\mathit{q}},t).$$

(7)

During ADRC construction, usually $\mathit{f}(\mathit{q},\dot{\mathit{q}},t)$ is regarded as the comprehensive acceleration disturbance of the system, including the dynamic characteristic disturbance of the robot and other uncertain disturbances. In the high-speed large-inertia changing the movement of robots, the real change $\mathit{f}(\mathit{q},\dot{\mathit{q}},t)$ is very large, and the large-amplitude disturbance variation may induce the slow convergence or even instability of ESO, thereby leading to large following errors or even system vibration. Thus, it needs to solve the problems to decrease the observed values of acceleration and increase the robustness of ESO.

The analysis showed there were two ways: (1) Designing stable ESO ensured it could effectively predict all the dynamic disturbance; (2) fully utilizing the known theoretical dynamic models and conducting uncertainty compensation would ensure ESO only observed the relatively small error part except the model. The real output torque $\mathit{\tau }$ consists of the model-estimated torque ${\mathit{\tau }}_{pre}$ and torque errors $\mathsf{\Delta }\mathit{\tau }$.

$$\mathit{\tau }={\mathit{\tau }}_{pre}+\mathsf{\Delta }\mathit{\tau }.$$

(8)

Based on this idea, starting from the motor end to the joint end, the real output torque $\mathit{\tau }$ can be regarded as the disturbance of the output shaft from the motor, where ${\mathit{\tau }}_{pre}$ can be compensated by the identification model, and the uncertainty except the model $\mathsf{\Delta }\mathit{\tau }$ can be observed by the ESO. We have:

$$\{\begin{array}{l}{\mathit{B}}_0={\mathit{J}}_m{}^{-1}{\mathit{K}}_m\\ {\mathit{F}}_1=-{\mathit{J}}_m{}^{-1}\mathit{\Lambda }{\mathit{\tau }}_{pre}\\ {\mathit{F}}_2=-{\mathit{J}}_m{}^{-1}(\mathit{\Lambda }\mathsf{\Delta }\mathit{\tau }+{\mathit{\tau }}_{mf})\\ \mathit{F}={\mathit{F}}_1+{\mathit{F}}_2\\ \mathit{u}={\mathit{I}}_q\end{array},$$

(9)

where ${\mathit{B}}_0$ is the system gain, and ${\mathit{F}}_1$ is the theoretical disturbance related to a known dynamic model and can be used into feedforward compensation; ${\mathit{F}}_2$ is the uncertain acceleration disturbance except for the model and can be observed via the ESO. Noticeably, ${\mathit{F}}_2$ includes the joint torque errors, which may contain minor time-variable acceleration component ${\ddot{q}}_m$ that cannot be observed by ESO, and, theoretically, the corresponding control current should be compensated. $\mathit{F}$ can be considered as the total disturbance of the motor system. Admittedly, the robot system is a second order multiple-input multiple-output (MIMO) system, $\mathit{u}$ is the real input of the controlled object or namely the current control quantity of the motor driven system.

Let $\mathit{\Lambda }{\mathit{\tau }}_{pre}$ be the theoretical output torque at the motor end, and ${\mathit{I}}_{pre}$ be the corresponding drive current, then:

$$\mathit{\Lambda }{\mathit{\tau }}_{pre}={\mathit{K}}_m{\mathit{I}}_{pre},{\mathit{F}}_1=-{\mathit{B}}_0{\mathit{I}}_{pre},$$

(10)

Let

$${\mathit{u}}_{ff}={\mathit{I}}_{pre},\mathit{U}={\mathit{B}}_0\mathit{u}.$$

(11)

Thereby the motor output state equation can be expressed as:

$$\{\begin{array}{l}{\dot{\mathit{X}}}_1={\mathit{X}}_2\\ {\dot{\mathit{X}}}_2={\mathit{B}}_0\mathit{u}+{\mathit{F}}_1+{\mathit{F}}_2=\mathit{U}+\mathit{F}\\ \mathit{Y}={\mathit{X}}_1\end{array},$$

(12)

where $\mathit{U}$ can be seen as the virtual control quantity of the system; $\mathit{Y}$ is the output from the system. The real inertia demand can be met by modifying the system gain ${\mathit{B}}_0$:

$${\mathit{B}}_0={\mathit{J}}_m{}^{-1}{\mathit{K}}_m\mathit{\zeta },$$

(13)

where $\mathit{\zeta }$ is the diagonal matrix of the correction coefficient, ${\zeta }_i\ge 1$. Many simulation studies show during ADRC control, the estimation demand of ${\mathit{B}}_0$ is not high, and the relative error is within 30%, and when it is higher, it does not affect the closed-loop control quality. Thus, $\mathit{\zeta }$ is usually considered as constant in practical applications [19].

2.2. Robot System Decoupling

The decoupling of multi-joints could ease the difficulty of controlling. In the ADRC system, the model part except the system-controlled quantity $\mathit{F}$ is called the ‘dynamic coupling part’ and $\mathit{U}$ is called the ‘static coupling part’. In the MIMO system, the input and output relation of channel i is:

$$\{\begin{array}{l}{\dot{x}}_{i1}=x_{i2}\\ {\dot{x}}_{i2}=U_i+F_i\\ y_i=x_{i1}\end{array}.$$

(14)

It is assumed $U_i$ is the ‘virtual control quantity’ of channel i, then it and the output $y_i$ form a single-input - single-output relation, or namely the controlled output $y_i$ and the controlled quantity $U_i$ of channel i can be completely decoupled: $F_i$ is considered as the total disturbance of channel i, including the acceleration disturbance of robot dynamics, and the uncertain disturbance except for the model. Thereby, n ADRC controllers implemented in parallel between the control quantity $\mathit{U}$ and the output vector $\mathit{Y}$ can control the multivariate system structure. The decoupling process is shown below (Figure 3):

The conversion relation between the real control quantity $\mathit{u}$ and the virtual control quantity $\mathit{U}$ is shown as:

$${\mathit{u}}_{}={\mathit{B}}_0{}^{-1}\mathit{U}.$$

(15)

Admittedly, ${\mathit{B}}_0$ is reversible, time-variable and bounded, and in ADRC control, its required estimation precision is not high. It should be noted the dynamic coupling part $\mathit{F}$ during decoupling can be considered as the total disturbance to be estimated and compensated, and its estimation precision decides the control performance of ADRC. Due to the very large inertia change during robot movement, the corresponding change of acceleration disturbance is also large, so it will intensify the burden on the ESO if it is all observed by ESO. According to the torque feedforward compensated total disturbance, only the unknown small amount is undertaken by ESO, which thereby largely reduces the burden on ESO and enhanced the system robustness. Then based on the principles of ADRC, we study the structure and algorithm of independent motion controllers.

3. Motion Controller Design and Stability Analysis

3.1. Design of Controller

The decoupled robot system is transformed into sive independent single-input single- output (SISO) systems, degrees of freedom of which formed independent control channels. A computed torque feedforward control strategy has been adopted to improve the control performance and stability of ADRC. It should be noted the controlled object here is no longer the robot joint position, but is the institution ontology and servo drivers under the torque mode (current mode).

The robot system is second order and usually has two choices in the ADRC structure: A second order system structure (Figure 4) and a cascade system structure (Figure 5). In the second order system, the control variable $u$ (current) directly drives the output of displacement $x_1$, without any transitional loop, and the corresponding uniaxial servo feedforward control structure is shown in Figure 4. This structure consists of two loops—a position loop and a current loop. The position loop directly offers a current command to the current loop implemented in a motor driver. The current feedforward path, as the main path, can offer the motor servo system with real-time theoretical current corresponding to the movement command, while the real-time current errors have been observed by ESO and regulated and compensated by the PID.

Since the current loop bandwidth is large and the current order from the position loop should be rapidly updated, the position order should be more refine and kept continuous, otherwise, the control variable $u$ would be discontinuous, thereby inducing systematic vibration.

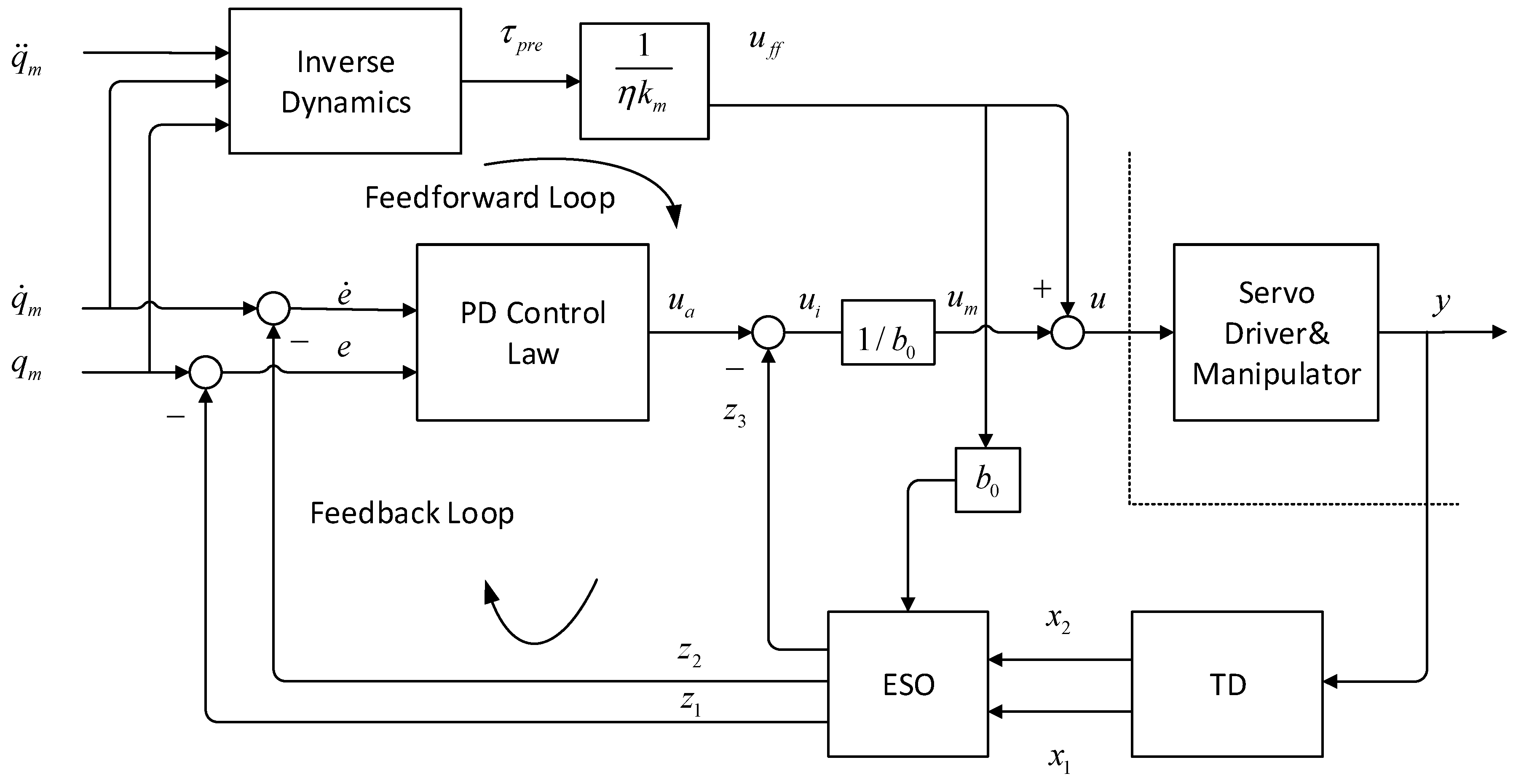
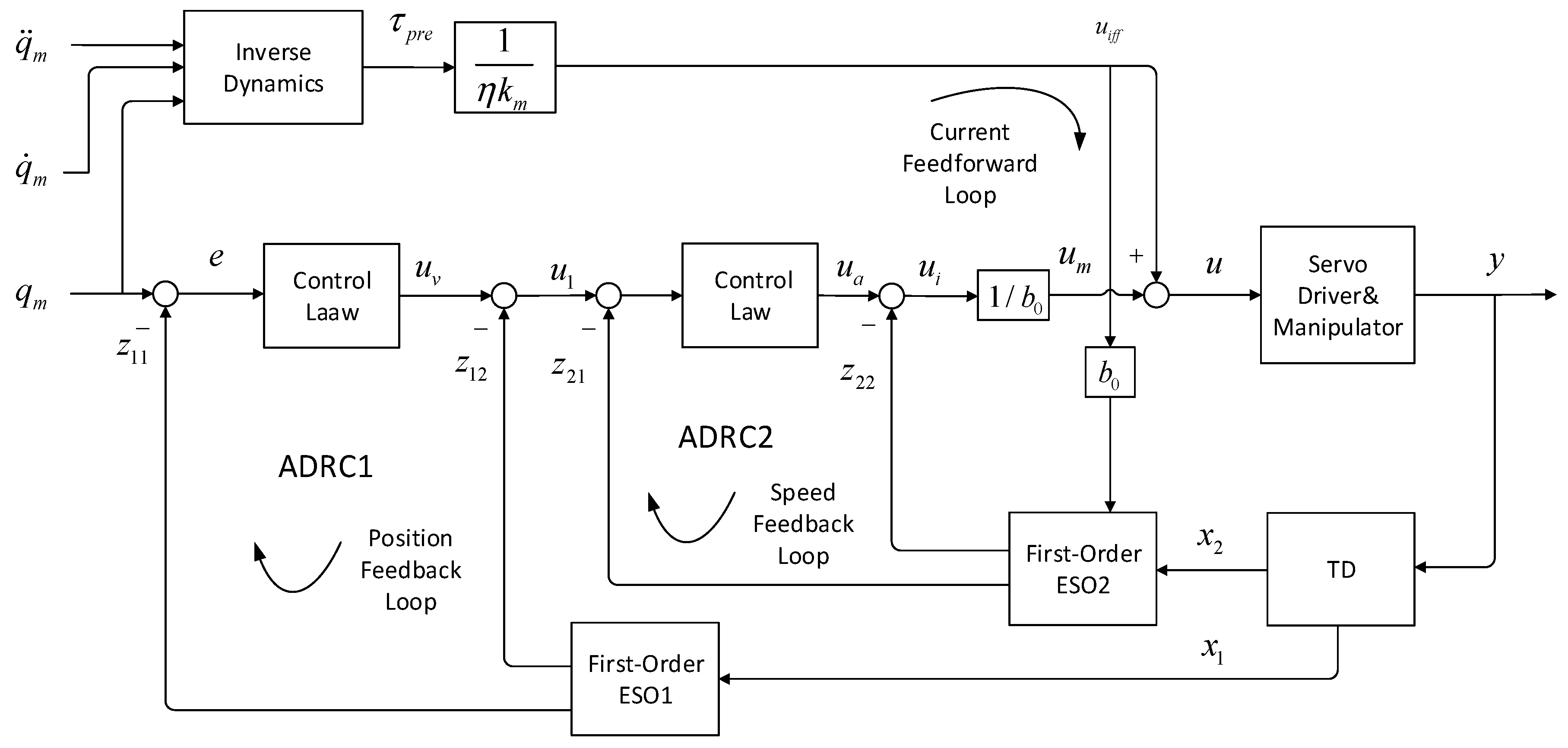
In the structure of the ADRC cascade system, the control variable $u$ (current) first drives the intermediate variable $x_2$ (velocity) and then $x_2$ drives position $x_1$, so as to control the target (Figure 6). In real servo control, this structure is the most common. Its idea is similar to the back-stepping method of modern control theories: The complex nonlinear system is decomposed into a number of subsystems (not larger than the system order); the difference is that back-stepping selects an appropriate Lyapunov function for each subsystem, and builds an assistant virtual control variable, so as to compensate the effects of uncertain factors and thereby loop-wise reverse back to the system control input. On the contrary, through a first-order ADRC method, each loop of ADRC compensates uncertain disturbance and regulates errors, avoiding the construction of Lyapunov function and being relatively simple. Based on the ideas of ADRC cascade structure, we design an ADRC cascade controller based on inertia feedforward (Figure 6).

This ADRC feedforward controller is composed of a position loop and a velocity loop, and each loop is based on the ADRC feedforward control technology. The interior velocity loop mainly produced comprehensive current command $u$, which is $u_{ff}$ mainly supplied by the current feedforward path. Then the acceleration corresponding to the uncertain errors is partially observed and compensated by the ESO2 and partially regulated by the velocity error feedback control law. The ESO disturbance observation and current feedforward can effectively reduce the power consumption, due to error control, improving the system robustness and response speed. Similarly, the exterior position loop mainly provides velocity order $u_1$, which mainly consists of the position error feedback control law output $u_v$ and the ESO1 velocity disturbance $z_{12}$. Moreover, the loop bandwidth can be also improved to some extent by the velocity feedforward method, which ensures the rapid response to the velocity order. As for the feedback, TD has been used to acquire information about robot position and velocity, and its estimation precision modestly affects the controller performance.

It should be noted in a cascade system, the movement change of the velocity loop is faster than the position loop, which is decided by the physical properties of the controlled system. Thus, during digital computation, the velocity loop and position loop are set at different sampling step sizes (sampling period), so as to prevent the system from high-frequency vibration. Usually, the sampling period of the position loop is set as an integral multiple of that of the velocity loop and is at the millisecond level. Such setting of order density avoids the restraint of current bandwidth as faced by second order systems. Moreover, to avoid overshoot and excessive noise in each loop control order, the amplitude limiting, and low-pass filtering can be used, respectively. By combining the analyses of two control structures, we can find that each stage of the cascade controller can be considered as a first order system. Its preliminary design of control algorithm is shown below:

• Basic function

  $$fal(e,\alpha ,\delta )=\{\begin{array}{ll}{\left|e\right|}^{\alpha }sign(e),& \left|e\right|>\delta \\ \frac{e}{{\delta }^{1-\alpha }},& \left|e\right|\le \delta \end{array};$$

  (16)
• Tracking differentiator [19]

  $$\{\begin{array}{l}fsg(x,d)=[sign(x+d)-sign(x-d)]/2\\ d=R{h}_0{}^2\\ a_0=h_0\cdot x_2\\ y=x_1+a_0\\ a_1=\sqrt{d(d+8\left|y\right|)}\\ a_2=a_0+sign(y)(a_1-d)/2\\ a=(a_0+y)fsg(y,d)+a_2(1-fsg(y,d))\\ fhan(x_1,x_2,R,h_0)=-R(a/d)fsg(a,d)-Rsign(a)\cdot (1-fsg(a,d))\end{array};$$

  (17)
• Differential state

  $$\{\begin{array}{l}fh=fhan(x_1-y,x_2,r,h_0)\\ x_1=x_1+h_0\cdot x_2\\ x_2=x_2+h_0\cdot fh\end{array}.$$

  (18)

ADRC is divided into three parts. The first part is about arranging the transition process, which is implemented in tracking differentiator, as in Equations (17) and (18), used to produce smooth instruction curves and differential curves. The second part is the design of ESO, as the first three equations in Equations (19) and (20), which are used to observe the disturbance in the corresponding loop.

• Position loop control using first order ESO1

  $$\{\begin{array}{l}e=z_{11}-x_1,fe=fal(e,0.5,h_1)\\ z_{11}=z_{11}+h_1(z_{12}-{\beta }_{01}\cdot e+u_1)\\ z_{12}=z_{12}+h_1(-{\beta }_{02}\cdot fe)\\ e_1=q_m-z_{11}\\ u_v={\beta }_{1}fal(e_1,0.5,1.0)\\ u_1=u_v-z_{12}\end{array};$$

  (19)
• Velocity loop control using first order ESO2

  $$\{\begin{array}{l}e=z_{21}-x_2,fe=fal(e,0.5,h_2)\\ z_{21}=z_{21}+h_2(z_{22}-{\beta }_{03}\cdot e+b_0{u}_i-b_0{u}_{ff})\\ z_{22}=z_{22}-h_2{\beta }_{04}\cdot fe\\ e_2=u_1-z_{21}\\ u_a={\beta }_{2}fal(e_2,0.5,1.0)\\ u_i=u_a-z_{22}\\ u_m=u_i/b_0\\ u=u_m+u_{ff}\end{array};$$

  (20)

  where $h_0,h_1,h_2$ are the sampling step sizes of TD, position loop and velocity loop, respectively; $z_{11},z_{12}$ are the values of position and velocity disturbance observed by first-order ESO1, respectively; $z_{11},z_{12}$ are the values of velocity and acceleration ‘unknown disturbance’ observed by first-order ESO2, respectively. The third part of ADRC is the feedback controller. The control laws $u_v$ in Equation (19) and $u_i$ in Equation (20) adopt the simple P control laws combing basic function fal(). When the controller structure has been determined, appropriate ESO and PID control laws could be designed/selected according to real situations, so as to improve the system robustness. More details can be found in [11,12,15,19].

3.2. System Stability Analysis

The closed-loop stability is very significant for the application of ADRC. However, the nonlinear structure of ADRC is very complex, and its stability verification is very complicated, which become the concerns in ADRC theoretical research. Guo strictly verified the convergence of high-gain ESO in nonlinear SISO systems mathematically and explored the convergence of nonlinear ESO in uncertain MIMO systems [20]. He used the absolute theory to analyze the stability of the simplified first-order ADRC closed-loop systems [21]. Zhao defined the convergence of ADRC controllers in SISO nonlinear systems and built and verified the convergence conditions of ADRC [22]. For simplification, we will analyze the necessary influence factors on system stability on the basis of system transformation, so as to characterize system stability.

3.2.1. System Dynamic Compensation Linearization

The shafts in the decoupled robot system are mutually independent. A mono-joint system can be described as a nonlinear system:

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=bu(t)+f(x,\dot{x},t)+\omega (x,t)\\ y=x_1\end{array},$$

(21)

where $f(x,\dot{x},t)$ is the acceleration function corresponding to the theoretical model; $\omega (x,t)$ is the comprehensive acceleration disturbance except for the model; $b$ was the system gain; $u(t)$ is the control variable. The closed-loop controller is expected to have the following dynamic properties:

$$\ddot{x}=g(x,\dot{x}).$$

(22)

When the theoretical model $f(x,\dot{x},t)$ has been known, the acceleration order could be compensated by the feedforward way, and the disturbance part is compensated by the observation of ESO, or namely $z(t)\approx \omega (t)$. Then the system control quantity is:

$$u=\frac{(u_0-z)}{b}-\frac{f}{b}.$$

(23)

At this moment, the closed-loop system became an integrator series system:

$$\ddot{x}\approx u_0(x,\dot{x}).$$

(24)

Admittedly, the system disturbance is compensated by the real-time estimation, which would forcefully transform the original nonlinear system into a classic linear system. Then an efficient error feedback control law $u_0$ (e.g., nonlinear PID control law) could be used to regulate the closed-loop performance and stabilize the system. However, the premise is that the feedback from the closed-loop control system could well estimate the uncertain disturbance and could promptly pre-estimate and compensate for the acceleration disturbance to the system. Thus, ESO is a core component of ADRC, and its convergence and anti-disturbance abilities directly affect the closed-loop performance and stability of ADRC [23]. Here we further analyzed the anti-disturbance ability of ESO.

3.2.2. Anti-disturbance Ability of ESO

Lemma 1 [21].

For a first-order controlled object,

$$\dot{x}=w(x,t)+u,$$

(25)

where $x$ is a state variable; $u$ is the controlled amount; $w(x,t)$ is the bounded disturbance of the system, and $\left|w(x,t)\right|\le {\omega }_0$. When this system is treated with nonlinear state feedback:

$$u(x)=-k{\left|x\right|}^{\alpha }sign(x),\alpha >0,k>0.$$

(26)

The system state $x$ under disturbance could rapidly converge to a small range of steady-state errors, then the solution domain of the closed-loop system meets:

$$\underset{t\to \infty }{\lim }\left|x\right|\le {({\omega }_0/k)}^{1/\alpha }.$$

(27)

For an nth order nonlinear SISO system:

$$\{\begin{array}{l}{x}^{(n)}=b_{0}u(t)+f(x,\dot{x},\cdots ,x^{(n-1)},t)+w(t)\\ y=x(t)\end{array},$$

(28)

where $f(\cdot )$ is an unknown function; $w(t)$ is the unknown disturbance; $b_0$ is the system gain; $u(t)$ is the system input; $y$ is the system output.

Let $x_1(t)=x(t),\cdots ,x_n(t)=x^{(n-1)}(t),$ $x_{n+1}(t)=a(t)=f(x,\dot{x},\cdots ,x^{(n-1)},t)+w(t)$, then the state equation of the above system ${\Sigma }_1$ becomes:

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ \cdots \cdots \\ {\dot{x}}_{n-1}=x_n\\ {\dot{x}}_n=x_{n+1}^{}+b_{0}u\\ {\dot{x}}_{n+1}=c(t)\\ y=x_1\end{array},$$

(29)

where $c(t)=d[a(t)]/dt$. For the above system, we can build an nth order ESO system ${\Sigma }_2$:

$$\{\begin{array}{l}e=z_1-x_1\\ {\dot{z}}_1=z_2-g_1(e)\\ \cdots \cdots \\ {\dot{z}}_n=z_{n+1}-g_n(e)+b_{0}u\\ {\dot{z}}_{n+1}=-g_{n+1}(e)\end{array}.$$

(30)

The state of system ${\Sigma }_1$ is followed: $z_1\to x_1,\dots z_n\to x_n,z_{n+1}\to x_{n+1}=a$. Let $\delta x_1=z_1-x_1,\cdots ,$ $\delta x_{n+1}=z_{n+1}-x_{n+1}$, then the following error system ${\Sigma }_3$ can be determined.

$$\{\begin{array}{l}\delta {\dot{x}}_1=\delta x_2-g_1(\delta x_1)\\ \dots \\ \delta {\dot{x}}_n=\delta x_{n+1}-g_n(\delta x_1)\\ \delta {\dot{x}}_{n+1}=-c(t)-g_{n+1}(\delta x_1)\end{array},$$

(31)

For a bounded variation $c(t)$, we can select an appropriate nonlinear function $g_i(\cdot )$ to make system ${\Sigma }_3$ always stabilize at the origin and thereby make the state observation variable follow the system status. When the controlled amount coefficient $b$ is inaccurate, its estimated value $b_0$ could be used, and the estimation errors $(b-b_{0}u)$ is included in $z_{n+1}(t)$. Expression of $g_i(\cdot )$ decides the anti-disturbance performance of ESO and is unrelated to the system, but is only related to the changing rate $c(t)$ of the comprehensive acceleration $a(t)$ and changing range. Thus, $g_i(\cdot )$ could be built by using different forms of nonlinear function. Usually the following function has been selected:

$$g(\epsilon )={\beta }_{0i}fal(\epsilon ,{\alpha }_i,{\delta }_i)(i=1,2,\cdots ,n+1),$$

(32)

where ${\beta }_{0i}$ is the gain factor, and ${\alpha }_i$ designed here meets $0<{\alpha }_i\le 1$, ${\delta }_i=\delta \ge 0$. From the above equation, it is the function $fal(\cdot )$ consisted of a small-range linear interval and a large-range ${\left|x\right|}^{\alpha }sign(x)$. For convenience of analysis, we set:

$$g(\delta x_1)={\beta }_{0i}{\left|\delta x_1\right|}^{\alpha }sign(\delta x_1).$$

(33)

Then the error system ${\Sigma }_3$ becomes:

$$\{\begin{array}{l}\delta {\dot{x}}_1=\delta x_2-{\beta }_{01}{\left|\delta x_1\right|}^{{\alpha }_1}sign(\delta x_1)\\ \dots \\ \delta {\dot{x}}_n=\delta x_{n+1}-{\beta }_{0n}{\left|\delta x_1\right|}^{{\alpha }_n}sign(\delta x_1)\\ \delta {\dot{x}}_{n+1}=-c(t)-{\beta }_{0(n+1)}{\left|\delta x_1\right|}^{{\alpha }_{n-1}}sign(\delta x_1)\end{array}.$$

(34)

Let the changing function of the comprehensive acceleration $c(t)$ be bounded and satisfy $c(t)\le {\omega }_0$; according to the prerequisite of ESO convergence, when $t\to \infty$, then $\delta {\dot{x}}_i\to 0$, and according to Lemma 1, the range of system steady-state error is:

$$\{\begin{array}{l}\underset{t\to \infty }{\lim }\left|\delta x_1\right|=\underset{t\to \infty }{\lim }\left|z_1-x_1\right|<{({\omega }_0/{\beta }_{0(n+1)})}^{\frac{1}{{\alpha }_{n+1}}}\\ \cdots \cdots \\ \underset{t\to \infty }{\lim }\left|\delta x_n\right|=\underset{t\to \infty }{\lim }\left|z_n-x_n\right|<{\beta }_{0(n-1)}{({\omega }_0/{\beta }_{0(n+1)})}^{\frac{{\alpha }_{n-1}}{{\alpha }_{n+1}}}\\ \underset{t\to \infty }{\lim }\left|\delta x_{n+1}\right|=\underset{t\to \infty }{\lim }\left|z_{n+1}-x_{n+1}\right|<{\beta }_{0n}{({\omega }_0/{\beta }_{0(n+1)})}^{\frac{{\alpha }_n}{{\alpha }_{n+1}}}\end{array}.$$

(35)

The right size of the above inequality presented the limits of steady-state errors in a closed-loop system. Clearly, the anti-disturbance ability of ESO is decided by the parameter setting. Let $\sigma ={\beta }_{0i}{({\omega }_0/{\beta }_{0(n+1)})}^{\frac{{\alpha }_i}{{\alpha }_{n+1}}}$, when ${\beta }_{0(n+1)}$ is large enough, the system steady-state error is very small, but easily leads to vibration of ESO system. When $0<{\alpha }_i<{\alpha }_{i+1}<\cdots {\alpha }_{n+1}<1$, we have $\sigma <{\beta }_{0i}({\omega }_0/{\beta }_{0(n+1)})$, indicating compared with linear feedback, the nonlinear feedback showed smaller steady-state error and stronger following ability and anti-disturbance ability. Moreover, the high-order system usually adopts a high-order ESO, but the amplitude ${\omega }_0$ of highest-order changing rate is very large, leading to larger ${\beta }_{0(n+1)}$, which not only complicates the parameter adjustment, but also easily makes the ESO unable to converge, or even the ADRC system unstable. Thus, ADRC systems at 3rd order or above are usually decomposed by the time scale into cascade systems, while the ESO adopts the low-order series form. Thereby, it is indicated a low-order cascade system contributes to improving the anti-disturbance ability of ESO and thereby improves the stability of ADRC systems.

4. Experimental Results and Analysis

To validate the effectiveness of the new control method, space arc trajectory follow-up experiments were conducted in a six-degree-of-freedom robot platform, in which the 6R industrial robots HSR-JR605-C (its parameters are in

Table 1. Modified D-H parameters of Robot.

Joint $\mathit{i}$	Link Twist ${\mathit{\alpha }}_{\mathit{i}}$ (°)	Link Length ${\mathit{a}}_{\mathit{i}}$ (mm)	Link Offset ${\mathit{d}}_{\mathit{i}}$ (mm)	Joint Angle
1	0	0	0	$q_1$
2	−90	0	0	$q_2$
3	0	360	0	$q_3$
4	−90	90	376.5	$q_4$
5	90	0	0	$q_5$
6	−90	0	0	$q_6$

) were used. Cartesian space arc trajectory was selected. The robot load was 3.6 kg, the initial attitude was $\mathit{q}={[0,-\pi /2,0,0,\pi /2,0]}^T$; the space arc trajectory was determined from the three space coordinates of the end-point P, where, $\mathrm{A}=[376.5,0,331]$, $\mathrm{B}=[396.5,20,331]$, $\mathrm{C}=[416.5,0,331]$, and arc center $\mathrm{O}=[396.5,20,331]$ in mm, as shown in Figure 7.

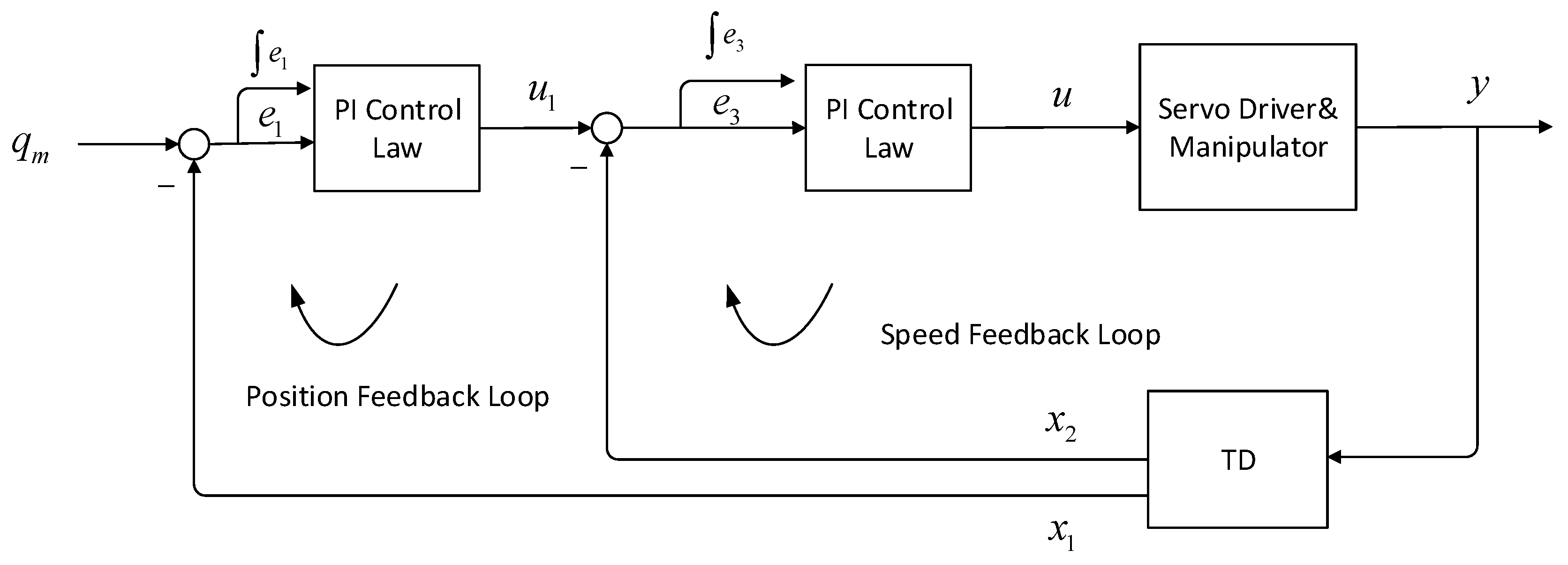
Point P is accelerated and clockwise along an arc from point A to point C, and then returns clockwise along from point C to point A. With the Cartesian space circular interpolation algorithm and the inverse kinematics computation, we could determine the joint motion status order. The input of this order is to convert the transmission ratio into motor end motion. It should be noted the on-line computation of the inverse dynamic model is much time-consuming, which may affect the timeliness of the controlled loops. Thus, here it is set as ‘background program’, and the computation memory is pre-stored and extracted in real-time. To validate the superiority of the new control algorithm in Figure 8, we select the commonly-used PI control algorithm as a comparison:

Its control algorithm consists of:

• Differential state estimation

  $$\{\begin{array}{l}fh=fhan(x_1-y,x_2,R,h_0)\\ x_1=x_1+h_0\cdot x_2\\ x_2=x_2+h_0\cdot fh\end{array};$$

  (36)
• Position loop control algorithm

  $$\{\begin{array}{l}{e}_1=q_m-x_1\\ e_0={\displaystyle \int e_{1}dt}\\ u_1={\beta }_{0}fal(e_0,0.25,1.0)+{\beta }_{1}fal(e_1,0.5,1.0)\end{array};$$

  (37)
• Velocity loop control algorithm

  $$\{\begin{array}{l}{e}_3=u_1-x_2,e_2={\displaystyle \int e_{3}dt}\\ u={\beta }_{2}fal(e_2,0.25,1.0)+{\beta }_{3}fal(e_3,0.5,1.0)\end{array}.$$

  (38)

As for the indices of response speed and trajectory following precision, we investigate the following trajectories of different joints in the joint coordinate system and the following trajectory of the end-point position in the Cartesian coordinate system. To reasonably evaluate the controller performance, we have to acquire accurate real-time robot joint position and attitude states and the Cartesian coordinates of the end-point ends, and when the joint flexibility has been ignored and for simplification, we recognize that the coder positional information directly reflected the joint positional information. The end-point Cartesian coordinates were acquired from robot forward kinematics, without any external measuring tool. Based on the semi-closed-loop control structure, we regulate the parameters of the two controllers to optimize the following performance. The parameters of the two controllers in Equations (15–20) and (36–38) are listed in

Table 2. Robot controller parameters.

Electromechanical Parameters	Torque constant $k_m=[0.354,0.354,0.283,0.276,0.276,0.226]$ (Nm/A), Gear ratio $\eta =[81,100,80,76.5,81,50]$, Motor shaft rotary inertia $J_m^{}=[0.130,0.130,0.044,0.027,0.027,0.005]$ ($\mathrm{kg}{m}^2\times {10}^{-3}$)
ADRC feedforward controller (6-shafts)	TD	$R=40,h_0=0.0002$
	ESO	$\begin{array}{cc}\hfill \mathrm{ESO}1:& {\beta }_{01}=[500,500,500,500,500,500]\hfill \\ & {\beta }_{02}=[5000,5000,5000,5000,5000,5000]\hfill \\ & h_1=0.002\hfill \end{array}$ $\begin{array}{cc}\hfill \mathrm{ESO}2:& {\beta }_{03}=[5000,5000,5000,5000,5000,5000]\hfill \\ & {\beta }_{04}=[50000,50000,45000,40000,40000,40000]\hfill \\ & h_2=0.0002\hfill \end{array}$ $b_0=J_m{}^{-1}{k}_m\zeta$, $\zeta =[0.950,0.950,0.980,0.980,0.980,0.990]$
	P	Position Loop: ${\beta }_1=[400,400,350,250,200,200]$ Speed Loop: ${\beta }_2=[5000,5000,4000,4000,4000,4000]$
	$\delta =1/\eta k_m$	$\delta =[0.03487,0.02824,0.04427,0.04736,0.04473,0.08850]$
PI controller (6-shafts)	TD	$R=40,h_0=0.0002$
	PI	Position Loop: $\begin{array}{l}{\beta }_0=[0,0,0,0,0,0]\\ {\beta }_1=[1000,1000,800,500,500,500]\end{array}$ Speed Loop: $\begin{array}{l}{\beta }_2=[0,0,0,0,0,0]\\ {\beta }_3=[10000,10000,8000,8000,5000,5000]\end{array}$

.

The servo periods of the position loop and the velocity loop were 2 ms and 200 µs, respectively, and the sampling period was 200 µs. Let the angular velocity of the end-point P of the operating arm resolving around the circle center O be $w=2,4,6,8(rad/s)$. 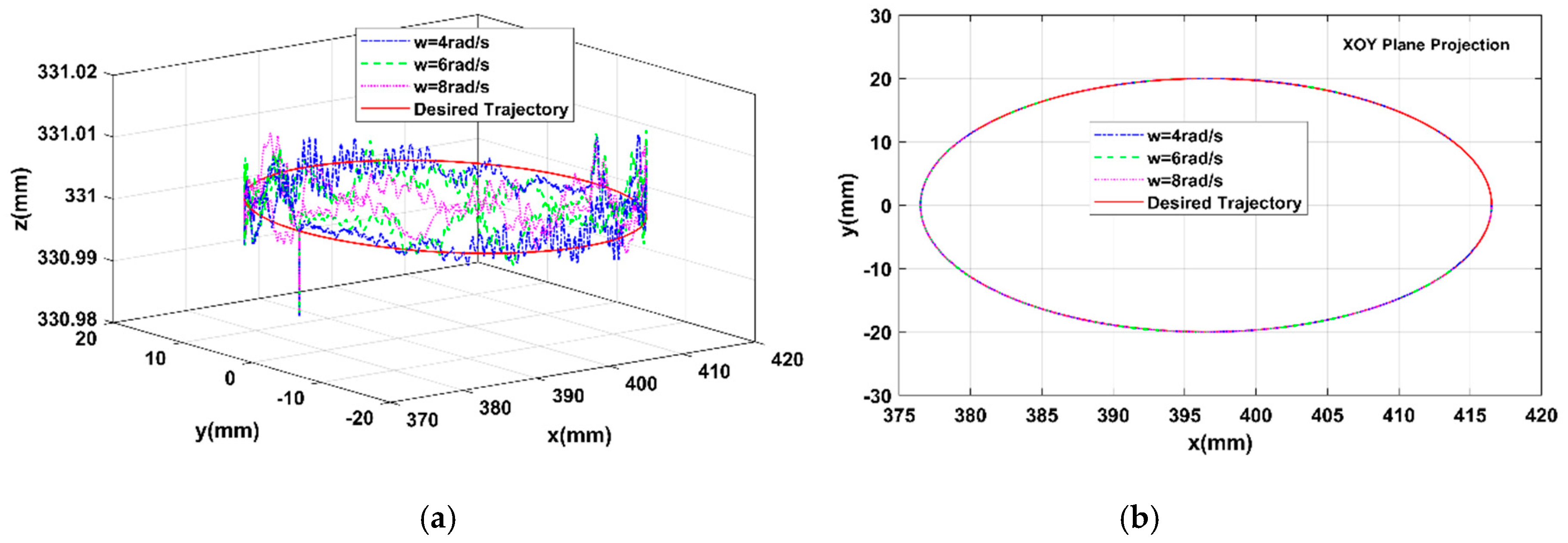The representative joint trajectory follow-up results and end-point Cartesian trajectory follow-up results of joint 2 are shown in Figure 9, Figure 10 and Figure 11. The end-point trajectory follow-up results at different speeds are shown in Figure 12.

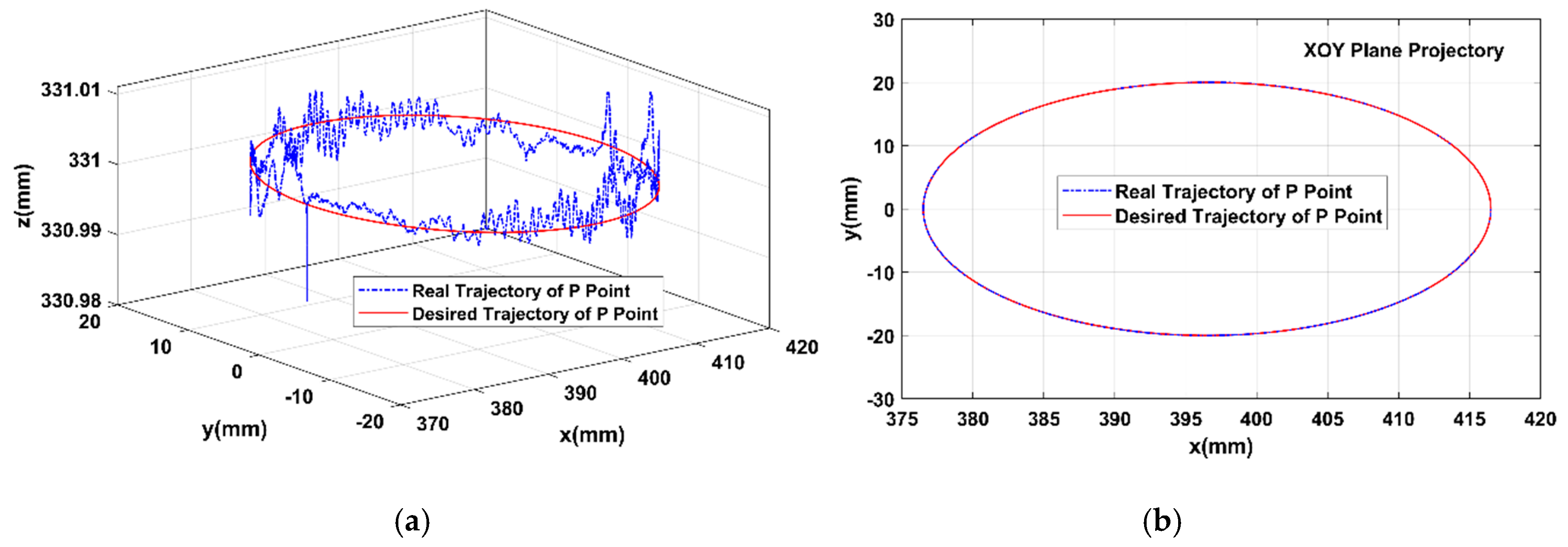
The above figures show the PI controller and the ADRC controller based on dynamic feedforward (or ADRC controller for short) both could stably follow the trajectory, but the following precision and response speeds both differed. In the joint coordinate system, for the large-inertia joint 2, the trajectory following error of the PI controller was very large (about 0.005 rad) (Figure 9b), which was higher than that of the ADRC controller (Figure 9d). As for the response speed, the new controller also outperformed the PI controller (Figure 9a,c). 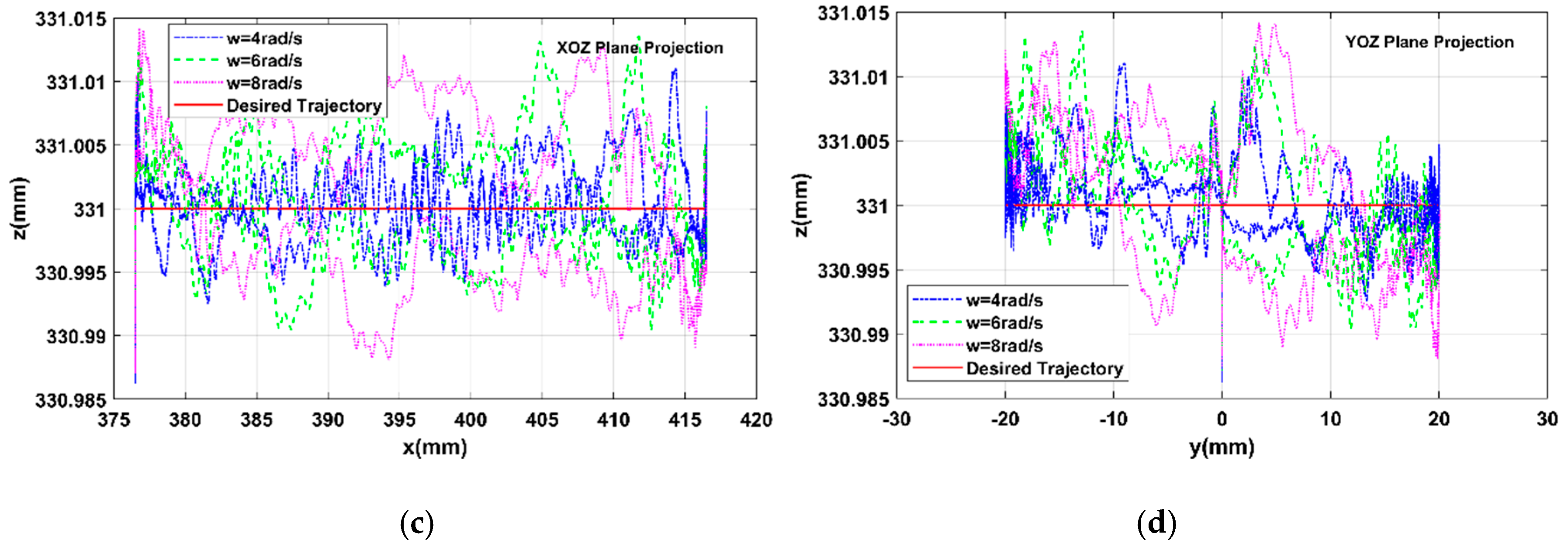Clearly, the ADRC controller outperformed the PI controller in both control precision and response speed, but the joint end-point following trajectory was more precise in the Cartesian coordinate system (Figure 10). As for planar projection, the ADRC feedforward showed control precision over the robot end-point end up to 0.015 mm (Figure 10c,d), which was far higher than the PI controller (0.3 mm, Figure 11c,d). As for error distributions, the end-point following error of the robot was very large upon the start-up, which was largely induced by the joint friction. Firstly, the joint static friction after the start of movement was very large, which could not be rapidly adjusted by a pure PI controller; secondly, due to the errors of the friction model, the static friction at the time of mutation was hard to be monitored or compensated promptly. Admittedly, relative to the PI controller, our new ADRC controller could well inhibit the friction uncertain disturbance, and generally, was outstanding in terms of control precision and response speed. Moreover, at different speeds, especially high speed (8 rad/s), the ADRC controller showed both high-quality trajectory follow-up and robustness (Figure 12).

To verify the position repeatability of robot, we set the start/stop point A (376.5, 0, 331), and control the robot end-point to perform a periodic circular motion to stop at point A for 20 times (w = 2 rad/s). The end-point Cartesian coordinates ($\overline{x}$, $\overline{y}$ and $\overline{z}$ in

Table 3. Position repeatability of robot end-point.

Samples	$\overline{\mathbf{x}}$ (mm)	$\overline{\mathbf{y}}$ (mm)	$\overline{\mathbf{z}}$ (mm)	${\mathit{t}}_{\mathit{i}}$ (mm)
1	376.505	0.004	331.008	0.010
2	376.497	0.002	331.001	0.003
3	376.495	−0.006	331.004	0.008
4	376.497	0.004	331.004	0.006
5	376.505	0.001	330.994	0.008
6	376.502	0.007	331.005	0.009
7	376.501	−0.005	331.002	0.005
8	376.503	−0.003	330.992	0.009
9	376.492	−0.004	331.003	0.009
10	376.494	−0.004	330.995	0.009
11	376.505	0.007	331.005	0.010
12	376.508	0.002	330.998	0.008
13	376.501	0.009	331.005	0.010
14	376.498	0.005	331.002	0.006
15	376.505	0.005	330.998	0.007
16	376.501	−0.004	330.995	0.006
17	376.502	0.003	331.006	0.007
18	376.503	0.01	330.999	0.010
19	376.498	−0.005	331.001	0.005
20	376.502	0.007	331.003	0.007
δ	0.0079 (mm)
3δ	0.0237 (mm)

) were acquired from robot forward kinematics based on the sampled information of encoders.

The $t_i$ and δ are expressed in Equations (39) and (40), respectively.

$$t_i=\sqrt{{(x-\overline{x})}^2+{(y-\overline{y})}^2+{(z-\overline{z})}^2},$$

(39)

where (x, y, z) = (376.5, 0, 331); i = 1, 2, 3, …, 20.

$$\delta =\sqrt{\frac{{\displaystyle \sum _{i=1}^n{(\overline{t}-t_i)}^2}}{n-1}},$$

(40)

where $\overline{t}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{t}_i}$, n = 20.

It can be seen that the repetitive position accuracy is slightly higher than the trajectory following accuracy. However, it should be noted that the actual repetitive position accuracy will be slightly worse because we acquire the end-point Cartesian coordinates from the encoders and theoretical calculation based on robot forward kinematics.

5. Conclusions

To improve the robustness of the dynamic feedforward control system, we put forward an ADRC strategy based on dynamic feedforward starting from the control perspective and combining the simple structure, strong anti-interference ability and no restraint from the control model of ADRC.

(1) Together with the dynamic characteristics of robots, we analyze the system disturbance compensation methods, and by regarding robots as motor output load, achieve multi-joint control decoupling through dynamic characteristic compensation and uncertain disturbance compensation.

(2) As for the uniaxial independent systems after decoupling, we study the ADRC series control structure and algorithm based on dynamic feedforward, and investigate the closed-loop stability by analyzing the dynamic linearization compensation and ESO anti-disturbance ability.

(3) Space arc trajectory following experiments have been conducted to comprehensively evaluate the 6-joint motion performances of robots. The ADRC controller based on dynamic feedforward outperforms traditional PI controllers in terms of trajectory following precision and response speed, and shows high values of practical engineering. It should be noted ADRC controllers are structurally diverse, and this study just proves the high efficiency of the P control law. To further improve the controller performance, other more advanced PD control law and ESO combination may be used, which is not elaborated here.