Radiation Properties of Conformal Antennas: The Elliptical Source
Abstract
:1. Introduction
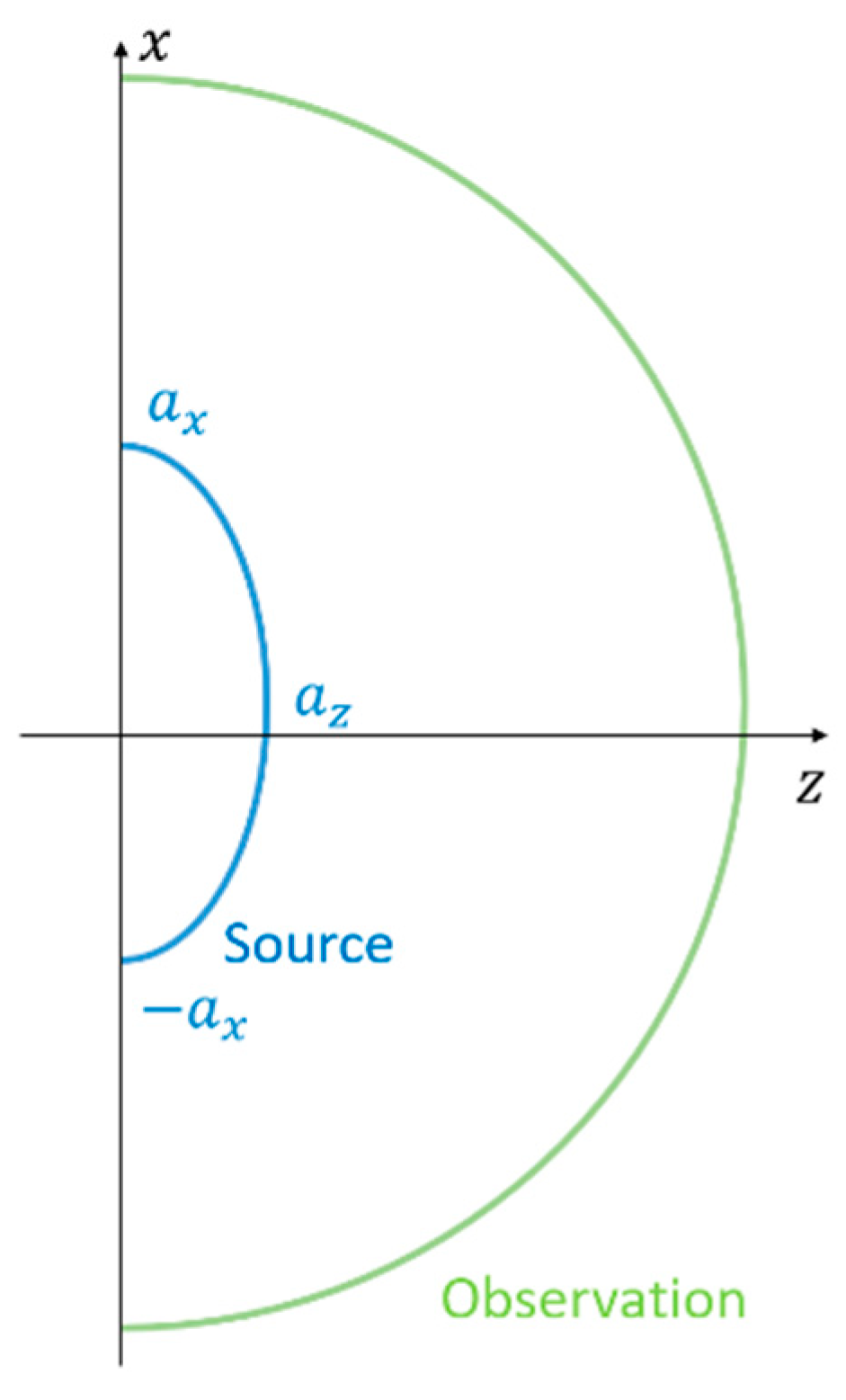
2. Problem Formulation and Method Description
3. Analysis of Some Source Geometries
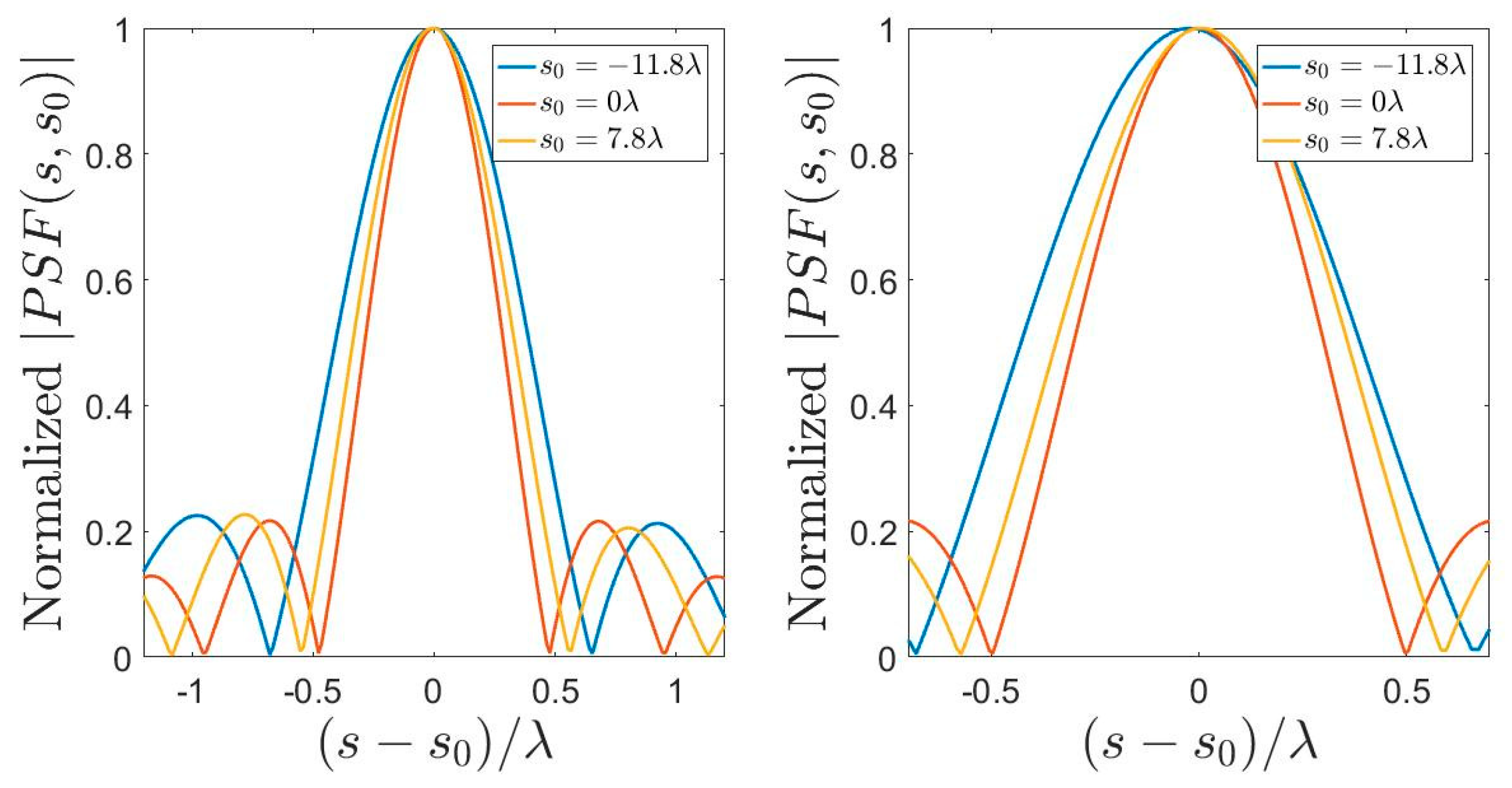
3.1. Linear Source
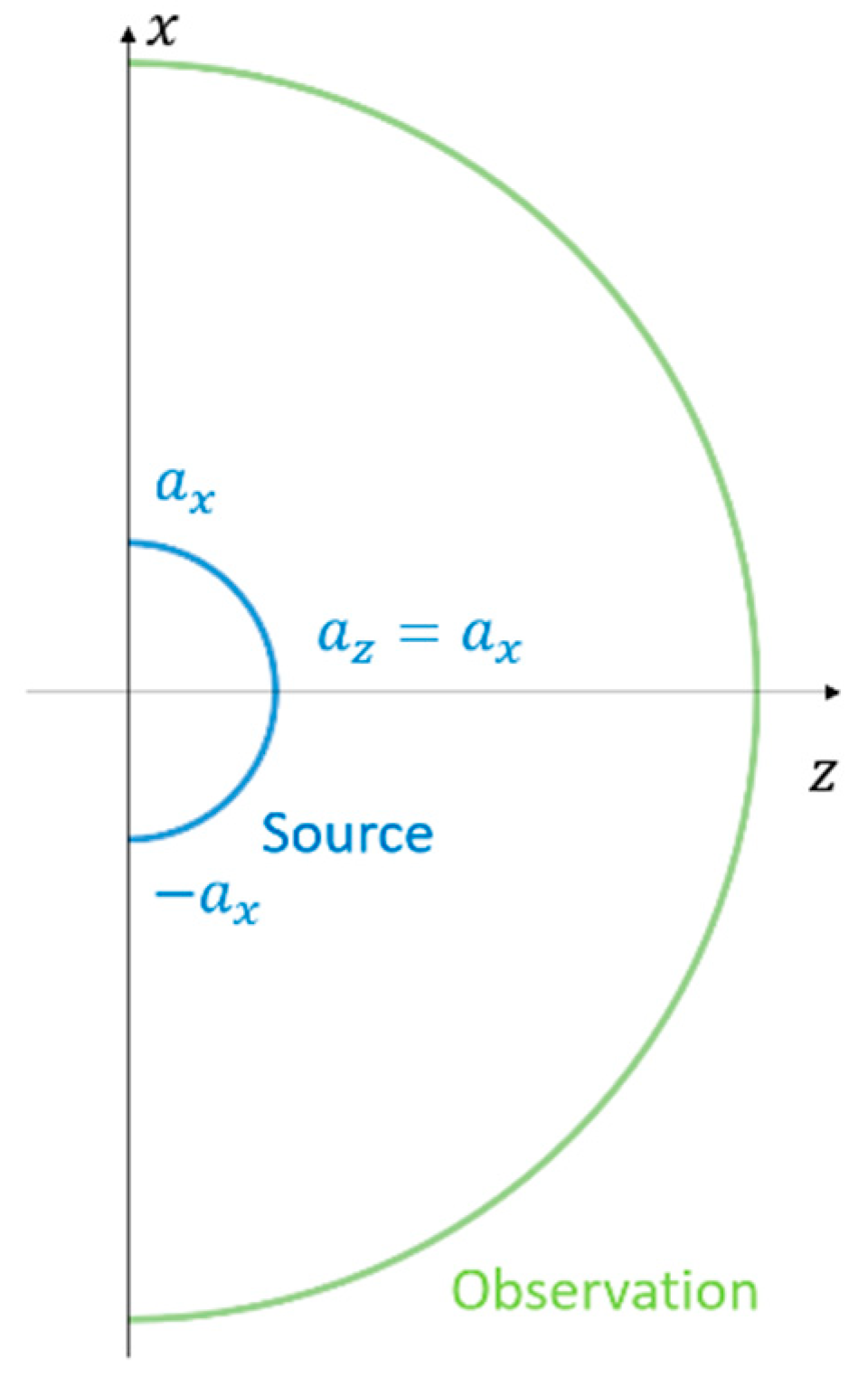
3.2. Semi-Circumference Source
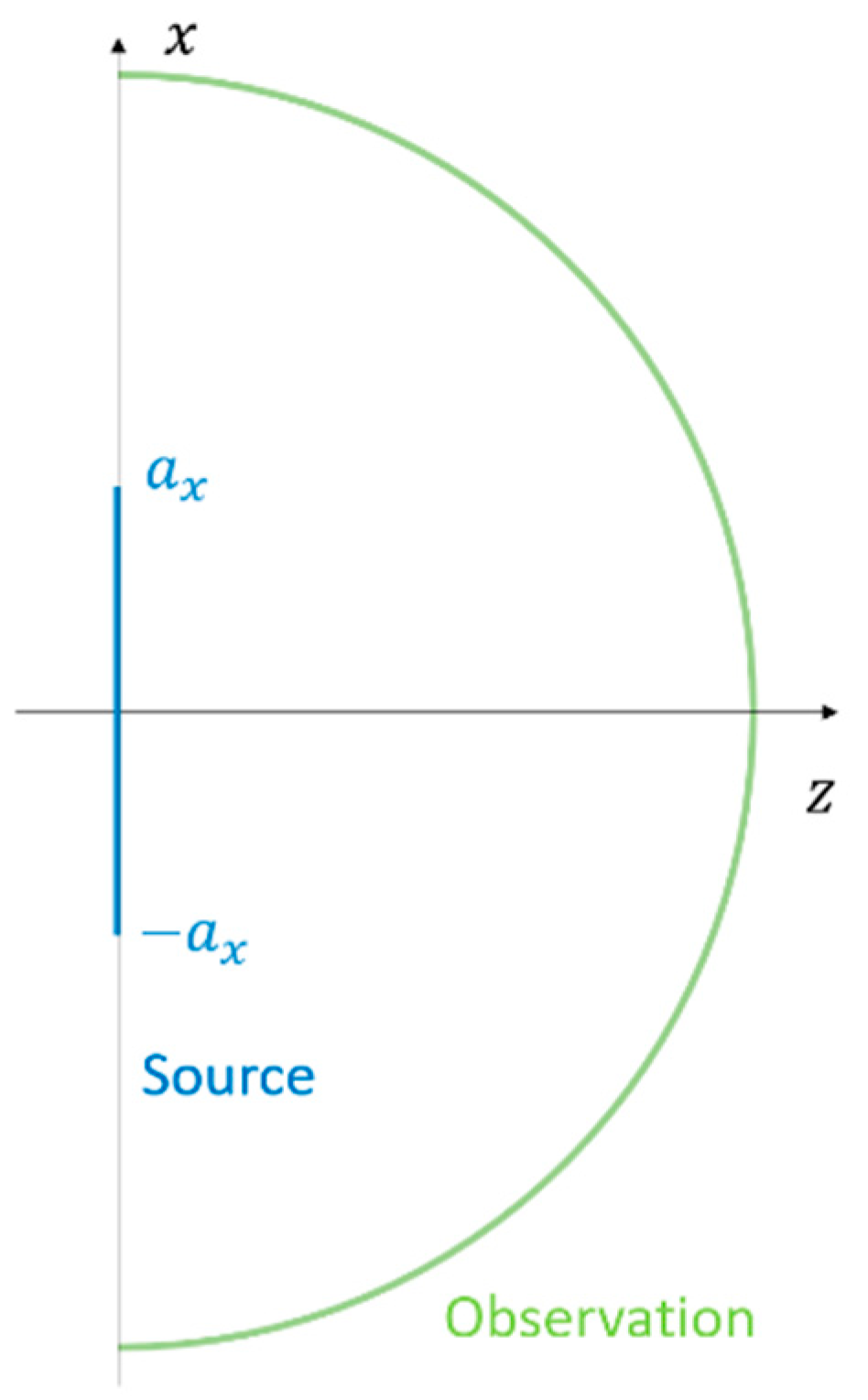
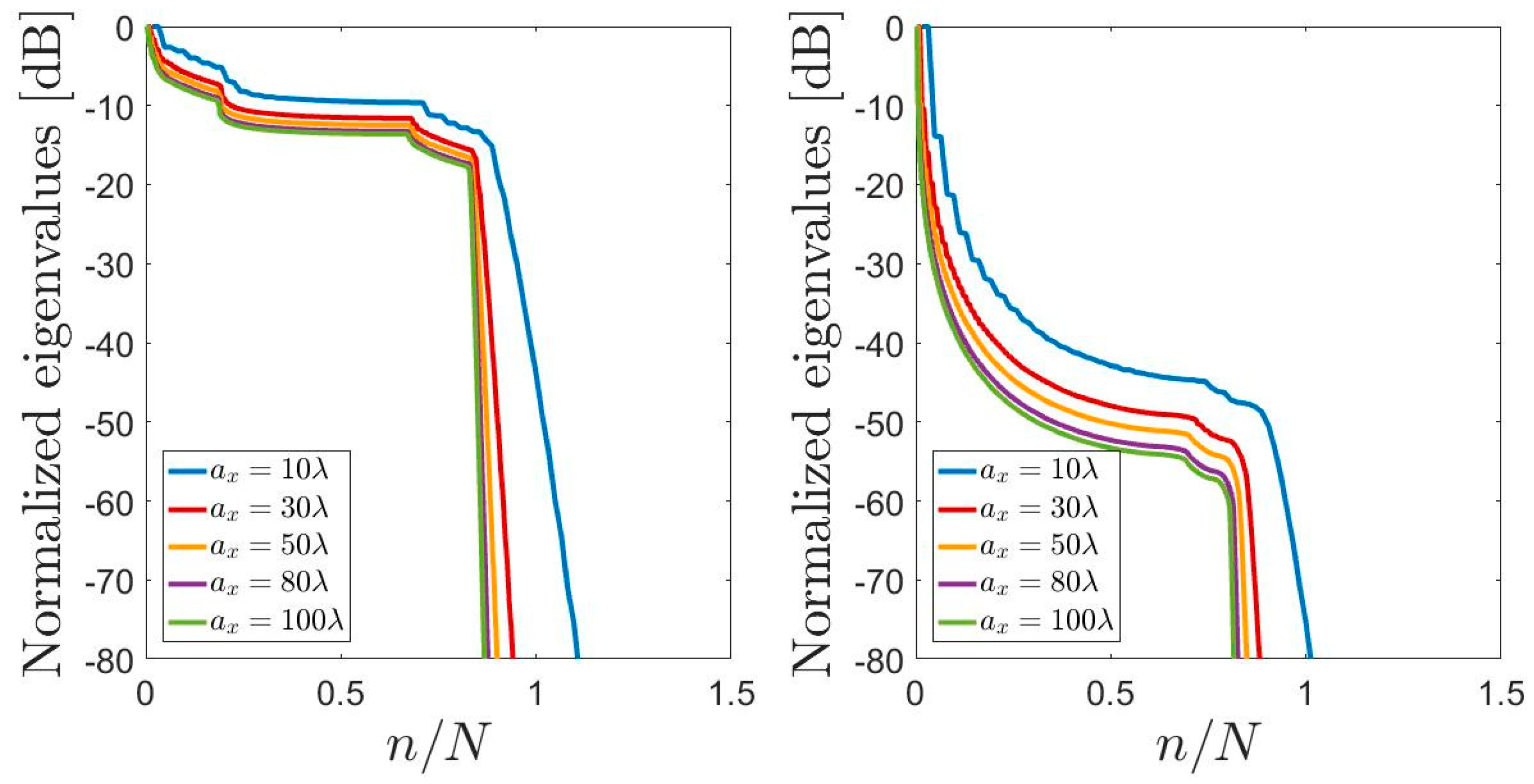
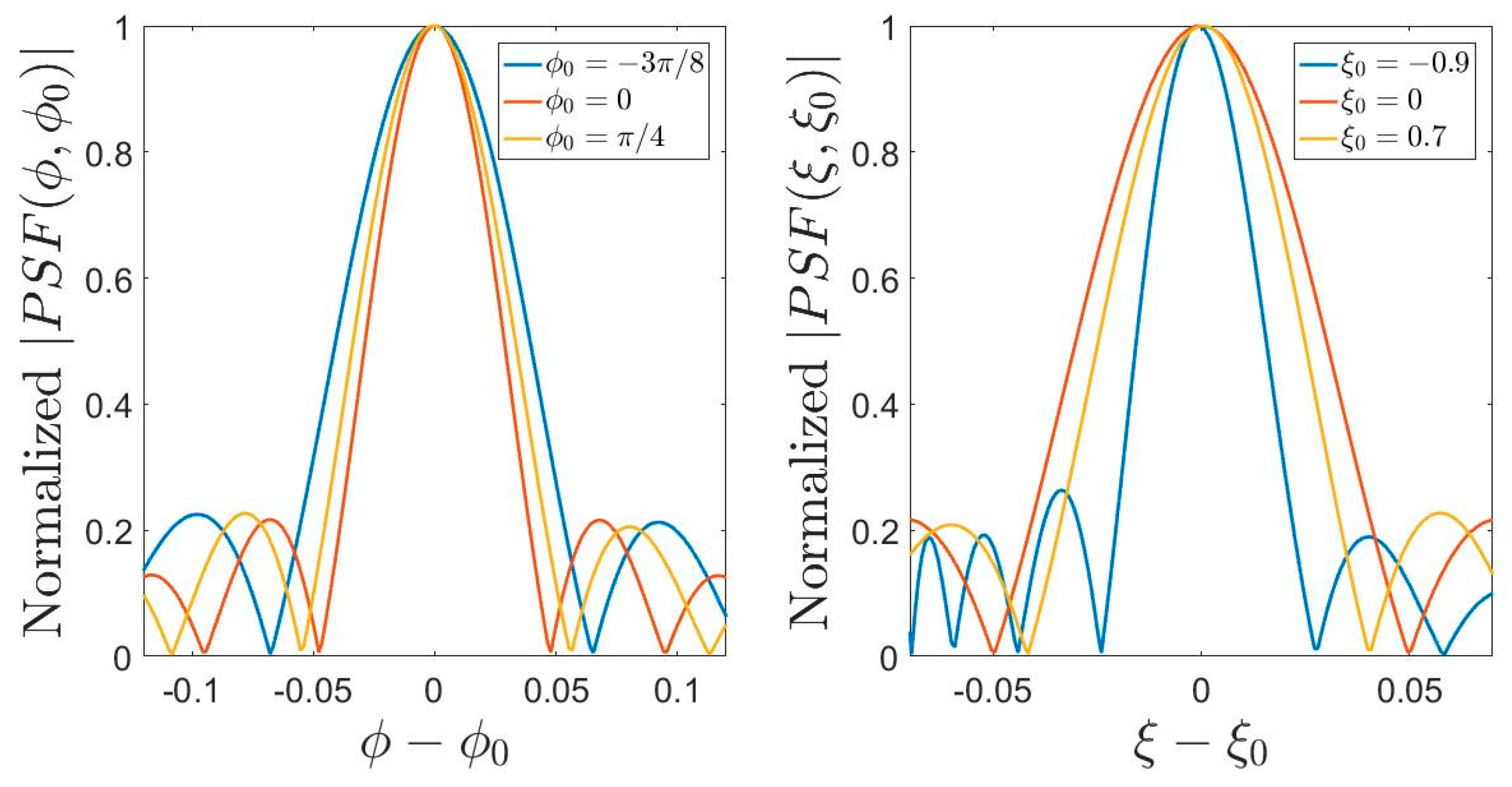
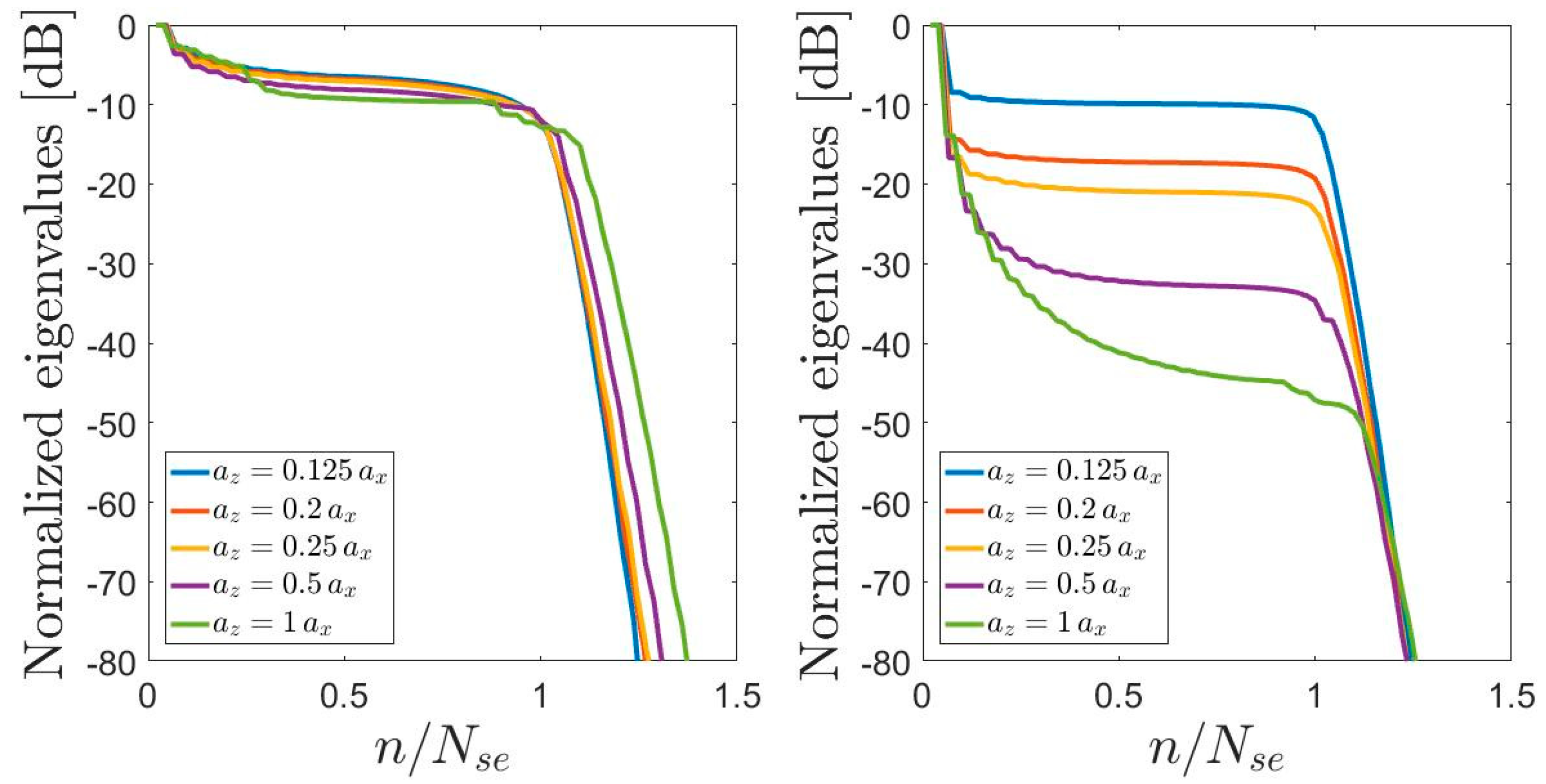
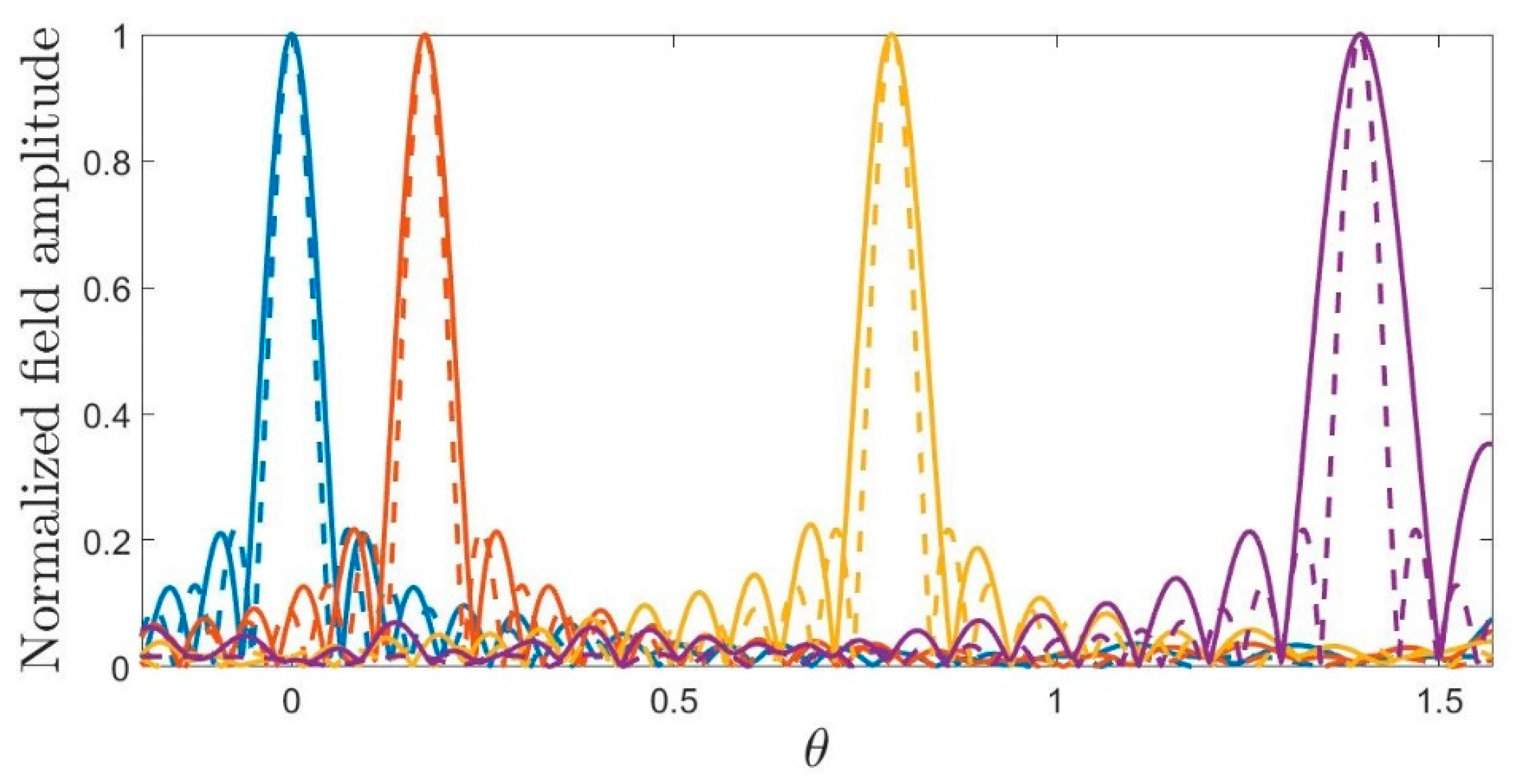
3.3. Semi-Elliptic Source
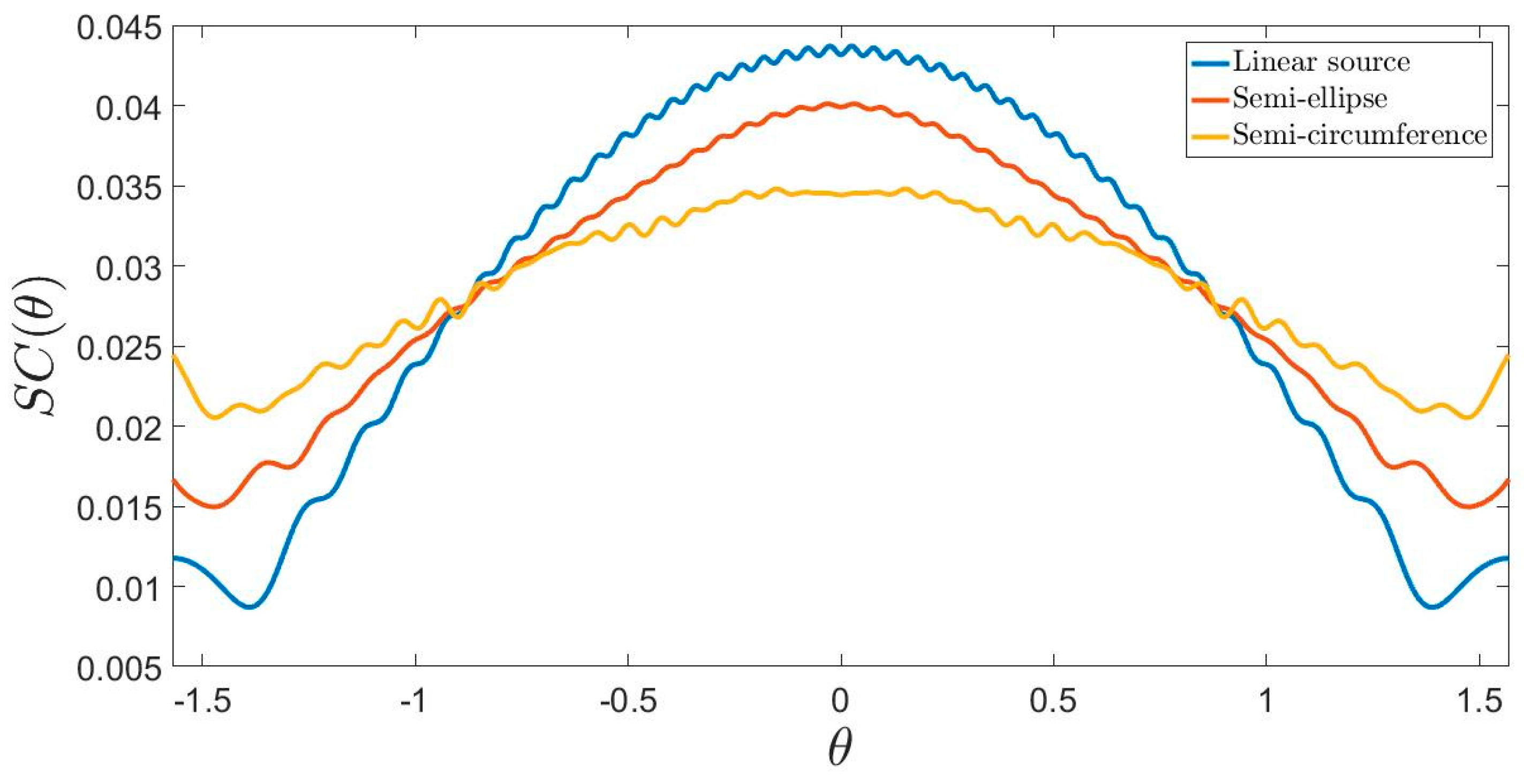
4. Discussion of the Results
- For a fixed extension of the source, increasing the dimension leads to an increase of the NDF dictated by (17).
- The NDF does not depend on the choice of the variables considered in this study.
- Equation (17) returns a more accurate estimation for the NDF of a semi-circumference source with respect to the upper bound (13) provided by [27].
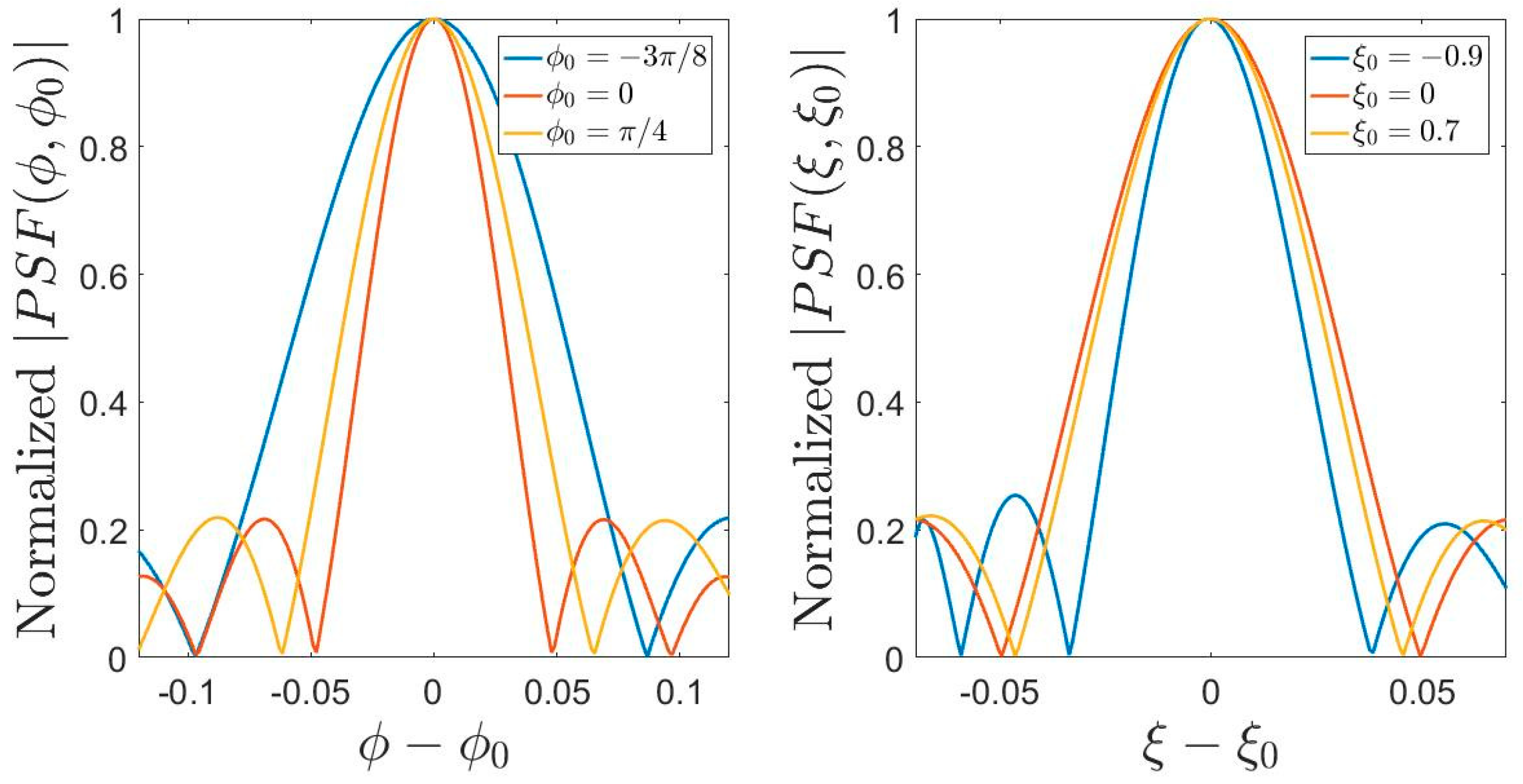
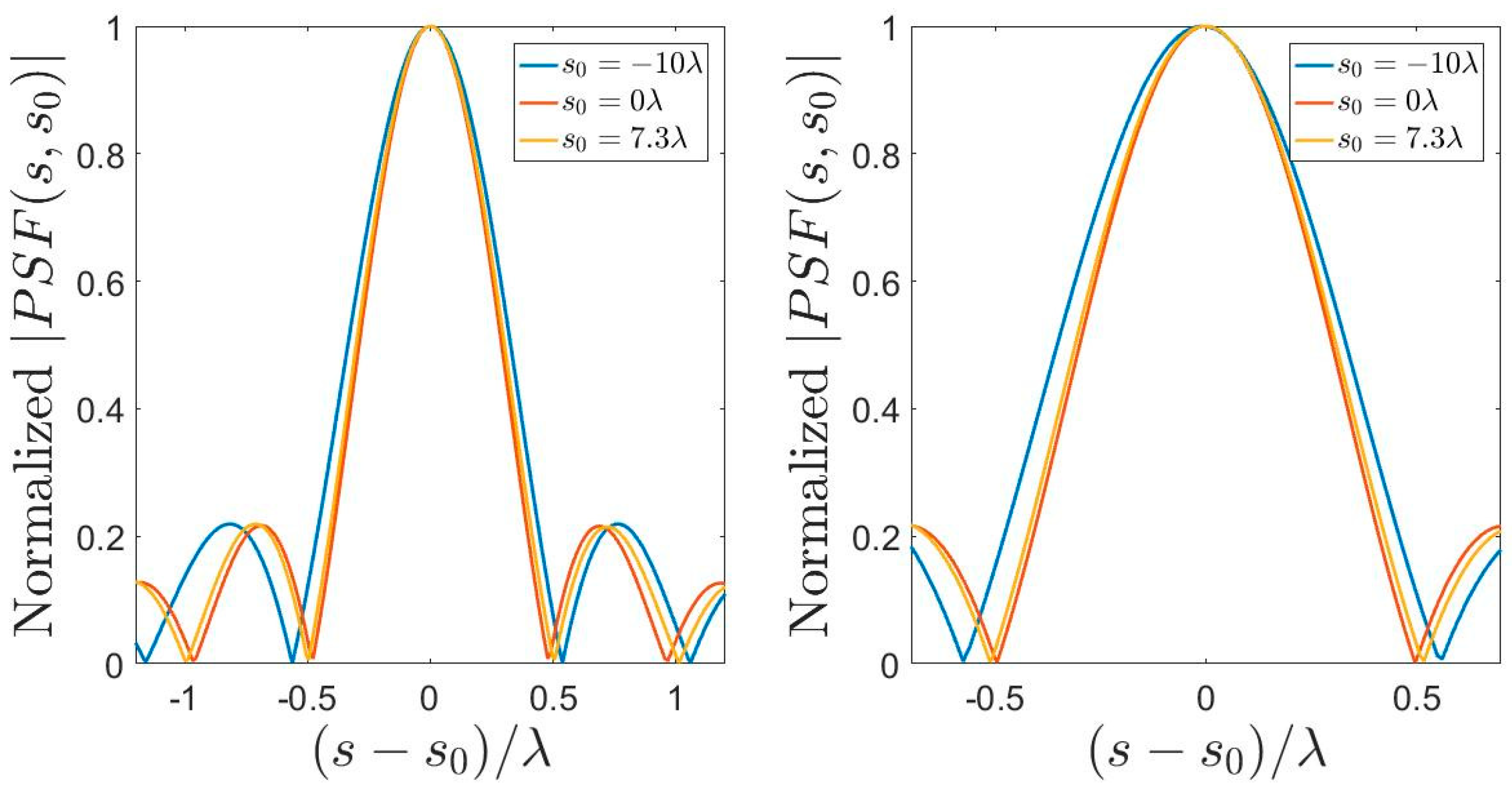
- Except for the limit case of a linear source that presents an invariant PSF for both the considered variable choices, increasing the dimension of the source leads to a variant PSF along the source domain, independent of the variables choice.
- The PSF is always variant along the observation domain, independent of the considered variables choice.
- Among all the possible variables choices discussed in this paper, the one ensuring a more invariant PSF is the arc length.
5. Examples of Antenna Applications
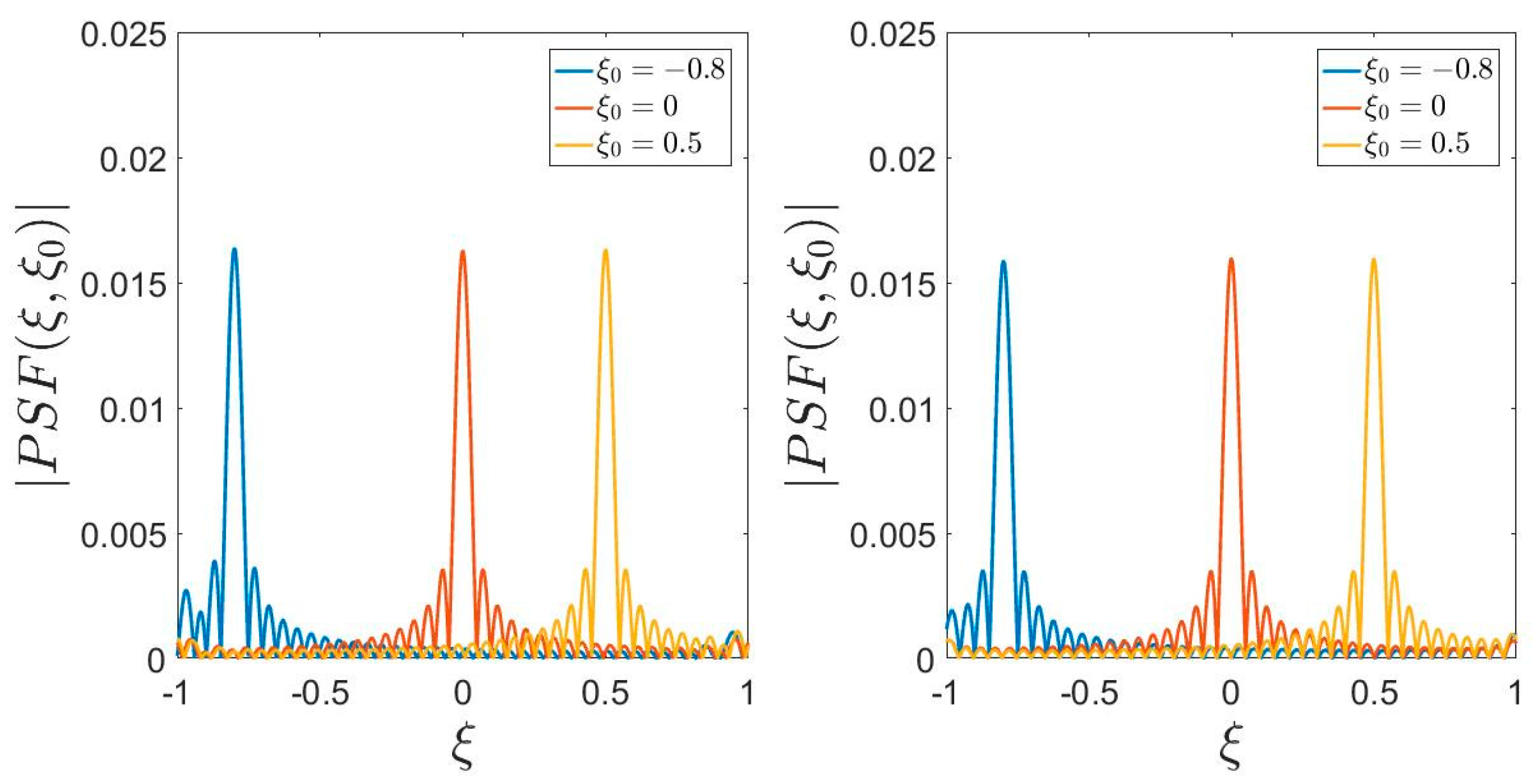
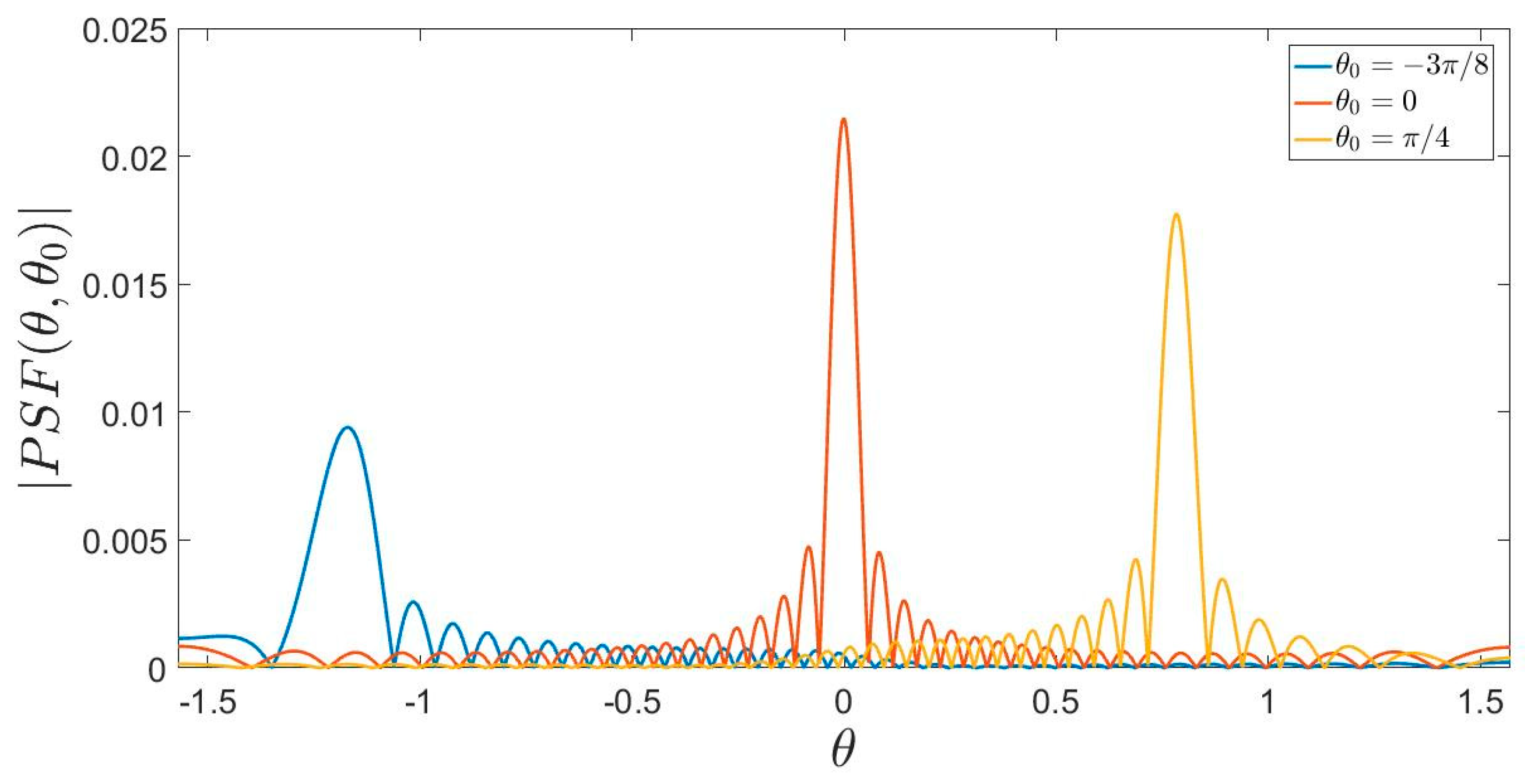
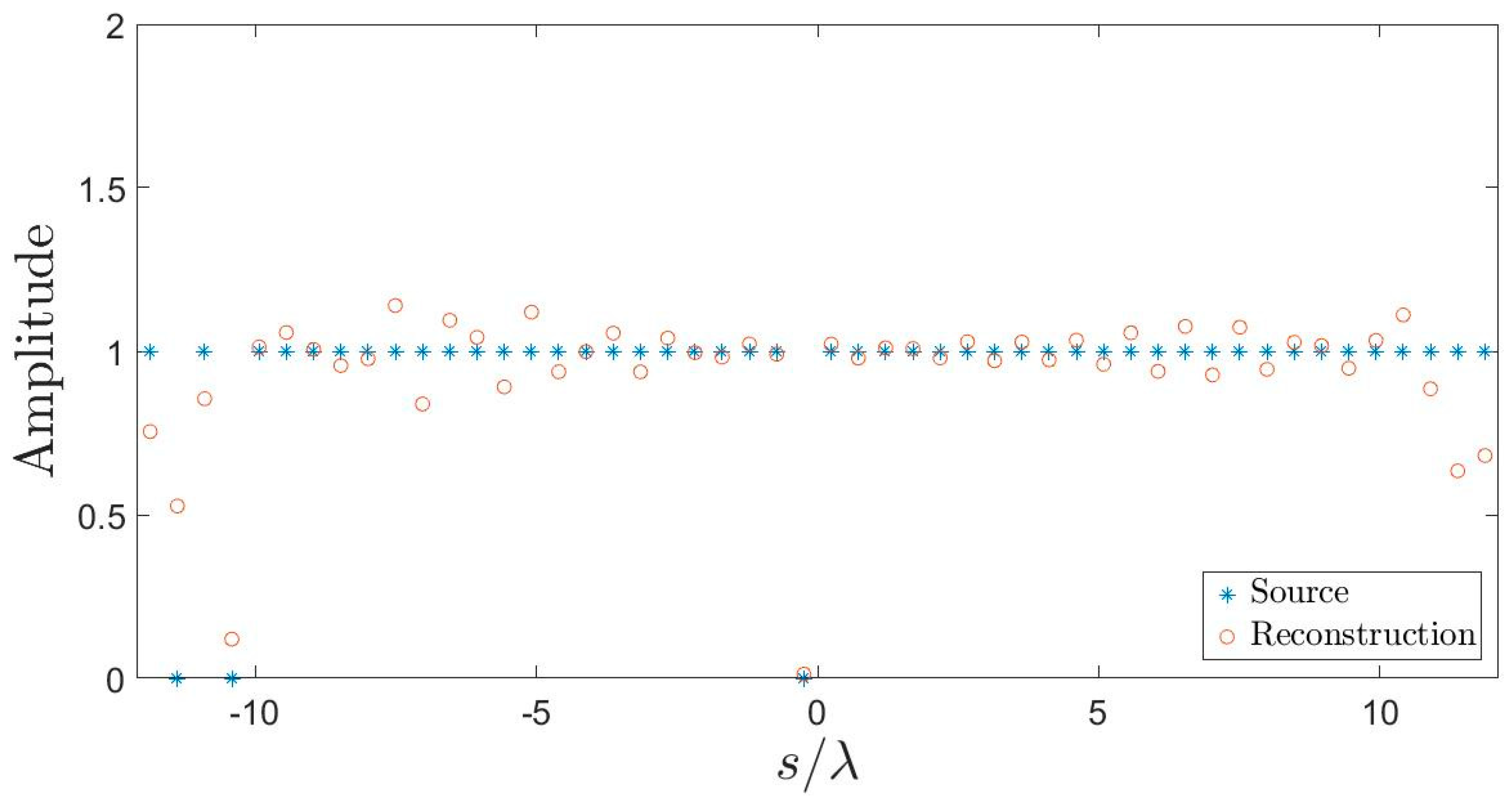
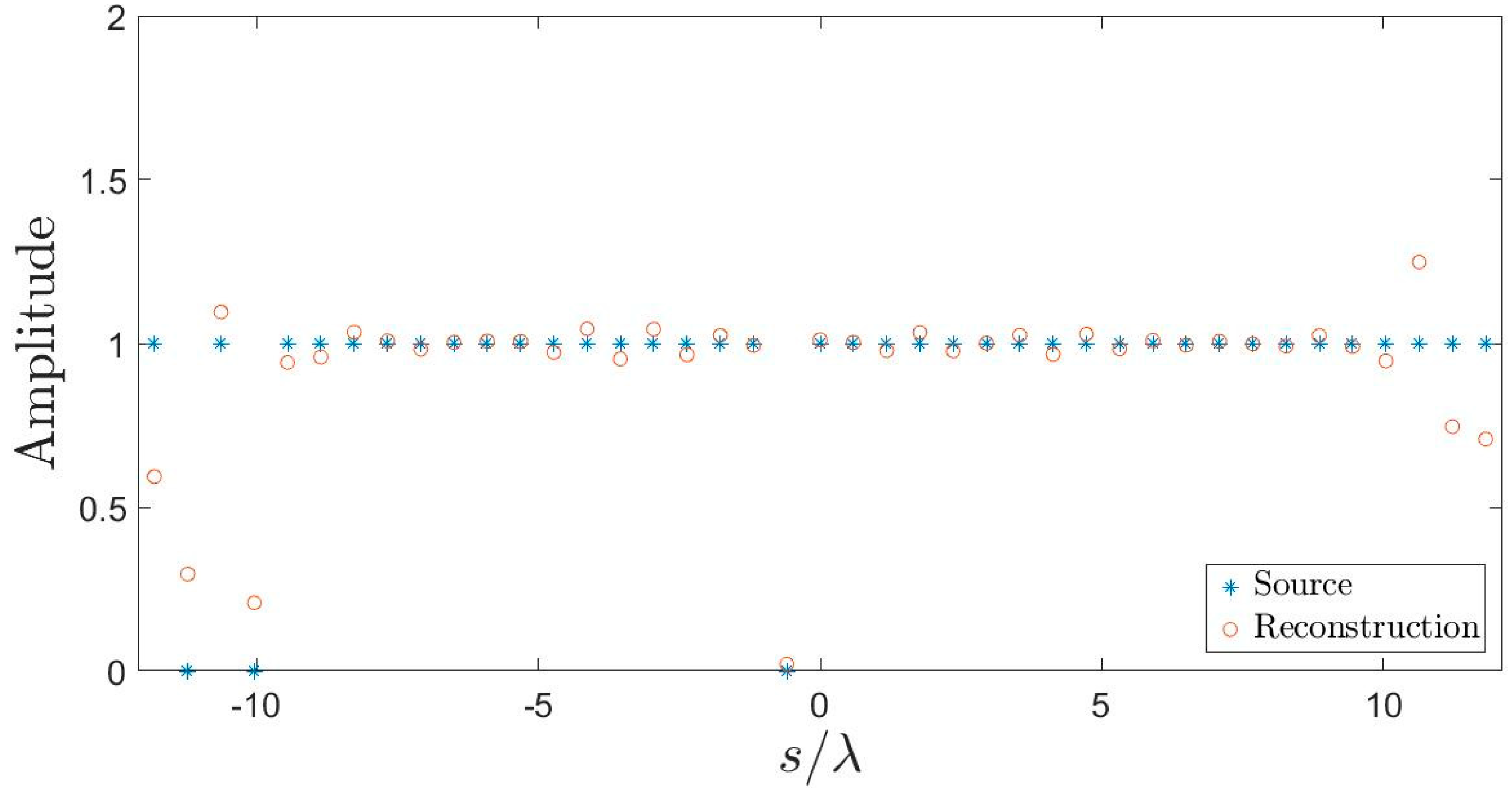
5.1. Array Diagnostics
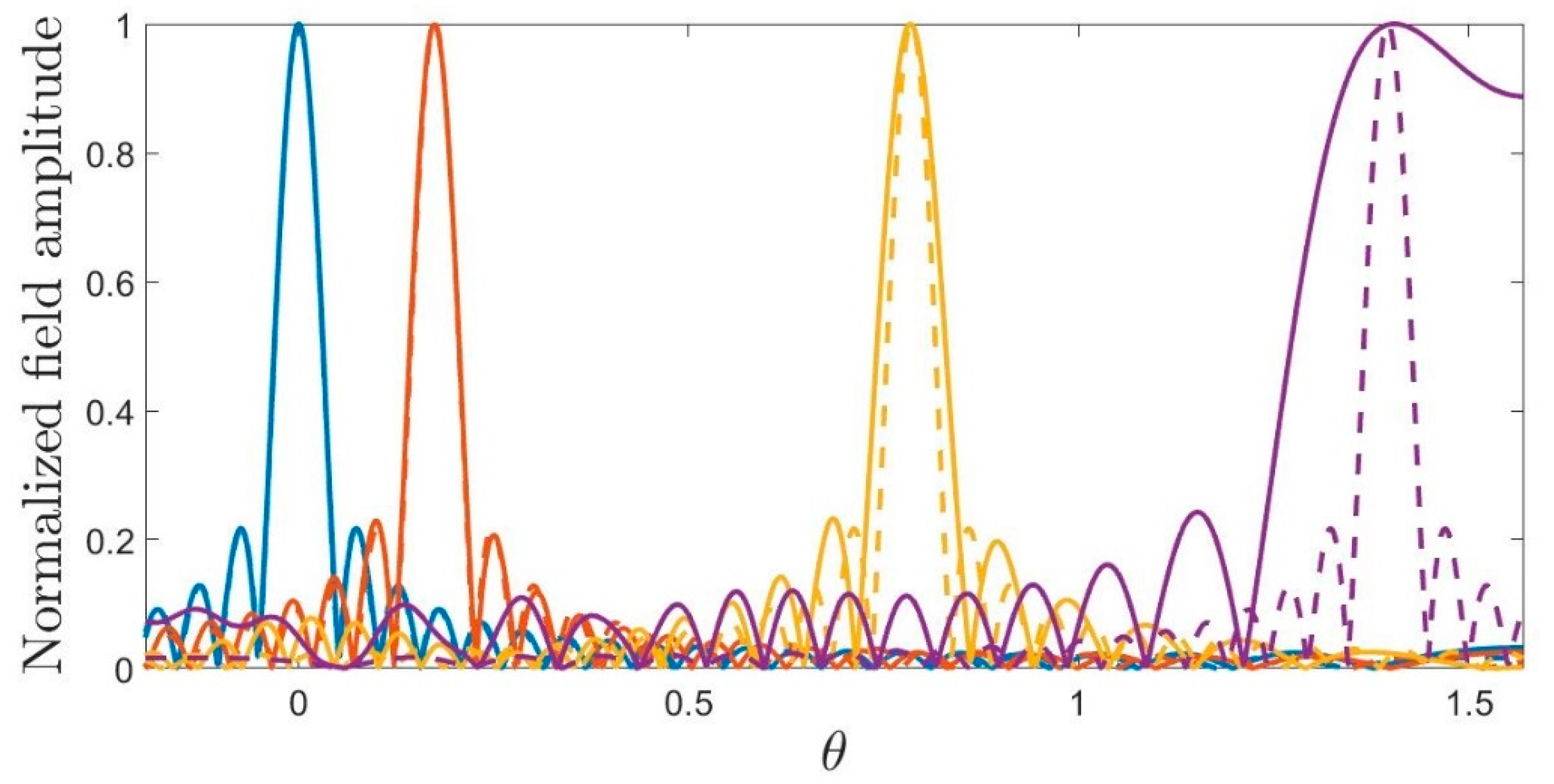
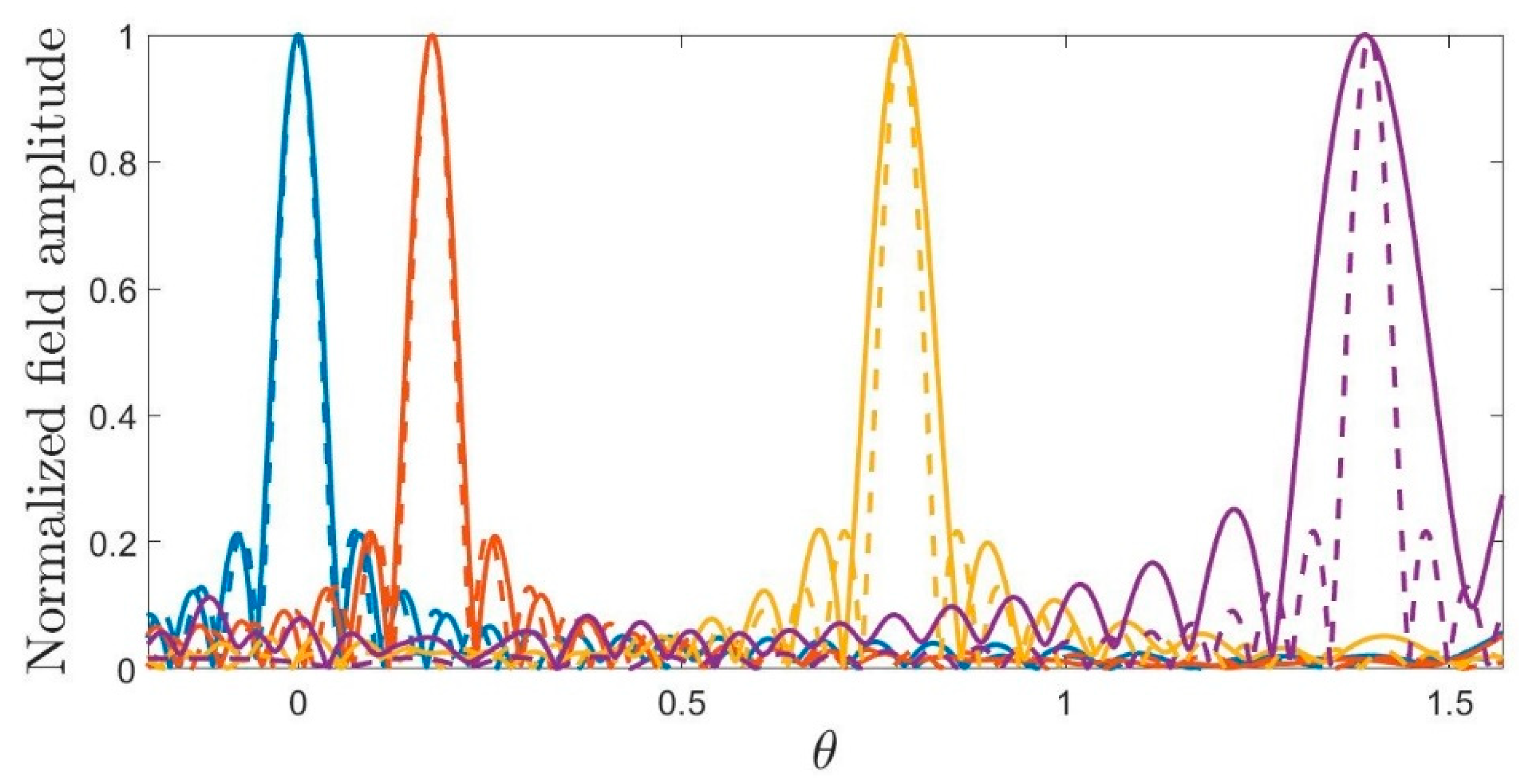
5.2. Pattern Synthesis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Josefsson, L.; Persson, P. Conformal Array Antenna Theory and Design; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Semkin, V.; Ferrero, F.; Bisognin, A.; Ala-Laurinaho, J.; Luxey, C.; Devillers, F.; Räisänen, A.V. Beam Switching Conformal Antenna Array for mm-Wave Communications. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 28–31. [Google Scholar] [CrossRef]
- Wang, Z.; Hall, P.S.; Kelly, J.R.; Gardner, P. Wideband Frequency-Domain and Space-Domain Pattern Reconfigurable Circular Antenna Array. IEEE Trans. Antennas Propag. 2017, 65, 5179–5189. [Google Scholar] [CrossRef]
- Rodriguez-Gonzalez, J.A.; Ares-Pena, F.; Fernandez-Delgado, M.; Iglesias, R.; Barro, S. Rapid method for finding faulty elements in antenna arrays using far field pattern samples. IEEE Trans. Antennas Propag. 2009, 57, 1679–1683. [Google Scholar] [CrossRef]
- Carlin, M.; Oliveri, G.; Massa, A. On the robustness to element failures of linear ADS-thinned arrays. IEEE Trans. Antennas Propag. 2011, 59, 4849–4853. [Google Scholar] [CrossRef]
- Buonanno, A.; D’urso, M. On the diagnosis of arbitrary geometry fully active arrays. In Proceedings of the Fourth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010. [Google Scholar]
- Cappellin, C.; Meincke, P.; Pivnenko, S.; Jorgensen, E. Array antenna diagnostics with the 3D reconstruction algorithm. In Proceedings of the 34th Annual Symposium of the Antenna Measurement Techniques Association, Bellevue, WA, USA, 21–26 October 2012. [Google Scholar]
- Cheng, G.G.; Zhu, Y.; Grzesk, J. Exact solutions in antenna holography using planar spherical or cylindrical near-field data. In Proceedings of the 34th Annual Symposium of the Antenna Measurement Techniques Association, Bellevue, WA, USA, 21–26 October 2012. [Google Scholar]
- Schnattinger, G.; Eibert, T.F. 3D image generation from arbitrary antenna measurement data by solving the full vectorial inverse source problem. In Proceedings of the 34th Annual Symposium of the Antenna Measurement Techniques Association, Bellevue, WA, USA, 21–26 October 2012. [Google Scholar]
- Bucci, O.M.; Migliore, M.D.; Panariello, G.; Sgambato, P. Accurate diagnosis of conformal arrays from near-field data using the matrix method. IEEE Trans. Antennas Propag. 2005, 53, 1114–1120. [Google Scholar] [CrossRef]
- Patnaik, A.; Choudhury, B.; Pradhan, P.; Mishra, R.K.; Christoulou, C. An ANN application for fault finding in antenna arrays. IEEE Trans. Antennas Propag. 2007, 55, 775–777. [Google Scholar] [CrossRef]
- Brégains, J.C.; Ares, F. Matrix pseudo-inversion technique for the diagnostics of planar arrays. In Proceedings of the First European Conference on Antennas and Propagation, Nice, France, 6–10 November 2006. [Google Scholar]
- Oliveri, G.; Rocca, P.; Massa, A. Reliable diagnosis of large linear arrays—A Bayesian compressive sensing approach. IEEE Trans. Antennas Propag. 2012, 60, 4627–4636. [Google Scholar] [CrossRef]
- LaHaie, I.J.; Cossmann, S.M.; Blischke, M.A. A Model-Based Technique with ℓ 1 Minimization for Defect Detection and RCS Interpolation from Limited Data. Appl. Comput. Electromagn. Soc. J. 2013, 28, 1171–1178. [Google Scholar]
- Di Francia, G.T. Degrees of freedom of an image. J. Opt. Soc. Am. 1969, 59, 799–804. [Google Scholar] [CrossRef]
- Miller, D.A. Communicating with waves between volumes: Evaluating orthogonal spatial channels and limits on coupling strengths. Appl. Opt. 2000, 39, 1681–1699. [Google Scholar] [CrossRef]
- Piestun, R.; Miller, D.A. Electromagnetic degrees of freedom of an optical system. J. Opt. Soc. Am. A 2000, 17, 892–902. [Google Scholar] [CrossRef]
- Somaraju, R.; Trumpf, J. Degrees of freedom of a communication channel: Using DOF singular values. IEEE Trans. Inf. Theory 2010, 56, 1560–1573. [Google Scholar] [CrossRef]
- Frazin, R.A.; Fischer, D.G.; Carney, P.S. Information content of the near field: Two-dimensional samples. J. Opt. Soc. Am. A 2004, 21, 1050–1057. [Google Scholar] [CrossRef]
- Fischer, D.G.; Frazin, R.A.; Asipauskas, M.; Carney, P.S. Information content of the near field: Three-dimensional samples. J. Opt. Soc. Am. A 2011, 28, 296–306. [Google Scholar] [CrossRef]
- Solimene, R.; Maisto, M.A.; Pierri, R. Information Content in Inverse Source with Symmetry and Support Priors. Prog. Electromagn. Res. 2018, 80, 39–54. [Google Scholar] [CrossRef]
- Bertero, M.; Boccacci, P. Introduction to Inverse Problems in Imaging; IOP Publishing: Bristol, UK, 1998. [Google Scholar]
- Newsam, G.; Barakat, R. Essential dimension as a well-defined number of degrees of freedom of finite-convolution operators appearing in optics. J. Opt. Soc. Am. A 1985, 2, 2040–2045. [Google Scholar] [CrossRef]
- Den Dekker, A.J.; van den Bos, A. Resolution: A survey. J. Opt. Soc. Am. A 1997, 14, 547–557. [Google Scholar] [CrossRef]
- Leone, G. Source Geometry Optimization for Hemispherical Radiation Pattern Coverage. IEEE Trans. Antennas Propag. 2016, 64, 2033–2038. [Google Scholar] [CrossRef]
- Leone, G.; Maisto, M.A.; Pierri, R. “Application of Inverse Source Reconstruction to Conformal Antennas Synthesis. IEEE Trans. Antennas Propag. 2018, 66, 1436–1445. [Google Scholar] [CrossRef]
- Leone, G.; Maisto, M.A.; Pierri, R. Inverse Source of Circumference Geometries: SVD Investigation based on Fourier Analysis. Prog. Electromagn. Res. 2018, 76, 217–230. [Google Scholar] [CrossRef]
- Slepian, D.; Pollack, H.O. Prolate spheroidal wave functions, Fourier analysis, and uncertainty—I. Bell Syst. Techn. J. 1961, 40, 43–63. [Google Scholar] [CrossRef]
- Landau, H.J.; Pollack, H.O. The eigenvalue distribution of time and frequency limiting. J. Math. Phys. 1980, 77, 469–481. [Google Scholar] [CrossRef]

| HPBW | Linear source (rad) | Semi-ellipse (rad) | Semi-circumference (rad) | Assigned pattern (rad) |
|---|---|---|---|---|
| 0.043 | 0.047 | 0.056 | 0.043 | |
| 0.045 | 0.049 | 0.054 | 0.043 | |
| 0.063 | 0.065 | 0.065 | 0.043 | |
| 0.267 | 0.117 | 0.092 | 0.043 |
| D | Linear source (dB) | Semi-ellipse (dB) | Semi-circumference (dB) | Assigned pattern (dB) |
|---|---|---|---|---|
| 35.60 | 34.93 | 33.65 | 35.76 | |
| 35.57 | 34.78 | 33.67 | 35.77 | |
| 32.74 | 32.27 | 32.26 | 35.77 | |
| 21.75 | 27.42 | 29.45 | 35.88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leone, G.; Munno, F.; Pierri, R. Radiation Properties of Conformal Antennas: The Elliptical Source. Electronics 2019, 8, 531. https://doi.org/10.3390/electronics8050531
Leone G, Munno F, Pierri R. Radiation Properties of Conformal Antennas: The Elliptical Source. Electronics. 2019; 8(5):531. https://doi.org/10.3390/electronics8050531
Chicago/Turabian StyleLeone, Giovanni, Fortuna Munno, and Rocco Pierri. 2019. "Radiation Properties of Conformal Antennas: The Elliptical Source" Electronics 8, no. 5: 531. https://doi.org/10.3390/electronics8050531
APA StyleLeone, G., Munno, F., & Pierri, R. (2019). Radiation Properties of Conformal Antennas: The Elliptical Source. Electronics, 8(5), 531. https://doi.org/10.3390/electronics8050531





