Research on Invulnerability Technology of Node Attack in Space-Based Information Network Based on Complex Network
Abstract
1. Introduction
2. Related Works
3. Model Construction and Parameter Analysis of Space-Based Information Network
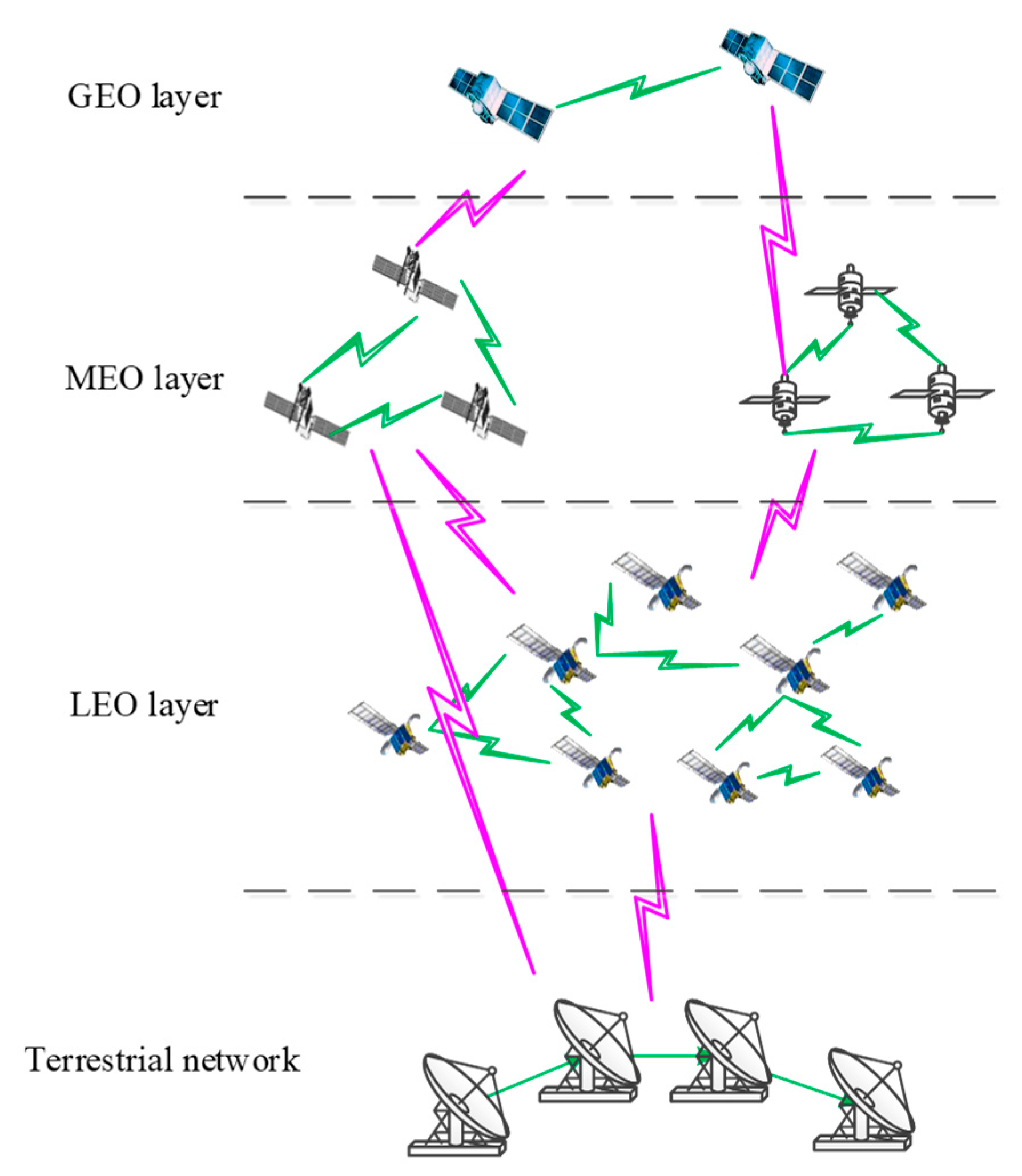
3.1. Construction of Space-Based Information Network Model
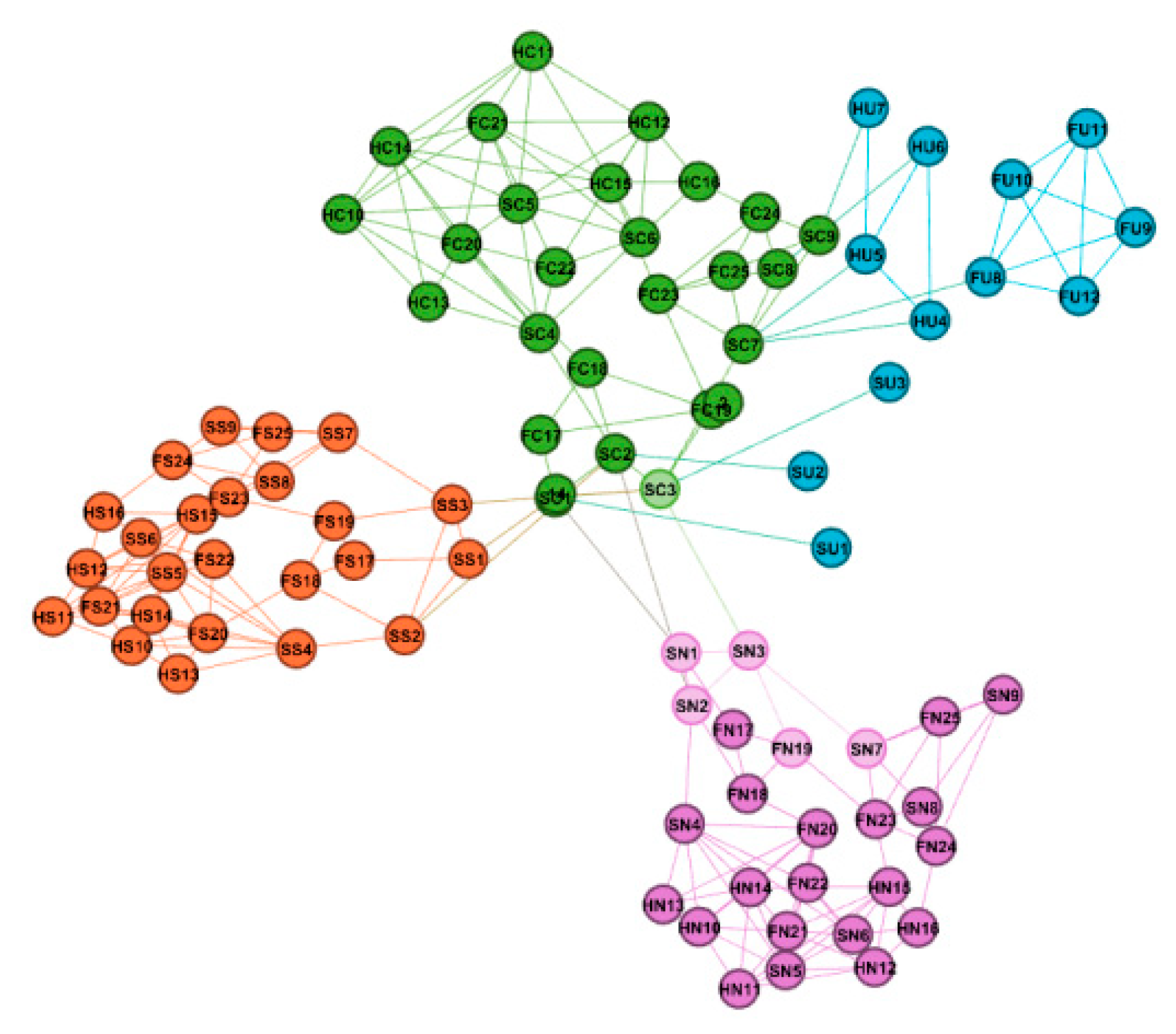
3.2. Model Mapping Based on Complex Network
3.2.1. Characteristics Analysis of SBIN
3.2.2. Parameter Analysis of SBIN
4. Algorithm Design of Improved Tree Attack Strategy
4.1. Methods and Meaning of Attacking Node
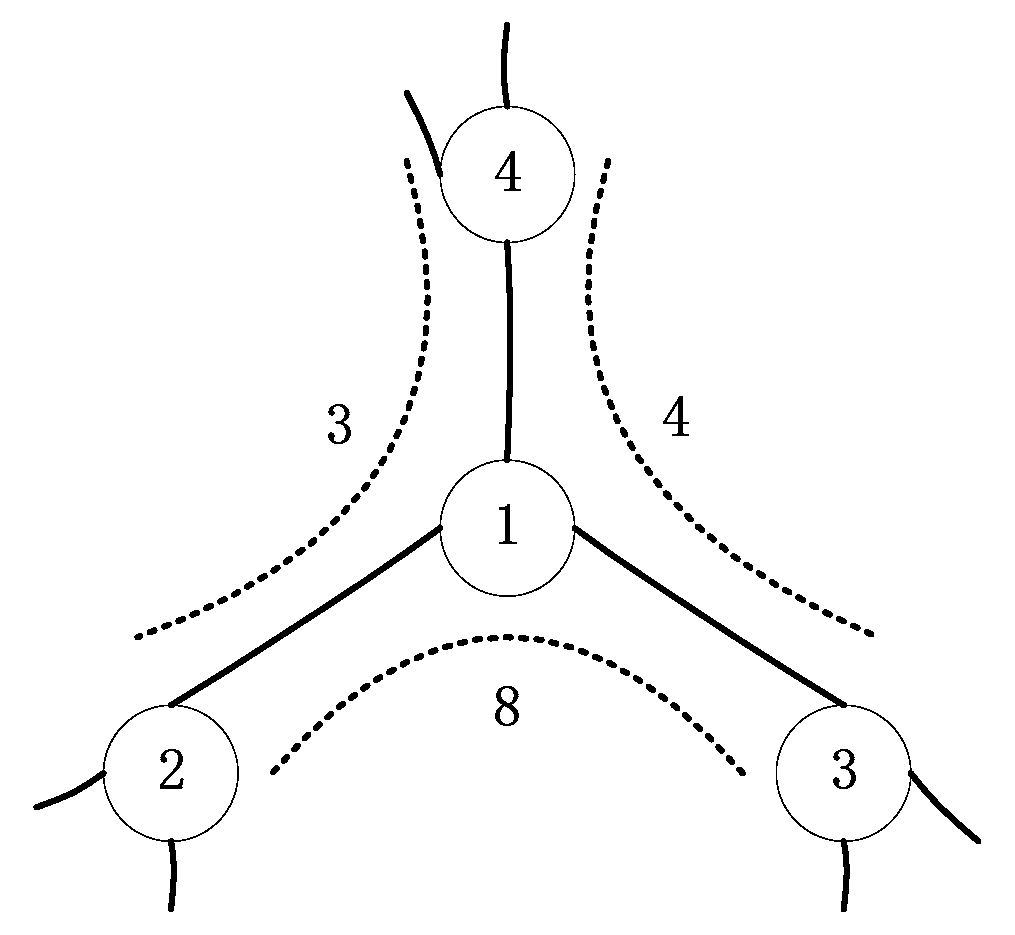
4.2. Study in Attack Information Metric Index
4.3. Attack Strategy Algorithm Research
- Traditional attack strategy (TAS):
- (1)
- Select node degree metric index to analyze the invulnerability of SBIN;
- (2)
- Select the attack node according to the breadth and accuracy of the attack information;
- (3)
- Attack the relevant nodes of SBIN in the appropriate steps according to the attack ratio;
- (4)
- Statistical metric index and perform a data analysis.
- Improved tree-attack strategy (ITAS):
- (1)
- Define the degree of the node as a measure index, selecting the non-isolated node in the network as a root node by a certain attack breadth and accuracy;
- (2)
- Invade all of the neighboring nodes of the root node as second layer nodes;
- (3)
- In the process of proportional deletion, the order of deletion is performed according to the root node, the root sibling node, the branch node, and the branch sibling node;
- (4)
- Attack the adjacent nodes of all of the second-layer nodes successively as third-layer nodes of the improved tree attack strategy until all nodes in SBIN are traversed.
4.4. Invulnerability Metric Index
5. Invulnerability Optimization Model of SBIN
5.1. Analysis Index of Invulnerability in SBIN
5.2. Optimization Methods of Invulnerability in SBIN
- Random edge-increasing method (RD).
- Step 1:
- Initialize , and abstract the SBIN into the graph ;
- Step 2:
- Randomly select two nodes with no edges connected in the graph G, the graph after adding the edge is , set and ;
- Step 3:
- If , go back to step 2 and continue to increase the edge until the end of the edge increasing process;
- Step 4:
- Calculate the of all nodes and the maximum value in SBIN after adding the edges.
- Low nodes degree with high priority (LDF).
- Step 1:
- Initialize , and abstract the SBIN into the graph ;
- Step 2:
- Arrange all nodes in SBIN from small to large according to the degree value;
- Step 3:
- Select two nodes with the smallest degree value and no edges connected in the graph , the graph after adding the edge is , set and ;
- Step 4:
- If , go back to step 2, or go to step 5;
- Step 5:
- Calculate the of all nodes and the maximum value in SBIN after adding the edges.
- Low nodes betweenness centrality with high priority (LBF).
- Step 1:
- Initialize , and abstract the SBIN into the graph ;
- Step 2:
- Arrange all nodes in SBIN from small to large according to the betweenness centrality value;
- Step 3:
- Select two nodes with the smallest betweenness centrality value and no edges connected in the graph , the graph after adding the edge is , set and ;
- Step 4:
- If , go back to step 2, or go to step 5;
- Step 5:
- Calculate the of all nodes and the maximum value in SBIN after adding the edges.
- Adding shortcut in nodes with the maximum betweenness centrality method (SMB).
- Step 1:
- Initialize , and abstract the SBIN into the graph ;
- Step 2:
- Calculate the betweenness centrality value of all nodes in SBIN, find the node with the largest betweenness centrality value , and the edge set connected to the node ;
- Step 3:
- Sort the betweenness centrality value of all the edges in the order from largest to smallest, and record the corresponding node set as at the other end of these edges;
- Step 4:
- Select the two nodes with no edges connected in the top from , add an edge between the nodes, the graph after adding the edge is , set and ;
- Step 5:
- If , go back to step 2, or go to step 6;
- Step 6:
- Calculate the of all nodes and the maximum value in SBIN after adding the edges.
6. Experimental Section and Analysis
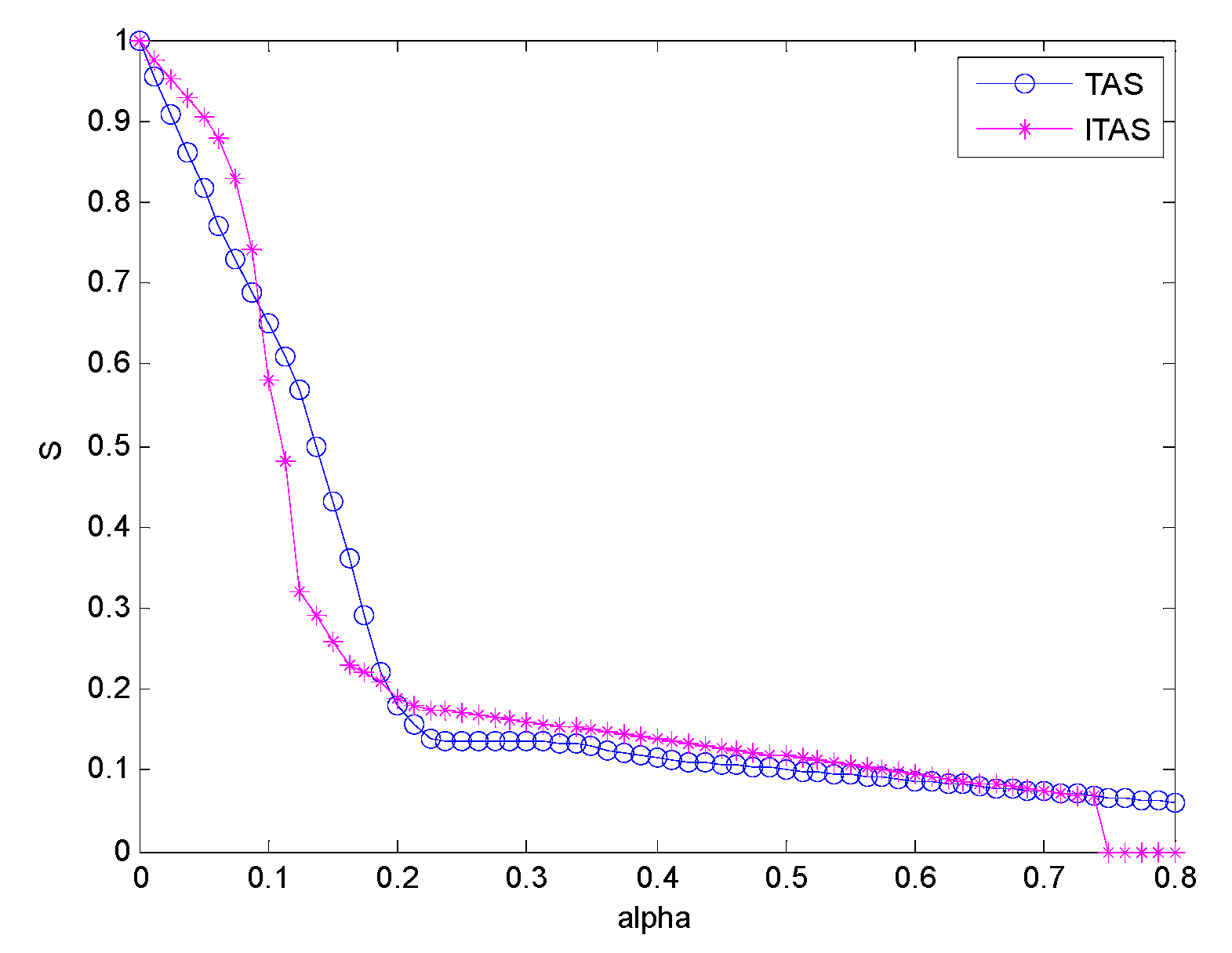
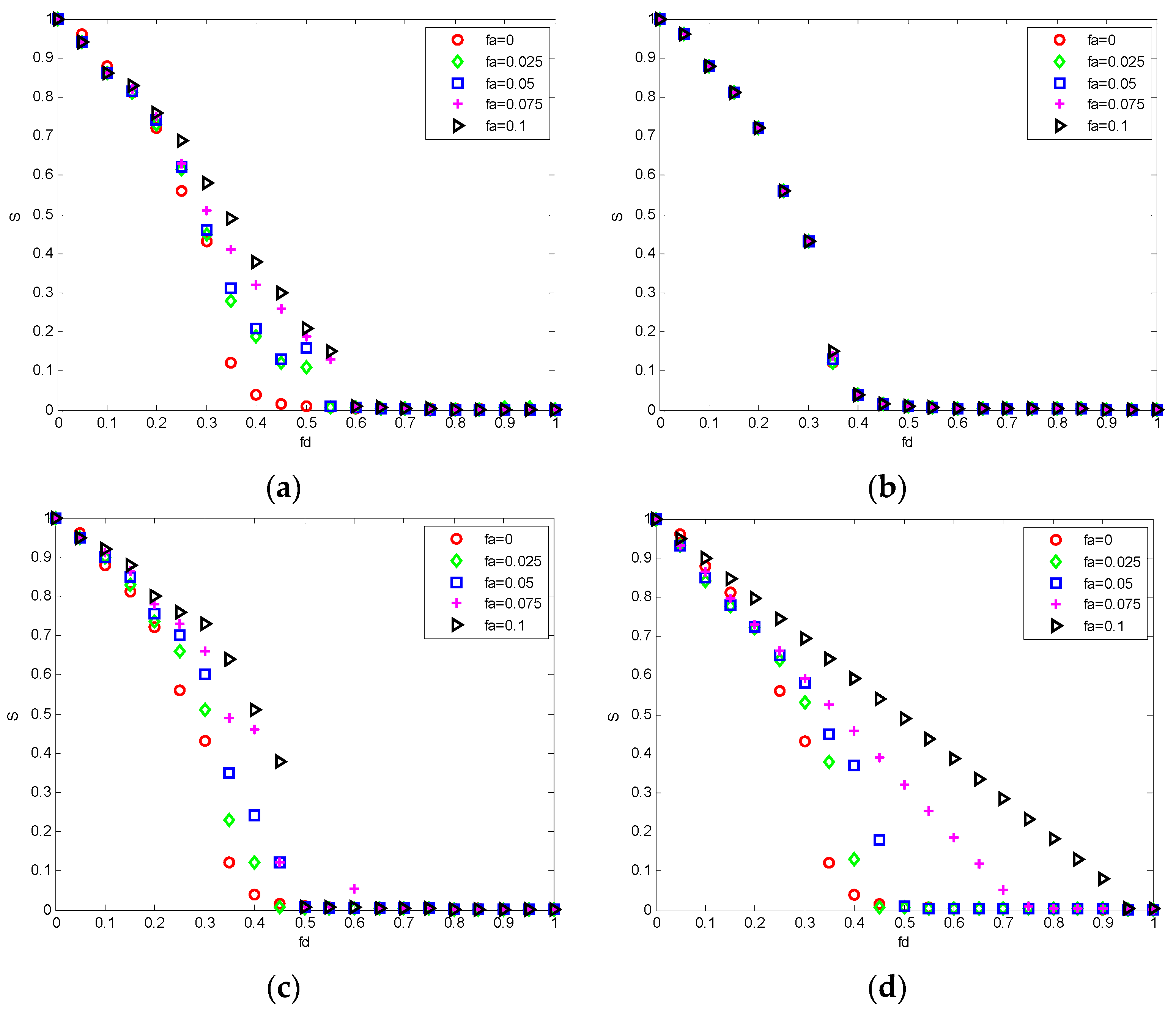
6.1. Comparison Experiments of Invulnerability Analysis
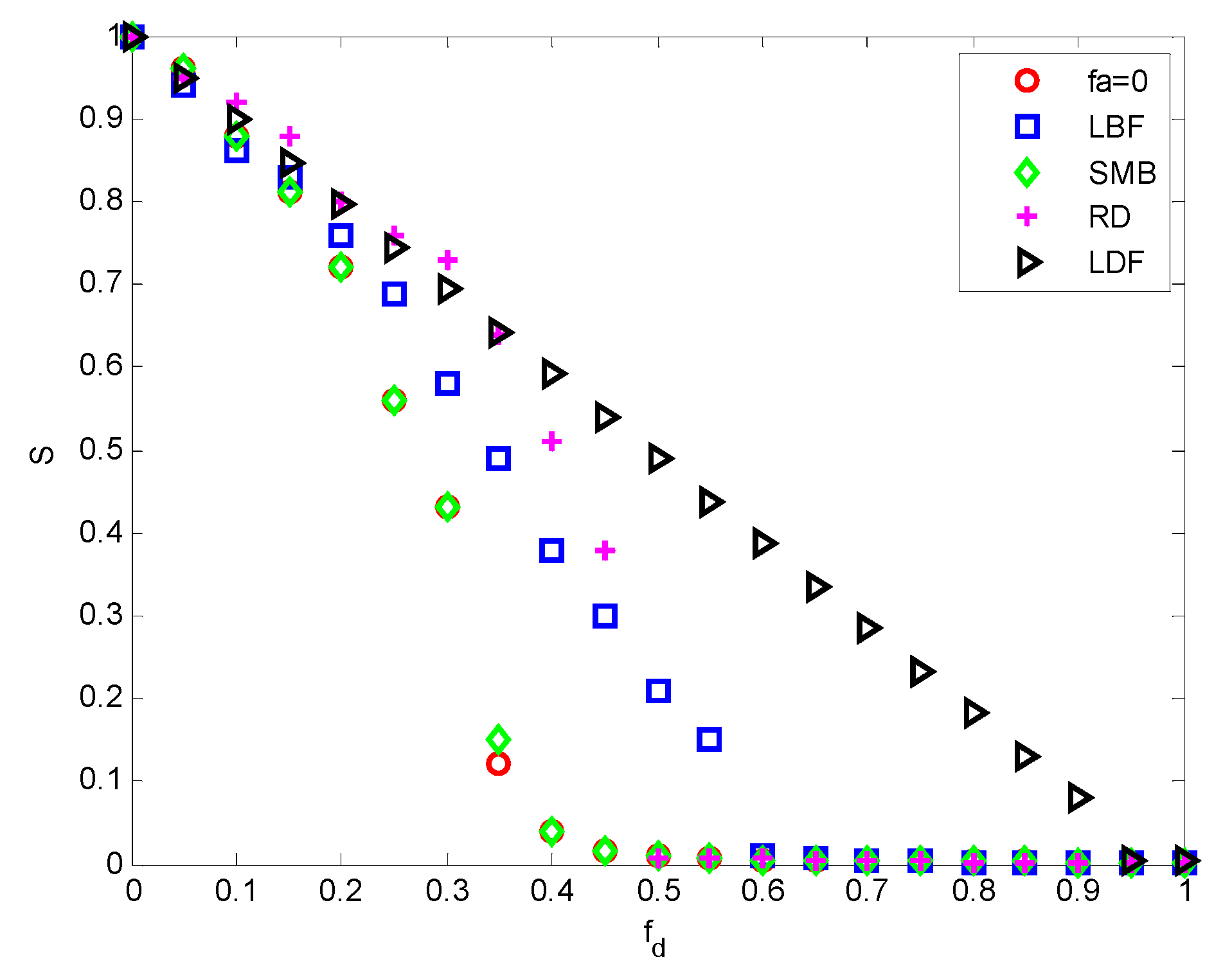
6.2. Experiment of Invulnerability Optimization Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Xiao, X.; Chen, J. Impact of Information Network Damage on Overload-based Cascading Failures of Power Grid. Autom. Electr. Power Syst. 2017, 41, 14–21. [Google Scholar]
- Ryzhov, Y.; Sakovych, L.; Vankevych, P.; Yakovlev, M.; Nastishin, Y. Optimization of requirements for measuring instruments at metrological service of communication tools. Measurement 2018, 123, 19–25. [Google Scholar] [CrossRef]
- Knorr, F.; Baselt, D.; Schreckenberg, M. Reducing Traffic Jams via VANETs. IEEE Trans. Veh. Technol. 2012, 61, 3490–3498. [Google Scholar] [CrossRef]
- Schurkus, H.F.; Luenser, A.; Ochsenfeld, C. Communication: Almost error-free resolution-of-the-identity correlation methods by null space removal of the particle-hole interactions. J. Chem. Phys. 2017, 146, 211106. [Google Scholar] [CrossRef]
- Shcherbinin, A.G.; Mansurov, A.S. Numerical studies of the electromagnetic reciprocal influences of symmetric communication cable. Russ. Electr. Eng. 2014, 85, 673–676. [Google Scholar] [CrossRef]
- Popovski, P.; Nielsen, J.J.; Stefanovic, C.; De Carvalho, E.; Ström, E.; Trillingsgaard, K.F.; Bana, A.-S.; Kim, D.M.; Kotaba, R.; Park, J.; et al. Wireless Access for Ultra-Reliable Low-Latency Communication: Principles and Building Blocks. IEEE Netw. 2018, 32, 16–23. [Google Scholar] [CrossRef]
- Wang, K.; Shao, Y.; Shu, L.; Zhu, C.; Zhang, Y. Mobile big data fault-tolerant processing for ehealth networks. IEEE Netw. 2016, 30, 36–42. [Google Scholar] [CrossRef]
- Guo, Q.; Yan, J.; Xu, W. Localized Fault Tolerant Algorithm Based on Node Movement Freedom Degree in Flying Ad Hoc Networks. Symmetry 2019, 11, 106. [Google Scholar] [CrossRef]
- Vespignani, A. Complex networks: The fragility of interdependency. Nature 2010, 464, 984. [Google Scholar] [CrossRef]
- Nepusz, T.; Vicsek, T. Controlling edge dynamics in complex networks. Nat. Phys. 2011, 8, 568–573. [Google Scholar] [CrossRef]
- Krioukov, D.; Papadopoulos, F.; Kitsak, M.; Vahdat, A.; Boguñá, M. Hyperbolic geometry of complex networks. Physics E 2010, 82, 36106. [Google Scholar] [CrossRef]
- Li, S.B.; Cao, D.N.; Dang, W.X. Variable speed limit strategies analysis with mesoscopic traffic flow model based on complex networks. Int. J. Mod. Phys. C 2018, 29, 1850014. [Google Scholar] [CrossRef]
- Reiss, K.; Morzan, U.N.; Grigas, A.T.; Batista, V.S. Water Network Dynamics Next to the Oxygen-Evolving Complex of Photosystem II. Inorganics 2019, 7, 39. [Google Scholar] [CrossRef]
- Memon, B.A.; Yao, H. Structural Change and Dynamics of Pakistan Stock Market During Crisis: A Complex Network Perspective. Entropy 2019, 21, 248. [Google Scholar] [CrossRef]
- Wang, P.; Xue, F.; Li, H. A Multi-Objective DV-Hop Localization Algorithm Based on NSGA-II in Internet of Things. Mathematics 2019, 7, 184. [Google Scholar] [CrossRef]
- Li, T.; Bai, J.; Yang, X. Co-Occurrence Network of High-Frequency Words in the Bioinformatics Literature: Structural Characteristics and Evolution. Appl. Sci. 2018, 8, 1994. [Google Scholar] [CrossRef]
- Ding, C.; Yang, L.; Wu, M. Localization-Free Detection of Replica Node Attacks in Wireless Sensor Networks Using Similarity Estimation with Group Deployment Knowledge. Sensors 2017, 17, 160. [Google Scholar] [CrossRef]
- Wan, J.; Xiong, N.; Zhang, W.; Zhang, Q.; Wan, Z. Prioritized Degree Distribution in Wireless Sensor Networks with a Network Coded Data Collection Method. Sensors 2012, 12, 17128–17154. [Google Scholar] [CrossRef]
- Zhang, Y.; Na, S. Research on the Topological Properties of Air Quality Index Based on a Complex Network. Sustainability 2018, 10, 1073. [Google Scholar] [CrossRef]
- Kasprzyk, R.; Najgebauer, A.; Pierzchała, D. Modelling and Simulation of an Infection Disease in Social Networks. In Proceedings of the International Conference on Computational Collective Intelligence (ICCCI 2011), Gdynia, Poland, 21–23 September 2011; pp. 388–398. [Google Scholar]
- Joshi, C.; Kumar, U. Security Testing and Assessment of Vulnerability Scanners in Quest of Current Information Security Landscape. Int. J. Comput. Appl. 2016, 145, 1–7. [Google Scholar] [CrossRef]
- Joshi, C.; Singh, U.K.; Singh, S.K. ZDAR system: Defending against the unknown. Int. J. Comput. Sci. Mob. Comput. 2016, 5, 143–149. [Google Scholar]
- Singh, U.K.; Joshi, C.; Sk, S. Zero day attacks defense technique for protecting system against unknown vulnerabilities. Int. J. Sci. Res. Comput. Sci. Eng. 2017, 5, 13–18. [Google Scholar]
- Kumar, U.; Joshi, C. Quantifying Security Risk by Critical Network Vulnerabilities Assessment. Int. J. Comput. Appl. 2016, 156, 26–33. [Google Scholar] [CrossRef]
- Kumar, U.; Joshi, C.; Gaud, N. Information Security Assessment by Quantifying Risk Level of Network Vulnerabilities. Int. J. Comput. Appl. 2016, 156, 37–44. [Google Scholar] [CrossRef]
- Singh, U.K.; Joshi, C. Quantitative Security Risk Evaluation Using CVSS Metrics by Estimation of Frequency and Maturity of Exploit. In Proceedings of the World Congress on Engineering and Computer Science (WCECS 2016), San Francisco, CA, USA, 19–21 October 2016. [Google Scholar]
- Joshi, C.; Singh, U.K. Information security risk management framework for university computing environment. Int. J. Netw. Secur. 2017, 19, 742–751. [Google Scholar]
- Lan, M.; Han, H. Study on invulnerability measure based on community structure of complex networks. Comput. Eng. Appl. 2012, 38, 23–28. [Google Scholar]
- Peng, X.; Hong, Y. Power-law-alterable SF networks’ cascading invulnerability under intentional attack. In Proceedings of the 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012. [Google Scholar] [CrossRef]
- Tian, T.; Jun, W.U.; Tan, Y.J. Simulation Optimization for Invulnerability of Complex Networks Based on Natural Connectivity. Complex Syst. Complex. Sci. 2013, 10, 88–94. [Google Scholar]
- Jiang, C.; Wang, X.; Wang, J.; Chen, H.-H.; Ren, Y. Security in space information networks. IEEE Commun. Mag. 2015, 53, 82–88. [Google Scholar] [CrossRef]
- Wang, X.; Du, J.; Wang, J.; Zhang, Z.; Jiang, C.; Ren, Y. Key Issues of Security in Space-Based Information Network Review. In Proceedings of the International Conferences on Cyberspace Technology (CCT 2014), Beijing, China, 8–10 November 2014. [Google Scholar] [CrossRef]
- Du, J.; Jiang, C.; Guo, Q.; Guizani, M.; Ren, Y. Cooperative earth observation through complex space information networks. IEEE Wirel. Commun. 2016, 23, 136–144. [Google Scholar] [CrossRef]
- Du, J.; Jiang, C.; Wang, J.; Ren, Y.; Yu, S.; Han, Z. Resource Allocation in Space Multi-Access Systems. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 598–618. [Google Scholar] [CrossRef]
- Wang, W.; Hu, B.; Di, P. Optimization of Network Invulnerability to Cascading Failure Based on Random-walk Betweenness Model. In Proceedings of the 2011 International Conference on Information Management, Innovation Management and Industrial Engineering (ICIII 2011), Shenzhen, China, 26–27 November 2011; pp. 231–234. [Google Scholar]
- Chen, S.; Jiang, J.; Pang, S.; Nie, S.; Lai, Y. Modeling and Optimization of Train Scheduling Network Based on Invulnerability Analysis. Appl. Math. Inf. Sci. 2013, 7, 113–119. [Google Scholar] [CrossRef]
- Li, F.; Hu, B.; Di, P. Optimization of dynamic invulnerability of scale-free networks based on limited resource model. Syst. Eng. Electron. 2012, 34, 175–178. [Google Scholar]
- Petrillo, A.; Pescapé, A.; Santini, S. A collaborative approach for improving the security of vehicular scenarios: The case of platooning. Comput. Commun. 2018, 122, 59–75. [Google Scholar] [CrossRef]
- Petrillo, A.; Salvi, A.; Santini, S.; Valente, A.S. Adaptive multi-agents synchronization for collaborative driving of autonomous vehicles with multiple communication delays. Transp. Res. Part C Emerg. Technol. 2018, 86, 372–392. [Google Scholar] [CrossRef]
- Fiengo, G.; Petrillo, A.; Salvi, A.; Santini, S.; Tufo, M. A control strategy for reducing traffic waves in delayed vehicular networks. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 2462–2467. [Google Scholar]
- Petrillo, A.; Pescape, A.; Santini, S. A collaborative control strategy for platoons of autonomous vehicles in the presence of message falsification attacks. In Proceedings of the 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Naples, Italy, 26–28 June 2017; pp. 110–115. [Google Scholar]
- Liu, C.; Xiong, W. Research on Internet of Things Vulnerability Based on Complex Network Attack Model. In Proceedings of the 3rd International Conference on Space Information Network (SINC 2018), Changchun, China, 9–10 August 2018; pp. 21–29. [Google Scholar]



| Complex-Network Characteristics | SBIN Features |
|---|---|
| Multi-layer features | Information transmission process involves the resource layer, service layer, function layer and mission layer |
| Multi-stage characteristics | Mainly composed of the bottom distribution sensor, convergence network and terminal application |
| Multi-dimensional traffic | Transmitted information includes data, images, voice, and video |
| Multiple attributes/guidelines | Different attributes and guidelines for abstract entities and interactions |
| Congestion | Network communication capabilities and user information transmission requirements lead to data transmission congestion control problems |
| Coordinating optimization issues | Global optimization results of data applications under limited resources may not satisfy the optimal data service requirements of individual nodes |
| Parameter Index | Node Number n | Edge Number m | Average Degree k | Average Clustering Coefficient C | Average Path Length L | Network Diameter D |
|---|---|---|---|---|---|---|
| Data Analysis | 107 | 324 | 3.028 | 0.502 | 2.829 | 3 |
| Identification | Name | Meaning |
|---|---|---|
| A1 | Physical node attack | The physical destruction of the terminal node is performed by various means such as tearing, scratching, and high temperature. |
| A2 | Transmission signal analysis | Crack the encryption information by algorithm, and then analyze the information characteristics to determine the data type and effect. |
| A3 | Signal interception and node reconstruction | The node is reconstructed by tapping the communication data of the network node to acquire sensitive information in the channel. |
| A4 | Communication interference | Block all levels of nodes from receiving normal communication signals, resulting in a link interruption by using flooding attacks, wormhole attacks, etc. |
| A5 | Network Protocol Attack | Through pseudo-terminal technology, send random data that receiving nodes cannot identify, parse, and recover.It also sends malformed data causing a crash. |
| A6 | Spurious data injection | Send false information that completely complies with the communication mechanism and network protocol so that it can process and distribute false information. |
| A7 | Wireless RF injection | Send information of virus-carrying, Trojans, or other malicious programs that fully comply with the communication mechanism and network protocol, and inject it into the data processing system to infect hosts, industrial computers, etc. |
| A8 | Data copying, tampering, and deletion | Use the injected malicious code and software vulnerabilities to complete the copying, tampering, and deletion on the target database. |
| A9 | Network paralysis | Cause the entire network data to lose normal application pass rates by maliciously attackingmultiple pseudo-terminals. |
| A10 | Illegal control | Obtain root privileges of the system and achieve complete control of the system, including system operation, service provision, network management, etc. |
| = 0 | = 2 | = 10 | |
|---|---|---|---|
| 0.92 | 0.904 | 0.816 | |
| 0.88 | 0.844 | 0.65 | |
| 0.82 | 0.776 | 0.43 | |
| 0.67 | 0.648 | 0.18 | |
| 0.61 | 0.51 | 0.1365 | |
| 0.53 | 0.438 | 0.1357 | |
| 0.5 | 0.354 | 0.1311 | |
| 0.44 | 0.282 | 0.1144 | |
| 0.37 | 0.234 | 0.1077 | |
| 0.28 | 0.21 | 0.1009 | |
| 0.22 | 0.186 | 0.0941 | |
| 0.18 | 0.168 | 0.0873 | |
| 0.15 | 0.148 | 0.0805 | |
| 0.12 | 0.116 | 0.0737 | |
| 0.1 | 0.091 | 0.0669 | |
| 0.08 | 0.076 | 0.06 |
| TAS | ITAS | |
|---|---|---|
| 0.816 | 0.904 | |
| 0.65 | 0.58 | |
| 0.43 | 0.26 | |
| 0.18 | 0.19 | |
| 0.1365 | 0.171 | |
| 0.1357 | 0.16 | |
| 0.1311 | 0.149 | |
| 0.1144 | 0.1386 | |
| 0.1077 | 0.1278 | |
| 0.1009 | 0.117 | |
| 0.0941 | 0.1062 | |
| 0.0873 | 0.0954 | |
| 0.0805 | 0.0846 | |
| 0.0737 | 0.0738 | |
| 0.0669 | 0 | |
| 0.06 | 0 |
| fa = 0 | RD (fa = 1) | SMB (fa = 1) | LBF (fa = 1) | LDF (fa = 1) | |
|---|---|---|---|---|---|
| fd = 0 | 1 | 1 | 1 | 1 | 1 |
| fd = 0.05 | 0.96 | 0.94 | 0.96 | 0.95 | 0.949 |
| fd = 0.1 | 0.88 | 0.86 | 0.88 | 0.92 | 0.898 |
| fd = 0.15 | 0.81 | 0.83 | 0.81 | 0.88 | 0.847 |
| fd = 0.2 | 0.72 | 0.76 | 0.72 | 0.8 | 0.796 |
| fd = 0.25 | 0.56 | 0.69 | 0.56 | 0.76 | 0.744 |
| fd = 0.3 | 0.43 | 0.58 | 0.43 | 0.73 | 0.693 |
| fd = 0.35 | 0.12 | 0.49 | 0.15 | 0.64 | 0.642 |
| fd = 0.4 | 0.04 | 0.38 | 0.04 | 0.51 | 0.591 |
| fd = 0.45 | 0.015 | 0.3 | 0.015 | 0.38 | 0.54 |
| fd = 0.5 | 0.01 | 0.21 | 0.01 | 0.01 | 0.489 |
| fd = 0.55 | 0 | 0.15 | 0 | 0 | 0.438 |
| fd = 0.6 | 0 | 0.01 | 0 | 0 | 0.387 |
| fd = 0.65 | 0 | 0.007 | 0 | 0 | 0.336 |
| fd = 0.7 | 0 | 0 | 0 | 0 | 0.284 |
| fd = 0.75 | 0 | 0 | 0 | 0 | 0.233 |
| fd = 0.8 | 0 | 0 | 0 | 0 | 0.182 |
| fd = 0.85 | 0 | 0 | 0 | 0 | 0.131 |
| fd = 0.9 | 0 | 0 | 0 | 0 | 0.08 |
| fd = 0.95 | 0 | 0 | 0 | 0 | 0 |
| fd = 1 | 0 | 0 | 0 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Xiong, W.; Zhang, Y.; Sun, Y.; Xiong, M.; Guo, C. Research on Invulnerability Technology of Node Attack in Space-Based Information Network Based on Complex Network. Electronics 2019, 8, 507. https://doi.org/10.3390/electronics8050507
Liu C, Xiong W, Zhang Y, Sun Y, Xiong M, Guo C. Research on Invulnerability Technology of Node Attack in Space-Based Information Network Based on Complex Network. Electronics. 2019; 8(5):507. https://doi.org/10.3390/electronics8050507
Chicago/Turabian StyleLiu, Chengxiang, Wei Xiong, Ying Zhang, Yang Sun, Minghui Xiong, and Chao Guo. 2019. "Research on Invulnerability Technology of Node Attack in Space-Based Information Network Based on Complex Network" Electronics 8, no. 5: 507. https://doi.org/10.3390/electronics8050507
APA StyleLiu, C., Xiong, W., Zhang, Y., Sun, Y., Xiong, M., & Guo, C. (2019). Research on Invulnerability Technology of Node Attack in Space-Based Information Network Based on Complex Network. Electronics, 8(5), 507. https://doi.org/10.3390/electronics8050507





