A Design Methodology and Analysis for Transformer-Based Class-E Power Amplifier
Abstract
1. Introduction
2. Methodology and Implementation on Transformer-Based Class-E PA
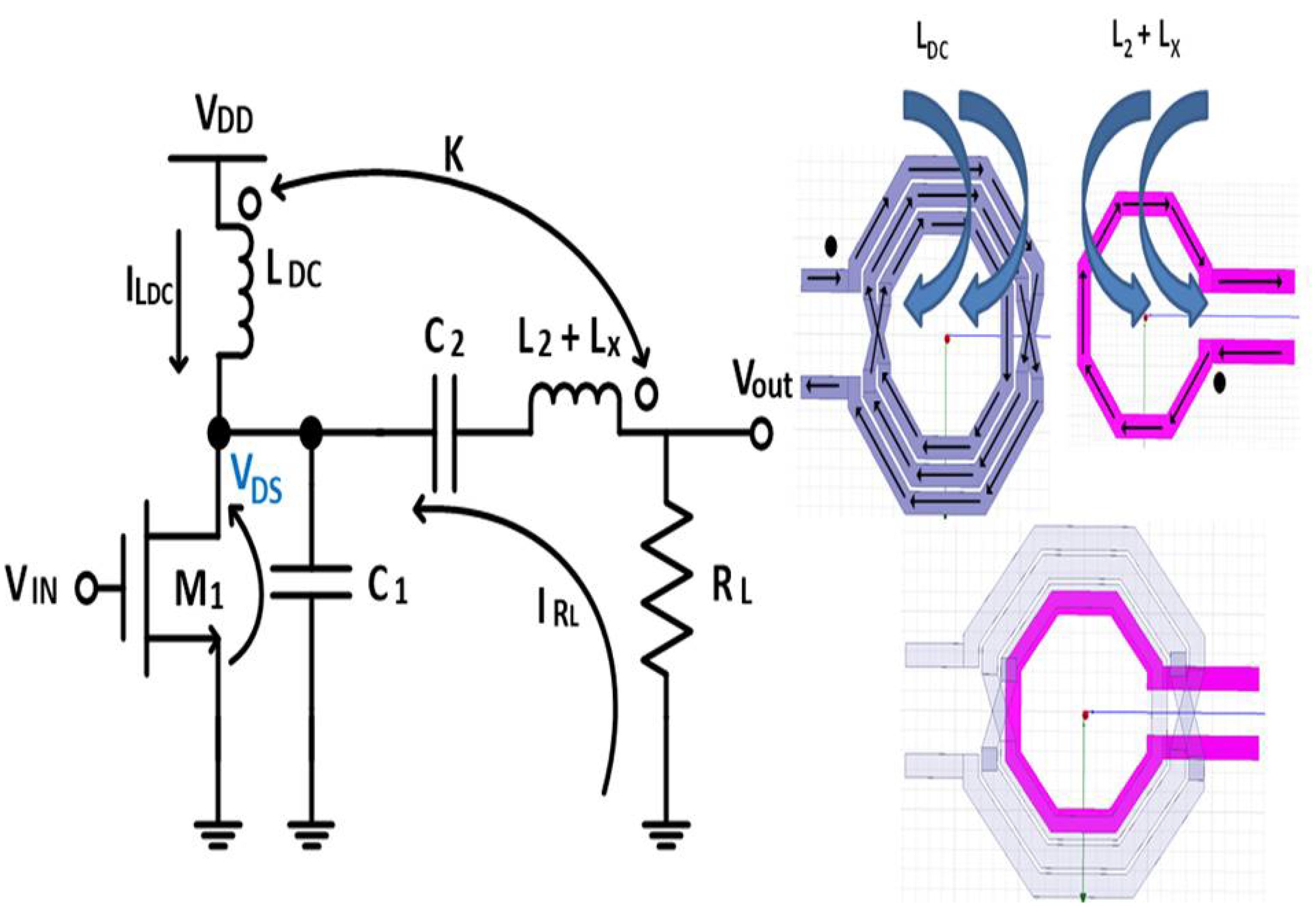
2.1. Design of the Inductors with Magnetic Coupling
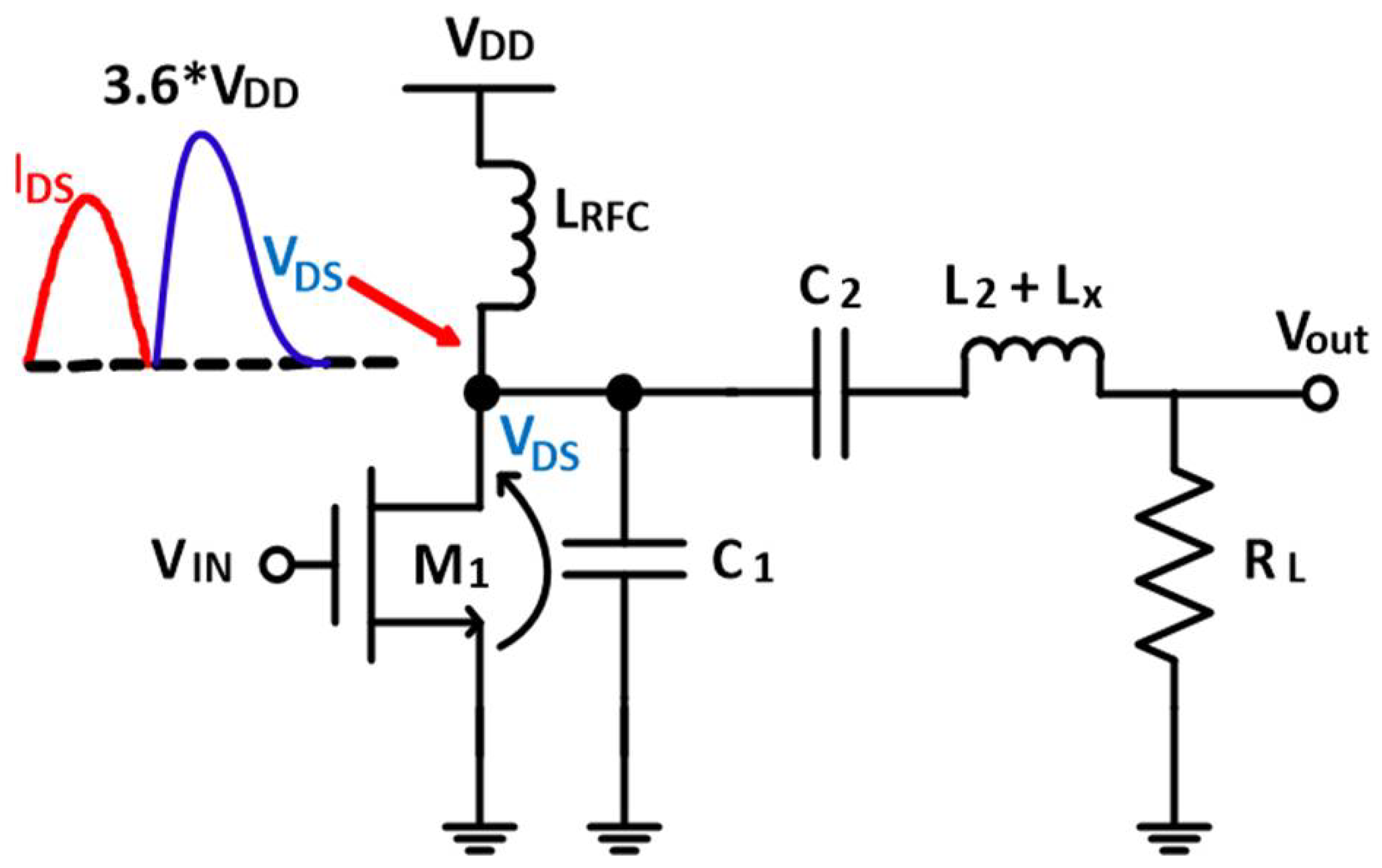
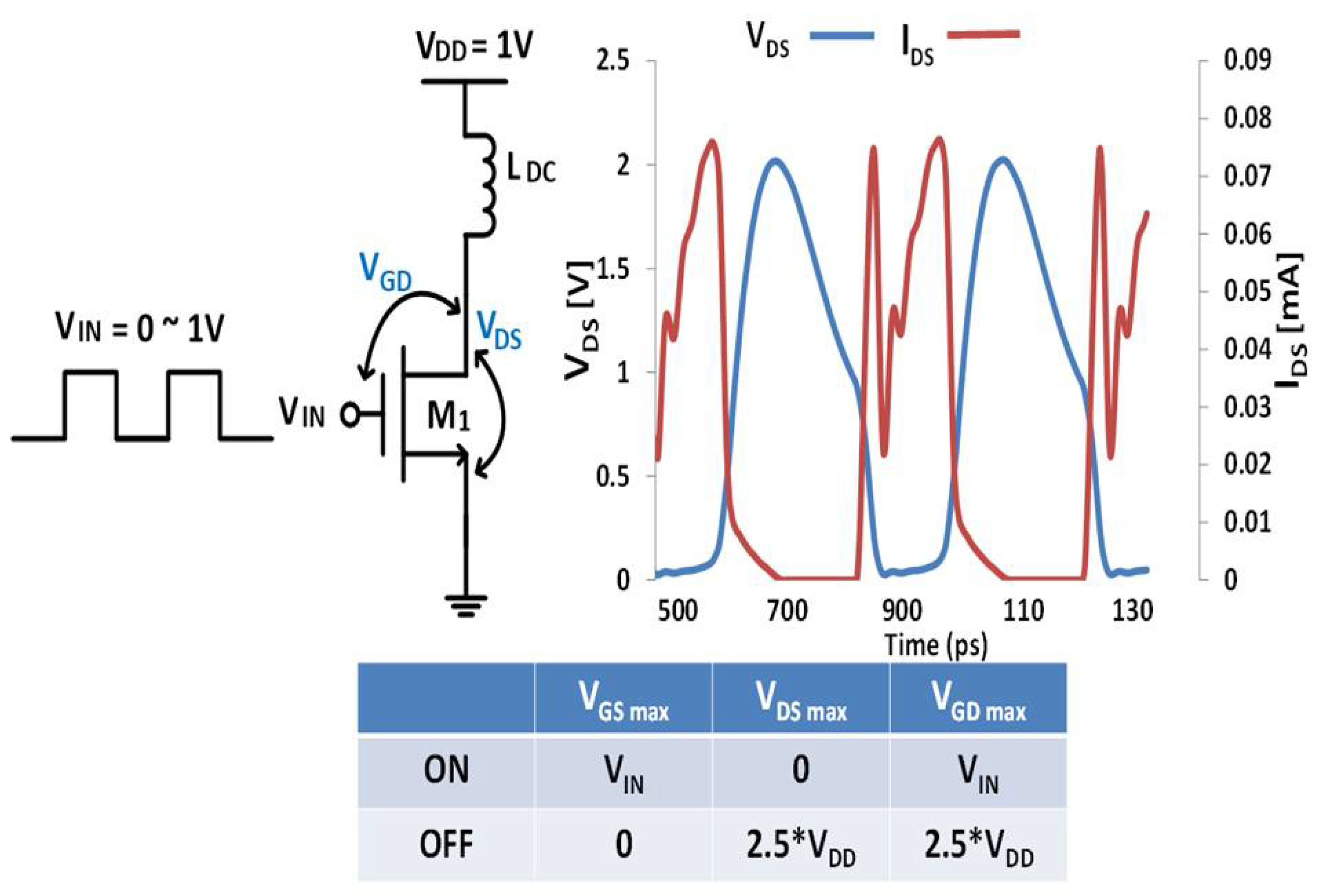
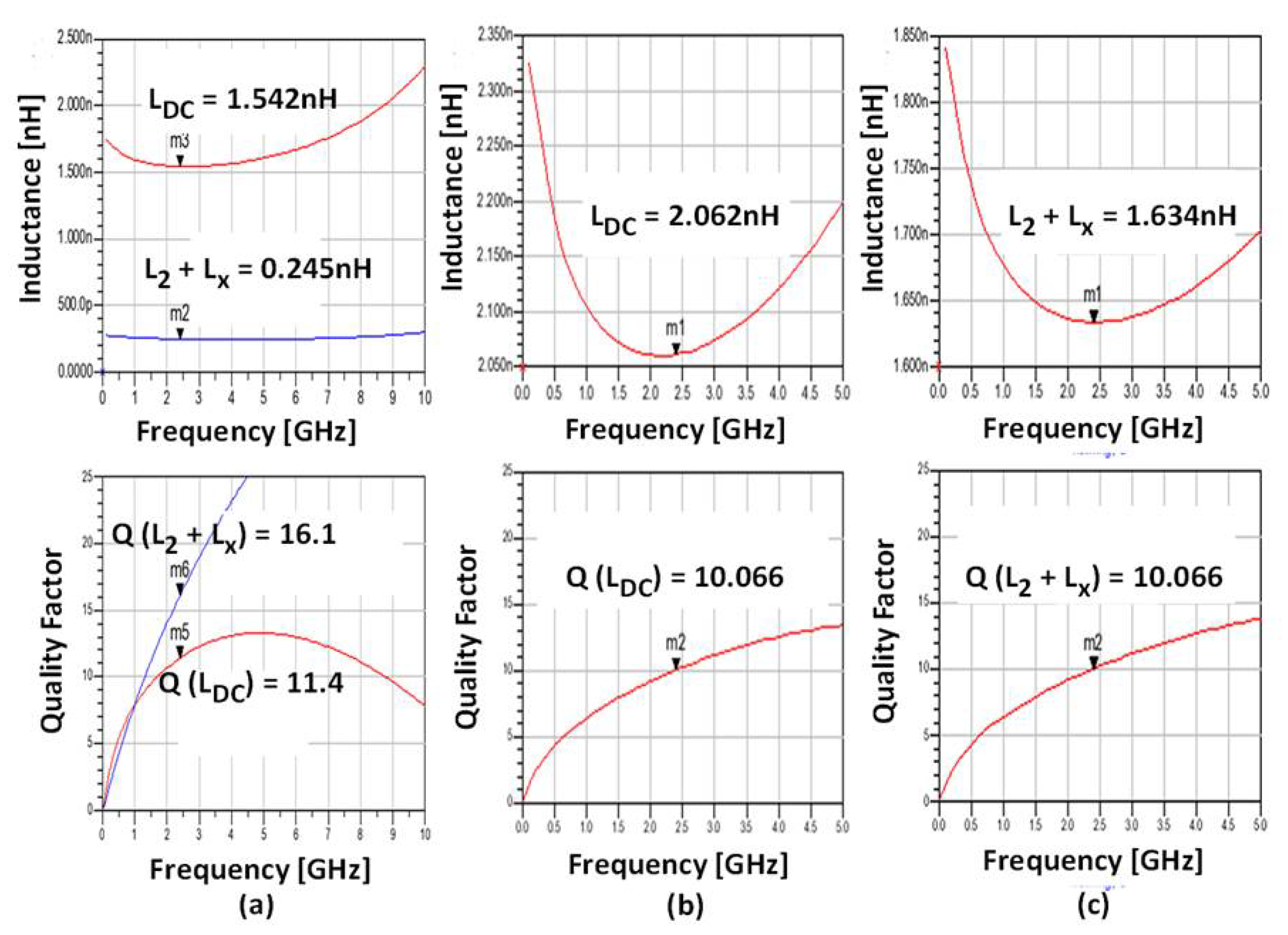
2.2. Design of the DC-Feed Inductance
- Greatly reduce the loss due to a smaller electrical series resistance
- A reduction in overall size and cost
- Simplifying the design of the matching network
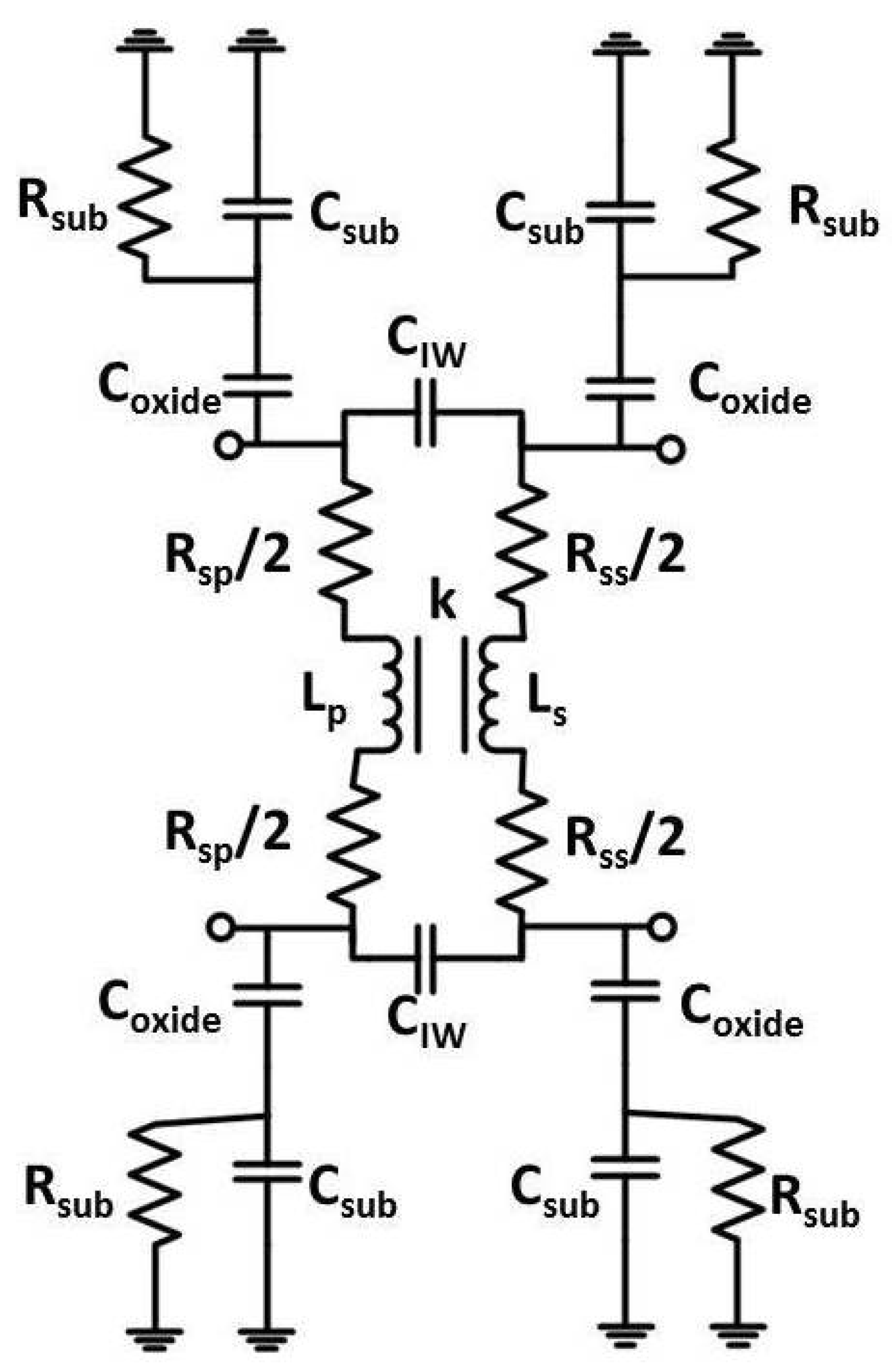
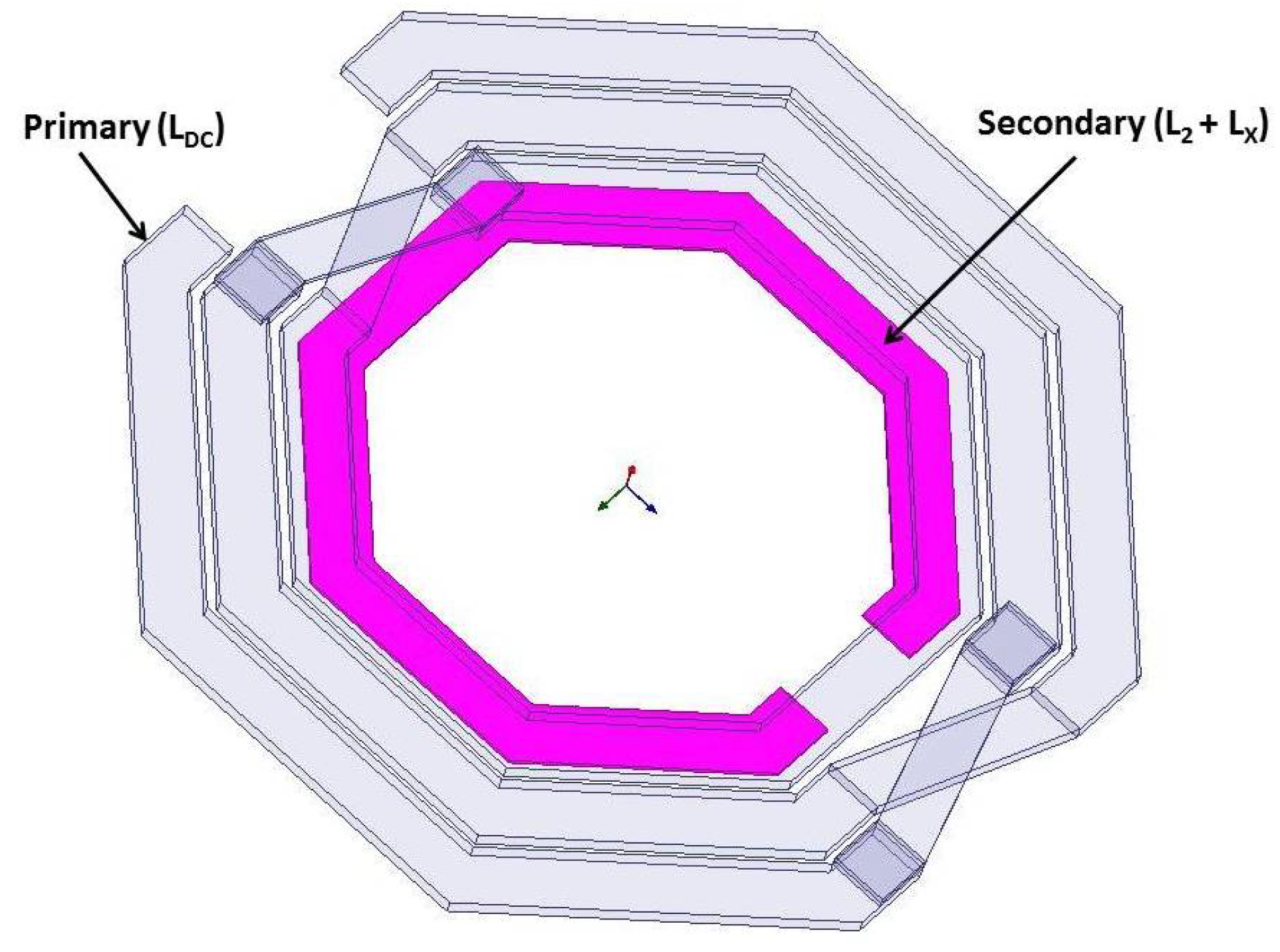
2.3. Design of Inductors and Transformers
- Low series resistance in the primary and secondary windings
- High magnetic coupling between the primary and the secondary coils
- Low capacitive coupling between primary and the secondary coils
- Low parasitic capacitances to the substrate
- To minimize the series resistance and the parasitic capacitance, the spiral is implemented in the top metal layer (which is the thickest) [13]
- It is desirable to minimize the outer dimensions of inductors, and this can be accomplished by decreasing W (line width) or incresing N (numbers of turns) [14]
- A diameter of 5 to 6 times W should be chosen for the inner opening to ensure negligible coupling [15]
- Differential geometry (driven by differential signals) also exhibits a higher Q [16], because each half experiences its own substrate loss and it will be reduced by a factor of two
- Choose a line spacing S of approximately three times the minimum allowable value for the particular technology being used to fabricate the design
- As a general rule of thumb, Din (inner dimension) lower than 50 m should be avoided unless it is mandatory to obtain very low inductance values (L < 0.5 nH) [17]
- For multi-turn inductors, do not use very tight metal spacing (i.e., coil thickness/line spacing < 3) to limit the performance degradation as this will cause the proximity effects to become worse [18]
2.4. Transformer Layouts in Class-E PA
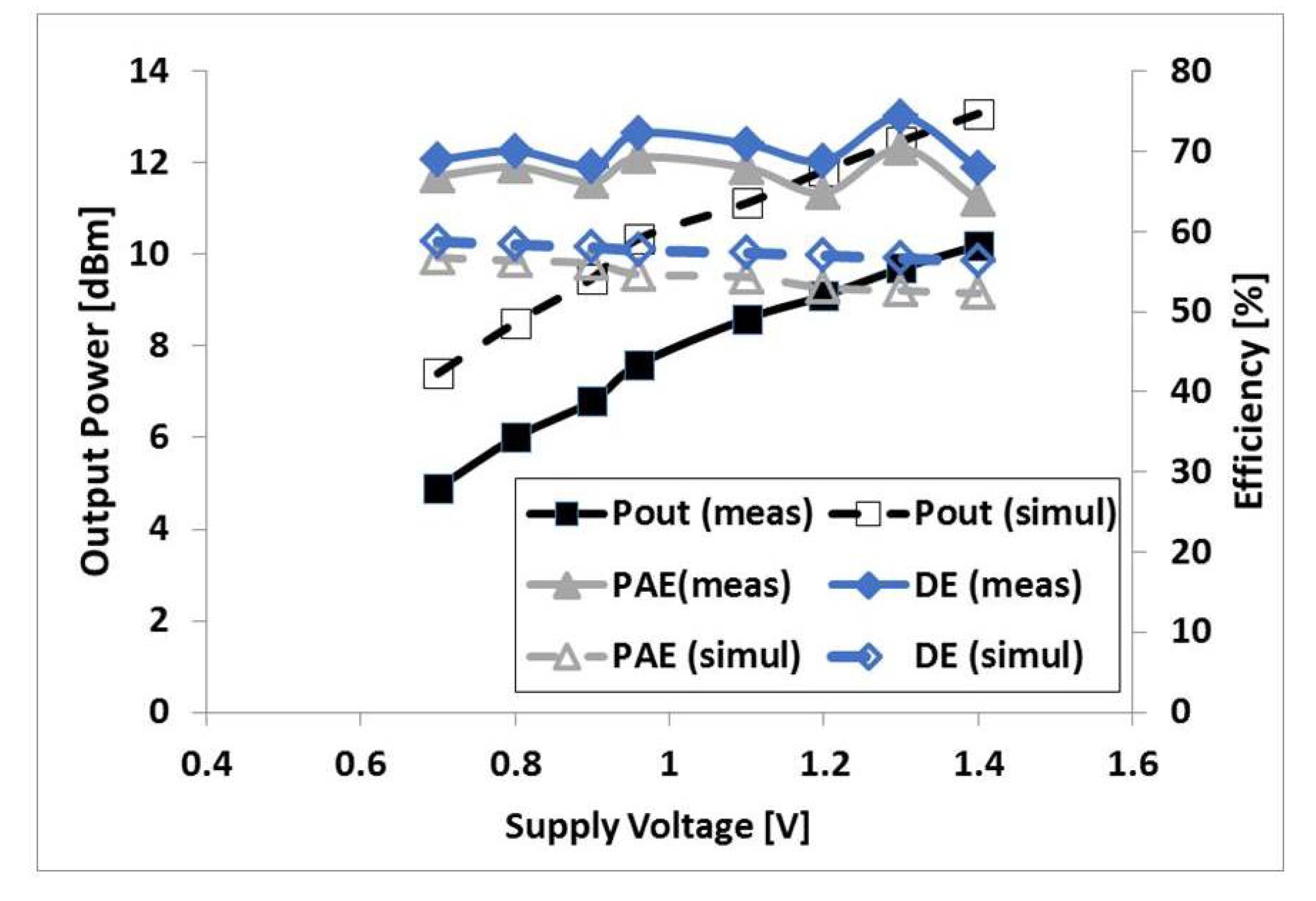
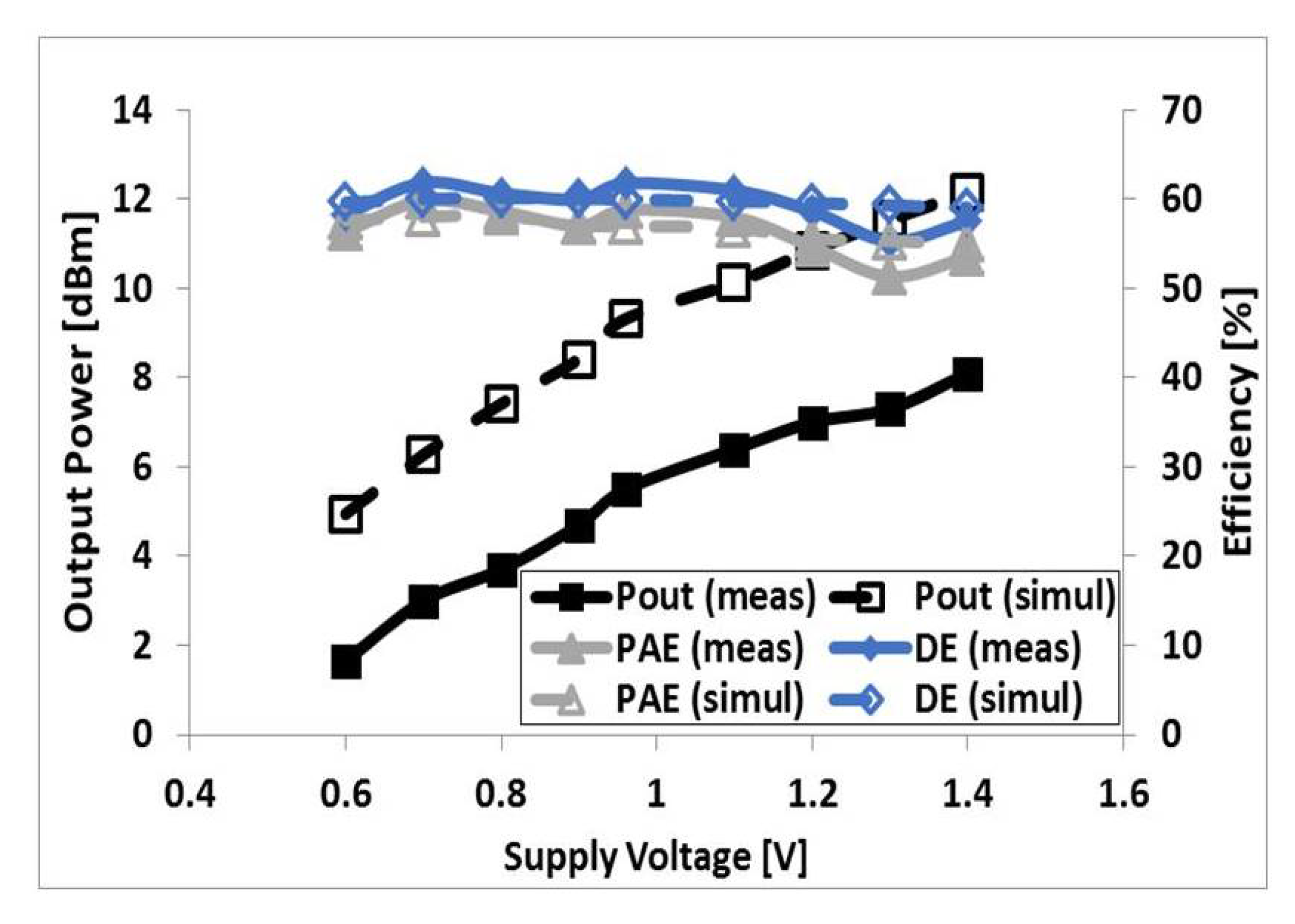
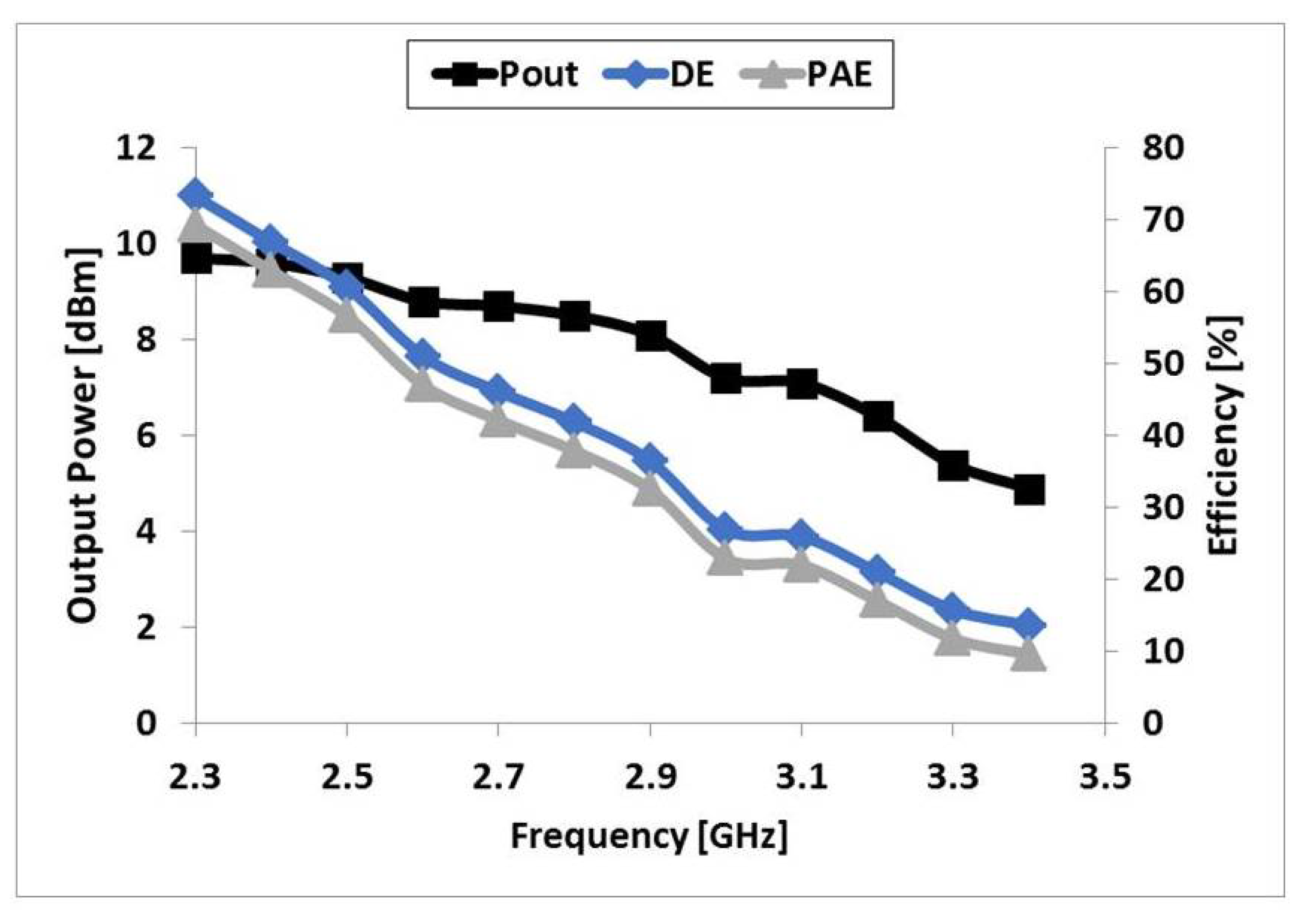
3. Measurement Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sokal, N.O.; Sokal, A.D. Class E-A new class of high-efficiency tuned single-ended switching power amplifiers. IEEE J. Solid-State Circuits 1975, 10, 168–176. [Google Scholar] [CrossRef]
- Raab, F. Idealized operation of the class E tuned power amplifier. IEEE Trans. Circuits Syst. 1977, 24, 725–735. [Google Scholar] [CrossRef]
- Kazimierczuk, M. Exact analysis of class E tuned power amplifier with only one inductor and one capacitor in load network. IEEE J. Solid-State Circuits 1983, 18, 214–221. [Google Scholar] [CrossRef]
- Milosevic, D.; van der Tang, J.; van Roermund, A. Explicit design equations for class-E power amplifiers with small DC-feed inductance. In Proceedings of the 2005 European Conference on Circuit Theory and Design, Cork, Ireland, 2 September 2005; Volume 3, pp. 101–104. [Google Scholar] [CrossRef]
- Kazimierczuk, M. Collector amplitude modulation of the class E tuned power amplifier. IEEE Trans. Circuits Syst. 1984, 31, 543–549. [Google Scholar] [CrossRef]
- Johansson, T.; Fritzin, J. A Review of Watt-Level CMOS RF Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2014, 62, 111–124. [Google Scholar] [CrossRef]
- Long, J.R.; Copeland, M.A. The modeling, characterization, and design of monolithic inductors for silicon RF IC’s. IEEE J. Solid-State Circuits 1997, 32, 357–369. [Google Scholar] [CrossRef]
- Sadiku, M.N. Elements of Electromagnetics; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Gamo, H. A general formulation of Faraday’s law of induction. Proc. IEEE 1979, 67, 676–677. [Google Scholar] [CrossRef]
- Mazzanti, A.; Larcher, L.; Brama, R.; Svelto, F. Analysis of reliability and power efficiency in cascode class-E PAs. IEEE J. Solid-State Circuits 2006, 41, 1222–1229. [Google Scholar] [CrossRef]
- Acar, M.; Annema, A.J.; Nauta, B. Analytical Design Equations for Class-E Power Amplifiers with Finite DC-Feed Inductance and Switch On-Resistance. In Proceedings of the 2007 IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 27–30 May 2007; pp. 2818–2821. [Google Scholar] [CrossRef]
- Lopez-Villegas, J.M.; Sieiro, J. Modeling of integrated inductors and transformers for RF applications. In Proceedings of the 6th International Conference on Thermal, Mechanial and Multi-Physics Simulation and Experiments in Micro-Electronics and Micro-Systems (EuroSimE 2005), Berlin, Germany, 18–20 April 2005; pp. 19–23. [Google Scholar] [CrossRef]
- Razavi, B.; Behzad, R. RF Microelectronics; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 1. [Google Scholar]
- Jenei, S.; Nauwelaers, B.K.J.C.; Decoutere, S. Physics-based closed-form inductance expression for compact modeling of integrated spiral inductors. IEEE J. Solid-State Circuits 2002, 37, 77–80. [Google Scholar] [CrossRef]
- Mohan, S.S.; del Mar Hershenson, M.; Boyd, S.P.; Lee, T.H. Simple accurate expressions for planar spiral inductances. IEEE J. Solid-State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
- Danesh, M.; Long, J.R.; Hadaway, R.A.; Harame, D.L. A Q-factor enhancement technique for MMIC inductors. In Proceedings of the 1998 IEEE MTT-S International Microwave Symposium Digest, Baltimore, MD, USA, 7–12 June 1998; Volume 1, pp. 183–186. [Google Scholar] [CrossRef]
- Sia, C.; Ong, B.; Chan, K.; Yeo, K.; Ma, J.; Do, M.A. Physical layout design optimization of integrated spiral inductors for silicon-based RFIC applications. IEEE Trans. Electron Devices 2005, 52, 2559–2567. [Google Scholar] [CrossRef]
- Scuderi, A.; Biondi, T.; Ragonese, E.; Palmisano, G. Analysis and modeling of thick-metal spiral inductors on silicon. In Proceedings of the 2005 European Microwave Conference, Paris, France, 4–6 October 2005; Volume 1. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Chan, A.; Razavi, B. Stacked inductors and transformers in CMOS technology. IEEE J. Solid-State Circuits 2001, 36, 620–628. [Google Scholar] [CrossRef]
- Long, J.R. Monolithic transformers for silicon RF IC design. IEEE J. Solid-State Circuits 2000, 35, 1368–1382. [Google Scholar] [CrossRef]
- Wei, M.; Kalim, D.; Erguvan, D.; Chang, S.; Negra, R. Investigation of Wideband Load Transformation Networks for Class-E Switching-Mode Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2012, 60, 1916–1927. [Google Scholar] [CrossRef]
- Tan, J.; Heng, C.; Lian, Y. Design of Efficient Class-E Power Amplifiers for Short-Distance Communications. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2210–2220. [Google Scholar] [CrossRef]
- Apostolidou, M.; van der Heijden, M.P.; Leenaerts, D.M.W.; Sonsky, J.; Heringa, A.; Volokhine, I. A 65 nm CMOS 30 dBm Class-E RF Power Amplifier With 60PAE at 16 dB Back-Off. IEEE J. Solid-State Circuits 2009, 44, 1372–1379. [Google Scholar] [CrossRef]
- Song, Y.; Lee, S.; Cho, E.; Lee, J.; Nam, S. A CMOS Class-E Power Amplifier With Voltage Stress Relief and Enhanced Efficiency. IEEE Trans. Microw. Theory Tech. 2010, 58, 310–317. [Google Scholar] [CrossRef]
- Ren, J.; Dai, R.; He, J.; Xiao, J.; Kong, W.; Zou, S. A novel stacked class-E-like power amplifier with dual drain output power technique in 0.18 μm RFSOI CMOS technology. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kreißig, M.; Kostack, R.; Pliva, J.; Paulo, R.; Ellinger, F. A fully integrated 2.6 GHz cascode class-E PA in 0.25 μm CMOS employing new bias network for stacked transistors. In Proceedings of the 2016 IEEE MTT-S Latin America Microwave Conference (LAMC), Puerto Vallarta, Mexico, 12–14 December 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Li, P.; Xia, Q.; Chen, Z.; Geng, L. High efficiency triple-stacked class-E power amplifier with novel dynamic biasing network. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Zhai, C.; Cheng, K.M. Fully-integrated CMOS differential class-E Power Amplifier with combined waveform-shaping network and transformer-based balun. In Proceedings of the 2014 Asia-Pacific Microwave Conference, Sendai, Japan, 4–7 November 2014; pp. 738–740. [Google Scholar]

| Configurations | Area | k | Capacitance | Electrical Symmetry | |
|---|---|---|---|---|---|
| Interleaved | Medium | Medium | Excellent | Excellent | Excellent |
| Stacked | Excellent | Excellent | Medium | Poor | Medium |
| Reference | [dBm] | PAE [%] | f [GHz] | Die Area [mm] | Process [nm] | FoM |
|---|---|---|---|---|---|---|
| [21] | 28.7 | 48 | 2.3 | 1.2 | 90 | 121.74 |
| [22] | 5.7 | 55 | 2.4 | 1 | 130 | 100.37 |
| [23] | 30 | 60 | 2 | 0.3 | 65 | 423 |
| [24] | 31.5 | 51 | 1.8 | 1 | 130 | 111.23 |
| [25] | 29.6 | 51 | 1.8 | 1.5 | 180 | 70 |
| [26] | 21.7 | 37.9 | 2.6 | 1.21 | 250 | 70.7 |
| [27] | 22.3 | 49.5 | 5 | 0.235 | 250 | 560 |
| [28] | 29 | 38.7 | 1.8 | 1.53 | 350 | 52 |
| This Work | 10.7 | 70 | 2.4 | 0.21 | 65 | 735 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, A.; Tan, A.; Kong, Z.-H.; Ma, K. A Design Methodology and Analysis for Transformer-Based Class-E Power Amplifier. Electronics 2019, 8, 494. https://doi.org/10.3390/electronics8050494
Lim A, Tan A, Kong Z-H, Ma K. A Design Methodology and Analysis for Transformer-Based Class-E Power Amplifier. Electronics. 2019; 8(5):494. https://doi.org/10.3390/electronics8050494
Chicago/Turabian StyleLim, Alfred, Aaron Tan, Zhi-Hui Kong, and Kaixue Ma. 2019. "A Design Methodology and Analysis for Transformer-Based Class-E Power Amplifier" Electronics 8, no. 5: 494. https://doi.org/10.3390/electronics8050494
APA StyleLim, A., Tan, A., Kong, Z.-H., & Ma, K. (2019). A Design Methodology and Analysis for Transformer-Based Class-E Power Amplifier. Electronics, 8(5), 494. https://doi.org/10.3390/electronics8050494





