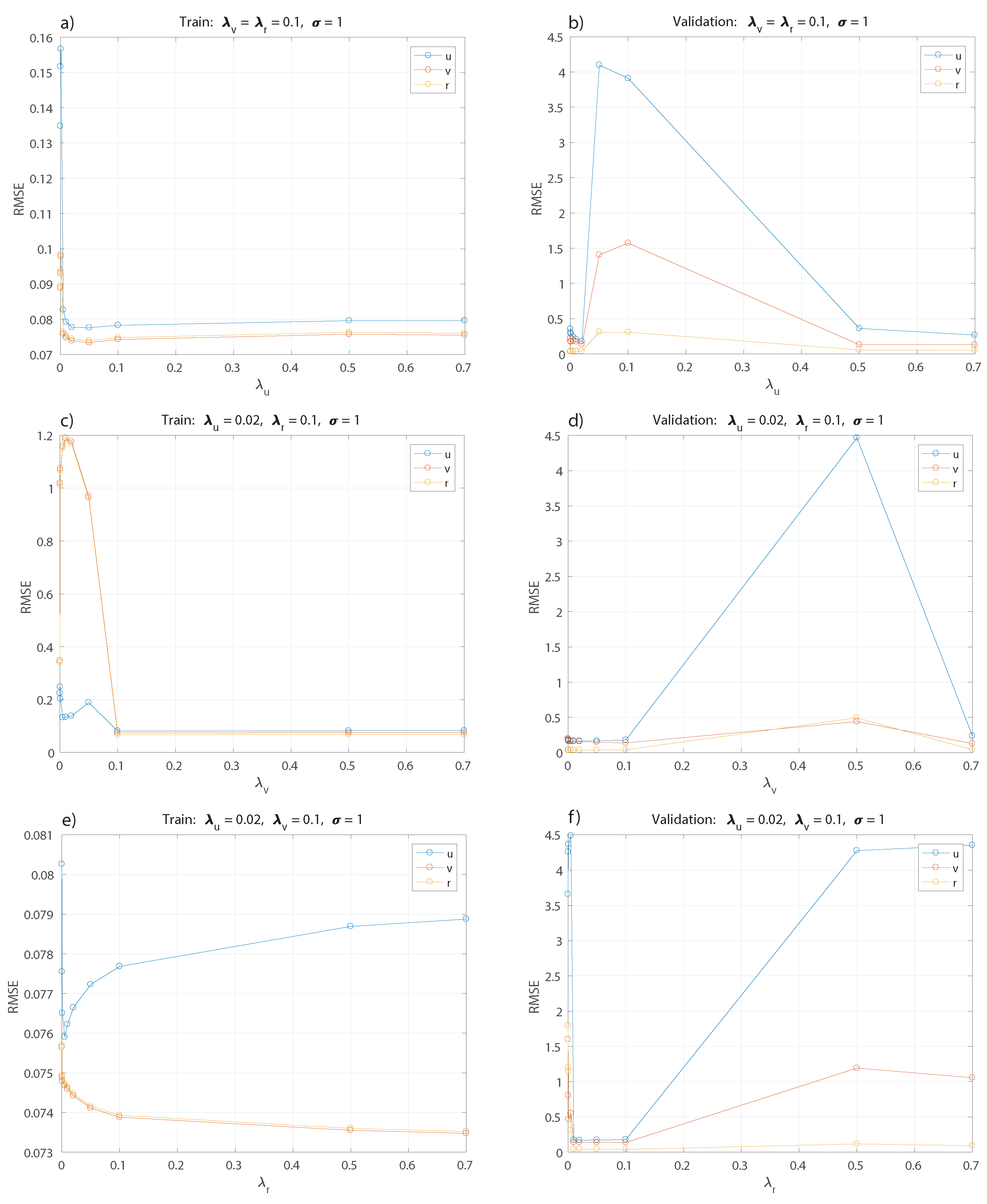1. Introduction
System identification, also known in industrial design as
surrogate modelling, is one of the most important phases in multiple engineering areas, where reliable mathematical models, and tools are needed for a wide range of applications [
1,
2]. The goal of system identification is to build mathematical models that, given the same inputs, yield the best fit between the measured response of the systems and the model outputs. Specifically, identification of mathematical models is of great importance for an efficient control design for autonomous vehicles, and therefore, this paper focuses on the identification of marine vehicles for control purposes.
It is important to remark that a real experiment in the sea involves a lot of people and infrastructures, with a high cost in terms of time and money. In this sense, the development of efficient models may provide accurate simulations which help to tackle real experiments with higher confidence, avoiding the realization of multiple and costly tests at sea. These models can be used to simulate new control systems and predict the behaviour of the real vehicles with high accuracy before real tests are carried out.
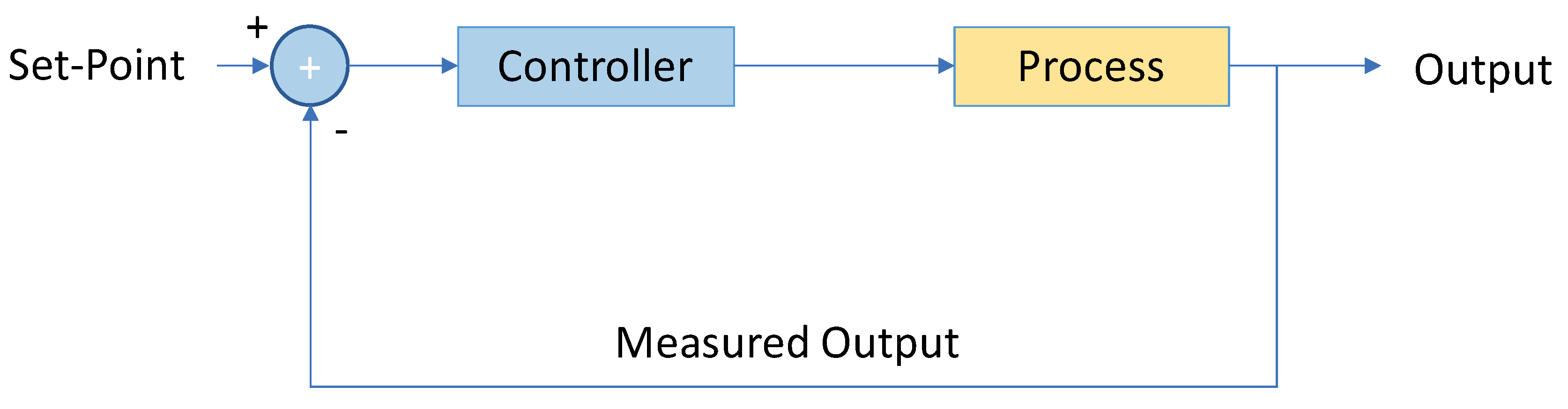
In control system applications, a closed-loop system is composed of the physical system or process, the feedback loop and the controller, as shown in
Figure 1. The objective is to obtain a good performance of the closed-loop control system based on simulations carried out with the computed model, for example [
3] where a course-keeping algorithm based on a knowledge base is developed for control tasks that can be applied for the simulation of nonlinear ship models. Therefore, the identification of the mathematical model should be sufficiently accurate and easily implementable so that these simulations can provide useful information. Although the performance of the vehicle can be improved when the control system is designed and implemented, the better the performance of the model computed in the identification phase, the better the performance of the closed-loop system once it is translated to the real world.
A good survey on identification can be found in [
4,
5]. It is possible to find different kinds of models in the literature, such as the gray-box models, which estimate parameters from data given a generic model structure, i.e., the model is based on the physics of the system and data, or the black-box models, which determine the model structure and estimate the parameters from data. For a survey on black-box identification, the reader is referred to [
6]. There are plenty of techniques that may be applied for black-box identification, for example, in the present work Symbolic Regression, Kernel Ridge Regression and also models computed with Support Vector Machines are considered. Among other techniques, an important technique for black-box system identification is the high resolution spectral estimation technique, where the modelling of time series is made over a limited window size of measurements. Different divergence measures can be employed, such as the beta divergence [
7], which is used to develop highly robust models with respect to outliers in learning algorithms. These information-theoretic divergences are commonly used in fields such as pattern recognition, sound speech analysis, or image processing [
8]. In this paper, the well known Root Mean Square Error (RMSE), which is closely related to
-norm, has been considered as a cost function to optimize the models.
Much work has been carried out in marine vehicle identification for different types of marine vehicles, for example, for surface marine vessels some of the most popular are Nomoto and Blanke models [
9]. For the computation of an accurate model, a large experimental dataset is usually needed so that the model computed may be able to characterize the hydrodynamics of the vehicle. In this sense, the identification of an accurate model may be a very complex task that entails great computational effort. There are different methods to estimate these models in the state-of-the-art such as Kalman Filter (KF) [
10], Extended Kalman Filter (EKF) [
11], or AutoRegresive Moving Average (ARMA) [
12]. For some other interesting related works, the reader is referred to [
9,
13,
14,
15], and the references therein.
Machine learning (ML) techniques have recently gained popularity in system identification and control problems, for example, we can find some works using Support Vector Machines (SVM) [
16], Support Vector Regression (SVR) for linear regression models [
17], the application of SVM to time series modelling [
18], and Least-Squares Support Vector Machines (LS-SVM) for nonlinear system identification [
19]. We can also find interesting works using Gaussian Processes for identification, such as [
20], where Gaussian Processes are used to model non-linear dynamics systems [
21], in which model identification is applied including prior knowledge as local linear models, or [
22], where a new approach of Gaussian Processes regression is described to handle large datasets for approximation. For a survey on Gaussian Processes identification, see [
23], and for an interesting survey on kernel methods for system identification, the reader is referred to [
24].
We can find some works where neural networks have been employed in marine system identification [
25,
26,
27], and other interesting works include the training of Abkowitz models using LS-SVM [
28] and
-SVM [
29]. However, most of these works use synthetic data without noise, simulating basic trajectories for training and testing the models, without proving the efficiency of the model in real experiments.
As far as the authors know, the state-of-the-art shows only a few works using real datasets for marine vehicle identification with ML techniques. Some of the works that have modelled surface marine vehicles using real experimental datasets are, for example, [
30] where LS-SVM is used for training a Nomoto second-order linear model, and a Blanke model in [
31]. In [
32], SVM is used for modelling a torpedo AUV, and symbolic regression is applied in [
33]. Finally, in [
34] a surface marine vehicle is modelled using Kernel Ridge Regression with Confidence Machine (KRR-CM). However, they use a small number of basic and simple trajectories to train and test the models.
In this work, the aim is to provide general and robust black-box models of a ship by applying different regression techniques. Unlike other studies in the state-of-the-art that employ synthetic data without noise or small experimental datasets of basic movements, the work described in this paper uses experimental data from different random manoeuvres and trajectories. In these previous works, models have been trained using specific trajectories, such as evolution circles or Zig Zags, and have been tested on the same type of movement. In contrast, in our study, we train and test the model with different random trajectories to ensure its robustness. Among the different techniques available from the Machine Learning field, we have selected the well-known Ridge Regression (RR) technique, since it is a basic regression technique widely used in many applications with good results. Alternatively, as an extension of RR, we have also applied Kernel Ridge Regression (KRR) with two different kernels: Radial Basis Function (RBF) and polynomial. The last approach applied is Symbolic Regression (SR), which is based on Genetic Programming (GP), obtaining a full expression for the equations of the model. While not as simple as RR models, it is more interpretable than kernel methods.
This paper is organized as follows. In
Section 2, the experimental system and dataset are presented.
Section 3 explains the techniques used to train the different models. In particular, parameter selection for RR and KRR are detailed, and the scheme followed for the SR models is described. The results of the different models are shown in
Section 4, and finally the conclusions and future work are discussed in
Section 5.
3. Machine Learning Techniques
In this section, an overview of the regression techniques applied is provided. First, an introduction on Ridge Regression (RR) is given, and then extended to Kernel Ridge Regression (KRR). Finally, Symbolic Regression (SR) using Genetic Programming (GP) is explained. Notation: In the following, matrices appear in bold and capital letters, while vectors appear in bold and lower case letters. We denote by the identity matrix, and by the transpose of matrix .
3.1. Ridge Regression
Ridge Regression (RR) is a well known regression shrinkage method proposed in [
36]. The original motivation of this technique is to cope with the presence of too many predictors, i.e., the number of input variables exceeds the number of observations. Although this is not the case for our problem, applying a regularization on the predictor estimation nevertheless helps to achieve a better model. The parameters of standard linear regression can be obtained as
, where
is input data,
is its transpose matrix, and
is output data. The estimates depend on
and small changes in
produce large changes in
when
is nearly singular. The model estimated may fit the training data but may not fit the test data. The conditioning of the problem can be improved by adding a small constant
to the diagonal of the matrix
before taking its inverse:
Then, RR is a modified version of least squares that adds an regularization to the estimators to reduce the variance. This shrinkage parameter controls the penalization over the variables (). If , we will have least squares, and if , the constraints on the variables are very high.
3.2. Kernel Ridge Regression
Dual ridge regression was proposed in [
37] using kernels. RR is combined with the kernel trick, i.e., the substitution of dot products in the optimization problem with kernel functions. This allows to transform a non-linear problem into a higher dimensional feature space where the problem is linearly separable. A kernel function is expressed as
, with
. Applying the kernel trick on the expression of RR, Equation (
5), by substituting all
with
yields:
where
is the kernel matrix. Then, the general form for Kernel Ridge Regression (KRR) becomes:
where
is a sample,
with
are the learned weights,
is the identity matrix, and
is the kernel function.
KRR and Support Vector Regression (SVR) are similar. Both use
regularization but have different loss functions and KRR seems to be faster for medium datasets. The main motivation to use KRR, rather than SVR or LS-SVM, is the good results obtained in a previous work [
34], where a KRR Confidence Machine (Conformal Predictors) was applied.
There are plenty of kernel functions available, however we have selected two of the main kernel functions widely used in the literature, namely, Radial Basis Function (RBF) and polynomial. The RBF kernel presents the following form:
where
denotes the euclidean distance, and the
parameter should be carefully tuned since it plays a major role in the performance. If
is overestimated, the exponential would behave linearly, losing its non-linear properties in the higher dimensional space; but if it is underestimated, the kernel will present a lack of regularization and will be sensitive to noise.
The polynomial kernel has the form:
where the parameters are the slope
, a constant term
c and the polynomial degree
p. In general, polynomial kernels behave well for normalized data.
3.3. Symbolic Regression
Genetic Programming (GP) is a supervised learning method based on the idea of biological evolution, i.e., the survival of the fittest individuals [
38,
39]. In GP, the possible solutions of the problem are presented as individuals who are evaluated using a fitness function to select the best candidates. These candidates are then mixed to combine the genes and generate new solutions in an iterative process. The basic algorithm works as follows:
A random initial population is created.
The fitness of the members of the population is evaluated.
The ’stop if’ condition is evaluated (a given accuracy, number of generations, etc.).
A next generation of solutions is formed by combining the selected members of the population using different operators (crossover, mutation, reproduction, etc.). Go back to step 2.
The operators basically mix the characteristics of the solutions, called genes, to generate new candidates. The combination of the best individuals along the generations should converge to an optimal solution. Symbolic Regression (SR) is a particular case of GP where the candidates are defined by functions and the objective is to fit empirical data without
a priori assumptions on the model structure. The fitness function in SR is the accuracy of the individuals fitting the empirical data, in our case RMSE, and the possible solutions are presented in a tree-based structure where nodes represent operators and variables. See [
40] for further description of SR. The library used for SR is the toolbox GPTIPS 1.0 in Matlab [
41].
Following a similar process to [
33], the operations allowed between variables are sum, difference, multiplication, protected division, protected root square and square. More operations can be used but the purpose is to keep the model simple while obtaining a good representation of the system.
In the following section, we have set the population to 600 and the generations to 500, with a tournament selection. The maximum number of genes per individual is fixed to 5 without the computation of the bias term, and the maximum depth of trees is 3.
These parameters could be changed with a large number of possible combinations. However, the values selected are a tradeoff election between very complex and very simple models after running a battery of experiments conducting a search grid over these parameters. By doing this, and with the selected parameters, the models proposed by the SR algorithms provide high accuracy while keeping the model structure relatively simple. For smaller values than those selected (genes or depth tree), the individuals (models) were quite simple, providing a reduced variety of individuals, thus constraining the optimal solutions to a few members. For larger values, the models became quite complex and also encountered the problem of over-fitting, modelling even the noise of the signals. Therefore, the above parameters have been set to the specified values to obtain interpretable models while not being excessively complex.
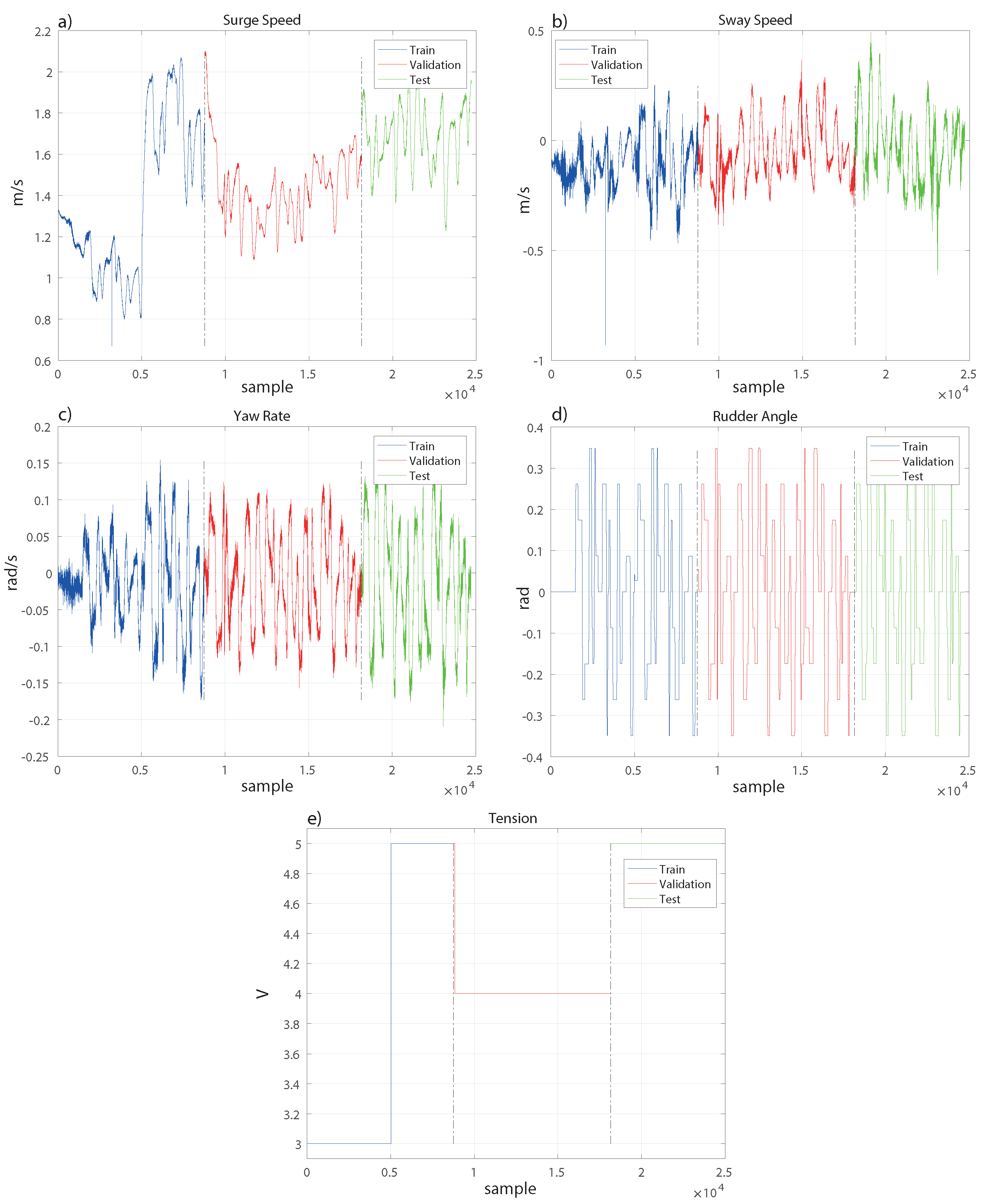
4. Results
To evaluate the performance of the models, Root Mean Squared Error (RMSE) has been used as a fitness function as mentioned in
Section 2.2.
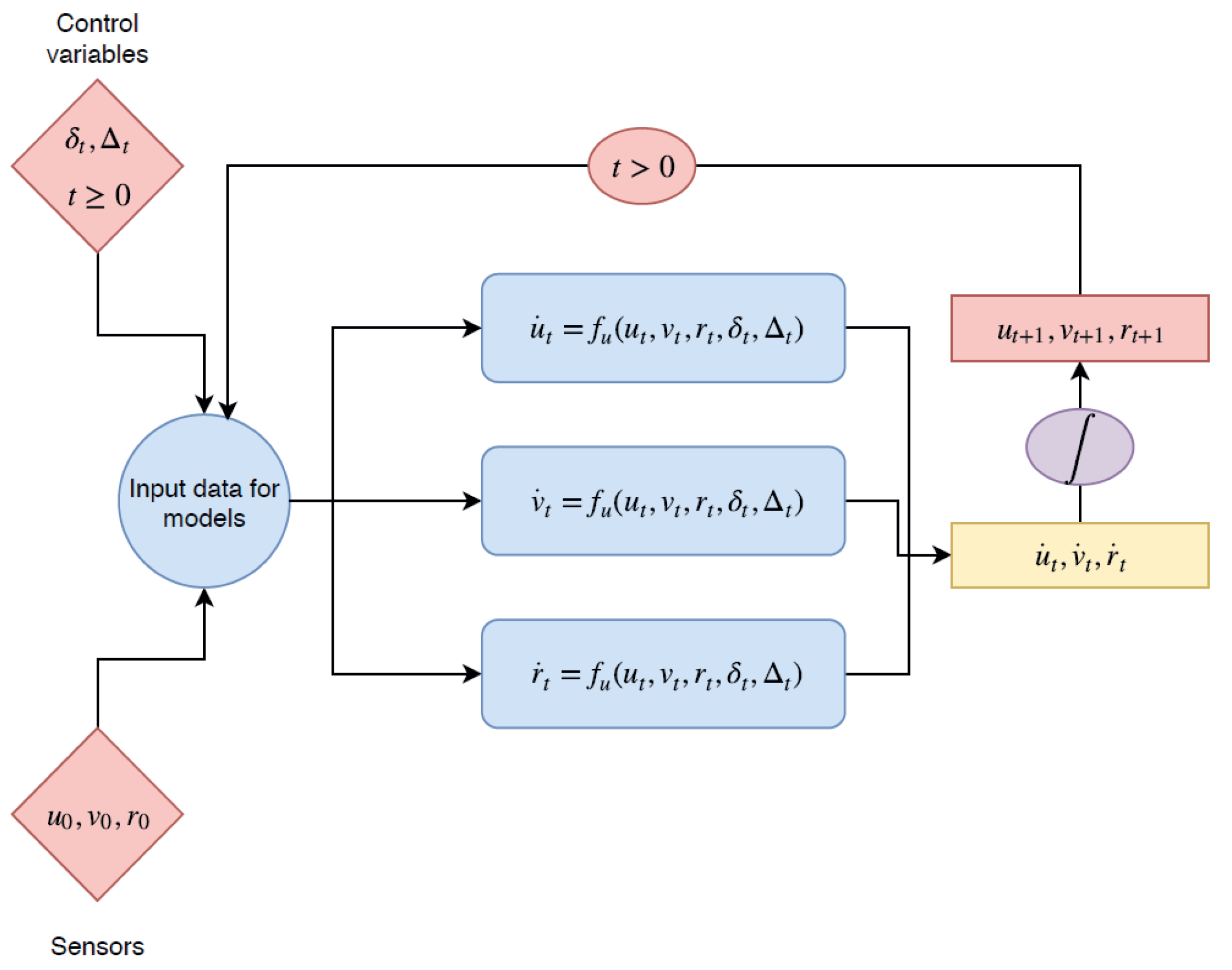
Two different approaches for the parameter selection of KRR with the RBF kernel have been applied. Firstly, each model was optimized independently, the parameters were tuned using the recursive regression only for the variable being optimized while the other variables were set to their true values from the training data, rather than their previous predicted values. In other words, if we are performing a freerun simulation, as shown in
Figure 4, the recursive regression uses as initial input
and for
the inputs used are
from the dataset and the predicted speed values
. However, if we are training the surge speed model
, the inputs for
are
from the dataset and the predicted value for
. This was done for each model
for the parameter selection. Nevertheless, this approach does not work once the optimal models are used together in a recursive regression for the validation and test.
Therefore, a second approach has been used. The
,
and
parameters and
,
and
hyperparameters selection has been carried out training the three models together by means of an exhaustive grid search. Training data are used to optimize our cost function and compute our model parameters
given specific values of the kernel hyperparameters and
s parameters. These specific parameters are computed as follows: first, a quick search was done to evaluate the range of the parameters where models show a coherent behaviour, i.e., low values for RMSE. Then, an exhaustive grid search for each parameter is performed by fixing the rest of the parameters at the values obtained in the previous process, as shown in
Figure 5 and
Figure 6. Each model obtained in this search is validated using the validation set, and the parameter values with the best performance are selected.
Figure 5a,b show the selection of
keeping fixed the rest of the parameters for the training and validation set. The best value obtained is
, then this parameter is kept fixed for tuning the others in the following optimization of
and
in
Figure 5c,d and
Figure 5e,f respectively.
The best values correspond to
. Now, keeping these values fixed, a range of values for
,
, and,
is tested; see
Figure 6, with the best results obtained for
. For simplification, only the result for
is shown as the analysis applies the same value for
and
, since changing the parameter for each model does not show a significant difference.
The polynomial kernel shows acceptable results with degrees using constant parameters and . The values used for are the same as the best result from the previous analysis for kernel RBF.
The results are shown in
Table 2 with the best model obtained from the parameter selection of kernel RBF, polynomial kernel and SR. The polynomial kernel shows slightly better results than RBF for both cases,
and
. The case of
corresponds to the standard RR approach.
The last model is computed applying GP with symbolic regression, where the following equations are obtained:
These equations show a dependency that is inversely proportional to the applied tension. It is important to note that the operation applied is a protected division, i.e., the tension variable will never be 0. Then, this model is useful for manoeuvres when the tension applied to the motor is , which makes perfect sense since there is no interest in modelling the boat with , and very low values of are not considered, since a minimum tension is needed to start or keep running the motor.
Table 3 shows the performance of the two best models obtained for validation and test sets. These models correspond to the polynomial kernel with degree
and the best model obtained with SR following the process explained in
Section 3.3. It can be seen that both results are really close and the polynomial kernel with
obtains slightly better performance in the validation and test sets. Although the difference between the models and the real data is not so small, it is important to consider that we are modelling experimental data. The noise has not been removed from the data, since we try to simulate the real experiment as close as possible. Thus, if the performance had been very accurate, it would indicate that we are over-fitting the noise in the data.
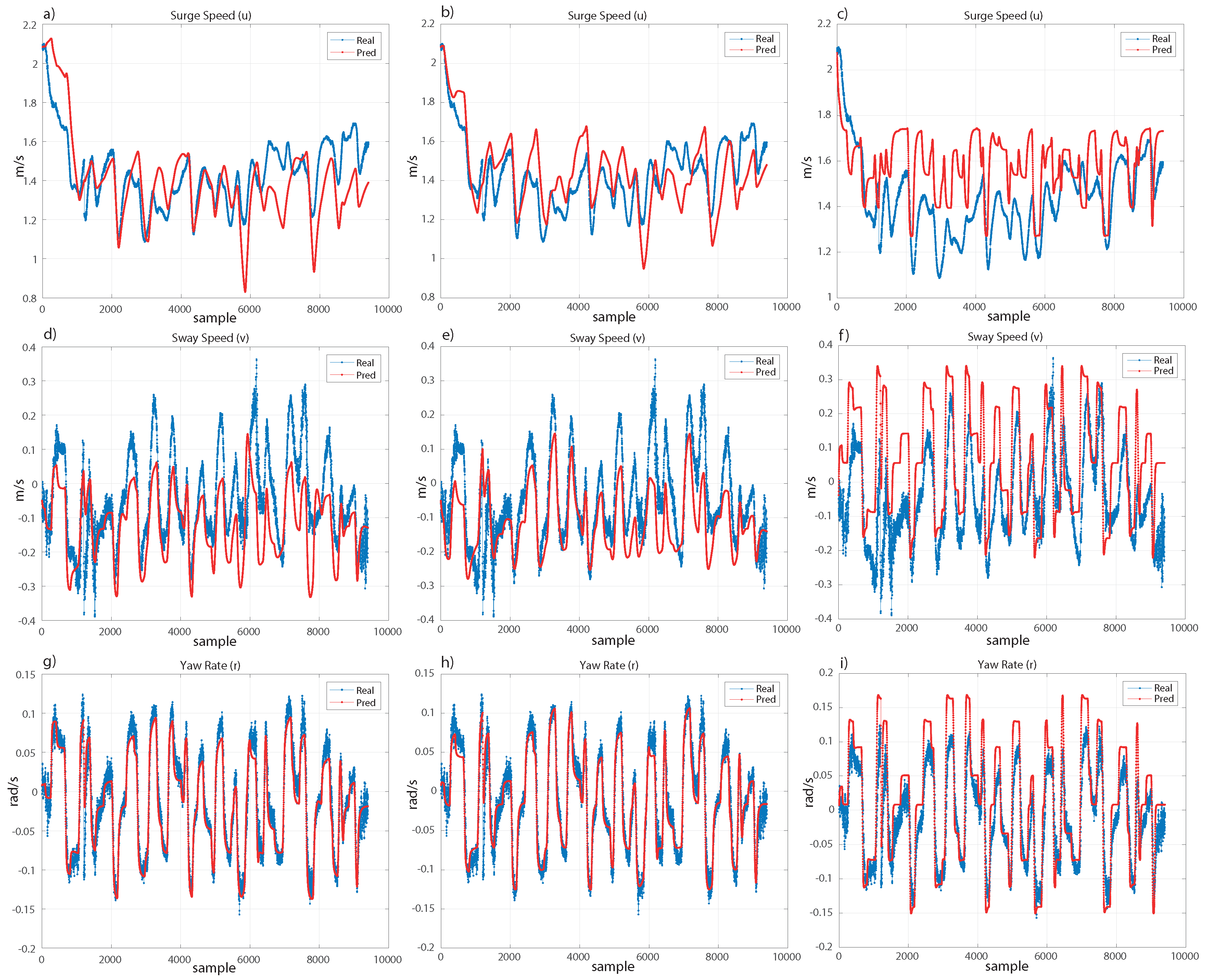
Therefore, since we are not interested in modelling the experimental data completely to avoid fitting the noise, and we just search for fitting the real movement of the ship, the models should follow with small error the trend of the real movement. Under these considerations, both models are really close, as shown in
Figure 7 and
Figure 8. For the validation set (see
Figure 7), the surge speed (
u) and sway speed (
v) are very similar for both models. In the case of the yaw rate (
r), both models are very efficient. For the test set (see
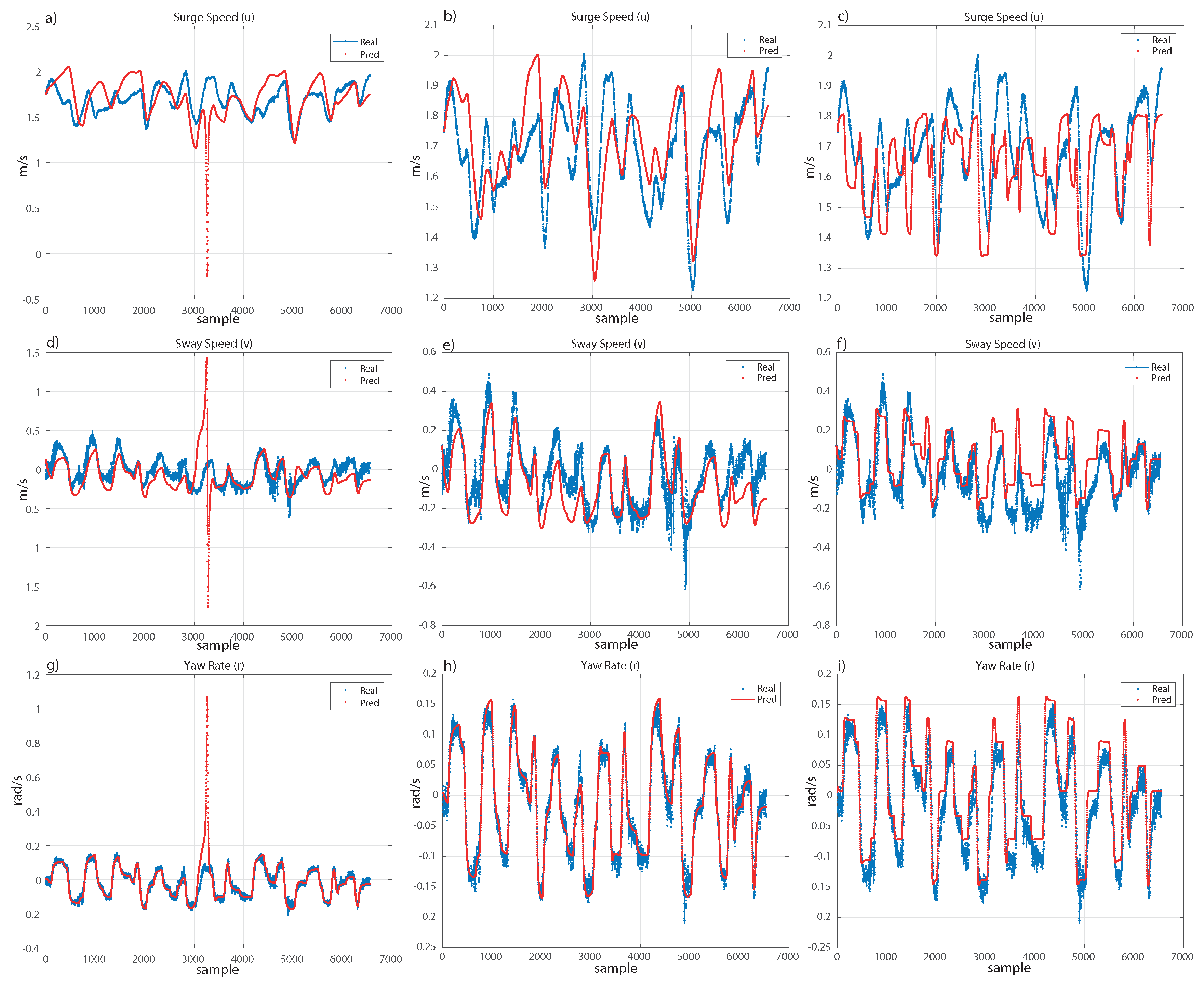
Figure 8), we can see a similar result. However, the polynomial kernel shows a peak where only one sample has been extremely poorly fitted. Despite this, the models are robust and recover the trend of the real movement.
As mentioned, there are not many works with experimental data for marine vehicle identification, and a comparison with models computed from synthetic data without noise or basic manoeuvres of a different ship would not be a rigorous analysis. A reasonable comparison with models from the state-of-the-art would be to compare the models computed in the present work with those from two works using the same ship and experimental data with basic movements for training them. Therefore, we have considered the models trained in [
33] with SR and in [
31] with LS-SVM. We will call these models, from the state-of-the-art, SOA-SR and SOA-LSSVM, respectively. hlOn one hand, SOA-SR is trained using experimental data from a 20/20 degree Zig-Zag manoeuvre and a similar process in the GP setup. On the other hand, SOA-LSSVM uses a Blanke model with LS-SVM and a 20/20 degree Zig-Zag manoeuvre for the training. These models have been tested on the validation and test sets; see
Table 3 where SOA-LSSVM shows a worse fitting on both datasets. However, SOA-SR shows results that are slightly worse than those of the best models selected in this work, and following the previous discussion, we analyze the fitting in both datasets in
Figure 7 and
Figure 8, to show graphically the performance of the model from the state-of-the-art in comparison with the models computed in this paper.
5. Conclusions and Future Work
This paper showed alternatives for black-box marine identification using different regression techniques. The main objective was to develop robust and simple models from experimental data of a real ship using random manoeuvres instead of predefined and simple manoeuvres. Three different datasets from different random trajectories have been used for training, validation and test, respectively. On the one hand, we have used kernel ridge regression with RBF and polynomial kernels with their respective parameter selection to train the models. The standard RR has been treated as a particular case of polynomial kernel with . On the other hand, GP with SR has been used with some constraints on the operations and on the depth of the trees and nodes to keep the complexity of the model low and, at the same time, obtain a good performance. Among all the models obtained, SR and KRR with the polynomial kernel with showed the best results. Although they present similar performance, we conclude that SR shows a slightly better approach since the equation form is not constrained to a polynomial, and it gives more flexibility to obtain different equations and to apply different operations. Furthermore, being able to generalize better a wider range of manoeuvres, the models provided seem to be more robust than classical models from the state-of-the-art such as SOA-LSSVM which is based on a Blanke model. Although the models presented in this work obtain better results than the SOA-SR model, it is important to note that this model obtains satisfactory results testing random trajectories. This shows how SR is an effective approach to obtain black-box identification models, and deserves further experimentation and efforts to further improve the modelling accuracy and its generalization performance.
An extended analysis on black-box identification models will be carried out as future work, where a wider variety of different approaches will be tested. Different techniques can be applied for black-box identification, and identifying which ones are more suitable for this problem would help to obtain more efficient models. The models presented in this work are formulated as differential equations of the speed variables, however it is interesting to develop discrete models based only on the speed variables. In addition, the identification is carried out using only the previous time step to predict the new incoming sample. The application of models trained with different temporal window sizes as input should be studied in the future.