1. Introduction
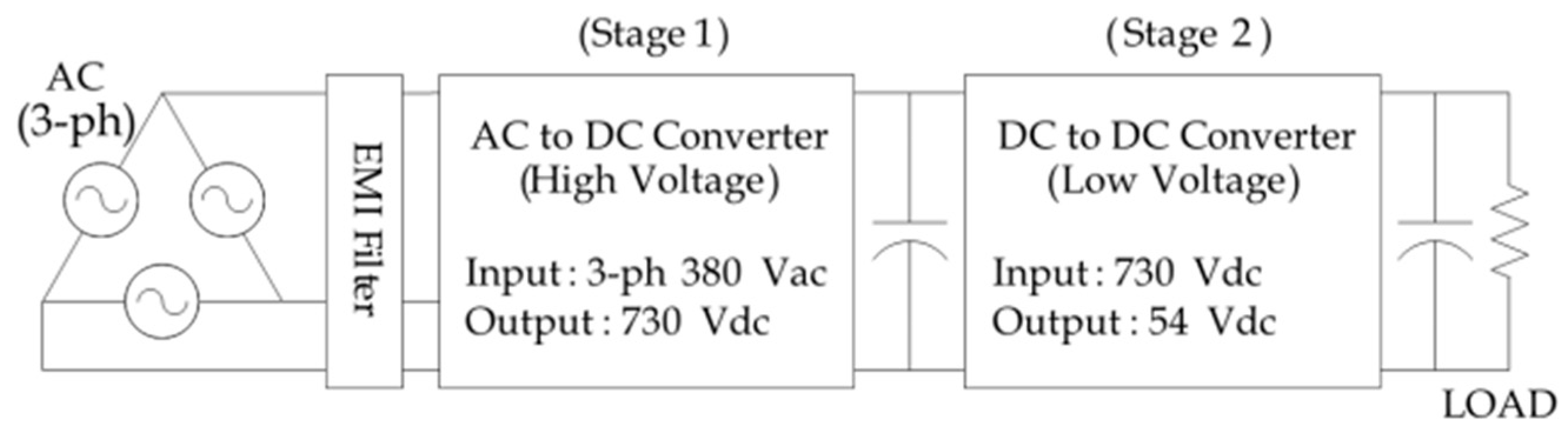
Generally, a power-supply system for communications requires a high power factor and wide bandwidth response characteristics. For this reason, the majority of power-supply systems for communications have a two-stage configuration, as shown in
Figure 1, including an AC/DC rectifier with a power-factor correction (PFC) function and a DC/DC converter with insulation between the primary and secondary circuits. The high-capacity power-supply system using a large input voltage usually applies three-phase power. The PFC circuit uses a boost-type two-level pulse-width modulation rectifier or three-level Vienna rectifier. The insulation-type DC/DC converter is typically designed by using a soft-switching topology to consider efficiency and size.
Because a rectifier using three-phase power as an input has a large DC link voltage, a DC/DC converter needs to use a power-switching element with a large breakdown voltage and low conduction loss, like an insulated gate bipolar mode transistor (IGBT). However, as IGBT undergoes a drastic increase in switching loss due to the tail current, it is not appropriate for fast switching. Accordingly, a low switching frequency is generally used to minimize the loss of the switching element, which increases the volumes and capacities of the inductor and capacitor. Furthermore, a high output-to-input voltage ratio causes a large transformer loss. Various studies have attempted to minimize the loss of the transformer by constructing a high-capacity converter. To solve this issue, a Vienna rectifier was used to dissolve a voltage imbalance by controlling the voltage of the center point of the link capacitor in the AC/DC rectifier on the basis of a three-level space-voltage vector [
1], and the series-connected DC/DC converter used a metal–oxide–semiconductor field-effect transistor (MOSFET) element for soft switching [
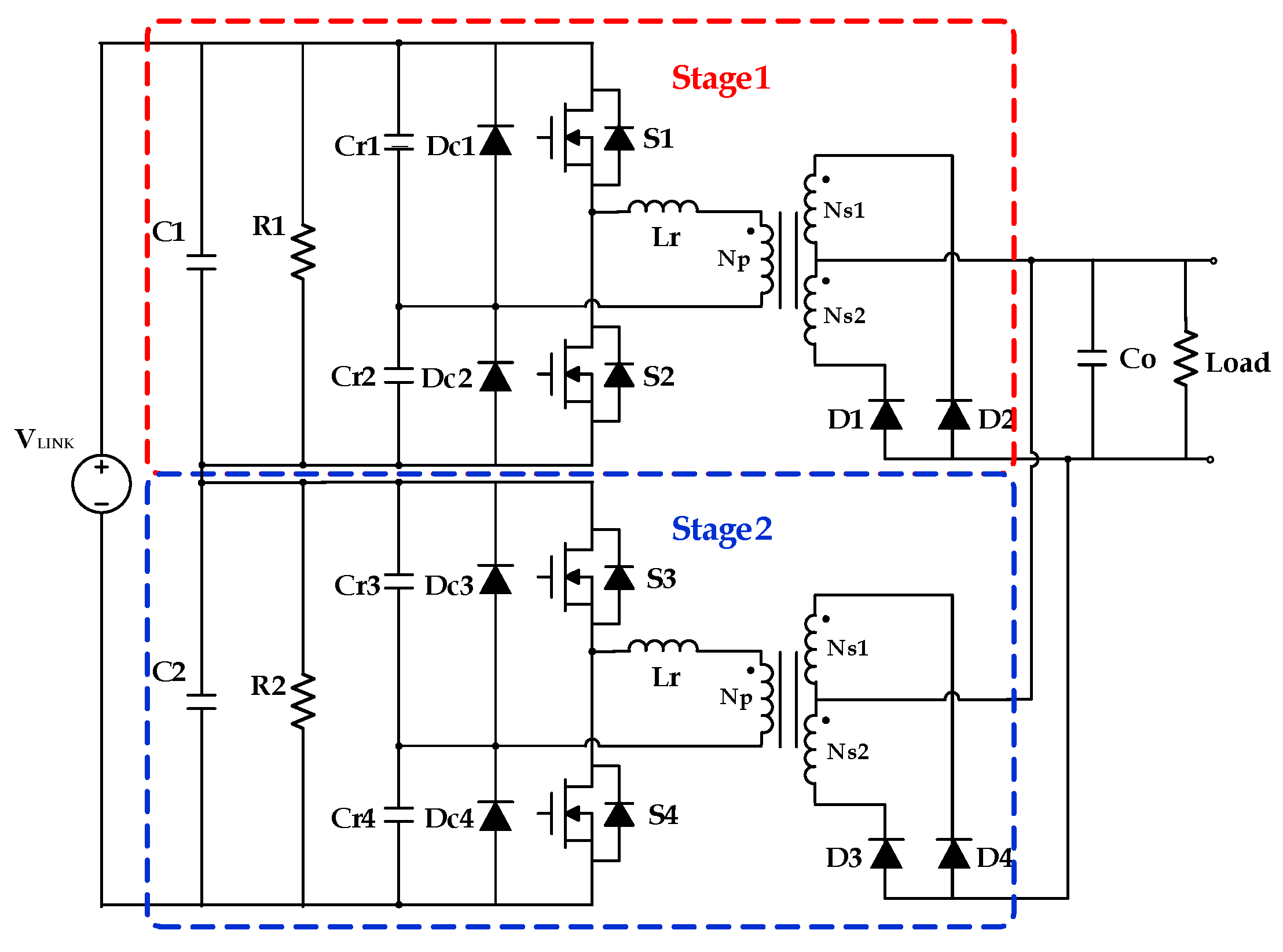
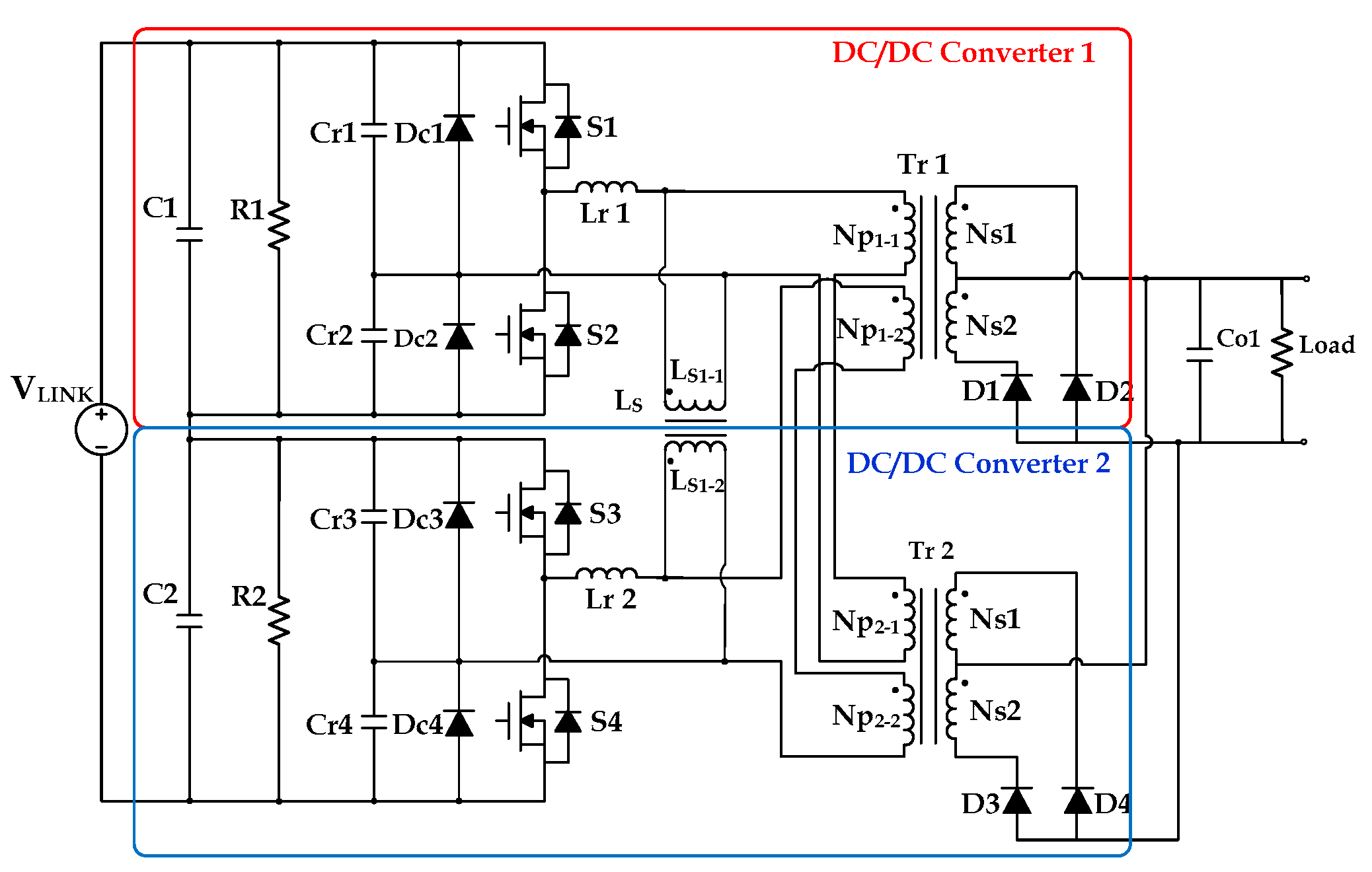
2] so called input series and output parallel (ISOP), which divides a large DC link voltage into smaller voltages and has a low withstand voltage and good switching performance as shown in
Figure 2.
In this way, the efficiency was improved and the volume was minimized. Moreover, to solve the problem of miniaturization, converters with the same module were connected by input serial and output parallel (ISOP) topology [
3,
4,
5,
6,
7,
8,
9]. However, this method may cause a problem of power imbalance between equivalent modules connected by ISOP. Among representative methods of solving this problem, Reference [
3] permits a certain imbalance between ISOP converter modules by permitting an imbalance of DC link voltage which called the auto-balancing method in that patent, and other methods divide the currents by independently controlling DC/DC converters [
4,
5,
6] or utilizing a coupling inductor [
7]. Unfortunately, these methods cannot perfectly solve the fundamental problem of power imbalance, which is attributable to complex circuits or control and the difference among elements. Another method used a single multiple-input transformer to solve the problem of power imbalance [
8]. However, this method cannot also solve the problem of increasing volume due to the heat concentrated in the transformer. This study proposes a new solution to the power imbalance of the DC/DC converter, which applies a new topology for the magnetic coupling of the transformer.
Section 2 analyzes the cause of the power imbalance of LLC resonant DC/DC converter with an ISOP auto-balancing configuration. The power imbalance of each converter is caused by passive elements, active elements, and the control signal. Among these factors, the difference in the magnetic elements is most influential.
Section 3 proposes a new topology for LLC resonant DC/DC converters, which uses a coupled shunt inductor and multiple-input transformers that share magnetic coupling in order to solve the problems of miniaturization and power imbalance in DC/DC converters.
Section 4 presents the proposed winding method for a multi-input transformer.
Section 5 applies the design parameters of the proposed LLC resonant DC/DC converter using a coupled shunt inductor and multiple-input transformers sharing magnetic coupling to a PSIM simulation tool to comparatively analyze the power imbalances.
Section 6 designs the prototype power-supply system by applying the proposed topology and verifies the effectiveness of the proposed method through simulation and experiment.
2. Power Imbalance Problem of ISOP Auto-balancing Converter
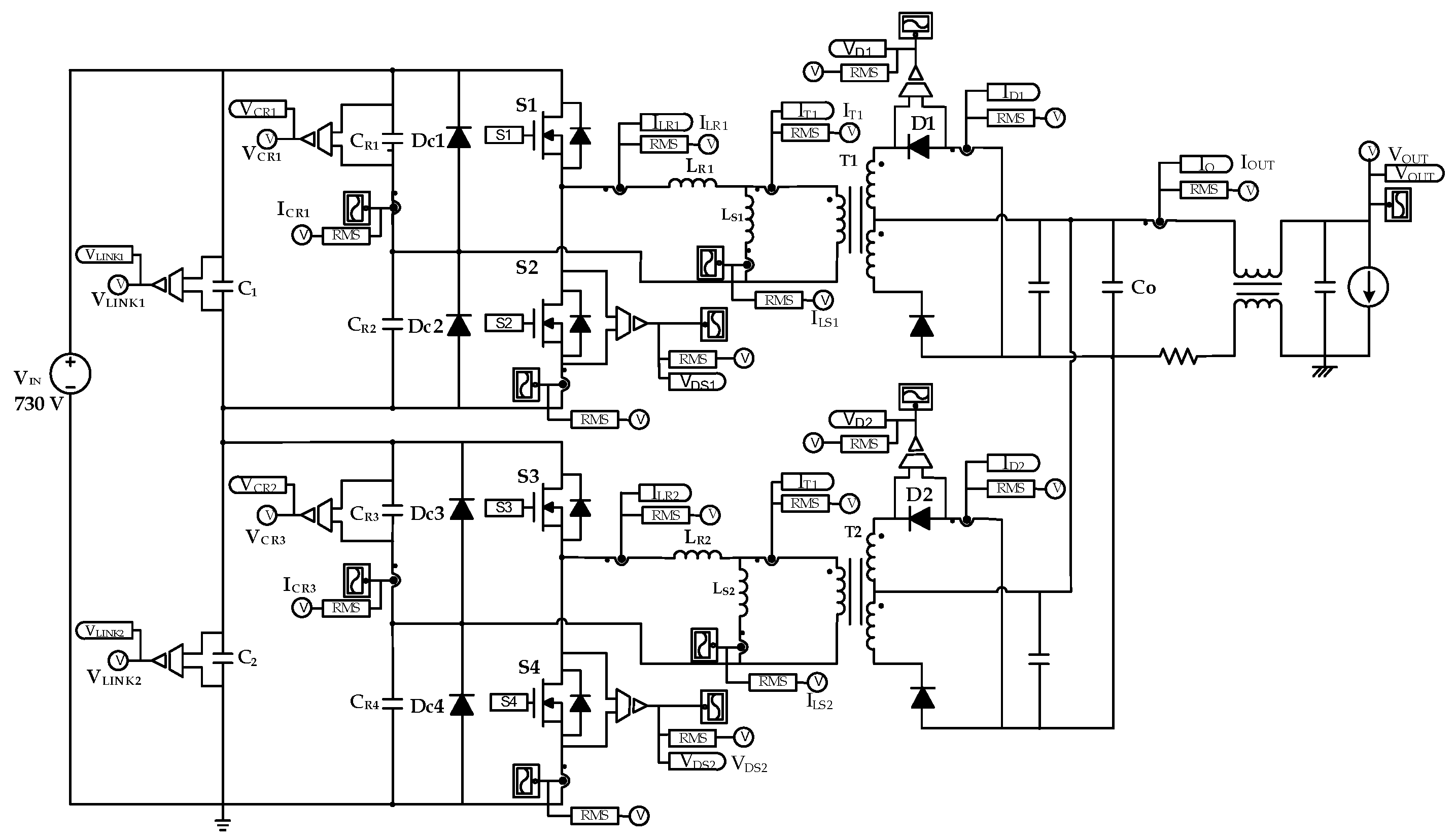
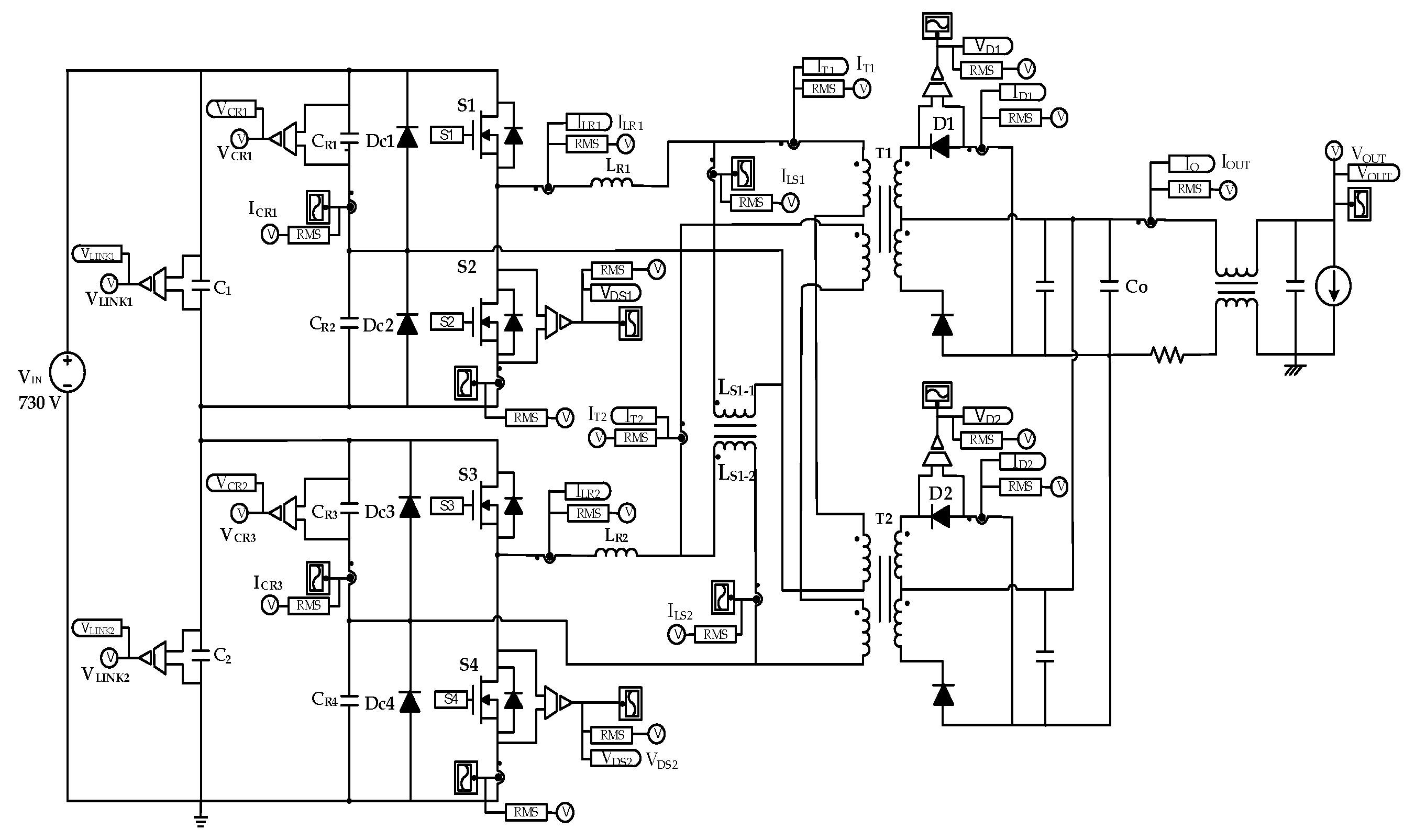
One of the most representative methods for solving the problem of DC/DC converters with a large output-to-input voltage ratio is configuring two DC/DC converters with the ISOP auto-balancing configuration shown in
Figure 2. In this figure, resonant capacitors C
r1 and C
r2, and C
r3 and C
r4 are separated, which was reported in References [
10,
11,
12,
13]. By this configuration, the voltage of the resonant capacitors with anti-parallel diodes can be limited by the diode clamping feature under the over load condition. As LLC resonant DC/DC converter 1 of stage 1, which is connected in series, and LLC resonant DC/DC converter 2 of stage 2 can be easily controlled by the same control circuit and pulse signal, this method is widely used. The auto-balancing method uses two series-connected DC link capacitors C
1 and C
2 and two series-connected DC/DC converters to divide a large voltage into smaller ones. The secondary circuit is connected in parallel, while the primary circuit of the DC/DC converter is connected in series. If the load current increases at the DC/DC converter 1 due to power imbalance, the voltage of C
1 decreases and that of C
2 increases. This reduced voltage of C
1 can reduce the load current of the DC/DC converter 1. On the other hand, as the load current increases at DC/DC converter 2 due to power imbalance, the voltage of C
2 decreases and this reduced voltage of C
2 can reduce the load current of the DC/DC converter 2. In this circular structure, the voltages of C
1 and C
2 are automatically adjusted according to the power imbalance condition. The power imbalance of each DC/DC converter is attributable to deviations related to passive and active elements and control signals. However, this auto-balancing method cannot solve this imbalance of the DC link voltage, perfectly. Power imbalance results in various problems. Firstly, higher DC link voltage can be generated, causing a high withstand voltage of the link capacitors, thereby selecting a large capacitor voltage rating. When power balancing, the DC link voltage can be exactly divided by 1/2V
dc for every series-connected capacitor C
1 and C
2, but if power imbalance occurs, a voltage higher than 1/2V
dc is applied to either C
1 or C
2. Secondly, the DC/DC converter where the high voltage is applied needs to use a switching device having a high voltage and a large capacity because of high power. Thirdly, converters with biased power lead to designs to ensure margins for heat dissipation as losses also increase. This problem of power imbalance increases the overall volume and cost. Another problem of the auto-balancing method can occur when a three-level Vienna rectifier is used as the PFC rectifier. Three-level Vienna rectifier can control the DC link capacitor voltage unbalance [
14]. When the DC link voltage unbalance can be controlled, auto-balancing cannot be actively operated.
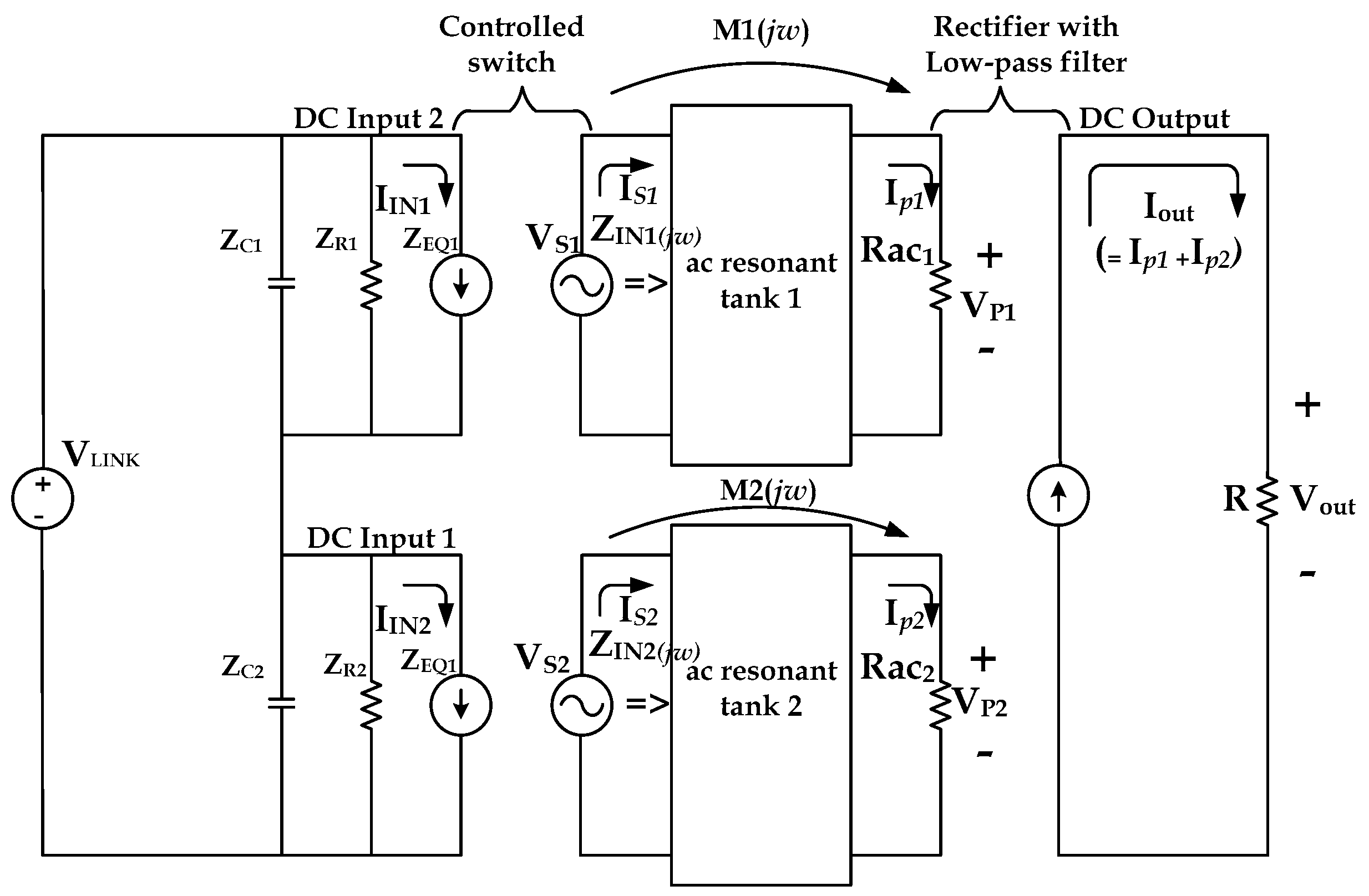
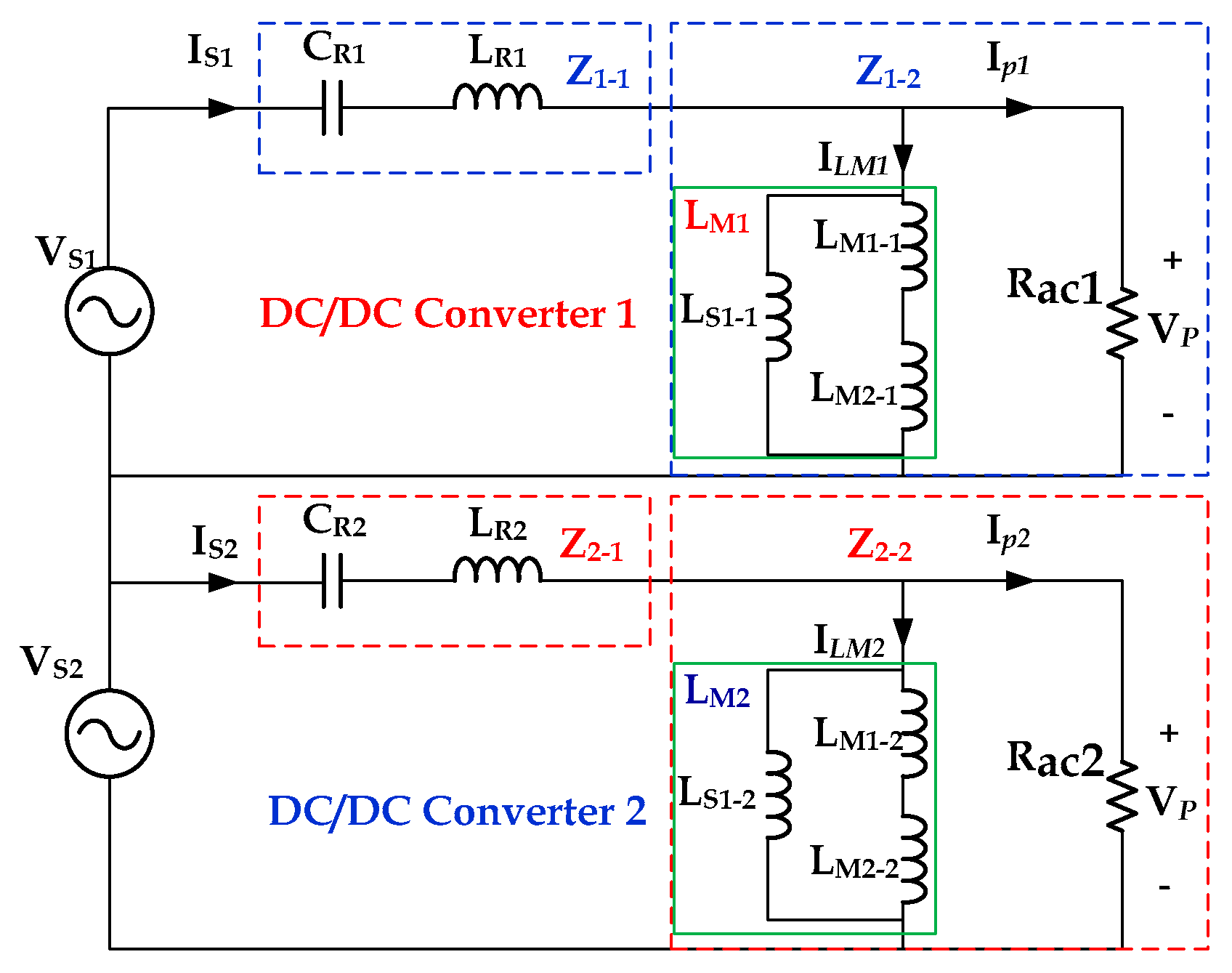
The power imbalance is mainly caused by a leakage inductor deviation, which determines the input impedance of a resonant tank, and a magnetizing inductor deviation of the transformer delivering power. The AL-value of the ferrite core, which determines the leakage and magnetizing inductances, has a maximum deviation of ±25%. For this reason, using two different shunt inductors and a transformer leads to the factor that causes the largest power deviation. An equivalent circuit can be expressed as in
Figure 3 [
15,
16]. In this figure, the circuit of the auto-balancing LLC resonant converter includes DC link capacitors (C
1, C
2) to divide a large input voltage and balance resistances (R
1, R
2) to prevent voltage imbalance under no load condition; LLC resonant networks (AC resonant tank) that are independent from each other and a low-pass filter of the parallel structure sharing output can be seen in
Figure 2.
In
Figure 3, the input impedance
of DC/DC converter 1 can be defined as follows.
where
is the DC link voltage and
is the input current of DC/DC converter 1 and represented as Equation (2),
In this equation,
represents the primary side current of the DC/DC converter, and the primary side voltage and current are in phase. On the simplified impedance model of the DC link side shown in
Figure 3, the condition for power balance can be expressed by Equation (3) below.
where Z
C1 and Z
C2 denote the impedances of DC link capacitors; Z
R1 and Z
R2 are the impedances for preventing imbalance; and Z
EQ1 and Z
EQ2 are the input impedances of the resonant tanks. In order to obtain the power balance, DC/DC converters 1 and 2 should have the same parallel impedance. However, the power imbalance occurs due to an impedance deviation among these impedance elements. In this article, it is assumed that the DC link capacitance values are exactly the same. Generally, the electrolytic capacitor used as a DC link capacitor has small parameter deviations compared to magnet elements. Besides, if a three-level Vienna rectifier is used as the PFC, the DC link capacitor unbalance can be controlled. So, there is no need to consider the DC link capacitance unbalance problem for the case of using a three-level Vienna rectifier. On the other hand, the impedance (Z
R1, Z
R2) of the resistances for preventing imbalance are much larger than the input impedances (Z
EQ1, Z
EQ2) of the resonant tank; they have little influence on power imbalance as shown in Equation (4).
As the resistance for preventing imbalance ranges from dozens to hundreds of kilo-ohms depending on voltage, the impedance (ZR) of resistance is also much larger than the equivalent impedance (ZEQ) of the LLC resonant converter.
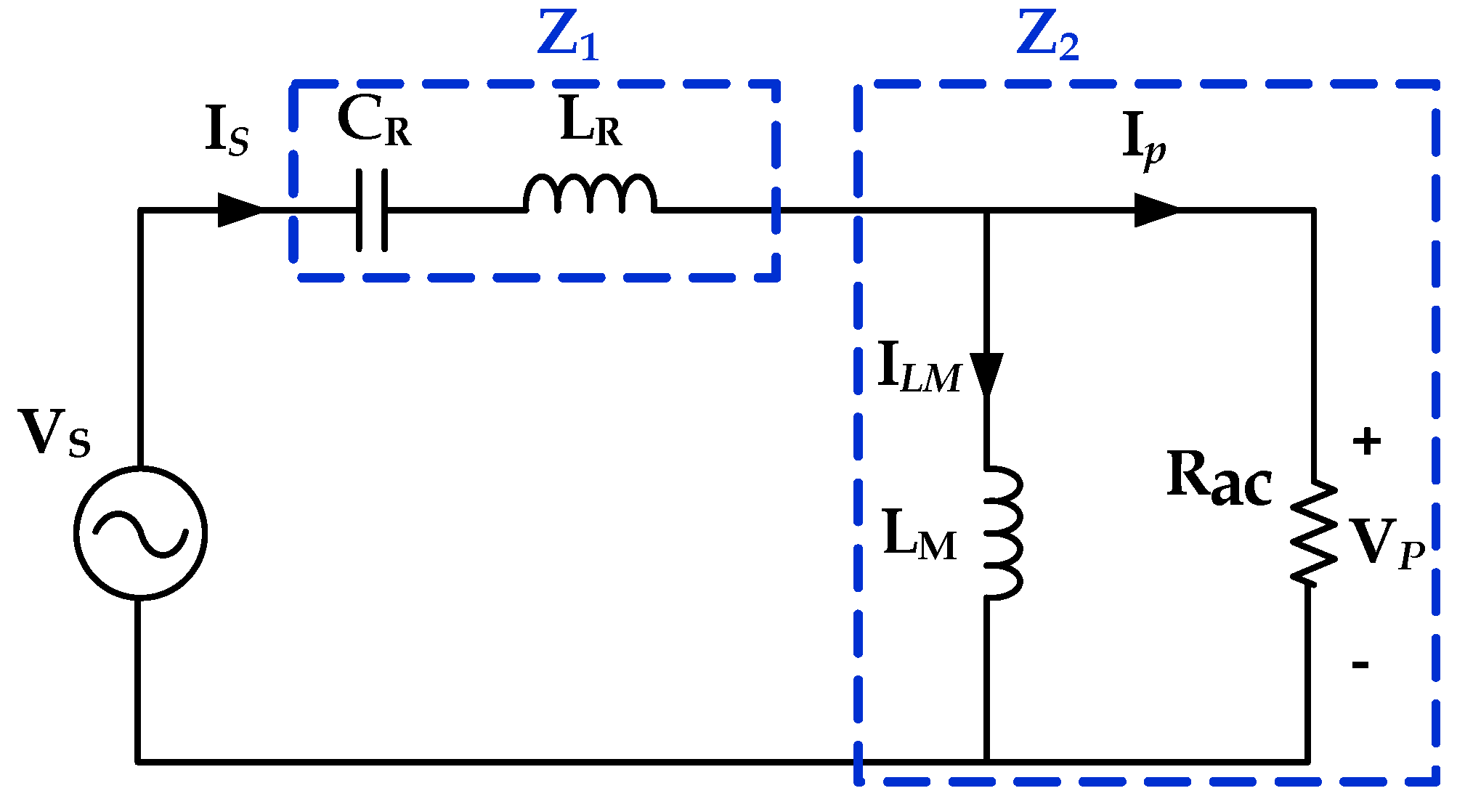
Figure 4 shows the equivalent circuit of the AC resonant tank. If the series impedance of the resonant capacitor (C
R) and the resonant inductance (L
R) is Z
1 and the parallel impedance of the magnetizing inductance (L
M) and the AC impedance (Rac) is Z
2, the input impedance (Z
IN) of the resonant tank can be expressed by the following equation.
where
represents the AC source voltage of LLC converter and is made by half of the DC link voltage
; Z
1 and Z
2 can be expressed as following:
From Equations (5) and (6), the input impedance of the LLC converter can be expressed as
where
is the switching frequency of the LLC converter,
is the resonant frequency of the resonant inductance (L
R) and the resonant capacitance (C
R), and Zo is the characteristic impedance of resonant inductance (L
R) and resonant capacitance (C
R).
is a normalized angular frequency indicating the ratio between the switching frequency (
) and the resonant switching frequency (
), Rac is a load resistance, and K
L is the constant indicating the ratio between the resonant inductance (L
R) and the magnetizing inductance (L
M), as expressed in Equation (8) below.
From the input impedance (Z
IN) of Equation (7), the normalized impedance (Zn) according to frequency can be obtained as shown in following equation.
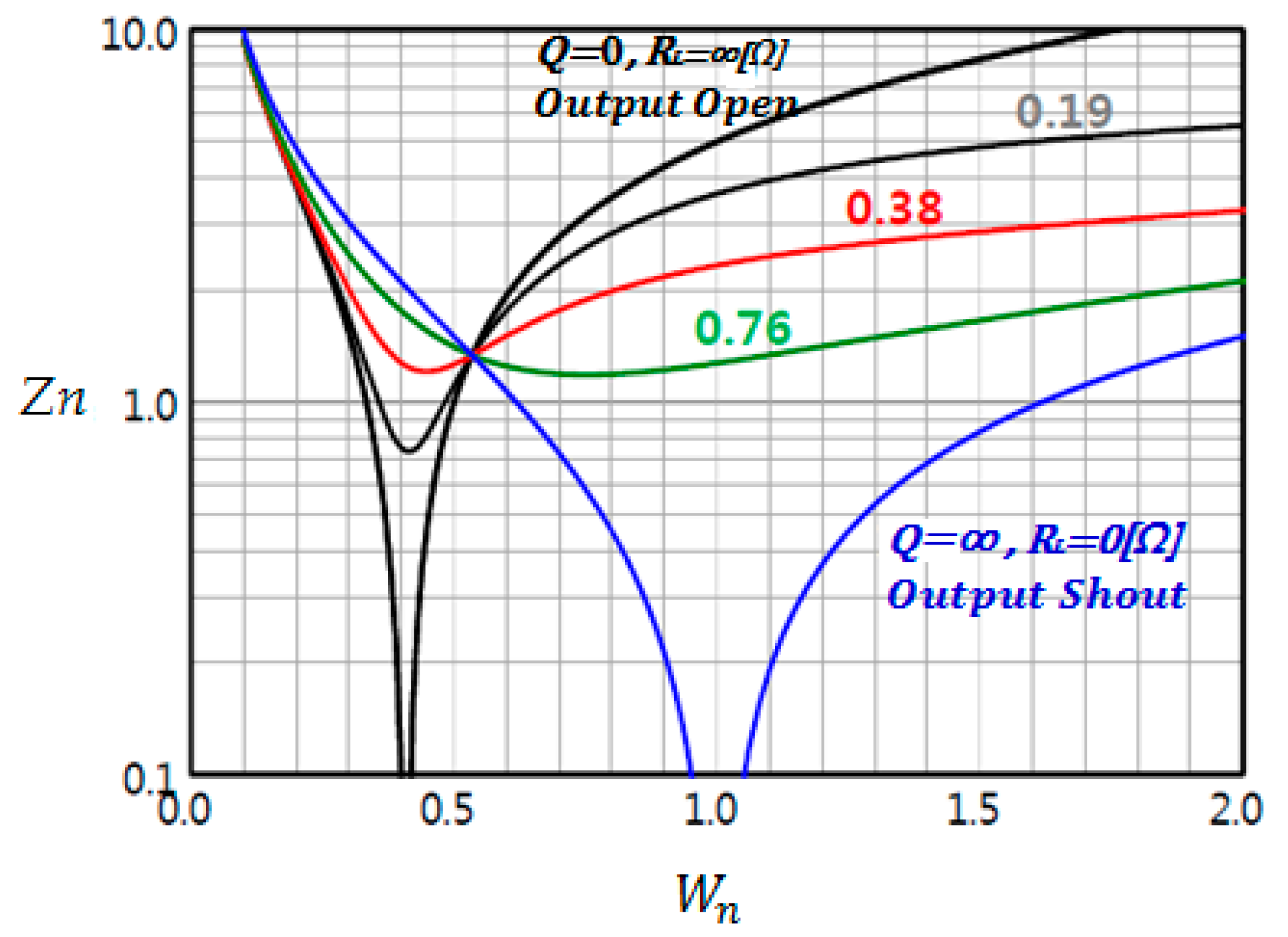
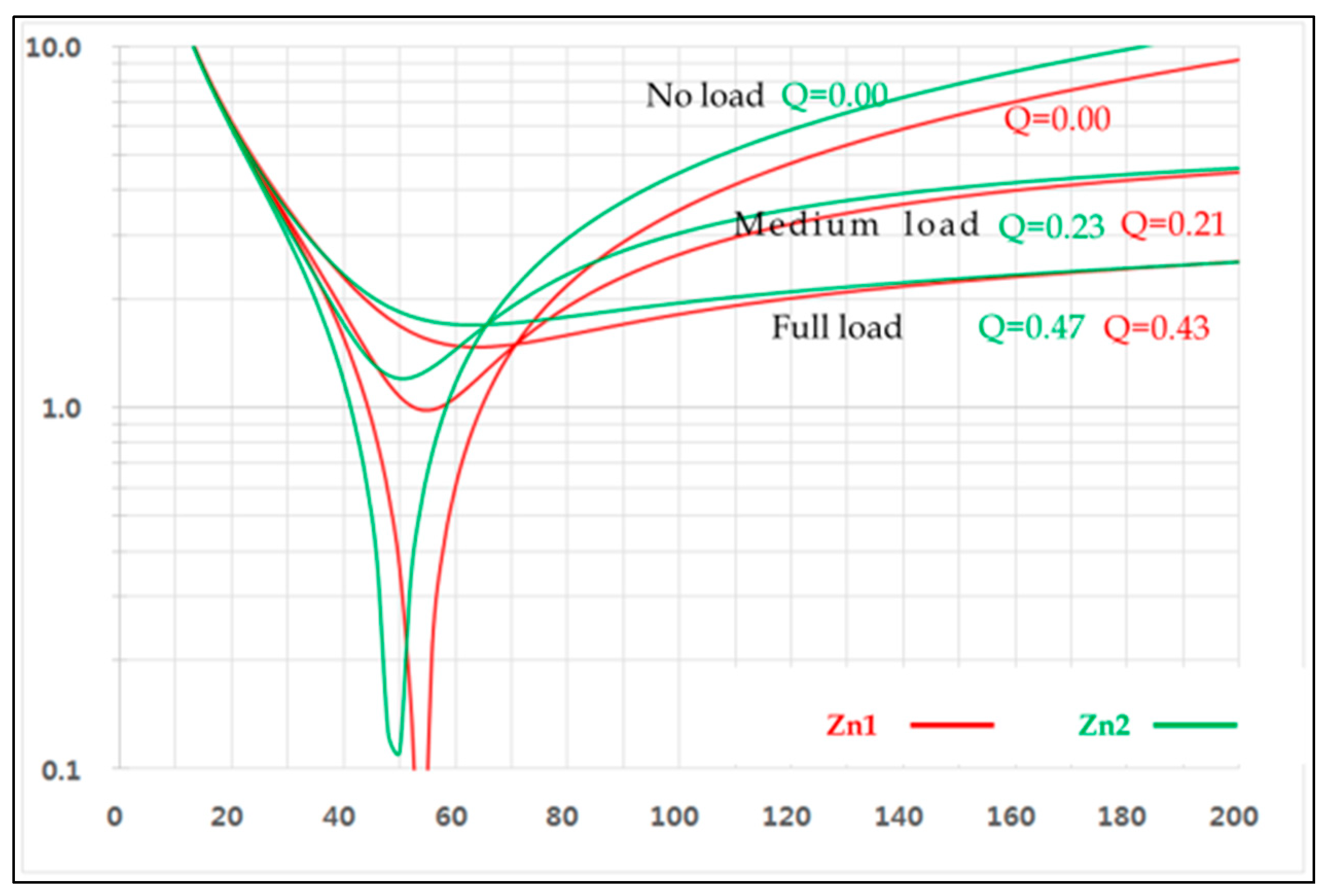
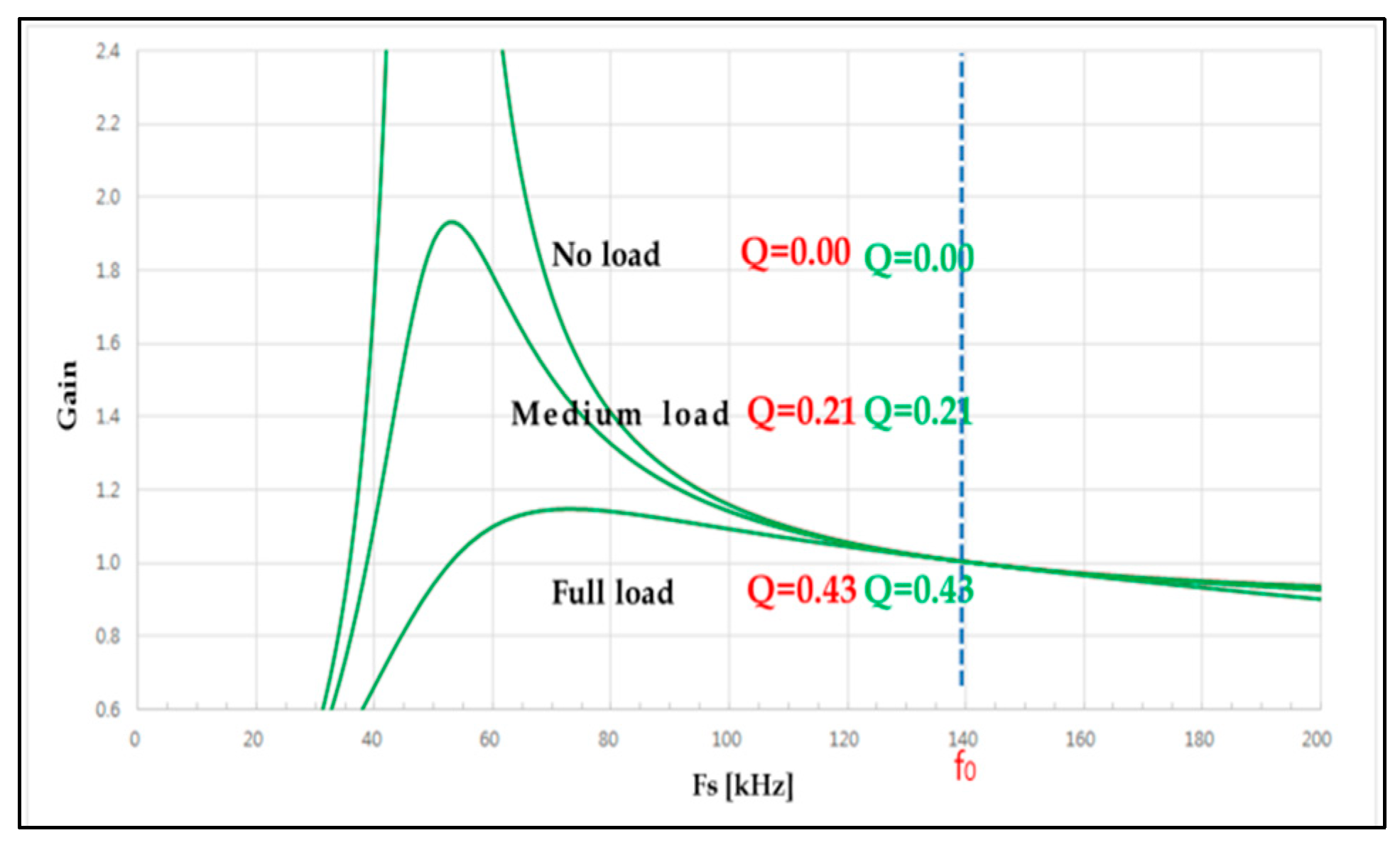
The input impedance characteristics at each switching frequency of the LLC resonant converter can be obtained by varying the switching frequency in Equation (9) under the condition of Q = ∞ (Rac = 0), as described in following Equation (10). The characteristic graph is V-shaped and depicted in blue. In the case of
, the input impedance becomes 0, and when
and
,
.
In addition, Equation (11) can be obtained by varying the switching frequency in Equation (9) under the condition of Q = 0 (Rac = ∞). The characteristic graph is V-shaped and depicted in black, where
results in the input impedance of K
L and, when both
and
are 0, the result is
.
From the above two conditions, the input impedance characteristic graph of the LLC converter according to frequency and Q can be expressed as in
Figure 5.
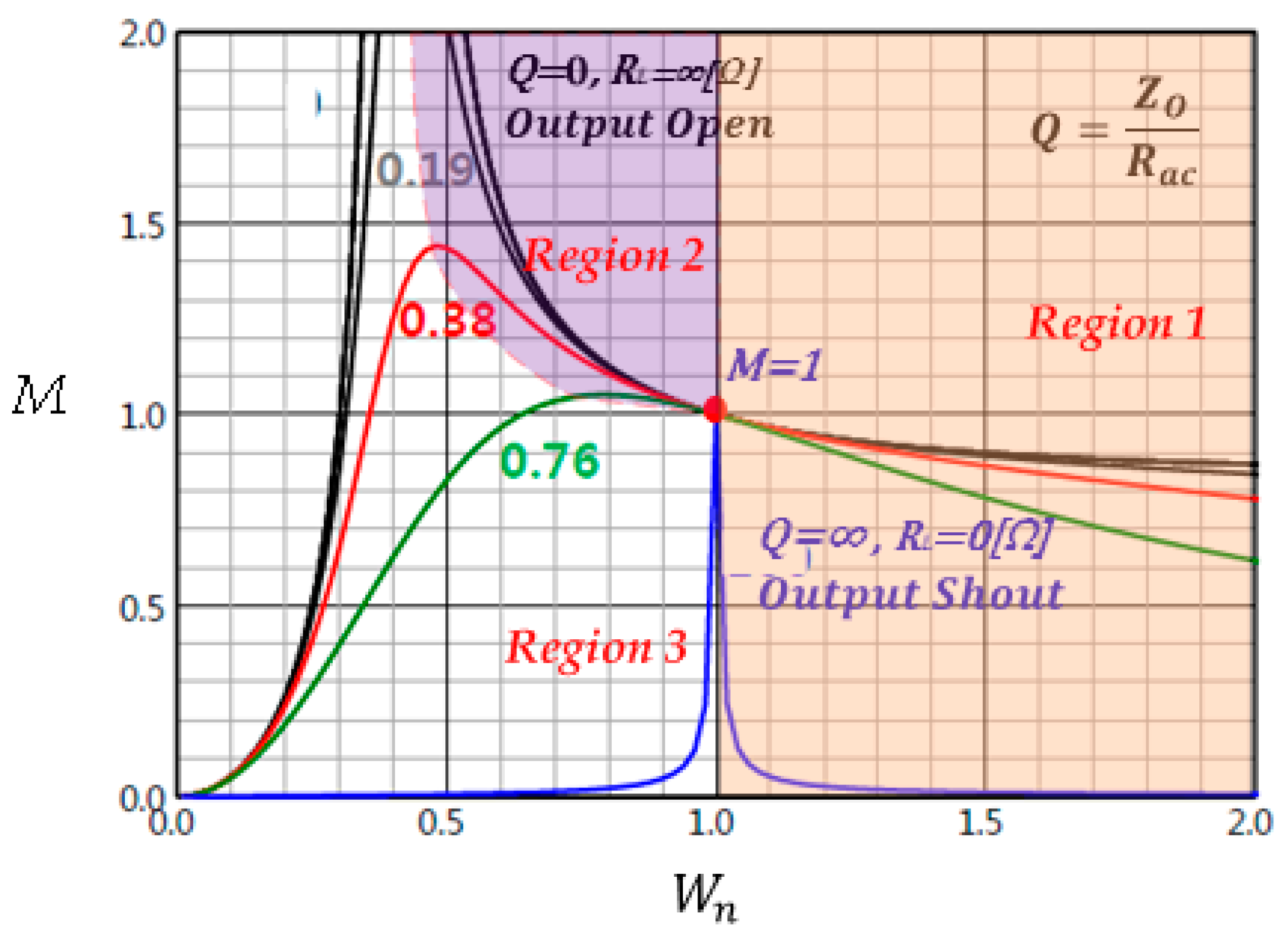
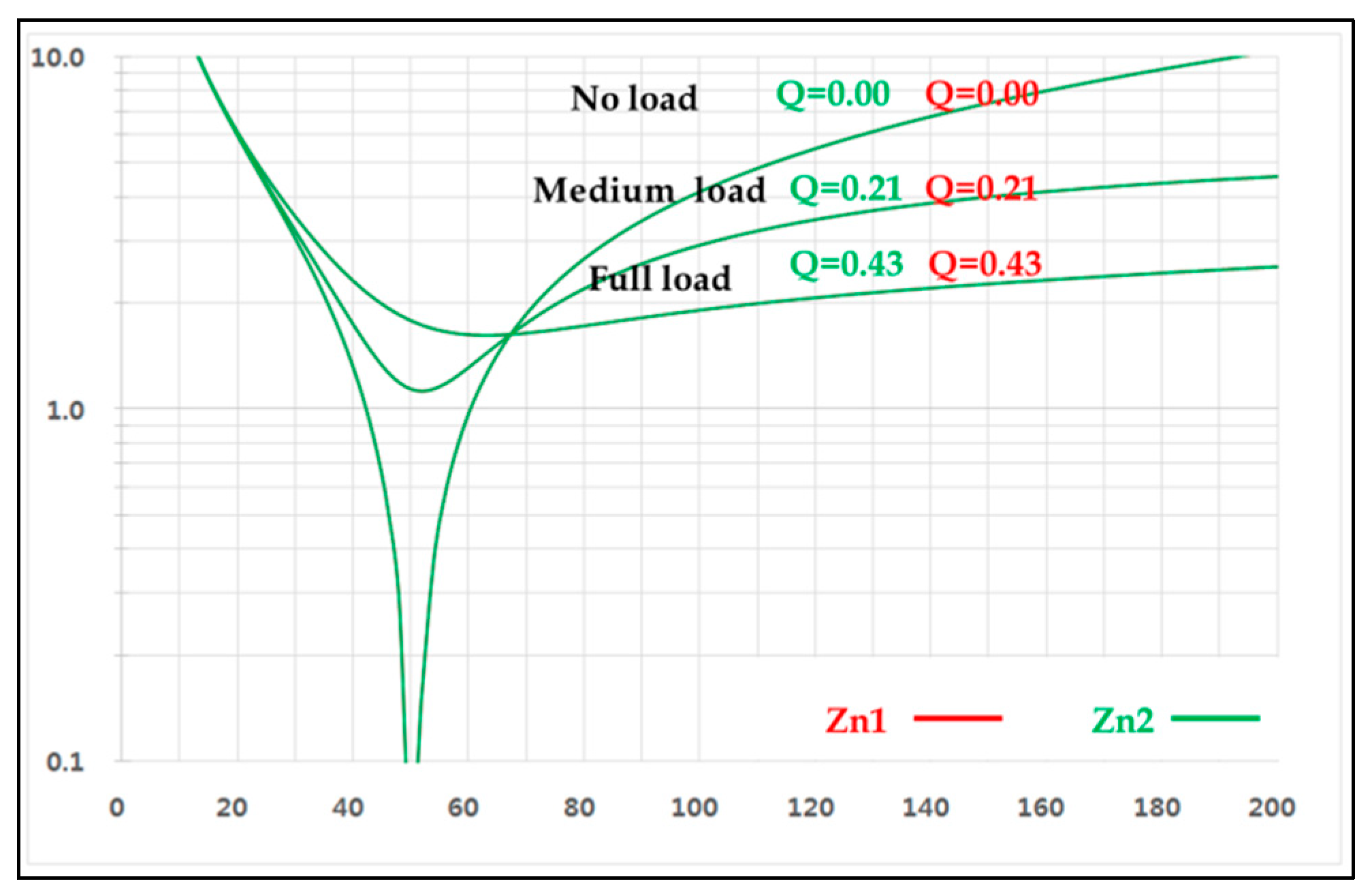
On the other hand, the input–output voltage gain of the LLC resonant converter can be expressed by Equation (12).
where
denotes the output voltage and n is the number of turns of the transformer. From Equation (12), the input–output voltage gain needs to be changed to change the output voltage, when the input voltage is fixed. When the circuit of the LLC converter is designed, every value is fixed including winding ratio (n), ratio between resonant inductance (L
R) and magnetizing inductance (L
M), resonant frequency (
), and characteristic impedance (Zo). As the quality factor (Q) at a specific load resistance (Rac) is also fixed, the switching frequency (
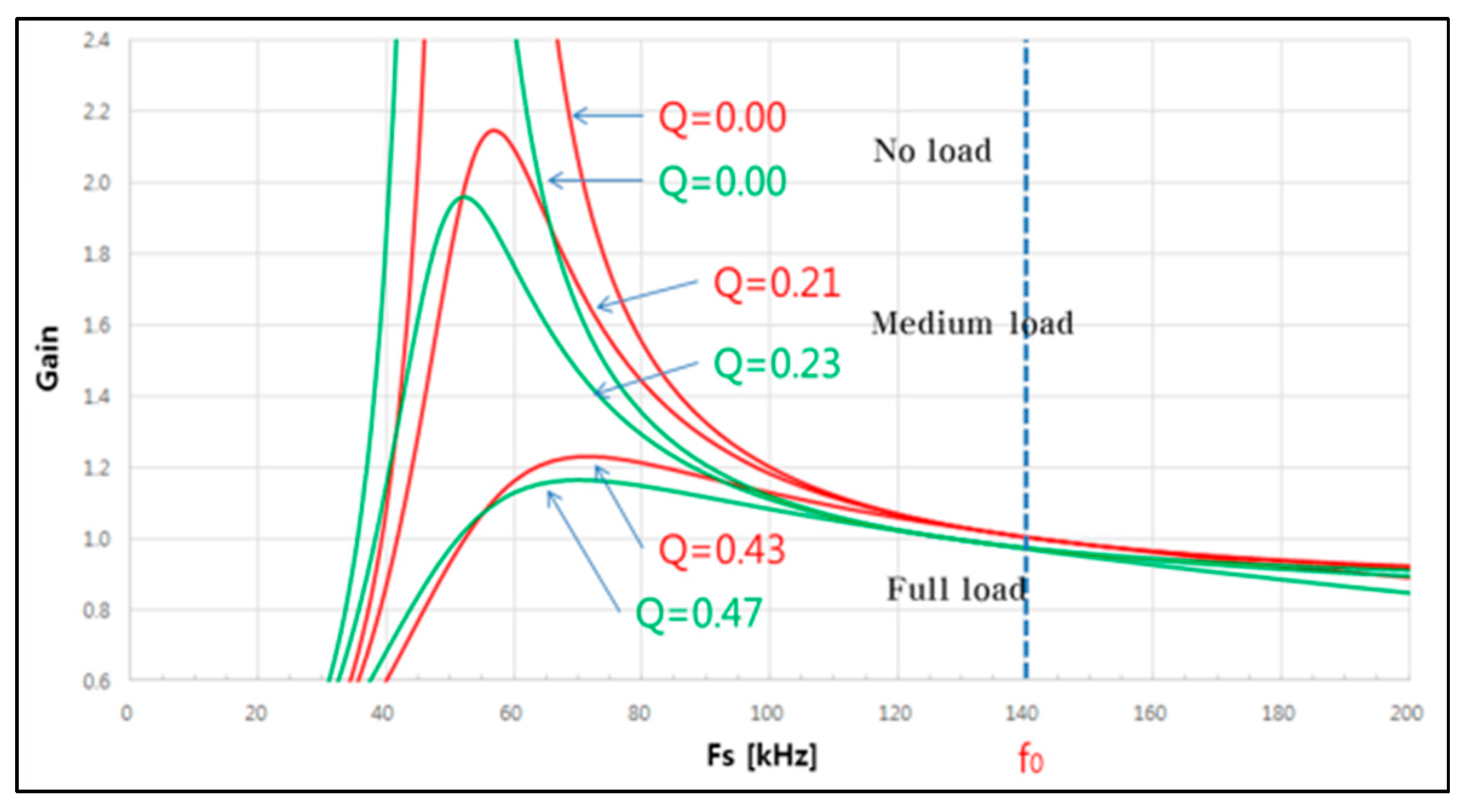
) needs to be changed in order to modify the input–output voltage gain (M). As shown in
Figure 6, the characteristic graph of the input–output voltage gains according to the frequency variation at a specific load resistance (Rac) can be expressed through Excel. The characteristic graph of
Figure 6 shows that the value of Q is inversely proportional to the gain. The switching frequency and the resonant frequency meet at the point of M = 1. Both frequencies pass this point under every load.
The input impedance and frequency characteristic graph (
Figure 5), which was derived from Equations (9) and (11), and the input–output voltage gain and frequency characteristic graph (
Figure 6) show that the voltage gain (M) characteristic and the input impedance (Z
IN) characteristic change according to variation of the quality factor (Q). The independent transformers used for two auto-balancing LLC resonant DC/DC converters generate a deviation between magnetizing inductance (L
M) and leakage inductance by winding method and ferrite-core characteristic. The deviation between magnetizing inductance (L
M) and leakage inductance in a transformer changes the constant K
L, that is the ratio between resonant inductance (L
R) and magnetizing inductance (L
M), and thus, not only does the resonant frequency of the AC resonant tank change, but also the quality factor (Q) is affected, which results in a difference in the input characteristic impedance according to the frequency characteristic. In other words, when independent transformers are used, the deviation between magnetizing inductance (L
M) and leakage inductance becomes the primary cause of power imbalance, because it generates a difference between the input–output voltage gain characteristic and the input impedance (Z
IN).
5. Prototype Test and Verification of the Proposed DC/DC Converter
A prototype was fabricated for an experiment in order to verify the proposed resonant LLC converter using a coupled shunt inductor and multiple input transformers. No separate controller was used to solve the problem of power imbalance occurring to the auto-balancing circuit with primary-series and secondary-parallel connection. However, a multiple input transformer was used at each stage to cross different input windings and connect them in series. Accordingly, the magnetizing inductance (L
M) of AC resonant tank 1 and 2 could be magnetically coupled. The input voltage was 730 Vdc, the output voltage was 48 Vdc, and the maximum power capacity was 4.8 kW. These were the same as the simulation and design parameters in
Table 3.
Figure 18 presents the image of the prototype LLC resonant converter using multiple input transformers, which is proposed in this study. The primary side consists of the power conversion units of DC/DC converter 1 and 2, and the rectifiers on the secondary side were configured in parallel.
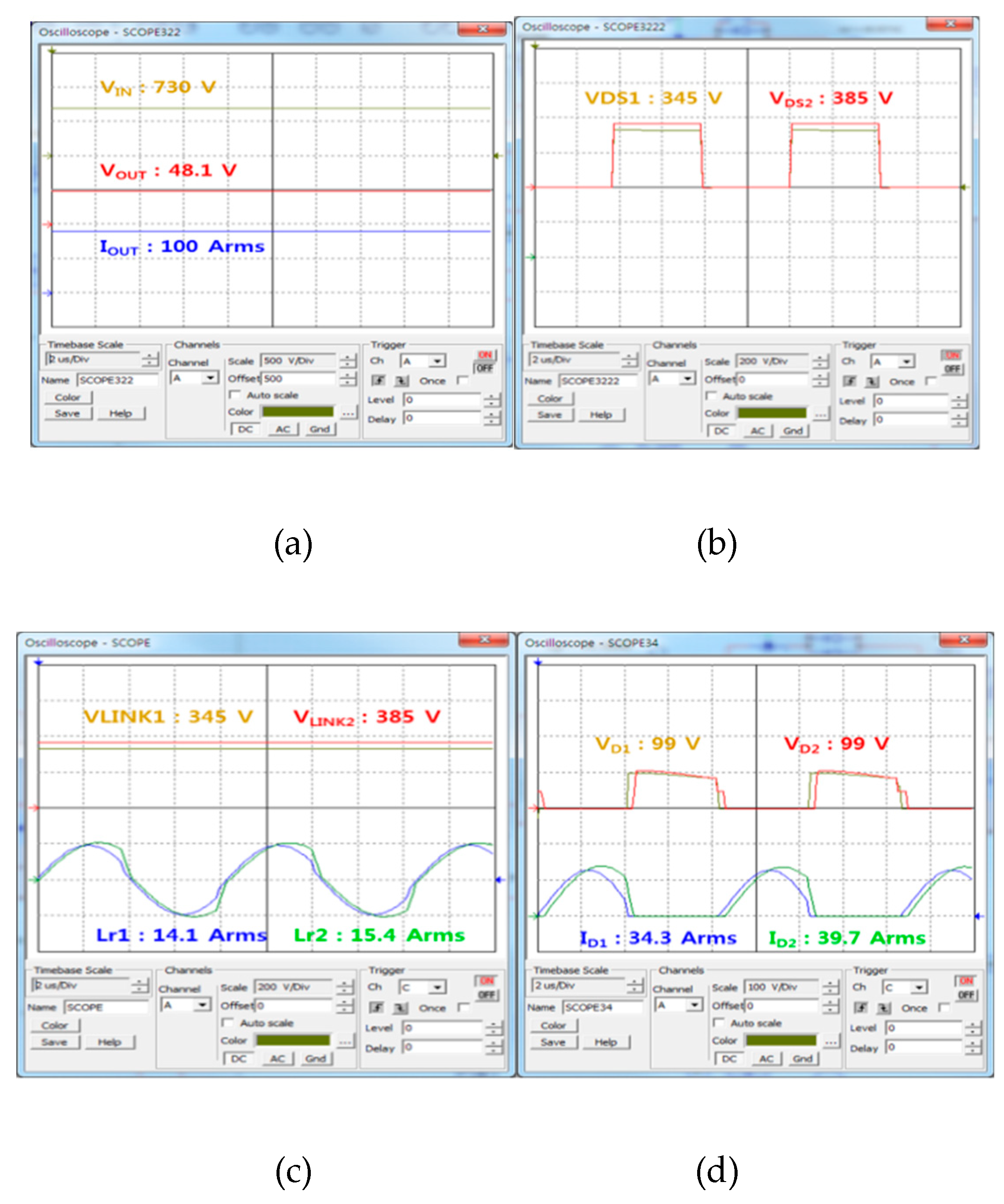
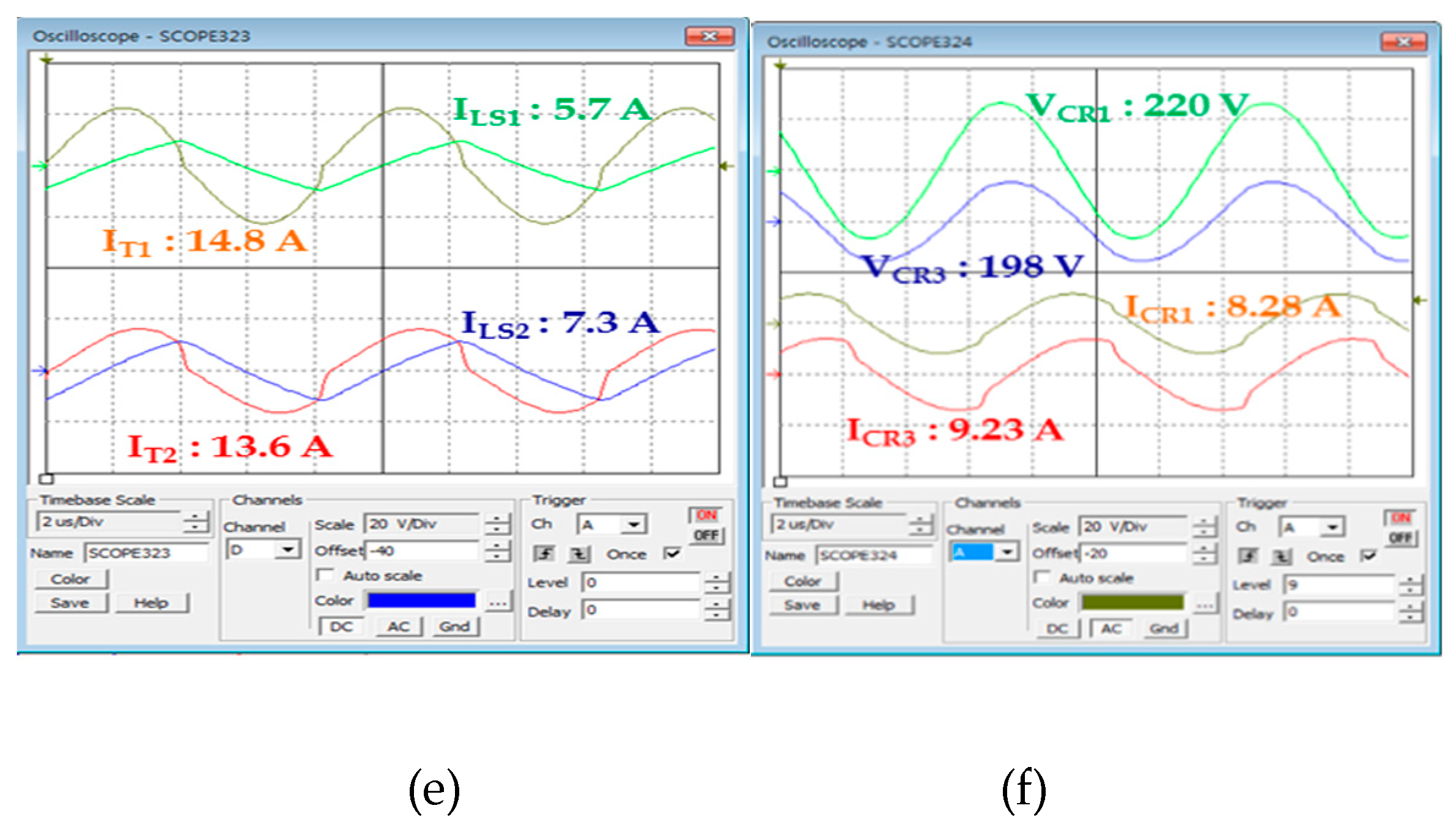
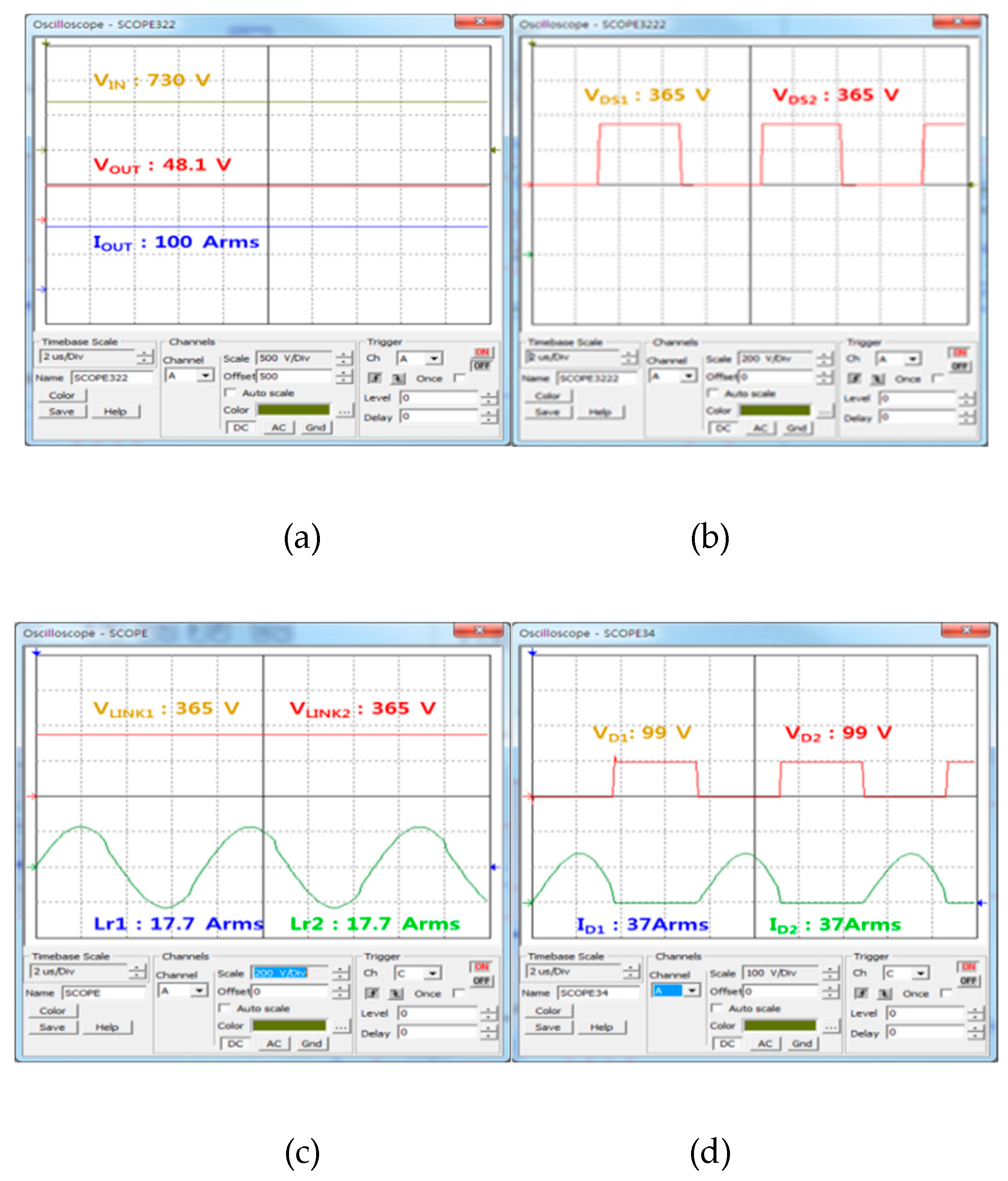
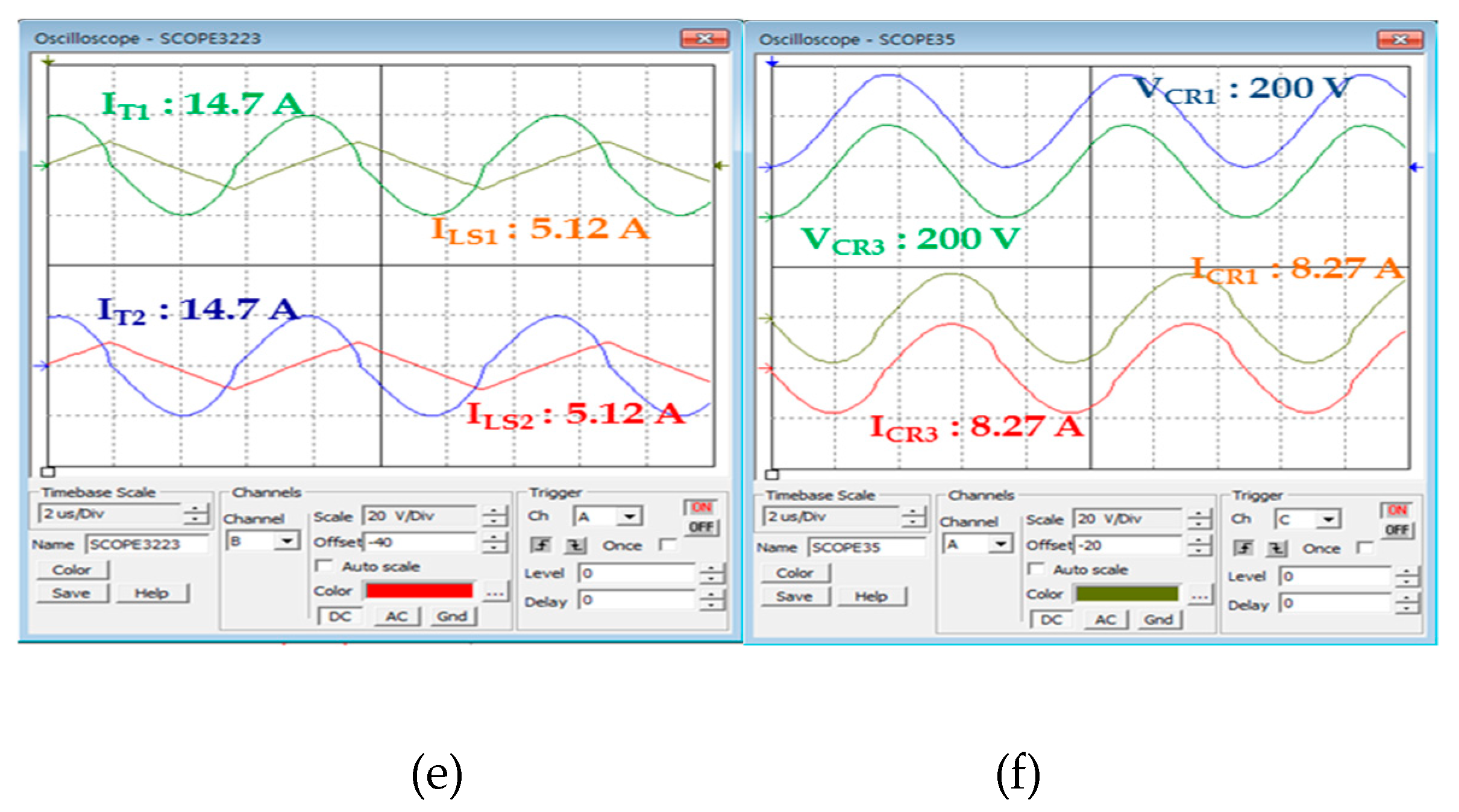
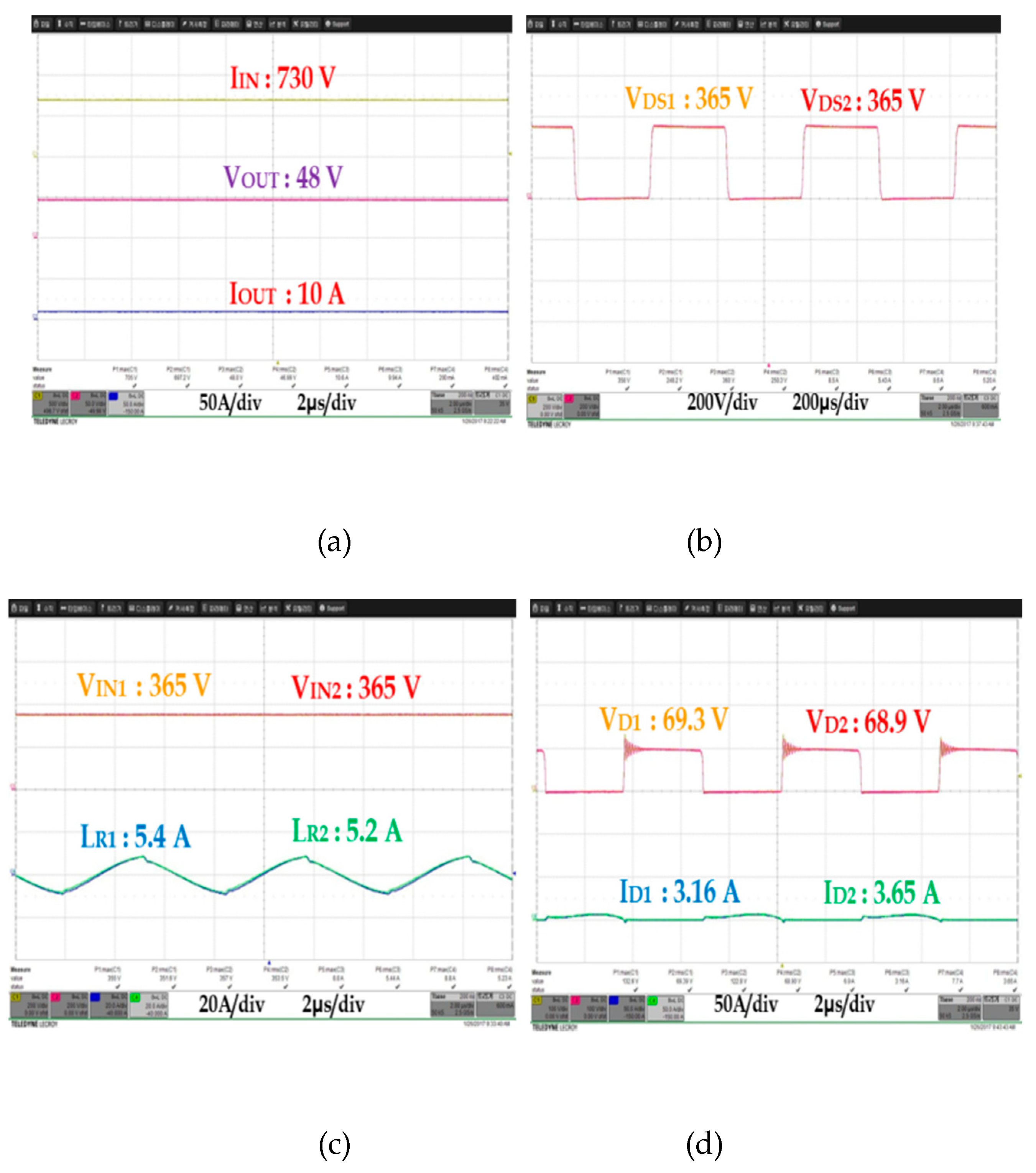
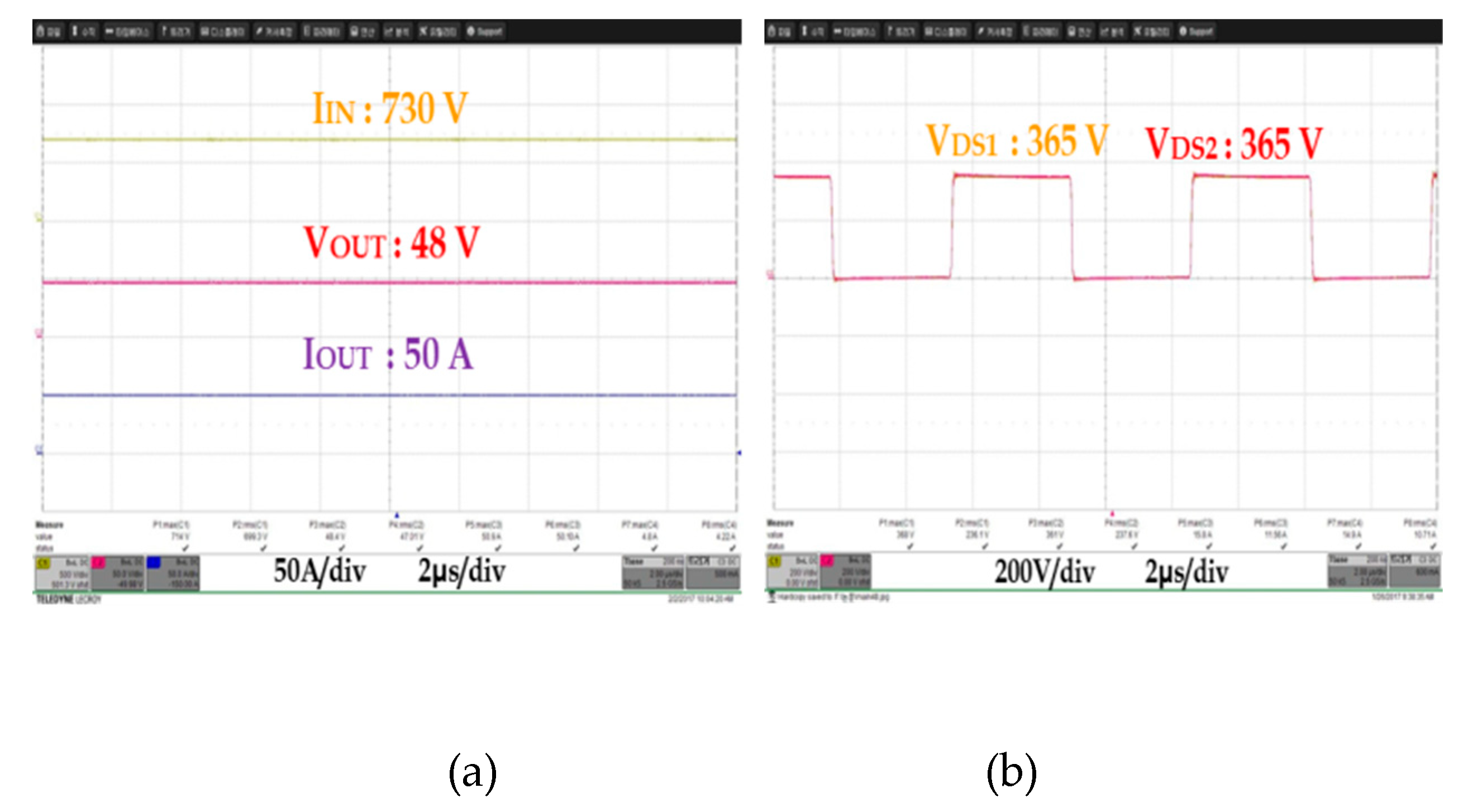
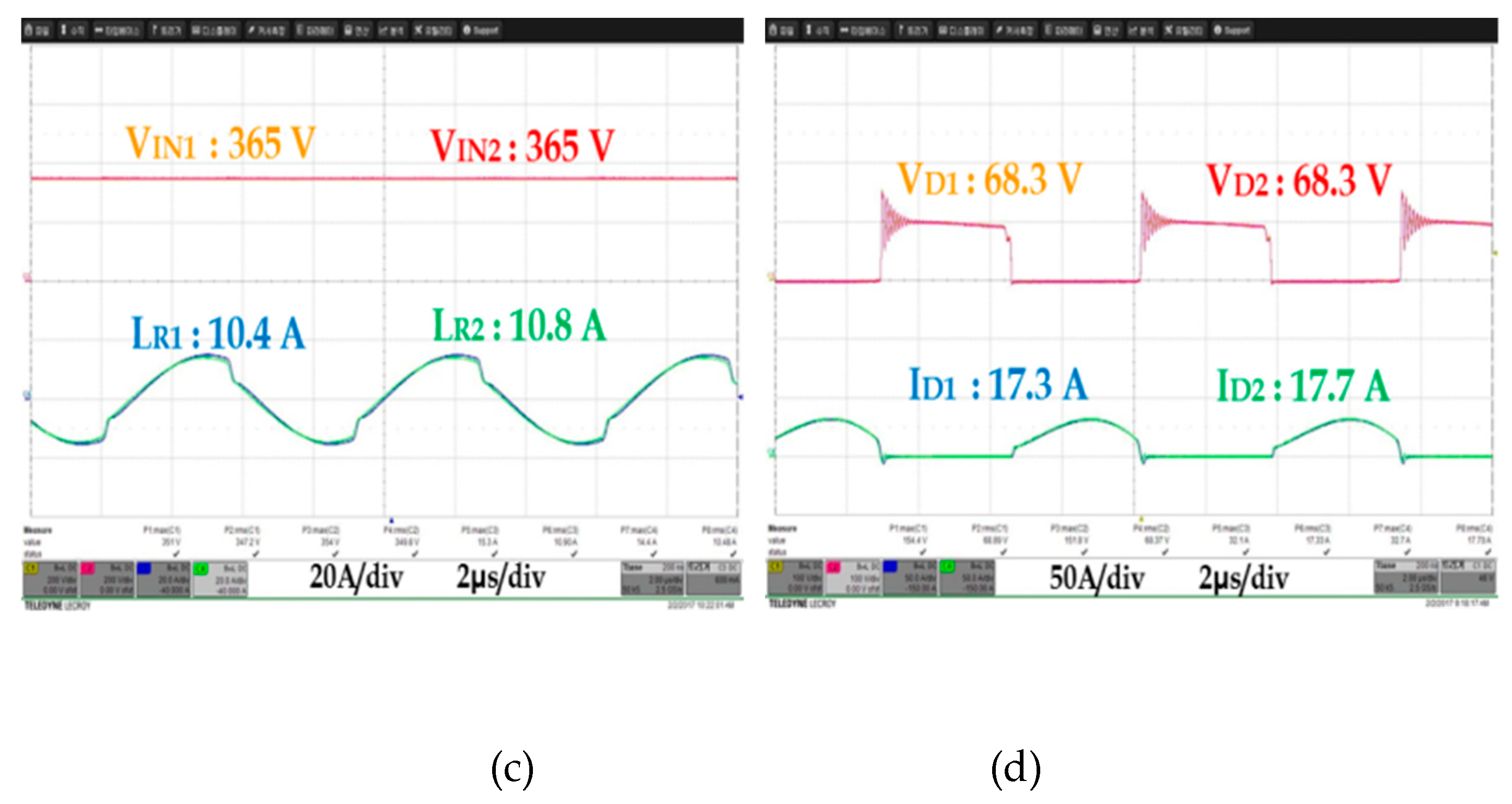
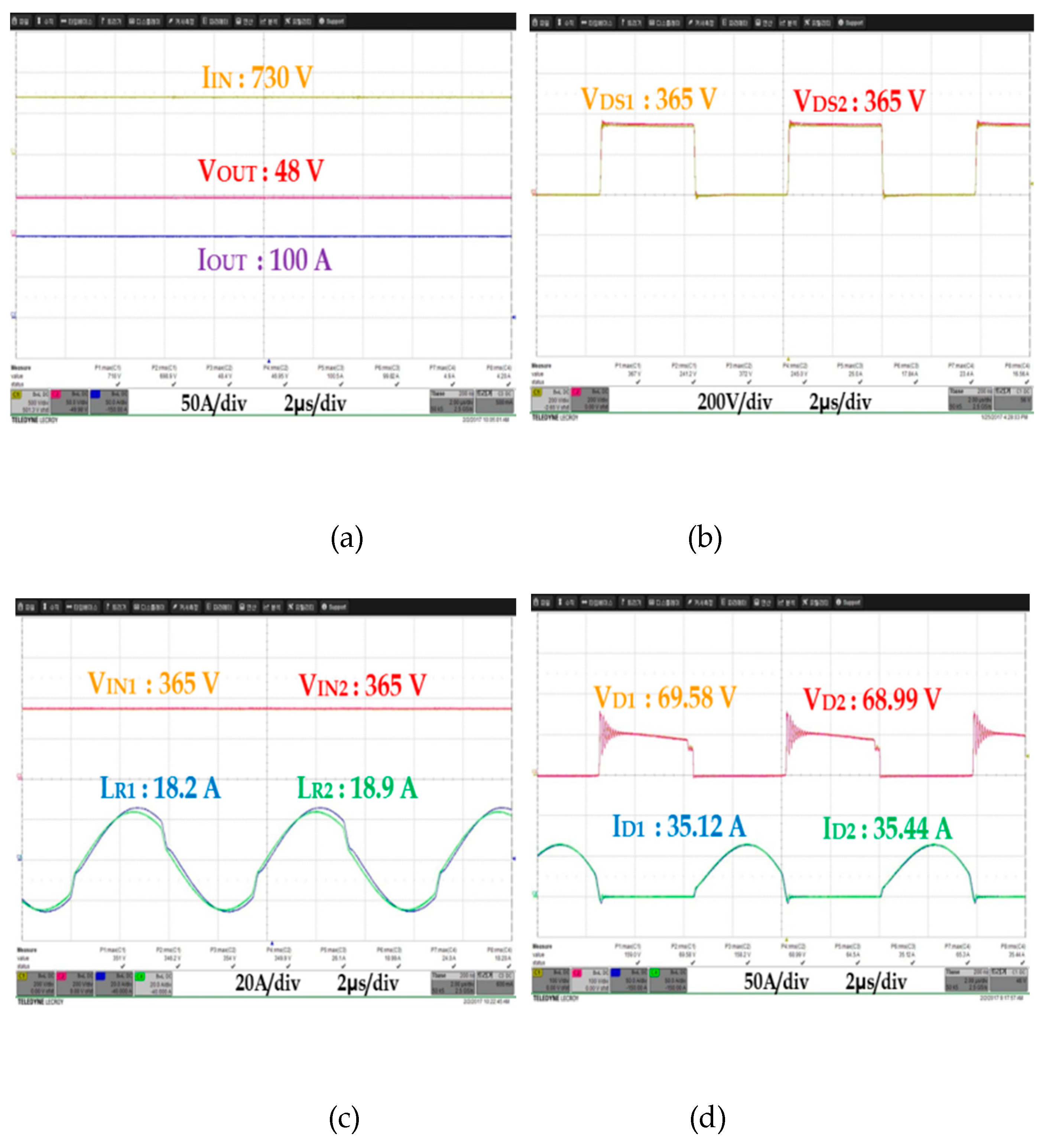
As was in the above simulation, input and output voltages, output current, FET DS waveform (VDS), input capacitor voltage (VIN), resonant current (IR) waveform, and the voltage (VD) and current (ID) waveform of the secondary rectifier diode were measured and compared at 10%, 50%, and 100% load current in order to see whether the power imbalance occurred in DC/DC converter 1 and 2.
Figure 19,
Figure 20 and
Figure 21 show experimental waveforms obtained under different load conditions. Unlike the simulation result, the waveforms of the proposed converter using multiple input transformers showed a few deviations in input voltage and resonant current. As for such deviations, which were generated in the ideal simulation, the deviation between the resonant capacitor and the resonant inductor, which were used for AC resonant tank 1 and 2, and the deviation of parasite components occurring to PCB design caused an error between input impedance and quality factor (Q), which resulted in a slight power imbalance between DC/DC converter 1 and 2. However, unlike the existing auto-balancing converter, no power imbalance occurred, which is attributable to the deviation between the magnetizing inductance and leakage inductance of two independent transformers.
Table 4 presents the comparison result for the input capacitor voltage (V
IN), the resonant current (L
R), and the voltage (V
D) and current (I
D) at the secondary rectifier diode of the proposed converter using multiple input transformers. In the experimental results of the proposed ISOP converter, the DC/DC converter 1 and the 2 input capacitor voltage (V
IN) are equal to 365 V
DC. The resonance tank resonance current (L
R) has a deviation of 0.7 A at the maximum load, the secondary rectifier diode voltage (V
D) Deviation was 0.4 V, and the diode current (I
D) deviation was 0.3 A; it was confirmed that a small deviation occurred.
Table 5 shows a comparison of the major features of the proposed converter and the automatic balancing converter. By using the windings of multiple input transformers crossing each other, the two converters are magnetically coupled to minimize power imbalance. As a result, the core size of the transformer could be reduced from EE7066 to EE6565. The Shunt Inductor uses magnetic inductors in two independent inductors to reduce the deviation and secure the mounting space. As a result, efficiency is improved by 0.7% and power imbalance is minimized by minimizing the heat dissipation area, resulting in a smaller size and an improved power density of 87%.
Simulation results using the PSIM tool show that the power imbalance does not occur. However, the power imbalance in the actual experimental results occurs with the slight error. The experimental results are different because the simulations do not take into consideration the environmental factors such as the deviation of the resonant inductor and the resonant capacitor and the leakage impedance on the actual PCB design.
6. Conclusions
This study has proposed a new circuit for improving the problem of power imbalance by using two DC/DC converters with ISOP structures, where there are a coupled shunt inductor and multiple input transformers sharing magnetic coupling. In addition, both simulation and experiment were conducted for the proposed circuit in order to measure and comparatively analyze the input and output voltage, output current, FET DS switching waveform, DC link capacitor voltage, resonant current waveform, and the voltage and current waveforms of the secondary rectifier diode.
The auto-balancing converter showed a deviation of quality factor (Q) due to the deviation between the magnetizing inductance (LM) and leakage inductance in the shunt inductor and the transformer, which were independently used. Accordingly, DC/DC converter 1 and 2 had different characteristics of input–output voltage gain (M) and input impedance (Zn) at the same frequency, which caused the power imbalance. On the other hand, the proposed topology made DC/DC converter 1 and 2, which used a coupled shunt inductor and multiple input transformers, share the magnetic coupling with each other. Accordingly, no deviation of quality factor (Q) occurred and the input–output voltage gain (M) has the same characteristic as the input impedance (Zn). Thus, it was verified that no power imbalance occurred. As a result, it can be seen that the power imbalance problem of the previous ISPO circuit mentioned in Session 2 is improved using a multi-input transformer that shares magnetic coupling with the combined shunt inductor. The problem of ensuring the breakdown voltage margin of the input capacitor due to the voltage imbalance is improved. The proposed circuit improves the voltage margin and current margin of the switching device due to the voltage rise. The reduced power conversion efficiency is improved due to biased power and thermal issues.
The proposed LLC resonant DC/DC converter is characterized by the magnetic coupling. Therefore, in designing coupled shunt inductors and multiple input transformers, a winding method in which each input winding has the same length to avoid inductance variation should be used. Also, when designing the PCB, the power line for sharing the magnetic coupling of the transformer is complicated, so care must be taken in the design.