1. Introduction
The population structure in Europe will change significantly over the next 40 years, with the elderly (defined as people over 65 years of age) increasing to 30% of the population by 2060 [
1]. The growth of this population will introduce new demands for managing quality of life and promoting independence. Home care monitoring offers the potential for continuous health and well-being supervision at home. This supervision is particularly important for people who are frail or have chronic diseases such as Parkinson’s disease (PD). When falls occur, such a system can alert a nurse, family member, or security staff [
2]. Several monitoring systems have been presented for the detection of falls or motion disorders in PD patients using on-body accelerometers [
3,
4]. Many of the falls in PD patients are caused by a locomotion and postural disorder called freezing of gait (FOG) [
5]. FOG is a frequent PD symptom that affects almost 50% of Parkinson’s patients, and it is defined as a “brief, episodic absence or marked reduction of forward progression of the feet despite the intention to walk” [
6]. This problem can last from a few seconds to a minute [
7]. FOG events appear more often during turns, with gait initiation, and in stressful situations. A successful intervention for reducing the duration and frequency of FOG episodes is to induce external cues, such as a rhythmic acoustic beat. The cueing system provides real-time auditory stimuli, helping the patient to maintain speed and amplitude of movements when walking. These cueing systems are more effective when applied only during FOG episodes [
8,
9] and, therefore, a system for reliably detecting FOG events is required.
The accurate supervision of patients is also important for monitoring the progression of PD. PD patients need to visit a physician every few months to monitor the illness progression. During their visit, the physician evaluates each patient by asking them to perform a set of activities specified in the Movement-Disorder-Society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS) [
10]. The information gathered by the doctor is subjective because it is limited to a short session every few months, so the physician evaluation can be influenced by the patient’s mood that day [
11] or nontypical patient behavior during the session [
12]. Automatic tools for continuously supervising PD symptoms during daily activities would provide objective long-term data to improve the physician’s assessment. One of the symptoms that must be monitored to assess disease progression is FOG.
This paper describes some advances in using body-worn accelerometers to detect FOG in Parkinson’s patients. We compared different feature sets and machine learning (ML) algorithms using a leave-one-subject-out (LOSO) cross validation. This type of evaluation is necessary to assess the robustness of these algorithms when monitoring patients whose data are not present in the training set. We evaluated two feature sets already applied to FOG detection and two new feature sets adapted from speech processing: mel frequency cepstral coefficients (MFCCs) and speech quality assessment (SQA) metrics. We analyzed four ML algorithms: random forest, multilayer perceptron, hidden Markov models (HMMs), and deep neural networks with convolutional layers. This study was performed using the Daphnet dataset [
13], which includes recordings from ten patients. Our best result shows a reduction from 17.3% to 12.5% of the equal error rate, relative to the best reported results on this dataset with a LOSO evaluation.
2. Related Work
In this section, we review related work in body-worn sensors for monitoring Parkinson’s patients. We also survey previous studies where several feature sets and classification algorithms were proposed and compared for FOG detection. We pay special attention to previous studies that used the Daphnet dataset.
Previous studies have placed ultrathin force-sensitive switches inside the subject’s shoes [
14] or used vertical ground reaction force sensors [
15] or multiaxis accelerometers [
16]. Accelerometers located on the patient’s body have been widely used to detect FOG [
7,
13,
17,
18]. The recent widespread availability of wearable devices (fit bands, smartwatches, and smartphones) equipped with accelerometers has facilitated this approach. The Daphnet dataset has also played a key role in this development. Daphnet is a public dataset that includes inertial signals from ten patients registered through three accelerometer sensors situated on the ankle, knee, and lower back. Several papers have been published using this dataset [
13,
17,
18,
19].
The detection of FOG requires the application of specific signal processing and classification methods adapted to this type of phenomenon. Initial efforts were focused on extracting good features [
13,
17,
20]. Moore et al. [
20] found that frequency components of leg movements in the 3–8 Hz band during FOG episodes are characteristic of this symptom and do not appear during normal walking. They introduced a freeze index (FI) to objectively identify FOG. This FI is defined as the power in the “freeze” band (3–8 Hz) divided by the power in the “locomotor” band (0.5–3 Hz). FOG episodes were detected using an FI threshold, and this feature was used in later experiments [
13,
18]. Assam and Seidl [
21] presented a study of wavelet features with different windows lengths, and Hammerla et al. [
17] proposed the empirical cumulative distribution function as feature representation. Mazilu et al. [
18] described a detailed analysis of different features using the Daphnet dataset. The first set included FOG-oriented features such as the freezing index and the sum of energy in the freezing (3–8 Hz) and locomotor (0.5–3 Hz) frequency bands. The second set contained some features often used in activity recognition: 18 features extracted from each of the three accelerometer axes (
x,
y, and
z) and 6 features using data from all three axes. The best features in the second set were the signal variance, range, root mean square, and eigenvalues of dominant directions in the three accelerometer axes. However, the performance of these features was lower than using FOG-specific features. Mazilu et al. also evaluated principal component analysis (PCA) applied to the raw accelerometer signal for obtaining unsupervised features. In this paper, the authors reported a pre-FOG status where some freezing characteristics became apparent a few seconds before the FOG occurs.
In another paper [
22], Mazilu et al. selected the best features for FOG detection: mean, standard deviation, variance, entropy, energy, freeze index, and power in freeze and locomotion bands. They evaluated different algorithms: random trees, random forest, decision trees and pruned decision trees (C4.5), naive Bayes, Bayes nets, k-nearest neighbor with one and two neighbors, multilayer perceptron (MLP), boosting (AdaBoost), and bagging with pruned C4.5. The best performance was obtained with AdaBoost (with pruned C4.5 as a base classifier) and random forest classifiers. All the ensemble methods (boosting, bagging, random forests) obtained better results than the single classifiers, with the boosting classifiers obtaining slightly better performance than the bagging classifiers. In this evaluation, the authors used a random 10-fold cross validation (R10Fold) for each patient, including data from the same patient in training and testing. The authors also reported an isolated result using LOSO evaluation. This result is our baseline using the same dataset and LOSO evaluation. We compare our results to it in
Section 4.2.In the literature, there are also papers proposing conditional random fields [
21] and deep learning algorithms for FOG detection. Ravi et al. [
23] used a convolutional neural network (CNN) with one convolutional layer for feature extraction and one fully connected layer for classification. They obtained a specificity and a sensitivity of 0.967 and 0.719, respectively, for their R10Fold experiments. Alsheikh et al. [
19] used a deep neural network with five fully connected layers obtaining a specificity and sensitivity of 0.915 in a R10Fold validation. The weights of the fully connected layers were initialized using the weights of a previously trained autoencoder.
In most of these experiments, the authors used a random 10-fold cross validation including data from the same patient in training and testing. Our paper addresses this flaw in the analysis by using a LOSO cross validation. LOSO evaluation is required to develop a robust FOG detection system that can handle new patients.
3. Methods
In this section, we detail the dataset, the signal preprocessing step, and the algorithms for feature extraction and FOG detection. For feature extraction, we used four feature sets. The first was the set proposed by Mazilu et al [
22]. The second consisted of features used in human activity recognition (HAR). The third set was composed of MFCCs, and the fourth included features derived from the SQA literature, such as harmonicity, predictability, and spectral flux. For classification algorithms, we compared random forest, multilayer perceptron, hidden Markov models, and deep neural networks with convolutional layers.
3.1. Gait Dataset
We used the Daphnet dataset [
13] in our experiments. This public dataset contains recordings from ten PD subjects (7 males, 66.5 ± 4.8 years) diagnosed with PD showing large variability in their motor performance. Some participants maintained regular gait during nonfreezing episodes, while others had a slow and unstable gait. The recordings include 3D accelerations (
x,
y, and
z axes) obtained from three sensors located on the ankle, thigh, and trunk (lower back) for a total of nine inertial signals.
The data were collected more than 12 h after the participants had taken their medication to ensure that treatment did not prevent FOG symptoms from being observed. Participants 2 and 8 reported frequent FOG episodes with medication, so they were not asked to skip any medication intake. The protocol consisted of several sessions, including three walking tasks performed in a laboratory: (1) Walking back and forth in a straight line, including several 180° turns. (2) Random walking, including a series of starts and stops and several 360° turns. (3) Walking simulating activities of daily living (ADL), such as entering and leaving rooms or carrying a glass of water while walking.
All sessions were recorded on a digital video camera. The ground truth labels were generated by a physiotherapist using the video recordings. The beginning of a FOG event was specified when the gait pattern disappeared, and the end of FOG was defined as the point in time at which the pattern was resumed. A total of 237 FOG episodes were recorded with durations between 0.5 and 40.5 s (time while the subject was blocked and could not walk). Two subjects in the dataset (4 and 10), did not have FOG. These subjects were excluded from all experiments except for the results in
Section 4.1, where all subjects were considered for a better comparison with the results in the literature.
3.2. Preprocessing
The raw accelerometer signals were recorded with a sampling rate of 64 Hz. This sampling rate was adequate because the information for FOG event detection is below 20 Hz [
20]. To remove the influence of gravity, we filtered the data with a high-pass third-order Butterworth filter at 0.3 Hz. The sample sequence was divided into a sequence of 4-s windows (256 samples) with 3-s overlap and 1-s advance. A window was labeled as a FOG window if more than 50% of its samples were labeled as FOG.
3.3. Feature Extraction
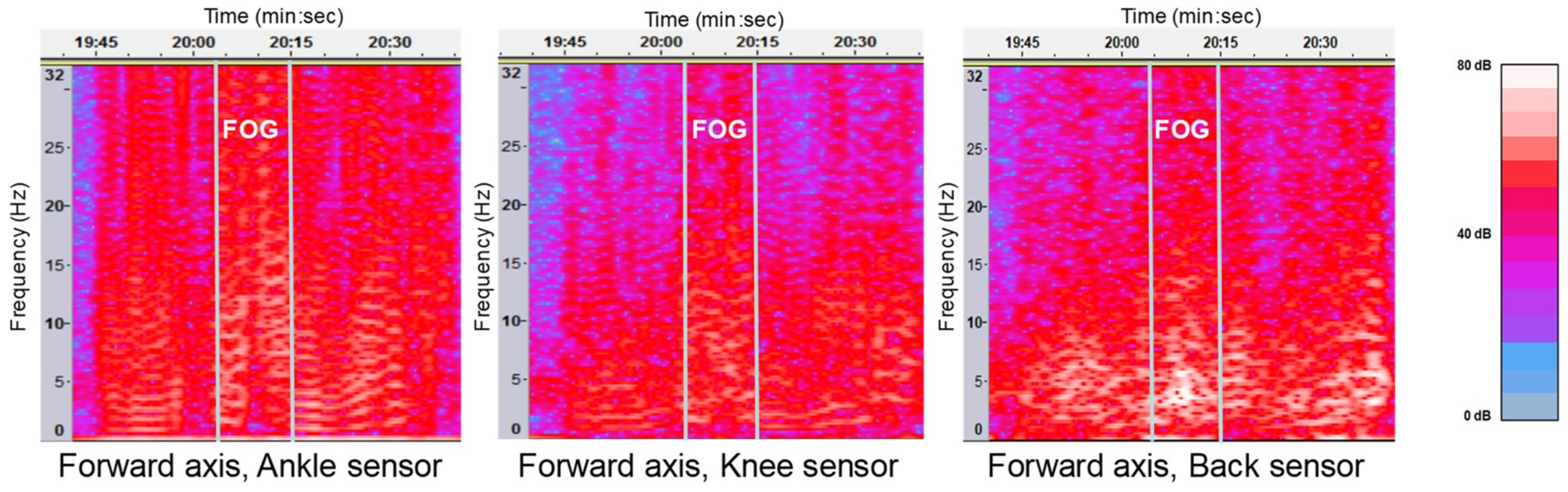
The main characteristic of FOG is the power increment in the frequency band of 3–8 Hz that does not appear during normal walking [
20]. When patients wanted to walk and they could not because of freezing, a vibration often appeared in all sensors (
Figure 1).
Table 1 summarizes the four features sets considered in this study. The first set of features contained the seven features per signal used in Mazilu et al. [
22]. With nine signals, we obtained a 7 × 9 feature vector for each 4-s window. The second set of features was composed of 90 features per signal (90 × 9 signals) that have often been used in HAR [
24]. This set included metrics obtained from the accelerometer signals in the time and frequency domains. The third set of features consisted of MFCCs adapted to inertial signals [
25]: 12 coefficients were considered from every inertial signal (12 × 9 signals).
The fourth set consisted of three metrics adapted from the SQA field [
26]. Many of these metrics are based on the speech signal periodicity presented during vowel pronunciation. When a person walks naturally, the accelerometer signal has high levels of periodicity and harmonicity and this structure is broken during a FOG event. The first quality metric used was harmonicity. This metric was computed as the autocorrelation of every window in time and frequency domains, generating two features. Lower autocorrelation values can be observed during FOG episodes. The second quality metric was signal predictability. This metric, which tries to measure how easy is to predict the signal using a linear model, was calculated by applying a linear prediction model with three coefficients and computing the error between the real signal and the prediction, both in time and frequency domains, generating two features. Higher errors are expected when FOG occurs. Finally, the spectral flux was computed as the Euclidean distance between two normalized consecutive window spectrums. A higher spectral flux can be observed when a FOG event starts. A total of five features per signal (5 × 9 signals) were included in this feature set.
3.4. Classification Algorithms
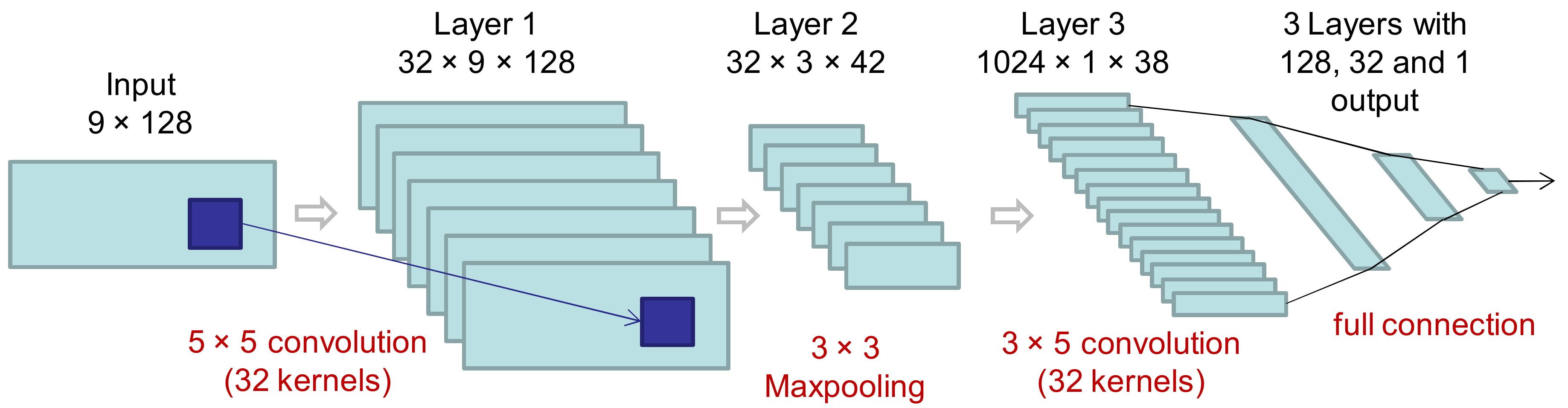
We analyzed several classification algorithms: random forest (baseline) with 100 decision trees, a multilayer perceptron with three fully connected layers, and five-state hidden Markov models. Additionally, a deep neural network was evaluated. This deep neural network was composed of six layers (
Figure 2) organized in two parts: the first part included two convolutional layers with an intermediate maxpooling layer for feature extraction, and the second part integrated three fully connected layers for classification (CNN + MLP). The inputs were the nine spectra (one for every accelerometer signal and direction) with 128 points each. In the first and second convolutional layers, 32 5 × 5 filters and 32 3 × 5 filters were considered, respectively. The configuration that achieved the best performance in the training set (using part of the training set for validation) was three epochs, batch size equal to 50, and ReLU as the activation function in all layers except the output layer that used a sigmoid function instead. The loss function was the binary cross entropy and the optimizer was the root-mean-square propagation method [
27].
4. Experiments
The majority of the experiments in this work were carried out with a LOSO cross validation. We created the training set including sessions from all subjects except the one used for testing. This process was iterated several times using a different subject for testing in each experiment. The final results were computed by averaging all the experiments. In order to create baseline performance numbers, we used a random 10-fold cross validation (R10Fold) for each subject independently. This evaluation methodology was used in Mazilu et al. [
22]. In this methodology, the sessions from every subject were randomly divided into 10 folds; 9 folds were used for training and 1 for testing. The process was repeated 10 times for each subject and the results were averaged. Only data from one subject was used. The final results were computed by averaging across the subjects included in the study. We computed specificity (true negative rate, the ratio of negatives that are correctly identified) versus sensitivity (true positive rate, the ratio of positives that are correctly identified) curves to compare the performance. These measurements are the most common metrics used in human sensing studies. We also calculated F1-score, area under the curve (AUC), and equal error rate (EER) in some experiments for an additional comparison.
4.1. Baseline and Comparison with Previous Work
The best results on the Daphnet dataset were reported by Mazilu et al. [
22]. The authors used seven features extracted from each acceleration signal: signal mean, standard deviation, variance, frequency entropy, energy, the ratio of the power in the freeze band to that in the locomotor band (i.e., the freeze index), and the power in both bands individually. Mazilu et al. [
22] compared several ML algorithms and reported that the best results were with the random forest algorithm. They also reported experiments with different window sizes in order to evaluate different latencies when detecting FOG events. They achieved a sensitivity, specificity, and F1-score of 0.995, 0.999, and 0.998, respectively, for their R10Fold experiments using a 4-s window. With LOSO evaluation, the sensitivity and specificity decreased to 0.663 and 0.954, respectively.
Most results in the literature used R10Fold evaluation rather than the more rigorous LOSO evaluation. R10Fold validation, with overlapped windows, is a weak evaluation because consecutive windows share data. Therefore, when the windows are shuffled before computing the folds, there is a high probability that windows in training and testing sets include some of the same raw data (
Figure 3). Some of the previous results in the literature did not report the overlap when using the R10Fold evaluation [
22]. Others proposed alternatives for dividing the 10 folds in a manner that avoids the inclusion of the same data in training and testing [
18]. For comparison with previous studies, we did some experiments using R10Fold with 4-s windows without excluding subjects 4 and 10 and considering several overlaps.
Table 2 shows that Mazilu and colleagues’ results [
22] could be reproduced only with a significant overlap.
The use of a single value metric for evaluating performance, such as sensitivity, specificity, accuracy, or F1-score, is problematic. These single value metrics depend on the threshold used by the classifier to make a decision, increasing the difficulty of comparing different systems. Additionally, some metrics (such as accuracy) have a strong dependency on the class balance in the testing dataset. In the Daphnet dataset, less than 10% of the data pertains to FOG episodes (positive examples), while the rest contains normal walking (negative examples), so classifying all examples as negative gives an accuracy higher than 90%. In this paper, we used specificity and sensitivity because these metrics do not depend on the class balance in testing.
4.2. Evaluation of the Different Feature Extraction Strategies
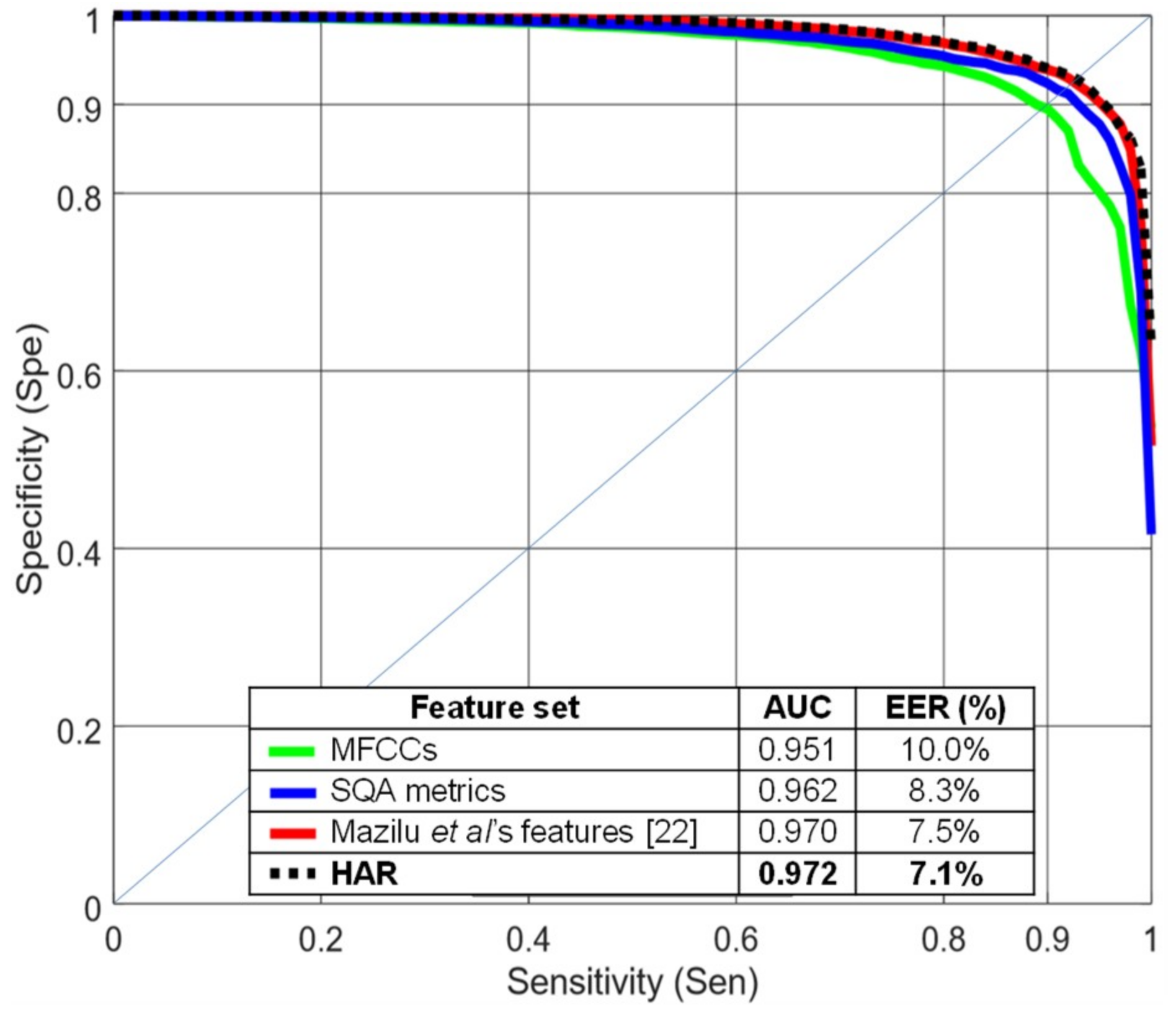
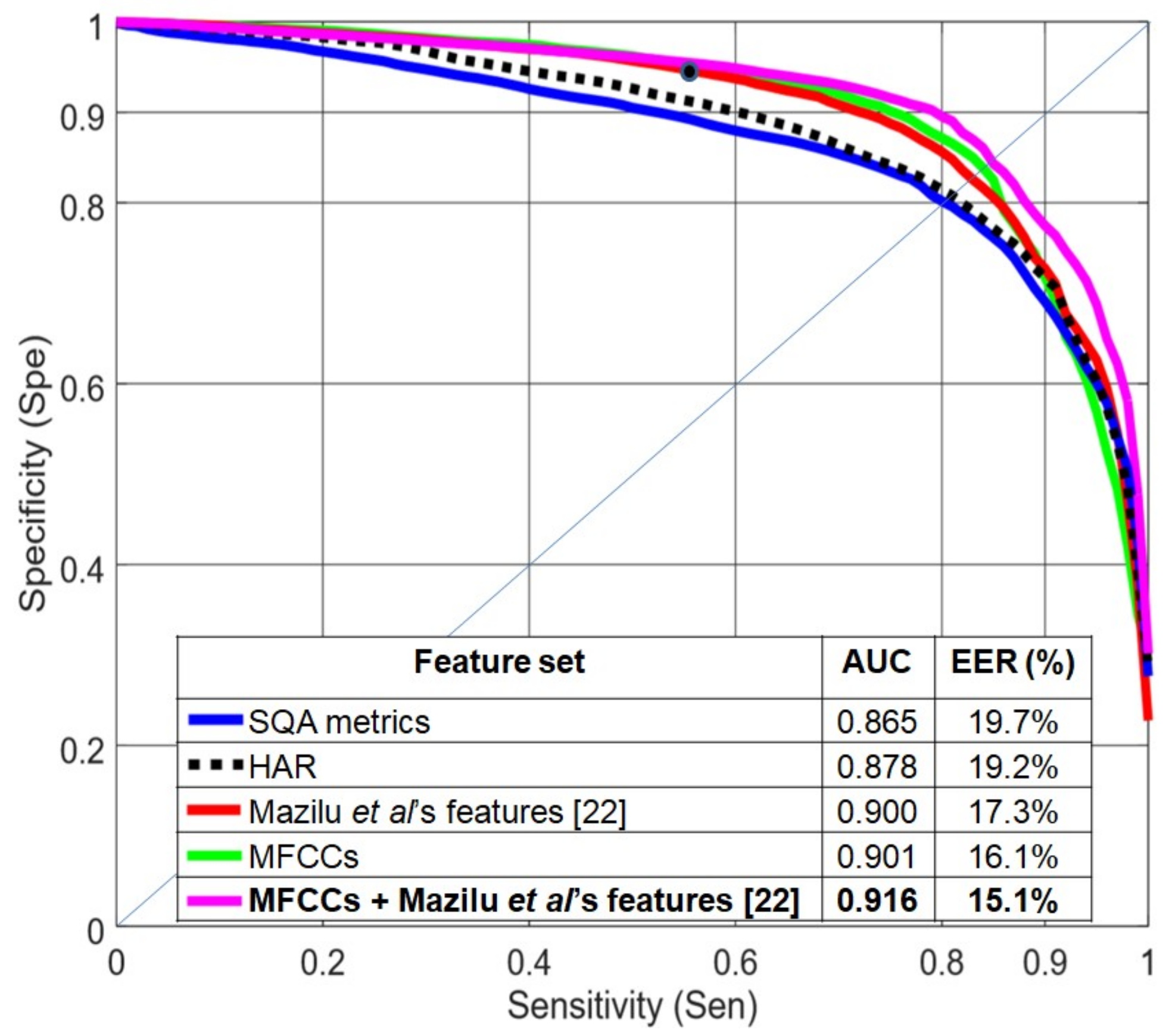
Figure 4 compares several feature sets using a random forest classifier with 4-s windows and 75% overlap.
Figure 4 shows specificity vs. sensitivity curves and AUC and EER values, all computed using R10Fold cross validation. HAR and Mazilu et al.’s [
22] feature sets performed better than MFCCs in this evaluation. The quality metrics (blue line) provided an intermediate level of performance. Mazilu et al.’s features, with only seven values per signal, obtained similar results compared to the HAR feature set with 90 features per signal.
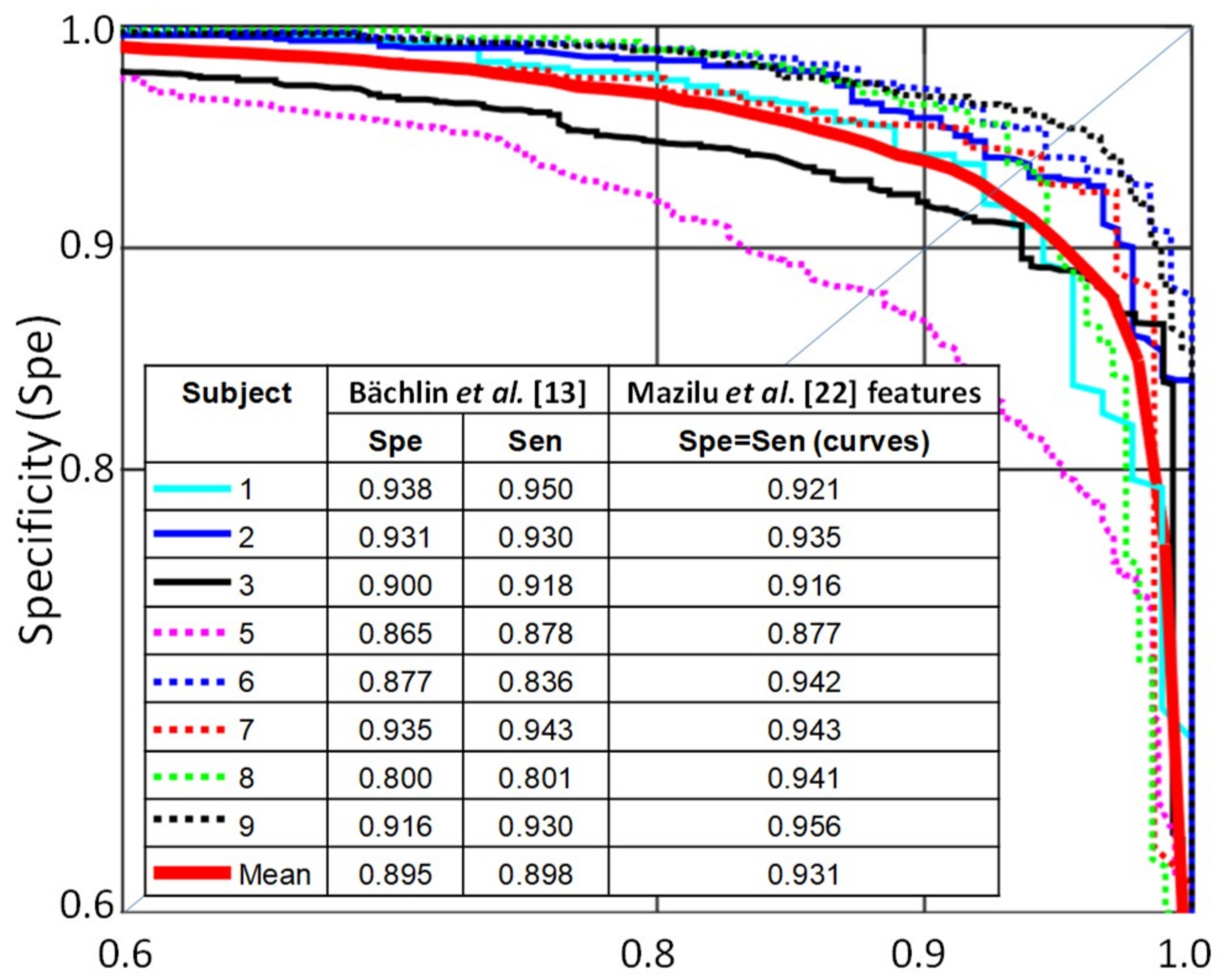
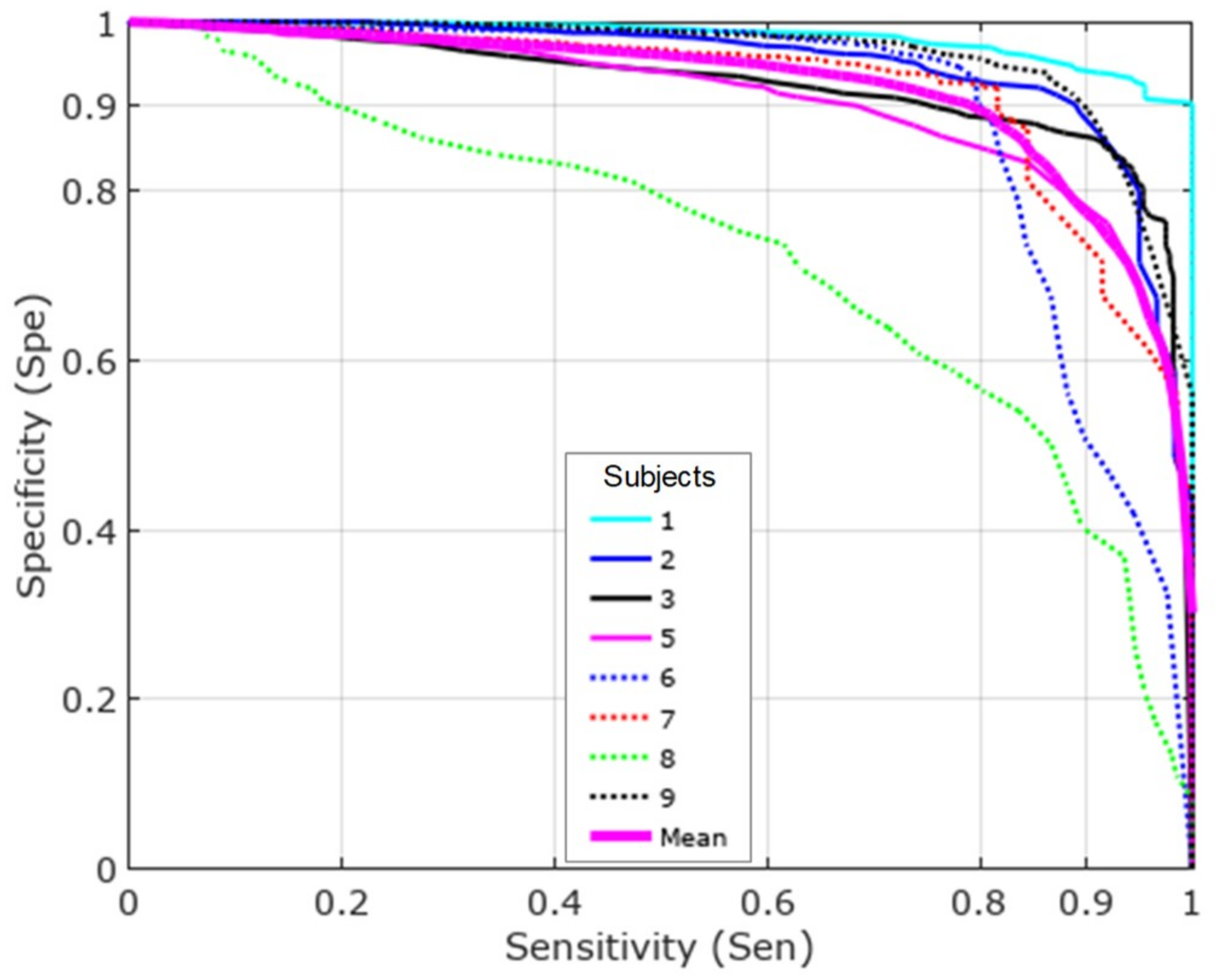
When we compared the results per subject using Mazilu et al.’s [
22] features with the results reported by Bächlin et al. [
13] (
Figure 5), we saw an improvement in all subjects except for subject 1.
Figure 6 compares the different feature sets with LOSO evaluation. MFCCs obtained slightly better results than Mazilu et al.’s features. MFCCs create a smooth distribution (very similar to a Gaussian distribution [
28]) which is less likely to overfit and, therefore, has better generalization behavior. HAR and quality metrics provided the worst results: they fit the data well in the R10Fold experiment but were not able to generalize to held-out subjects. The best results were obtained when combining Mazilu et al.’s [
22] and MFCC features (concatenating the two feature vectors). Mazilu et al. [
22] reported a sensitivity of 0.66 and a specificity of 0.95, but these values included subjects 4 and 10, each of whom were associated with a sensitivity of 1.0. Removing these two subjects, the sensitivity decreased to 0.55 for a specificity of 0.95 (isolated point in
Figure 6).
Figure 7 shows the results per subject using MFCCs and Mazilu et al.’s features together. Subject 8 provided the worst results. This subject had many FOG events with a different pattern than the other subjects, showing no increase in energy in the 3−8-Hz band. This unique pattern produced bad results in a LOSO scenario, as it did not appear sufficiently in the training set.
4.3. Evaluation of Different Classification Algorithms
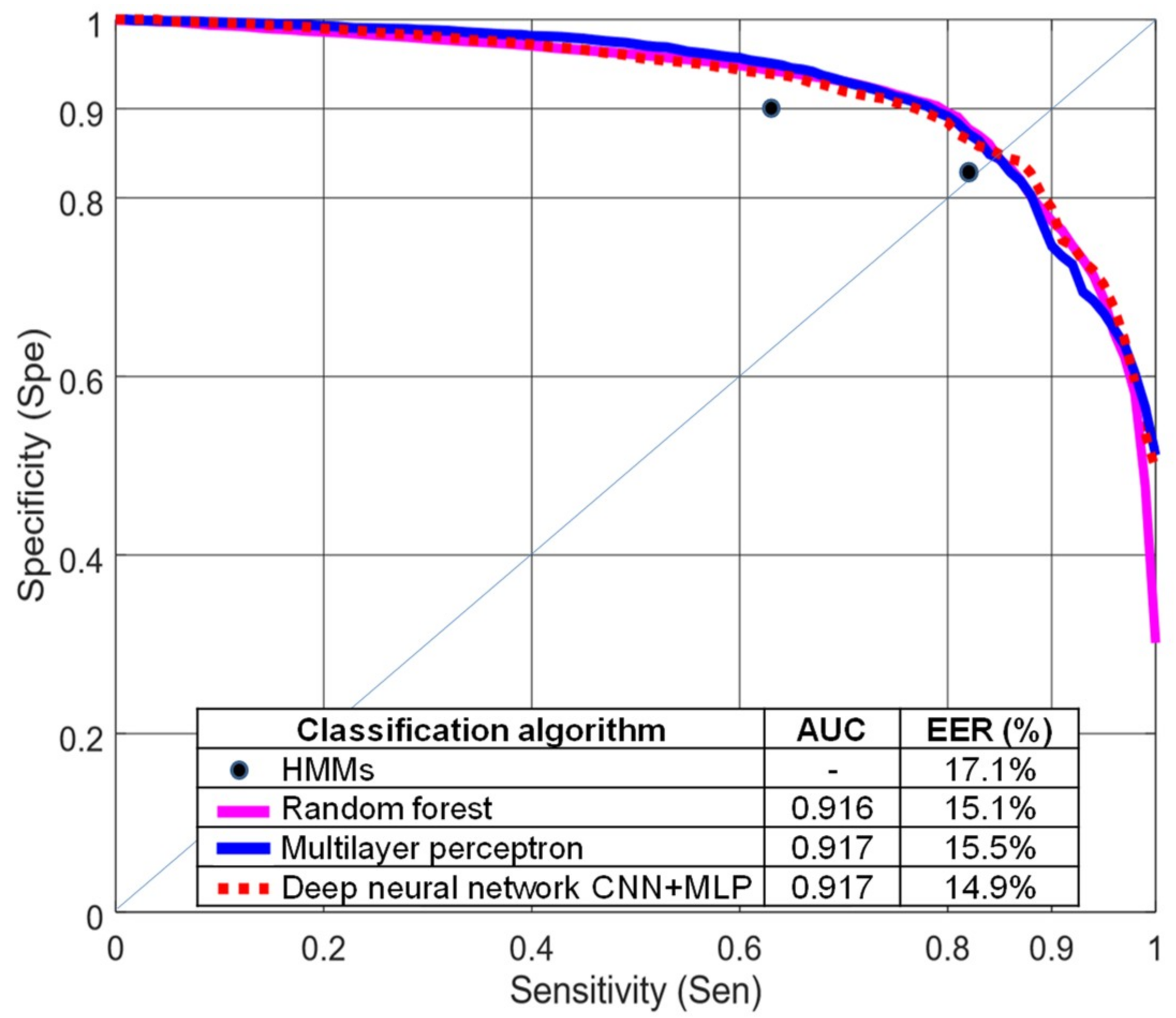
We tested four different classification algorithms: random forest, multilayer perceptron, and hidden Markov models (
Figure 8), using MFCCs and Mazilu et al.’s features, and the deep neural network described in
Section 3.3. The performance of the HMMs is represented with two isolated points corresponding to different probabilities for the transitions between FOG and non-FOG HMMs. Hidden Markov models are finite state machines. Every time
t that a state
j is entered, a feature vector
Ot is generated from the probability density
bj(Ot). The transition from state
i to state
j is also probabilistic and modeled by the discrete probability a
ij.
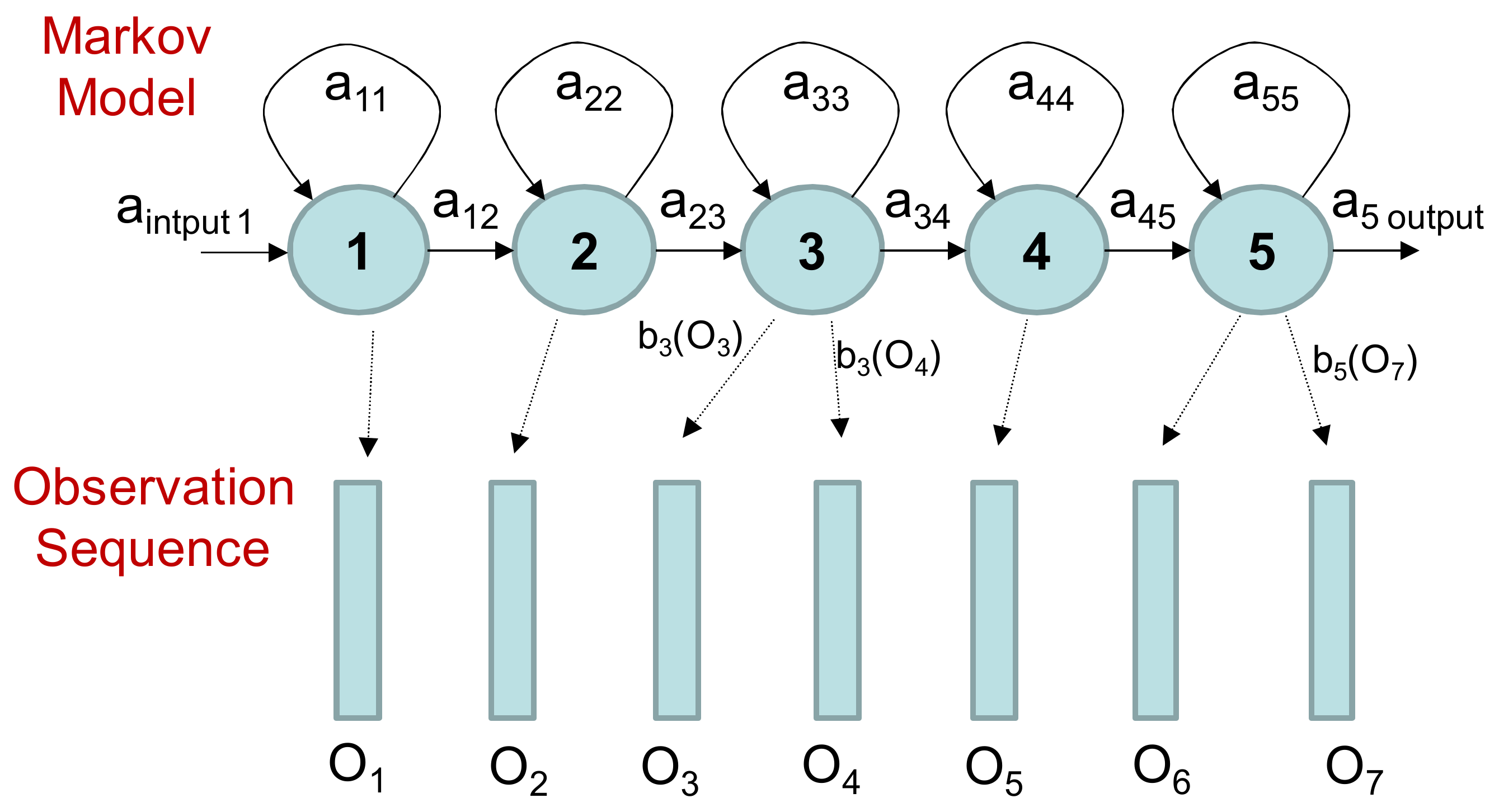
Figure 9 shows an example of this process where the five-state model moves through the state sequence X = 1; 2; 3; 3; 4; 5; 5 in order to generate the feature vector sequence
O1 to
O7. The weakest results were obtained with HMMs. The HMMs required defining a sequential model with five states to achieve reasonable discrimination. Therefore, a minimum number of windows (five windows corresponding to 5 s) was necessary to make a decision. Short FOG episodes were missed when they appeared in isolation, or consecutive FOG episodes were combined if the time between them was shorter than 5 s. In this dataset, more than 30% of the FOG episodes lasted less than 5 s.
The results obtained with random forest and multilayer perceptron were very similar and better than HMMs. Both classifiers are discriminative algorithms using the same set of features. We obtained slightly lower EER for the deep neural network.
4.4. Using Contextual Windows
In the time leading up to a FOG event, there is an initial phase where some of the FOG characteristics appear [
18]. With this idea in mind, we tested whether or not the inclusion of features from adjacent time windows, referred to here as contextual windows, would improve classification performance. The effect of including the contextual windows in the classification task was evaluated for the deep learning strategy with LOSO evaluation (CNN+MLP in
Figure 10). The results improved when previous and subsequent windows were included in the analysis but were saturated when using three previous and three subsequent 4-s windows with a 75% overlap. The CNN filters were able to find patterns between the spectra of consecutive windows. We did not obtain significant improvements when including contextual windows with MFCCs and Mazilu et al.’s features and a random forest classifier.
When using subsequent windows, a 1 second delay in the system response was introduced for each subsequent window included in the decision. In order to reduce this delay, we repeated the experiments using only previous windows (
Table 3). Although the results were slightly worse than when both previous and subsequent windows were included, we achieved significant improvement without increasing the system delay.
Table 4 shows the performance for independent sensors (ankle, knee, and back accelerometers) when including only previous windows. With the knee accelerometer, the results were very similar to the case of using the three sensors. The worst results were obtained when using only the back accelerometer.
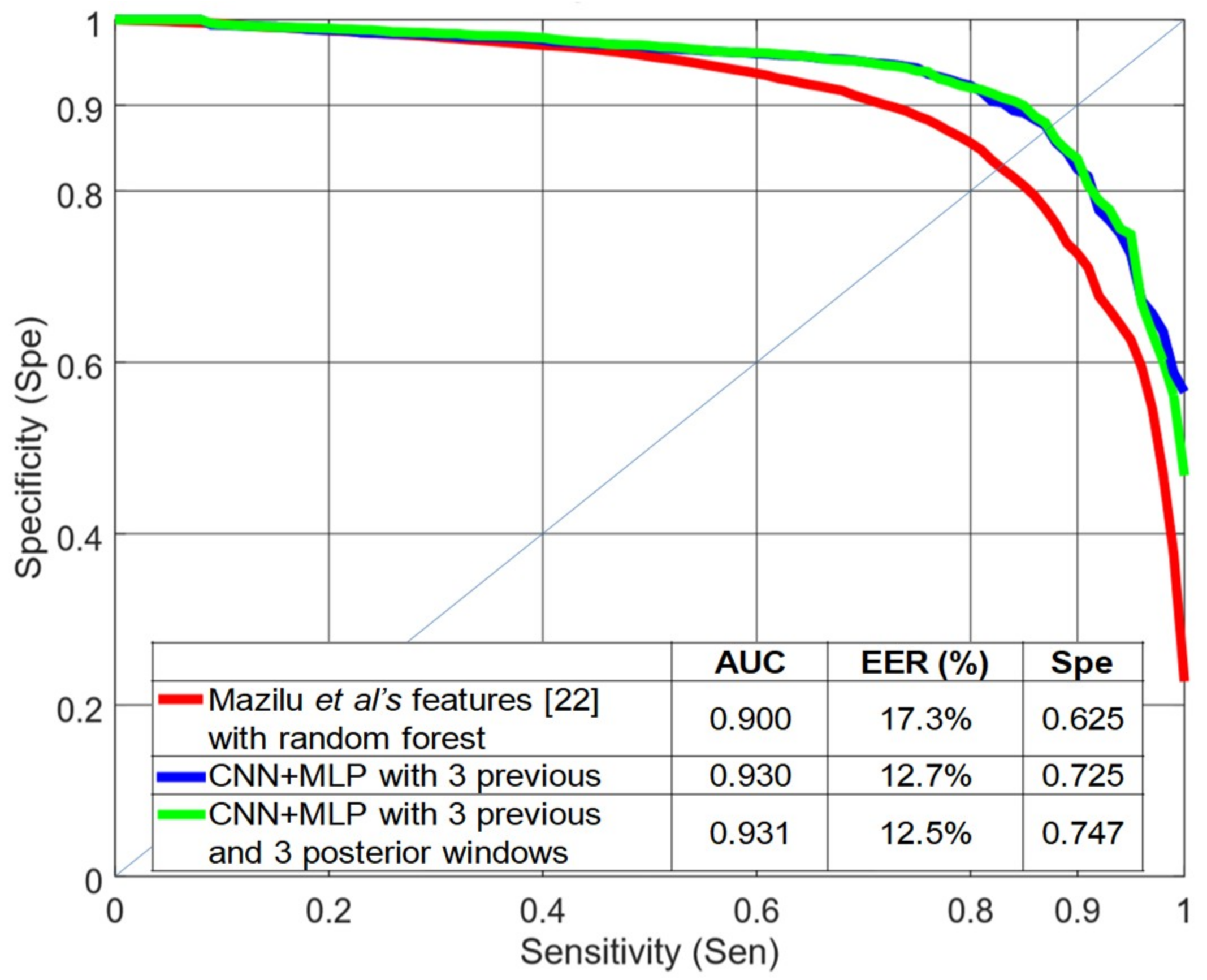
Figure 11 shows a comparison between the baseline (Mazilu et al.’s features [
22] with random forest) and the best system obtained in this paper (CNN+MLP with three previous and three subsequent windows) using a LOSO evaluation. This figure also includes the results for the CNN+MLP structure when including only three previous windows. The EER decreased from 17.3% to 12.5% and the AUC increased from 0.900 to 0.931. With this dataset, a difference of 0.015 (1.5%) in AUC can be considered significant with
p < 0.0005, according to Hanley’s method [
29]. For high levels of sensitivity (0.95), the specificity increased more than 0.12 when using previous and subsequent windows and more than 0.10 when using only previous windows.
5. Discussion and Conclusions
We evaluated the robustness of different feature sets and ML algorithms for FOG detection using body-worn accelerometers. The evaluation was carried out with subjects whose data was held out from the training set (LOSO evaluation). We found that MFCCs were very good features in the LOSO evaluation. The combination of the features proposed by Mazilu et al. [
22] and MFCCs were the best set of handcrafted features evaluated in this paper.
Hidden Markov models did not work well in this task because, in order to increase their discrimination capability, the number of states had to be increased, losing resolution in the segmentation process. The best results were obtained with a deep neural network that included two convolutional layers combined with a maxpooling layer (for extracting features from the accelerometer signal spectra) and three fully connected layers for classification. We obtained a further improvement when we included temporal information in the detection process via contextual windows. When comparing Mazilu et al.’s system [
22] with our best system, the EER decreased from 17.3% to 12.5% and the AUC increased from 0.900 to 0.931, obtaining the best results for this dataset with a LOSO evaluation. Regarding the sensor placement, when using only the knee accelerometer, the performance was very close to the case of using the three accelerometers.
A FOG detection system can be used to activate external cues, such as rhythmic acoustic ones. These cueing systems help the patient to maintain a certain speed and amplitude of movements when walking, reducing the duration and frequency of FOG episodes. These cues are more effective when applied only during FOG episodes or in difficult walking situations. Therefore, FOG event detection must have a high sensitivity (true positive rate) in order to activate the cueing system. For high levels of sensitivity (95%), our best system increased the specificity from 0.63 to 0.73 without adding delays to the detection process.
The main characteristic of FOG is a significant power increment in the 3−8 Hz band. However, the FOG pattern varies across subjects. For example, for subject 8, some FOG episodes did not show an increase in power in the 3−8-Hz band. Differences among subjects present a challenge for a system that must maintain high accuracy for unseen subjects. For future work, we would like to validate these results using a larger number of subjects to deal with FOG variability across subjects. With more data from a larger subject pool, it might be possible to train more complex deep learning models and achieve better performance. Moreover, we could analyze different FOG patterns in order to define distinct classes of this symptom that might help in designing better detection systems.