Radar Waveform Optimization for Joint Radar Communications Performance
Abstract
1. Introduction
1.1. Contributions
- Extend previously derived spectral mask shaping method to employ the continuous spectral WF algorithm to maximize communications performance
- Employ more computationally efficient optimization solvers for the spectral mask shaping algorithm
- Introduce constraints on autocorrelation peak side-lobe to main-lobe ratio and spectral leakage for the spectral mask shaping waveform design method
- Conduct a preliminary study to compare the performance of the extended waveform design method against previously derived spectral-mask shaping method
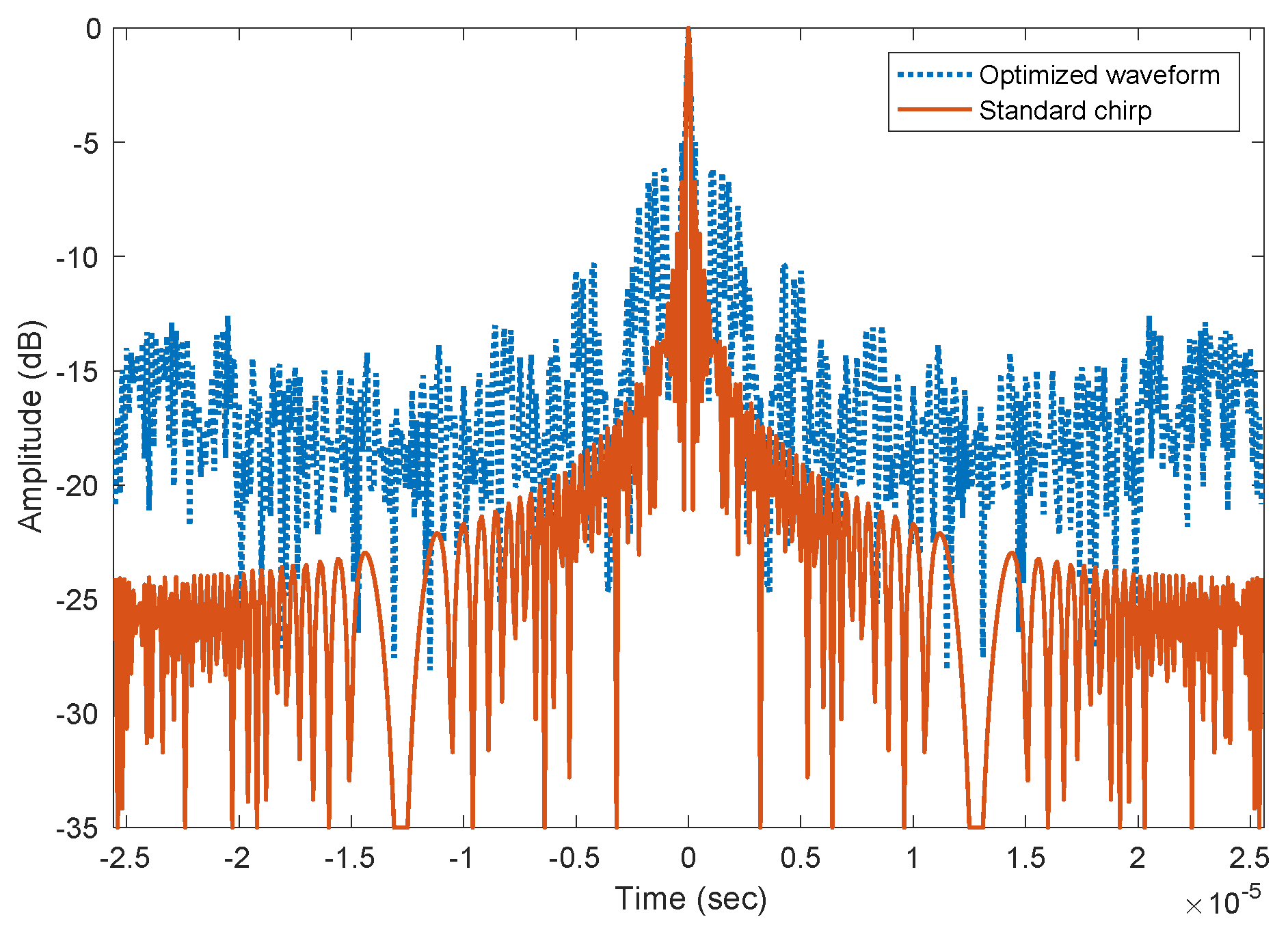
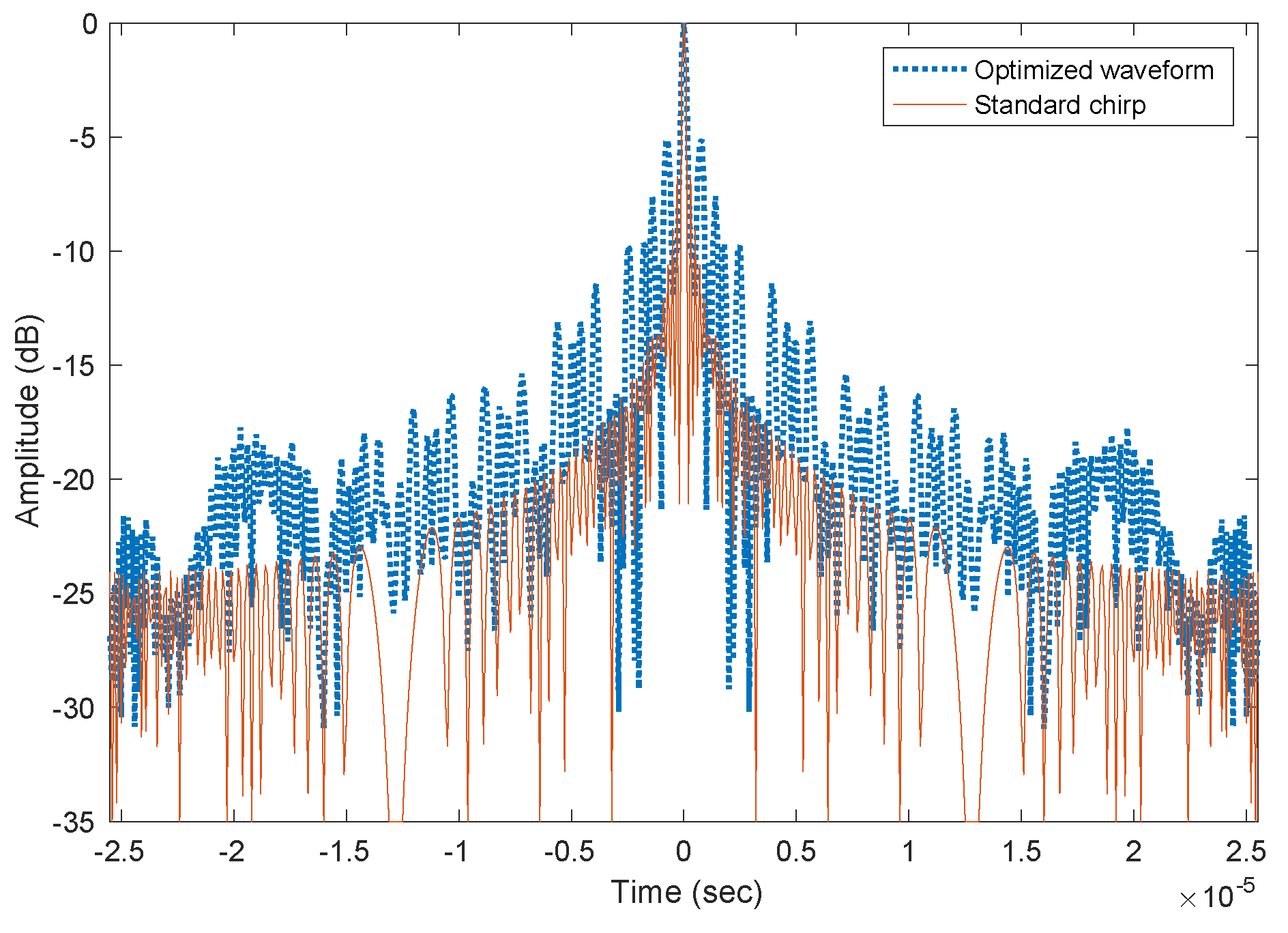
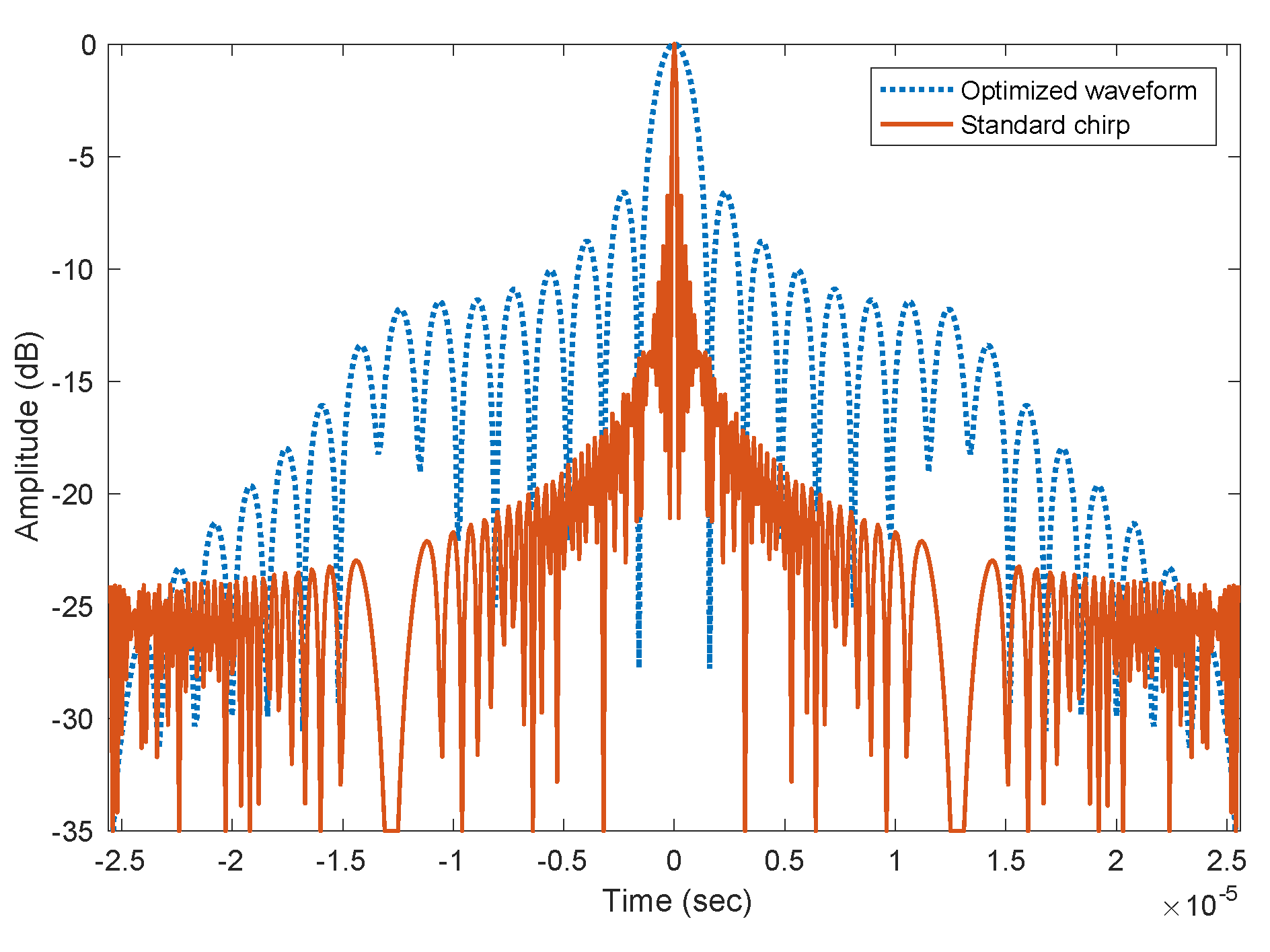
- Compare waveform properties of the optimally designed radar waveform with that of a LFM chirp waveform
- Derive a time-domain expression for a spectrally masked standard chirp signal
- Prove that the solution of the NLP waveform design problem is Pareto-optimal
1.2. Background
1.3. Problem Description
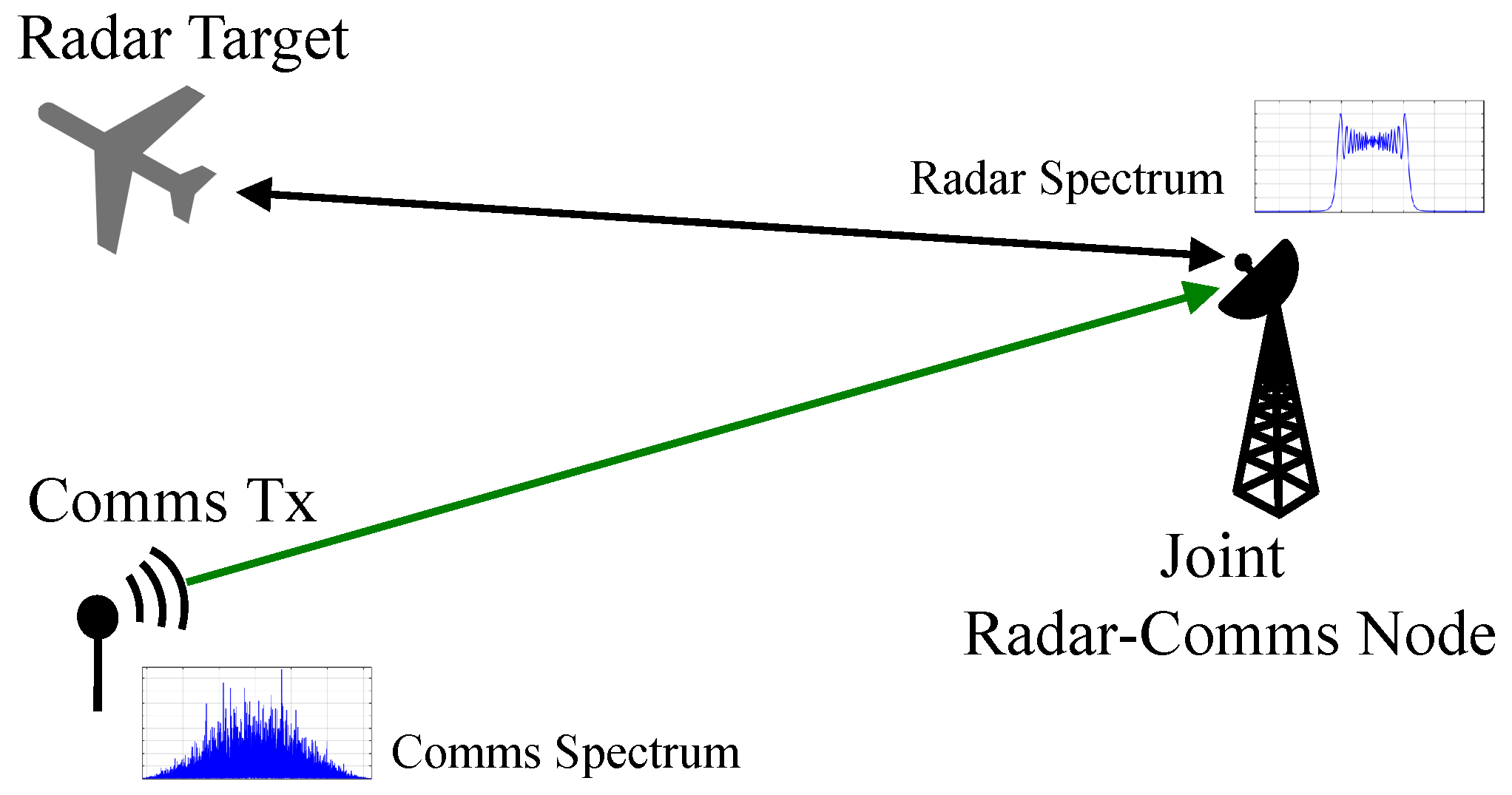
- Radar and communications operate in the same frequency allocation simultaneously
- Joint radar communications receiver is capable of simultaneously decoding a communications signal and estimating a target parameter
- Radar detection and track acquisition have already taken place
- Radar system is an active, single-input single-output (SISO), mono-static, and pulsed system
- Radar system operates without any maximum unambiguous range
- A single SISO communications transmitter is present
- Only one radar target is present
- Target range or delay is the only parameter of interest
- Target cross-section is well estimated
2. Joint Radar Communications Performance Metrics
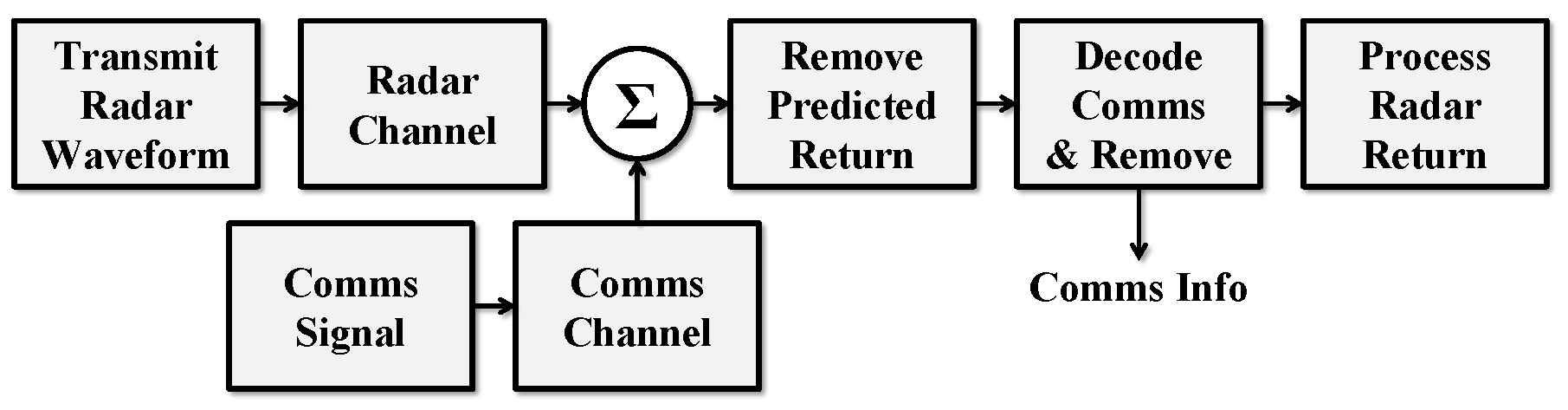
2.1. Successive Interference Cancellation Receiver Model
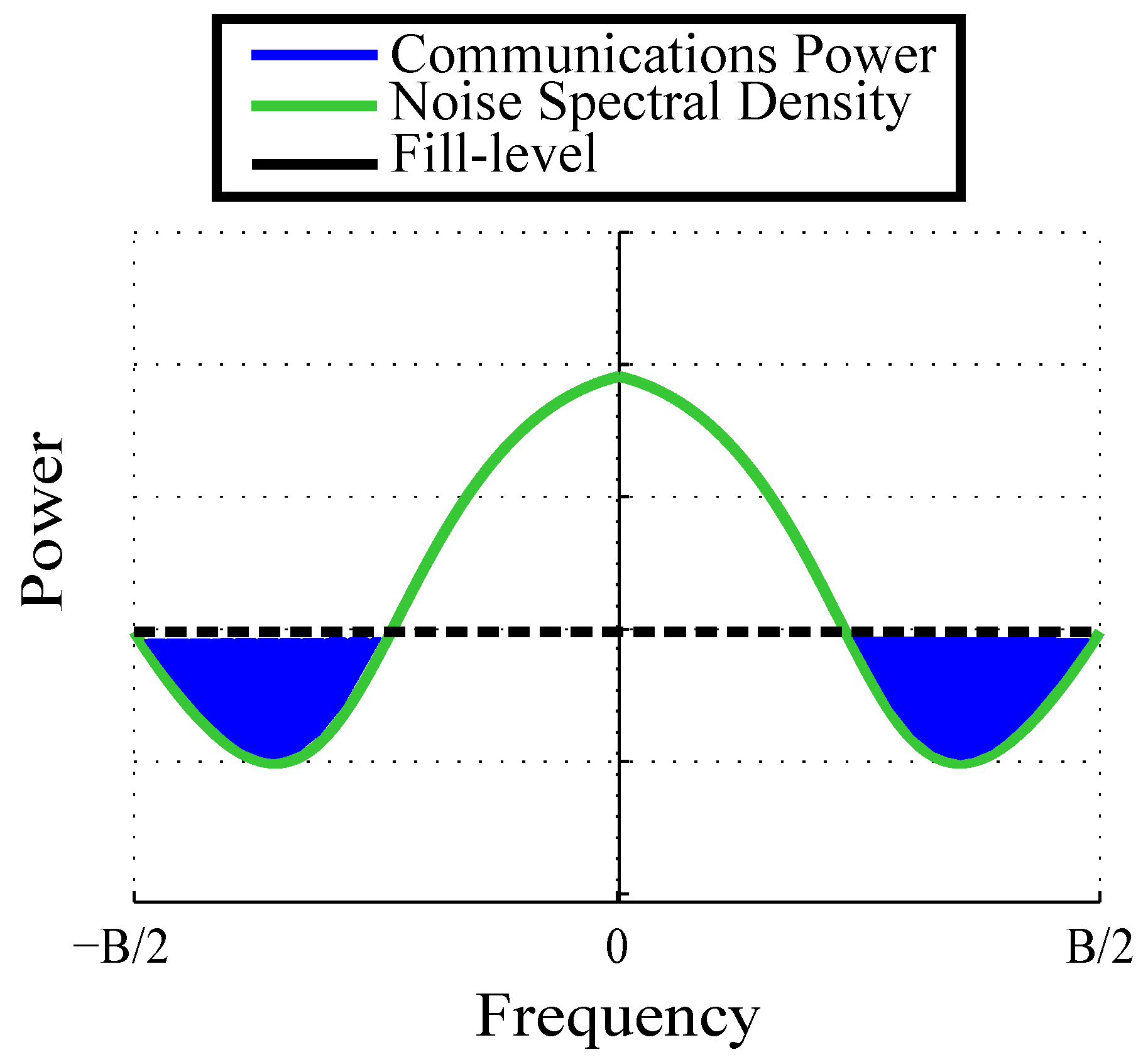
2.2. Spectral Water-Filling SIC Data Rate
2.3. Global Radar Estimation Rate
3. Joint Waveform Design Problem
- Peak side-lobe to main-lobe ratio (constraint ): in [8], the estimation rate was extended to consider global estimation errors (errors occurring when the radar waveform autocorrelation side-lobe is confused for the main-lobe) using the method of interval errors [60]. However, the method of interval errors only considers the errors occurring due to the peak side-lobe and ignores the rest. If the other side-lobes are high enough, they can still have a significant contribution to the global estimation error. By limiting the peak side-lobe to main-lobe ratio to be below a certain threshold, we can reduce the effect the peak side-lobe as well as any other high side-lobes will have on the global estimation error. This constraint is mathematically defined in Equation (11).
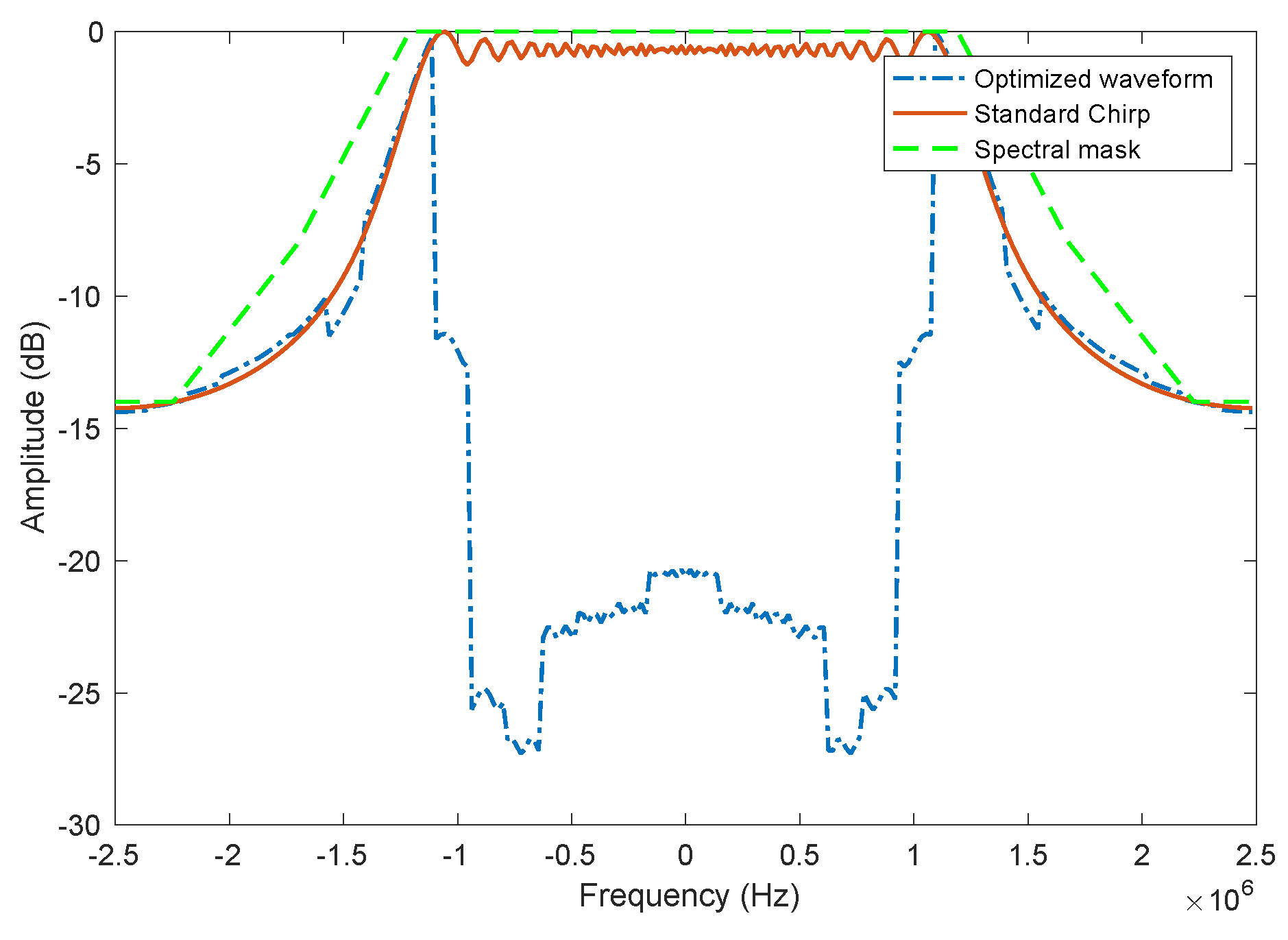
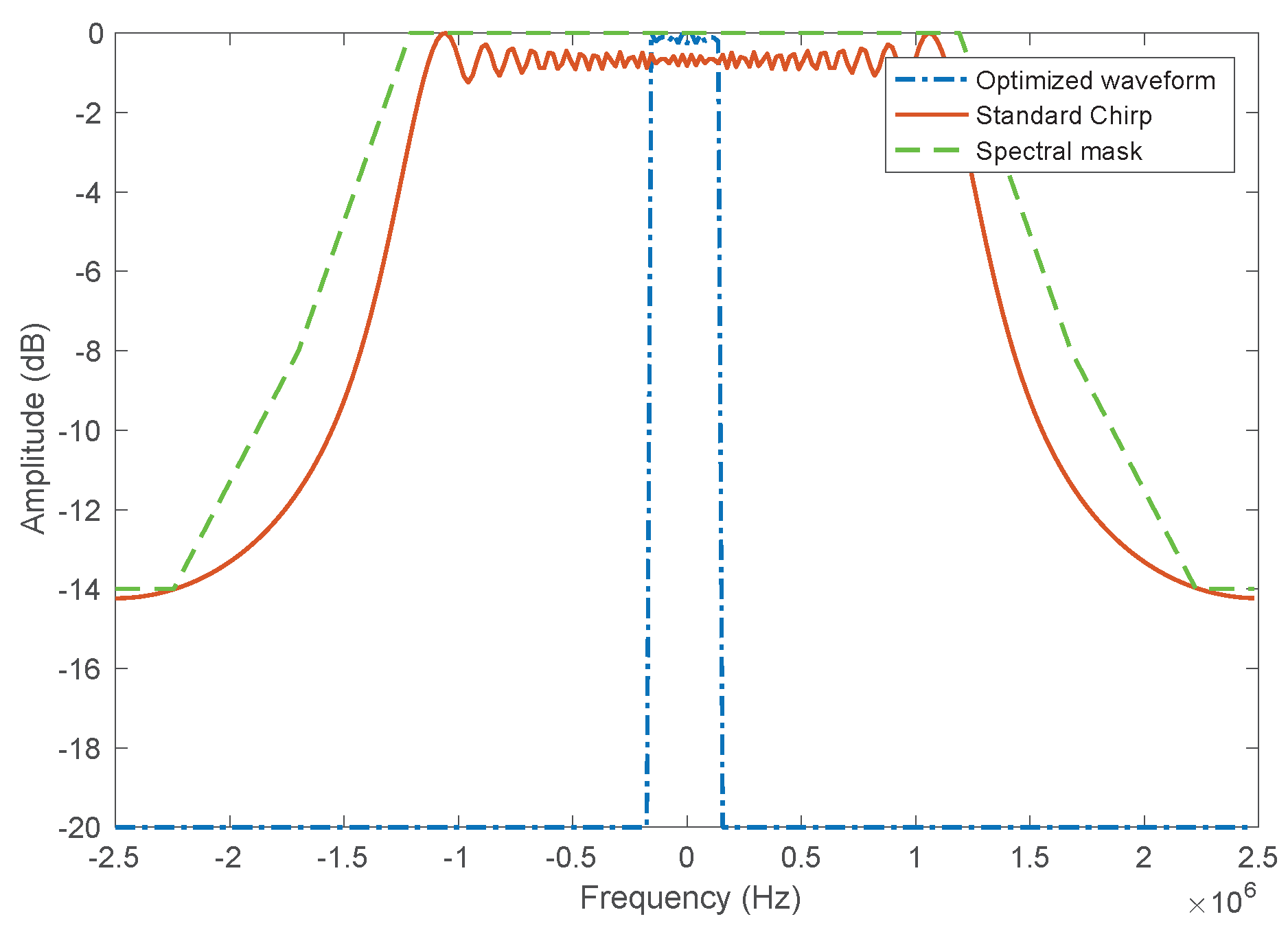
- Spectral leakage (constraint ): Since the system can only receive signals whose spectrum lies within the system’s bandwidth, any electromagnetic radio frequency (RF) energy that leaks outside of the bandwidth will be lost. To minimize this loss of RF energy, we introduce a constraint on the amount of energy present in the radar spectrum at frequencies out of the system bandwidth range. We enforce this constraint by having the radar spectrum be below a thresholding spectral mask such as the one seen in Figure 5. This constraint is mathematically defined in Equation (11).
4. Method
- and
- and .
Time Domain Form of Spectrally-Masked Chirp
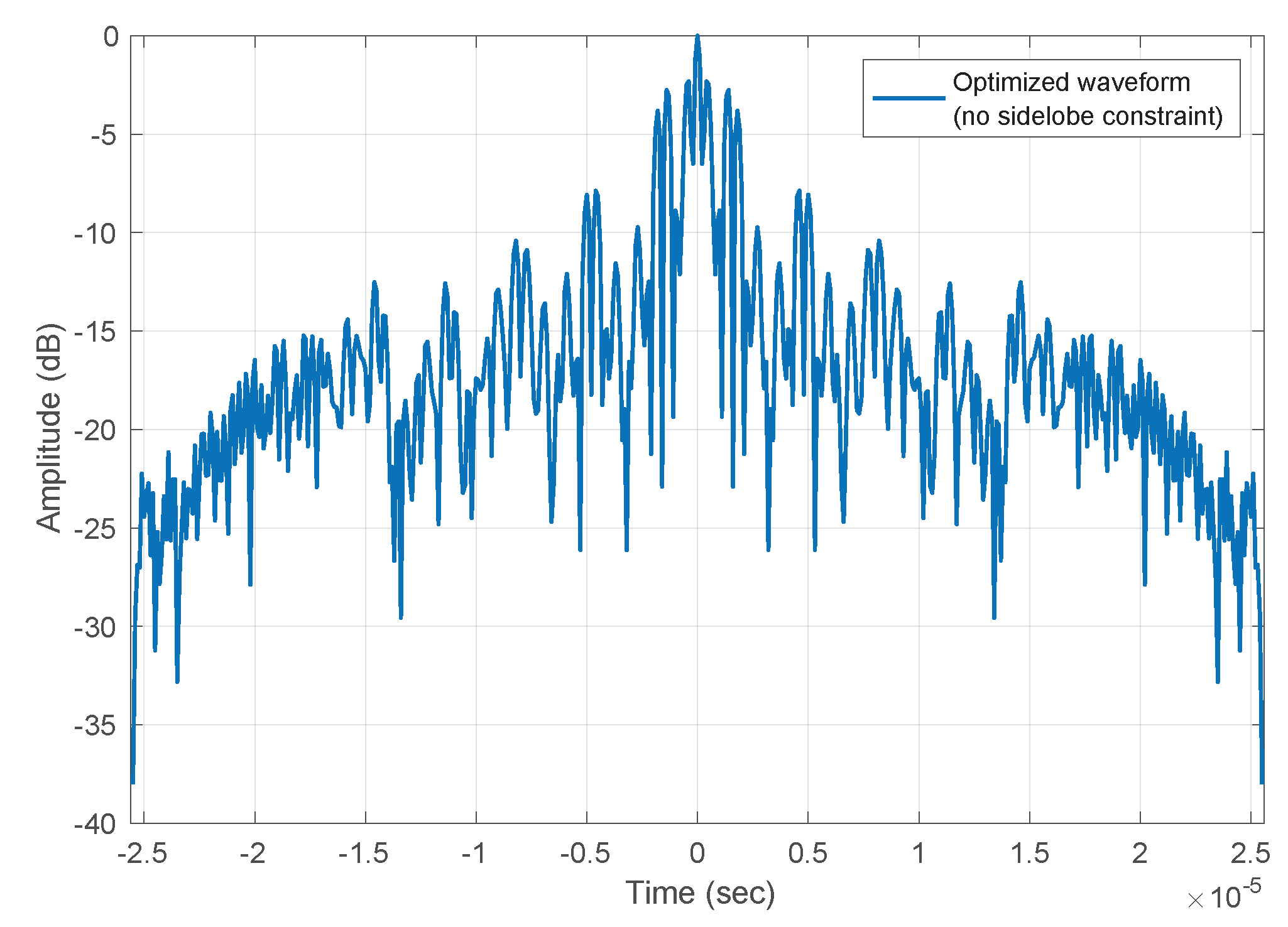
5. Simulation Results and Discussion
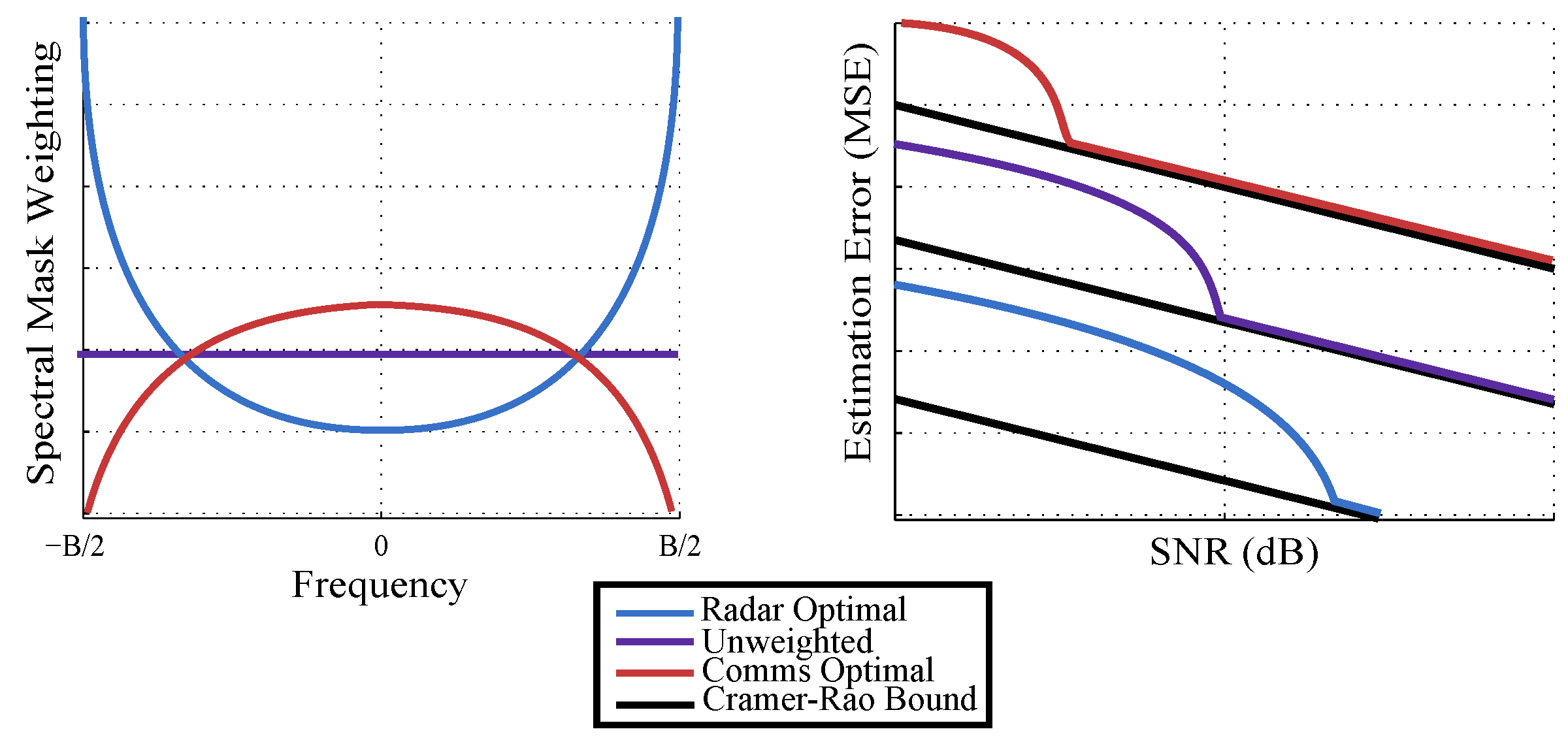
5.1. Spectral-Mask Shaping Method
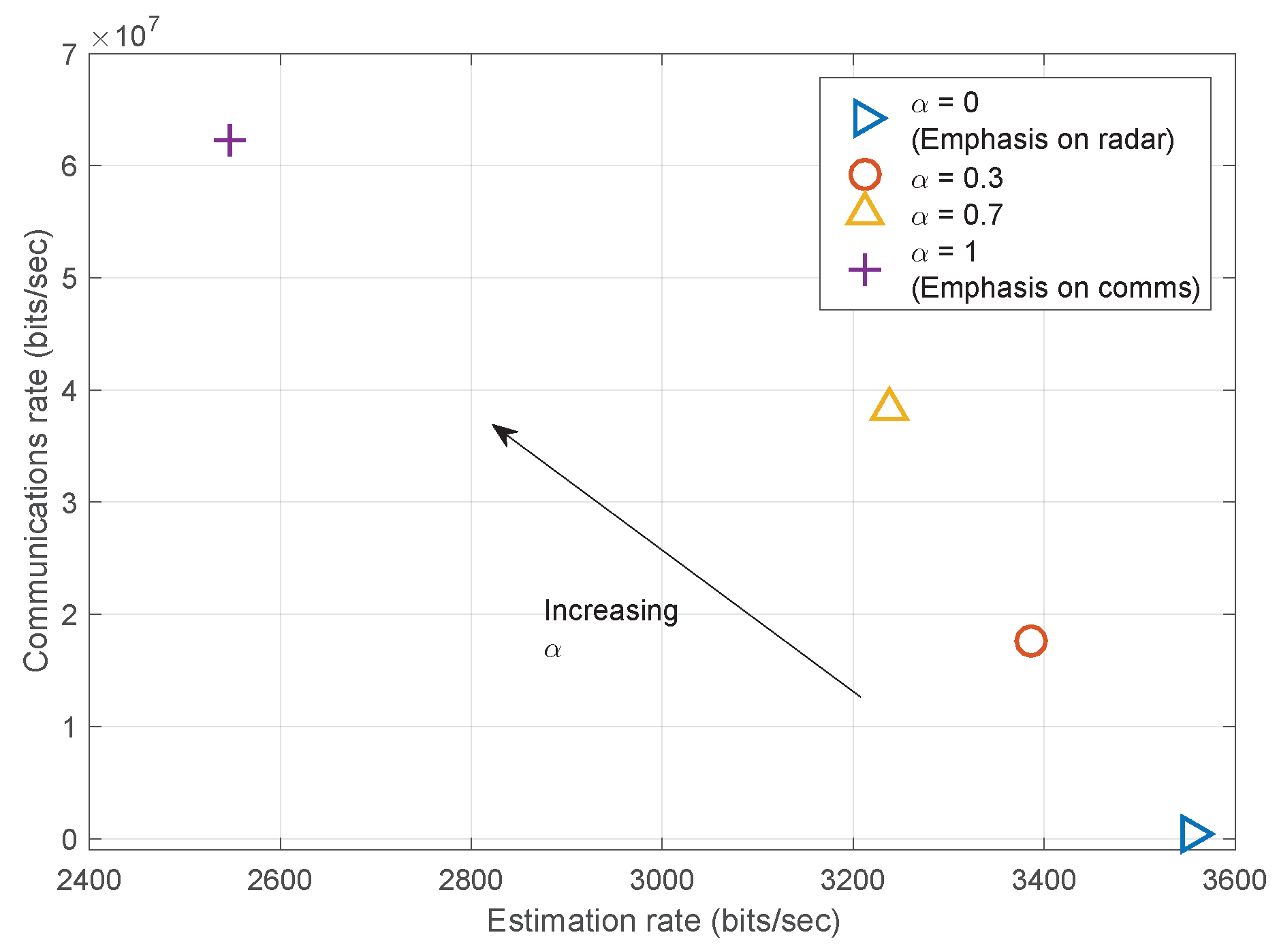
5.2. Performance Comparison of Waveform Design Algorithms
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BER | bit error rate |
| NLP | Nonlinear Programming |
| MMSE | Minimum Mean-Squared Error |
| OFDM | Orthogonal Frequency-Division Multiplexing |
| PSD | Power Spectral Density |
| RMS | Root Mean Square |
| RF | Electromagnetic Radio Frequency |
| SIC | Successive Interference Cancellation |
| SISO | Single-Input Single-Output |
| SNR | Signal-to-Noise Ratio |
| WF | Water-Filling |
References
- Paul, B.; Chiriyath, A.R.; Bliss, D.W. Survey of RF Communications and Sensing Convergence Research. IEEE Access 2016, 5, 252–270. [Google Scholar] [CrossRef]
- Griffiths, H.; Cohen, L.; Watts, S.; Mokole, E.; Baker, C.; Wicks, M.; Blunt, S. Radar Spectrum Engineering and Management: Technical and Regulatory Issues. Proc. IEEE 2015, 103, 85–102. [Google Scholar] [CrossRef]
- Bliss, D.W. Cooperative Radar and Communications Signaling: The Estimation and Information Theory Odd Couple. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 50–55. [Google Scholar]
- Deng, H.; Himed, B. Interference mitigation processing for spectrum-sharing between radar and wireless communications systems. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1911–1919. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Jacyna, G.M.; Bliss, D.W. Inner Bounds on Performance of Radar and Communications Co-existence. IEEE Trans. Signal Process. 2016, 64, 464–474. [Google Scholar] [CrossRef]
- Paul, B.; Bliss, D.W. The Constant Information Radar. Entropy 2016, 18, 338. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Bliss, D.W. Radar-communications convergence: Coexistence, cooperation, and co-design. IEEE Trans. Cognit. Commun. Netw. 2017, 3, 1–12. [Google Scholar] [CrossRef]
- Paul, B.; Chiriyath, A.R.; Bliss, D.W. Joint Communications and Radar Performance Bounds Under Continuous Waveform Optimization: The Waveform Awakens. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 865–870. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Chiriyath, A.R.; Bliss, D.W. Effect of Clutter on Joint Radar-Communications System Performance Inner Bounds. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 1379–1383. [Google Scholar]
- Chiriyath, A.R.; Bliss, D.W. Joint Radar-Communications Performance Bounds: Data versus Estimation Information Rates. In Proceedings of the 2015 IEEE Military Communications Conference, MILCOM, Tampa, FL, USA, 26–28 October 2015; pp. 1491–1496. [Google Scholar]
- Chiriyath, A.R.; Paul, B.; Bliss, D.W. Joint Radar-Communications Information Bounds with Clutter: The Phase Noise Menace. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 690–695. [Google Scholar]
- Sturm, C.; Wiesbeck, W. Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing. Proc. IEEE 2011, 99, 1236–1259. [Google Scholar] [CrossRef]
- Turlapaty, A.; Jin, Y.; Xu, Y. Range and Velocity Estimation of Radar Targets by Weighted OFDM Modulation. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1358–1362. [Google Scholar]
- Guo, T.; Qiu, R. OFDM Waveform Design Compromising Spectral Nulling, Side-lobe Suppression and Range Resolution. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1424–1429. [Google Scholar]
- Lellouch, G.; Mishra, A.; Inggs, M. Impact of the Doppler modulation on the Range and Doppler Processing in OFDM Radar. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 803–808. [Google Scholar]
- Thompson, S.C.; Stralka, J.P. Constant Envelope OFDM for Power-Efficient Radar and Data Communications. In Proceedings of the International Waveform Diversity and Design Conference, Kissimmee, FL, USA, 8–13 February 2009; pp. 291–295. [Google Scholar]
- Krier, J.R.; Norko, M.C.; Reed, J.T.; Baxley, R.J.; Lanterman, A.D.; Ma, X.; Barry, J.R. Performance Bounds for an OFDM-Based Joint Radar and Communications System. In Proceedings of the IEEE Military Communications Conference, Tampa, FL, USA, 26–28 October 2015; pp. 511–516. [Google Scholar]
- Hakobyan, G.; Yang, B. A novel OFDM-MIMO radar with non-equidistant subcarrier interleaving and compressed sensing. In Proceedings of the 17th International Radar Symposium (IRS), Krakow, Poland, 10–12 May 2016; pp. 1–5. [Google Scholar]
- Sit, Y.L.; Nuss, B.; Basak, S.; Orzol, M.; Zwick, T. Demonstration of interference cancellation in a multiple-user access OFDM MIMO Radar-Communication network using USRPs. In Proceedings of the IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), San Diego, CA, USA, 19–20 May 2016; pp. 1–4. [Google Scholar]
- Shi, C.; Wang, F.; Sellathurai, M.; Zhou, J.; Salous, S. Power minimization-based robust OFDM radar waveform design for radar and communication systems in coexistence. IEEE Trans. Signal Process. 2018, 66, 1316–1330. [Google Scholar] [CrossRef]
- Shaojian, X.; Bing, C.; Ping, Z. Radar-Communication Integration Based on DSSS Techniques. In Proceedings of the 8th International Conference on Signal Processing, Beijing, China, 16–20 November 2006; Volume 4, pp. 1–4. [Google Scholar]
- Xie, Y.; Tao, R.; Wang, T. Method of Waveform design for radar and communication integrated system based on CSS. In Proceedings of the First International Conference on Instrumentation, Measurement, Computer, Communication and Control, Beijing, China, 21–23 October 2011; pp. 737–739. [Google Scholar]
- Roberton, M.; Brown, E.R. Integrated radar and communications based on chirped spread-spectrum techniques. In Proceedings of the 2003 IEEE MTT-S International Microwave Symposium Digest, Philadelphia, PA, USA, 8–13 June 2003; Volume 1, pp. 611–614. [Google Scholar]
- Nusenu, S.Y.; Wang, W.Q.; Chen, H. Dual-Function MIMO Radar-Communications Employing Frequency-Hopping Chirp Waveforms. Prog. Electromagn. Res. 2018, 64, 135–146. [Google Scholar] [CrossRef]
- Aubry, A.; Carotenuto, V.; De Maio, A.; Farina, A.; Pallotta, L. Optimization theory-based radar waveform design for spectrally dense environments. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 14–25. [Google Scholar] [CrossRef]
- Huang, Y.; Piezzo, M.; Carotenuto, V.; De Maio, A. Radar waveform design under similarity, bandwidth priority, and spectral coexistence constraints. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1142–1147. [Google Scholar]
- Aubry, A.; Carotenuto, V.; De Maio, A. Radar waveform design with multiple spectral compatibility constraints. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Qian, J.; Lops, M.; Zheng, L.; Wang, X.; He, Z. Joint System Design for Coexistence of MIMO Radar and MIMO Communication. IEEE Trans. Signal Process. 2018, 66, 3504–3519. [Google Scholar] [CrossRef]
- Tang, B.; Naghsh, M.M.; Tang, J. Relative Entropy-Based Waveform Design for MIMO Radar Detection in the Presence of Clutter and Interference. IEEE Trans. Signal Process. 2015, 63, 3783–3796. [Google Scholar] [CrossRef]
- Zhu, Z.; Kay, S.; Raghavan, R.S. Information-Theoretic Optimal Radar Waveform Design. IEEE Signal Process. Lett. 2017, 24, 274–278. [Google Scholar] [CrossRef]
- Setlur, P.; Devroye, N. Adaptive waveform scheduling in radar: An information theoretic approach. Proc. SPIE 2012, 8361, 836103. [Google Scholar]
- Ravenscroft, B.; Owen, J.W.; Jakabosky, J.; Blunt, S.D.; Martone, A.F.; Sherbondy, K.D. Experimental demonstration and analysis of cognitive spectrum sensing and notching for radar. IET Radar Sonar Navig. 2018, 12, 1466–1475. [Google Scholar] [CrossRef]
- Nijsure, Y.; Chen, Y.; Yuen, C.; Chew, Y.H. Location-Aware Spectrum and Power Allocation in Joint Cognitive Communication-Radar Networks. In Proceedings of the Sixth International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM), Osaka, Japan, 1–3 June 2011; pp. 171–175. [Google Scholar]
- Kirk, B.H.; Narayanan, R.M.; Gallagher, K.A.; Martone, A.F.; Sherbondy, K.D. Avoidance of Time-Varying Radio Frequency Interference With Software-Defined Cognitive Radar. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1090–1107. [Google Scholar] [CrossRef]
- Palamà, R.; Griffiths, H.; Watson, F. Joint dynamic spectrum access and target-matched illumination for cognitive radar. IET Radar Sonar Navig. 2019, 13, 750–759. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Piezzo, M.; Naghsh, M.M.; Soltanalian, M.; Stoica, P. Cognitive Radar Waveform Design for Spectral Coexistence in Signal-Dependent Interference. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 474–478. [Google Scholar]
- Huang, K.W.; Bică, M.; Mitra, U.; Koivunen, V. Radar waveform design in spectrum sharing environment: Coexistence and cognition. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 1698–1703. [Google Scholar]
- Nijsure, Y.; Chen, Y.; Boussakta, S.; Yuen, C.; Chew, Y.H.; Ding, Z. Novel System Architecture and Waveform Design for Cognitive Radar Radio Networks. IEEE Trans. Veh. Technol. 2012, 61, 3630–3642. [Google Scholar] [CrossRef]
- Baylis, C.; Egbert, A.; Alcala-Medel, J.; Dockendorf, A.; Calabrese, C.; Langley, E.; Martone, A.; Gallagher, K.; Viveiros, E.; Peroulis, D.; et al. Reconfigurable and Adaptive Radar Amplifiers for Spectrum Sharing in Cognitive Radar. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–3. [Google Scholar]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Woodward, P. Information Theory and the Design of Radar Receivers. Proc. IRE 1951, 39, 1521–1524. [Google Scholar] [CrossRef]
- Bell, M.R. Information Theory and Radar Waveform Design. IEEE Trans. Inf. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef]
- Guo, D.; Shamai, S.; Verdú, S. The Interplay Between Information and Estimation Measures; Foundations and Trends in Signal Processing; Now Publishers Inc.: Hanover, MA, USA, 2012; Volume 6, pp. 243–429. [Google Scholar]
- Tian, T.; Zhang, T.; Kong, L.; Cui, G.; Wang, Y. Mutual Information based Partial Band Coexistence for Joint Radar and Communication System. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–5. [Google Scholar]
- Khawar, A.; Abdel-Hadi, A.; Clancy, T.C. Spectrum sharing between S-band radar and LTE cellular system: A spatial approach. In Proceedings of the IEEE International Symposium on Dynamic Spectrum Access Networks (DYSPAN), McLean, VA, USA, 1–4 April 2014; pp. 7–14. [Google Scholar]
- Sodagari, S.; Khawar, A.; Clancy, T.C.; McGwier, R. A Projection Based Approach for Radar and Telecommunication Systems Coexistence. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 5010–5014. [Google Scholar]
- Shajaiah, H.; Abdelhadi, A.; Clancy, C. Spectrum Sharing Approach between Radar and Communication Systems and its Impact on Radar’s Detectable Target Parameters. In Proceedings of the IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–6. [Google Scholar]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO communications with MIMO radar: From co-existence to joint transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- Zhang, W.; Vedantam, S.; Mitra, U. Joint Transmission and State Estimation: A Constrained Channel Coding Approach. IEEE Trans. Inf. Theory 2011, 57, 7084–7095. [Google Scholar] [CrossRef]
- Stinco, P.; Greco, M.; Gini, F.; Himed, B. Channel parameters estimation for cognitive radar systems. In Proceedings of the 2014 4th International Workshop on Cognitive Information Processing (CIP), Copenhagen, Denmark, 26–28 May 2014; pp. 1–6. [Google Scholar]
- Pezeshki, A.; Calderbank, A.R.; Moran, W.; Howard, S.D. Doppler Resilient Golay Complementary Waveforms. IEEE Trans. Inf. Theory 2008, 54, 4254–4266. [Google Scholar] [CrossRef]
- Li, B.; Petropulu, A. MIMO radar and communication spectrum sharing with clutter mitigation. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. A dual function radar-communications system using sidelobe control and waveform diversity. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 1260–1263. [Google Scholar]
- Ahmed, A.; Zhang, Y.D.; Himed, B. Distributed Dual-Function Radar-Communication MIMO System with Optimized Resource Allocation. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–5. [Google Scholar]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F.; Himed, B. Non-coherent PSK-based dual-function radar-communication systems. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Dokhanchi, S.H.; Shankar, M.B.; Nijsure, Y.A.; Stifter, T.; Sedighi, S.; Ottersten, B. Joint automotive radar-communications waveform design. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–7. [Google Scholar]
- Dokhanchi, S.H.; Mysore, B.S.; Mishra, K.V.; Ottersten, B. A mmWave Automotive Joint Radar-Communications System. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1241–1260. [Google Scholar] [CrossRef]
- Dokhanchi, S.H.; Bhavani Shankar, M.R.; Mishra, K.V.; Stifter, T.; Ottersten, B. Performance Analysis of mmWave Bi-static PMCW-based Automotive Joint Radar-Communications System. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Bliss, D.W.; Govindasamy, S. Adaptive Wireless Communications: MIMO Channels and Networks; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Gallager, R.G. Information Theory and Reliable Communication, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Chiriyath, A.R.; Ragi, S.; Mittelmann, H.D.; Bliss, D.W. Novel Radar Waveform Optimization for a Cooperative Radar-Communications System. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1160–1173. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory, 1st ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Paul, B.; Bliss, D.W. Extending Joint Radar-Communications Bounds for FMCW Radar with Doppler Estimation. In Proceedings of the IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 89–94. [Google Scholar]
- Van Trees, H. Detection, Estimation, and Modulation Theory: Part 1, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Richards, M.A. Principles of Modern Radar: Basic Principles; SciTech Publishing: Raleigh, NC, USA, 2010. [Google Scholar]
- Mathworks. MATLAB’s fmincon. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html?requestedDomain=www.mathworks.com (accessed on 15 November 2019).



| Variable | Description |
|---|---|
| Expectation | |
| L2-norm or absolute value | |
| Marcum Q-function | |
| Dirac-delta function | |
| f | Frequency |
| t | Time |
| B | Full bandwidth of the system |
| Root-mean-squared radar bandwidth | |
| Unit-variance transmitted radar signal | |
| Radar signal frequency response | |
| Radar power | |
| Time delay to target | |
| a | Target complex combined antenna, cross-section, and propagation gain |
| T | Radar pulse duration |
| Radar duty factor | |
| Total communications power | |
| Optimal communications transmit distribution | |
| b | Complex combined antenna gain and communications propagation loss |
| Receiver thermal noise | |
| Post-SIC radar residual | |
| Thermal noise power | |
| Boltzmann constant | |
| Absolute temperature | |
| Variance of range fluctuation process | |
| Cramèr-Rao lower bound or estimation error variance | |
| Integrated radar SNR |
| Parameter | Value |
|---|---|
| Bandwidth (B) | 5 MHz |
| Center frequency | 3 GHz |
| Effective temperature () | 1000 K |
| Communications range | 10 km |
| Communications power () | 1 W |
| Communications antenna Gain | 20 dBi |
| Communications receiver Side-lobe Gain | 10 dBi |
| Radar target range | 11.2 km |
| Radar antenna gain | 30 dBi |
| Radar power () | 1 kW |
| Target cross section | 10 m2 |
| Target process standard deviation () | 100 m |
| Time–bandwidth product () | 128 |
| Radar duty factor () | 0.01 |
| Performance Metric (Average Values) | CW Spectral-Mask Shaping | Spectral-Mask Shaping |
|---|---|---|
| Final objective value | ||
| (b/s) | ||
| (b/s) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiriyath, A.R.; Ragi, S.; Mittelmann, H.D.; Bliss, D.W. Radar Waveform Optimization for Joint Radar Communications Performance. Electronics 2019, 8, 1498. https://doi.org/10.3390/electronics8121498
Chiriyath AR, Ragi S, Mittelmann HD, Bliss DW. Radar Waveform Optimization for Joint Radar Communications Performance. Electronics. 2019; 8(12):1498. https://doi.org/10.3390/electronics8121498
Chicago/Turabian StyleChiriyath, Alex R., Shankarachary Ragi, Hans D. Mittelmann, and Daniel W. Bliss. 2019. "Radar Waveform Optimization for Joint Radar Communications Performance" Electronics 8, no. 12: 1498. https://doi.org/10.3390/electronics8121498
APA StyleChiriyath, A. R., Ragi, S., Mittelmann, H. D., & Bliss, D. W. (2019). Radar Waveform Optimization for Joint Radar Communications Performance. Electronics, 8(12), 1498. https://doi.org/10.3390/electronics8121498






