Analysis of an SDN-Based Cooperative Caching Network with Heterogeneous Contents
Abstract
1. Introductione
1.1. Related Work
1.2. Contributions and Outcomes
- With consideration of the content heterogeneity, we model the content attributes as [file popularity, MU preference, file size], where file popularity denotes the global probability that the file will be requested in the network, the MU preference for file category is the local probability for which category the MU prefers, and the file size represents the scale heterogeneity. Based on these definitions, we define a new local file block library and calculate the local popularity of each file block.
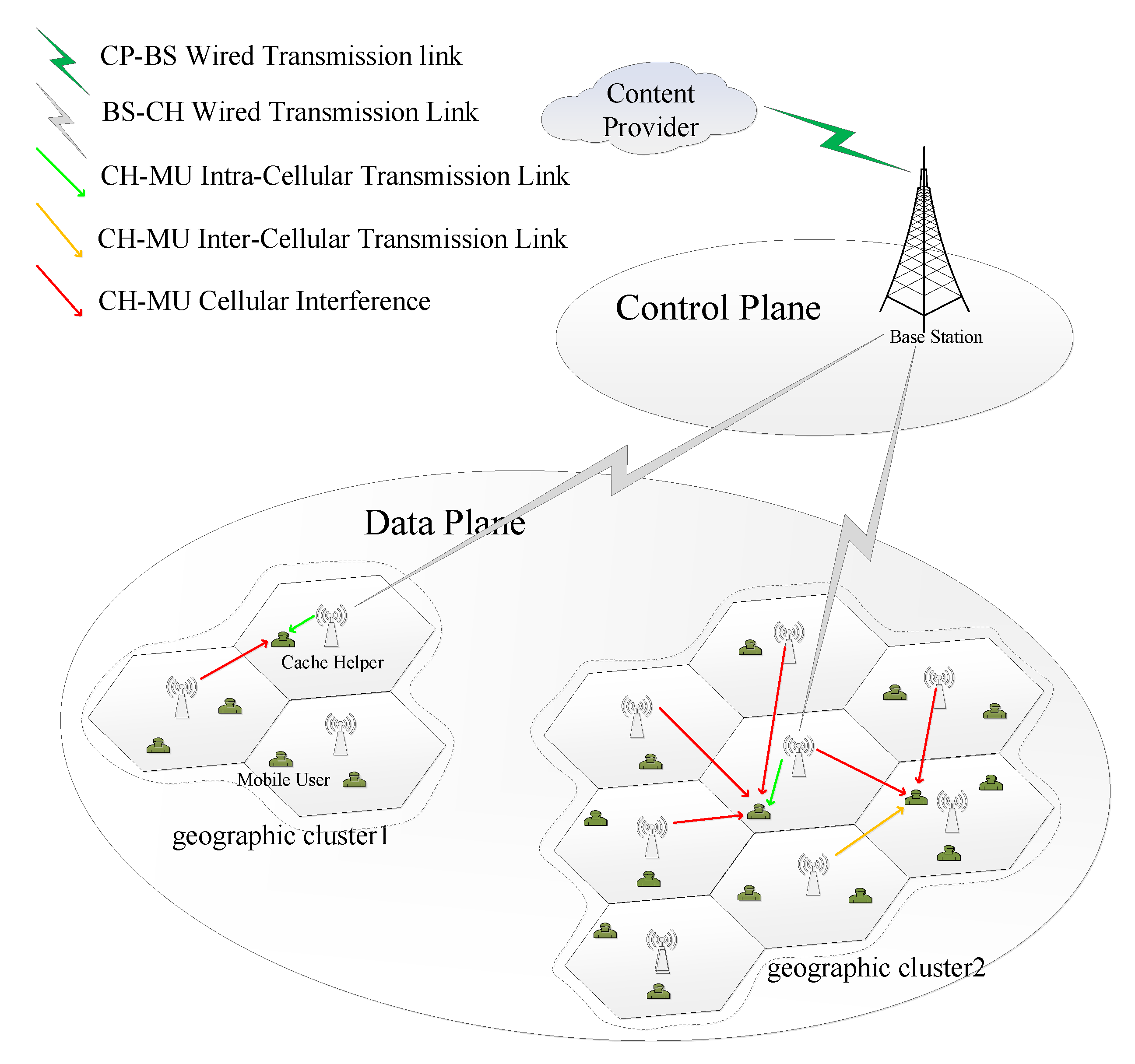
- We proposed an SDN-based three-tier network. In the base station tier (BS-Tier), the BS centered at the macrocell supplies the entire cell with control coverage. In the cache helper tier (CH-tier) and mobile user tier (MU-tier) with cache capacity, CHs distributed in the center of hexagonal grids and randomly distributed MUs supply data coverage together. Taking the ‘most popular content’ (MPC) and ‘largest diversity content’ (LDC) into consideration synthetically, a distributed cooperative caching strategy is proposed in which the caches of the MUs store the most popular blocks in the file block library to mitigate the effect of MU mobility and those of the CHs store the remainder in a probabilistic caching manner to enrich the diversity of stored contents and reduce the MU caching pressure.
- Based on the above caching system, we derive the request meet probability (RMPro) and obtain the optimal caching distribution of the contents in a probabilistic caching manner via RMPro optimization. Using the optimization result, we also analyze the content retrieval delays that occur when a typical MU requests a file block or a whole file. A key intermediate step in the analysis is the derivation of the SINR distribution.
2. System Model
2.1. Heterogeneous Content Model
2.2. Caching Network Architecture
2.3. Cooperative Cache Placement Strategy
- Local-Cache-provide: If the requested file block belongs to the first in the local file block library, the typical MU can obtain it directly from its local cache without any delay.
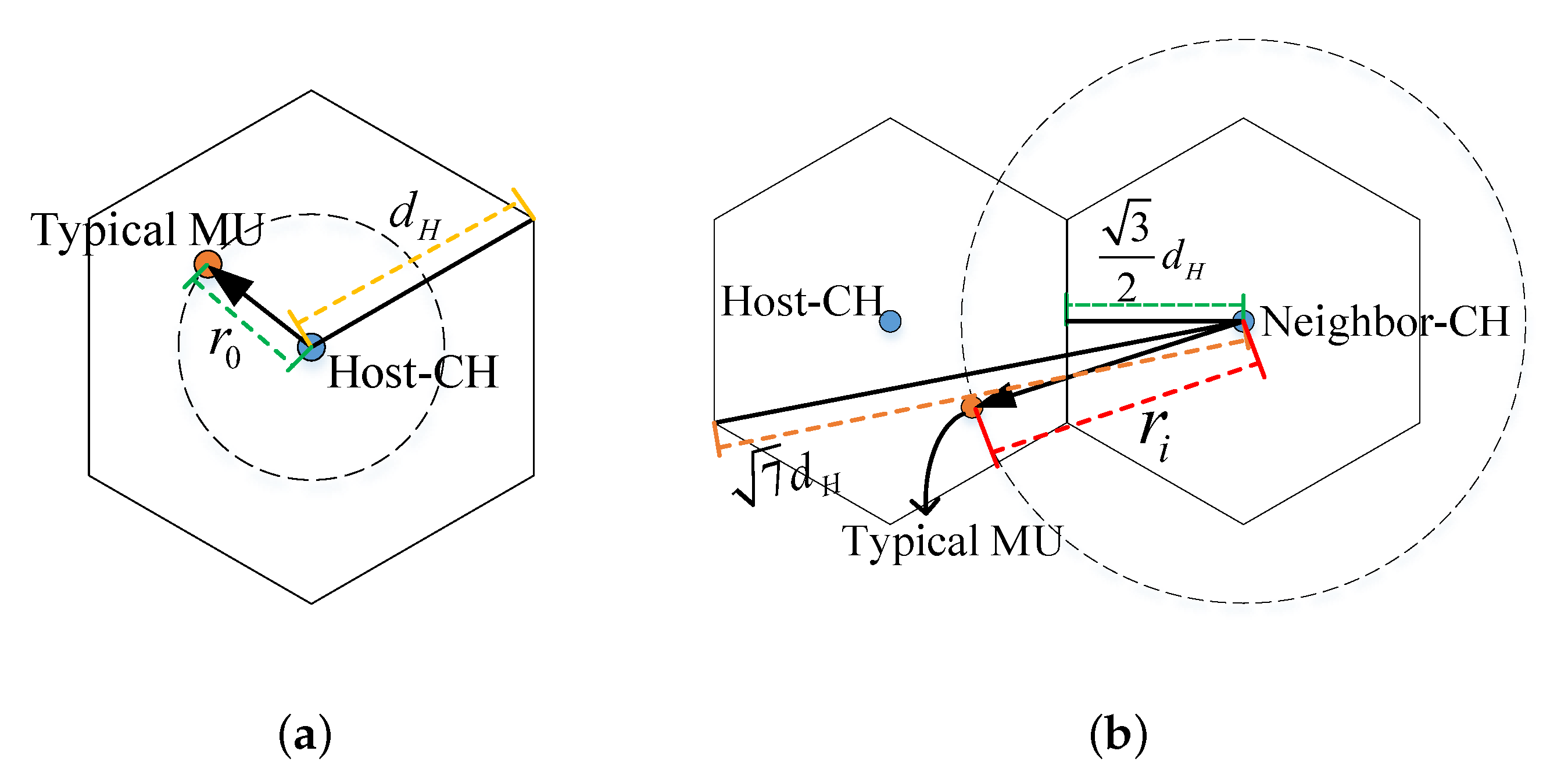
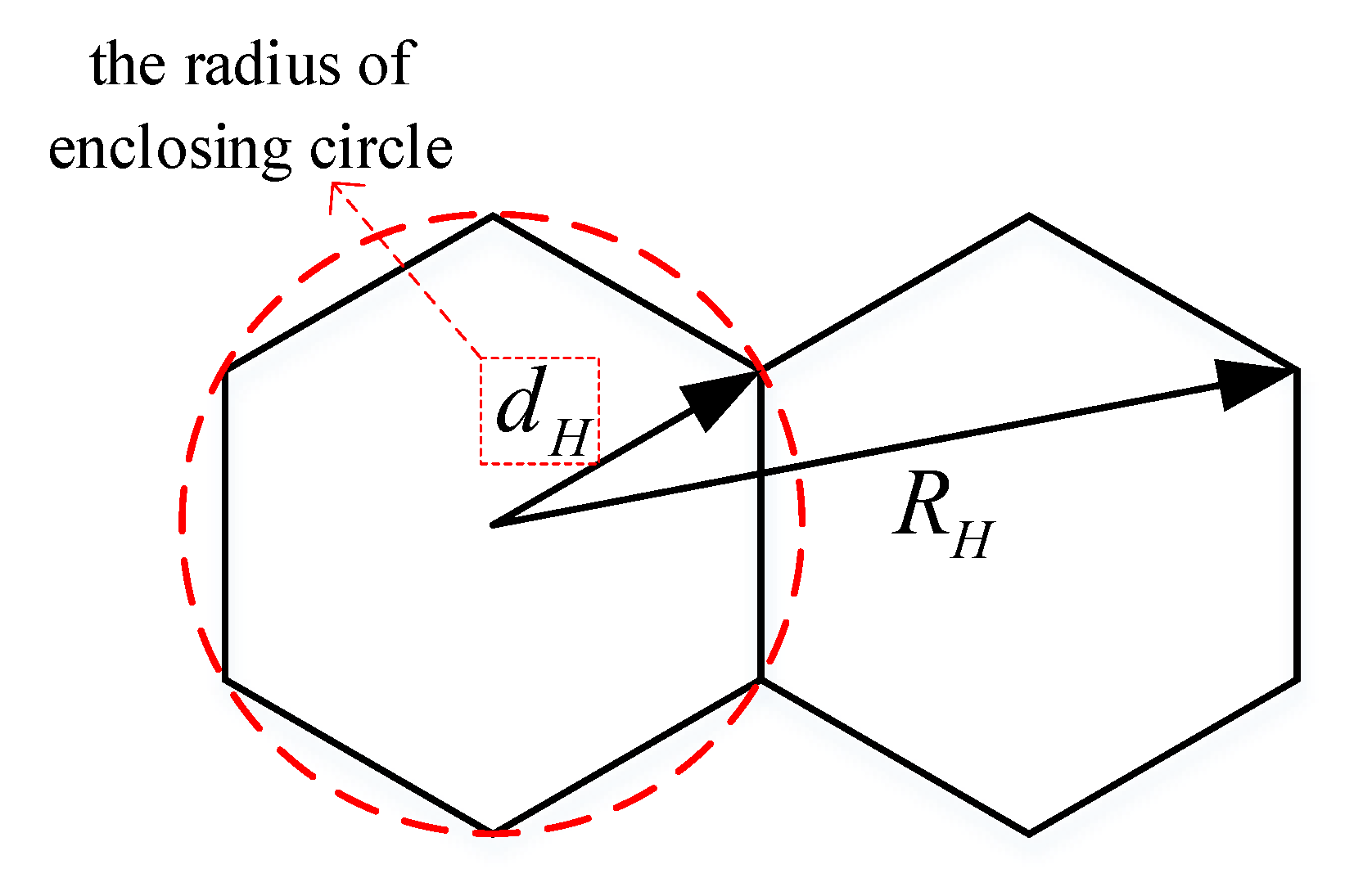
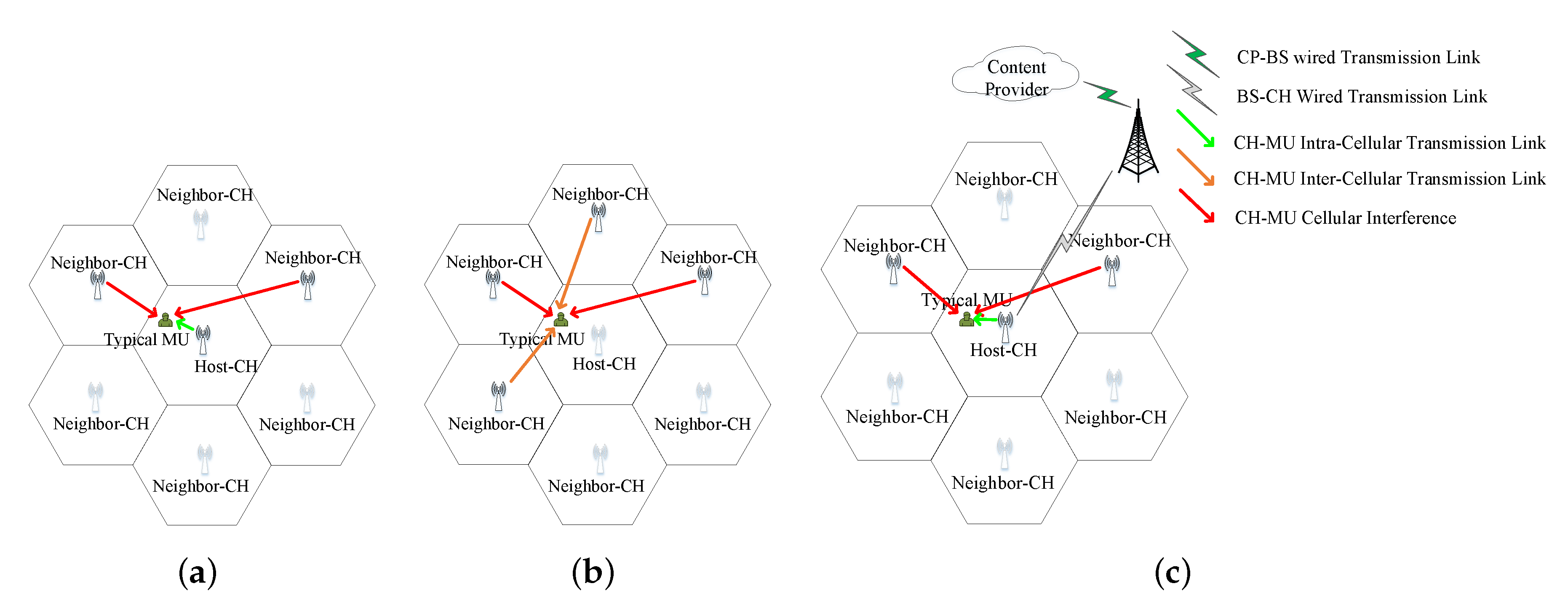
- Host-CH-provide: If the popularity order of the requested file block ranges from to in the local file block library, it might be stored in the host-CH or neighbor-CHs. If it is stored in the host-CH, the block can be obtained from the host-CH through the CH-MU intra-cellular transmission link with a delay time. Considering that it is impossible that all CHs are always idle and waiting to send requested contents, let () denote the proportion of active CHs. Because the communication range is larger than the microcell radius , there is a probability of CH-MU cellular interference from one of the six neighbor-CHs.
- Neighbor-CH-provide: The popularity order of the requested file block also ranges from to , but it is cached in the neighbor-CHs instead, and thus, it can be obtained from certain neighbor-CHs through the CH-MU inter-cellular transmission link with delay. The probability exists that CH-MU cellular interference comes from one of the remaining neighbor-CHs.
- CP-BS-provide: When the content request cannot be met in the above three ways, the BS should obtain the contents from CP and transmit it to the host-CH via a wired link with a constant delay . The host-CH retransmits the contents to typical MU.
2.4. Delivery Model
3. Performance Metrics and Problem Formulation
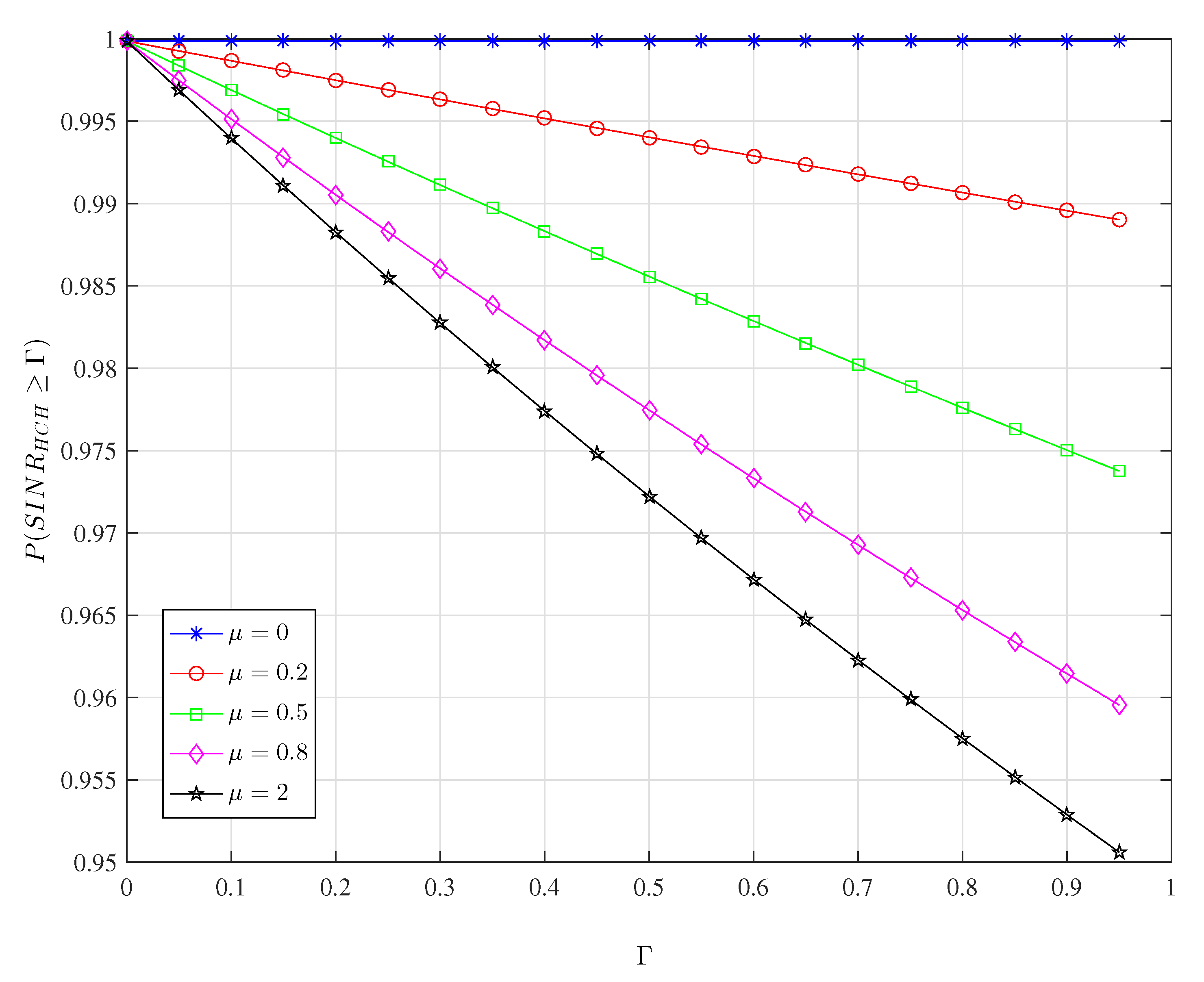
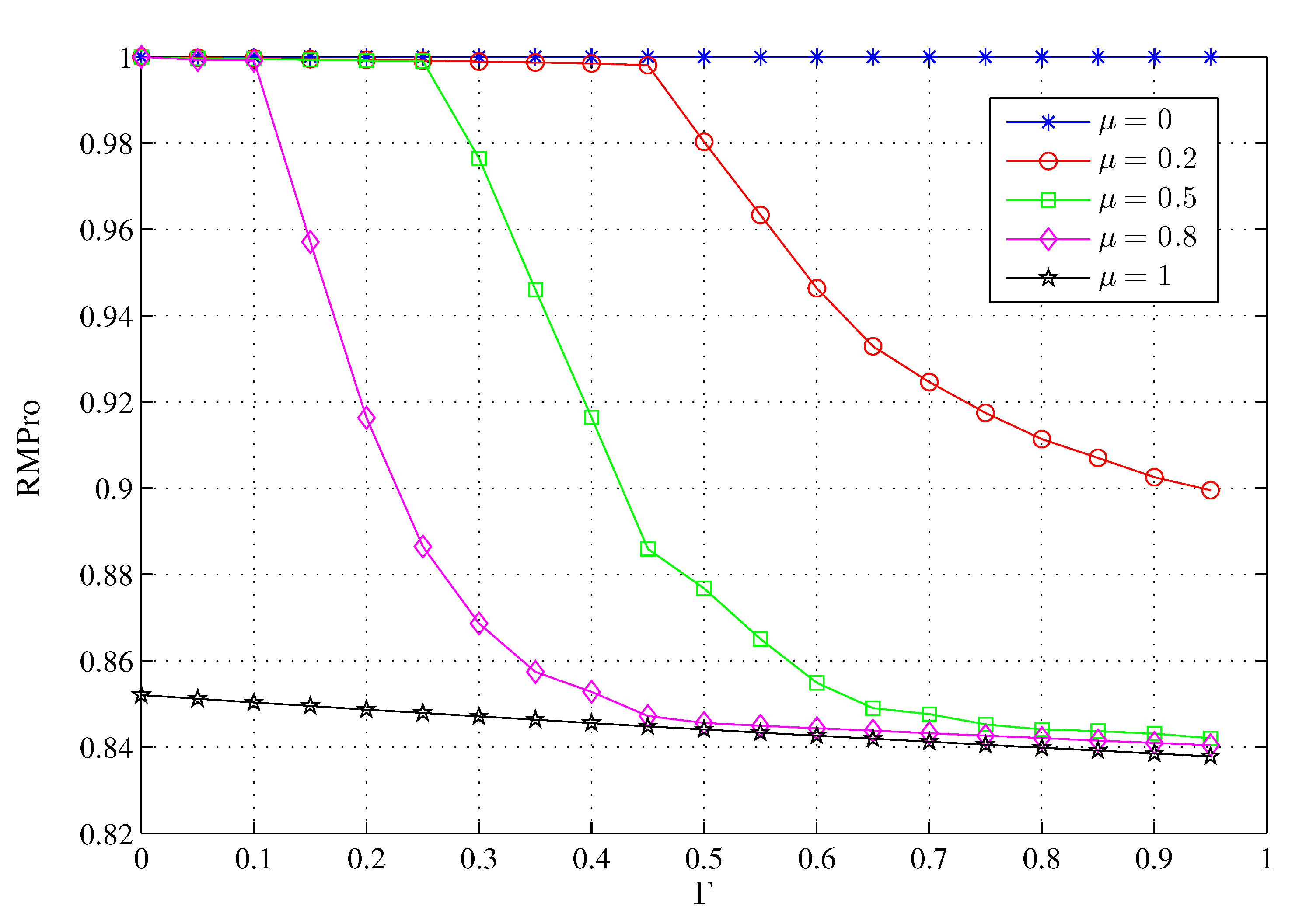
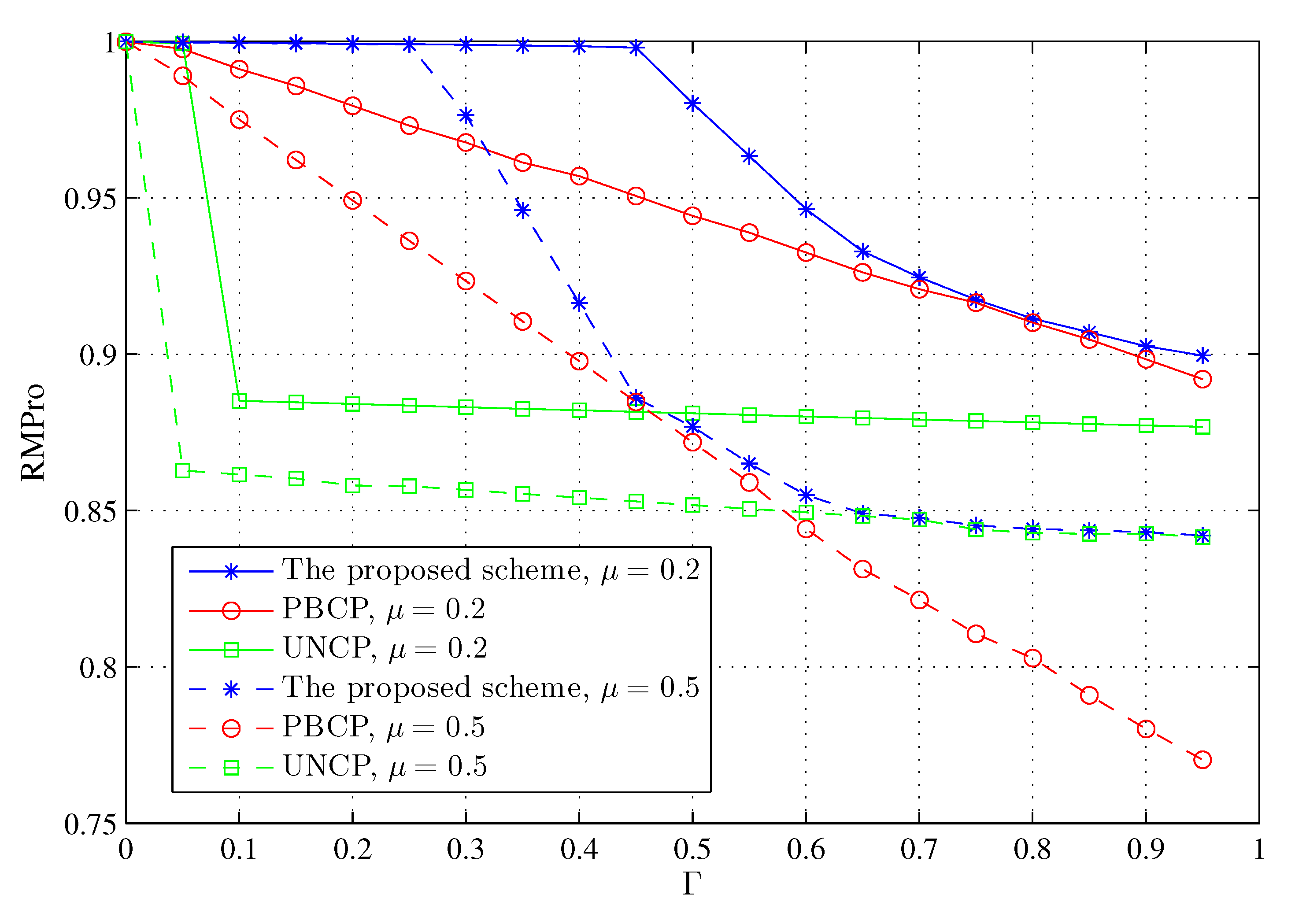
3.1. Request Meet Probability
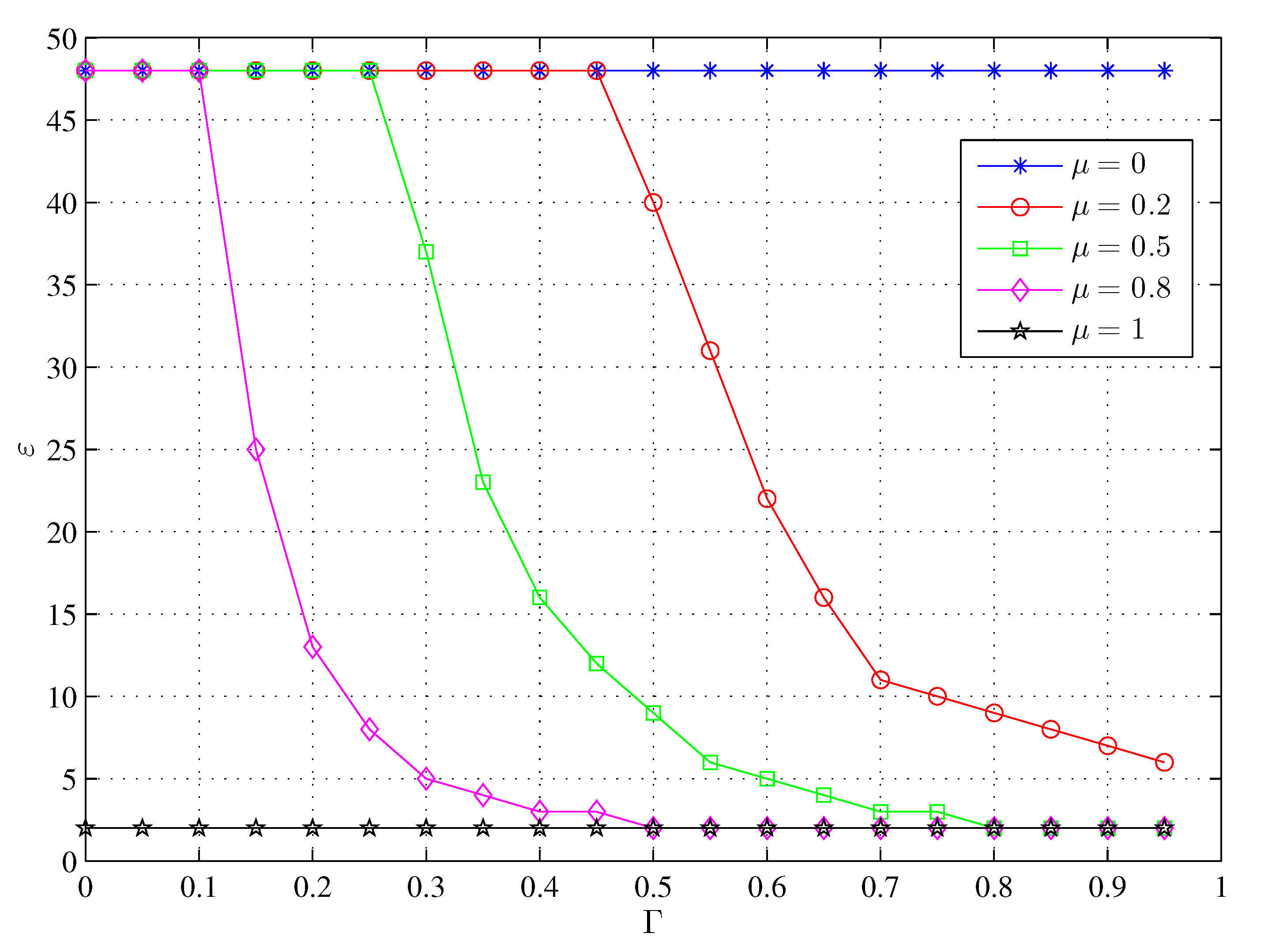
3.2. Problem Formulation
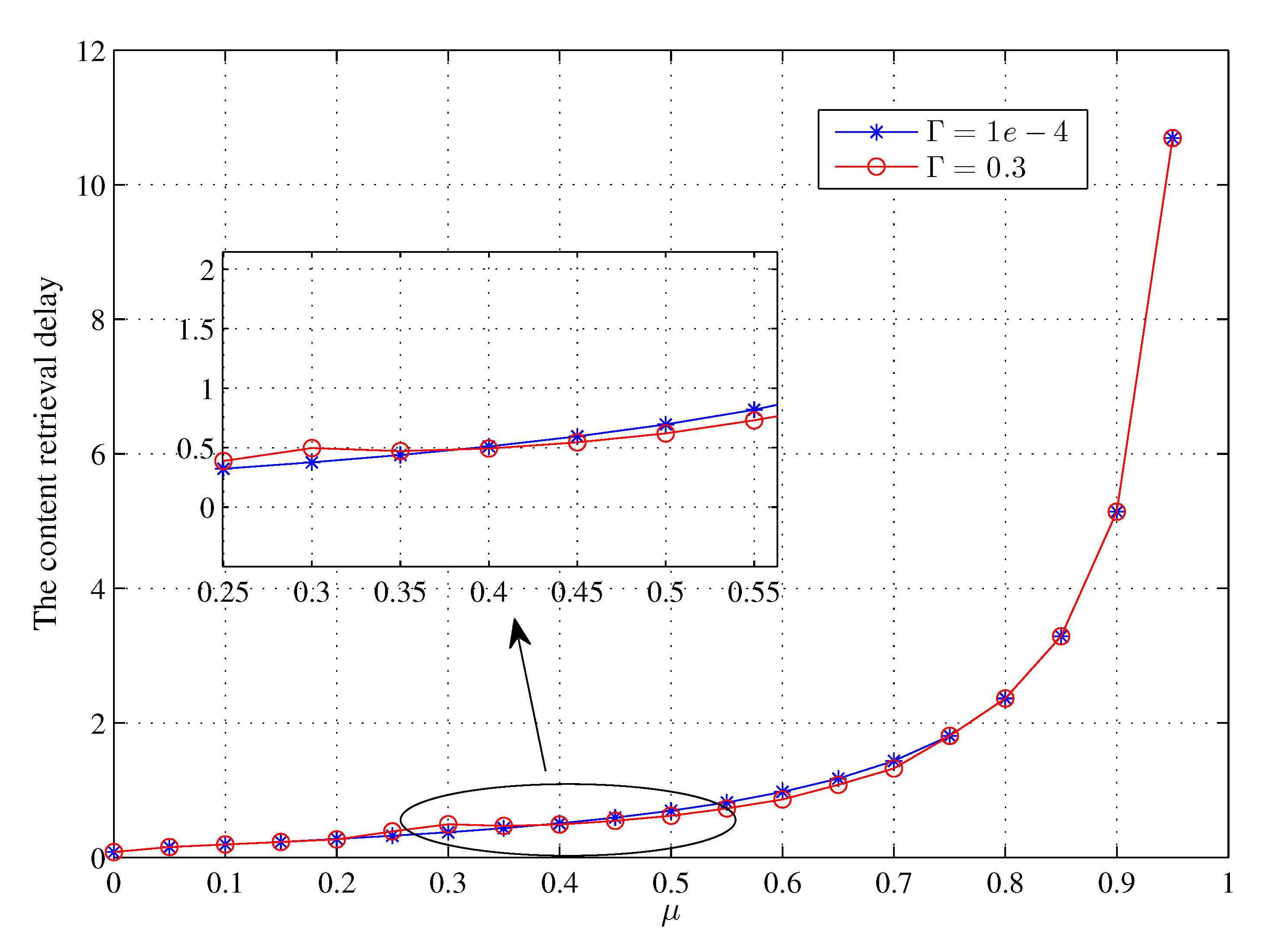
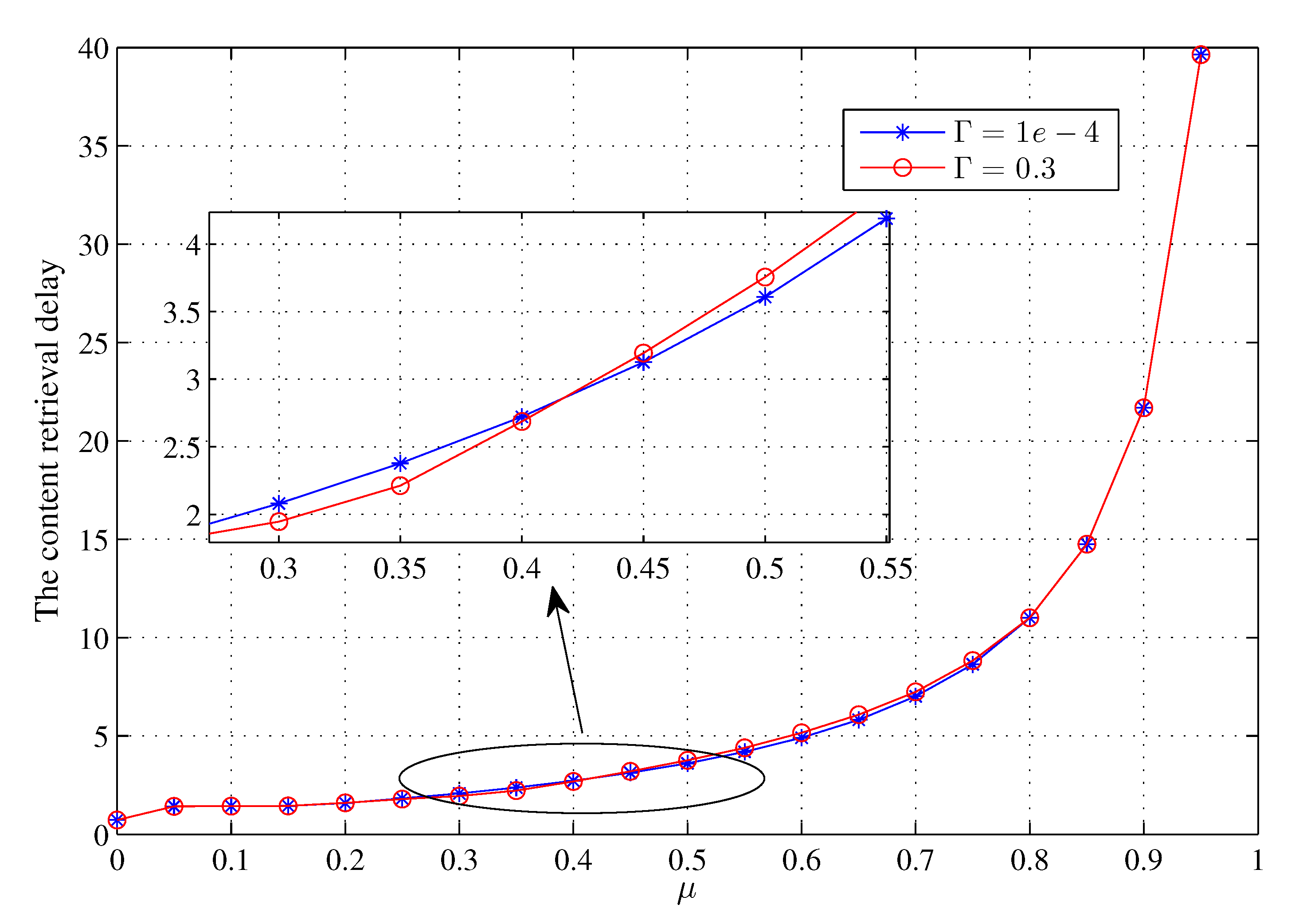
4. Analysis of the Content Retrieval Delay
4.1. Content Retrieval Delay Of Request For A File Block
- When the requested file block is stored in the local cache of typical MU, it is assumed that the transmission rate is infinite, and the delay time tends to be 0, i.e.,
- When the requested file block is obtained in the manner of Host-CH-provide, the delay time iswhere is the average transmission rate when the host-CH is the transmitter and certain neighbor-CHs act as interference-makers, W is the transmission bandwidth of CH and is the mean of ∗.
- When the requested file block is transmitted to the typical MU by Neighbor-CH-provide, the delay time iswhere is the average transmission rate while the neighbor-CHs are not only transmitters but interference-makers.
- When the requested file block is supplied by CP-BS-provide, the delay time includes two components. One component is the time spent on the transmission from CP to the host-CH via the BS, which is assumed as a constant value , and the other is the transmission time from the host-CH to the typical MU, which is the same as .Combining the four cases, the content retrieval delay of a random request for a file block is
4.2. Content Retrieval Delay of Request for a Whole File
5. Performance Evaluation
5.1. Simulation Setup
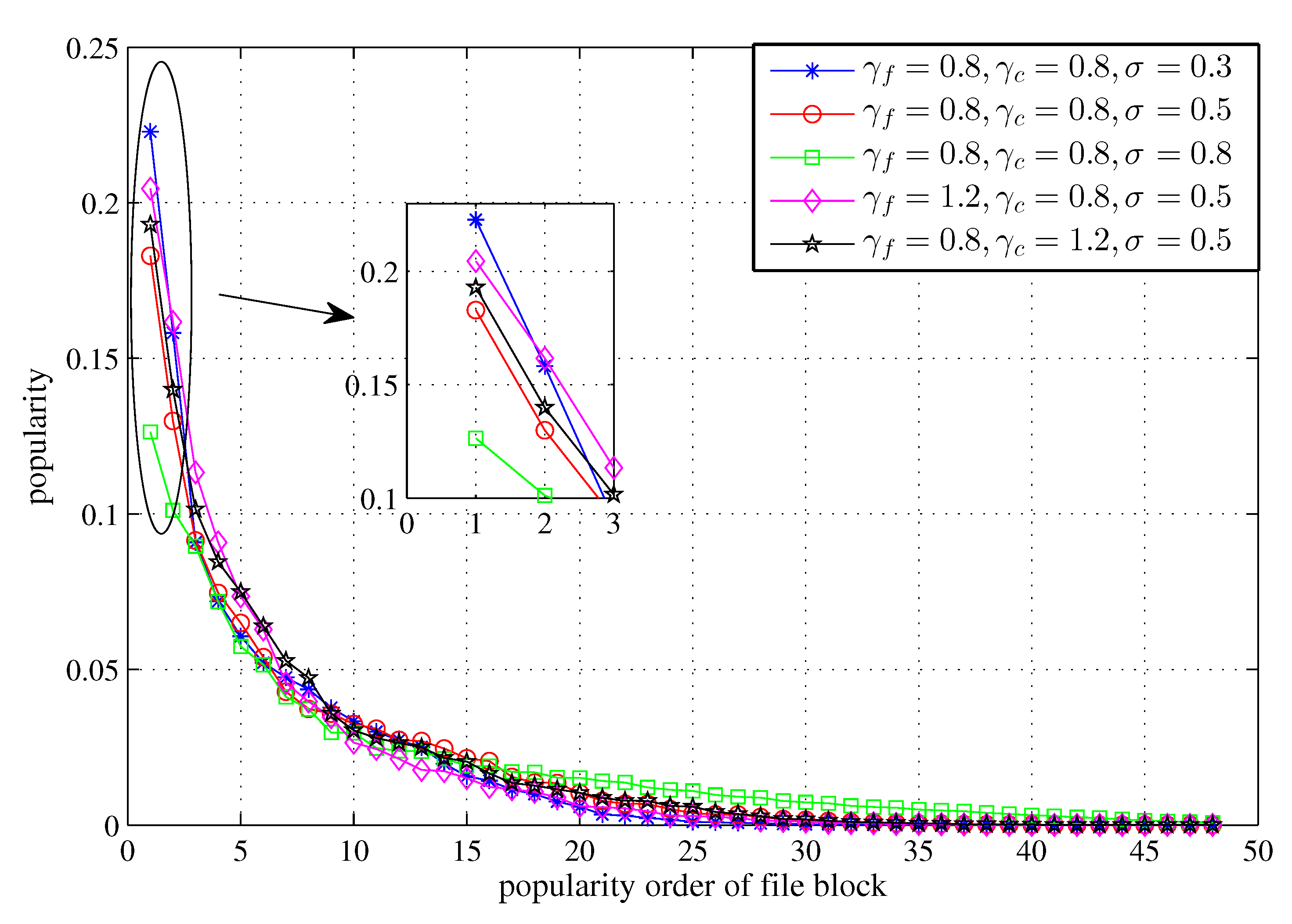
5.2. Simulation Result And Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SDN | Software-Defined Network |
| MU | Mobile User |
| CH | Cache Helper |
| RMPro | Request Meet Probability |
| BS | Base Station |
| QoE | Quality of Experience |
| D2D | Device-to-Device |
| SBS | Small-BS |
| F-RAN | Fog Ratio Access Network |
| PPP | Poisson Point Processe |
| SINR | Signal to Interference plus Noise Ratio |
| BS-Tier | Base Station Tier |
| CH-Tier | Cache Helper Tier |
| MU-Tier | Mobile User Tier |
| MPC | Most Popular Content |
| LDC | Largest Diversity Content |
| CP | Content Provider |
| Probability Density Function | |
| PBCP | Popularity-Based Caching Policy |
| UNCP | UNiform Caching Policy |
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
Appendix C. Proof of Lemma 3
Appendix D. Proof of Lemma 4
References
- CISCO. CISCO Visual Networking Index: Global Mobile Data Traffic Forcast Update, 2015–2020. Available online: https://www.cisco.com/c/dam/m/en_in/innovation/enterprise/assets/mobile-white-paper-c11-520862.pdf (accessed on 14 October 2019).
- Deng, N.; Haenggi, M. The benefits of hybrid caching in Gauss–Poisson D2D networks. IEEE J. Sel. Areas Commun. 2018, 36, 1217–1230. [Google Scholar] [CrossRef]
- Bąstug, E.; Bennis, M.; Debbah, M. Living on the edge: The role of proactive caching in 5G wireless networks. IEEE Commun. Mag. 2014, 52, 82–89. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.; Taleb, T.; Ksentini, A.; Leung, V. Cache in the air: Exploiting content caching and delivery techniques for 5G systems. IEEE Trans. Commun. Mag. 2014, 52, 131–139. [Google Scholar] [CrossRef]
- Lei, L.; Xiong, X.; Hou, L.; Zheng, K. Collaborative edge caching through service function chaining: Architecture and challenges. IEEE Wirel. Commun. 2018, 25, 94–102. [Google Scholar] [CrossRef]
- Song, J.; Song, H.; Choi, W. Optimal caching placement of caching system with helpers. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1825–1830. [Google Scholar]
- Blaszczyszyn, B.; Giovanidis, A. Optimal geographic caching in cellular networks. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015. [Google Scholar]
- Bastug, E.; Bennis, M.; Debbah, M. Cache-enabled small cell networks: Modeling and tradeoffs. In Proceedings of the 2014 11th International Symposium on Wireless Communications Systems (ISWCS), Barcelona, Spain, 26–29 August 2014; pp. 649–653. [Google Scholar]
- Chae, S.H.; Ryu, J.Y.; Quek, T.Q.S.; Choi, W. Cooperative transmission via caching helpers. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015. [Google Scholar]
- Li, J.; Chen, Y.; Lin, Z.; Chen, W.; Vucetic, B.; Hanzo, L. Distributed caching for data dissemination in the downlink of heterogeneous networks. IEEE Trans. Commun. 2015, 63, 3553–3568. [Google Scholar] [CrossRef]
- Shanmugam, K.; Golrezaei, N.; Dimakis, A.G.; Molisch, A.F.; Caire, G. Femtocaching: Wireless content delivery through distributed caching helpers. IEEE Trans. Inform. Theory 2012, 59, 8402–8413. [Google Scholar] [CrossRef]
- Chen, Z.; Lee, J.; Quek, T.Q.S.; Kountouris, M. Cooperative caching and transmission design in cluster-centric small cell networks. IEEE Trans. Wirel. Commun. 2017, 16, 3401–3415. [Google Scholar] [CrossRef]
- Afshang, M.; Dhillon, H.S.; Chong, P.H.J. Modeling and performance analysis of clustered device-to-device networks. IEEE Trans. Wirel. Commun. 2016, 15, 4957–4972. [Google Scholar] [CrossRef]
- Golrezaei, N.; Mansourifard, P.; Molisch, A.F.; Dimakis, A.G. Base-station assisted device-to-device communications for high-throughput wireless video networks. IEEE Trans. Wirel. Commun. 2014, 13, 3665–3676. [Google Scholar] [CrossRef]
- Chen, Z.; Pappas, N.; Kountouris, M. Probabilistic caching in wireless D2D networks: Cache hit optimal versus throughput optimal. IEEE Commun. Lett. 2017, 21, 584587. [Google Scholar] [CrossRef]
- Golrezaei, N.; Dimakis, A.G.; Molisch, A.F. Scaling behavior fo device-to-device communications with distributed caching. IEEE Trans. Inform. Theory 2014, 60, 4286–4298. [Google Scholar] [CrossRef]
- Amer, R.; Butt, M.M.; Bennis, M.; Marchetti, N. Inter-Cluster Cooperation for Wireless D2D Caching Networks. IEEE Trans. Wirel. Commun. 2018, 17, 6108–6121. [Google Scholar] [CrossRef]
- Yang, C.; Yao, Y.; Chen, Z.; Xia, B. Analysis on cache-enabled wireless heterogeneous networks. IEEE Trans. Wirel. Commun. 2016, 15, 131–145. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z.; Liu, H. Push-based wireless converged networks for massive multimedia content delivery. IEEE Trans. Wirel. Commun. 2014, 13, 2894–2905. [Google Scholar]
- Wang, R.; Hajiaghajani, F.; Biswas, S. Incentive Based Cooperative Content Caching in Social Wireless Networks. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Jiang, Y.; Ma, M.; Bennis, M.; Zheng, F.; You, X. User Preference Learning Based Edge Caching for Fog Radio Access Network. IEEE Trans. Commun. 2019, 67, 1268–1283. [Google Scholar] [CrossRef]
- Peng, A.; Jiang, Y.; Bennis, M.; Zheng, F.C.; You, X. Performance analysis and caching design in fog radio access networks. In Proceedings of the IEEE Globecom Workshops, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Baek, J.; Kaddoum, G.; Garg, S.; Kaur, K.; Gravel, V. Managing Fog Networks using Reinforcement Learning Based Load Balancing Algorithm. In Proceedings of the IEEE 2019 IEEE WCNC, Marrakech, Morocco, 15–19 April 2019. [Google Scholar]
- Wang, R.; Li, R.; Wang, P.; Liu, E. Analysis and Optimization of Caching in Fog Radio Access Networks. IEEE Trans. Veh. Technol. 2019, 68, 8279–8283. [Google Scholar] [CrossRef]
- Rao, J.; Feng, H.; Yang, C.; Chen, Z.; Xia, B. Optimal caching placement for D2D assisted wireless caching networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016. [Google Scholar]
- Zhuang, Y.; Luo, Y.; Cai, L.; Pan, J. A geometric probability model for capacity analysis and interference estimation in wireless mobile cellular systems. In Proceedings of the Global Telecommunications Conference 2011 (GLOBECOM 2011), Kathmandu, Nepal, 5–9 December 2011. [Google Scholar]
- Zhang, Y.; Wang, X.; Wang, D.; Zhang, Y.; Lan, Y. BER Performance of Multicast SCMA Systems. IEEE Wirel. Commun. Lett. 2018, 8, 1073–1076. [Google Scholar] [CrossRef]
- Cohen, H. Numerical Approximation Methods; Springer: New York, NY, USA, 2011. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 6th ed.; Academic Press: New York, NY, USA, 2000. [Google Scholar]
| Parameters | Values |
|---|---|
| Number of files in the library (L) | 10 |
| Number of file categories in the library (K) | 3 |
| The Zipf distribution coefficient of global file popularity () | 0.8, 1.2 (default) |
| The Zipf distribution coefficient of local file category popularity () | 0.8 (default), 1.2 |
| The transition probability between two adjacent file blocks () | 0.3, 0.5 (default), 0.8 |
| The exponential distribution coefficient of file scale distribution () | 4 |
| Size of file blocks in the library (M) | 5 (Mbit) |
| Number of file blocks in the library () | 48 |
| Parameters | Values |
|---|---|
| Number of file blocks that can be cached in the CH cache () | 5 |
| Number of file blocks that can be cached in the MU cache () | 2 |
| The density of MU PPP distribution () | |
| The communication range of CH () | 100 (m) |
| The radius of microcell () | (m) |
| The proportion of active CHs () | 1 , 0.2, 0.5, 0.8, 1 |
| The pathloss coefficient () | 4 |
| The SINR threshold () | 1 , 0.3 |
| The transmission power of CH () | 0.2 (W) |
| The bandwidth of CH transmission (W) | 1 (Mbps) |
| The transmission time from CP to host-CH via BS () | 5 (s) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, X.; Wang, D.; Zhang, Y.; Lan, Y.; Liu, Q.; Song, L. Analysis of an SDN-Based Cooperative Caching Network with Heterogeneous Contents. Electronics 2019, 8, 1491. https://doi.org/10.3390/electronics8121491
Li Q, Wang X, Wang D, Zhang Y, Lan Y, Liu Q, Song L. Analysis of an SDN-Based Cooperative Caching Network with Heterogeneous Contents. Electronics. 2019; 8(12):1491. https://doi.org/10.3390/electronics8121491
Chicago/Turabian StyleLi, Qi, Xiaoxiang Wang, Dongyu Wang, Yibo Zhang, Yanwen Lan, Qiang Liu, and Lei Song. 2019. "Analysis of an SDN-Based Cooperative Caching Network with Heterogeneous Contents" Electronics 8, no. 12: 1491. https://doi.org/10.3390/electronics8121491
APA StyleLi, Q., Wang, X., Wang, D., Zhang, Y., Lan, Y., Liu, Q., & Song, L. (2019). Analysis of an SDN-Based Cooperative Caching Network with Heterogeneous Contents. Electronics, 8(12), 1491. https://doi.org/10.3390/electronics8121491





