Abstract
The original multi-target multi-Bernoulli (MeMBer) filter for multi-target tracking (MTT) is shown analytically to have a significant bias in its cardinality estimation. A novel cardinality balance multi-Bernoulli (CBMeMBer) filter reduces the cardinality bias by calculating the exact cardinality of the posterior probability generating functional (PGFl) without the second assumption of the original MeMBer filter. However, the CBMeMBer filter can only have a good performance under a high detection probability, and retains the first assumption of the MeMBer filter, which requires measurements that are well separated in the surveillance region. An improved MeMBer filter proposed by Baser et al. alleviates the cardinality bias by modifying the legacy tracks. Although the cardinality is balanced, the improved algorithm employs a low clutter density approximation. In this paper, we propose a novel structure for a multi-Bernoulli filter without a cardinality bias, termed as a novel multi-Bernoulli (N-MB) filter. We remove the approximations employed in the original MeMBer filter, and consequently, the N-MB filter performs well in a high clutter intensity and low signal-to-noise environment. Numerical simulations highlight the improved tracking performance of the proposed filter.
1. Introduction
Considering the multi-target tracking (MTT) environments, the unknown number of targets changes with time because of the presence of target deaths and births. Moreover, the ambiguities in track-to-measurement association, which involves the missed detection and clutters, increase the difficulty of the joint estimation of the target cardinality and target states [1,2,3]. Based on the finite set statistics (FISST) theory, Mahler proposed a rigorous formulation of random finite set (RFS)-type filters. The RFS-based algorithms model the targets and the measurements as RFSs [3]. Compared with the conventional multiple hypothesis tracker (MHT) and joint probability data association (JPDA) algorithms [4,5,6], they avoid data association, which has a high computation burden. In the past few years, several RFS-based methods, such as the well-known probability hypothesis density (PHD) filter [7,8,9], cardinality PHD (CPHD) filter [10,11,12], and MeMBer filter [3] have been created. For example, the PHD filter models both targets and measurements as Poisson RFSs, and sequentially propagates the first moment of the multi-target density (PHD intensity) over time. The CPHD filter improves the cardinality-estimating performance of the PHD filter by propagating the cardinality distribution with the PHD of the multi-target density. The MeMBer filter parameterizes the multi-target distribution that models each potential target as a single Bernoulli RFS [3], which is characterized by the probability of existence and the probability density function (pdf). Accordingly, the multi-Bernoulli (MB) RFS is a union of multiple independent Bernoulli components. Since the Gaussian mixture implementations are proposed for the RFS-based filters, various extensions are found in many papers [3,13]. However, some inherent problems brought about by the assumptions made in these filters limit their applications.
Recently, the conjugate distributions in the framework of Bayesian probability theory has generated substantial interest. A conjugate distribution means that the Bayesian recursion is closed. Those filters based on conjugate priors derived under the labeled RFS [14,15,16] and unlabeled RFS theory [17,18,19,20] can approximate the exact multi-target distributions accurately and were compared in Vo et al. [21]. The Poisson multi-Bernoulli mixture (PMBM) filter is derived based on the unlabeled distributions, where the filter models multi-target using a hybrid form of Poisson and MB mixture (MBM) RFSs. The prior multi-target distribution is the same with the posterior multi-target distribution in the PMBM filter [17,18]. Another Bayes-closed filter is derived based on the well-known generalized labeled multi-Bernoulli distribution (GLMB) [14,15,16], along with a relatively efficient version, the well-known δ-GLMB filter, which propagates the whole data association history together with track sets; consequently, it is computationally expensive. The LMB filter was proposed in Williams [16] based on approximating the GLMB density. However, the prediction step in the standard form of the δ-GLMB and the LMB filter involves truncating prediction density by a K-shortest path algorithm, which brings in additional computational burden and influences the efficiency of performance. Thus, combining the prediction and update step of these filters is necessary for practical application [22,23].
However, the RFS formulation using the FISST theory is free of the huge computational burden due to the data association in MTT [3,24]. Some approximations made in the MeMBer filter may bring in a significant performance degradation. For example, the MeMBer filter has a positive cardinality bias due to the approximations made in the derivation of the MeMBer corrector to obtain a posterior multi-Bernoulli density (second approximation). The CBMeMBer filter achieves the cardinality balance by preserving the PHD of each Bernoulli component [25]; however, this approximation has destroyed the posterior density, especially in low-detection (low signal-to-noise) environments. An improved form of the MeMBer (I-MeMBer) filter models the spurious targets in the legacy tracks and removes them after the update step [26]. Consequently, the cardinality is balanced. However, both CBMeMBer and I-MeMBer filters retain the first approximation of the MeMBer filter [3], which requires measurements that are well-separated in surveillance region. Thus, they cannot perform well in a surveillance region with proximity targets and/or high clutter density environments. The measurement-driven MeMBer filter removes the cardinality bias by modifying the legacy parameters, but it is not an analytical solution [27].
In this paper, an analytical solution to the Bayesian multi-target filter is proposed. The targets are modeled as an MB RFS, where each target is modeled as a Bernoulli RFS with an individual existence probability and pdf. The prior multi-Bernoulli distribution shifts the combinatorial problem to that of associating measurements to a corresponding Bernoulli component. Thus, the approximation employed in the original MeMBer filter is relaxed. The proposed novel structure of the multi-Bernoulli (N-MB) filter employs a Gibbs sampler [28] to solve the data association problem, i.e., it finds a finite number of best global hypothesis.
The remainder of this paper is organized as follows. In Section 2, we review the background information on RFS theory. In Section 3, we derive our N-MB filter. In Section 4, we present the implementation details for the N-MB filter. In Section 5, we show the performance of our proposed N-MB filter. Conclusions are given in Section 6.
2. Random Finite Set Statistics
The RFS is a finite-set-valued random variable, and throughout this paper, we model the multi-target as the union of a Poisson RFS and a MB RFS. An RFS includes a random number and unordered targets and represents individual states as random vectors. A finite set of state vectors is used to denote multi-target states, where . The cardinality of a finite set is . Denote the probability density of the RFS with and the set of all finite subsets of the state space
with , then for a function , the set integral is given as:
Defining a multi-target exponential notation , where is a real-valued function with . The PGFl is given as:
A Bernoulli RFS with an existence probability and pdf has a multi-target density and PGFl:
where denotes the inner product of two functions and . An MB density is the union of multiple independent Bernoulli densities:
where is the number of single Bernoulli components in an MB and . Furthermore, its PGFl is given as:
Throughout this paper, an MB distribution is abbreviated as:
Given a Dirac delta density , we define the functional derivative of in the direction of as and given as:
If the functional is of the form , then we have .
The first-order moment, i.e., the PHD function of a multi-target density , is given as:
The PHD function of an MB is given as [3]:
A key result of the functional derivative utilized in our derivation process is the product rule [3]:
where indicates the sum is over all disjoint sets and , which permits the calculation of the derivative of a product of an MB PGFl.
3. Novel Structure of an MB Filter
In this section, the derivation process of the proposed algorithm is presented. Before we commence, the following assumptions are presented, which are used in the derivation of the algorithm.
Assumptions:
- Birth target distribution is denoted by .
- The survival probability conditioned on the target state is . The transition pdf is , where denotes the previous target state.
- The clutter distribution is modeled as a Poisson distribution with a clutter rate .
- A single target may generate at most one measurement, where the detection probability is and the measurement likelihood is .
3.1. Derivation of the Predictor
At each time , the PGFl of the posterior MB density and the PGFl of the birth density take the form of Equation (6). The predicted multi-target distribution is also a multi-target multi-Bernoulli process [3]:
Here, is the PGFl of the birth process, which follows Assumption 1:
Also, the predicted parameters of the surviving targets are given as:
3.2. Derivation of the Corrector
For notational simplicity, in the following derivation, we omit the time index. As given in the above subsection, the PGFl of the predicted distribution is the MB process:
where .
Denoting the multi-target measurement likelihood function conditioned on the target state set as , the PGFl of the likelihood is:
where . Thus, the functional is defined as:
The PGFl of the updated density (updated by ) is given as [3]:
where is the functional derivative of in WRT the set .
Using the product rule given in Equation (11), we rewrite Equation (19) as:
where
where
The notation denotes the set of clutters, i.e., the measurements not associated with any targets. The set can have any cardinality (the number of clutter alarms) that meets the constraint . For , the set denotes the set of measurements associated with the corresponding target (represented by the Bernoulli component). The cardinality of the set is , where means the target is not detected. The set is given as:
where if the target is not detected, and if the target is associated with measurement . The number of measurements is . Defining an to denote a choice of a one-to-one mapping, i.e., there are no distinct , with . The set of all assignment vectors is denoted as .
The functional derivative of in WRT the set is given as:
where denotes the “volume” of the surveillance region. For , the functional derivative of in WRT the set is given as:
Furthermore, set :
Using the association notations and the results of Equations (24) and (26), we rewrite Equation (20) as:
Note that the PGFl with the same form as Equation (27) is not an MB PGFl because of the additional sum according to different associations . A multi-Bernoulli PGFl is shown in Equation (13), which is the product of single Bernoulli PGFls.
The original MeMBer filter [3] approximates the derivative of in WRT the whole measurement set . Moreover, in the derivation of the corrector for the original MeMBer filter, the CBMeMBer filter, and the I-MeMBer filter, the approximation that there is no more than one measurement near a true target is indispensable; a performance degradation occurs when targets in the surveillance region are too close, or the clutter intensity is very high. In contrast, the form as given in Equation (27) is exact. However, the combinatorial problem in this formulation is tractable. Thus, we utilize a Gibbs sampler to find the best associations .
3.3. PHD Intensity of the Posterior
Moreover, we approximate the posterior density with an MB distribution by calculating the PHD intensity (first-order moment). Thus, an MB RFS is constructed with an identical PHD intensity to the truncated distribution (truncated with a finite number of best association ).
The PHD of the updated posterior is:
We define the function:
The derivative of the functional in WRT the target state and measurement set is given as:
where
Thus, we rewrite Equation (28) as:
Equation (32) shows that the PHD function of the updated posterior has a similar structure to that of an MB PHD function, which is given in Equation (10). Thus, the Bernoulli components of can be calculated from Equation (32) by merging the parameters of the Bernoulli component under different data associations . The final MB parameters of are given as:
where
and
From the right-hand side of Equation (33), we can see that there are many choices for the updated Bernoulli RFSs, but we can merge all the choices of associations for the Bernoulli components.
Compared to the LMB filter, our N-MB filter employs a straightforward prediction step. Thus, a different cost matrix needs to be designed to find the best data association. Moreover, the derivation of the LMB filter was based on approximating the GLMB density, which employs the labeled RFS notation. While our N-MB filter models the targets as an unlabeled multi-Bernoulli distribution, the Gibbs sampler is employed to get an approximate multi-Bernoulli distribution for the posterior density. Our N-MB filter was derived by using the theory of probability generating functionals and functional derivatives, which are very important tools for deriving RFS-based filters, for example, the PHD filter, CPHD filter, MeMBer filter, and PMBM filter.
4. Gaussian Implementation
In the previous section, we derived the recursion for the N-MB filter. Intuitively, the filter is intractable; therefore, approximations are necessary. In this section, we propose a closed-form Gaussian mixture (GM)-based implementation for the derived filter.
We assume that targets follow linear Gaussian dynamics, and measurements follow models with MB births:
where denotes the transition matrix, denotes the process noise covariance, denotes the observation matrix, and denotes the observation noise covariance. Furthermore, the survival and detection probability were assumed to be constant, which is given as and .
The birth model is also an MB with the parameter set and the pdf is a GM of the form:
where , , and denote the weights, means, and covariances of the Gaussian component. Note that and denotes the number of components.
4.1. Update
The prediction step of the proposed filter is the same with that in Baser et al. [25]. Given the predicted MB density and each pdf is in the form of Gaussian mixtures:
then, for each association , the updated posterior MB density is:
For , the updated means and covariances of the posterior MB density stay unchanged. For , the means and covariances of the posterior MB density are updated by the associated measurement :
Then, the updated parameters in Equation (40) can be calculated using:
where
The derivation of the above steps involves analytically calculating the products of Gaussians and integrals of Gaussians using the standard results of Gaussian functions [9].
4.2. Gibbs Sampling
We employ the Gibbs sampling algorithm to solve the data association problem, which is an efficient algorithm for finding the best choices for the assignment of targets to measurements [28]. This subsection presents the implementation of the integrated Gibbs sampler in detail.
After the prediction step, there are predicted Bernoulli components (representing targets), and the number of measurements is . We define:
where denotes the index of whichever measurement is assigned to the target. For , .
Consider a realization of a random variable that distributes according to a probability distribution on . A Gibbs sampler is used to generate positive one-to-one vectors by independently sampling from . The distribution is:
where is the set of one-to-one mapping vectors in .
It is difficult to sample from the distribution in Equation (49) directly. The Markov chain Monte Carlo (MCMC) method is the well-known algorithm for sampling from a complex distribution [29]. The Gibbs sampling algorithm is an efficient case of the so-called Metropolis–Hasting MCMC algorithm [30]. The proposed samples in a Gibbs sampler are always adopted; therefore, the Gibbs sampler is considered to be an efficient tool for generating the best associations [22,28,30,31]. Given results obtained using Equation (48), the assignment problem can be immediately solved by utilizing a Gibbs sampler.
Finally, the pseudocode for the filter is summarized in Algorithm 1.
| Algorithm 1: Pseudocode for the filter |
| 1. Step 1: (prediction) 2. Input birth density and posterior density 3. Output 4. Step 2: (find best ) 5. Calculate according to Equation (48) 6. 7. Step 3: (update for each ) 8. for 9. Calculate , according to Equations (45) and (46) 10. end 11. Step 4: (reconstruction) 12. Reconstruct the MB density according to Equation (33) |
5. Simulation
This section demonstrates the simulation results of the proposed N-MB filter conducted on linear Gaussian models. We set the simulation environments similar those in Baser et al. [25]. Consider a 2-D cartesian coordinate system where targets’ births and deaths occurred in a surveillance region of . A sensor was located at and provided point measurements to a controller at each time step. The sample interval was and both the number and states of the multi-target at each time step were unknown. Figure 1 shows the true tracks of targets.
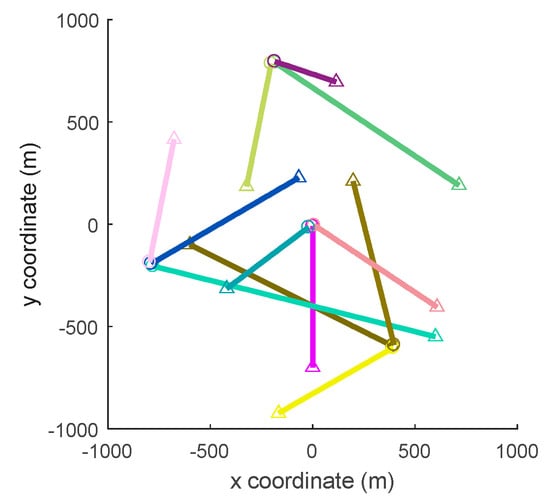
Figure 1.
Trajectories in the -plane; —locations of target births, —locations of target deaths.
5.1. Targets Model
The kinematic state is given as . The Gaussian target dynamics were modeled using the constant velocity (CV) model:
where the standard deviation (std) was set as .
The survival probability was and the detection probability was set as a constant . Consider the surveillance region including four locations where targets may birth from: , , , and . The birth process was modeled as a Poisson RFS with intensity , where , , , , and , and the covariance matrix was given by .
Measurements followed the observation function in Equation (37) with parameters:
where was the std of the measurement noise. Clutters were modeled as a Poisson process with a clutter rate and uniformly distributed according to the spatial probability density over the surveillance region, where was the “volume” of the surveillance region.
We used a threshold for the target state extraction and we removed those Gaussian components whose weights were lower than . Those Gaussian components in a Bernoulli component whose distances were lower than were merged.
5.2. Performance Evaluation
Simulations were performed using MTT filters implemented in MATLAB (9.1.0.441655 R2016b, MathWorks, Beijing, China) on computers with an Intel Core i7-7700K CPU @ 4.20GHz and 16 GB RAM. We analyzed the performance in terms of the position estimates obtained by the proposed N-MB filer and CBMeMBer filter proposed in Baser et al. [25], the CPHD filter proposed in Vo et al. [13], and the track-oriented marginal MeMBer-Poisson (TOMB/P) filter proposed in García-Fernández et al. [17] using Monte Carlo simulations. We employed the optimal sub-pattern assignment (OSPA) distance as the error metric [32] to compare the performance of these filters. The OSPA is a distance metric for denoting the difference between two sets of points. The generalized OSPA (GOSPA), which was proposed recently, was also employed to verify the simulation’s performance. GOSPA penalizes localization errors for detected targets and the errors due to missed and false targets [33], which is not considered in OSPA. The GOSPA metric with parameter is given by
where denotes the set of all possible assignments, is the cut-off value, and determines the severity of penalizing the outliers in the localization component. We compared the root mean square (RMS) OSPA and the RMS GOSPA for the position estimation across all time steps. The Euclidean metric was used as the base metric and we set and . In this case, could be decomposed as: , which denotes the localization error; , which denotes the miss-detection error; and , which denotes the false-detection error.
5.3. Simulation Results
In Figure 2, the decomposed - and -components of the true tracks, state estimates generated by the N-MB filter, and measurements across all the time steps are shown versus time. The results showed that the proposed filter could correctly track the targets with individual motions throughout the targets’ births and deaths. Three targets crossed with each other at time step , and two targets crossed with each other at time step , and the proposed filter had no difficulty handling these situation.
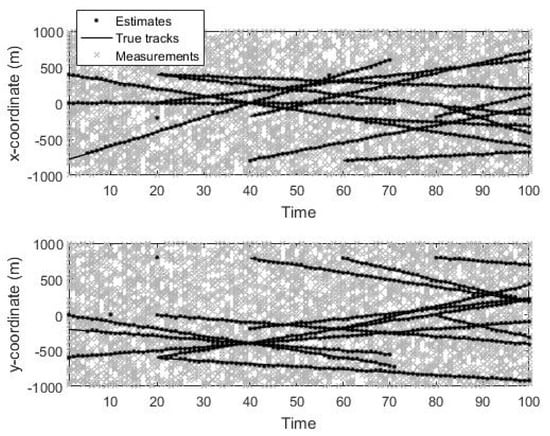
Figure 2.
Measurements, true tracks, and novel multi-Bernoulli (N-MB) filter estimates.
We further showed the performance of our proposed N-MB filter over Monte Carlo (MC) runs with a fixed set of target trajectories (shown in Figure 1) but randomly generated measurement data (the generated measurements over all time steps for one MC run is shown in Figure 2). Considering an environment with a high clutter intensity (the clutter rate was set to and the detection probability was set as ), the mean and std of the estimated cardinality versus time for the CBMeMBer, CPHD, TOMB/P, and N-MB filters are shown in Figure 3. The CBMeMBer filter suffers from false estimations greatly. This phenomenon is easy to explain because the CBMeMBer employed the assumption that measurements were well separated [3,25]. In contrast, both TOMB/P and the proposed N-MB filter performed well in the cardinality estimation, and had a lower variance than the CPHD filter.
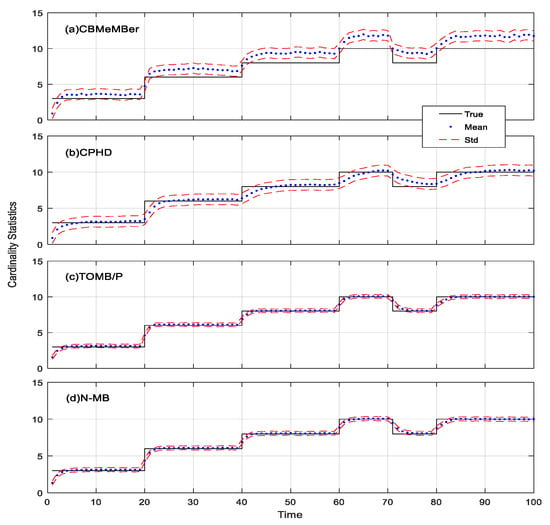
Figure 3.
Statistics for a high clutter rate (, ) for filters.
Moreover, the MC average of the RMS OSPA distances are given in Figure 4, where the clutter rate was set to and the detection probability was set to (i.e., a low signal-to-noise environment). The CBMeMBer filter suffered a great performance degradation when the detection probability was low. This was because the filter required the approximation of a high detection probability to correct for the negative term involved in the existence probability of the resulting MB components [25,34]. In contrast, the proposed N-MB filter performed well in the environment with a low detection probability. Compared to the TOMB/P filter, the N-MB filter had a better performance in most of time steps, but the TOMB/P filter outperformed the N-MB filter in terms of removing death targets at . The CPHD filter was also not suitable for application in the low-signal-to-noise environment.
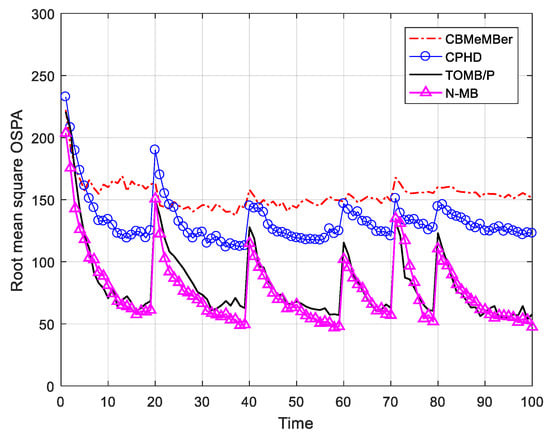
Figure 4.
Optimal sub-pattern assignment (OSPA) distances versus time for filters.
In Figure 5, we give the averages of 200 MC trials for the RMS OSPA distance for the CBMeMBer, CPHD, TOMB/P, and N-MB filters for various clutter rates from to . In Figure 6, we give the results for various detection probabilities from to . As expected, the OSPA error increased with the increased clutter rates and a lower detection probability. Overall, these results showed that the N-MB filter had a better performance compared to the other filters. The performance of the CBMeMBer filter was greatly influenced by the increased clutter rate
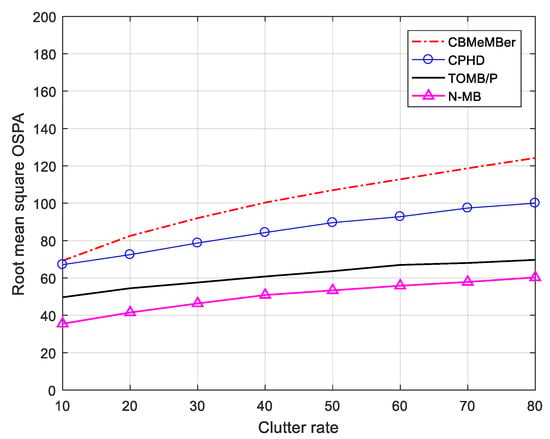
Figure 5.
Time-averaged OSPA distances for varying clutter rates.
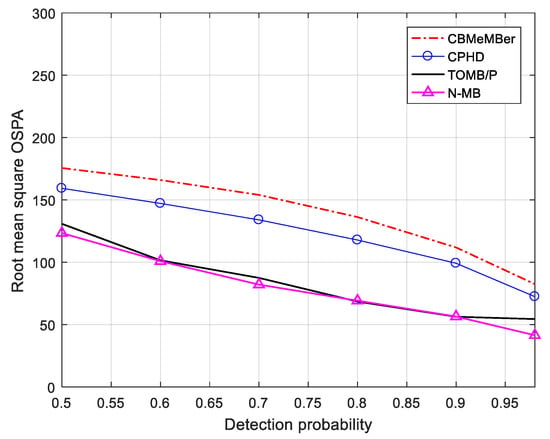
Figure 6.
Time-averaged OSPA distances for varying detection probabilities.
Although OSPA is a good method for measuring the performance of RFS-based MTT filters, we do not know whether the difference in performance of OSPA error comes from a better detection ability, a lower number of false targets, or a lower number of missed targets, which is key information regarding the analysis of filters. As mentioned in Section 5.2, we employed decomposed GOSPA components to verify the performance of filters in terms of location estimations, false estimations, and missed estimations. The RMS OSPA/GOSPA error averaged over all time steps of the filters in different situations are given in Figure 7 and Figure 8. These results prove that the N-MB filter had a similar performance to the TOMB/P filter regarding location accuracy, but outperformed the latter in evaluation of missed targets. The N-MB filter was more sensitive regarding initializing birth tracks; however, this feature meant the N-MB filter produced more false estimates. Overall, the N-MB filter outperformed the TOMB/P filter, especially in the high signal-to-noise environment. Again, the CBMeMBer filter showed its efficient performance in environment with a high signal-to-noise ratio and low clutter intensity, but the performance degraded dramatically in challenging environments.
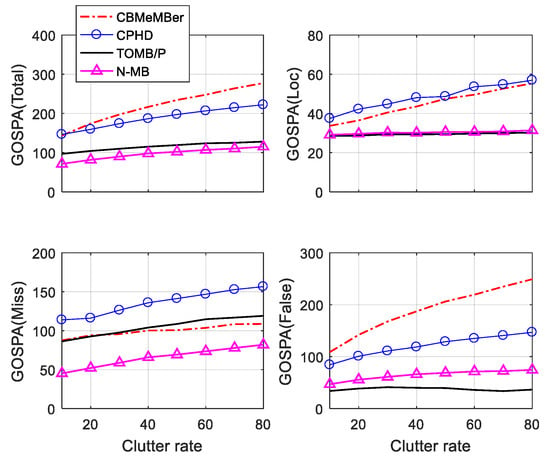
Figure 7.
Time-averaged generalized OSPA (GOSPA) error for varying clutter rates. Filters: CBMeMBer—cardinality balance multi-Bernoulli, CPHD—cardinality probability hypothesis density, TOMB/P—track-oriented marginal MeMBer-Poisson, N-MB—novel multi-Bernoulli.
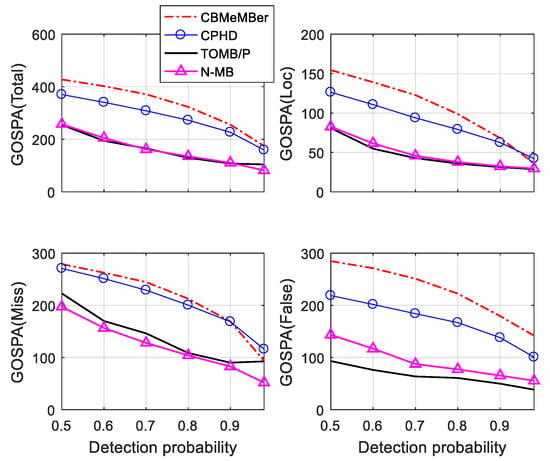
Figure 8.
Time-averaged GOSPA error for varying detection probabilities.
5.4. Comparison with the LMB Filter
As summarized in Section 3.3, the proposed N-MB filter has a similar structure with the LMB filter, while it has a straightforward prediction step because the N-MB filter was derived based on the theory of PGFls and functional derivatives, while the LMB filter is based on approximating the GLMB density. An efficient implementation method that combines the prediction and update steps of the LMB filter is proposed in Mahler [23], which avoids the complex calculation burden of the prediction step. We compared the time-averaged GOSPA error and computation times (seconds) of the proposed N-MB filter and the LMB filter [23] in different situations, and the results are given in Table 1. Both filters employ the gating technique, which is widely used in many papers [15,16,22].

Table 1.
Comparison with the LMB filter.
Intuitively, the proposed N-MB filter had a similar performance to the LMB filter in high signal-to-noise environments. However, the N-MB filter had a more stable performance in more challenging environments (low signal-to-noise environments with a high clutter intensity). In contrast, a serious leak-tracking problem occurred in the tracking results of the LMB filter when applied in challenging environments.
6. Conclusions
Although the CBMeMBer filter was cardinality balanced, the derivation of which removes the second approximation employed in the original MeMBer filter [3]. It employs the first approximation in Mahler [3], which assumes that measurements are well-separated in the surveillance region. A filter based on this approximation cannot be applied in an environment with high clutter intensity. Moreover, the approximation of a high detection probability is required in the derivation of the CBMeMBer filter; therefore, the filter cannot be applied in the low signal-to-noise environment.
In this paper, we derived a novel-structured MB filter based on PGFl theory and unlabeled RFSs. The proposed filter removed the assumptions utilized in deriving the MeMBer filter. Thus, the filter performed well in the low signal-to-noise and high clutter density environments. Compared to filters based on a GLMB distribution, the proposed filter did not extract explicit tracks for targets. The theory of tracking based on sets of trajectories [35] was utilized to solve this problem. Various simulation results showed that the proposed filter outperformed the LMB filter in low signal-to-noise environments with a little higher computational cost.
Author Contributions
W.S. and H.Z. conceived and designed the experiments; Z.Q. performed the experiments; W.S. and H.Z. analyzed the data; Z.Q. contributed reagents/materials/analysis tools; H.Z. wrote the paper.
Funding
This work was supported in part by the National Natural Science Foundation of China under grants 61671168 and 61801143, in part by the National Natural Science Foundation of Heilongjiang Province under grant LH2019F005, and in part by the Fundamental Research Funds for the Central Universities under grants 3072019CF0801 and 3072019CFM0802.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bar-Shalom, Y.; Willett, P.K.; Tian, X. Tracking and Data Fusion; YBS Publishing: Storrs, CT, USA, 2011. [Google Scholar]
- Koch, W. Tracking and Sensor Data Fusion; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Mahler, R.P. Statistical Multisource-Multitarget Information Fusion; Artech House, Inc.: Norwood, MA, USA, 2007. [Google Scholar]
- Bar-Shalom, Y.; Li, X.-R. Multitarget-Multisensor Tracking: Principles and Techniques; YBS: Storrs, CT, USA, 1995. [Google Scholar]
- Pulford, G. (Ed.) Taxonomy of multiple target tracking methods. IEEE Proc. Radar Sonar Navig. 2005, 152, 291–304. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.-N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multitarget filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Vo, B.-N.; Ma, W.-K. The Gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Mahler, R. (Ed.) A theory of PHD filters of higher order in target number. In Signal Processing, Sensor Fusion, and Target Recognition XV; International Society for Optics and Photonics: Orlando, FL, USA, 2006. [Google Scholar]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- De Melo, F.E.; Maskell, S. A CPHD approximation based on a discrete-Gamma cardinality model. IEEE Trans. Signal Process. 2018, 67, 336–350. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.-N.; Vo, B.-T.; Phung, D. Labeled random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.-T.; Vo, B.-N.; Dietmayer, K. The labeled multi-Bernoulli filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar]
- Williams, J.L. Marginal multi-bernoulli filters: RFS derivation of MHT, JIPDA, and association-based member. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1664–1687. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Williams, J.L.; Granström, K.; Svensson, L. Poisson multi-Bernoulli mixture filter: direct derivation and implementation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1883–1901. [Google Scholar] [CrossRef]
- Williams, J.L. An efficient, variational approximation of the best fitting multi-Bernoulli filter. IEEE Trans. Signal Process. 2014, 63, 258–273. [Google Scholar] [CrossRef]
- Correa, J.; Adams, M.; Perez, C. (Eds.) A dirac delta mixture-based random finite set filter. In Proceedings of the 2015 IEEE International Conference on Control, Automation and Information Sciences (ICCAIS), Changshu, China, 29–31 October 2015. [Google Scholar]
- Xia, Y.; Granstrcom, K.; Svensson, L.; García-Fernández, Á.F. (Eds.) Performance evaluation of multi-Bernoulli conjugate priors for multi-target filtering. In Proceedings of the 2017 IEEE 20th International Conference on Information Fusion (Fusion), Xi′an, China, 10–13 July 2017. [Google Scholar]
- Vo, B.-N.; Vo, B.-T.; Hoang, H.G. An efficient implementation of the generalized labeled multi-Bernoulli filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Reuter, S.; Danzer, A.; Stübler, M.; Scheel, A.; Granström, K. (Eds.) A fast implementation of the Labeled Multi-Bernoulli filter using gibbs sampling. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017. [Google Scholar]
- Mahler, R. “Statistics 102” for multisource-multitarget detection and tracking. IEEE J. Sel. Top. Signal Process. 2013, 7, 376–389. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Baser, E.; Kirubarajan, T.; Efe, M.; Balaji, B. Improved multi-target multi-Bernoulli filter with modelling of spurious targets. IET Radar Sonar Navig. 2016, 10, 285–298. [Google Scholar] [CrossRef]
- Ouyang, C.; Ji, H.; Li, C. Improved multi-target multi-Bernoulli filter. IET Radar Sonar Navig. 2012, 6, 458–464. [Google Scholar] [CrossRef]
- Hue, C.; Cadre, J.P.L.; Perez, P. Tracking multiple objects with particle filtering. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 791–812. [Google Scholar] [CrossRef]
- Oh, S.; Russell, S.; Sastry, S. Markov chain Monte Carlo data association for multi-target tracking. IEEE Trans. Autom. Control 2009, 54, 481–497. [Google Scholar]
- Casella, G.; George, E. Explaining the Gibbs sampler. Am. Stat. 1992, 46, 167–174. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 564–584. [Google Scholar]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. Analytic implementations of the cardinalized probability hypothesis density filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Schuhmacher, D.; Vo, B.-T.; Vo, B.-N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- Rahmathullah, A.S.; García-Fernández, Á.F.; Svensson, L. (Eds.) Generalized optimal sub-pattern assignment metric. In Proceedings of the 2017 IEEE 20th International Conference on Information Fusion (Fusion), Xi′an, China, 10–13 July 2017. [Google Scholar]
- Saucan, A.-A.; Coates, M.J.; Rabbat, M. A multisensor multi-Bernoulli filter. IEEE Trans. Signal Process. 2017, 65, 5495–5509. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Svensson, L.; Morelande, M.R. Multiple target tracking based on sets of trajectories. arXiv 2016, arXiv:08163. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).