Electroporation Modelling of Irregular Nucleated Cells Including Pore Radius Dynamics
Abstract
1. Introduction
2. Mathematical Formulation
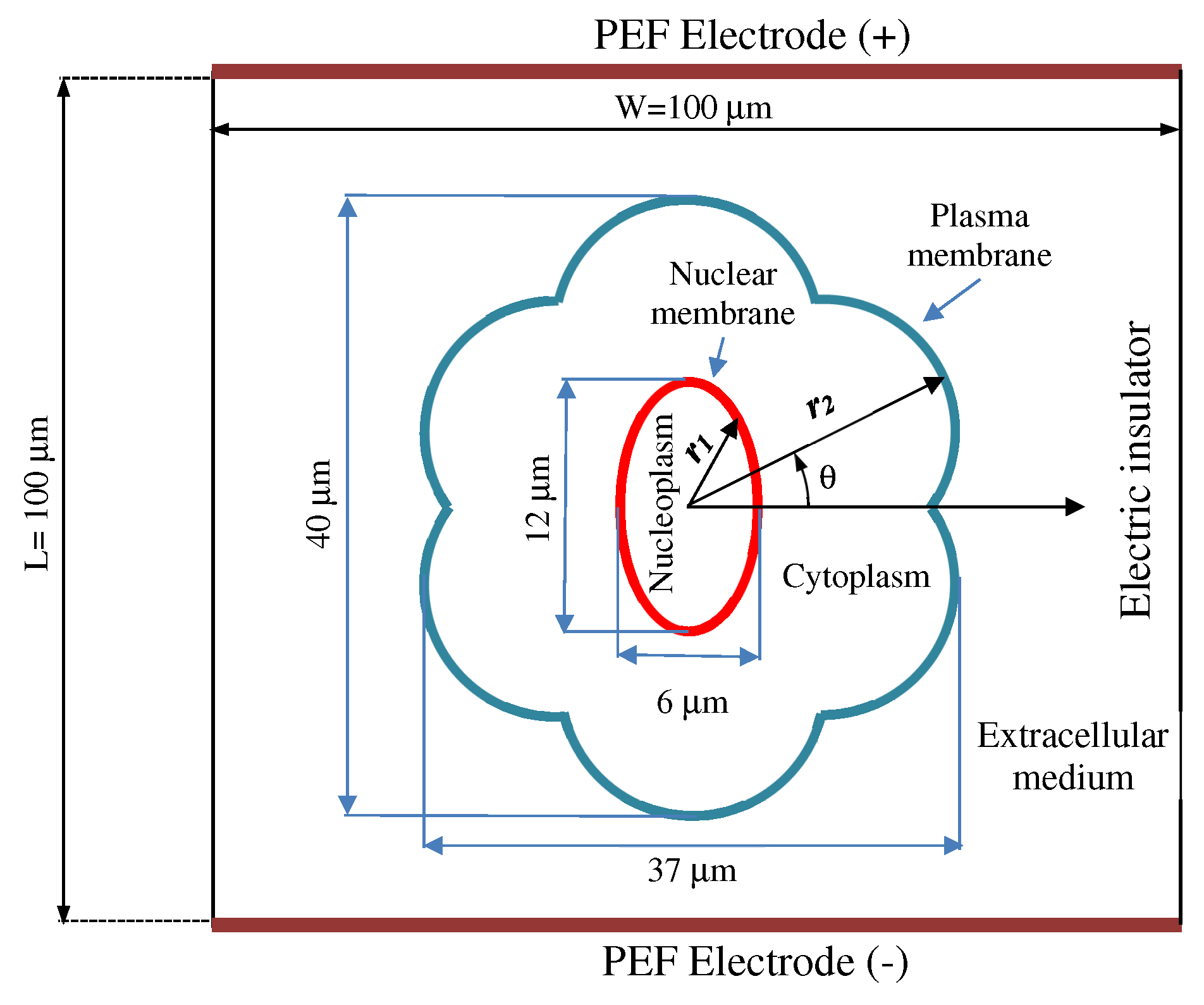
2.1. Cell Geometry Model
2.2. Pores Radius Model
2.3. Complex Permittivity Model
2.4. Electromagnetic Model
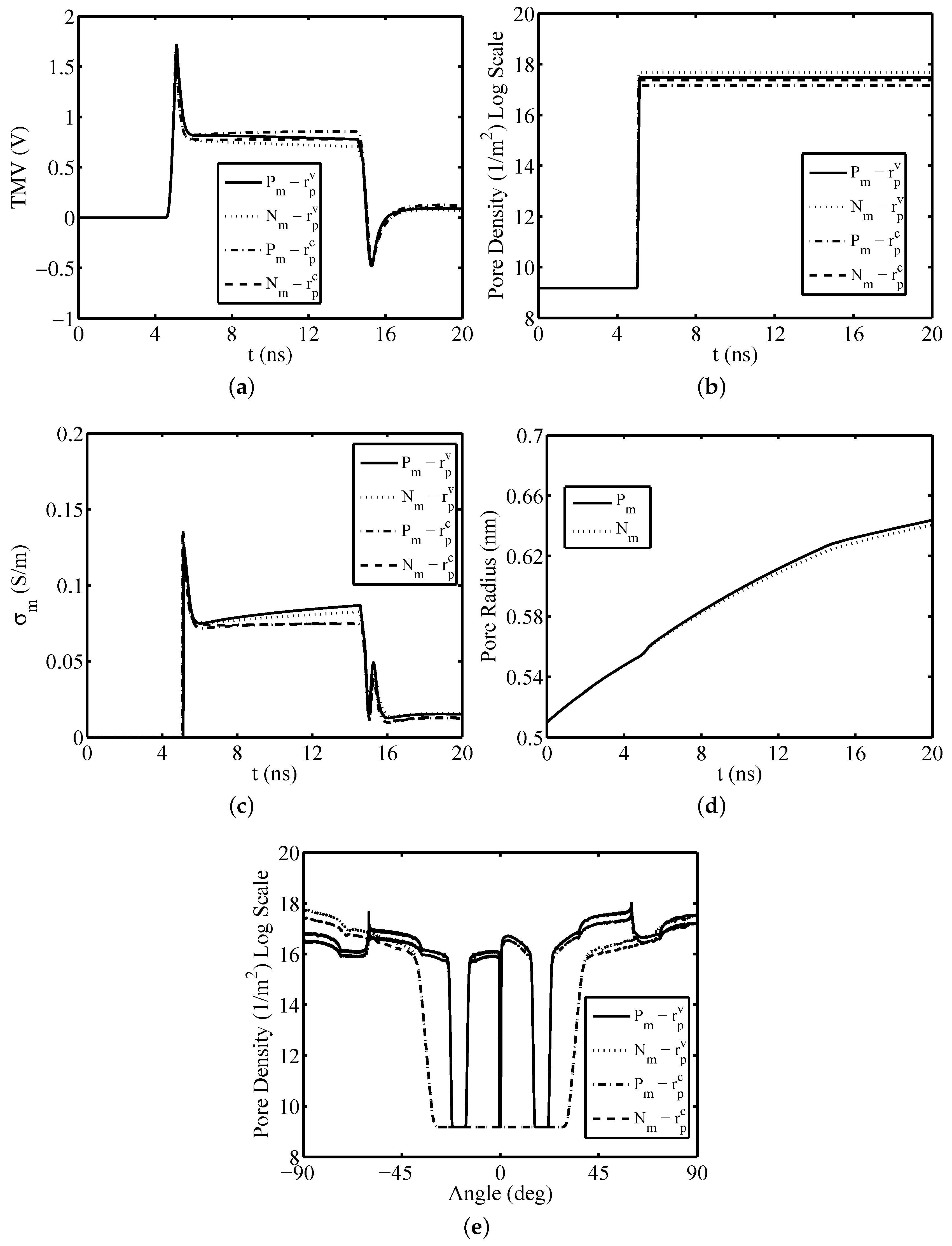
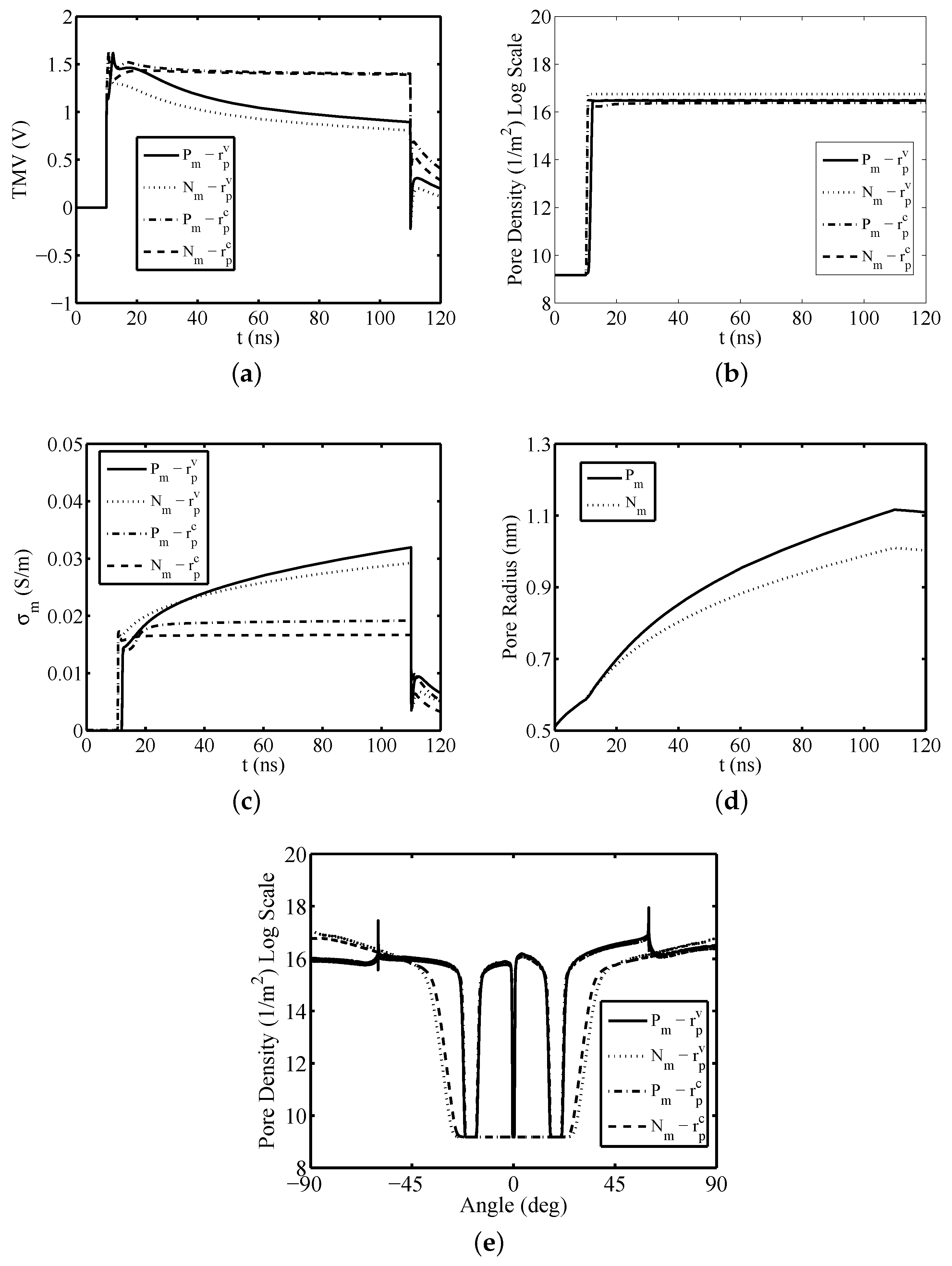
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ECT | Electrochemotherapy |
| EP | Electroporation |
| NTIRE | Nonthermal irreversible electroporation |
| PEF | Pulsed electric field |
| TMV | Transmembrane voltage |
References
- Kranjc, M.; Bajd, F.; Serša, I.; Miklavčič, D. Magnetic resonance electrical impedance tomography for monitoring electric field distribution during tissue electroporation. IEEE Trans. Med. Imag. 2011, 30, 1771–1778. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Ma, Y.; Zhu, J.; Chen, Y.; Sun, Y.; Yao, Y.; Yang, Z.; Xie, J. A Review on Electroporation-Based Intracellular Delivery. Molecules 2018, 23, 3044. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, G.A.; Dev, S.B.; Dimmer, S.; Nanda, G.S. Electroporation therapy: A new approach for the treatment of head and neck cancer. IEEE Trans. Biomed. Eng. 1999, 46, 752–759. [Google Scholar] [CrossRef] [PubMed]
- Mescia, L.; Chiapperino, M.A.; Bia, P.; Gielis, J.; Caratelli, D. Modeling of Electroporation induced by pulsed electric fields in irregularly shaped cells. IEEE Trans. Biomed. Eng. 2018, 65, 414–423. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, P.; Romeo, S.; Sannino, A.; Zeni, L.; Zeni, O. The Role of Pulse Repetition Rate in nsPEF-Induced Electroporation: A Biological and Numerical Investigation. IEEE Trans. Biomed. Eng. 2015, 62, 2234–2243. [Google Scholar] [CrossRef] [PubMed]
- Chiapperino, M.A.; Bia, P.; Caratelli, D.; Gielis, J.; Mescia, L.; Dermol-Černe, J.; Miklavčič, D. Nonlinear dispersive model of electroporation for irregular nucleated cells. Bioelectromagnetics 2019, 40, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Mescia, L.; Chiapperino, M.A.; Lamacchia, C.M.; Bia, P.; Gielis, J.; Caratelli, D. Design of electroporation process in irregularly shaped multicellular systems. Electronics 2019, 8, 37. [Google Scholar] [CrossRef]
- Krassowska, W.; Filev, P.D. Modeling electroporation in a single cell. Biophys. J. 2007, 92, 404–417. [Google Scholar] [CrossRef] [PubMed]
- Leguebe, M.; Silve, A.; Mir, L.M.; Poignard, C. Conducting and permeable states of cell membrane submitted to high voltage pulses: Mathematical and numerical studies validated by the experiments. J. Theor. Biol. 2014, 360, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Mescia, L.; Bia, P.; Chiapperino, M.A.; Caratelli, D. Fractional calculus based FDTD modeling of layered biological media exposure to wideband electromagnetic pulses. Electronics 2017, 6, 106. [Google Scholar] [CrossRef]
- Bia, P.; Caratelli, D.; Mescia, L.; Gielis, J. Analysis and synthesis of supershaped dielectric lens antennas. IET Microwaves Antennas Propag. 2015, 9, 1497–1504. [Google Scholar] [CrossRef]
- Neu, J.C.; Krassowska, W. Asymptotic model of electroporation. Phys. Rev. E 1999, 59, 471–482. [Google Scholar] [CrossRef]
- Jiang, C.; Davalos, R.V.; Bischof, J.C. Review of basic to clinical studies of irreversible electroporation therapy. IEEE Trans. Biomed. Eng. 2015, 62, 4–20. [Google Scholar] [CrossRef] [PubMed]
- Martinsen, G.; Grimnes, S.; Schwan, H.P. Interface phenomena and dielectric properties of biological tissues. In Encyclopedia of Surface and Colloid Science; Marcel Dekker, Inc.: New York, NY, USA, 2002; pp. 2643–2652. [Google Scholar]
- Rems, L.; Ušaj, M.; Kandušer, M.; Reberšek, M.; Miklavčič, D.; Pucihar, G. Cell electrofusion using nanosecond electric pulses. Sci. Rep. 2013, 3, 3382. [Google Scholar] [CrossRef] [PubMed]
- Salimi, E.; Thomson, D.J.; Bridges, G.E. Membrane dielectric dispersion in nanosecond pulsed electroporation of biological cells. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1256–1265. [Google Scholar] [CrossRef]
- Kotnik, T.; Miklavcic, D. Theoretical evaluation of the distributed power dissipation in biological cells exposed to electric fields. Bioelectromagnetics 2000, 21, 385–394. [Google Scholar] [CrossRef]
- Polevaya, Y.; Ermolina, I.; Schlesinger, M.; Ginzburg, B.Z.; Feldman, Y. Time domain dielectric spectroscopy study of human cells ii. normal and malignant white blood cells. Biochim. Biophys. Acta 1999, 1419, 257–271. [Google Scholar] [CrossRef]
| Title 1 | Title 2 | Title 3 |
|---|---|---|
| First relaxation time of plasma membrane [16] | ||
| First relaxation time of nuclear membrane [16] | ||
| Second relaxation time of plasma membrane [16] | ||
| Second relaxation time of nuclear membrane [16] | ||
| Relaxation time of extracellular medium [17] | ||
| Relaxation time of cytoplasm [17] | ||
| Relaxation time of nucleoplasm [17] | ||
| First relaxation amplitude of plasma membrane [16] | ||
| First relaxation amplitude of nuclear membrane [16] | ||
| Second relaxation amplitude of plasma membrane [16] | ||
| Second relaxation amplitude of nuclear membrane [16] | ||
| Relaxation amplitude of extracellular medium [17] | ||
| Relaxation amplitude of cytoplasm [17] | ||
| Relaxation amplitude of nucleoplasm [17] | ||
| High frequency permittivity [16] | ||
| Dielectric permittivity of vacuum | ||
| Conductivity of the extracellular medium [8] | ||
| Passive Conductivity of the plasma membrane [16] | ||
| Conductivity of cytoplasm [18] | ||
| Passive Conductivity of the nuclear membrane [15] | ||
| Conductivity of nucleoplasm [18] | ||
| Conductivity of solution inside the pore for plasma membrane [15] | ||
| Conductivity of solution inside the pore for nuclear membrane [15] | ||
| Minimum radius of hydrophilic pores [8] | ||
| Minimum energy radius at [8] | ||
| q | 2.46 | Electroporation constant [8] |
| D | Diffusion coefficient for pore radius [8] | |
| Steric repulsion energy [8] | ||
| Edge energy [8] | ||
| Tension of the bilayer without pores [8] | ||
| Tension of hydrocarbon-water interface [8] | ||
| F | Maximum electric force for [8] | |
| First costant for advection velocity [8] | ||
| Second costant for advection velocity [8] | ||
| Pore creation rate density [16] | ||
| Characteristic voltage of electroporation [8] | ||
| Equilibrium pore density [8] | ||
| Equivalent pore density for one pore [8] | ||
| 3.2 | Energy barrier inside the pore [16] | |
| 0.15 | Relative length of pore entrance area [16] | |
| 7.82 × 10−3 | Costant used in Equations (19) and (25) [8] | |
| Electron electric charge | ||
| k | Boltzmann constant | |
| T | Temperature [8] | |
| Plasma membrane thickness [15] | ||
| Nuclear membrane thickness [15] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiapperino, M.A.; Bia, P.; Lamacchia, C.M.; Mescia, L. Electroporation Modelling of Irregular Nucleated Cells Including Pore Radius Dynamics. Electronics 2019, 8, 1477. https://doi.org/10.3390/electronics8121477
Chiapperino MA, Bia P, Lamacchia CM, Mescia L. Electroporation Modelling of Irregular Nucleated Cells Including Pore Radius Dynamics. Electronics. 2019; 8(12):1477. https://doi.org/10.3390/electronics8121477
Chicago/Turabian StyleChiapperino, Michele Alessandro, Pietro Bia, Claudio Maria Lamacchia, and Luciano Mescia. 2019. "Electroporation Modelling of Irregular Nucleated Cells Including Pore Radius Dynamics" Electronics 8, no. 12: 1477. https://doi.org/10.3390/electronics8121477
APA StyleChiapperino, M. A., Bia, P., Lamacchia, C. M., & Mescia, L. (2019). Electroporation Modelling of Irregular Nucleated Cells Including Pore Radius Dynamics. Electronics, 8(12), 1477. https://doi.org/10.3390/electronics8121477







