Analysis and Classification of Motor Dysfunctions in Arm Swing in Parkinson’s Disease
Abstract
1. Introduction
- (a)
- classifies between subjects with motor dysfunctions and a control group based exclusively on arm motions
- (b)
- uses 3D data from the accelerometer, gyroscope, and magnetometer
- (c)
- includes new parameters
- (d)
- is small and easy to use
- (e)
- is not bound to a location
- (f)
- requires a small number of sensors
- (g)
- is low cost
2. Materials
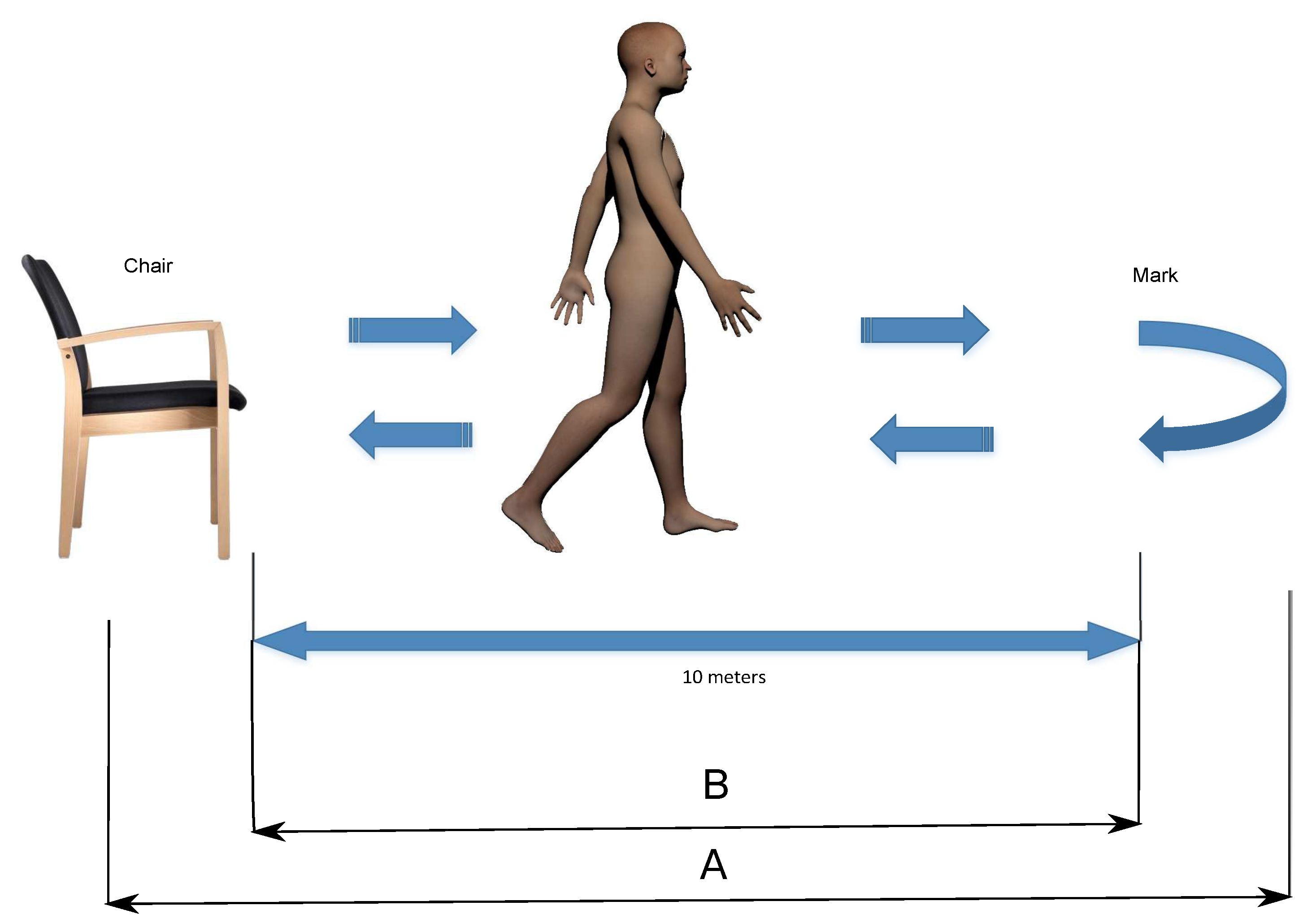
2.1. Protocol
2.2. Hardware
2.3. Data
2.3.1. Dataset
2.3.2. Sensor Data
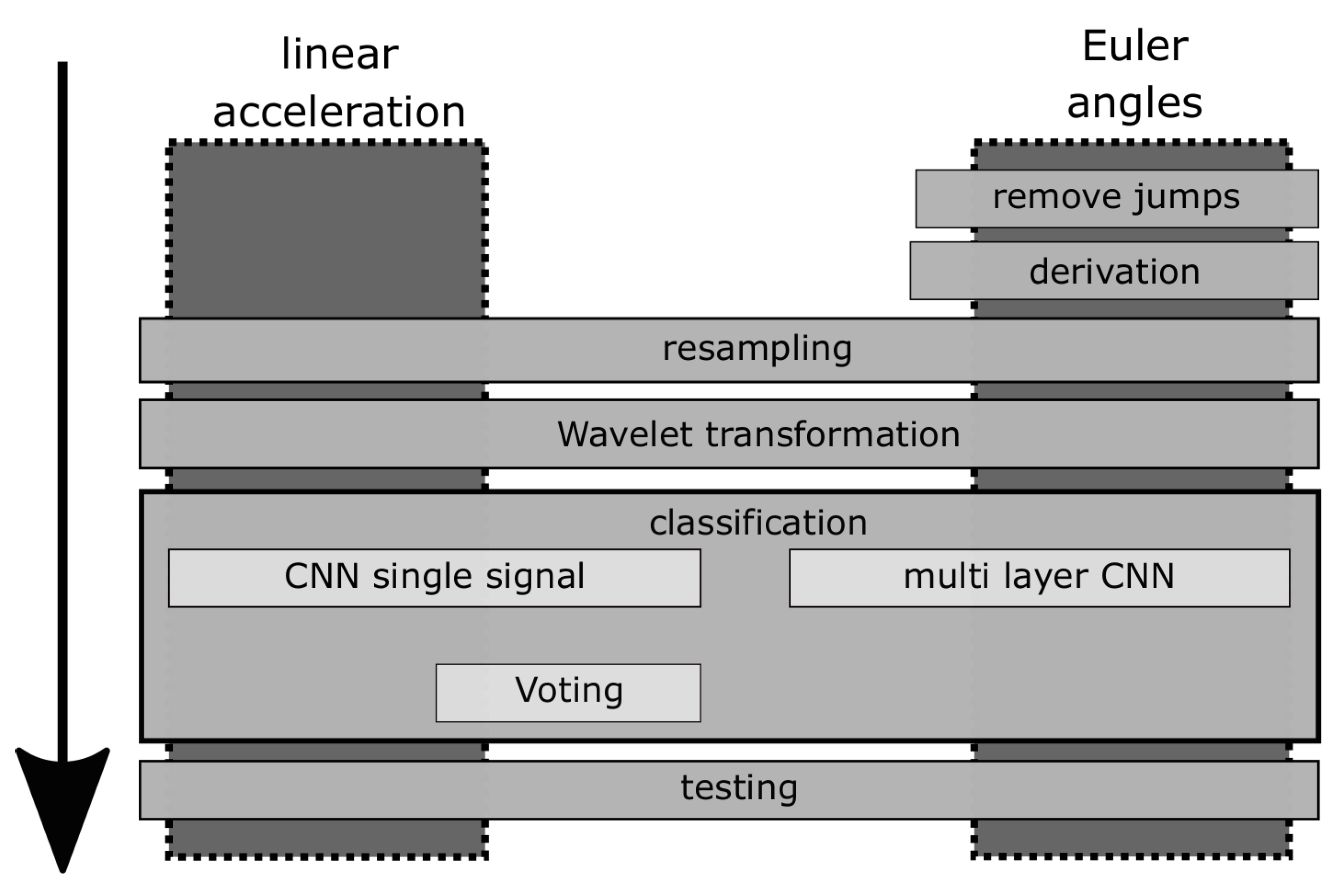
3. Methods
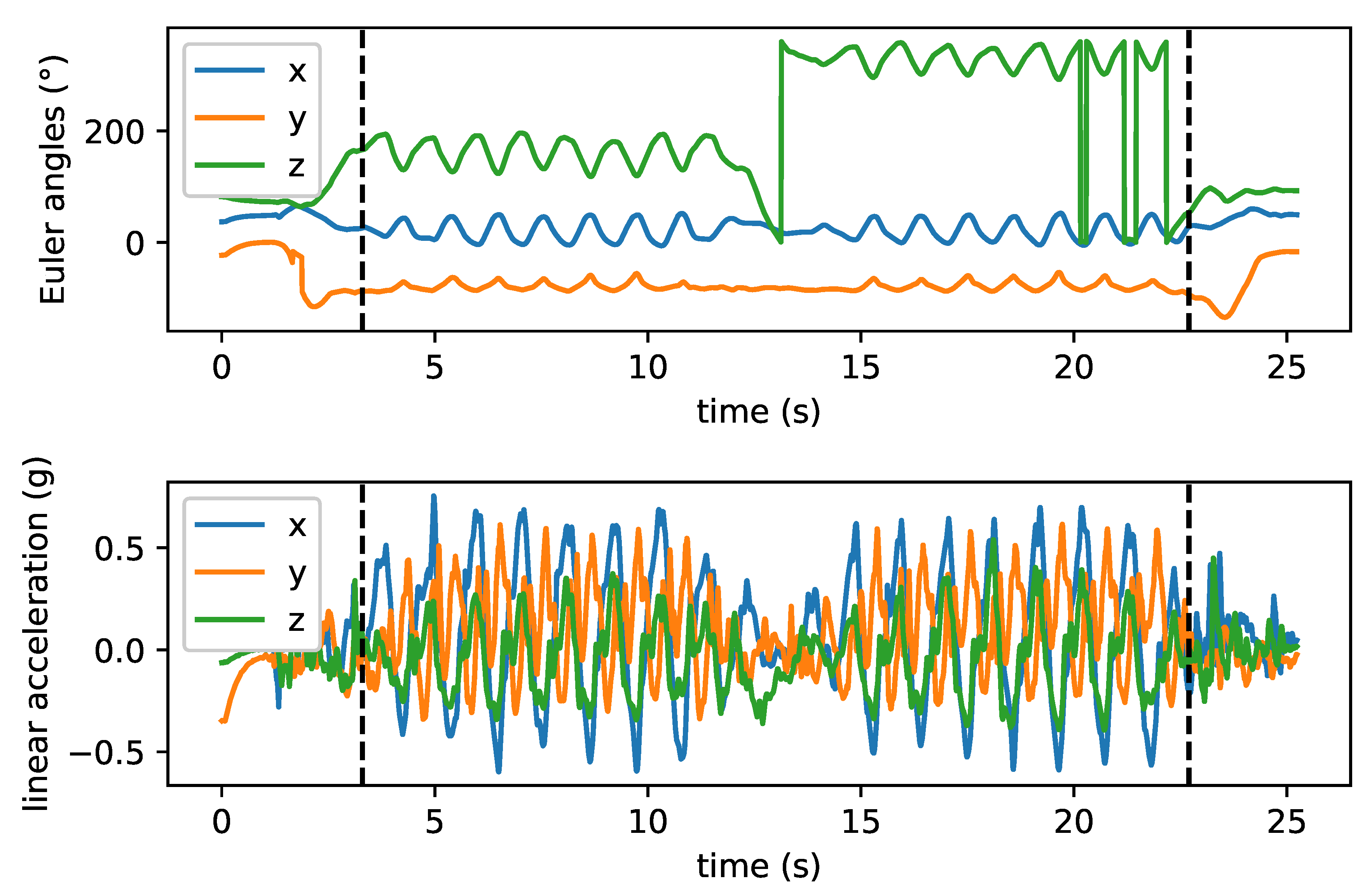
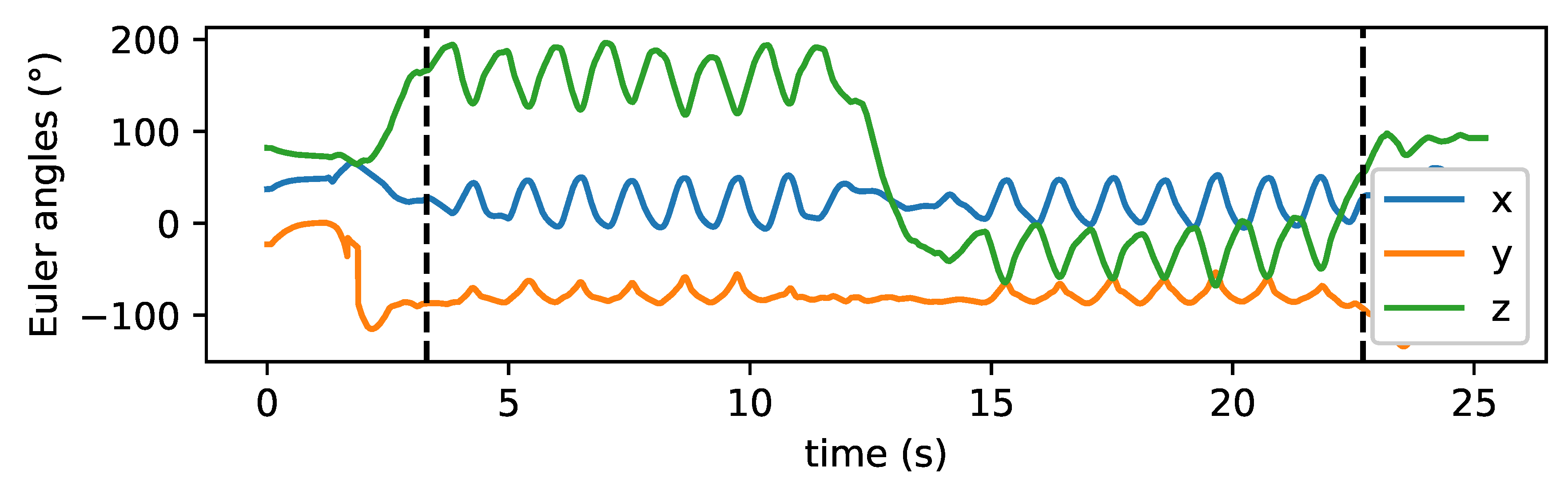
3.1. Removing Jumps
3.2. Derivation
3.3. Resampling
3.4. Wavelet Transformation
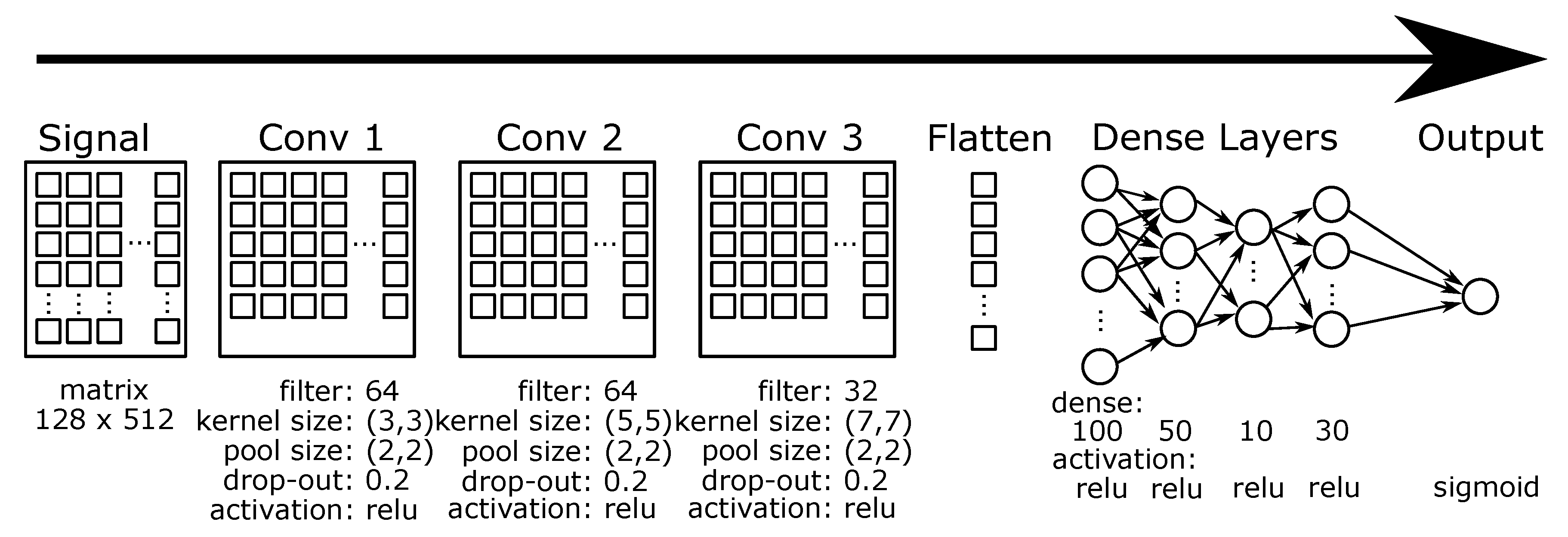
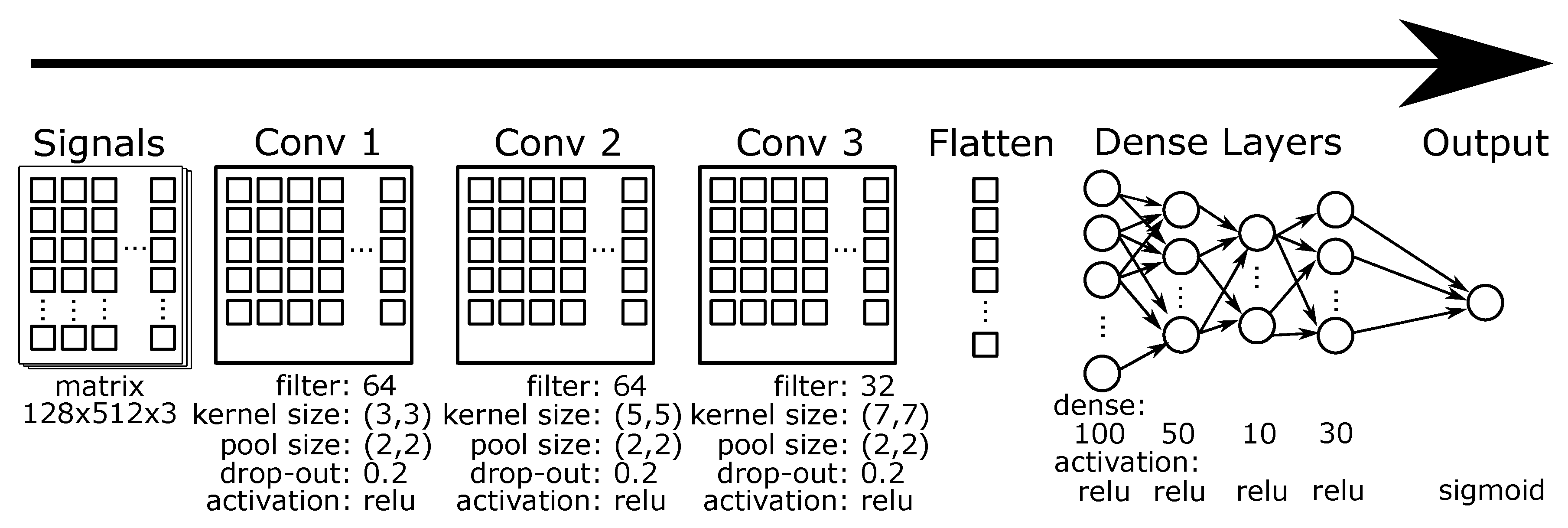
3.5. CNN
3.6. Multi-Channel CNN
3.7. Weight Voting
3.8. Evaluation
3.9. Methodology
4. Results
4.1. Parts (A) and (B) of TUG
4.1.1. Single Layer
4.1.2. Signal Combination
4.2. Part (B) of TUG
4.2.1. Single Layer
4.2.2. Signal Combination
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kontis, V.; Bennett, J.E.; Mathers, C.D.; Li, G.; Foreman, K.; Ezzati, M. Future life expectancy in 35 industrialised countries: Projections with a Bayesian model ensemble. Lancet 2017, 389, 1323–1335. [Google Scholar] [CrossRef]
- Parkinson’s Foundation. Available online: https://www.parkinson.org/Understanding-Parkinsons/Statistics (accessed on 1 October 2019).
- Goetz, C.G.; Tilley, B.C.; Shaftman, S.R.; Stebbins, G.T.; Fahn, S.; Martinez-Martin, P.; Poewe, W.; Sampaio, C.; Stern, M.B.; Dodel, R.; et al. Movement Disorder Society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale presentation and clinimetric testing results. Mov. Disord. 2008, 23, 2129–2170. [Google Scholar] [CrossRef] [PubMed]
- Mazumder, O. Development and Control of Active Lower Limb Exoskeleton for Mobility Regeneration and Enhancement. Ph.D. Thesis, Indian Institute of Engineering Science and Technology, Shibpur, India, 2018. [Google Scholar]
- Jasni, F.; Hamzaid, N.A.; Al-Nusairi, T.Y.; Yusof, N.H.M.; Shasmin, H.N.; Cheok, N.S. Feasibility of A Gait Phase Identification Tool for Transfemoral Amputees using Piezoelectric-Based In-Socket Sensory System. IEEE Sens. J. 2019, 19, 6437–6444. [Google Scholar] [CrossRef]
- Stoelben, K.J.V.; Pappas, E.; Mota, C.B. Lower extremity joint moments throughout gait at two speeds more than 4 years after ACL reconstruction. Gait Posture 2019, 70, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Balzer, J.; Marsico, P.; Mitteregger, E.; van der Linden, M.L.; Mercer, T.H.; van Hedel, H.J. Influence of trunk control and lower extremity impairments on gait capacity in children with cerebral palsy. Disabil. Rehabil. 2018, 40, 3164–3170. [Google Scholar] [CrossRef] [PubMed]
- Prakash, C.; Sujil, A.; Kumar, R.; Mittal, N. Linear Prediction Model for Joint Movement of Lower Extremity. In Recent Findings in Intelligent Computing Techniques; Springer: Singapore, 2019; pp. 235–243. [Google Scholar]
- Steinmetzer, T.; Bonninger, I.; Priwitzer, B.; Reinhardt, F.; Reckhardt, M.C.; Erk, D.; Travieso, C.M. Clustering of Human Gait with Parkinson’s Disease by Using Dynamic Time Warping. In Proceedings of the 2018 IEEE International Work Conference on Bioinspired Intelligence (IWOBI), San Carlos, Costa Rica, 18–20 July 2018; pp. 1–6. [Google Scholar]
- Steinmetzer, T.; Bönninger, I.; Reckhardt, M.; Reinhardt, F.; Erk, D.; Travieso, C.M. Comparison of algorithms and classifiers for stride detection using wearables. Neural Comput. Appl. 2019, 1–12. [Google Scholar] [CrossRef]
- Ospina, B.M.; Chaparro, J.A.V.; Paredes, J.D.A.; Pino, Y.J.C.; Navarro, A.; Orozco, J.L. Objective arm swing analysis in early-stage Parkinson’s disease using an RGB-D camera (Kinect). J. Parkinson’s Dis. 2018, 8, 563–570. [Google Scholar] [CrossRef] [PubMed]
- Spasojević, S.; Santos-Victor, J.; Ilić, T.; Milanović, S.; Potkonjak, V.; Rodić, A. A vision-based system for movement analysis in medical applications: The example of Parkinson disease. In International Conference on Computer Vision Systems; Springer: Cham, Switzerland, 2015; pp. 424–434. [Google Scholar]
- Baron, E.I.; Koop, M.M.; Streicher, M.C.; Rosenfeldt, A.B.; Alberts, J.L. Altered kinematics of arm swing in Parkinson’s disease patients indicates declines in gait under dual-task conditions. Parkinsonism Relat. Disord. 2018, 48, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Lewek, M.D.; Poole, R.; Johnson, J.; Halawa, O.; Huang, X. Arm swing magnitude and asymmetry during gait in the early stages of Parkinson’s disease. Gait Posture 2010, 31, 256–260. [Google Scholar] [CrossRef] [PubMed]
- Tsipouras, M.G.; Tzallas, A.T.; Rigas, G.; Tsouli, S.; Fotiadis, D.I.; Konitsiotis, S. An automated methodology for levodopa-induced dyskinesia: Assessment based on gyroscope and accelerometer signals. Artif. Intell. Med. 2012, 55, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Castaño, Y.; Navarro, A.; Arango, J.; Muñoz, B.; Orozco, J.L.; Valderrama, J. Gait and Arm Swing Analysis Measurements for Patients Diagnosed with Parkinson’s Disease, using Digital Signal Processing and Kinect. In Proceedings of the SSN2018, Valdivia, Chile, 29–31 October 2018; pp. 71–74. [Google Scholar]
- Dranca, L.; de Mendarozketa, L.D.A.R.; Goñi, A.; Illarramendi, A.; Gomez, I.N.; Alvarado, M.D.; Rodríguez-Oroz, M.C. Using Kinect to classify Parkinson’s disease stages related to severity of gait impairment. BMC Bioinform. 2018, 19, 471. [Google Scholar] [CrossRef] [PubMed]
- Castaño-Pino, Y.J.; Navarro, A.; Muñoz, B.; Orozco, J.L. Using Wavelets for Gait and Arm Swing Analysis. In Wavelet Transform and Complexity; IntechOpen: London, UK, 2019. [Google Scholar]
- Roggendorf, J.; Chen, S.; Baudrexel, S.; Van De Loo, S.; Seifried, C.; Hilker, R. Arm swing asymmetry in Parkinson’s disease measured with ultrasound based motion analysis during treadmill gait. Gait Posture 2012, 35, 116–120. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Mahoney, J.M.; Lewis, M.M.; Du, G.; Piazza, S.J.; Cusumano, J.P. Both coordination and symmetry of arm swing are reduced in Parkinson’s disease. Gait Posture 2012, 35, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Bertomeu-Motos, A.; Lledó, L.; Díez, J.; Catalan, J.; Ezquerro, S.; Badesa, F.; Garcia-Aracil, N. Estimation of human arm joints using two wireless sensors in robotic rehabilitation tasks. Sensors 2015, 15, 30571–30583. [Google Scholar] [CrossRef] [PubMed]
- Viteckova, S.; Kutilek, P.; Lenartova, J.; Kopecka, J.; Mullerova, D.; Krupicka, R. Evaluation of movement of patients with Parkinson’s disease using accelerometers and method based on eigenvectors. In Proceedings of the 2016 17th International Conference on Mechatronics-Mechatronika (ME), Prague, Czech Republic, 7–9 December 2016; pp. 1–5. [Google Scholar]
- MbientLab. MetaWear RG/RPro. 2016. Available online: https://mbientlab.com/docs/MetaWearRPROPSv0.8.pdf (accessed on 4 January 2016).
- BOSCH Sensortec, Data Sheet BMI160. 2015. Available online: https://ae-bst.resource.bosch.com/media/_tech/media/datasheets/BST-BMI160-DS000-07.pdf (accessed on 2 December 2019).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy: Open Source Scientific Tools For Python. 2019. Available online: http://www.scipy.org/ (accessed on 2 December 2019).
- Hausdorff, J.M.; Cudkowicz, M.E.; Firtion, R.; Wei, J.Y.; Goldberger, A.L. Gait variability and basal ganglia disorders: Stride-to-stride variations of gait cycle timing in Parkinson’s disease and Huntington’s disease. Mov. Disord. 1998, 13, 428–437. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.R.; Gommers, R.; Wasilewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Abadi, M.; Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 11 October 2019).
- Tafazzoli, F.; Safabakhsh, R. Model-based human gait recognition using leg and arm movements. Eng. Appl. Artif. Intell. 2010, 23, 1237–1246. [Google Scholar] [CrossRef]
- Zhang, R.; Vogler, C.; Metaxas, D. Human gait recognition at sagittal plane. Image Vis. Comput. 2007, 25, 321–330. [Google Scholar] [CrossRef]



| Label | Persons | Records |
|---|---|---|
| Motor dysfunction | 15 | 80 |
| Control | 24 | 170 |
| Classes | ||
|---|---|---|
| Positive | Negative | |
| predicted | TP | FP |
| positive | true positive | false positive |
| predicted | FN | TN |
| negative | false negative | true negative |
| Signal | Sensitivity | Specificity | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|
| x Euler angles | |||||
| y Euler angles | |||||
| z Euler angles | |||||
| x linear acceleration | |||||
| y linear acceleration | |||||
| z linear acceleration |
| Layer | Sensitivity | Specificity | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|
| 3 channel CNN | |||||
| 3 signal voting |
| Signal | Sensitivity | Specificity | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|
| x Euler angles | |||||
| y Euler angles | |||||
| z Euler angles | |||||
| x linear acceleration | |||||
| y linear acceleration | |||||
| z linear acceleration |
| Layer | Sensitivity | Specificity | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|
| 3 layer CNN | |||||
| 3 signal voting |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinmetzer, T.; Maasch, M.; Bönninger, I.; Travieso, C.M. Analysis and Classification of Motor Dysfunctions in Arm Swing in Parkinson’s Disease. Electronics 2019, 8, 1471. https://doi.org/10.3390/electronics8121471
Steinmetzer T, Maasch M, Bönninger I, Travieso CM. Analysis and Classification of Motor Dysfunctions in Arm Swing in Parkinson’s Disease. Electronics. 2019; 8(12):1471. https://doi.org/10.3390/electronics8121471
Chicago/Turabian StyleSteinmetzer, Tobias, Michele Maasch, Ingrid Bönninger, and Carlos M. Travieso. 2019. "Analysis and Classification of Motor Dysfunctions in Arm Swing in Parkinson’s Disease" Electronics 8, no. 12: 1471. https://doi.org/10.3390/electronics8121471
APA StyleSteinmetzer, T., Maasch, M., Bönninger, I., & Travieso, C. M. (2019). Analysis and Classification of Motor Dysfunctions in Arm Swing in Parkinson’s Disease. Electronics, 8(12), 1471. https://doi.org/10.3390/electronics8121471






