Aging-Resilient Topology Synthesis of Heterogeneous Manycore Network-On-Chip Using Genetic Algorithm with Flexible Number of Routers
Abstract
1. Introduction
2. Related Works
2.1. Aging-Resilient Design for NoC
2.2. Error Recovery Scheme in NoC Datapath
2.3. Topology Synthesis of NoC
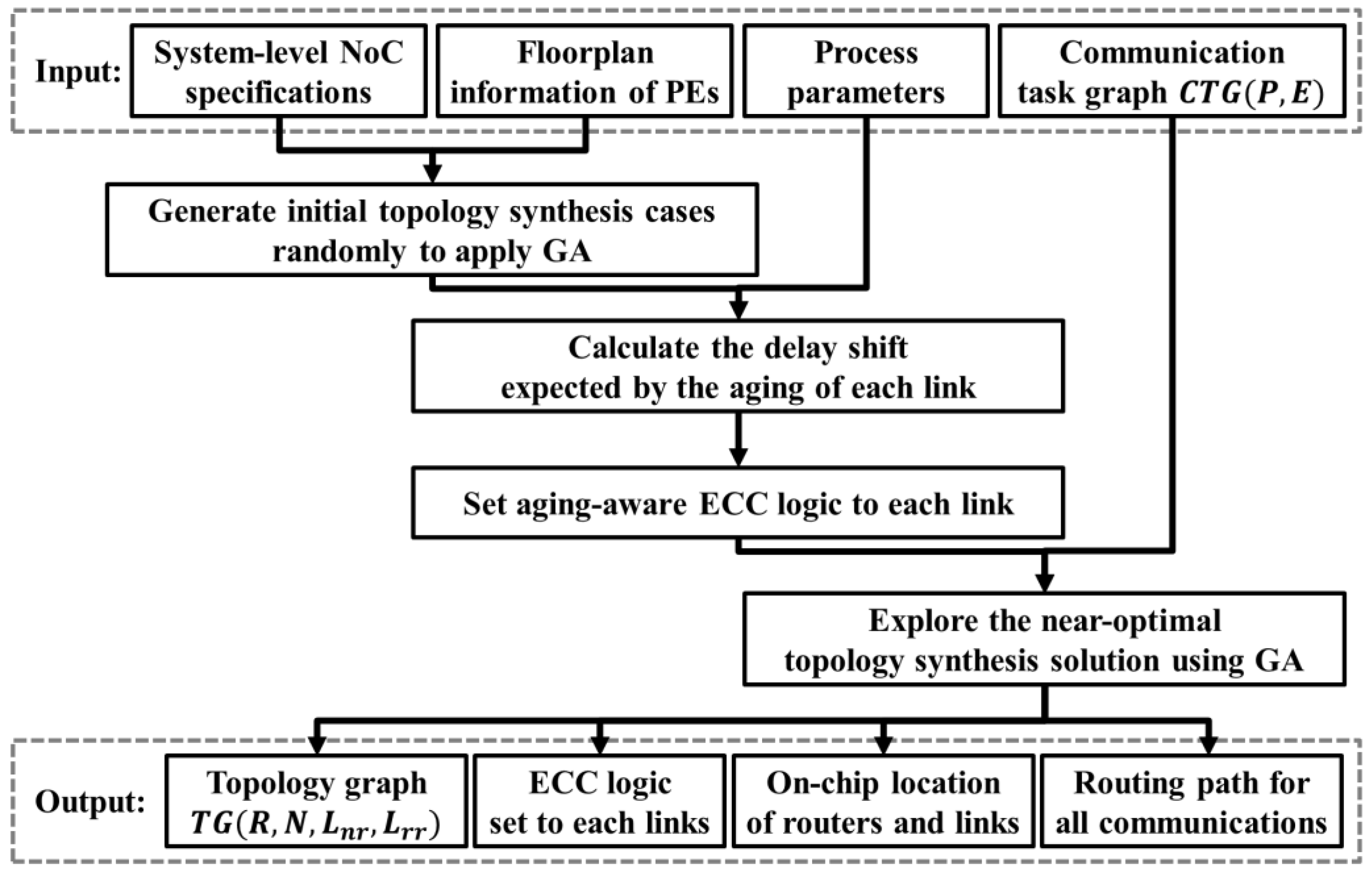
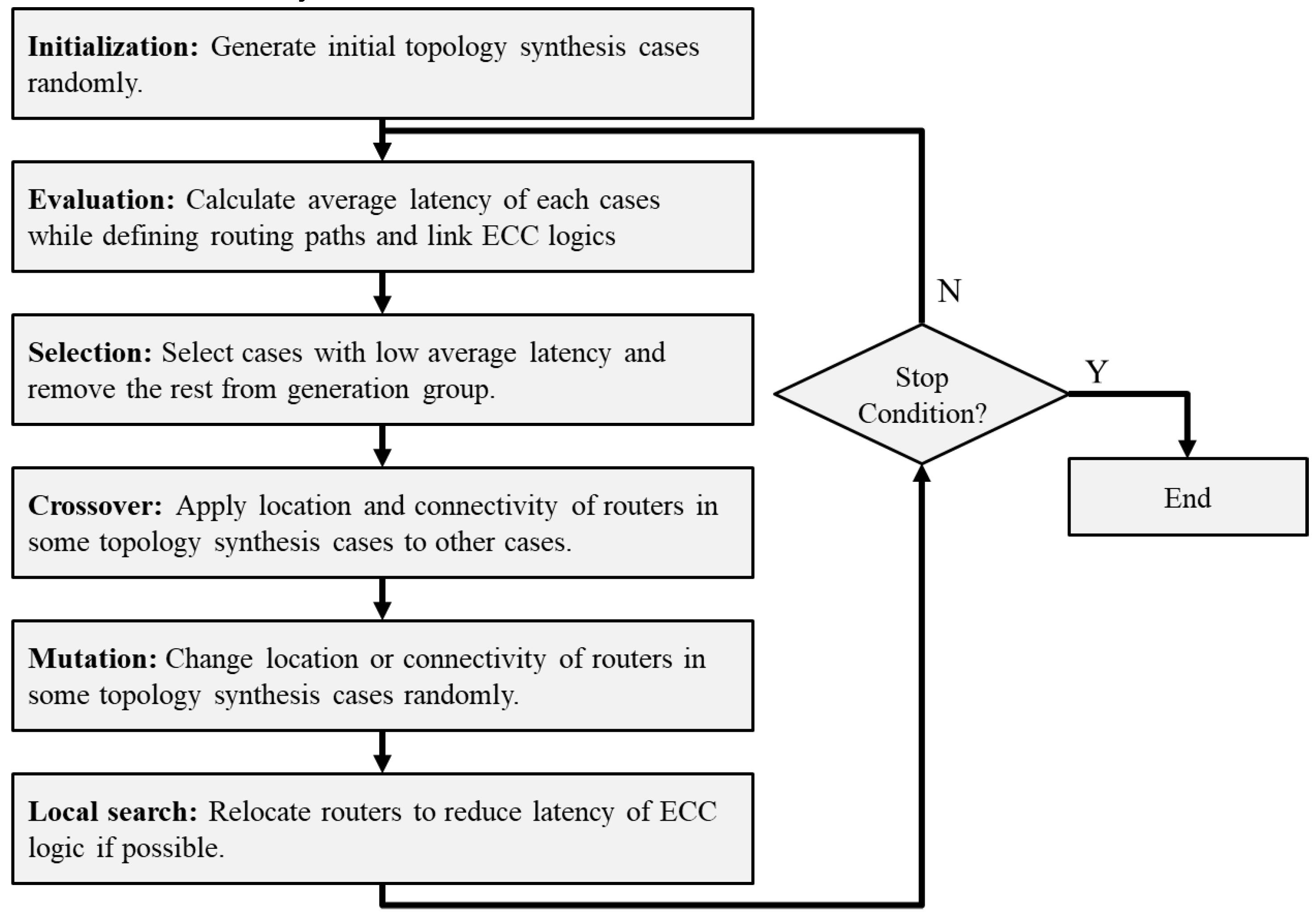
3. Overall Flow of Proposed Topology Synthesis
- The location of all routers cannot exist in the area where PEs are placed (i.e., router position constraint).
- The physical path of all links cannot exist in the area where PEs are placed (i.e., link position constraint).
- Each PE must be connected to only one router (i.e., PE connection constraint).
- Routers must be connected such that a communication path with each other exists (i.e., link connection constraint).
- The length of the link between the PEs, routers, and between routers must be less than (i.e., maximum link length constraint).
- The number of ports in each router must not exceed (i.e., maximum router port constraint).
4. Aging-Resilient Design of NoC with Non-Uniform ECC Assignment
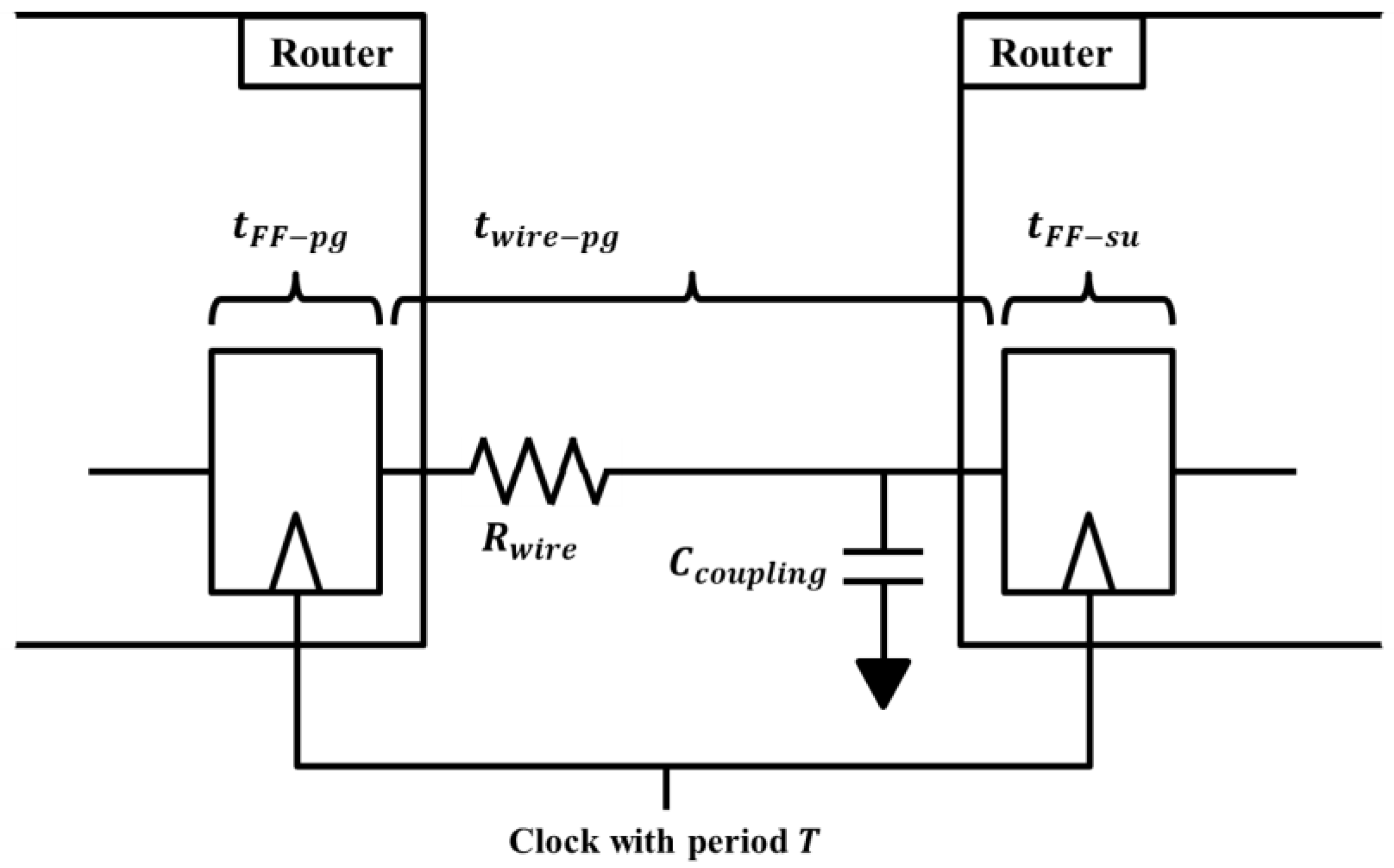
4.1. Time Constraint of NoC Links
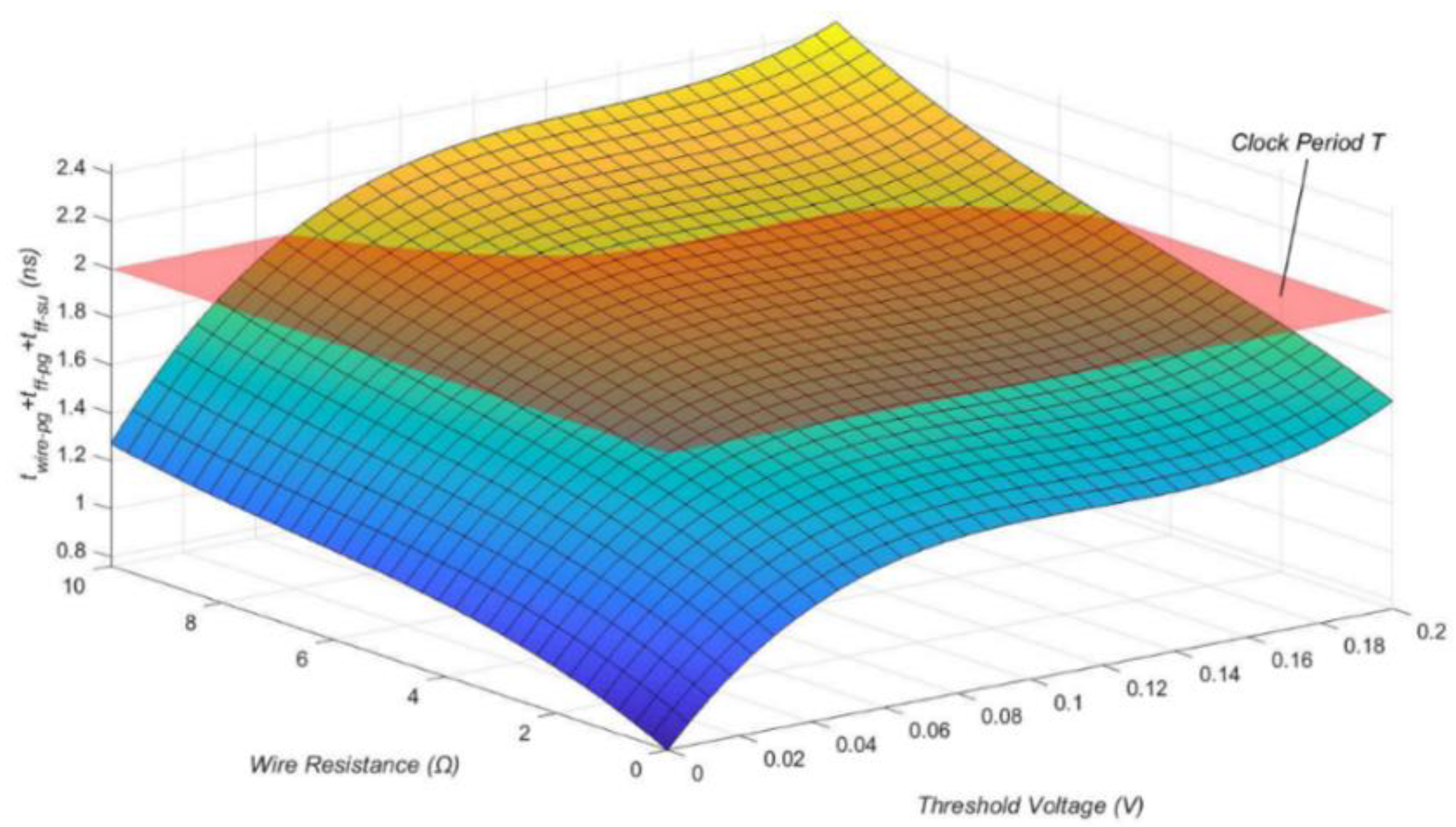
4.2. Aging-Induced Delay Model
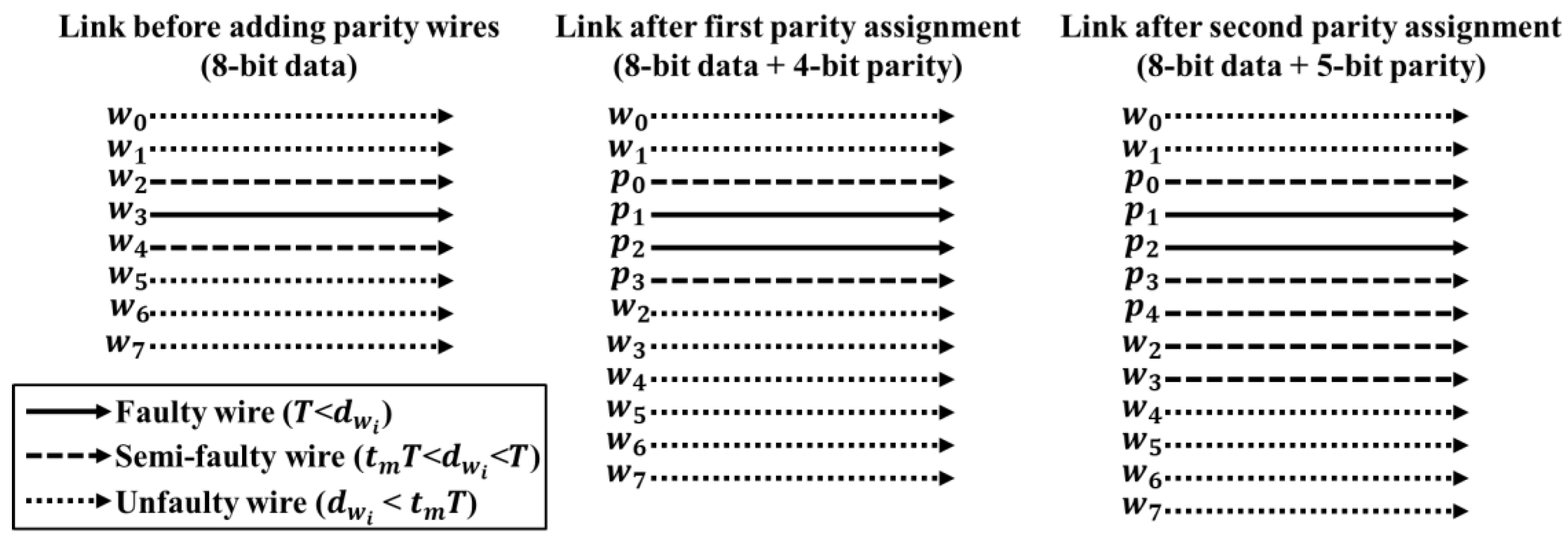
4.3. Non-Uniform ECC Generation
- Condition (1). Each column of the matrix must be unique.
- Condition (2). The result of the bitwise XOR operation between columns belonging to the faulty wire group should be unique.
- Condition (3). The result of bitwise XOR operation between all the columns generated in Condition (2) and the columns belonging to the semi-faulty wire group must be unique.
5. Average Latency Optimization Using Genetic Algorithm
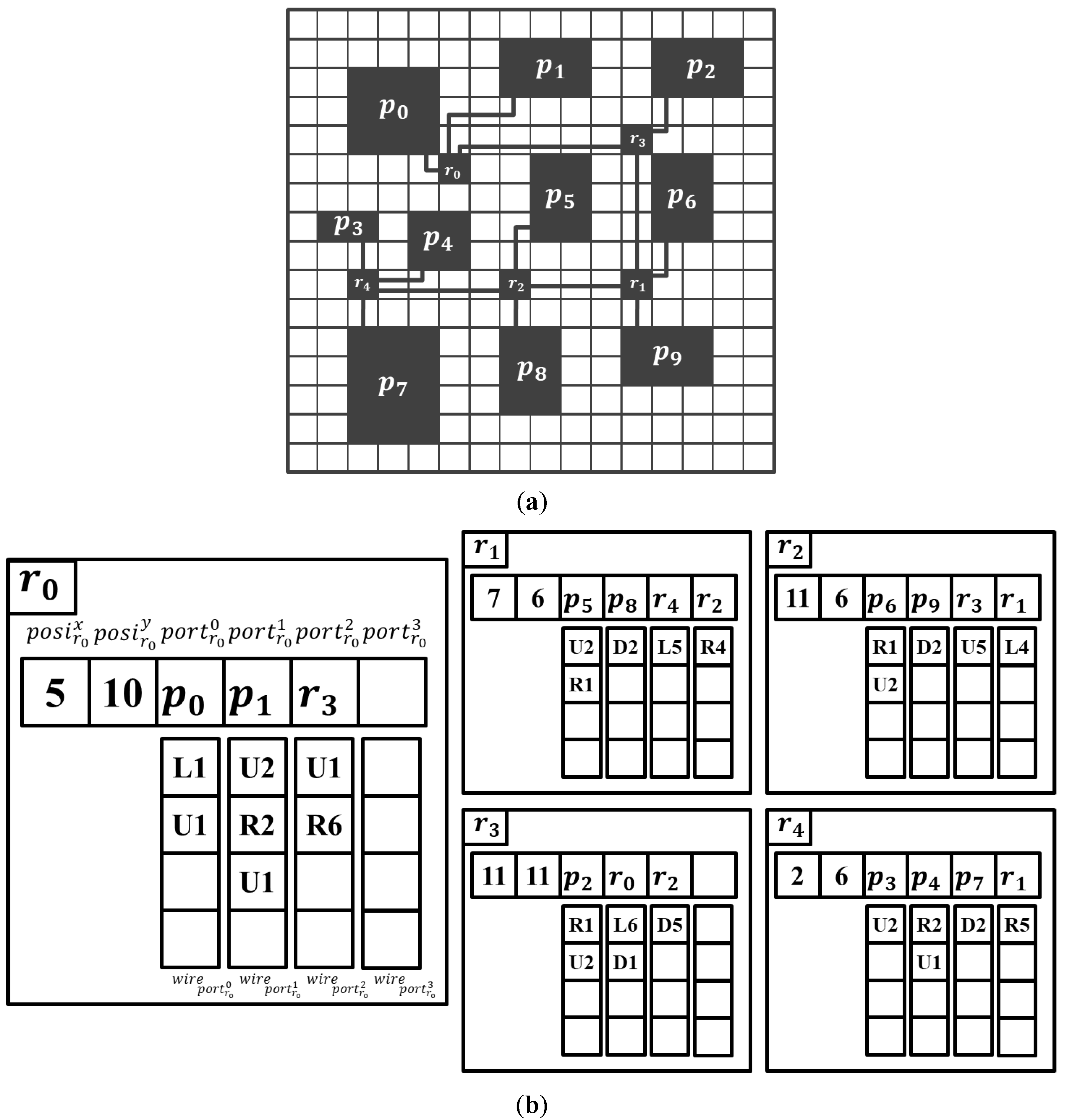
5.1. Data Representation of Topology Synthesis Case
5.2. Initialization
- Connectable router must satisfy the maximum link length constraint and the maximum router port constraint.
- Connectable router and the selected router must not exist in the same group.
5.3. Evaluation and Selection
5.4. Crossover
- Violation (1). For removing the cross-router, the links to the router are not removed.
- Violation (2). For removing the cross-router, the nodes connected to the router are disconnected.
- Violation (3). For creating a cross-router, PEs connected to the router are connected to two routers.
- Violation (4). For creating a cross-router, the router is disconnected from other routers.
5.5. Mutation
5.6. Local Search
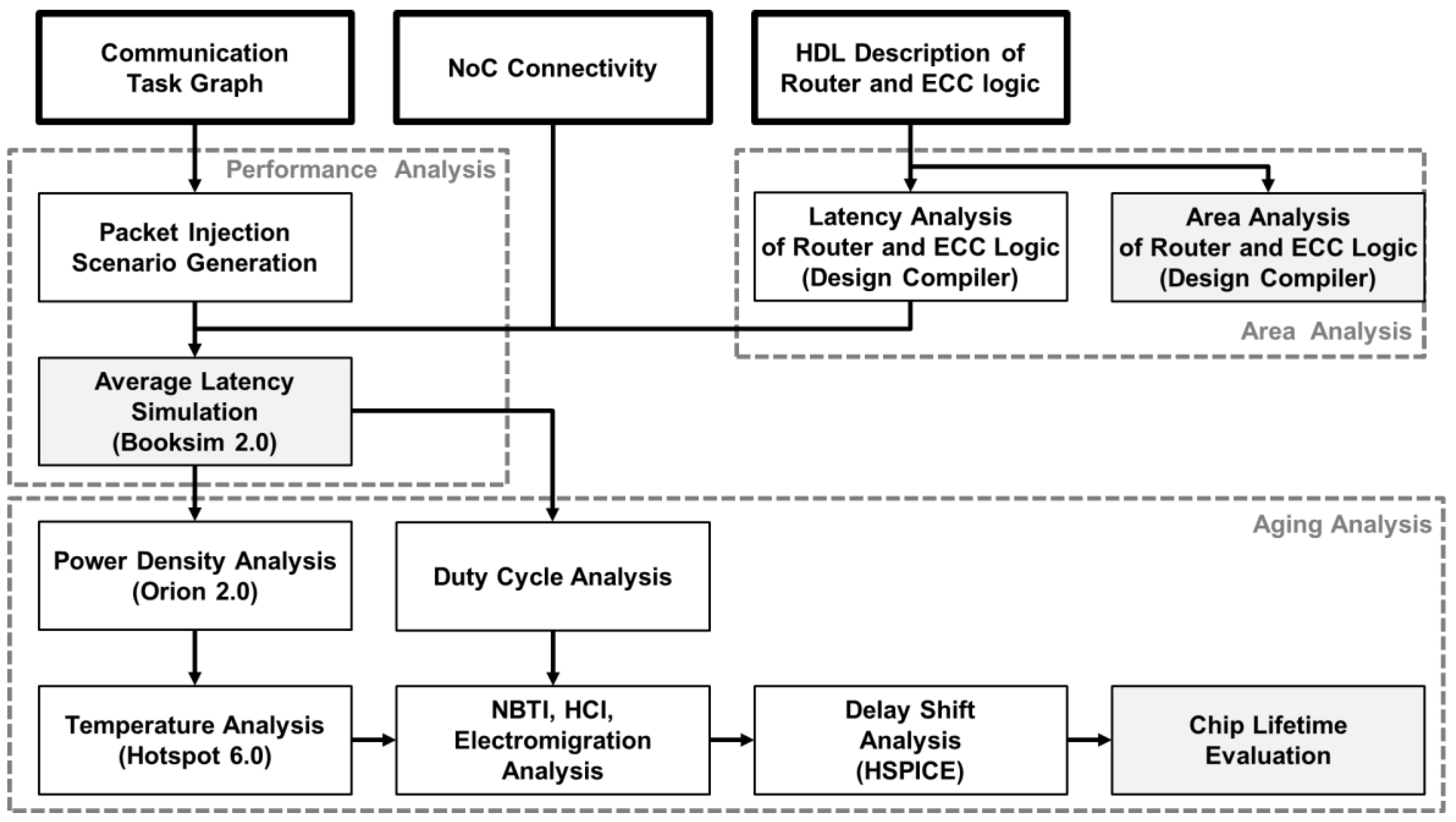
6. Simulation Results
6.1. Simulation Setup
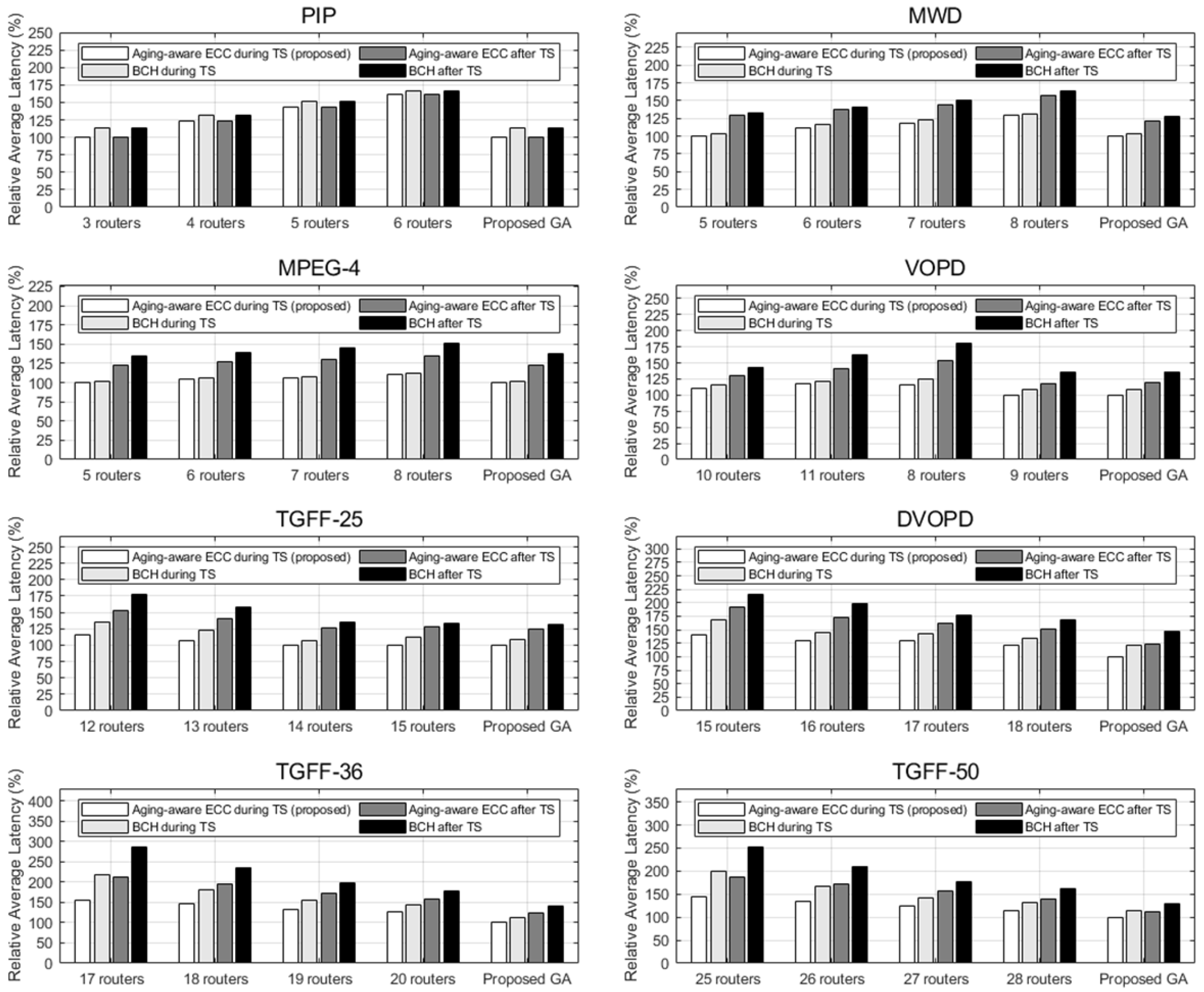
- To verify the average latency and area savings of aging-aware ECC, we created a topology synthesis solution that uses BCH logic at each link instead of aging-aware ECC. BCH logics are designed to correct all expected aging-induced delay faults within the lifetime of each link.
- To verify the improvement of the average latency and lifetime of the solution considering aging in the NoC design, we created an existing design solution that undergoes aging analysis after defining NoC connectivity. To ignore the aging element in GA, there is no local search that adds ECC logic and adjusts routers during the evaluation process. After the location and connectivity of routers and links are defined, the aging effect of each link is analyzed, and ECC logic is added to the links. Both cases with aging-aware ECC logics and cases with BCH logics are created.
- To verify the solution search efficiency of GA, we created a conventional GA-based topology synthesis model with a fixed number of routers. Because the reasonable number of routers in each network is not initially known, the average latency and computation speed were measured by adding up to three routers from the smallest number of routers.
6.2. Average Latency Analysis
6.3. Lifetime Analysis
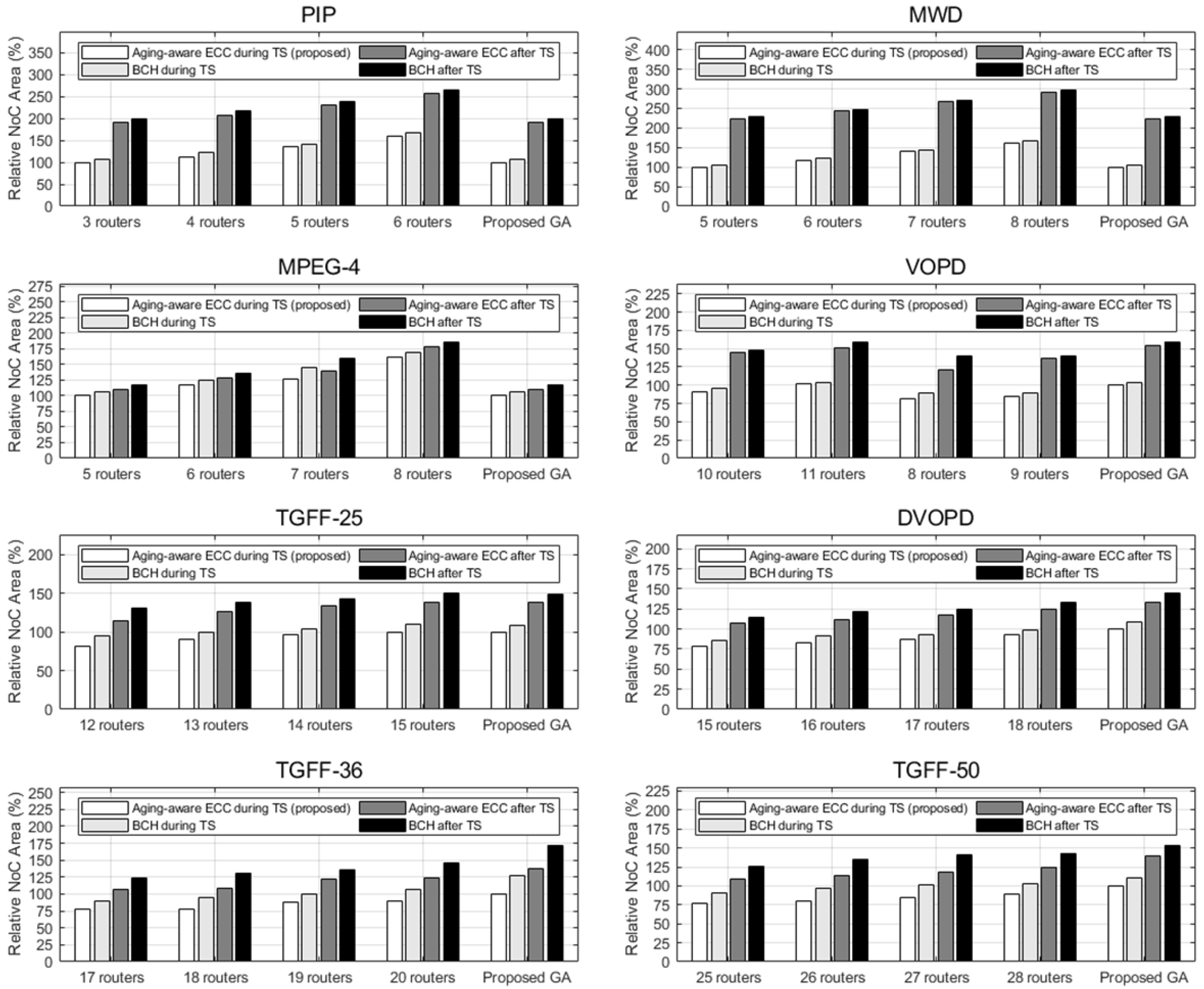
6.4. Area Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, S.; Jantsch, A.; Soininen, J.-P.; Forsell, M.; Millberg, M.; Oberg, J.; Tiensyrja, K.; Hemani, A. A network on chip architecture and design methodology. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI. New Paradigms for VLSI Systems Design. ISVLSI 2002, Pittsburgh, PA, USA, 25–26 April 2002; pp. 117–124. [Google Scholar]
- Cilardo, A.; Fusella, E. Design automation for application-specific on-chip interconnects: A survey. Integration 2016, 52, 102–121. [Google Scholar] [CrossRef]
- Bjerregaard, T.; Mahadevan, S. A survey of research and practices of network-on-chip. ACM Comput. Surv. (CSUR) 2006, 38, 1. [Google Scholar] [CrossRef]
- Venkataraman, N.; Kumar, R. Design and analysis of application specific network on chip for reliable custom topology. Comput. Netw. 2019, 158, 69–76. [Google Scholar] [CrossRef]
- Soumya, J.; Chattopadhyay, S. Application-Specific Network-on-Chip synthesis with flexible router Placement. J. Syst. Archit. 2013, 59, 361–371. [Google Scholar] [CrossRef]
- Jun, M.; Ro, W.W.; Chung, E.-Y. Exploiting implementation diversity and partial connection of routers in application-specific network-on-chip topology synthesis. IEEE Trans. Comput. 2012, 63, 1434–1445. [Google Scholar] [CrossRef]
- Seiculescu, C.; Murali, S.; Benini, L.; De Micheli, G. Sunfloor 3d: A tool for networks on chip topology synthesis for 3-d systems on chips. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2010, 29, 1987–2000. [Google Scholar] [CrossRef]
- Schonwald, T.; Zimmermann, J.; Bringmann, O.; Rosenstiel, W. Fully adaptive fault-tolerant routing algorithm for network-on-chip architectures. In Proceedings of the 10th Euromicro Conference on Digital System Design Architectures, Methods and Tools (DSD 2007), Lubeck, Germany, 29–31 August 2007; pp. 527–534. [Google Scholar]
- Ancajas, D.M.; Bhardwaj, K.; Chakraborty, K.; Roy, S. Wearout resilience in NoCs through an aging aware adaptive routing algorithm. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2014, 23, 369–373. [Google Scholar] [CrossRef]
- Park, D.; Nicopoulos, C.; Kim, J.; Vijaykrishnan, N.; Das, C.R. Exploring fault-tolerant network-on-chip architectures. In Proceedings of the International Conference on Dependable Systems and Networks (DSN’06), Philadelphia, PA, USA, 25–28 June 2006; pp. 93–104. [Google Scholar]
- Sengupta, D.; Sapatnekar, S.S. Estimating circuit aging due to BTI and HCI using ring-oscillator-based sensors. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 36, 1688–1701. [Google Scholar] [CrossRef]
- Chen, C.-C.; Liu, T.; Milor, L. System-level modeling of microprocessor reliability degradation due to bias temperature instability and hot carrier injection. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2016, 24, 2712–2725. [Google Scholar] [CrossRef]
- Gao, R.; Manut, A.B.; Ji, Z.; Ma, J.; Duan, M.; Zhang, J.F.; Franco, J.; Hatta, S.W.M.; Zhang, W.D.; Kaczer, B. Reliable time exponents for long term prediction of negative bias temperature instability by extrapolation. IEEE Trans. Electron Devices 2017, 64, 1467–1473. [Google Scholar] [CrossRef]
- Raparti, V.Y.; Kapadia, N.; Pasricha, S. ARTEMIS: An aging-aware runtime application mapping framework for 3D NoC-based chip multiprocessors. IEEE Trans. Multi Scale Comput. Syst. 2017, 3, 72–85. [Google Scholar] [CrossRef]
- Rohbani, N.; Shirmohammadi, Z.; Zare, M.; Miremadi, S.-G. LAXY: A location-based aging-resilient Xy-Yx routing algorithm for network on chip. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 36, 1725–1738. [Google Scholar] [CrossRef]
- Das, S.; Basu, K.; Doppa, J.R.; Pande, P.P.; Karri, R.; Chakrabarty, K. Abetting planned obsolescence by aging 3D networks-on-chip. In Proceedings of the 2018 Twelfth IEEE/ACM International Symposium on Networks-on-Chip (NOCS), Turin, Italy, 4–5 October 2018; pp. 1–8. [Google Scholar]
- Boraten, T.; Kodi, A.K. Runtime techniques to mitigate soft errors in Network-on-Chip (NoC) architectures. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 37, 682–695. [Google Scholar] [CrossRef]
- Poluri, P.; Louri, A. Shield: A reliable network-on-chip router architecture for chip multiprocessors. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 3058–3070. [Google Scholar] [CrossRef]
- Shamshiri, S.; Ghofrani, A.; Cheng, K.-T. End-to-end error correction and online diagnosis for on-chip networks. In Proceedings of the 2011 IEEE International Test Conference, Anaheim, CA, USA, 20–22 September 2011; pp. 1–10. [Google Scholar]
- Campos-Cruz, A.; Espinosa-Flores-Verdad, G.; Torres-Jacome, A.; Tlelo-Cuautle, E. On the Prediction of the Threshold Voltage Degradation in CMOS Technology Due to Bias-Temperature Instability. Electronics 2018, 7, 427. [Google Scholar] [CrossRef]
- Chen, P.; Keutzer, K. Towards true crosstalk noise analysis. In Proceedings of the 1999 IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 7–11 November 1999; pp. 132–138. [Google Scholar]
- Chen, W.; Gupta, S.K.; Breuer, M.A. Analytic models for crosstalk delay and pulse analysis under non-ideal inputs. In Proceedings of the International Test Conference 1997, Washington, DC, USA, 6 November 1997; pp. 809–818. [Google Scholar]
- Bhardwaj, S.; Wang, W.; Vattikonda, R.; Cao, Y.; Vrudhula, S. Predictive modeling of the NBTI effect for reliable design. In Proceedings of the IEEE Custom Integrated Circuits Conference 2006, San Jose, CA, USA, 10–13 September 2006; pp. 189–192. [Google Scholar]
- Bravaix, A.; Guerin, C.; Huard, V.; Roy, D.; Roux, J.; Vincent, E. Hot-carrier acceleration factors for low power management in DC-AC stressed 40 nm NMOS node at high temperature. In Proceedings of the 2009 IEEE International Reliability Physics Symposium, Montreal, QC, Canada, 26–30 April 2009; pp. 531–548. [Google Scholar]
- Sun, M.; Pecht, M.G.; Barbe, D. Lifetime rc time delay of on-chip copper interconnect. IEEE Trans. Semicond. Manuf. 2002, 15, 253–259. [Google Scholar] [CrossRef]
- Murali, S.; Theocharides, T.; Vijaykrishnan, N.; Irwin, M.J.; Benini, L.; De Micheli, G. Analysis of error recovery schemes for networks on chips. IEEE Des. Test Comput. 2005, 22, 434–442. [Google Scholar] [CrossRef]
- Yu, Q.; Ampadu, P. Dual-layer adaptive error control for network-on-chip links. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2011, 20, 1304–1317. [Google Scholar] [CrossRef]
- Poluri, P.; Louri, A. A soft error tolerant network-on-chip router pipeline for multi-core systems. IEEE Comput. Archit. Lett. 2014, 14, 107–110. [Google Scholar] [CrossRef]
- Srinivasan, K.; Chatha, K.S. ISIS: A genetic algorithm based technique for custom on-chip interconnection network synthesis. In Proceedings of the 18th International Conference on VLSI Design held jointly with 4th International Conference on Embedded Systems Design, Kolkata, India, 3–7 January 2005; pp. 623–628. [Google Scholar]
- Leary, G.; Srinivasan, K.; Mehta, K.; Chatha, K.S. Design of network-on-chip architectures with a genetic algorithm-based technique. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2009, 17, 674–687. [Google Scholar] [CrossRef]
- Lai, G.; Lin, X.; Lai, S. GA-based floorplan-aware topology synthesis of application-specific network-on-chip. In Proceedings of the 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems, Xiamen, China, 29–31 October 2010; pp. 554–558. [Google Scholar]
- Bahirat, S.; Pasricha, S. A software framework for rapid application-specific hybrid photonic network-on-chip synthesis. Electronics 2016, 5, 21. [Google Scholar] [CrossRef]
- Fang, J.; Zong, H.; Zhao, H.; Cai, H. Intelligent Mapping Method for Power Consumption and Delay Optimization Based on Heterogeneous NoC Platform. Electronics 2019, 8, 912. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Choi, J.Y. A genetic algorithm for job sequencing problems with distinct due dates and general early-tardy penalty weights. Comput. Oper. Res. 1995, 22, 857–869. [Google Scholar] [CrossRef]
- Offman, M.N.; Tournier, A.L.; Bates, P.A. Alternating evolutionary pressure in a genetic algorithm facilitates protein model selection. BMC Struct. Biol. 2008, 8, 34. [Google Scholar] [CrossRef] [PubMed]
- Manning, T.; Sleator, R.D.; Walsh, P. Naturally selecting solutions: The use of genetic algorithms in bioinformatics. Bioengineered 2013, 4, 266–278. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Michelogiannakis, G.; Becker, D.; Towles, B.; Dally, W.J. Booksim 2.0 User’s Guide; Standford University: Stanford, CA, USA, 2010. [Google Scholar]
- Wang, H.-S.; Zhu, X.; Peh, L.-S.; Malik, S. Orion: A power-performance simulator for interconnection networks. In Proceedings of the 35th annual ACM/IEEE international symposium on Microarchitecture, Istanbul, Turkey, 18–22 November 2002; pp. 294–305. [Google Scholar]
- Zhang, R.; Stan, M.R.; Skadron, K. Hotspot 6.0: Validation, Acceleration and Extension; University of Virginia: Charlottesville, VA, USA, 2015; (Tech. Rep.). [Google Scholar]
- Sanchez, D.; Michelogiannakis, G.; Kozyrakis, C. An analysis of on-chip interconnection networks for large-scale chip multiprocessors. ACM Trans. Archit. Code Optim. TACO 2010, 7, 4. [Google Scholar] [CrossRef]
- Dick, R.P.; Rhodes, D.L.; Wolf, W. TGFF: Task graphs for free. In Proceedings of the Sixth International Workshop on Hardware/Software Codesign (CODES/CASHE’98), Seattle, WA, USA, 18 March 1998; pp. 97–101. [Google Scholar]



| Parameters | Definitions |
| Horizontal position of left end of PE on chip | |
| Vertical position of bottom end of PE on chip | |
| Horizontal size of PE | |
| Vertical size of PE | |
| Maximum link length constraint in network | |
| Maximum number of ports in a router | |
| Latency of transmission of a router | |
| Variables | Definitions |
| Horizontal position of router | |
| Vertical position of router | |
| PE or router connected to -th port of router | |
| Wire placement information of link from router to | |
| Variable assigned value 1 if a link exists between PE and router . Otherwise, value is 0 | |
| Variable assigned value 1 if a link exists between routers and . Otherwise, value is 0 | |
| Link length between PE and router | |
| Link length between routers and | |
| Additional latency of link caused by ECC logic | |
| Variable that has value 1 if there is a routing path from routers to . Otherwise, value is 0 |
| Parameter | Value | Description |
|---|---|---|
| Time exponent for NBTI | ||
| Time exponent for HCI | ||
| Electron charge () | ||
| Oxide thickness () | ||
| Dielectric constant () | ||
| Fitting parameter () | ||
| Boltzmann constant () | ||
| Oxide capacitance per unit area ( | ||
| Operating voltage () | ||
| Initial threshold voltage () | ||
| Fitting parameter | ||
| Activation energy ( | ||
| Temperature ( | ||
| Electric field () | ||
| Peak electric field () | ||
| Duty cycle | ||
| Stress period () | ||
| Aging period () | ||
| Back diffusion constant | ||
| Healing factor | ||
| Height of wire () | ||
| Frequency factor in copper oxide () | ||
| Activation energy in copper oxide () | ||
| Gas constant () | ||
| Absolute temperature of wire () |
| Bit Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Encoded data | ||||||||||||||
| Parity bit coverage | - | - | 1 | 0 | 0 | 0 | 0 | 1 | 0 | - | - | - | - | |
| - | - | 0 | 1 | 0 | 0 | 0 | 0 | 1 | - | - | - | - | ||
| - | - | 0 | 0 | 1 | 0 | 0 | 1 | 0 | - | - | - | - | ||
| - | - | 0 | 0 | 0 | 1 | 0 | 0 | 1 | - | - | - | - | ||
| - | - | 0 | 0 | 0 | 0 | 1 | 1 | 1 | - | - | - | - | ||
| Decimal | - | - | 1 | 2 | 4 | 8 | 16 | 21 | 26 | - | - | - | ||
| Application | # of PEs | MAX() | AVG() | Chip Size | PE Size |
|---|---|---|---|---|---|
| Picture-in-Picture (PIP) | 8 | 540 | 215.6 | 10 × 10 | 2.5 × 1.5, 1 × 1, 1 × 2, 1 × 2.5, 1.5 × 1, 1 × 2.5, 2.5 × 1.5, 1 × 1 |
| Multi-Window Display (MWD) | 12 | 128 | 93.33 | 12 × 12 | 2.5 × 1, 2.5 × 2.5, 3 × 2.5, 2.5 × 1.5, 1 × 2.5, 1.5 × 1.5, 2 × 1.5, 2.5 × 2, 2 × 1, 2 × 1.5, 1.5 × 2, 1.5 × 2.5 |
| Moving Picture Experts Group Phase 4 (MPEG-4) | 12 | 910 | 266.6 | 12 × 12 | 1.5 × 2, 2 × 1, 2.5 × 1.5, 3 × 2.5, 1 × 3, 2 × 1.5, 2 × 1.5, 1 × 2, 1.5 × 3, 2 × 1.5, 2 × 2.5, 3 × 2.5 |
| Video Object Plane Decoder (VOPD) | 16 | 500 | 177.7 | 14 × 14 | 1 × 2.5, 3 × 1, 3 × 3, 2 × 2.5, 2 × 1, 2.5 × 1, 1.5 × 1, 2 × 2.5, 2 × 1.5, 2 × 1.5, 2.5 × 3, 2 × 1.5, 1 × 1, 2 × 1.5, 1 × 1, 2 × 1 |
| TGFF-25 | 25 | 526 | 245.8 | 16 × 16 | 1.5 × 1.5, 1 × 1.5, 1.5 × 1, 2 × 2.5, 3 × 1.5, 2 × 1, 1.5 × 2, 1 × 1.5, 1.5 × 2, 2.5 × 1, 2.5 × 2, 2.5 × 3, 1.5 × 3, 2.5 × 1.5, 2.5 × 1, 2.5 × 2.5, 3 × 2.5, 2.5 × 1.5, 1 × 2.5, 1.5 × 1.5, 2 × 1.5, 2.5 × 2, 2 × 1, 2 × 1.5, 1.5 × 2 |
| Dual Video Object Plane Decoder (DVOPD) | 32 | 540 | 215.6 | 20 × 20 | 1 × 2.5, 3 × 1, 3 × 3, 2 × 2.5, 2 × 1, 2.5 × 1, 1.5 × 1, 2 × 2.5, 2 × 1.5, 2 × 1.5, 2.5 × 3, 2 × 1.5, 1 × 1, 2 × 1.5, 1 × 1, 2 × 1, 1 × 2.5, 3 × 1, 3 × 3, 2 × 2.5, 2 × 1, 2.5 × 1, 1.5 × 1, 2 × 2.5, 2 × 1.5, 2 × 1.5, 2.5 × 3, 2 × 1.5, 1 × 1, 2 × 1.5, 1 × 1, 2 × 1 |
| TGFF-36 | 36 | 624 | 287.7 | 24 × 24 | 2.5 × 1, 2.5 × 2.5, 3 × 2.5, 2.5 × 1.5, 1 × 2.5, 1.5 × 1.5, 2 × 1.5, 2.5 × 2, 2 × 1, 2 × 1.5, 1.5 × 2, 1.5 × 2.5, 2.5 × 1.5, 1 × 1, 1 × 2, 1 × 2.5, 1.5 × 1, 1 × 2.5, 2.5 × 1.5, 1 × 1, 1 × 2.5, 3 × 1, 3 × 3, 2 × 2.5, 2 × 1, 2.5 × 1, 1.5 × 1, 2 × 2.5, 2 × 1.5, 2 × 1.5, 2.5 × 3, 2 × 1.5, 1 × 1, 2 × 1.5, 1 × 1, 2 × 1 |
| TGFF-50 | 50 | 676 | 313 | 30 × 30 | 1.5 × 2, 2 × 1, 2.5 × 1.5, 3 × 2.5, 1 × 3, 2 × 1.5, 2 × 1.5, 1 × 2, 1.5 × 3, 2 × 1.5, 2 × 2.5, 3 × 2.5, 1 × 2.5, 3 × 1, 3 × 3, 2 × 2.5, 2 × 1, 2.5 × 1, 1.5 × 1, 2 × 2.5, 2 × 1.5, 2 × 1.5, 2.5 × 3, 2 × 1.5, 1 × 1, 2 × 1.5, 1 × 1, 2 × 1, 2.5 × 1.5, 1 × 1, 1 × 2, 1 × 2.5, 1.5 × 1, 1 × 2.5, 2.5 × 1.5, 1 × 1, 1.5 × 1.5, 1 × 1.5, 1.5 × 1, 2 × 2.5, 3 × 1.5, 2 × 1, 1.5 × 2, 1 × 1.5, 1.5 × 2, 2.5 × 1, 2.5 × 2, 2.5 × 3, 1.5 × 3, 2.5 × 1.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.S.; Kim, S.; Han, T.H. Aging-Resilient Topology Synthesis of Heterogeneous Manycore Network-On-Chip Using Genetic Algorithm with Flexible Number of Routers. Electronics 2019, 8, 1458. https://doi.org/10.3390/electronics8121458
Lee YS, Kim S, Han TH. Aging-Resilient Topology Synthesis of Heterogeneous Manycore Network-On-Chip Using Genetic Algorithm with Flexible Number of Routers. Electronics. 2019; 8(12):1458. https://doi.org/10.3390/electronics8121458
Chicago/Turabian StyleLee, Young Sik, SoYoung Kim, and Tae Hee Han. 2019. "Aging-Resilient Topology Synthesis of Heterogeneous Manycore Network-On-Chip Using Genetic Algorithm with Flexible Number of Routers" Electronics 8, no. 12: 1458. https://doi.org/10.3390/electronics8121458
APA StyleLee, Y. S., Kim, S., & Han, T. H. (2019). Aging-Resilient Topology Synthesis of Heterogeneous Manycore Network-On-Chip Using Genetic Algorithm with Flexible Number of Routers. Electronics, 8(12), 1458. https://doi.org/10.3390/electronics8121458






