Rotation Angle Estimation of JPEG Compressed Image by Cyclic Spectrum Analysis
Abstract
1. Introduction
2. Image Cyclic Spectrum and Its Rotation Theory Trajectory
3. The Proposed Method
- (1)
- Calculate the second-order statistics (covariance) of the image (the rotated image processed by JPEG compression) and its cyclic spectral amplitude components.
- (2)
- Employ semi-soft threshold wavelet transform to denoise the four neighborhood amplitude components of the theoretical trajectory in the cyclic spectrum.
- (3)
- Perform a super sorting operation on the amplitude data.
- (4)
- Select the peak point according to the principle of amplitude–distance.
- (5)
- The rotation angle of the JPEG image is estimated according to the corresponding theoretical peak point position coordinates.
3.1. Cyclic Spectrum Preprocessing Based on Semi-Soft Threshold Wavelet
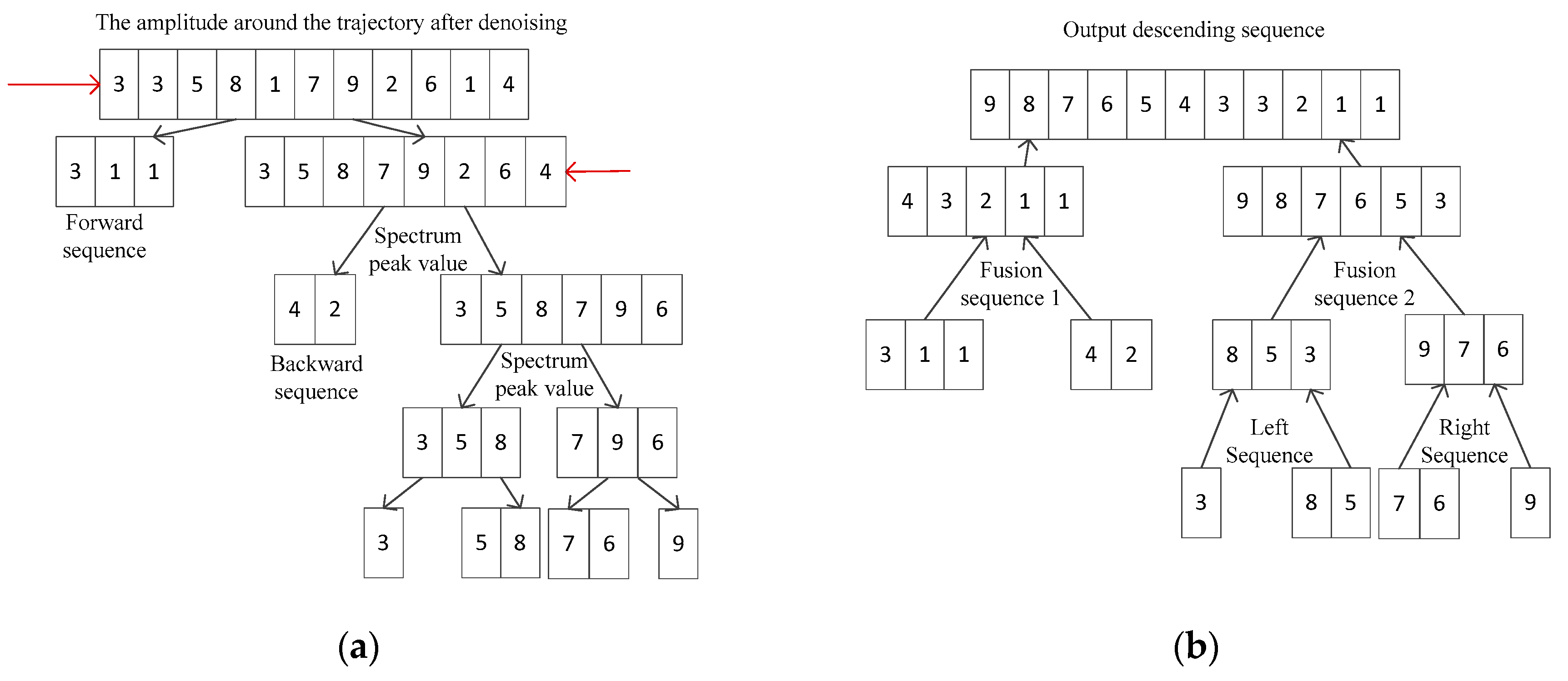
3.2. Image Rotation Angle Estimation Based on Super Sorting
| Algorithm 1 Super_Sort (L) |
| Input: Spectral data column L (containing n data) around trajectory paths after wavelet pretreatment |
| Output: Spectral data around trajectory paths in descending order |
| 1: If length (L) < 1 then |
| 2: Return () |
| 3: else |
| 4: Forward sequence ← empty matrix |
| 5: Backward sequence ← empty matrix |
| 6: /* Forward Selection*/ |
| 7: current minimum amplitude ← L [left] |
| 8: for i ← 1 to length (L) by 1 do |
| 9: if L[i] ≤ current minimum amplitude |
| 10: then current minimum amplitude ← L [i] |
| 11: remove L [i] to forward sequence |
| 12: end |
| 13: /*Backward Selection*/ |
| 14: if length(L) > 1 |
| 15: then current minimum amplitude ← L [length (L)] |
| 16: for i ← length (L) to 1 by 1 do |
| 17: if L [i] ≤ current minimum amplitude then |
| 18: then current minimum amplitude ← L [i] |
| 19: remove L [i] to backward sequence |
| 20: end |
| 21: sequence 1 ← Fusion of forward sequence and backward sequence fusion |
| 22: /* Partition*/ |
| 23: Middle ← empty matrix |
| 24: Middle1 ← empty matrix |
| 25: Middle2 ← empty matrix |
| 26: while length (L) > 1 |
| 27: do Middle ← length (L)/2 |
| 28: Middle1 ← (0, middle) |
| 29: Middle2 ← (middle + 1, length(L)) |
| 30: Middle1 ← call super_sort (Middle1) |
| 31: Middle2 ← call super_sort (Middle2) |
| 32: end |
| 33: sequence 2 ← the fusion of middle1 and middle2 |
| 34: Return the fusion of sequence 1 and 2 |
4. Experimental Results and Discussion
4.1. The Evaluation Criteria of Algorithm
| Algorithm 2 Image positioning algorithm |
| Input: The rotated image |
| Output: Locate the tampered part of the image |
| 1: Input the rotated image I |
| 2: /* Set the image block size B and lag range K */ |
| 3: B ← 128 × 128 |
| 4: K ← 9 |
| 5: /*Acquire the rows i and columns j of the rotated image*/ |
| 6: [i,j] ← size(I) |
| 7: X ← j:j + B + sqrt (K) − 1 |
| 8: Y ← i:I + B + sqrt (K) − 1 |
| 9: estimated angle ← call the angle estimator function |
| 10: If absolute (estimated angle − actual angle) < 1 |
| 11: then I (X,Y) ← the tamper part |
| 12: marked with red box |
| 13: end |
4.2. Rotation Angle Estimation Error and Positioning Results of Uncompressed Images
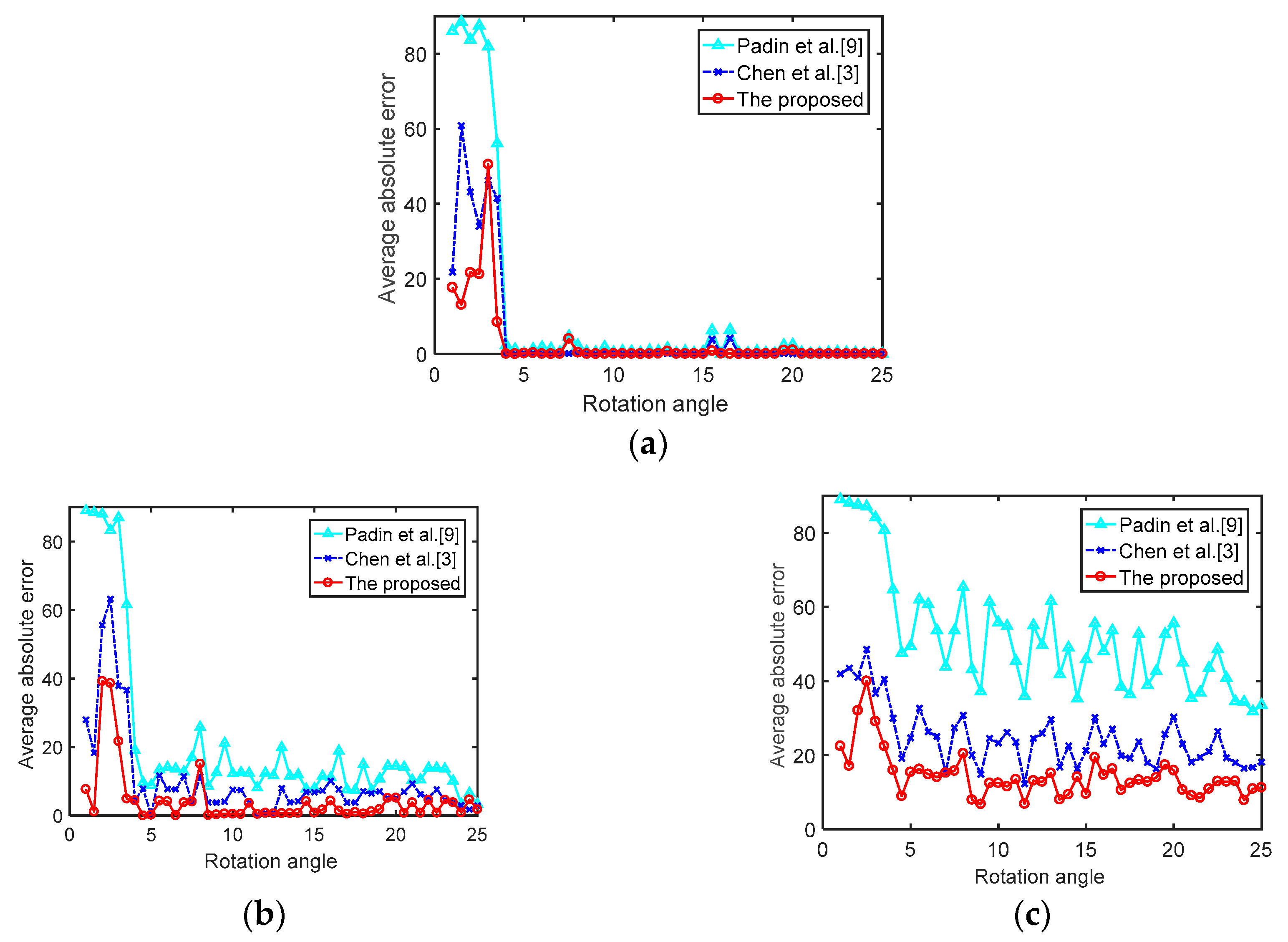
4.3. Image Rotation Estimation Results under JPEG Compression
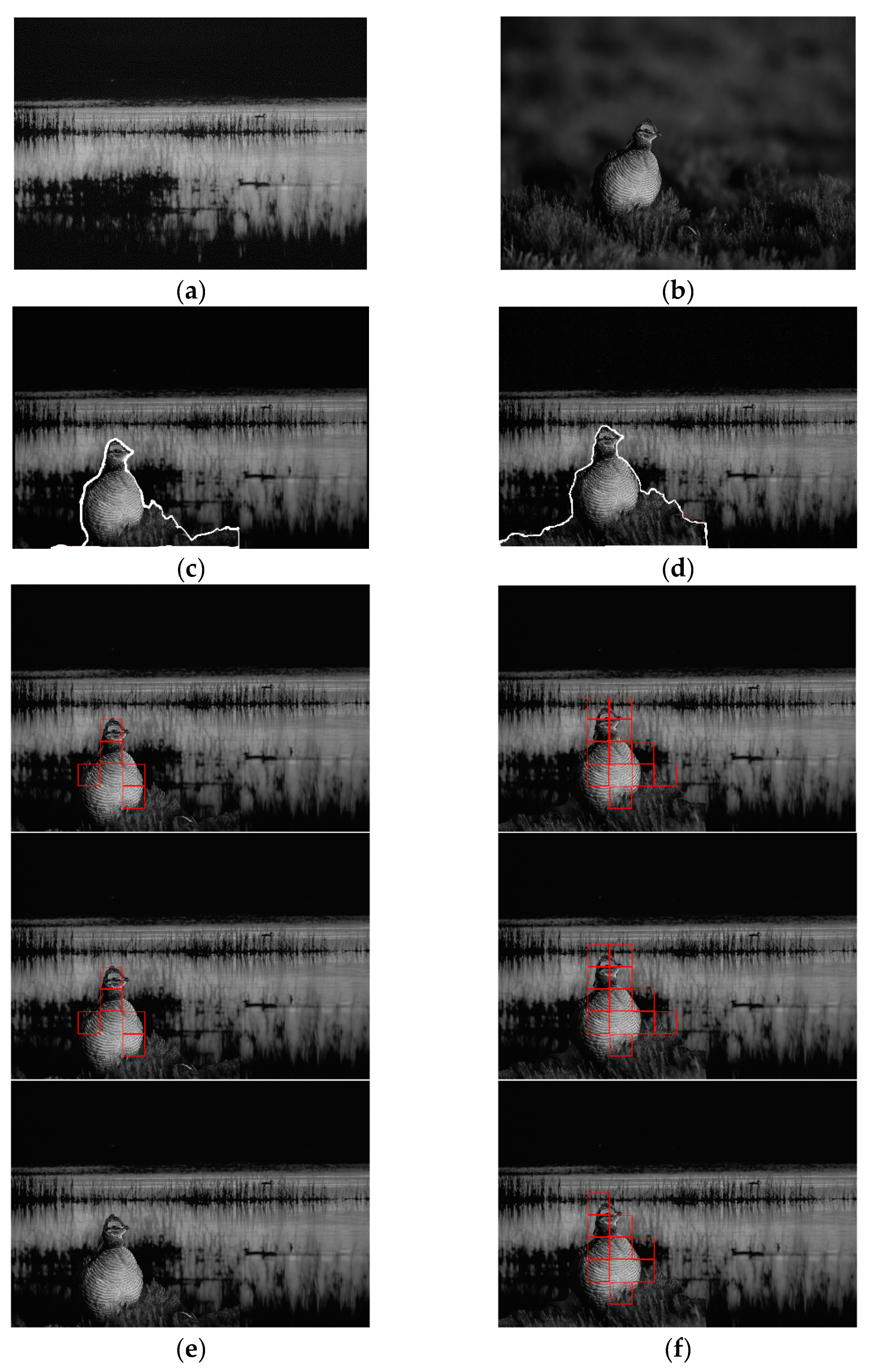
4.4. The Location Detection of Tampered Image
4.5. Analysis of Algorithm Complexity and Time Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Islam, M.M.; Karmakar, G.C.; Kamruzzaman, J.; Mueshed, M. Detecting Splicing and Copy-Move Attacks in Color Images. In Proceedings of the 2018 Digital Image Computing: Techniques and Applications (DICTA), Canberra, Australia, 10–13 December 2018; pp. 1–7. [Google Scholar]
- Marra, F.; Poggi, G.; Sansone, C.; Verdoliva, L. Blind PRNU-based Image Clustering for Source Identification. IEEE Trams. Inf. Foren. Sec. 2017, 12, 2197–2211. [Google Scholar] [CrossRef]
- Chen, C.L.; Ni, J.Q.; Shen, Z.Y.; Shi, Y.Q. Blind Forensics of Successive Geometric Transformations in Digital Images Using Spectral Method: Theory and Applications. IEEE Trans. Image Process. 2017, 26, 811–2824. [Google Scholar] [CrossRef] [PubMed]
- Popescu, A.C.; Farid, H. Exposing digital forgeries by detecting traces of resampling. IEEE Trans. Image Process. 2005, 53, 758–767. [Google Scholar] [CrossRef]
- Kirchner, M. Fast and reliable resampling detection by spectral analysis of fixed linear predictor residue. In Proceedings of the Workshop on Multimedia & Security, Oxford, UK, 22–23 September 2008; ACM: New York, NY, USA; pp. 11–20. [Google Scholar]
- Mahdian, B.; Saic, S. Blind Authentication Using Periodic Properties of Interpolation. IEEE Trams. Inf. Foren. Sec. 2008, 3, 529–538. [Google Scholar] [CrossRef]
- Gallagher, A.C. Detection of linear and cubic interpolation in JPEG compressed images. In Proceedings of the 2nd Canadian Conference on Computer and Robot Vision (CRV’05), Victoria, BC, Canada, 9–11 May 2005; IEEE: Piscataway, NJ, USA; pp. 65–72. [Google Scholar]
- Wei, W.M.; Wang, S.Z.; Zhang, X.P.; Tang, Z.J. Estimation of Image Rotation Angle Using Interpolation-Related Spectral Signatures With Application to Blind Detection of Image Forgery. IEEE Trams. Inf. Foren. Sec. 2010, 5, 507–517. [Google Scholar] [CrossRef]
- Vazquez-Padin, D.; Mosquera, C.; Fernando, P. Two-dimensional statistical test for the presence of almost cyclostationarity on images. In Proceedings of the International Conference on Image Processing, ICIP 2010, Hong Kong, China, 26–29 September 2010; IEEE: Piscataway, NJ, USA; pp. 1745–1748. [Google Scholar]
- Chen, C.L.; Ni, J.Q.; Shen, Z.Y. Effective Estimation of Image Rotation Angle Using Spectral Method. IEEE Signal. Pro. Lett. 2014, 21, 890–894. [Google Scholar]
- Vazquez-Padin, D.; Perez-Gonzalez, F.; Comesana-Alfaro, P. A Random Matrix Approach to the Forensic Analysis of Upscaled Images. IEEE T. Inf. Foren. Sec. 2017, 12, 2115–2130. [Google Scholar] [CrossRef]
- Nhan, L.; Florent, R. Statistical Detector of Resampled TIFF Images. In Proceedings of the 2018 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Louisville, KY, USA, 6–8 December 2018; IEEE: Piscataway, NJ, USA; pp. 331–335. [Google Scholar]
- Liu, X.J.; Lu, W.; Huang, T.; Liu, H.M.; Xue, Y.J.; Yeung, Y.L. Scaling factor estimation on JPEG compressed images by cyclostationarity analysis. Multimed. Tools Appl. 2018, 78, 7947–7964. [Google Scholar] [CrossRef]
- Liu, X.; Lu, W.; Zhang, Q.; Huang, J.W. Downscaling Factor Estimation on Pre-JPEG Compressed Images. IEEE Trans. Circ. Syst. Vid. 2019, 1. [Google Scholar] [CrossRef]
- Qian, Y. A Wavelet Denoising Method Based on Improved Threshold and Autocorrelation. In Proceedings of the 30th Chinese Control and Decision Making Conference (CCDC 2018), Shenyang, China, 9–11 June 2018. [Google Scholar]
- Zhang, Y.; He, N.; Zhen, X.; Xin, S. Image Denoising Based on the Wavelet Semi-soft Threshold and Total Variation. In Proceedings of the 2017 International Conference on Vision, Image and Signal Processing (ICVISP), Osaka, Japan, 22–24 September 2017; IEEE: Piscataway, NJ, USA; pp. 55–62. [Google Scholar]
- Shen, C.; Wu, A.; Bai, N.F.; Fan, H.H. TWT output signal denoising based on improved wavelet threshold. In Proceedings of the 2017 18th International Vacuum Electronics Conference (IVEC), London, UK, 1 April 2017; pp. 1–2. [Google Scholar]
- Khurana, M.; Faujdar, N.; Saraswat, S. Hybrid bucket sort switching internal sorting based on the data inside the bucket. In Proceedings of the 2017 6th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 1 September 2017; pp. 476–482. [Google Scholar]
- Gugale, Y. Super Sort Sorting Algorithm. In Proceedings of the 2018 3rd International Conference for Convergence in Technology (I2CT), Pune, India, 6–8 April 2018; pp. 1–5. [Google Scholar]
- Zhang, H.; Sindagi, V.; Patel, V.M. Image De-raining Using a Conditional Generative Adversarial Network. IEEE Trans. Circuits Syst. Video Technol. 2017, 1. [Google Scholar] [CrossRef]
- Morales-Cruz, E.; Garcia-Hernandez, J.J. Detection of JPEG compression on bitmap image based on phase spectrum statistical feature. In Proceedings of the 2017 International Conference on Information Society (I-Society), Dublin, Ireland, 1 July 2017; pp. 111–115. [Google Scholar]
- Wang, Z.; Zheng, L.; Junyuan, W. Research of novel bearing fault diagnosis method based on improved krill herd algorithm and kernel Extreme Learning Machine. Complexity 2019. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W.Q. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]




| θ ° | QF = 95 | QF = 90 | QF = 85 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Proposed Algorithm | Chen et al. [3] | Vazquez-Padin et al. [9] | Proposed Algorithm | Chen et al. [3] | Vazquez-Padin et al. [9] | Proposed Algorithm | Chen et al. [3] | Vazquez-Padin et al. [9] | |
| 1° | 0.640 | 0.485 | 0.000 | 0.435 | 0.260 | 0.000 | 0.190 | 0.095 | 0.000 |
| 2° | 0.450 | 0.470 | 0.000 | 0.340 | 0.300 | 0.000 | 0.200 | 0.175 | 0.005 |
| 3° | 0.380 | 0.465 | 0.000 | 0.335 | 0.260 | 0.000 | 0.175 | 0.110 | 0.000 |
| 4° | 0.910 | 0.885 | 0.000 | 0.665 | 0.615 | 0.000 | 0.370 | 0.280 | 0.000 |
| 5° | 0.910 | 0.915 | 0.910 | 0.775 | 0.725 | 0.700 | 0.530 | 0.465 | 0.420 |
| 6° | 0.890 | 0.855 | 0.000 | 0.640 | 0.620 | 0.000 | 0.340 | 0.275 | 0.000 |
| 7° | 0.975 | 0.955 | 0.930 | 0.880 | 0.885 | 0.730 | 0.800 | 0.795 | 0.470 |
| 8° | 0.925 | 0.890 | 0.000 | 0.845 | 0.705 | 0.000 | 0.650 | 0.565 | 0.005 |
| 9° | 0.965 | 0.940 | 0.935 | 0.810 | 0.785 | 0.770 | 0.655 | 0.575 | 0.540 |
| 10° | 0.905 | 0.890 | 0.885 | 0.700 | 0.640 | 0.625 | 0.455 | 0.345 | 0.300 |
| 11° | 0.945 | 0.935 | 0.930 | 0.775 | 0.715 | 0.690 | 0.520 | 0.465 | 0.425 |
| 12° | 0.930 | 0.905 | 0.885 | 0.730 | 0.690 | 0.630 | 0.415 | 0.315 | 0.280 |
| 13° | 0.915 | 0.830 | 0.600 | 0.655 | 0.530 | 0.400 | 0.340 | 0.215 | 0.140 |
| 14° | 0.945 | 0.925 | 0.910 | 0.760 | 0.700 | 0.680 | 0.545 | 0.390 | 0.345 |
| 15° | 0.920 | 0.920 | 0.915 | 0.740 | 0.700 | 0.680 | 0.515 | 0.400 | 0.380 |
| 16° | 0.915 | 0.900 | 0.900 | 0.700 | 0.665 | 0.635 | 0.425 | 0.405 | 0.345 |
| 17° | 0.950 | 0.930 | 0.930 | 0.790 | 0.775 | 0.745 | 0.580 | 0.525 | 0.470 |
| 18° | 0.955 | 0.935 | 0.930 | 0.760 | 0.680 | 0.625 | 0.520 | 0.350 | 0.265 |
| 19° | 0.940 | 0.925 | 0.920 | 0.755 | 0.735 | 0.715 | 0.525 | 0.485 | 0.395 |
| 20° | 0.940 | 0.915 | 0.860 | 0.725 | 0.595 | 0.540 | 0.450 | 0.245 | 0.299 |
| 21° | 0.960 | 0.945 | 0.940 | 0.850 | 0.785 | 0.750 | 0.655 | 0.525 | 0.485 |
| 22° | 0.950 | 0.925 | 0.925 | 0.780 | 0.750 | 0.680 | 0.545 | 0.410 | 0.360 |
| 23° | 0.950 | 0.935 | 0.930 | 0.765 | 0.730 | 0.680 | 0.570 | 0.465 | 0.390 |
| 24° | 0.970 | 0.945 | 0.940 | 0.850 | 0.810 | 0.805 | 0.685 | 0.560 | 0.480 |
| 25° | 0.955 | 0.950 | 0.950 | 0.840 | 0.810 | 0.479 | 0.640 | 0.525 | 0.485 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, S.; Zhang, Y.; Song, W.; Wu, F.; Zhang, L. Rotation Angle Estimation of JPEG Compressed Image by Cyclic Spectrum Analysis. Electronics 2019, 8, 1431. https://doi.org/10.3390/electronics8121431
Dai S, Zhang Y, Song W, Wu F, Zhang L. Rotation Angle Estimation of JPEG Compressed Image by Cyclic Spectrum Analysis. Electronics. 2019; 8(12):1431. https://doi.org/10.3390/electronics8121431
Chicago/Turabian StyleDai, Shuxian, Yujin Zhang, Wanqing Song, Fei Wu, and Lijun Zhang. 2019. "Rotation Angle Estimation of JPEG Compressed Image by Cyclic Spectrum Analysis" Electronics 8, no. 12: 1431. https://doi.org/10.3390/electronics8121431
APA StyleDai, S., Zhang, Y., Song, W., Wu, F., & Zhang, L. (2019). Rotation Angle Estimation of JPEG Compressed Image by Cyclic Spectrum Analysis. Electronics, 8(12), 1431. https://doi.org/10.3390/electronics8121431





