Lifetime Estimation and Failure Risk Analysis in a Power Stage Used in Wind-Fuel Cell Hybrid Energy Systems
Abstract
1. Introduction
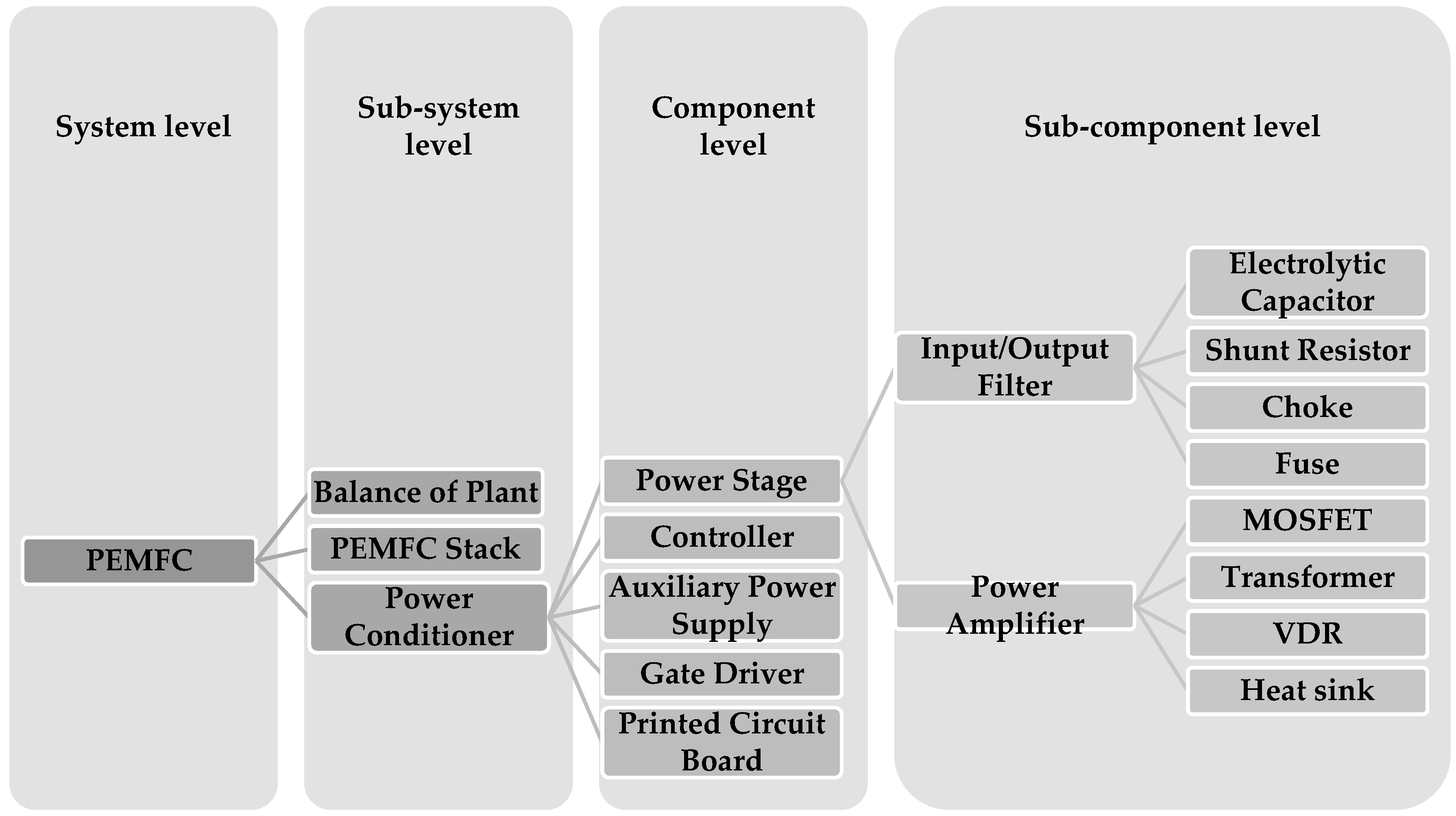
2. Power Stage Components
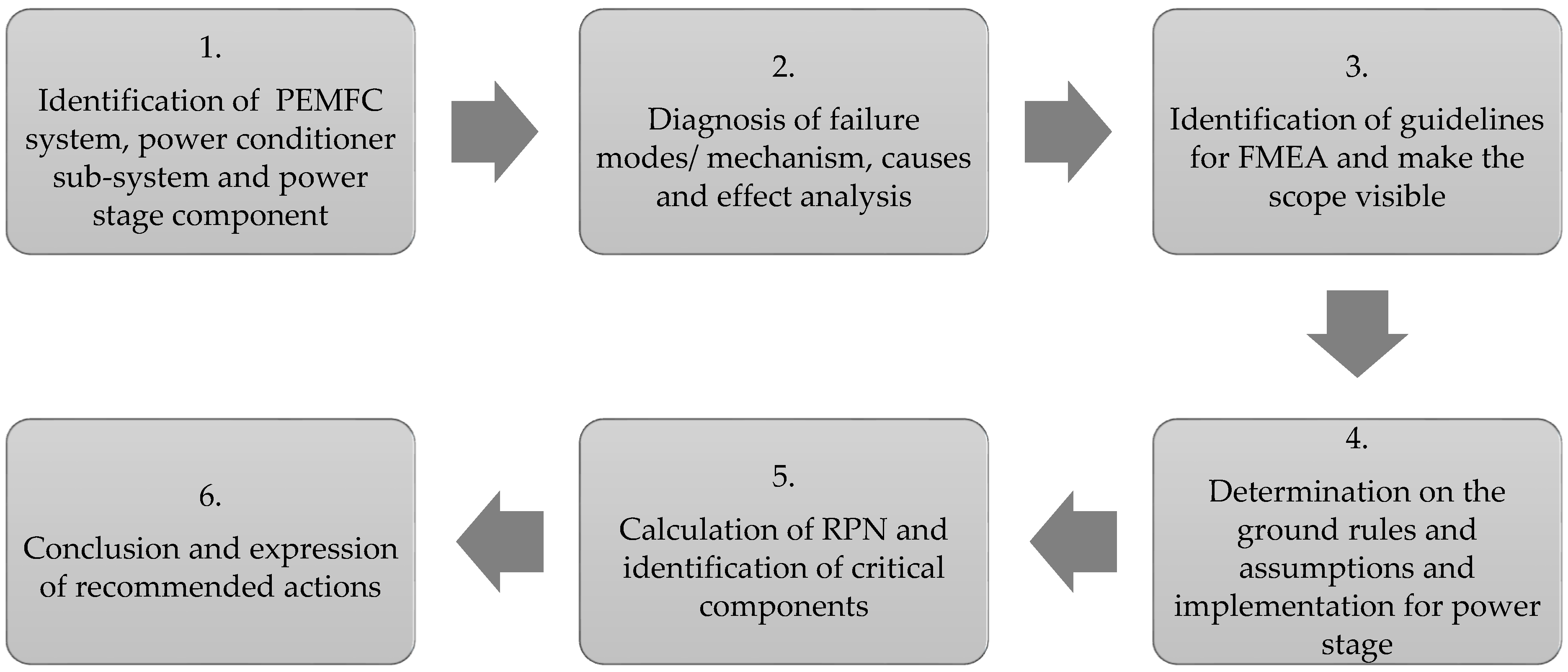
3. Failure Mechanisms and Failure Modes Analysis
4. Fault Tree Analysis
5. Results and Discussion of Reliability Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khan, F.I.; Hawboldt, K.; Iqbal, M.T. Life Cycle Analysis of wind-fuel cell integrated system. Renew. Energy 2005, 30, 157–177. [Google Scholar] [CrossRef]
- Eroglu, M.; Dursun, E.; Sevencan, S.; Song, J.; Yazici, S.; Kilic, O. A mobile renewable house using PV/wind/fuel cell hybrid power system. Int. J. Hydrogen Energy 2011, 36, 7985–7992. [Google Scholar] [CrossRef]
- Cetin, E.; Yilanci, A.; Ozturk, H.K.; Colak, M.; Kasikci, I.; Iplikci, S. A micro-DC power distribution system for a residential application energized by photovoltaic-wind/fuel cell hybrid energy systems. Energy Build. 2010, 42, 1344–1352. [Google Scholar] [CrossRef]
- Iqbal, M.T. Modeling and control of a wind fuel cell hybrid energy system. Renew. Energy 2003, 28, 223–237. [Google Scholar] [CrossRef]
- Haddad, A.; Ramadan, M.; Khaled, M.; Ramadan, H.S.; Becherif, M. Triple hybrid system coupling fuel cell with wind turbine and thermal solar system. Int. J. Hydrogen Energy 2019. [Google Scholar] [CrossRef]
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Dynamic modeling, design and simulation of a wind/fuel cell/ultra-capacitor-based hybrid power generation system. J. Power Sources 2006, 161, 707–722. [Google Scholar] [CrossRef]
- Khan, M.J.; Iqbal, M.T. Dynamic modeling and simulation of a small wind-fuel cell hybrid energy system. Renew. Energy 2005, 30, 421–439. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel standalone hybrid solar/wind/fuel cell/battery power generation system. Energy 2017, 140, 454–465. [Google Scholar] [CrossRef]
- Beuscher, U.; Cleghorn, S.J.C.; Johnson, W.B. Challenges for PEM fuel cell membranes. Int. J. Energy Res. 2005, 29, 1103–1112. [Google Scholar] [CrossRef]
- Zhang, J. PEM Fuel Cell Electrocatalysts and Catalyst Layers: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 9781848009356. [Google Scholar]
- Bahrebar, S.; Blaabjerg, F.; Wang, H.; Vafamand, N.; Khooban, M.-H.; Rastayesh, S.; Zhou, D. A Novel Type-2 Fuzzy Logic for Improved Risk Analysis of Proton Exchange Membrane Fuel Cells in Marine Power Systems Application. Energies 2018, 11, 721. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, H.; Blaabjerg, F. Mission Profile Based System-Level Reliability Analysis of DC/DC Converters for a Backup Power Application. IEEE Trans. Power Electron. 2018, 33, 8030–8039. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, H.; Blaabjerg, F.; Kor, S.K.; Blom-Hansen, D. System-level reliability assessment of power stage in fuel cell application. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar]
- Bahrebar, S.; Zhou, D.; Rastayesh, S.; Wang, H.; Blaabjerg, F. Reliability assessment of power conditioner considering maintenance in a PEM fuel cell system. Microelectron. Reliab. 2018, 88–90, 1177–1182. [Google Scholar] [CrossRef]
- Bahrebar, S.; Blaabjerg, F.; Wang, H.; Zhou, D.; Rastayesh, S. System-level Risk Analysis of PEM Fuel Cell Using Failure Mode and Effect Analysis. In Proceedings of the IRSEC 2018, 5th International Reliability and Safety Engineering Conference, Shiraz, Iran, 9–10 May 2018. [Google Scholar]
- Soliman, H.; Wang, H.; Blaabjerg, F. A Review of the Condition Monitoring of Capacitors in Power Electronic Converters. IEEE Trans. Ind. Appl. 2016, 52, 4976–4989. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F. Reliability of Capacitors for DC-Link Applications in Power Electronic Converters—An Overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef]
- Huai, W.; Liserre, M.; Blaabjerg, F.; De Place Rimmen, P.; Jacobsen, J.B.; Kvisgaard, T.; Landkildehus, J. Transitioning to physics-of-failure as a reliability driver in power electronics. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 97–114. [Google Scholar]
- Bahman, A.S.; Jensen, S.M.; Iannuzzo, F. Failure mechanism analysis of fuses subjected to manufacturing and operational thermal stresses. Microelectron. Reliab. 2018, 88–90, 304–308. [Google Scholar] [CrossRef]
- Rahimi, T.; Jahan, H.; Blaabjerg, F.; Bahman, A.; Hosseini, S. Fuzzy-Logic-Based Mean Time to Failure (MTTF) Analysis of Interleaved Dc-Dc Converters Equipped with Redundant-Switch Configuration. Appl. Sci. 2018, 9, 88. [Google Scholar] [CrossRef]
- Modarres, M.; Kaminskiy, M.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Pang, H.; Yu, T.; Song, B. Failure mechanism analysis and reliability assessment of an aircraft slat. Eng. Fail. Anal. 2016, 60, 261–279. [Google Scholar] [CrossRef]
- Pandey, A.; Singh, M.; Sonawane, A.U.; Rawat, P.S. FMEA Based Risk Assessment of Component Failure Modes in Industrial Radiography. Int. J. Eng. Trends Technol. 2016, 39, 216–225. [Google Scholar] [CrossRef]
- Krishnan, K.J.; Kalam, A.; Zayegh, A. Experimental investigation of H2 generator and PEM fuel cell as a remote area back-up power. In Proceedings of the Procedia Engineering; Elsevier Ltd.: Amsterdam, The Netherlands, 2012; Volume 49, pp. 66–73. [Google Scholar]
- Wang, Y.; Liu, H.; Lu, C.; Zhou, B. PEM fuel cell health state assessment using a geometrical approach and mahalanobis distance. In Proceedings of the Proceedings of the World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 1312–1316. [Google Scholar]
- Lee, S.; Zhou, D.; Wang, H. Reliablity assessment of fuel cell system—A framework for quantitative approach. In Proceedings of the ECCE 2016—IEEE Energy Conversion Congress and Exposition, Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Rabbani, A.; Rokni, M. Dynamic characteristics of an automotive fuel cell system for transitory load changes. Sustain. Energy Technol. Assess. 2013, 1, 34–43. [Google Scholar] [CrossRef]
- Javed, K.; Gouriveau, R.; Zerhouni, N.; Hissel, D. Improving accuracy of long-term prognostics of PEMFC stack to estimate remaining useful life. In Proceedings of the IEEE International Conference on Industrial Technology, Seville, Spain, 17–19 March 2015; pp. 1047–1052. [Google Scholar]
- Whiteley, M.; Fly, A.; Leigh, J.; Dunnett, S.; Jackson, L. Advanced reliability analysis of Polymer Electrolyte Membrane Fuel Cells using Petri-Net analysis and fuel cell modelling techniques. Int. J. Hydrogen Energy 2015, 40, 11550–11558. [Google Scholar] [CrossRef]
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure Modes and Effects Analysis (FMEA) for wind turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- Vesely, W.E.; Goldberg, F.F. Fault Tree Handbook, 16th ed.; U.S. Government Printing Office: Washington, DC, USA, 1981.
- Whiteley, M.; Dunnett, S.; Jackson, L. Failure Mode and Effect Analysis, and Fault Tree Analysis of Polymer Electrolyte Membrane Fuel Cells. Int. J. Hydrogen Energy 2016, 41, 1187–1202. [Google Scholar] [CrossRef]
- Collong, S.; Kouta, R. Fault tree analysis of proton exchange membrane fuel cell system safety. Int. J. Hydrogen Energy 2015, 40, 8248–8260. [Google Scholar] [CrossRef]
- Pourramazan, A.; Saffari, S.; Barghandan, A. Study of Failure Mode and Effect Analysis (FMEA) on Capacitor Bank Used in Distribution Power Systems. Ijireeice 2017, 5, 113–118. [Google Scholar]
- Larrucea, X.; Belmonte, F.; Welc, A.; Xie, T. Reliability Engineering. IEEE Softw. 2017, 34, 26–29. [Google Scholar] [CrossRef]
- Mathew, S.; Alam, M.; Pecht, M. Identification of failure mechanisms to enhance prognostic outcomes. J. Fail. Anal. Prev. 2012, 12, 66–73. [Google Scholar] [CrossRef]
- Young, A.L.; Hilmas, G.E.; Zhang, S.C.; Schwartz, R.W. Mechanical vs. electrical failure mechanisms in high voltage, high energy density multilayer ceramic capacitors. J. Mater. Sci. 2007, 42, 5613–5619. [Google Scholar] [CrossRef]
- Toh, S.L.; Tan, P.K.; Goh, Y.W.; Hendarto, E.; Cai, J.L.; Tan, H.; Wang, Q.F.; Deng, Q.; Lam, J.; Hsia, L.C.; et al. In-Depth Electrical Analysis to Reveal the Failure Mechanisms With Nanoprobing. IEEE Trans. Device Mater. Reliab. 2008, 8, 387–393. [Google Scholar] [CrossRef]
- Modarres, M. Risk Analysis in Engineering: Techniques, Tools, and Trends; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Feili, H.R.; Akar, N.; Lotfizadeh, H.; Bairampour, M.; Nasiri, S. Risk analysis of geothermal power plants using Failure Modes and Effects Analysis (FMEA) technique. Energy Convers. Manag. 2013, 72, 69–76. [Google Scholar] [CrossRef]
- Jensen, F.; Morris, A.S.; Levin, M.A.; Kalal, T.T.; Pascoe, N.; Carlson, C. Effective FMEAs; Wiely: Hoboken, NJ, USA, 2012. [Google Scholar]
- Berg, F.; Logistics, I.; Komenského, P. FMEA (failure mode and effects analysis) and proposal of risk minimizing in storage processes for automotive. Acta Logist. 2016, 3, 15–18. [Google Scholar]
- Rafie, M.; Namin, F.S. Prediction of subsidence risk by FMEA using artificial neural network and fuzzy inference system. Int. J. Min. Sci. Technol. 2015, 25, 655–663. [Google Scholar] [CrossRef]
- van Leeuwen, J.F.; Nauta, M.J.; de Kaste, D.; Odekerken-Rombouts, Y.M.C.F.; Oldenhof, M.T.; Vredenbregt, M.J.; Barends, D.M. Risk analysis by FMEA as an element of analytical validation. J. Pharm. Biomed. Anal. 2009, 50, 1085–1087. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Blaabjerg, F.; Wang, H.; Liserre, M. Overview of catastrophic failures of freewheeling diodes in power electronic circuits. Microelectron. Reliab. 2013, 53, 1788–1792. [Google Scholar] [CrossRef]
- Shafiee, M.; Dinmohammadi, F. An FMEA-based risk assessment approach for wind turbine systems: A comparative study of onshore and offshore. Energies 2014, 7, 619–642. [Google Scholar] [CrossRef]
- Placca, L.; Kouta, R. Fault tree analysis for PEM fuel cell degradation process modelling. Int. J. Hydrogen Energy 2011, 36, 12393–12405. [Google Scholar] [CrossRef]
- Rastayesh, S.; Bahrebar, S. Importance Analysis of a Typical Diesel Generator Using Dynamic Fault Tree. Int. J. Curr. Life Sci. 2014, 4, 697–700. [Google Scholar]
- Rastayesh, S.; Bahrebar, S.; Sepanloo, K. Time Dependent Reliability Of Emrgency Diesel Generator Station. Indian J. Sci. Res. 2014, 1, 453–460. [Google Scholar]
- Bahrebar, S.; Rastayesh, S.; Sepanloo, K. Dynamic Availability Assessment on Tehran Research Reactor Water Cooling System. Indian J. Sci.Res. 2014, 1, 471–474. [Google Scholar]





| Ranking | Criteria | Description |
|---|---|---|
| 1 | Very low | Unlikely to occur at all |
| 2 | Low | Remote—once in 1 to 10 number |
| 3 | Medium | Rare—once in 10 to 100 number |
| 4 | High | Occasional—once in 100 to 1000 number |
| Ranking | Criteria | Description |
|---|---|---|
| 1 | High | Detectable with a shutdown |
| 2 | Medium | Detectable according to the deviation |
| 3 | Low | Detectable by a sensor |
| 4 | Very low | Not physically detectable |
| Ranking | Criteria | Description |
|---|---|---|
| 1 | Very low | Negligible changes like temperature |
| 2 | Low | Reduction in ability to work |
| 3 | Medium | Loss of ability to work |
| 4 | High | Major damage to work |
| # | Sub-Components of Power Stage | Top Function | Top Failure Mode | Top Failure Cause | Top Failure Mechanism | Mechanism Type | S | O | D | RPN |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Fuse | Protecting | Fail to protect | High voltage/ temperature | Over voltage | Electrical tension mechanism/ overstress | 2 | 3 | 2 | 12 |
| 2 | Electrolytic capacitor | Filtering and storing | Does not filter and store | High current/ temperature | Leakage and Short/open circuit | Electrical tension mechanism/ overstress | 4 | 2 | 4 | 32 |
| 3 | Choke | Smoothing and resist changing | Fail to smooth and resist changing | Manufacturing defect and high temperature | Short/open circuit | Inherent failure mechanism/ wear out | 3 | 3 | 3 | 27 |
| 4 | Shunt resistor | Measuring of currents | Fail to measure currents | Manufacturing defect and high temperature | Overvoltage | Inherent failure mechanism/ wear out | 3 | 2 | 2 | 12 |
| 5 | MOSFET | Protection and regulation | Fail to switch and regulation | High voltage/current/temperature | Gate oxide short/breakdown, EOS, ESD | Electrical tension mechanism/ overstress | 4 | 3 | 4 | 48 |
| 6 | VDR | Compensating voltage | Does not compensate voltage | Manufacturing defect and high temperature | Overvoltage | Electrical tension mechanism/ overstress | 2 | 2 | 2 | 8 |
| 7 | Transformer | Inducting and reinforcing | Does not reinforce | Manufacturing defect and high temperature | Leakage and short/open circuit | Inherent failure mechanism/ wear out | 3 | 3 | 3 | 27 |
| 8 | Heatsink | Heat reducing | Does not heat reduce | Manufacturing defect | Thermal damage | External failure mechanism/ overstress | 2 | 1 | 2 | 4 |
| System | Components | Failure Rate (λ) | Weibull Parameters | |
|---|---|---|---|---|
| Shape Parameter (β) | Scaling Parameter (ɳ) | |||
| Power stage | Fuse | 0.02 × 10−6 | 1 | 5.00 × 107 |
| Electrolytic capacitor | 0.11 × 10−6 | 1 | 8.33 × 106 | |
| Choke | 0.16 × 10−9 | 1 | 5.95 × 109 | |
| Shunt resistor | 0.43 × 10−9 | 1 | 2.31 × 109 | |
| MOSFET | 0.58 × 10−6 | 1 | 1.91 × 106 | |
| VDR | 0.43 × 10−9 | 1 | 2.31 × 109 | |
| Transformer | 0.15 × 10−6 | 1 | 6.51 × 106 | |
| Heatsink | 0.06 × 10−6 | 1 | 1.66 × 107 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rastayesh, S.; Bahrebar, S.; Bahman, A.S.; Sørensen, J.D.; Blaabjerg, F. Lifetime Estimation and Failure Risk Analysis in a Power Stage Used in Wind-Fuel Cell Hybrid Energy Systems. Electronics 2019, 8, 1412. https://doi.org/10.3390/electronics8121412
Rastayesh S, Bahrebar S, Bahman AS, Sørensen JD, Blaabjerg F. Lifetime Estimation and Failure Risk Analysis in a Power Stage Used in Wind-Fuel Cell Hybrid Energy Systems. Electronics. 2019; 8(12):1412. https://doi.org/10.3390/electronics8121412
Chicago/Turabian StyleRastayesh, Sima, Sajjad Bahrebar, Amir Sajjad Bahman, John Dalsgaard Sørensen, and Frede Blaabjerg. 2019. "Lifetime Estimation and Failure Risk Analysis in a Power Stage Used in Wind-Fuel Cell Hybrid Energy Systems" Electronics 8, no. 12: 1412. https://doi.org/10.3390/electronics8121412
APA StyleRastayesh, S., Bahrebar, S., Bahman, A. S., Sørensen, J. D., & Blaabjerg, F. (2019). Lifetime Estimation and Failure Risk Analysis in a Power Stage Used in Wind-Fuel Cell Hybrid Energy Systems. Electronics, 8(12), 1412. https://doi.org/10.3390/electronics8121412








