Estimating the Information Source under Decaying Diffusion Rates
Abstract
1. Introduction
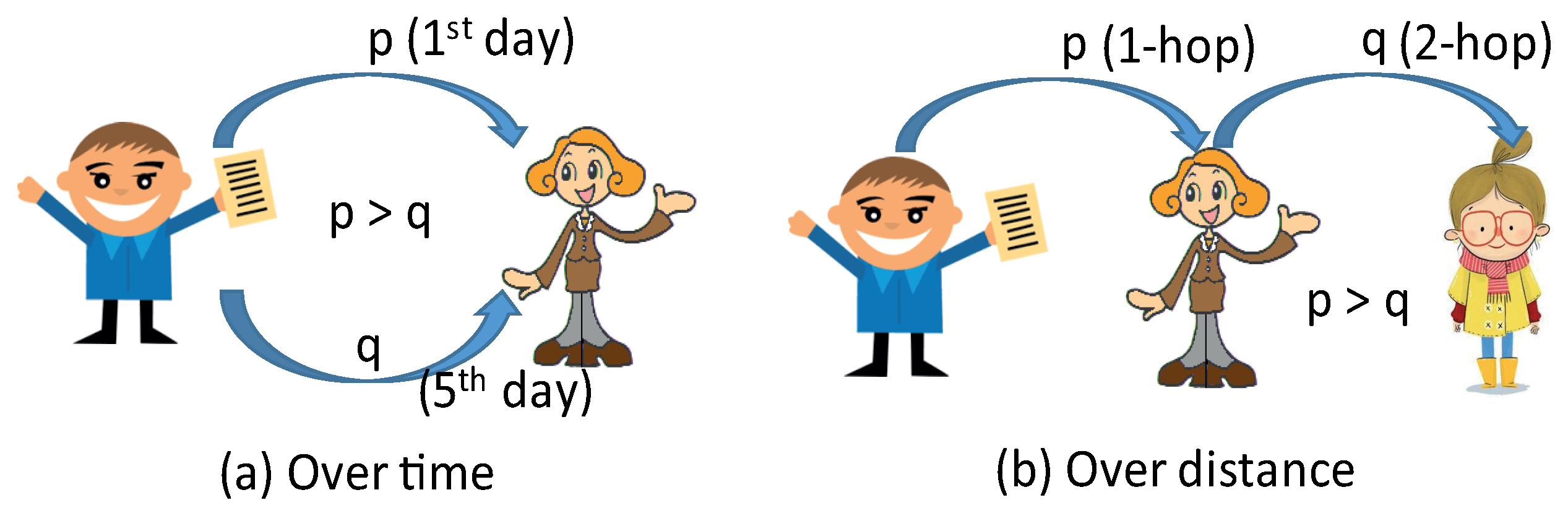
- First, we use the MLE to find the source for decaying diffusion and show that the MLE is same as that of the homogeneous diffusion rate of information if the diffusion decays with respect to the distance from the source. This implies that the MLE of our model also has the same graphical centrality property called rumor center in [1]. This enables us to analyze the detection performance for the decaying rate scenario.
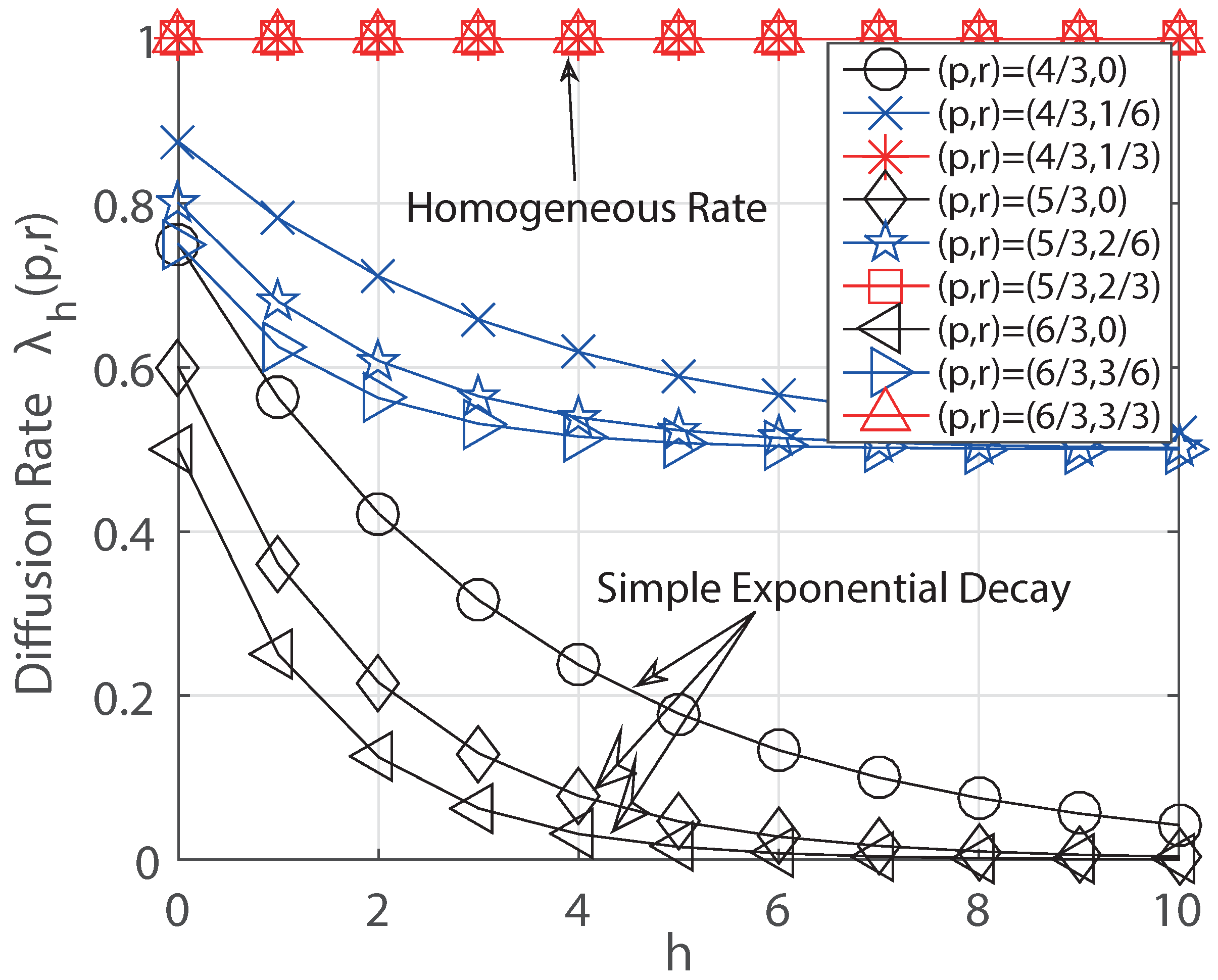
- Second, we define two exponential decaying models: Simple exponential decay and Generalized exponential decay. The simple exponential decay is a kind of light tail distribution, but the generalized exponential decay covers light and heavy tail distribution in the sense of the decaying pattern. We then obtain the closed-form of detection probability of the MLE when the underlying graph is a regular tree for both decaying models. Different to the prior result in [1], the detection probability is larger than zero in the line graph and there is a non-neglectable improvement of detection for any degree of a regular tree.
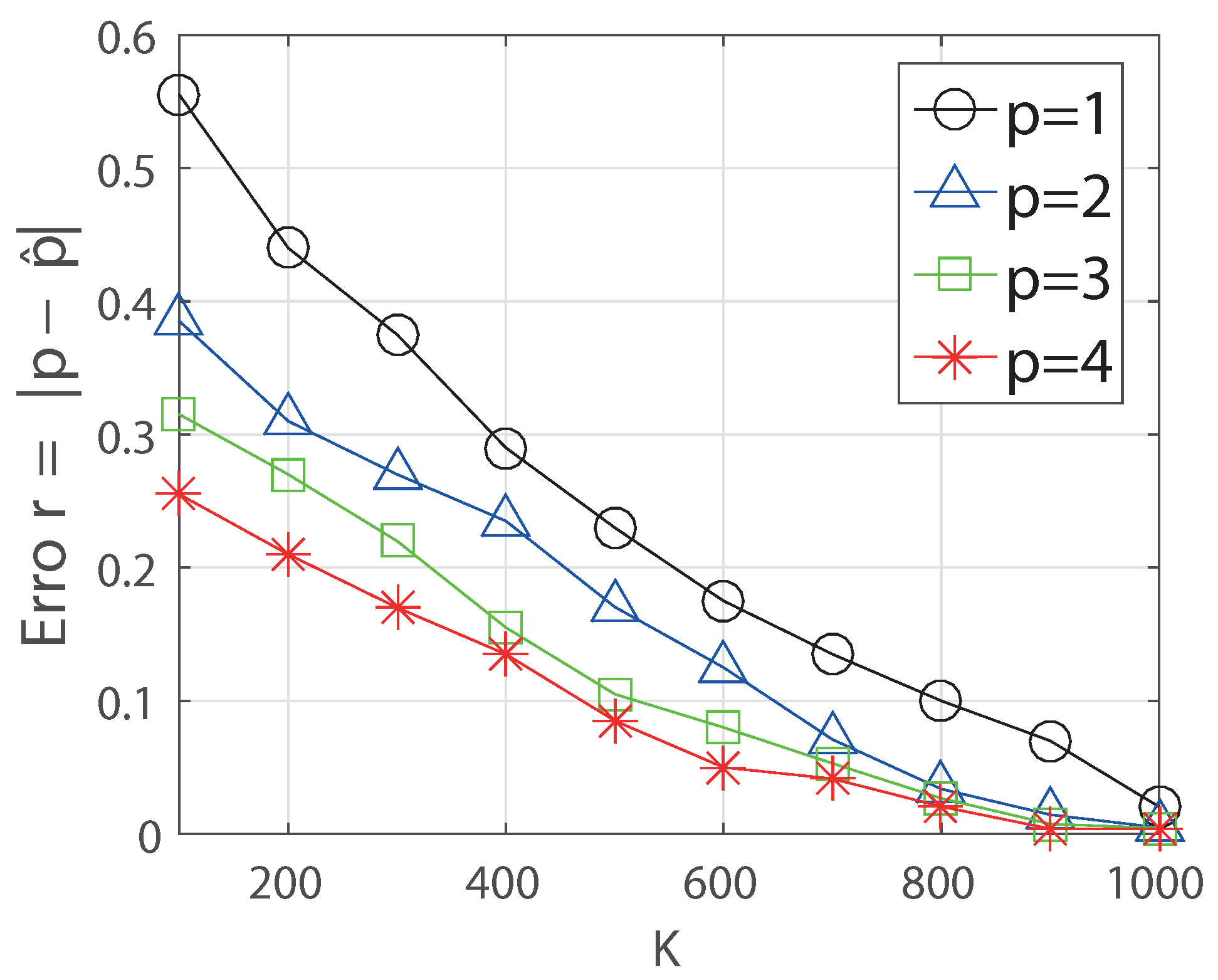
- Third, we consider the case that the decaying model parameter is hidden for two decaying models above. This is a more realistic scenario because knowing the exact parameter of the model is not easy in practice. To do that, we first derive MLE to estimate this parameter and show that it needs exponential computing time. Hence, we design a heuristic estimation algorithm for the true parameter by using the diffusion snapshot information, appropriately.
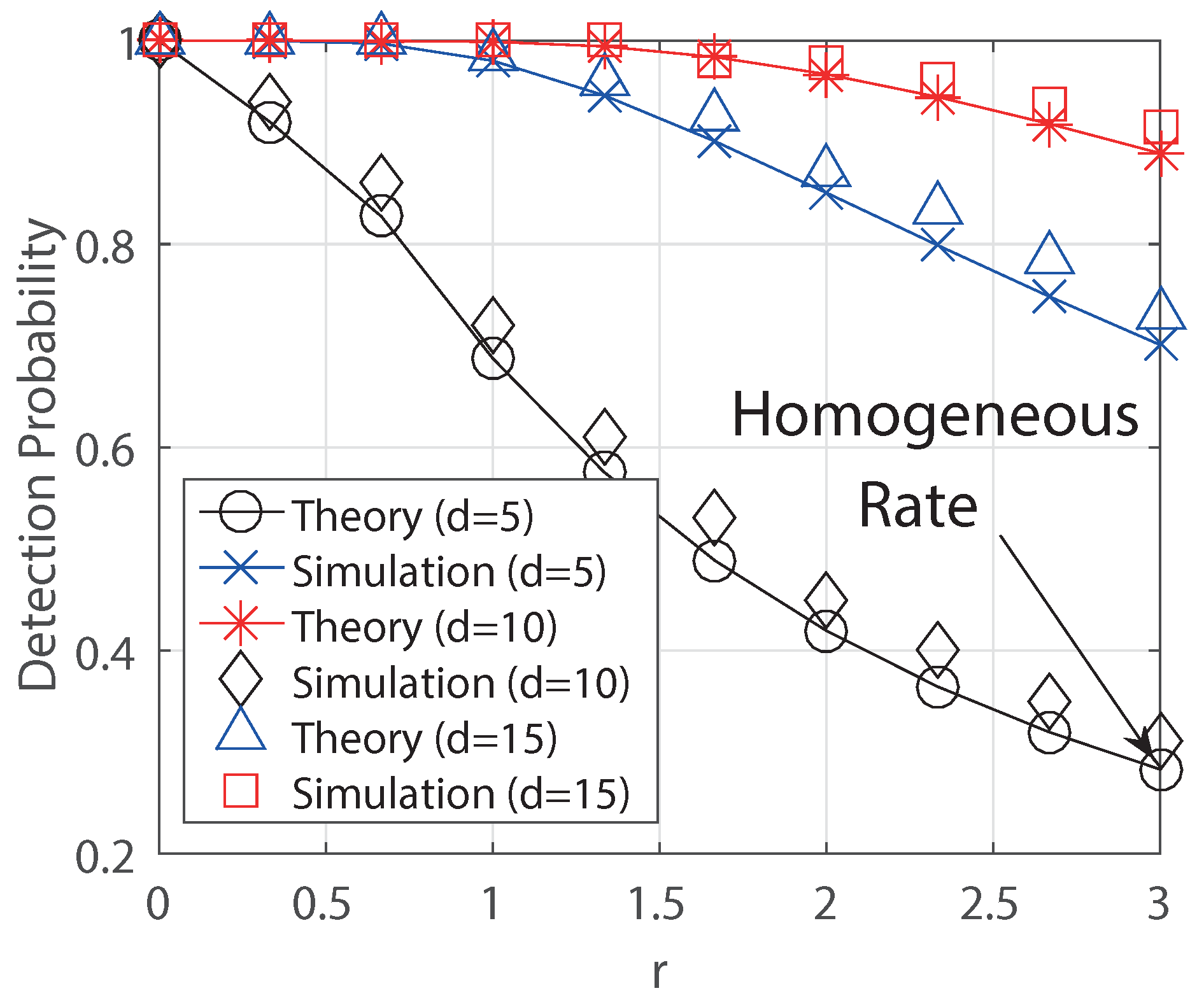
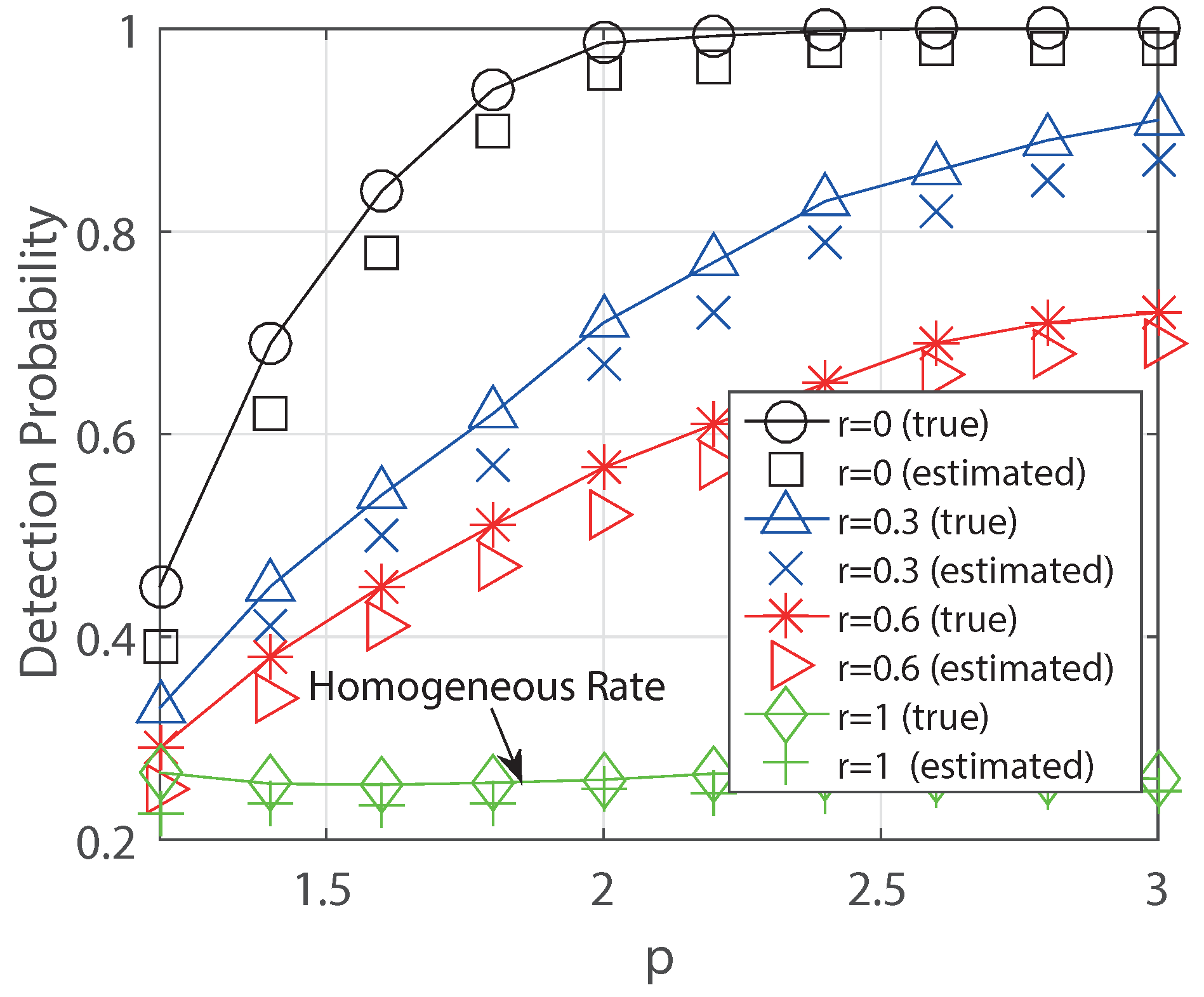
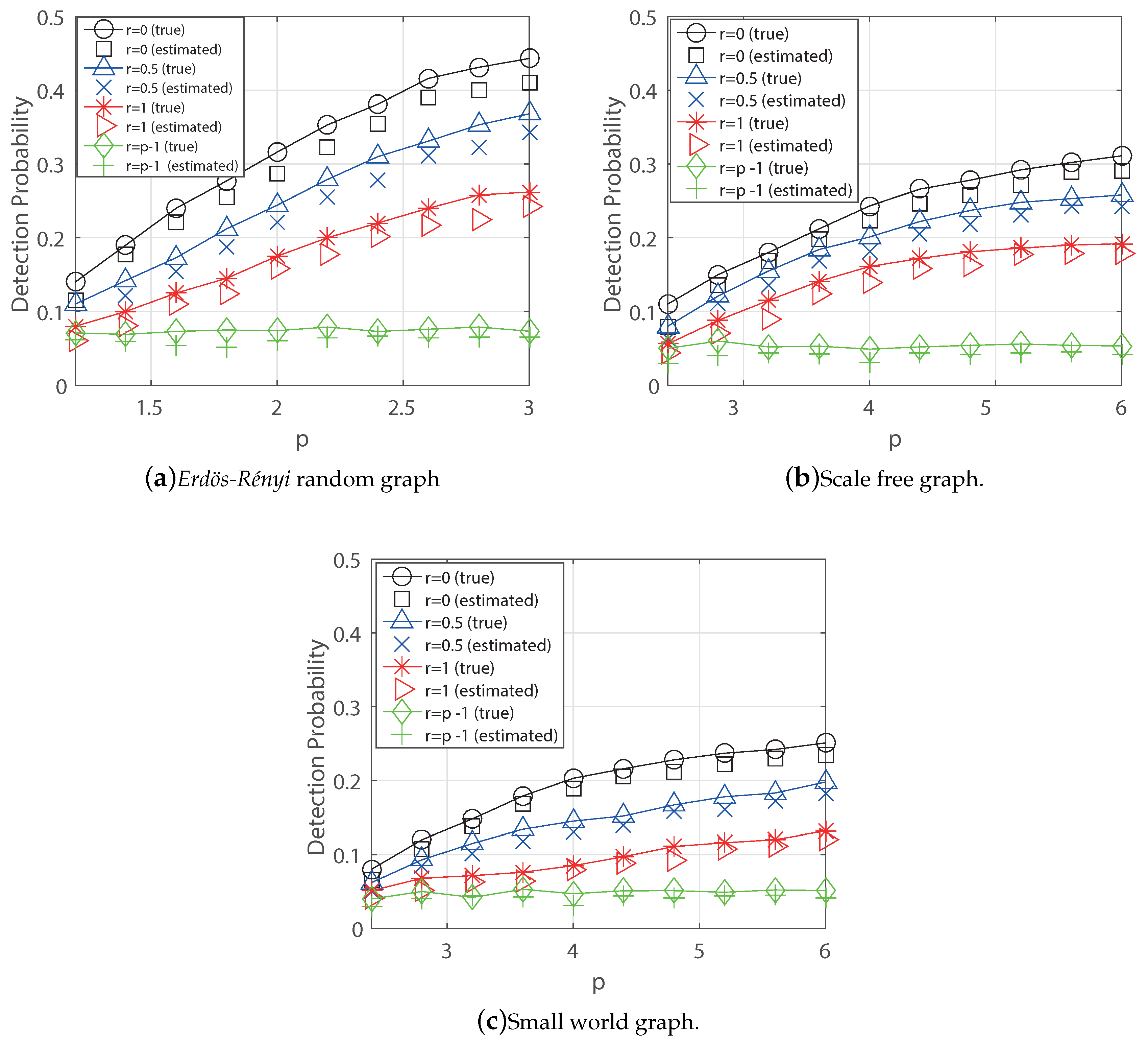
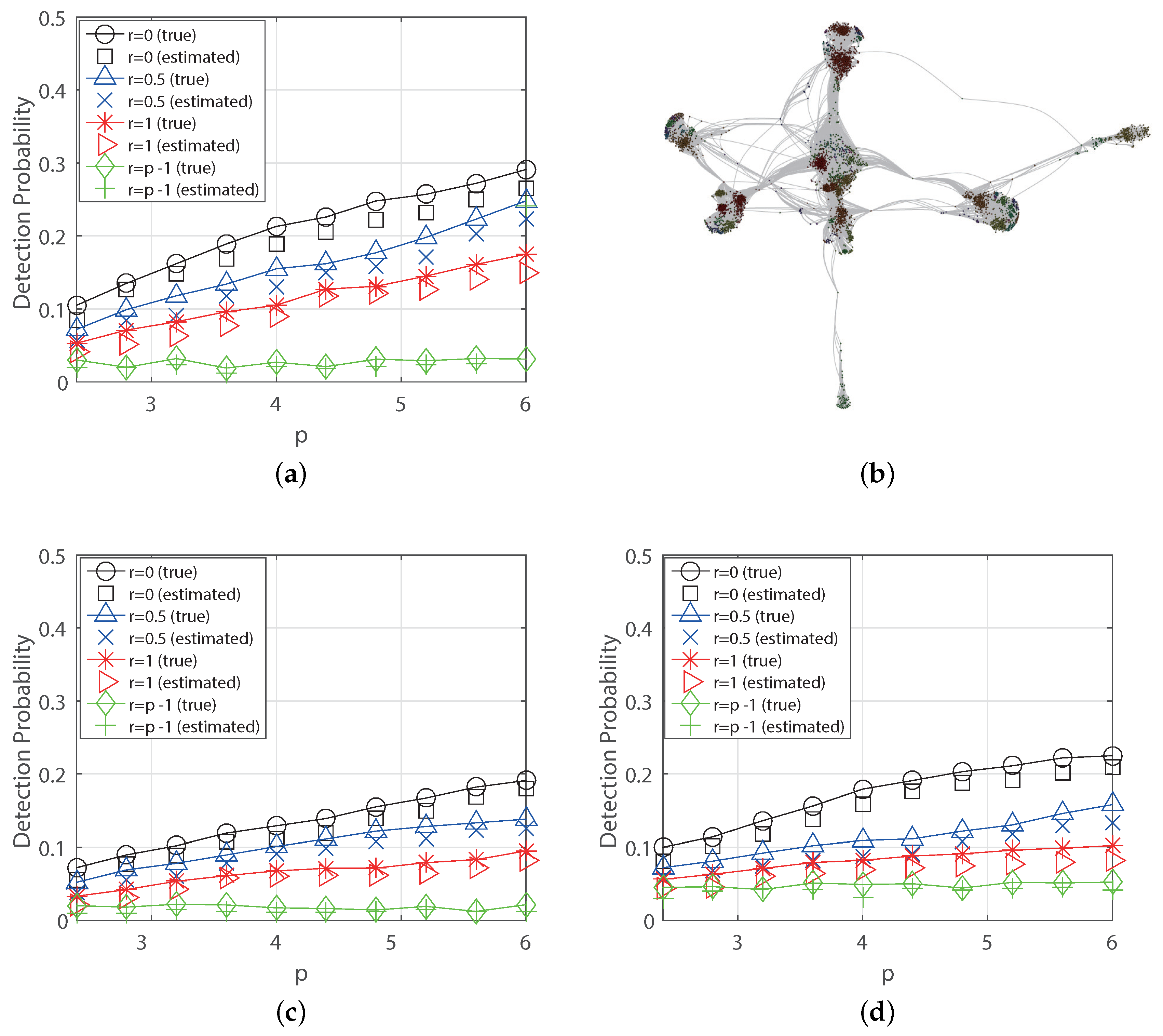
- Finally, we validate our theoretical result for the regular tree using the MLE and for over popular random graphs (Erdös-Rényi, scale-free and small-world graphs) and real-world networks (US-power grid, Facebook and Wiki vote) using the heuristic Breath-First-Search (BFS) estimator. As a result, we see that the detection probability can be above 80% for the regular tree and it can be above 30% if the diffusion rate decays, whereas it is about 20% without decaying in the Facebook graph.
2. Related Work
3. Model and Estimator
4. Main Results
4.1. Probability of Correct Detection of MLE
4.2. Decaying Parameter Estimation
| Algorithm 1 Decaying Parameter Estimation (DPE(K)) |
| Input: Diffusion snapshot , sampling cost K, , , increasing step size |
| Output: Estimation parameter |
| Set the initial decaying parameter ; |
| while do |
| for each do |
| Step1: Compute the rumor centrality by a message passing algorithm [1]; |
| Step2: Choose random samples K times and compute its mean by; |
| Step3: Set ; |
| end for |
| Set ←; |
| ; |
| end while |
| Compute ; |
| Return ; |
5. Proof of Results
5.1. Proof of Proposition 1
5.2. Proof of Theorem 1
5.3. Proof of Theorem 2
5.4. Proof of Theorem 3
6. Numerical and Simulation Results
6.1. Regular Trees
6.2. Random Graphs
6.3. Real World Graphs
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Lemmas
Appendix A.1. Proof of Lemma 2
Appendix A.2. Proof of Lemma 3
Appendix A.3. Proof of Lemma 4
Appendix A.4. Proof of Lemma 5
References
- Shah, D.; Zaman, T. Detecting Sources of Computer Viruses in Networks: Theory and Experiment. In Proceedings of the ACM SIGMETRICS, New York, NY, USA, 14–18 June 2010. [Google Scholar]
- Shah, D.; Zaman, T. Rumor Centrality: A Universal Source Detector. In Proceedings of the ACM SIGMETRICS, London, UK, 11–15 June 2012. [Google Scholar]
- Shah, D.; Zaman, T. Rumors in a Network: Who’s the Culprit? IEEE Trans. Inf. Theory 2011, 57, 5163–5181. [Google Scholar] [CrossRef]
- Zhu, K.; Ying, L. Information Source Detection in the SIR Model: A Sample Path Based Approach. In Proceedings of the IEEE Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 10–15 February 2013. [Google Scholar]
- Zhu, K.; Ying, L. A robust information source estimator with sparse observations. In Proceedings of the IEEE INFOCOM, Toronto, ON, Canada, 27 April–2 May 2014. [Google Scholar]
- Wang, Z.; Dong, W.; Zhang, W.; Tan, C.W. Rumor source detection with multiple observations: Fundamental limits and algorithms. In Proceedings of the ACM SIGMETRICS, Austin, TX, USA, 16–20 June 2014. [Google Scholar]
- Dong, W.; Zhang, W.; Tan, C.W. Rooting Out the Rumor Culprit from Suspects. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey, 7–12 July 2013. [Google Scholar]
- Choi, J.; Shin, J.; Yi, Y. Information Source Localization with Protector Diffusion in Networks. IEEE/KICS J. Commun. Netw. 2017, 21, 136–147. [Google Scholar] [CrossRef]
- Choi, J.; Moon, S.; Woo, J.; Son, K.; Shin, J.; Yi, Y. Rumor Source Detection under Querying with Untruthful Answers. In Proceedings of the IEEE INFOCOM, 2017 IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Choi, J.; Yi, Y. Necessary and Sufficient Budgets in Information Source Finding with Querying: Adaptivity Gap. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018. [Google Scholar]
- Ohsaka, N.; Yamaguchi, Y.; Kakimura, N.; Kwarabayashi, K. Maximizing Time-Decaying Influence in Social Networks. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, 19–23 September 2016; pp. 132–147. [Google Scholar]
- Bubeck, S.; Devroye, L.; Lugosi, G. Finding Adam in random growing trees. Random Struct. Algorithms 2017, 50, 158–172. [Google Scholar] [CrossRef]
- Khim, J.; Loh, P.-O. Confidence Sets for Source of a Diffusion in Regular Trees. IEEE Trans. Netw. Sci. Eng. 2015, 4, 27–40. [Google Scholar] [CrossRef]
- Luo, W.; Tay, W.P.; Leng, M. How to Identify an Infection Source With Limited Observations. IEEE J. Sel. Top. Signal Process. 2014, 8, 586–597. [Google Scholar] [CrossRef]
- Prakash, B.A.; Vreeken, J.; Faloutsos, C. Efficiently Spotting the Starting Points of an Epidemic in a Large Graph. In Proceedings of the IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017. [Google Scholar]
- Zhu, K.; Chen, Z.; Ying, L. Catch’Em All: Locating Multiple Diffusion Sources in Networks with Partial Observations. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Ji, F.; Tay, W.P. An Algorithmic Framework for Estimating Rumor Sources With Different Start Times. IEEE Trans. Signal Process. 2017, 65, 2517–2530. [Google Scholar] [CrossRef]
- Fanti, G.; Kairouz, P.; Oh, S.; Viswanath, P. Spy vs. In Spy: Rumor Source Obfuscation. In Proceedings of the ACM SIGMETRICS, Portland, OR, USA, 15–19 June 2015. [Google Scholar]
- Luo, W.; Tay, W.P.; Leng, M. Infection Sprading and Source Identification: A Hide and Seek Game. IEEE Trans. Signal Process. 2016, 64, 4228–4243. [Google Scholar] [CrossRef]
- Fanti, G.; Viswanath, P. Anonymity Properties of the Bitcoin P2P Network. arXiv 2017, arXiv:1703.08761. [Google Scholar]
- Leskovec, J.; McAuley, J. Learning to discover social circles in ego networks. In Proceedings of the Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–8 December 2012. [Google Scholar]
- Leskovec, J.; Huttenlocher, D.; Kleinberg, J. Predicting Positive and Negative Links in Online Social Networks. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010. [Google Scholar]
| True p | ER | SF | SW | PG | FB | WiKi |
|---|---|---|---|---|---|---|
| 2 | 1.82 | 2.23 | 2.08 | 1.93 | 1.81 | 1.93 |
| 3 | 3.26 | 3.72 | 3.35 | 2.83 | 2.84 | 3.11 |
| 4 | 3.71 | 3.83 | 4.23 | 4.32 | 3.81 | 4.13 |
| 5 | 4.84 | 4.72 | 4.73 | 5.28 | 4.93 | 4.91 |
| 6 | 5.84 | 5.82 | 5.88 | 6.28 | 5.83 | 5.91 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, J.; Choi, J. Estimating the Information Source under Decaying Diffusion Rates. Electronics 2019, 8, 1384. https://doi.org/10.3390/electronics8121384
Woo J, Choi J. Estimating the Information Source under Decaying Diffusion Rates. Electronics. 2019; 8(12):1384. https://doi.org/10.3390/electronics8121384
Chicago/Turabian StyleWoo, Jiin, and Jaeyoung Choi. 2019. "Estimating the Information Source under Decaying Diffusion Rates" Electronics 8, no. 12: 1384. https://doi.org/10.3390/electronics8121384
APA StyleWoo, J., & Choi, J. (2019). Estimating the Information Source under Decaying Diffusion Rates. Electronics, 8(12), 1384. https://doi.org/10.3390/electronics8121384






