Security Analysis of Multi-Antenna NOMA Networks Under I/Q Imbalance
Abstract
:1. Introduction
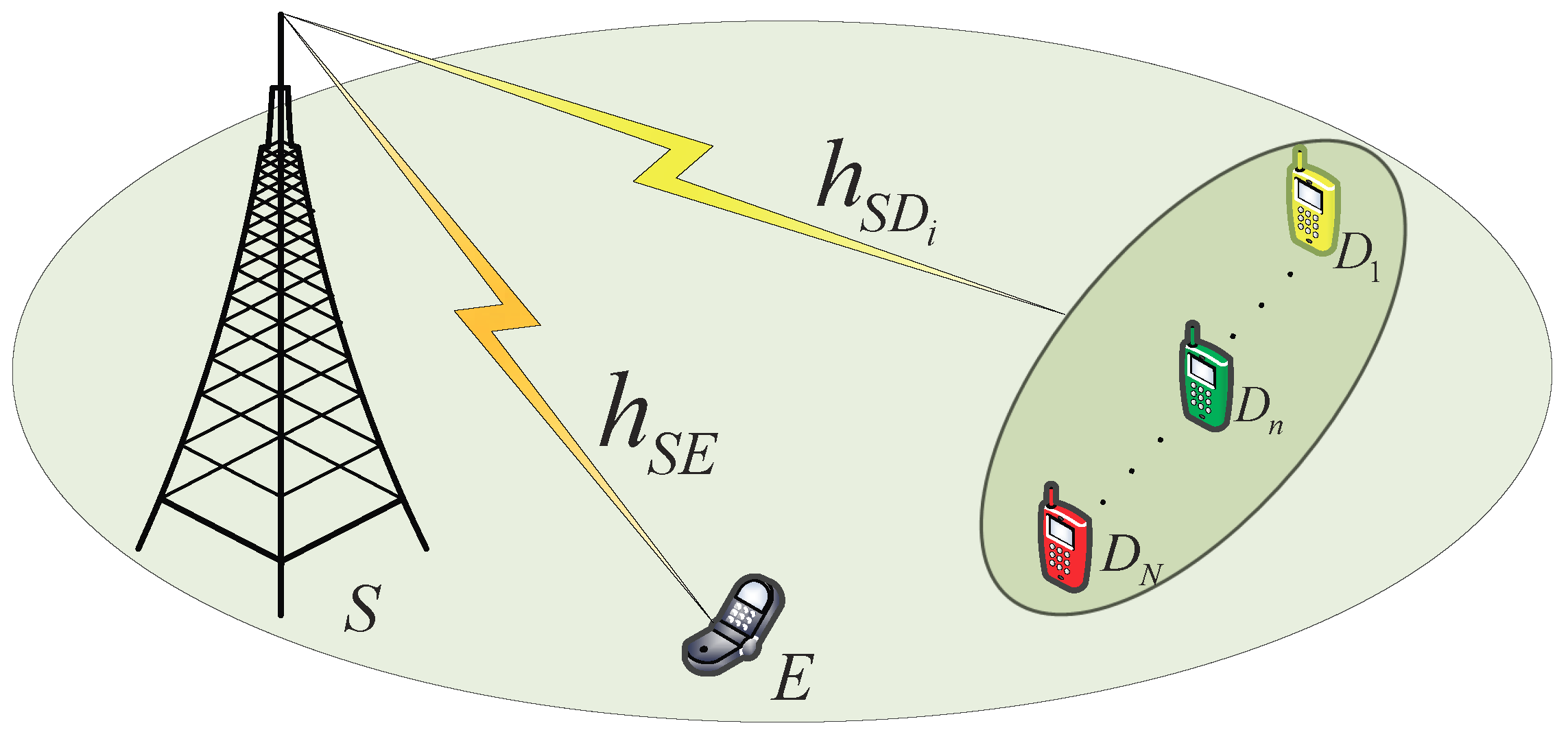
- Considering IQI at both transmitter (TX) and receiver (RX), we propose an AS scheme at the multiple-antenna legitimate users and eavesdropper to enhance reliability and security, in which the antenna of optimal quality link between the source and the receiver antennas is selected.
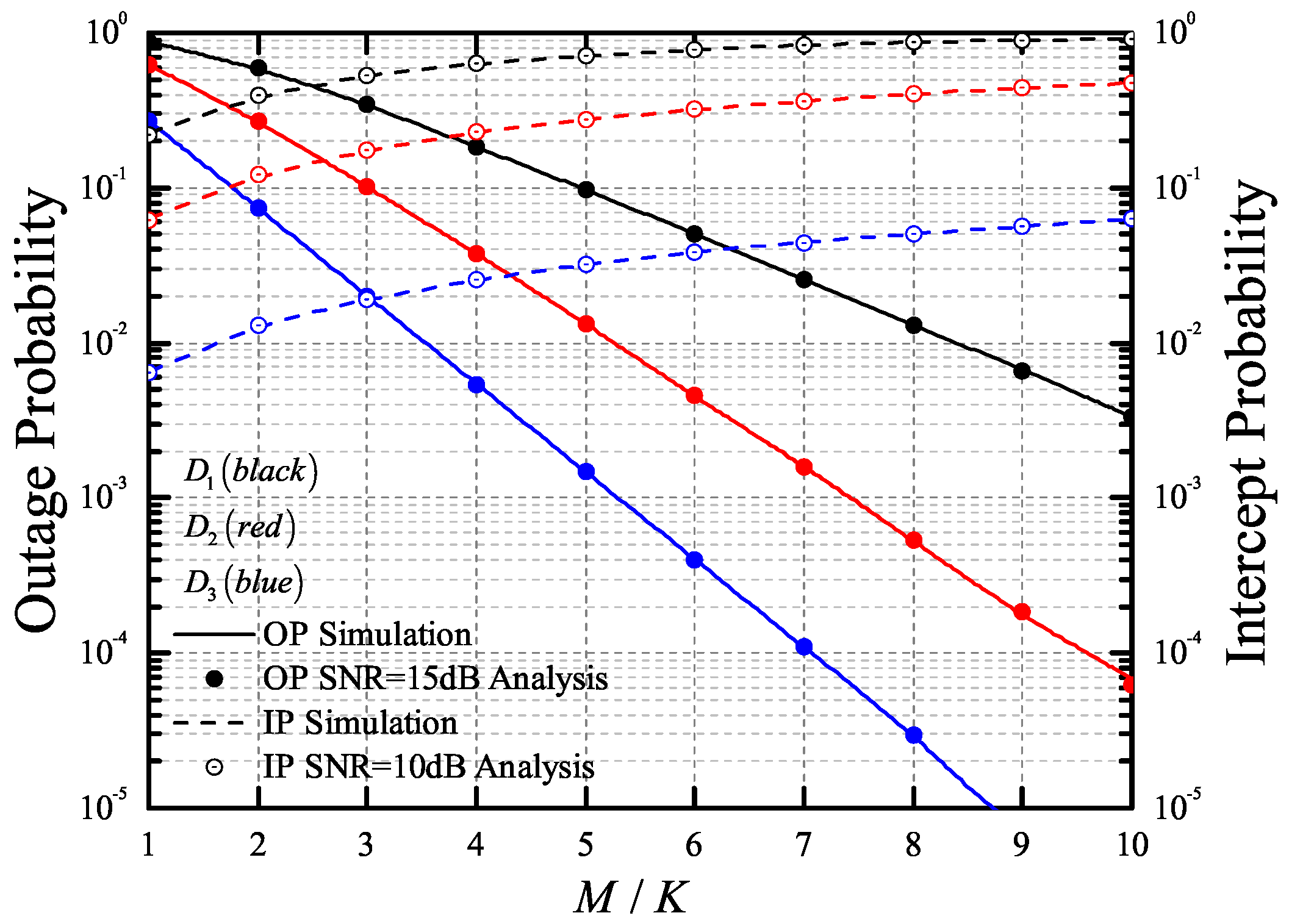
- Based on the proposed selection scheme, we derive the exact analytical expressions for the OP and intercept probability (IP) of the considered single-input multiple-output (SIMO)-NOMA system over the Nakagami-m fading channels. The results show that the reliability of the considered system can be improved by increasing the number of antennas at the receiver, while the security of the system will be reduced with the increase of the number of antennas at the eavesdropper.
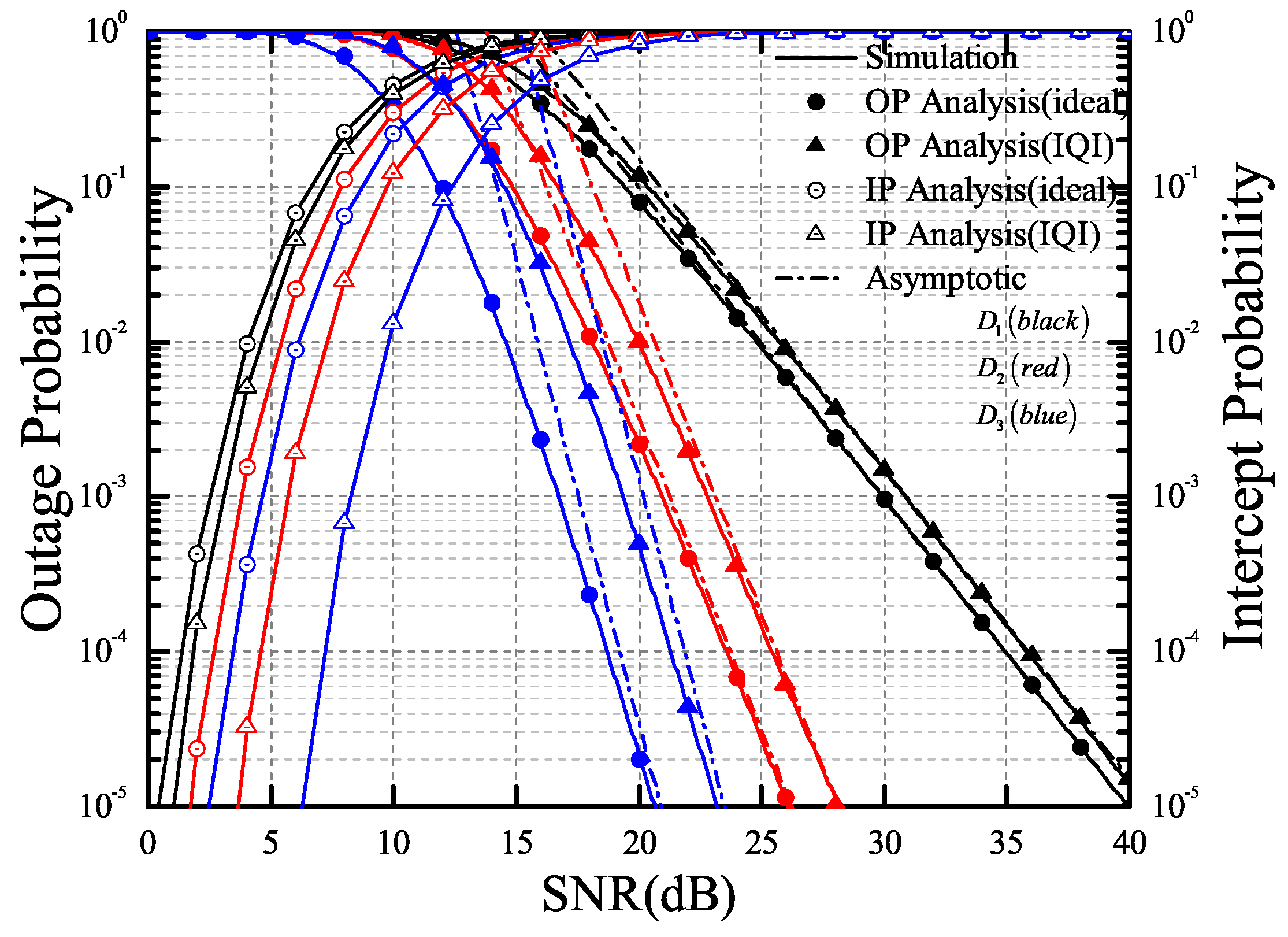
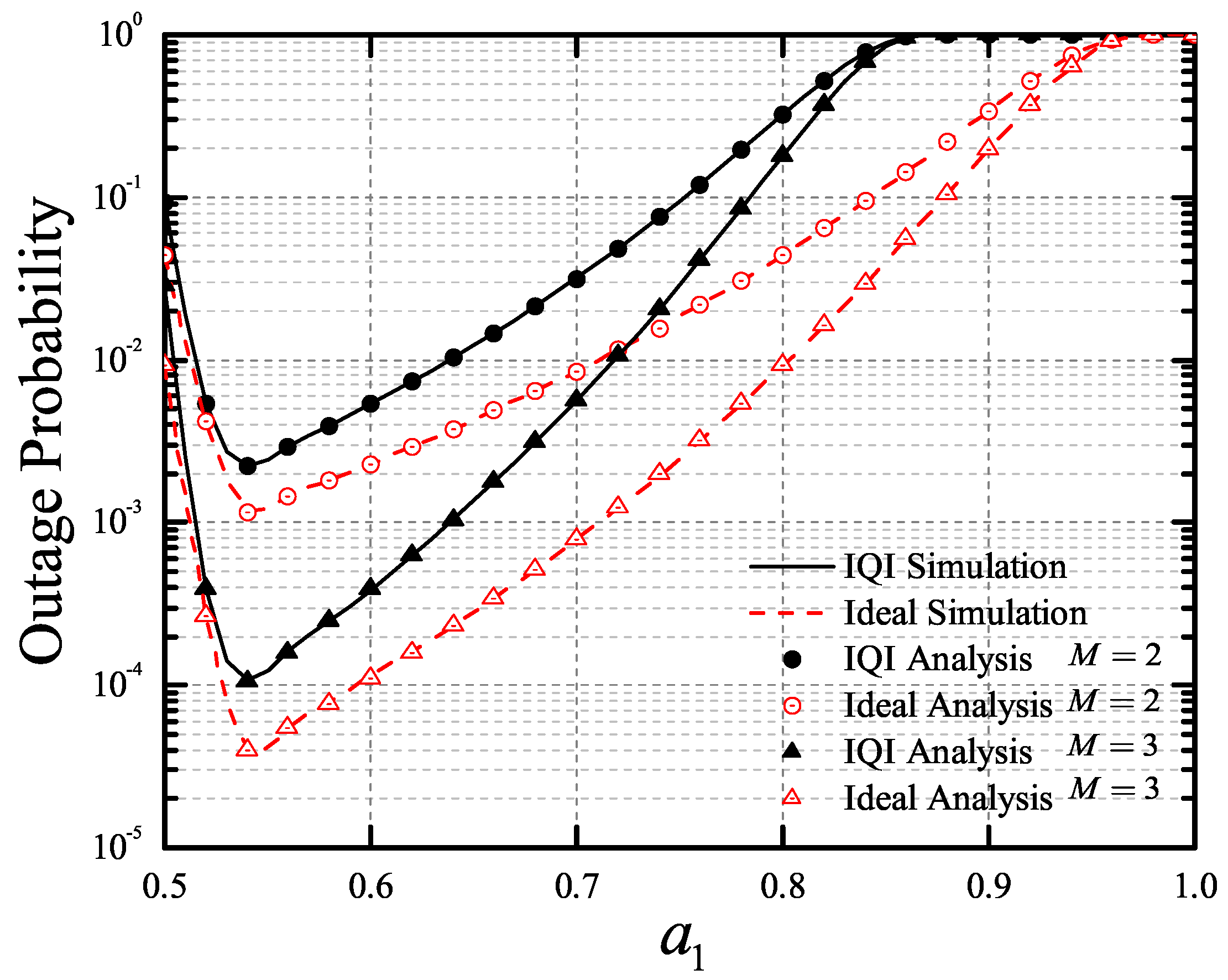
- In order to obtain deeper insights, we investigate the asymptotic behaviors of OP in the high SNR regime. Based on the derived asymptotic results, the diversity order for the OP can be derived and discussed. Specifically, it is proved that there is a trade-off between OP and IP. Moreover, considering the different degrees of impairment, the diversity order of the asymptotic OP for the considered system is derived, and the results demonstrate that IQI does not affect the diversity order of the considered system.
2. System Model
3. Performance Analysis
3.1. Outage Probability
- Non-ideal conditionsfor , and for .
- Ideal conditions (, )for , and for .
3.2. Intercept Probability
- Non-ideal conditionsfor , and for .
- Ideal conditions (, )for , and for .where .
3.3. Asymptotic Analysis
- Non-ideal conditions
- Ideal conditions (, )
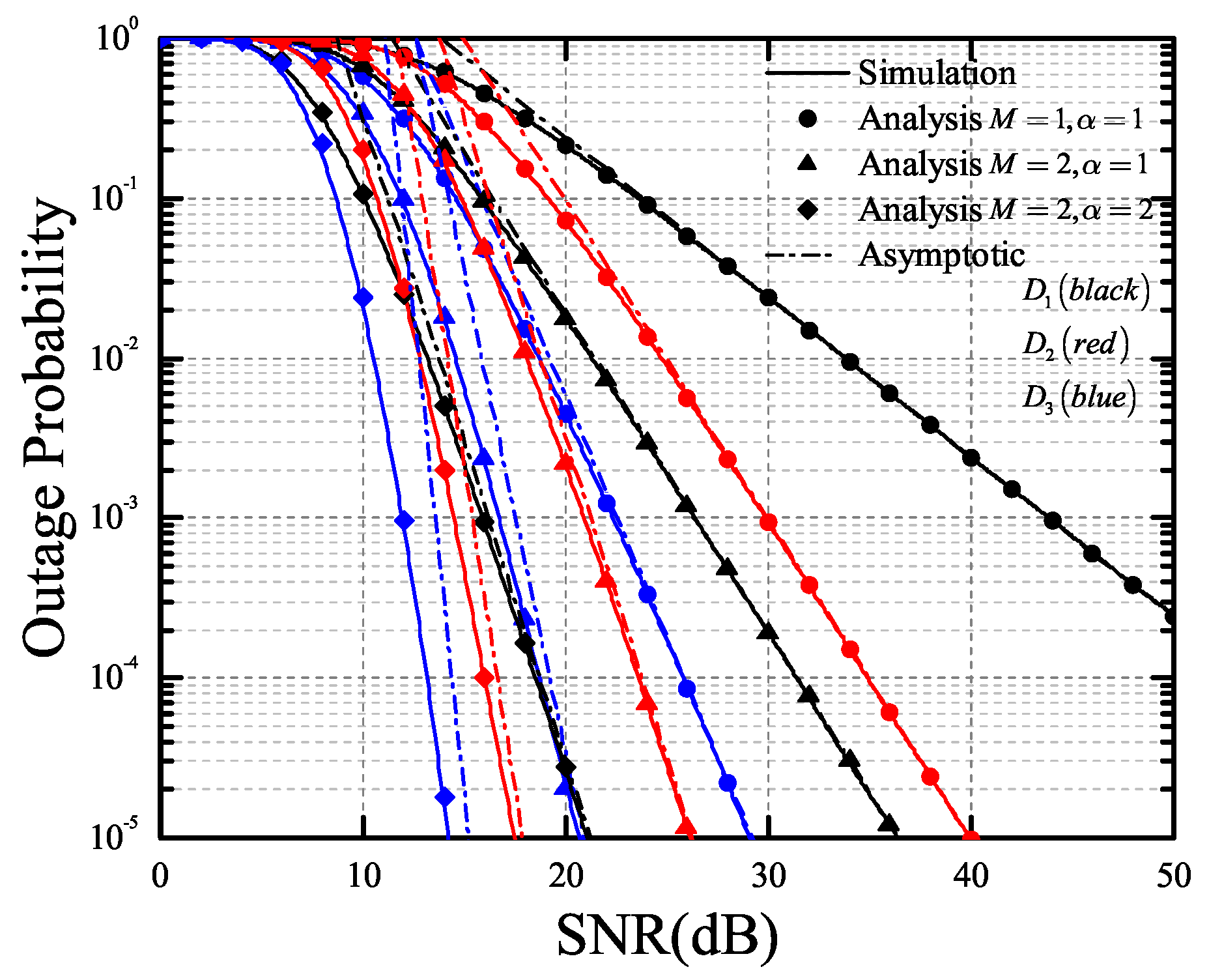
3.4. Diversity Order
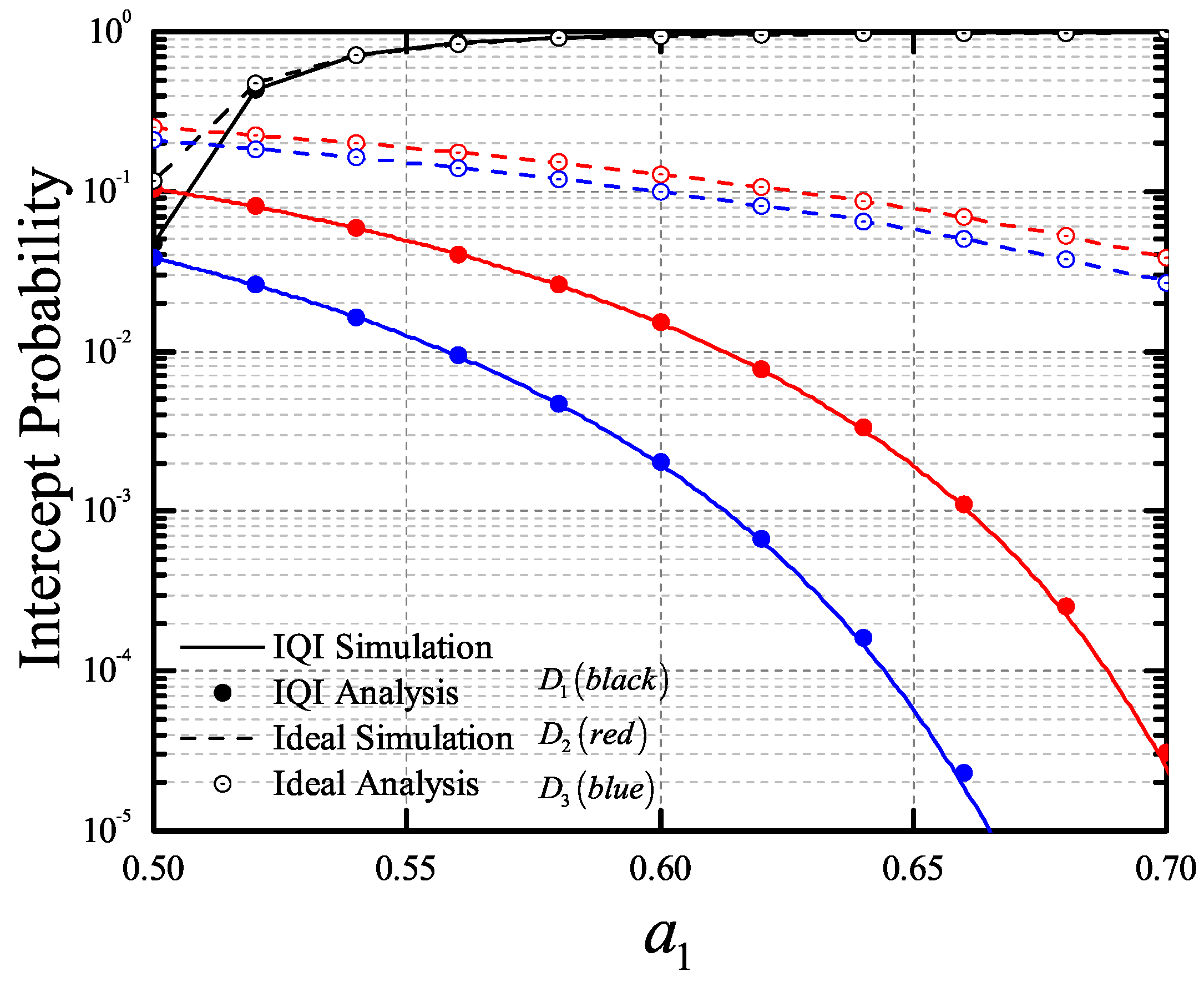
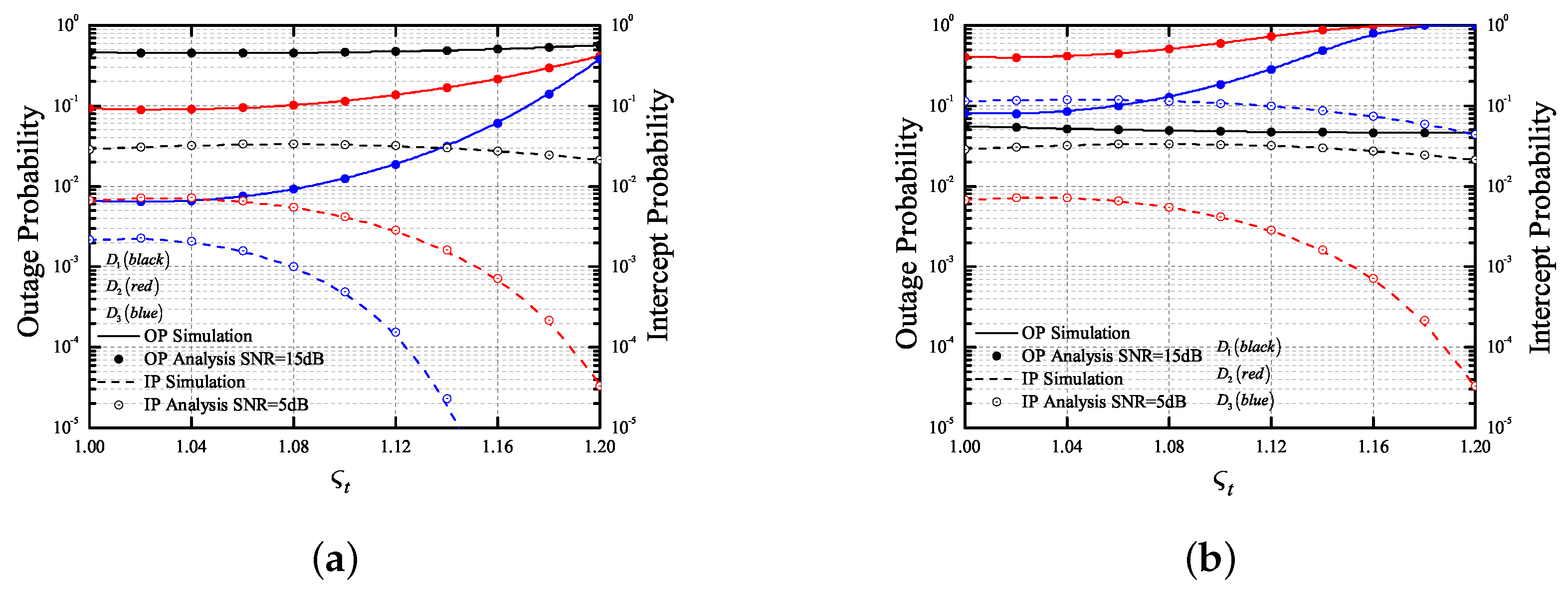
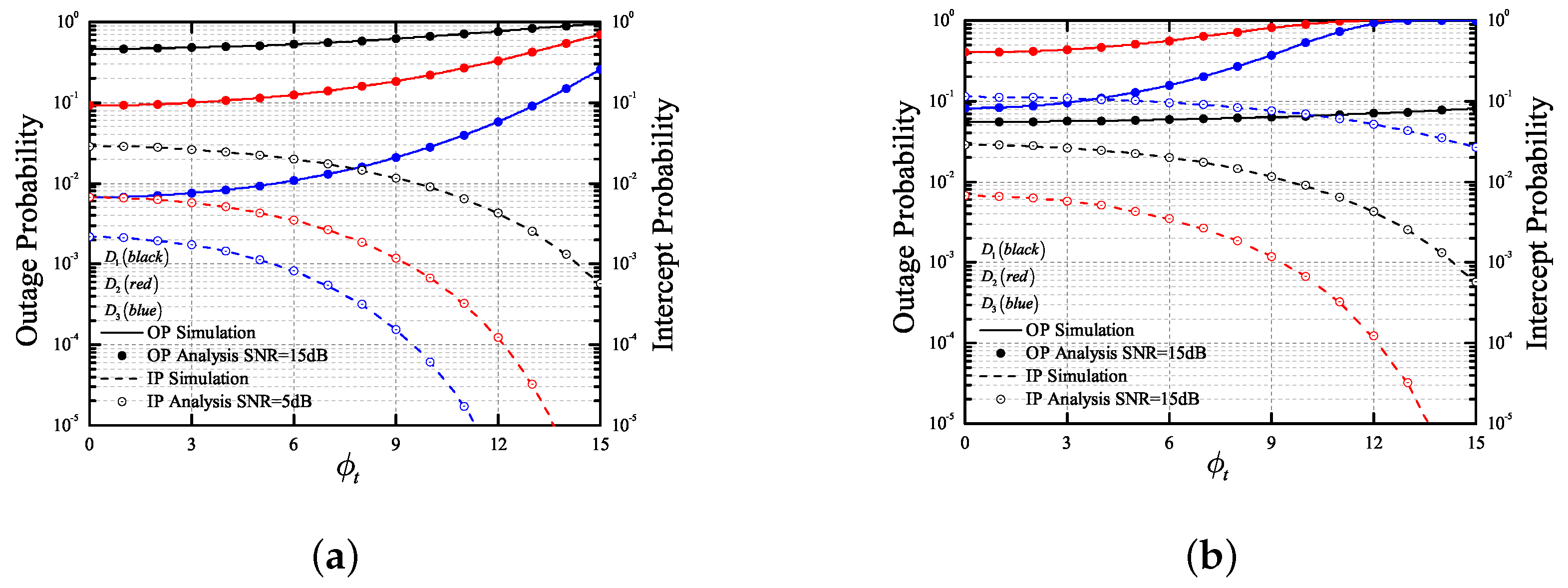
4. Numeric Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
References
- Li, X.; Li, J.; Mathiopoulos, P.T.; Zhang, D. Joint Impact of Hardware Impairments and Imperfect CSI on Cooperative SWIPT NOMA Multi-Relaying Systems. In Proceedings of the 2018 IEEE/CIC International Conference on Communications in China (ICCC), Beijing, China, 16–18 August 2018; pp. 95–99. [Google Scholar]
- Zeng, J.; Lv, T.; Liu, R.P. Investigation on Evolving Single-Carrier NOMA Into Multi-Carrier NOMA in 5G. IEEE Access 2018, 6, 48268–48288. [Google Scholar] [CrossRef]
- Li, X.; Liu, M.; Deng, C.; Mathiopoulos, P.T.; Ding, Z.; Liu, Y. Full-Duplex Cooperative NOMA Relaying Systems with I/Q Imbalance and Imperfect SIC. IEEE Wirel. Commun. Lett. 2019. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Liu, Y.; Ding, Z.; Nallanathan, A. Residual Transceiver Hardware Impairments on Cooperative NOMA Networks. IEEE Trans. Wirel. Commun. 2019. [Google Scholar] [CrossRef]
- Khan, W.U.; Jameel, F.; Ristaniemi, T.; Khan, S.; Sidhu, G.A.S.; Liu, J. Joint Spectral and Energy Efficiency Optimization for Downlink NOMA Networks. IEEE Trans. Cogn. Commun. Netw. 2019. [Google Scholar] [CrossRef]
- Niharika, G. Performance comparison of modulation schemes for Downlink NOMA. In Proceedings of the 2018 2nd International Conference Inventive System Control, Coimbatore, India, 19–20 January 2018; pp. 1431–1433. [Google Scholar]
- Abbasi, O.; Ebrahimi, A.; Mokari, N. NOMA Inspired Cooperative Relaying System Using an AF Relay. IEEE Wirel. Commun. Lett. 2019, 8, 261–264. [Google Scholar] [CrossRef]
- Yue, X.; Liu, Y.; Kang, S.; Nallanathan, A. Performance Analysis of NOMA with Fixed Gain Relaying Over Nakagami-m Fading Channels. IEEE Access 2017, 5, 5445–5454. [Google Scholar] [CrossRef]
- Men, J.; Ge, J. Performance analysis of non-orthogonal multiple access in downlink cooperative network. IET Commun. 2015, 9, 2267–2273. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. Random beamforming in millimeterwave NOMA networks. IEEE Access 2017, 5, 7667–7681. [Google Scholar] [CrossRef]
- Arzykulov, S.; Nauryzbayev, G.; Tsiftsis, T.A.; Maham, B.; Abdallah, M. On the Outage of Underlay CR-NOMA Networks with Detect-and-Forward Relaying. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 795–804. [Google Scholar] [CrossRef]
- Mirabbasi, S.; Martin, K. Classical and modern receiver architectures. IEEE Commun. Mag. 2000, 38, 132–139. [Google Scholar] [CrossRef]
- Li, J.; Matthaiou, M.; Svensson, T. I/Q Imbalance in AF Dual-Hop Relaying: Performance Analysis in Nakagami-m Fading. IEEE Trans. Commun. 2014, 62, 836–847. [Google Scholar] [CrossRef]
- Chen, L.; Helmy, A.G.; Yue, G.; Li, S.; Al-Dhahir, N. Performance Analysis and Compensation of Joint TX/RX I/Q Imbalance in Differential STBC-OFDM. IEEE Trans. Veh. Technol. 2017, 66, 6184–6200. [Google Scholar] [CrossRef]
- Hamila, R.; Özdemir, Ö.; Al-Dhahir, N. Beamforming OFDM Performance Under Joint Phase Noise and I/Q Imbalance. IEEE Trans. Veh. Technol. 2016, 65, 2978–2989. [Google Scholar] [CrossRef]
- Faruk, M.S.; Kikuchi, K. Compensation for In-Phase/Quadrature Imbalance in Coherent-Receiver Front End for Optical Quadrature Amplitude Modulation. IEEE Photon. J. 2013, 5, 7800110. [Google Scholar] [CrossRef]
- Ruihao, C.; Xiuli, Y.; Yuyao, S.; Yongqing, W. Method for the compensation of transmitter I/Q imbalance based on the pre-distortion of baseband signals. In Proceedings of the 2017 9th International Conference Advanced Infocomm Technology, Chengdu, China, 22–24 November 2017; pp. 313–317. [Google Scholar]
- Nam, W.; Roh, H.; Lee, J.; Kang, I. Blind Adaptive I/Q Imbalance Compensation Algorithms for Direct-Conversion Receivers. IEEE Signal Process. Lett. 2012, 19, 475–478. [Google Scholar] [CrossRef]
- Selim, B.; Muhaidat, S.; Sofotasios, P.; Sharif, B.; Stouraitis, T.; Karagiannidis, G.; Al-Dhahir, N. Performance Analysis of Non-Orthogonal Multiple Access Under I/Q Imbalance. IEEE Access 2018, 6, 18453–18468. [Google Scholar] [CrossRef]
- Khan, W.U. Maximizing physical layer security in relay-assisted multicarrier nonorthogonal multiple access transmission. Internet Technol. Lett. 2019, 2. [Google Scholar] [CrossRef]
- Chen, X.; Guo, L.; Li, X.; Dong, C.; Lin, J. Secrecy rate optimization for cooperative cognitive radio networks aided by a wireless energy harvesting jammer. IEEE Access 2018, 6, 34127–34134. [Google Scholar] [CrossRef]
- Yang, N.; Wang, L.; Geraci, G.; Elkashlan, M.; Yuan, J.; di Renzo, M. Safeguarding 5G wireless communication networks using physical layer security. IEEE Commun. Mag. 2015, 53, 20–27. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless information-theoretic security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Liang, L.; Wei, D.; Li, M. Wireless Physical Layer Security Based on Channel Pre-Compensation for PolSK Modulated Systems. In Proceedings of the 2017 IEEE International Conference Communication Software and Networks, Guangzhou, China, 6–8 May 2017; pp. 357–361. [Google Scholar]
- Wang, H.; Luo, M.; Yin, Q.; Xia, X. Hybrid Cooperative Beamforming and Jamming for Physical-Layer Security of Two-Way Relay Networks. IEEE Trans. Inf. Forensics Secur. 2013, 8, 2007–2020. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, J.; Zhao, H.; Xu, Y. Performance analysis of physical layer security over α − η − κ − μ fading channels. China Commun. 2018, 15, 138–148. [Google Scholar] [CrossRef]
- Ammari, M.; Fortier, P. Physical layer security of multiple-input-multiple-output systems with transmit beamforming in Rayleigh fading. IET Commun. 2015, 9, 1096–1103. [Google Scholar] [CrossRef]
- Abolpour, M.; Mirmohseni, M.; Aref, M. Outage Performance in Secure Cooperative NOMA. In Proceedings of the 2019 Iran Workshop on Communication and Information Theory (IWCIT), Tehran, Iran, 24–25 April 2019; pp. 1–6. [Google Scholar]
- Shim, K.; Do, T.; An, B. Improving Physical Layer Security of NOMA Networks by Using Opportunistic Scheduling. In Proceedings of the 2018 Tenth International Conference Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 3–6 July 2018; pp. 262–267. [Google Scholar]
- Satrya, G.B.; Shin, S.Y. Security enhancement to successive interference cancellation algorithm for non-orthogonal multiple access (NOMA). In Proceedings of the 2017 IEEE 28th Annual International Symposium Pers., Indoor, Mobile Radio Communications, Montreal, QC, Canada, 8–13 October 2017; pp. 1–5. [Google Scholar]
- Zheng, B.; Wen, M.; Chen, F.; Tang, J.; Ji, F. Secure NOMA Based Full-Duplex Two-Way Relay Networks with Artificial Noise against Eavesdropping. In Proceedings of the 2018 IEEE International Conference Communications, Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Lei, H.; Zhang, J.; Park, K.; Xu, P.; Zhang, Z.; Pan, G. Secrecy Outage of Max-Min TAS Scheme in MIMO-NOMA Systems. IEEE Trans. Veh. Technol. 2018, 67, 6981–6990. [Google Scholar] [CrossRef]
- Zaghdoud, N.; Alouane, W.; Boujemaa, H.; Touati, F. Secure Performance of AF and DF Relaying in Cooperative Noma Systems. In Proceedings of the 2019 19th International Conference Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 24–26 March 2019; pp. 614–619. [Google Scholar]
- Liu, Y.; Xing, H.; Pan, C.; Nallanathan, A.; Elkashlan, M.; Hanzo, L. Multiple-Antenna-Assisted Non-Orthogonal Multiple Access. IEEE Wirel. Commun. 2018, 25, 17–23. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, J.; Park, K.; Xu, P.; Ansari, I.S.; Pan, G.; Alomair, B.; Alouini, M.S. On Secure NOMA Systems WITH Transmit Antenna Selection Schemes. IEEE Access 2017, 5, 17450–17464. [Google Scholar] [CrossRef]
- Gomez, G.; Martin-Vega, F.; Javier, F.; Liu, Y.; Elkashlan, M. Physical Layer Security in Uplink NOMA Multi-Antenna Systems with Randomly Distributed Eavesdroppers. IEEE Access 2019, 7, 70422–70435. [Google Scholar] [CrossRef]
- Li, X.; Huang, M.; Zhang, C.; Deng, D.; Rabie, K.; Ding, Y.; Du, J. Security and Reliability Performance Analysis of Cooperative Multi-Relay Systems with Nonlinear Energy Harvesters and Hardware Impairments. IEEE Access 2019, 7, 102644–102661. [Google Scholar] [CrossRef]
- Korn, I.; Fonseka, J.P. FSK with Limiter-Discriminator Detector in Nakagami Fading Channels with and without Selection Combining. IEEE Trans. Veh. Technol. 2006, 55, 1934–1940. [Google Scholar] [CrossRef]
- Lei, H.; Ansari, I.S.; Pan, G.; Alomair, B.; Alouini, M.S. Secrecy Capacity Analysis Over α − μ Fading Channels. IEEE Commun. Lett. 2017, 21, 1445–1448. [Google Scholar] [CrossRef]
- Sun, J.; Li, X.; Huang, M.; Ding, Y.; Jin, J.; Pan, G. Performance analysis of physical layer security over κ − μ shadowed fading channels. IET Commun. 2018, 12, 970–975. [Google Scholar] [CrossRef]
- Bjornson, E.; Matthaiou, M.; Debbah, M. A New Look at Dual-Hop Relaying: Performance Limits with Hardware Impairments. IEEE Trans. Commun. 2013, 61, 4512–4525. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Li, L. Performance Analysis of Impaired SWIPT NOMA Relaying Networks Over Imperfect Weibull Channels. IEEE Syst. J. 2019, 1–4. [Google Scholar] [CrossRef]
- Schenk, T. RF Imperfections in High-Rate Wireless Systems; Springer: Berlin, Germany, 2008. [Google Scholar]
- Maham, B.; Tirkkonen, O.; Hjorungnes, A. Impact of Transceiver I/Q Imbalance on Transmit Diversity of Beamforming OFDM Systems. IEEE Trans. Commun. 2012, 60, 643–648. [Google Scholar] [CrossRef]
- Boulogeorgos, A.A.; Sofotasios, P.C.; Selim, B.; Muhaidat, S. Effects of RF Impairments in Communications Over Cascaded Fading Channels. IEEE Trans. Veh. Technol. 2016, 65, 8878–8894. [Google Scholar] [CrossRef]
- Qi, J.; Ai¨ssa, S.; Alouini, M. Impact of I/Q imbalance on the performance of two-way CSI-assisted AF relaying. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2507–2512. [Google Scholar]
- Li, X.; Liu, M.; Deng, D. Power Beacon Assisted Wireless Power Cooperative Relaying using NOMA with Hardware Impairments and Imperfect CSI. AEU-Int. J. Electron. Commun. 2019, 108, 275–286. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Liu, Y.; Ding, Z. Outage Performance of Cooperative NOMA Networks with Hardware Impairments. In Proceedings of the 2018 IEEE Global Communication Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Aloqaily, M.; Balasubramanian, V.; Zaman, F.; Al Ridhawi, I.; Jararweh, Y. Congestion mitigation in densely crowded environments for augmenting qos in vehicular clouds. In Proceedings of the 8th Symposium on Design and Analysis of Intelligent Vehicular Networks and Applications, Montreal, QC, Canada, 28 October–2 November 2018; pp. 49–56. [Google Scholar]
| Monte Carlo Simulations Repeated | Iterations |
|---|---|
| The number of legitimate destinations | |
| The number of antennas | |
| Power sharing coefficients of NOMA | , , |
| Noise power | |
| Targeted data rates (OP) | , , |
| Targeted data rates (IP) | , , and |
| The fading parameters of the channel | , |
| Ideal RF front end | , |
| IQI parameters | , |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhao, M.; Zhang, C.; Khan, W.U.; Wu, J.; Rabie, K.M.; Kharel, R. Security Analysis of Multi-Antenna NOMA Networks Under I/Q Imbalance. Electronics 2019, 8, 1327. https://doi.org/10.3390/electronics8111327
Li X, Zhao M, Zhang C, Khan WU, Wu J, Rabie KM, Kharel R. Security Analysis of Multi-Antenna NOMA Networks Under I/Q Imbalance. Electronics. 2019; 8(11):1327. https://doi.org/10.3390/electronics8111327
Chicago/Turabian StyleLi, Xingwang, Mengle Zhao, Changsen Zhang, Wali Ullah Khan, Jun Wu, Khaled M. Rabie, and Rupak Kharel. 2019. "Security Analysis of Multi-Antenna NOMA Networks Under I/Q Imbalance" Electronics 8, no. 11: 1327. https://doi.org/10.3390/electronics8111327
APA StyleLi, X., Zhao, M., Zhang, C., Khan, W. U., Wu, J., Rabie, K. M., & Kharel, R. (2019). Security Analysis of Multi-Antenna NOMA Networks Under I/Q Imbalance. Electronics, 8(11), 1327. https://doi.org/10.3390/electronics8111327








