SDR Based Indoor Beacon Localization Using 3D Probabilistic Multipath Exploitation and Deep Learning
Abstract
:1. Introduction
2. 3D Multipath Estimation and Probabilistic Learning
2.1. 3D CSI Estimation
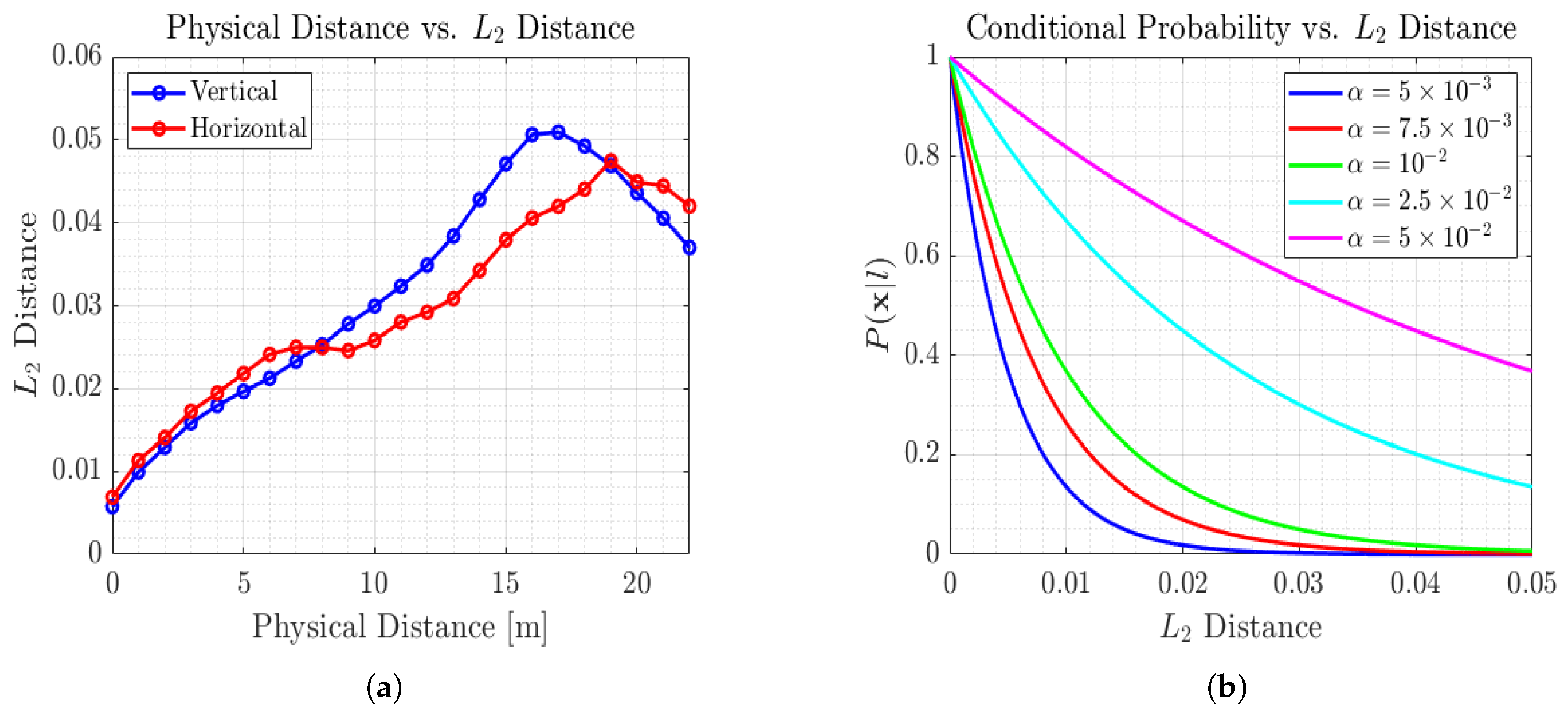
2.2. Probabilistic Localization Algorithm
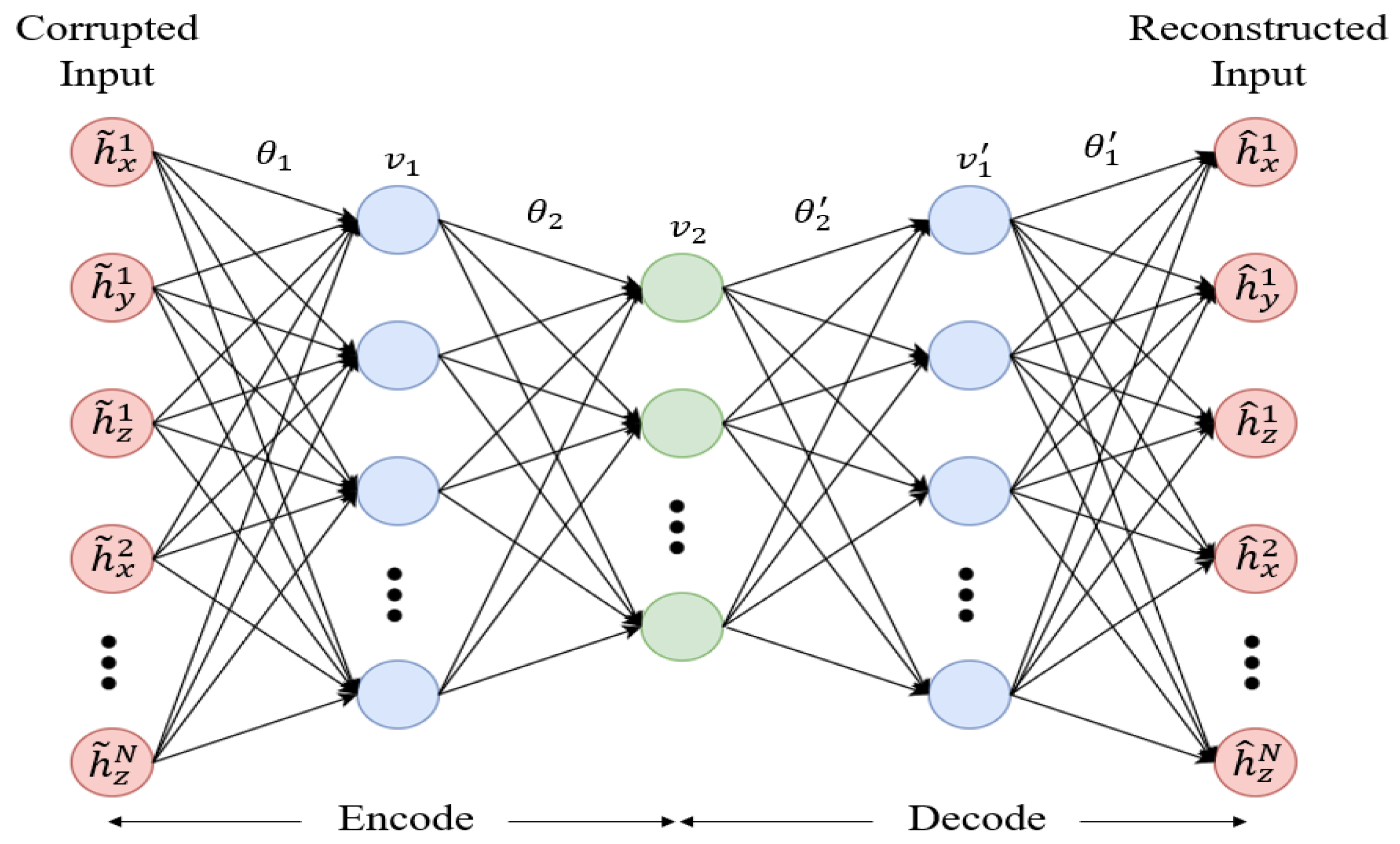
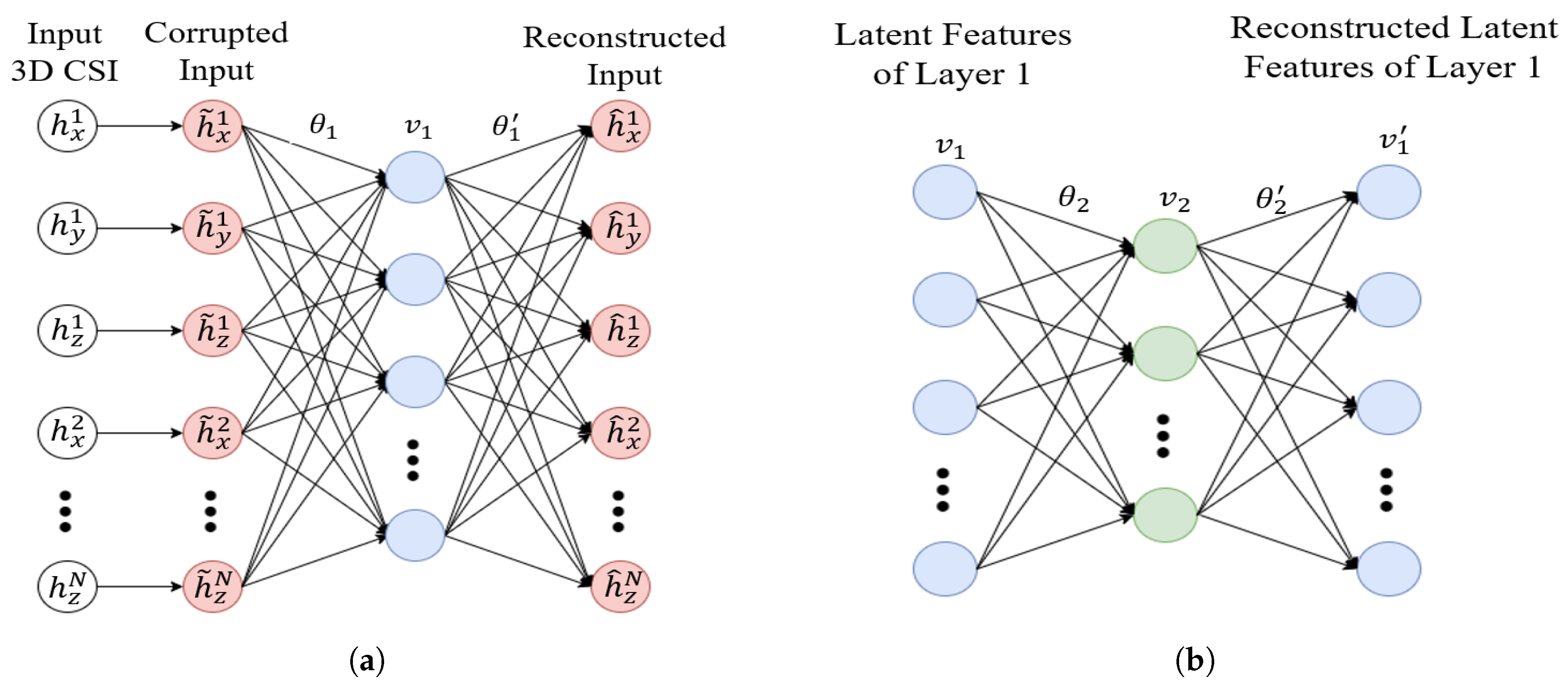
3. Deep Learning and Denoising Autoencoder
4. Indoor Localization Model
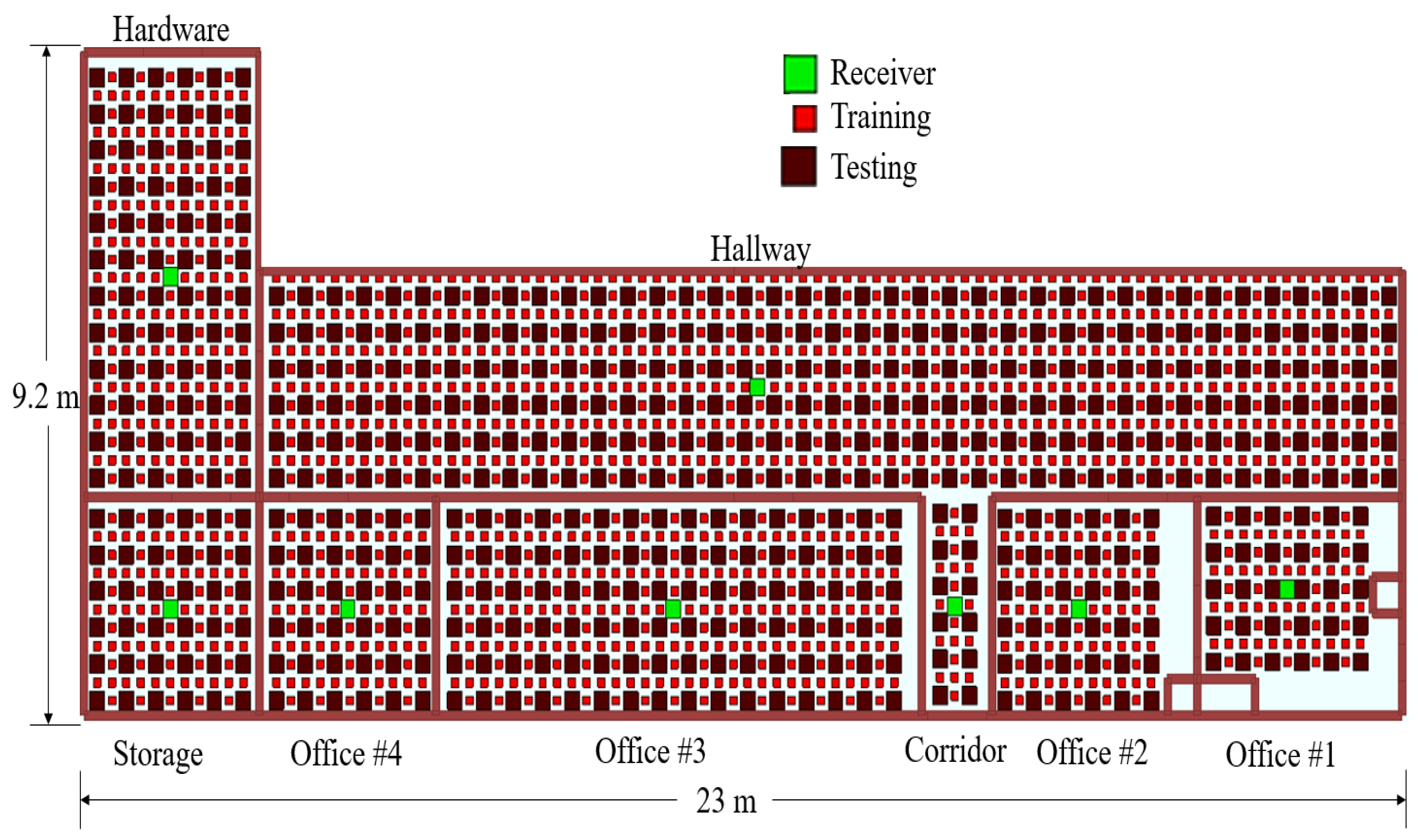
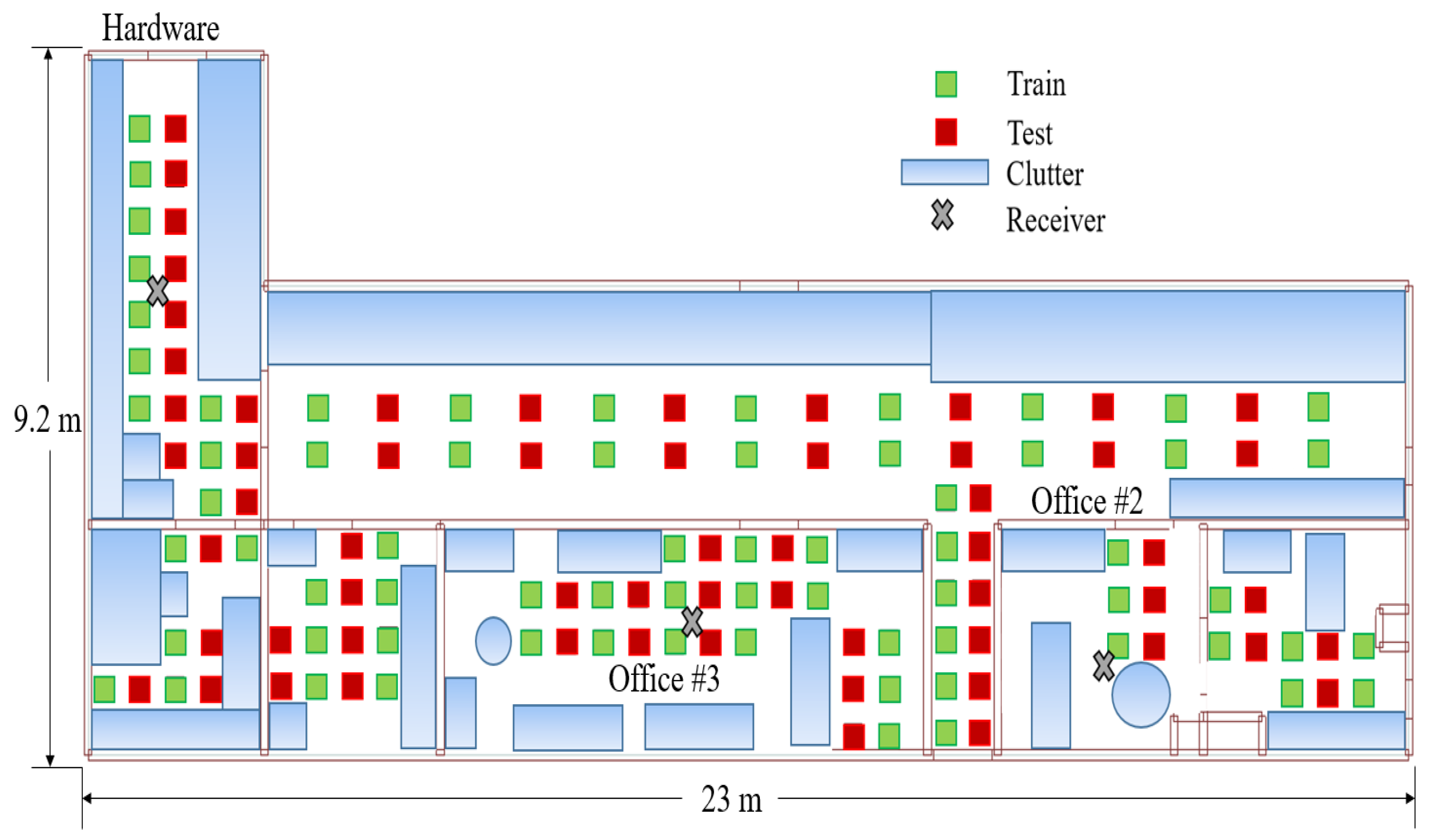
4.1. Indoor Model
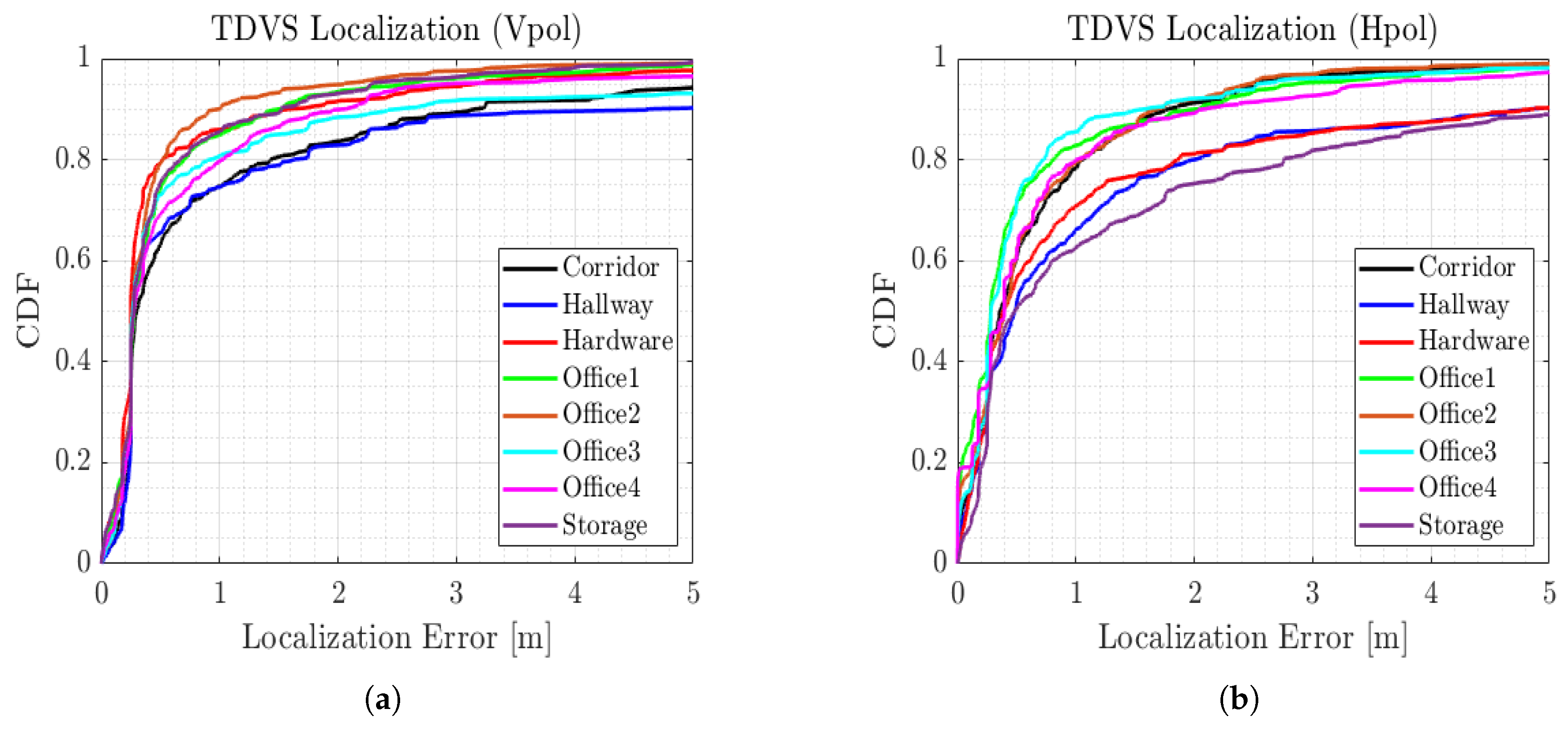
4.2. Simulation Results
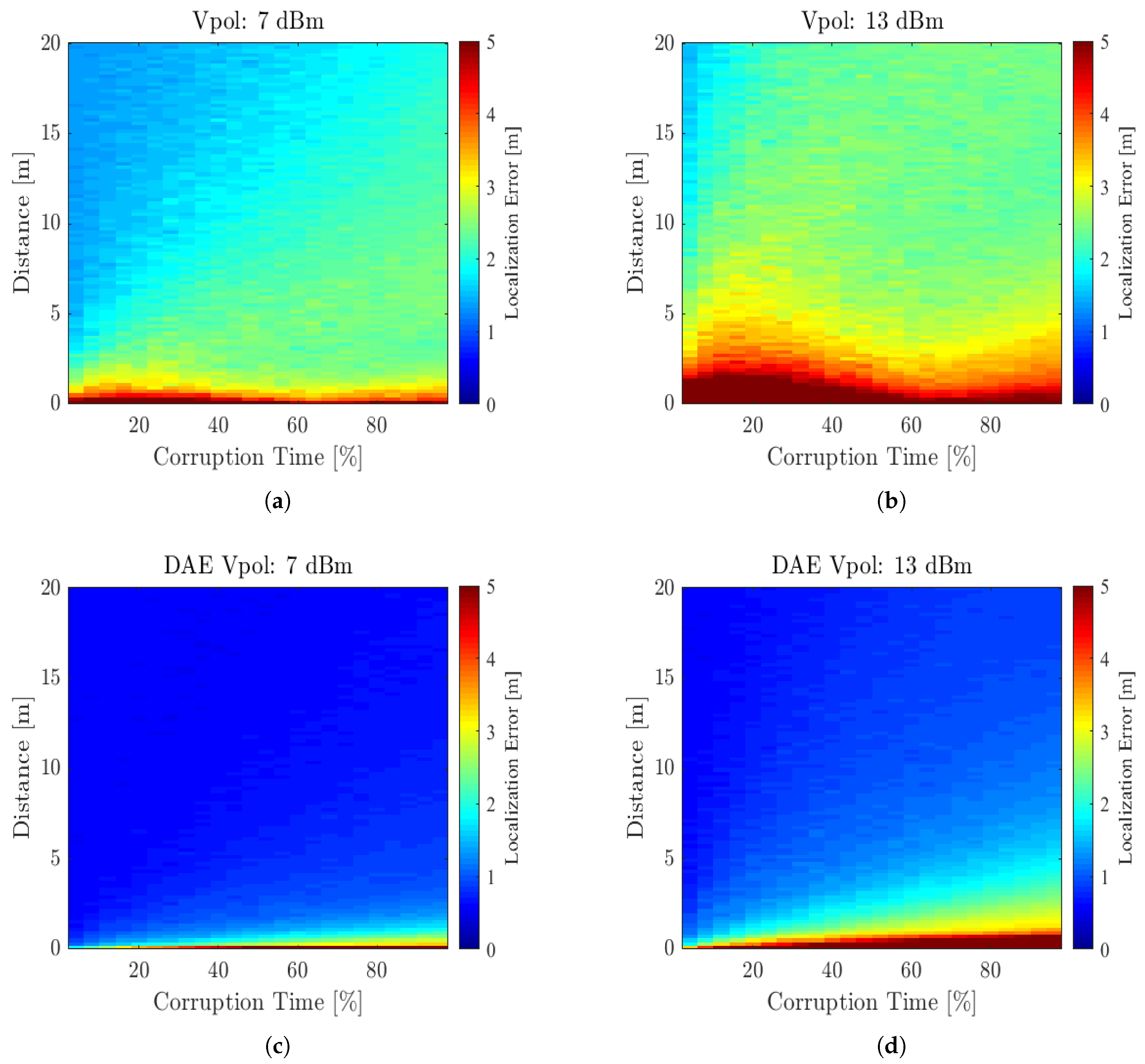
4.3. Interference Impacts on 3D CSI and Denoising Autoencoder
4.3.1. Interference Generation
4.3.2. Training 3D CSI Interference Based Denoising Autoencoder
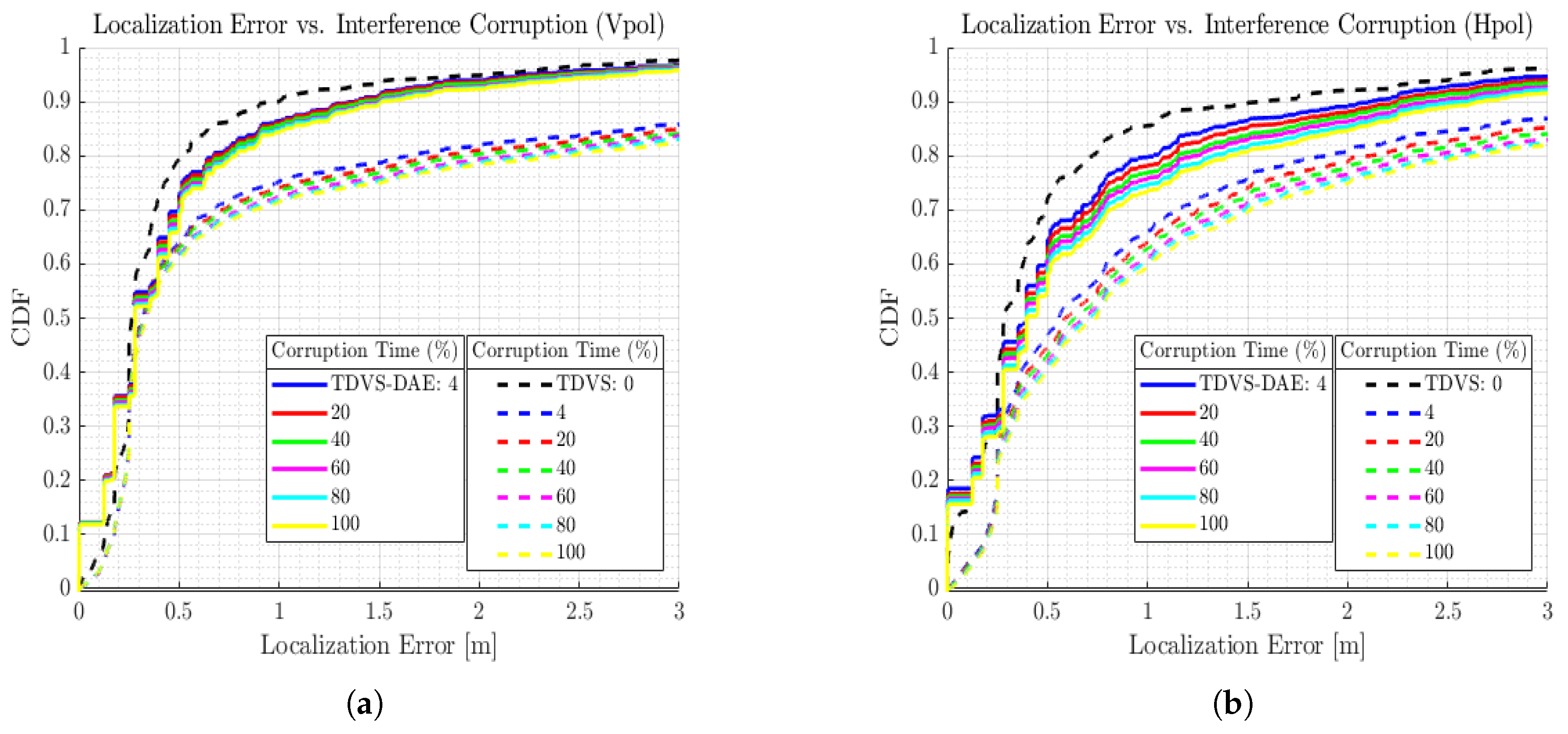
4.3.3. Localization Performance with Interference
5. Software Defined Radio Experimentation
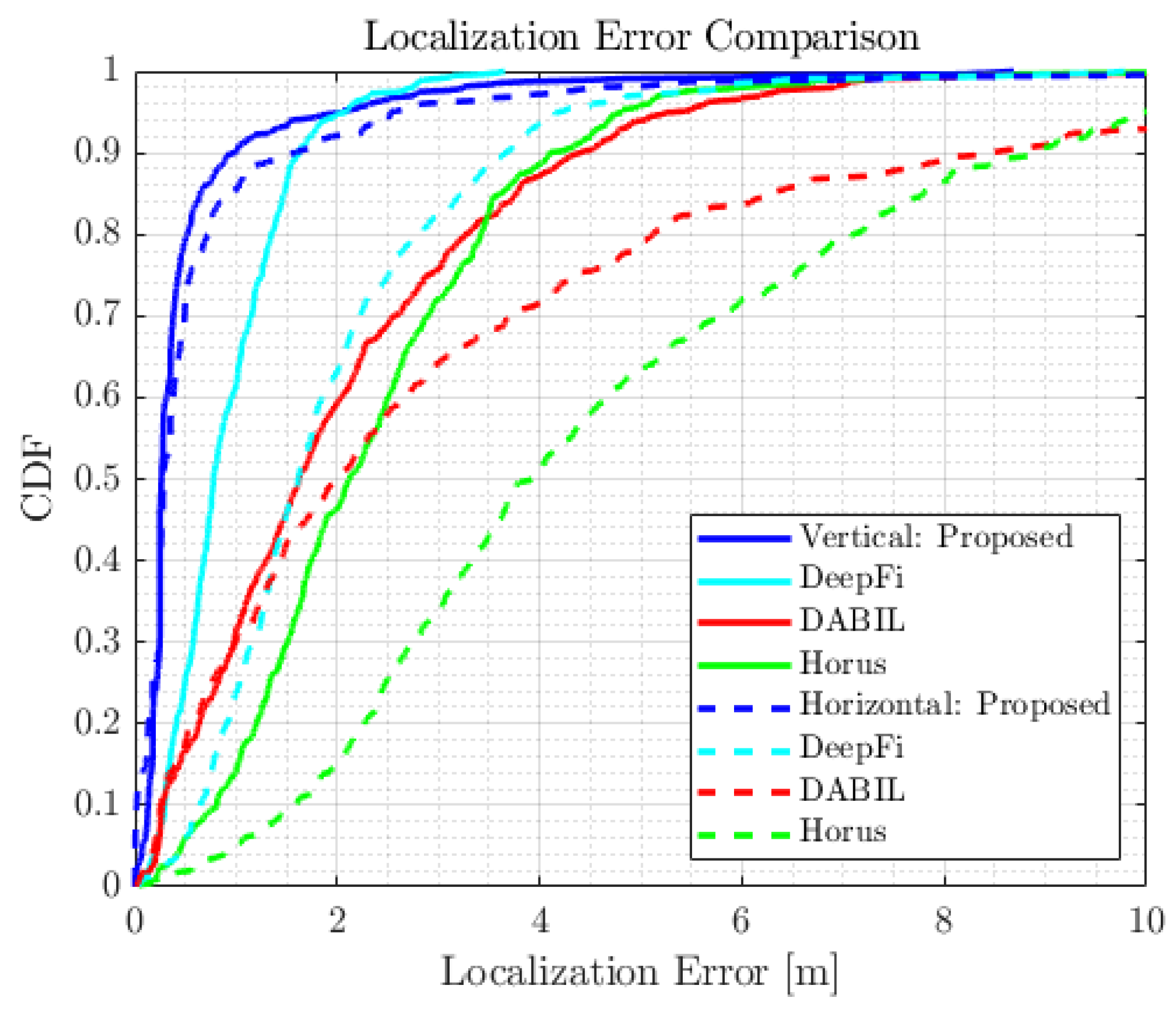
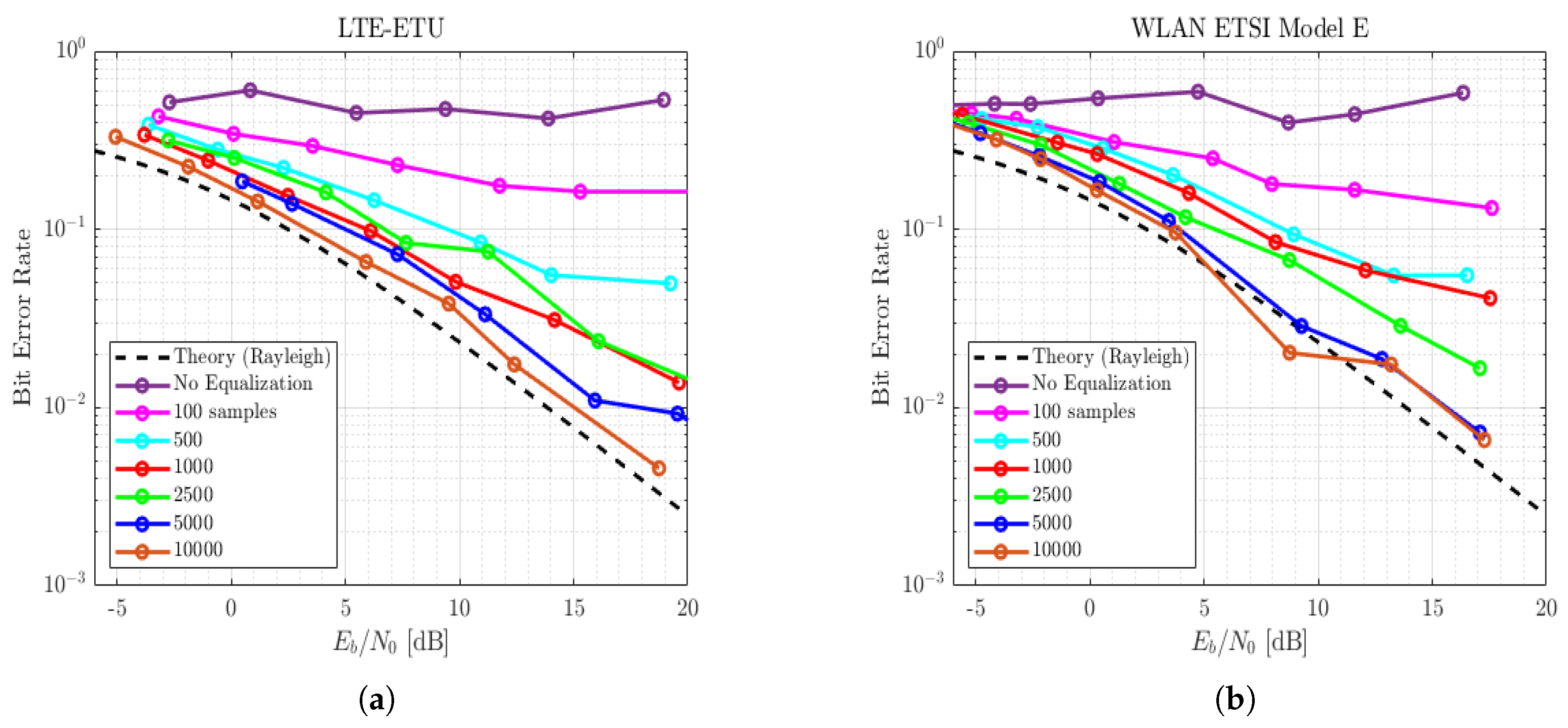
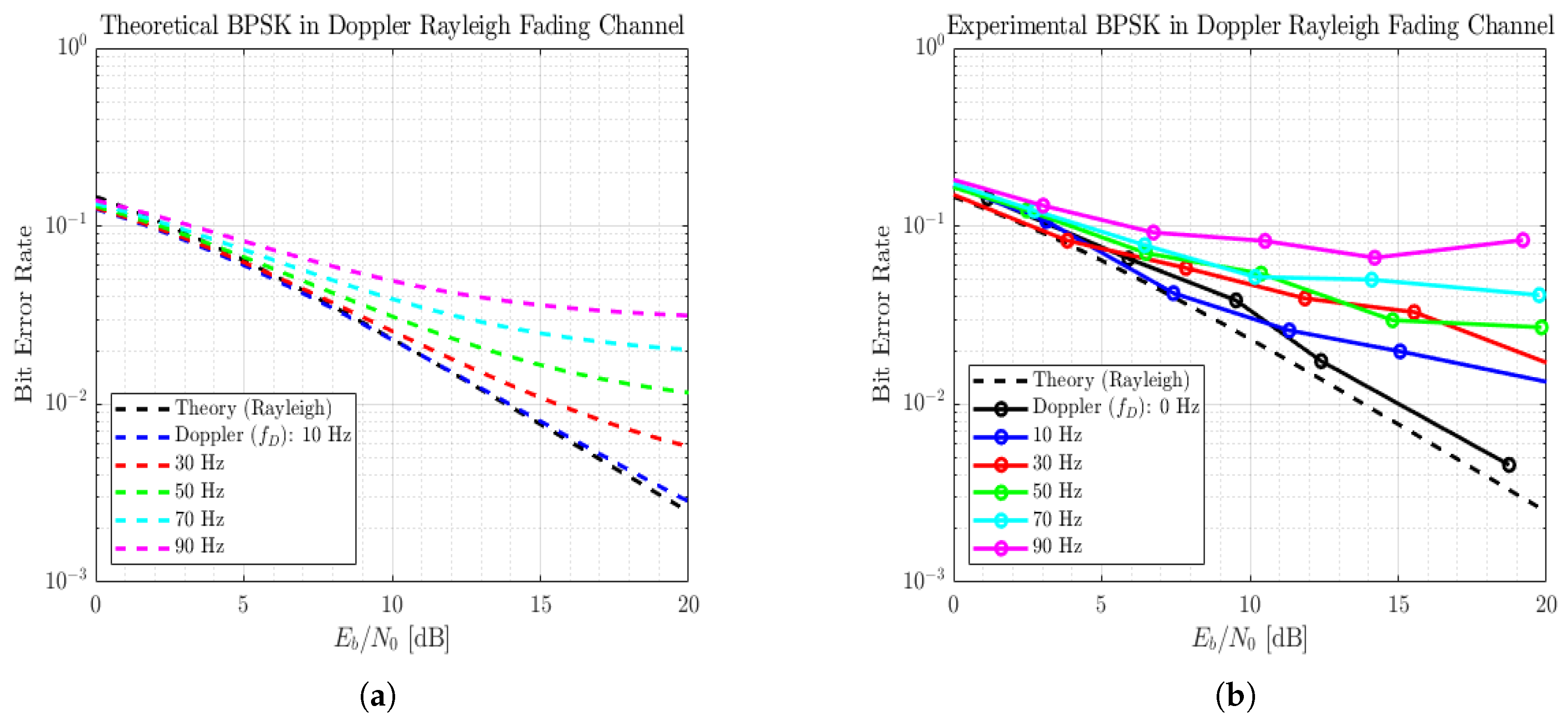
5.1. CSI Estimation
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AP | Access point |
| AWG | Arbitrary waveform generator |
| BPSK | Binary phase shift keying |
| CSI | Channel state information |
| DAE | Denoising autoencoder |
| DoA | Direction of arrival |
| GMM | Gaussian mixture model |
| IPS | Indoor positioning system |
| LoS | Line-of-sight |
| NIC | Network interface card |
| NLoS | Non-line-of-sight |
| PkNN | Probabilistic k nearest neighbor |
| RF | Radio frequency |
| RSS | Received signal strength |
| SDR | Software defined radio |
| TDVS | Triad dipole vector sensor |
| WLAN | Wireless local access network |
References
- Roos, T.; Myllymäki, P.; Tirri, H.; Misikangas, P.; Sievänen, J. A Probabilistic Approach to WLAN User Location Estimation. Int. J. Wirel. Inf. Netw. 2002, 9, 155–164. [Google Scholar] [CrossRef]
- Bulten, W.; Rossum, A.C.V.; Haselager, W.F.G. Human SLAM, Indoor Localisation of Devices and Users. In Proceedings of the 2016 IEEE First International Conference on Internet-of-Things Design and Implementation (IoTDI), Berlin, Germany, 4–8 April 2016; pp. 211–222. [Google Scholar] [CrossRef]
- Youssef, M.; Agrawala, A.K. The Horus WLAN location determination system. In Proceedings of the 3rd International Conference on Mobile Systems, Applications, and Services (MobiSys), Seattle, WA, USA, 6–8 June 2005. [Google Scholar]
- Khatab, Z.E.; Hajihoseini, A.; Ghorashi, S.A. A Fingerprint Method for Indoor Localization Using Autoencoder Based Deep Extreme Learning Machine. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Xiao, C.; Yang, D.; Chen, Z.; Tan, G. 3-D BLE Indoor Localization Based on Denoising Autoencoder. IEEE Access 2017, 5, 12751–12760. [Google Scholar] [CrossRef]
- Wu, K.; Xiao, J.; Yi, Y.; Chen, D.; Luo, X.; Ni, L.M. CSI-Based Indoor Localization. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1300–1309. [Google Scholar] [CrossRef]
- Yazdanian, P.; Pourahmadi, V. DeepPos: Deep Supervised Autoencoder Network for CSI Based Indoor Localization. arXiv 2018, arXiv:1811.12182. [Google Scholar]
- Wu, G.; Tseng, P. A Deep Neural Network-Based Indoor Positioning Method using Channel State Information. In Proceedings of the 2018 International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 5–8 March 2018; pp. 290–294. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. DeepFi: Deep learning for indoor fingerprinting using channel state information. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015; pp. 1666–1671. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Mao, S. CSI Phase Fingerprinting for Indoor Localization With a Deep Learning Approach. IEEE Internet Things J. 2016, 3, 1113–1123. [Google Scholar] [CrossRef]
- Nambiar, V.; Vattapparamban, E.; Yurekli, A.I.; Güvenç, İ; Mozaffari, M.; Saad, W. SDR based indoor localization using ambient WiFi and GSM signals. In Proceedings of the 2017 International Conference on Computing, Networking and Communications (ICNC), Santa Clara, CA, USA, 26–29 January 2017; pp. 952–957. [Google Scholar] [CrossRef]
- Schmidt, E.; Inupakutika, D.; Mundlamuri, R.; Akopian, D. SDR-Fi: Deep-learning-based Indoor Positioning via Software-defined Radio. IEEE Access 2019, 7, 145784–145797. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, C.; Wang, Z. WiFi TDoA indoor localization system based on SDR platform. In Proceedings of the 2017 IEEE International Symposium on Consumer Electronics (ISCE), Kuala Lumpur, Malaysia, 14–15 November 2017; pp. 82–83. [Google Scholar] [CrossRef]
- Vasudeva, K.; Çiftler, B.S.; Altamar, A.; Guvenc, I. An experimental study on RSS-based wireless localization with software defined radio. In Proceedings of the WAMICON 2014, Tampa, FL, USA, 6 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Hall, D.L.; Narayanan, R.M.; Lenzing, E.H.; Jenkins, D.M. Passive Vector Sensing for Non-Cooperative Emitter Localization in Indoor Environments. Electronics 2018, 7, 442. [Google Scholar] [CrossRef]
- Hall, D.L.; Narayanan, R.M.; Jenkins, D.M.; Lenzing, E.H. Non-cooperative emitter classification and localization with vector sensing and machine learning in indoor environments. In Radar Sensor Technology XXIII; Ranney, K.I., Doerry, A., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11003, pp. 280–293. [Google Scholar] [CrossRef]
- Daldorff, L.K.S.; Turaga, D.S.; Verscheure, O.; Biem, A. Direction of Arrival estimation using single tripole radio antenna. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 2149–2152. [Google Scholar] [CrossRef]
- Chen, L.; Aminaei, A.; Falcke, H.; Gurvits, L. Optimized estimation of the Direction of Arrival with single tripole antenna. In Proceedings of the 2010 Loughborough Antennas Propagation Conference, Loughborough, UK, 8–9 November 2010; pp. 93–96. [Google Scholar] [CrossRef]
- Compton, R. The tripole antenna: An adaptive array with full polarization flexibility. IEEE Trans. Antennas Propag. 1981, 29, 944–952. [Google Scholar] [CrossRef]
- Durgin, G. Space-Time Wireless Channels, 1st ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Baldi, P.; Hornik, K. Neural Networks and Principal Component Analysis: Learning from Examples Without Local Minima. Neural Netw. 1989, 2, 53–58. [Google Scholar] [CrossRef]
- Vlasenko, I.; Nikolaidis, I.; Stroulia, E. The Smart-Condo: Optimizing Sensor Placement for Indoor Localization. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 436–453. [Google Scholar] [CrossRef]
- Perez-Vega, C.; Zamanillo, J.M. Path-loss model for broadcasting applications and outdoor communication systems in the VHF and UHF bands. IEEE Trans. Broadcast. 2002, 48, 91–96. [Google Scholar] [CrossRef]
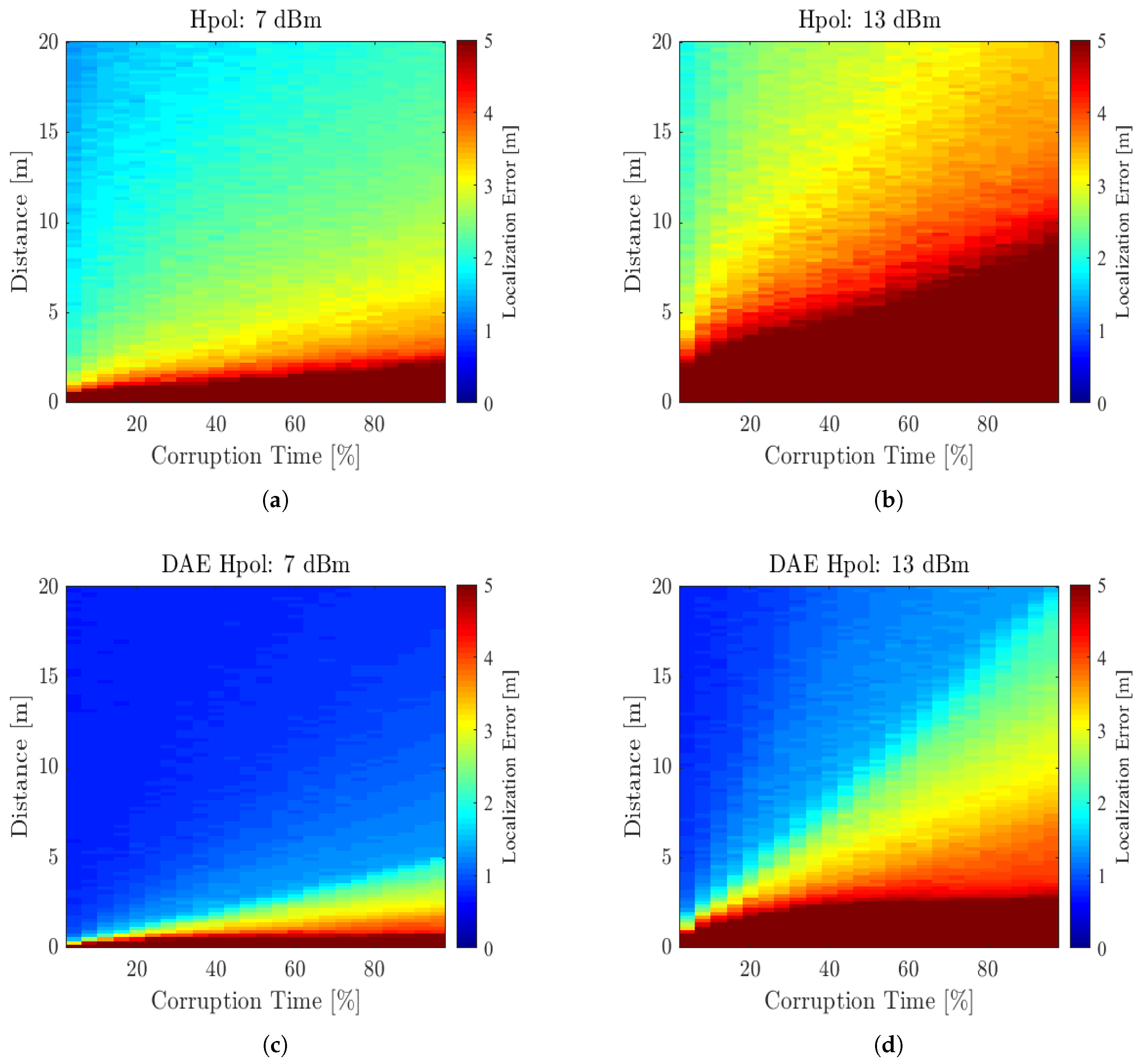
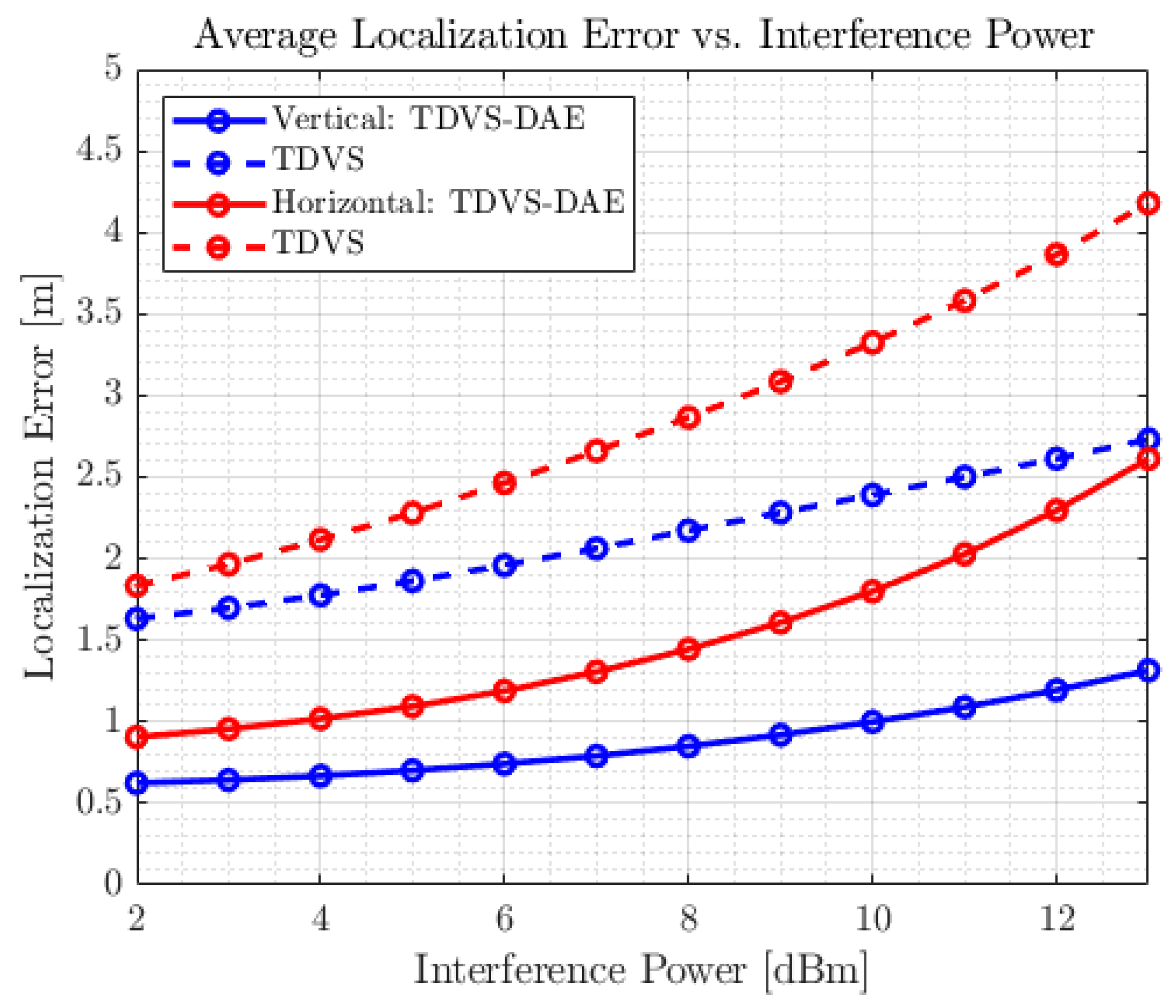

| Vertical Polarization | Horizontal Polarization | |||
|---|---|---|---|---|
| Room Location | (m) | (m) | (m) | (m) |
| Corridor | 1.251 | 2.454 | 0.762 | 1.217 |
| Hallway | 1.556 | 3.323 | 1.607 | 2.780 |
| Hardware | 0.693 | 1.462 | 1.687 | 3.283 |
| Office 1 | 0.643 | 1.066 | 0.703 | 1.335 |
| Office 2 | 0.528 | 0.910 | 0.694 | 0.935 |
| Office 3 | 1.242 | 2.908 | 0.683 | 1.315 |
| Office 4 | 0.893 | 1.847 | 0.823 | 1.398 |
| Storage | 0.600 | 0.921 | 1.943 | 3.319 |
| Vertical Polarization | Horizontal Polarization | |||
|---|---|---|---|---|
| Algorithm | (m) | (m) | (m) | (m) |
| 3D CSI | 0.528 | 0.910 | 0.694 | 0.935 |
| DeepFi | 0.924 | 0.597 | 1.946 | 1.365 |
| DABIL | 2.071 | 1.717 | 3.220 | 3.427 |
| Horus | 2.368 | 1.463 | 4.662 | 2.921 |
| Vertical Polarization | Horizontal Polarization | |||
|---|---|---|---|---|
| Room: Approach | (m) | (m) | (m) | (m) |
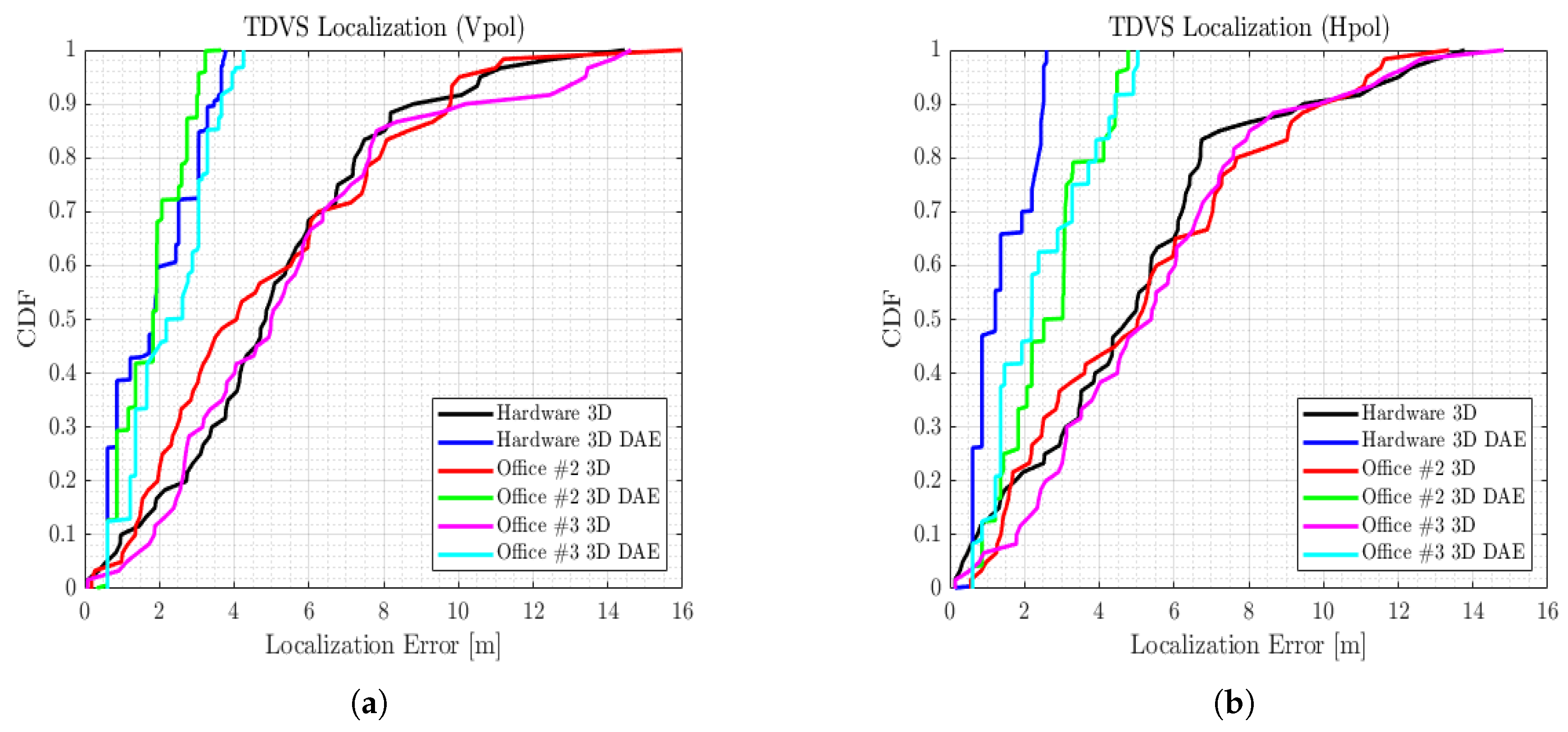
| Hardware: TDVS | 5.175 | 3.068 | 5.014 | 3.323 |
| Hardware: TDVS-DAE | 1.861 | 1.101 | 1.397 | 0.757 |
| Office 2: TDVS | 4.938 | 3.375 | 5.211 | 3.336 |
| Office 2: TDVS-DAE | 1.760 | 0.834 | 2.621 | 1.219 |
| Office 3: TDVS | 5.533 | 3.476 | 5.488 | 3.183 |
| Office 3: TDVS-DAE | 2.230 | 1.083 | 2.417 | 1.350 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hall, D.L.; Narayanan, R.M.; Jenkins, D.M. SDR Based Indoor Beacon Localization Using 3D Probabilistic Multipath Exploitation and Deep Learning. Electronics 2019, 8, 1323. https://doi.org/10.3390/electronics8111323
Hall DL, Narayanan RM, Jenkins DM. SDR Based Indoor Beacon Localization Using 3D Probabilistic Multipath Exploitation and Deep Learning. Electronics. 2019; 8(11):1323. https://doi.org/10.3390/electronics8111323
Chicago/Turabian StyleHall, Donald L., Ram M. Narayanan, and David M. Jenkins. 2019. "SDR Based Indoor Beacon Localization Using 3D Probabilistic Multipath Exploitation and Deep Learning" Electronics 8, no. 11: 1323. https://doi.org/10.3390/electronics8111323
APA StyleHall, D. L., Narayanan, R. M., & Jenkins, D. M. (2019). SDR Based Indoor Beacon Localization Using 3D Probabilistic Multipath Exploitation and Deep Learning. Electronics, 8(11), 1323. https://doi.org/10.3390/electronics8111323






