A Novel 3D Visible Light Positioning Method Using Received Signal Strength for Industrial Applications
Abstract
1. Introduction
2. Methodology
2.1. VLC System Model
2.2. Illumination Levels
2.3. Positioning Algorithms
2.3.1. Cayley–Menger Determinant
2.3.2. Linear Least Squares
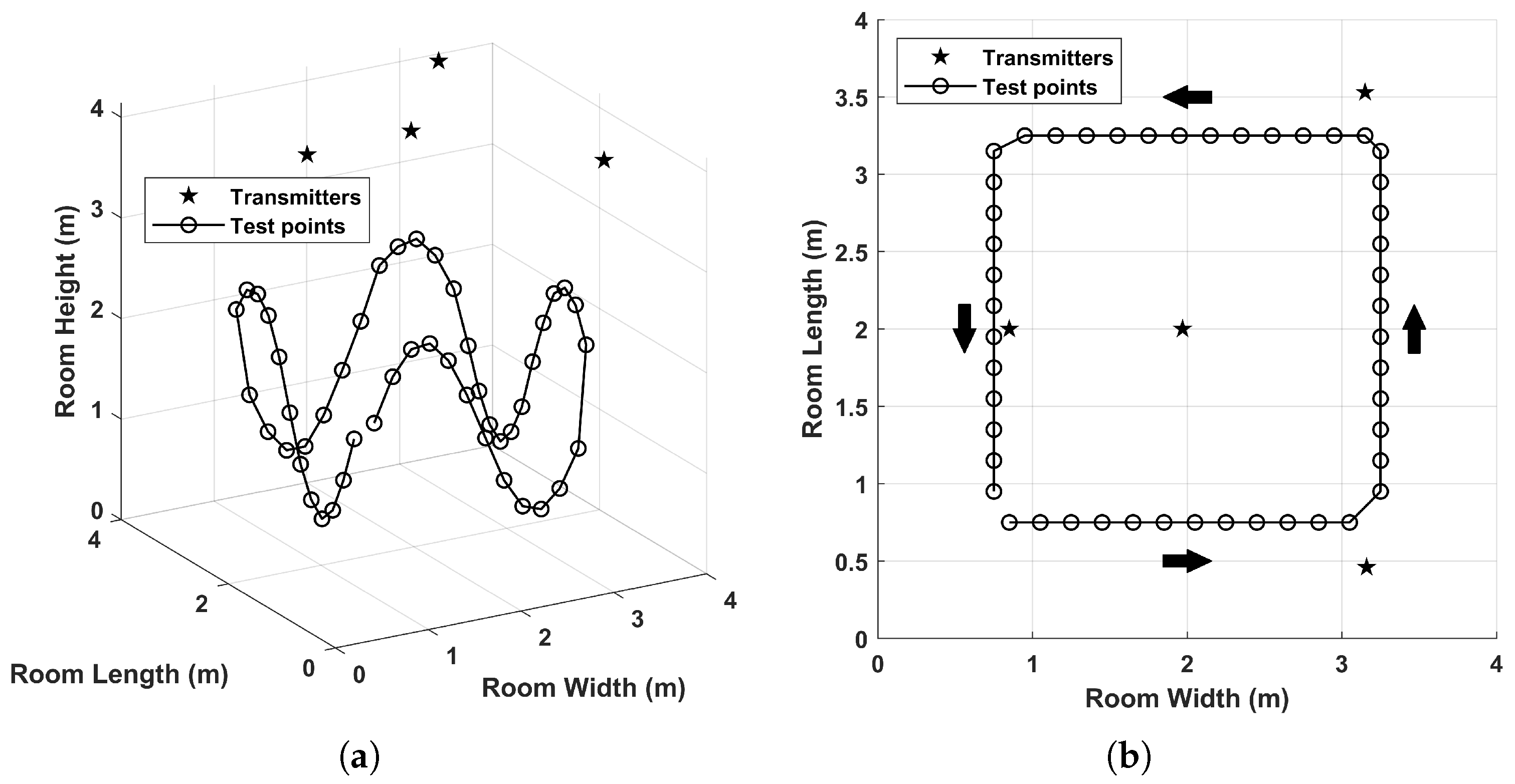
2.3.3. Experimental Validation: Configuration
3. Results and Discussion
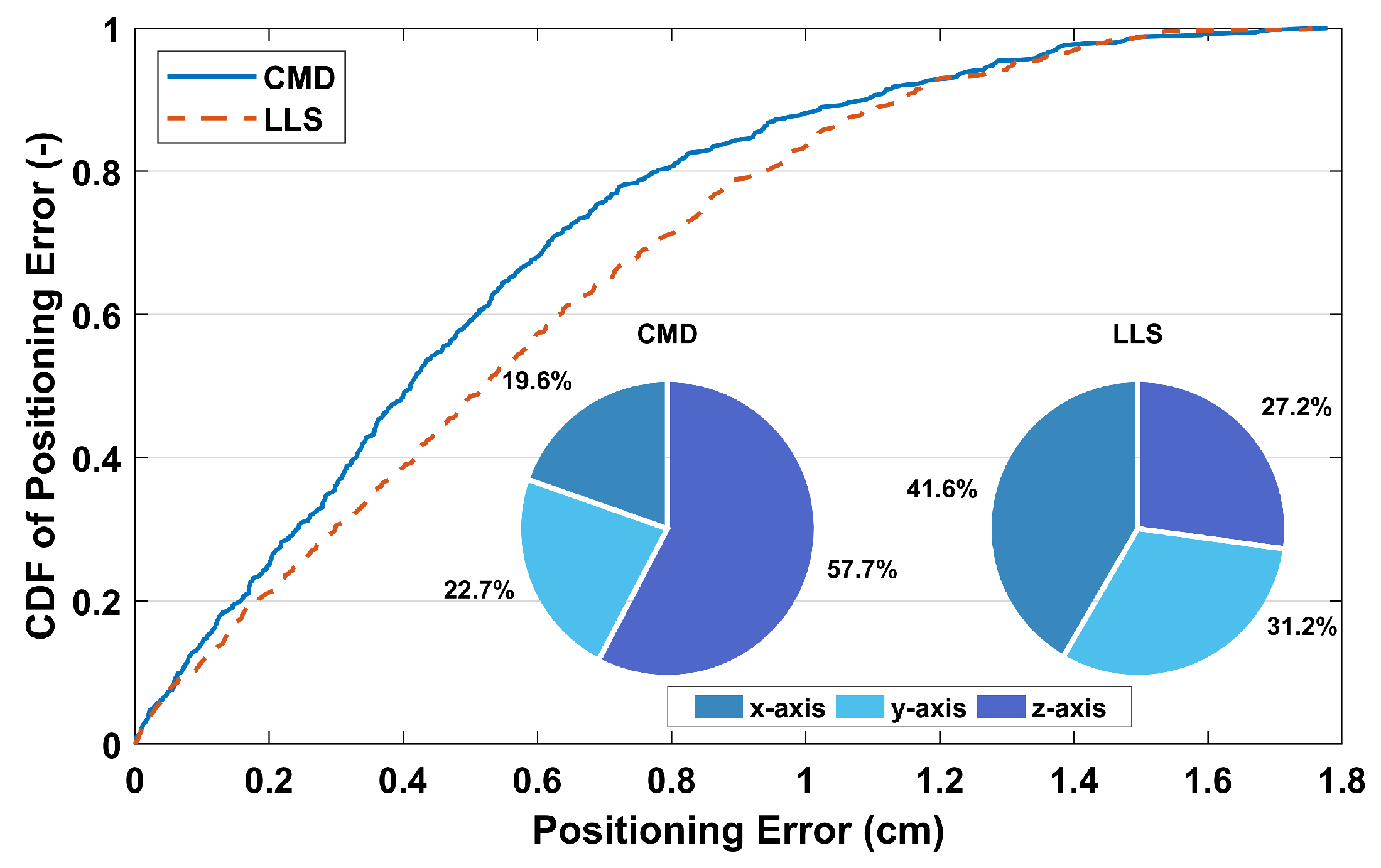
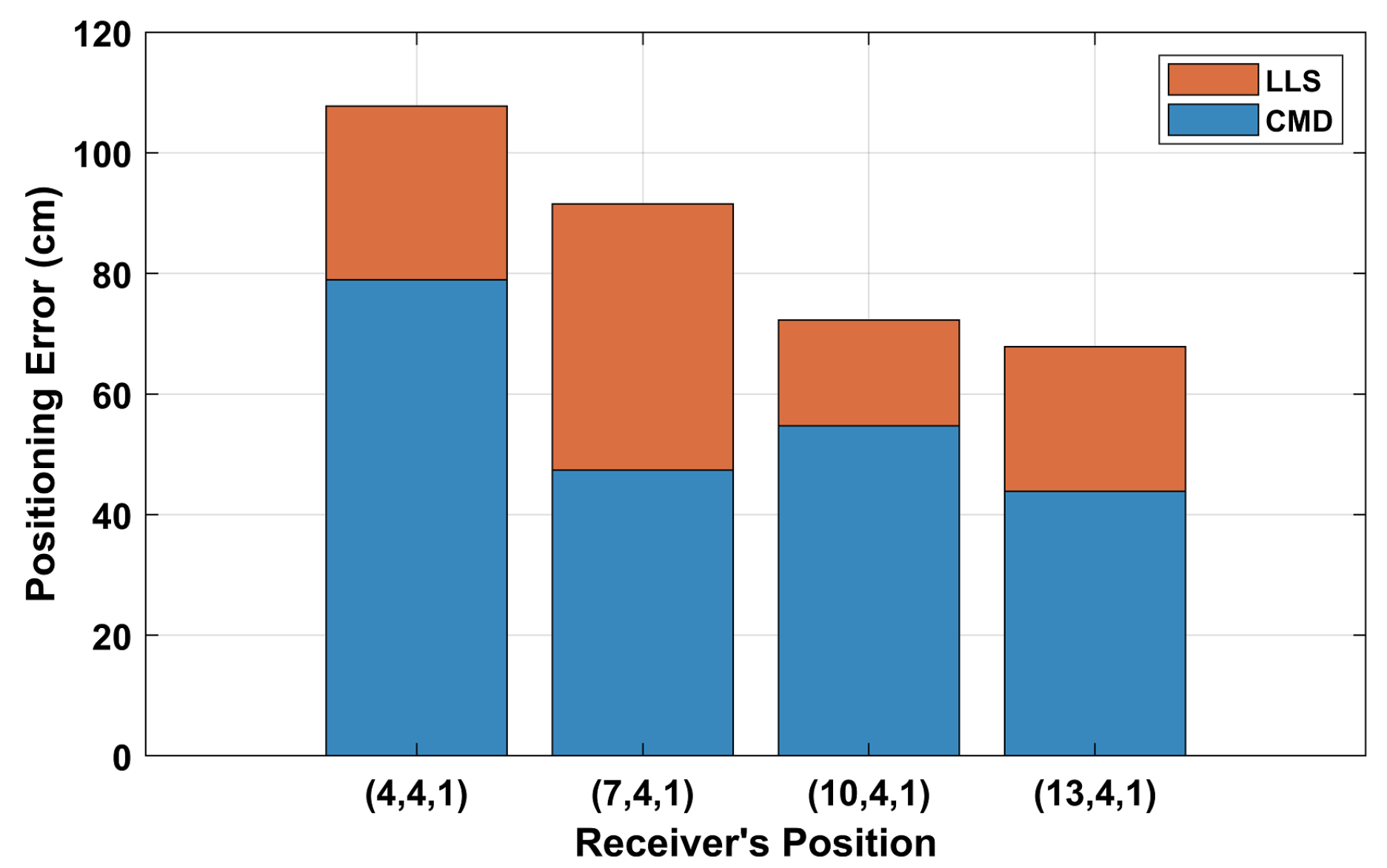
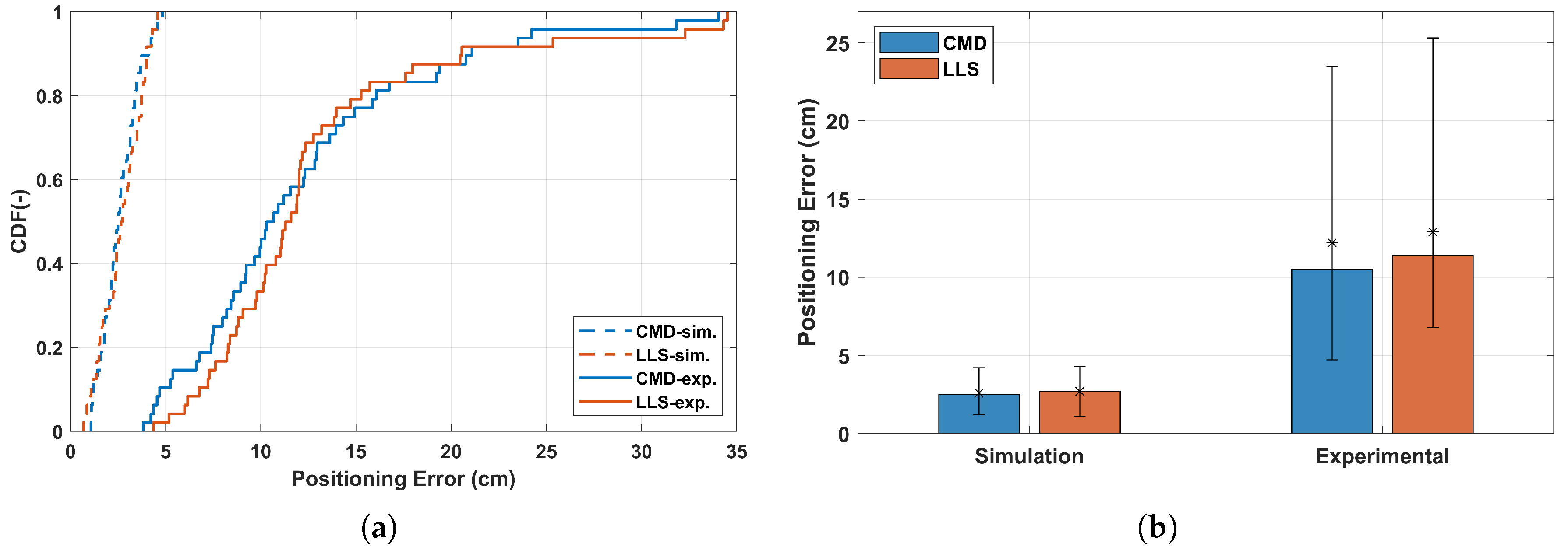
3.1. Positioning Accuracy for Line-of-Sight Reception with Untilted Receiver
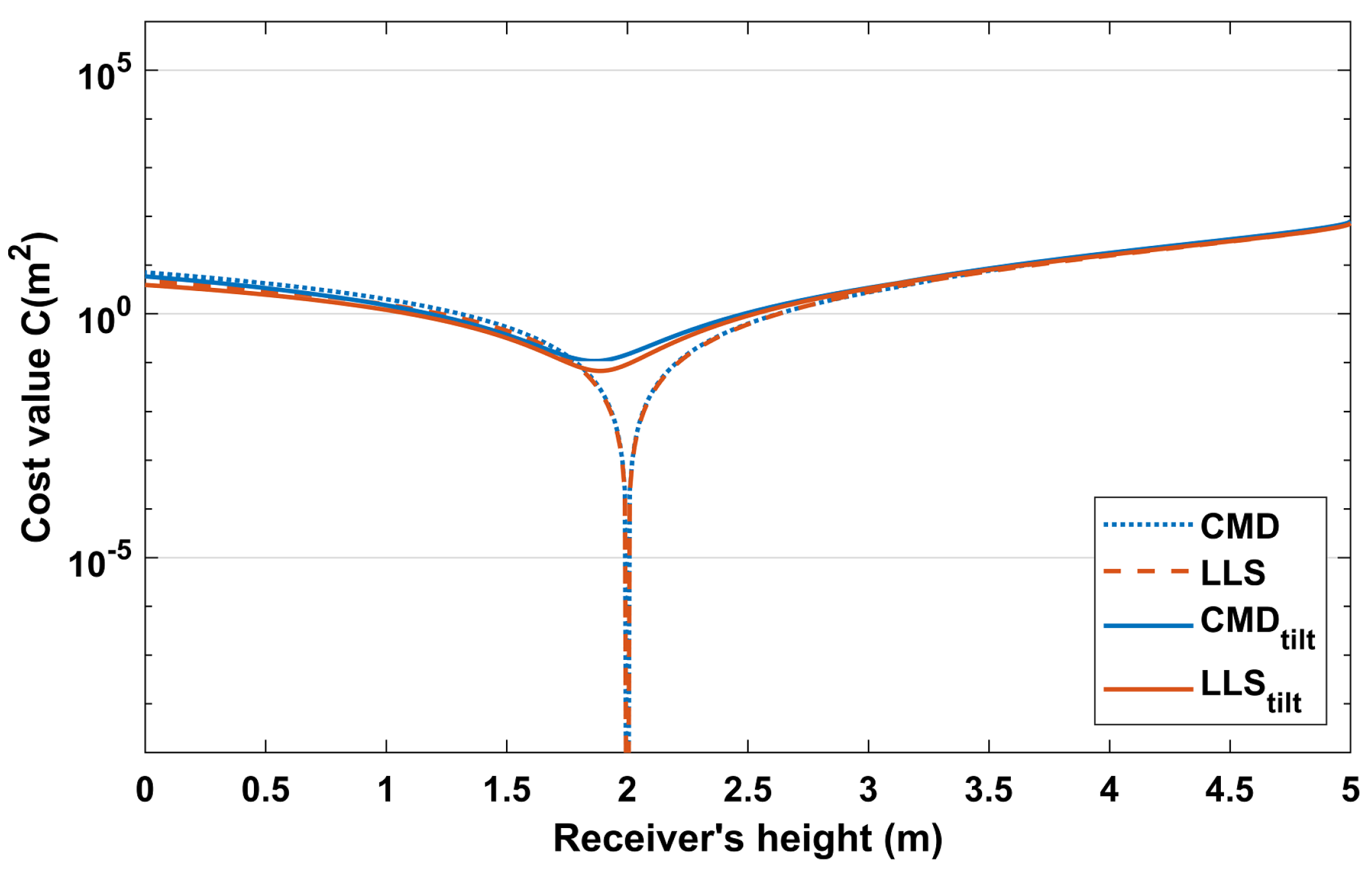
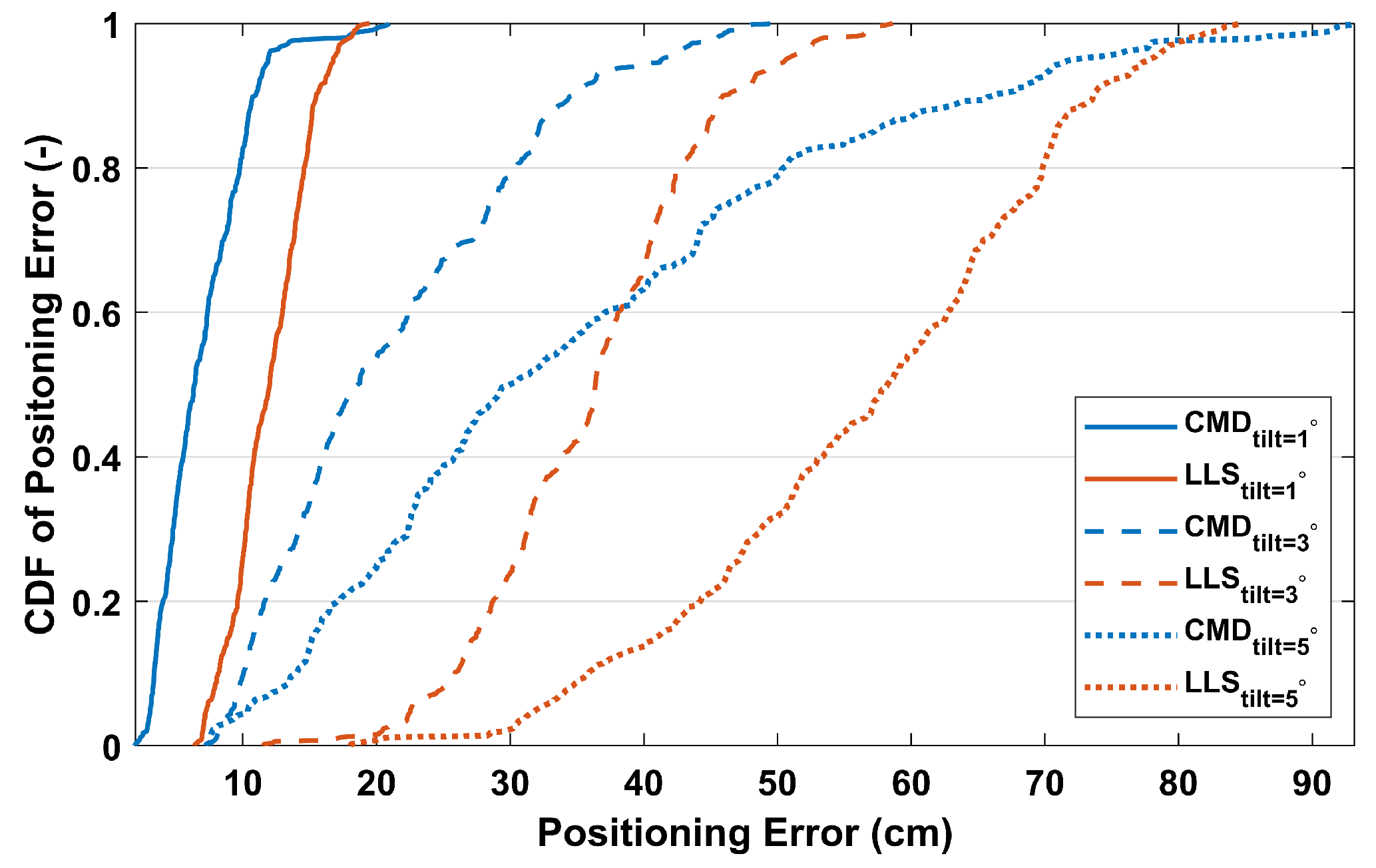
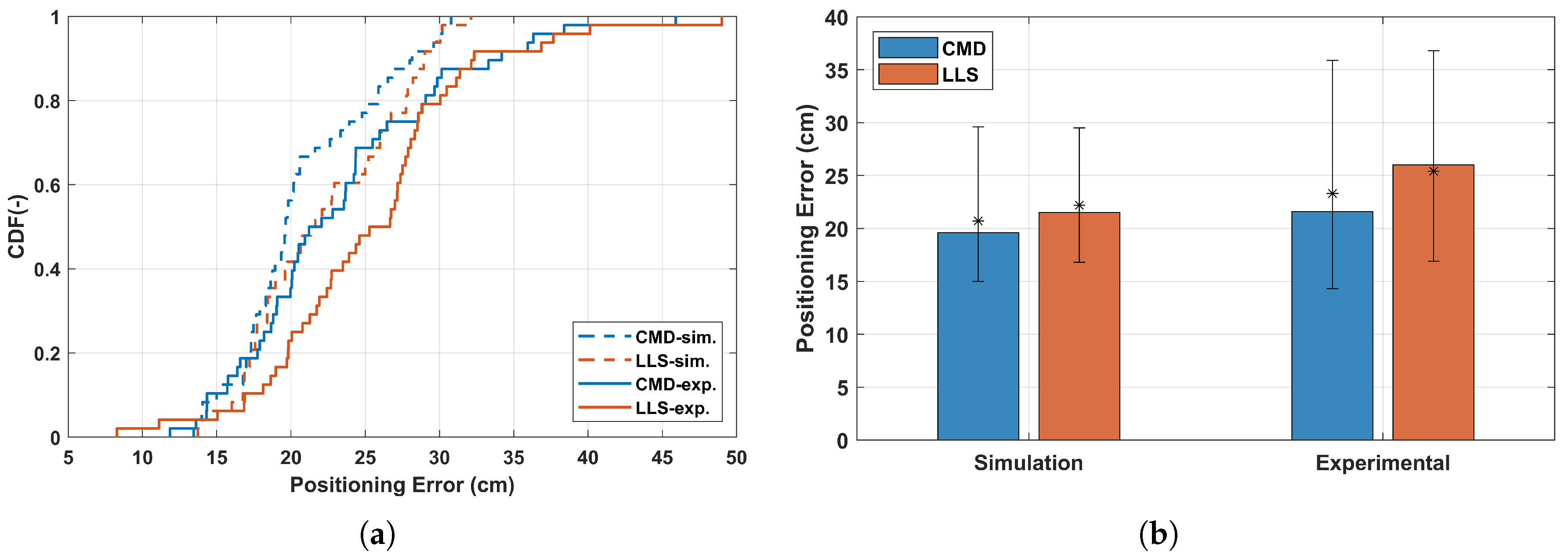
3.2. The Effect of Tilting
3.3. Positioning Accuracy with Multipath Reflections
3.4. Experimental Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| UWB | Ultra-wideband |
| RF | Radio frequency |
| VLP | Visible light positioning |
| LED | Light emitting diode |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| RSS | Received signal strength |
| AoA | Angle-of-arrival |
| CMD | Cayley–Menger determinant |
| LLS | Linear least squares |
| FOV | Field of view |
| SNR | Signal-to-noise ratio |
| CDF | Cumulative distribution function |
| FFT | Fast Fourier transform |
References
- Jordan, S.; Moore, J.; Hovet, S.; Box, J.; Perry, J.; Kirsche, K.; Lewis, D.; Tse, Z.T.H. State-of-the-art technologies for UAV inspections. IET Radar Sonar Navig. 2018, 12, 151–164. [Google Scholar] [CrossRef]
- Benini, A.; Mancini, A.; Longhi, S. An IMU/UWB/Vision-based Extended Kalman Filter for Mini-UAV Localization in Indoor Environment using 802.15.4a Wireless Sensor Network. J. Intell. Robot. Syst. 2013, 70, 461–476. [Google Scholar] [CrossRef]
- Wu, K.J.; Gregory, T.S.; Moore, J.; Hooper, B.; Lewis, D.; Tse, Z.T.H. Development of an indoor guidance system for unmanned aerial vehicles with power industry applications. IET Radar Sonar Navig. 2017, 11, 212–218. [Google Scholar] [CrossRef]
- Soria, P.R.; Palomino, A.F.; Arrue, B.C.; Ollero, A. Bluetooth network for micro-uavs for communication network and embedded range only localization. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL USA, 13–16 June 2017; pp. 747–752. [Google Scholar] [CrossRef]
- Ueyama, J.; Freitas, H.; Faical, B.S.; Filho, G.P.R.; Fini, P.; Pessin, G.; Gomes, P.H.; Villas, L.A. Exploiting the use of unmanned aerial vehicles to provide resilience in wireless sensor networks. IEEE Commun. Mag. 2014, 52, 81–87. [Google Scholar] [CrossRef]
- Yasir, M.; Ho, S.W.; Vellambi, B.N. Indoor Positioning System Using Visible Light and Accelerometer. J. Lightwave Technol. 2014, 32, 3306–3316. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, W.; Wu, Y.; Xie, C.; Chen, Y.; Fang, L. Indoor High Precision Three-Dimensional Positioning System Based on Visible Light Communication Using Particle Swarm Optimization. IEEE Photonics J. 2017, 9, 1–20. [Google Scholar] [CrossRef]
- Zhang, M.; Li, F.; Guan, W.; Wu, Y.; Xie, C.; Peng, Q.; Liu, X. A three-dimensional indoor positioning technique based on visible light communication using chaotic particle swarm optimization algorithm. Optik 2018, 165, 54–73. [Google Scholar] [CrossRef]
- Chen, H.; Guan, W.; Li, S.; Wu, Y. Indoor high precision three-dimensional positioning system based on visible light communication using modified genetic algorithm. Opt. Commun. 2018, 413, 103–120. [Google Scholar] [CrossRef]
- Yang, S.; Kim, H.; Son, Y.; Han, S. Three-Dimensional Visible Light Indoor Localization Using AOA and RSS With Multiple Optical Receivers. J. Lightwave Technol. 2014, 32, 2480–2485. [Google Scholar] [CrossRef]
- Gu, W.; Zhang, W.; Kavehrad, M.; Feng, L. Three-dimensional light positioning algorithm with filtering techniques for indoor environments. Opt. Eng. 2014, 53, 107107. [Google Scholar] [CrossRef]
- Gu, W.; Aminikashani, M.; Deng, P.; Kavehrad, M. Impact of Multipath Reflections on the Performance of Indoor Visible Light Positioning Systems. J. Lightwave Technol. 2016, 34, 2578–2587. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, J.; Chen, B.; Liu, Y.; Zuo, Y.; Liu, S.; Dai, Y. Analysis of indoor VLC positioning system with multiple reflections. In Proceedings of the 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Jeong, E.; Yang, S.; Kim, H.; Han, S. Tilted receiver angle error compensated indoor positioning system based on visible light communication. Electron. Lett. 2013, 49, 890–892. [Google Scholar] [CrossRef]
- Kahn, J.M.; Barry, J.R. Wireless infrared communications. Proc. IEEE 1997, 85, 265–298. [Google Scholar] [CrossRef]
- Plets, D.; Eryildirim, A.; Bastiaens, S.; Stevens, N.; Martens, L.; Joseph, W. A Performance Comparison of Different Cost Functions for RSS-Based Visible Light Positioning Under the Presence of Reflections. In Proceedings of the 4th ACM Workshop on Visible Light Communication Systems, Snowbird, UT, USA, 16 October 2017; pp. 37–41. [Google Scholar]
- Moreira, A.J.C.; Valadas, R.T.; de Oliveira Duarte, A.M. Optical Interference Produced by Artificial Light. Wirel. Netw. 1997, 3, 131–140. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling With Matlab; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- de Normalisation, C.E. EN 12464-1: Light and Lighting-Lighting of Work Places, Part 1: Indoor Work Places; Comité Européen de Normalisation: Brussels, Belgium, 2002. [Google Scholar]
- DIAL. DIALux. Available online: https://www.dial.de/en/dialux/ (accessed on 7 November 2019).
- Almadani, Y.; Ijaz, M.; Rajbhandari, S.; Adebisi, B.; Raza, U. Application of Visible Light Communication in an Industrial Environment. In Proceedings of the 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Thomas, F.; Ros, L. Revisiting trilateration for robot localization. IEEE Trans. Robot. 2005, 21, 93–101. [Google Scholar] [CrossRef]
- Plets, D.; Almadani, Y.; Bastiaens, S.; Ijaz, M.; Martens, L.; Joseph, W. Efficient 3D trilateration algorithm for visible light positioning. J. Opt. 2019, 21, 05LT01. [Google Scholar] [CrossRef]
- De Lausnay, S.; De Strycker, L.; Goemaere, J.; Stevens, N.; Nauwelaers, B. A Visible Light Positioning system using Frequency Division Multiple Access with square waves. In Proceedings of the 2015 9th International Conference on Signal Processing and Communication Systems (ICSPCS), Cairns, Australia, 14–16 December 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Fath, T.; Haas, H. Performance Comparison of MIMO Techniques for Optical Wireless Communications in Indoor Environments. IEEE Trans. Commun. 2013, 61, 733–742. [Google Scholar] [CrossRef]
- Al-Kinani, A.; Wang, C.; Haider, F.; Haas, H.; Zhang, W.; Cheng, X. Light and RF dual connectivity for the next generation cellular systems. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zeng, L.; Brien, D.O.; Le-Minh, H.; Lee, K.; Jung, D.; Oh, Y. Improvement of Date Rate by using Equalization in an Indoor Visible Light Communication System. In Proceedings of the 4th IEEE International Conference on Circuits and Systems for Communications, Shanghai, China, 26–28 May 2008; pp. 678–682. [Google Scholar] [CrossRef]
- Luo, J.; Fan, L.; Li, H. Indoor Positioning Systems Based on Visible Light Communication: State of the Art. IEEE Commun. Surv. Tutor. 2017, 19, 2871–2893. [Google Scholar] [CrossRef]
- Bin Junaid, A.; Diaz De Cerio Sanchez, A.; Betancor Bosch, J.; Vitzilaios, N.; Zweiri, Y. Design and Implementation of a Dual-Axis Tilting Quadcopter. Robotics 2018, 7, 65. [Google Scholar] [CrossRef]
- Francisco, J. Lopez-Hernandez, Rafael Perez-Jimenez, A.S. Ray-tracing algorithms for fast calculation of the channel impulse response on diffuse IR wireless indoor channels. Opt. Eng. 2000, 39, 2775–2780. [Google Scholar] [CrossRef]
- Aminikashani, M.; Gu, W.; Kavehrad, M. Indoor positioning with OFDM Visible Light Communications. In Proceedings of the 2016 13th IEEE Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2016; pp. 505–510. [Google Scholar] [CrossRef]
- Plets, D.; Bastiaens, S.; Martens, L.; Joseph, W. An Analysis of the Impact of LED Tilt on Visible Light Positioning Accuracy. Electronics 2019, 8, 389. [Google Scholar] [CrossRef]
- Plets, D.; Bastiaens, S.; Martens, L.; Joseph, W.; Stevens, N. On the impact of LED power uncertainty on the accuracy of 2D and 3D Visible Light Positioning. Optik 2019, 195, 163027. [Google Scholar] [CrossRef]
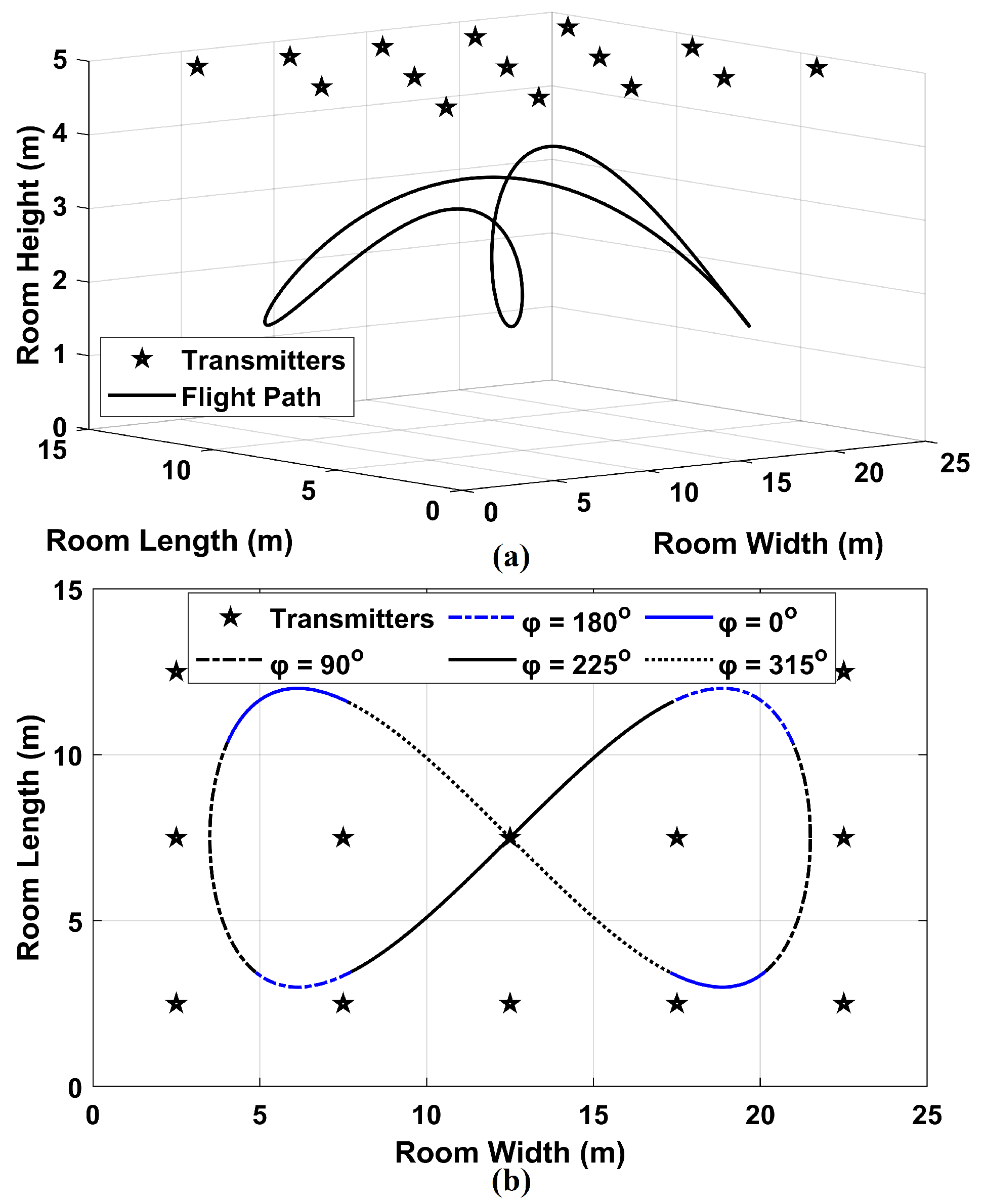
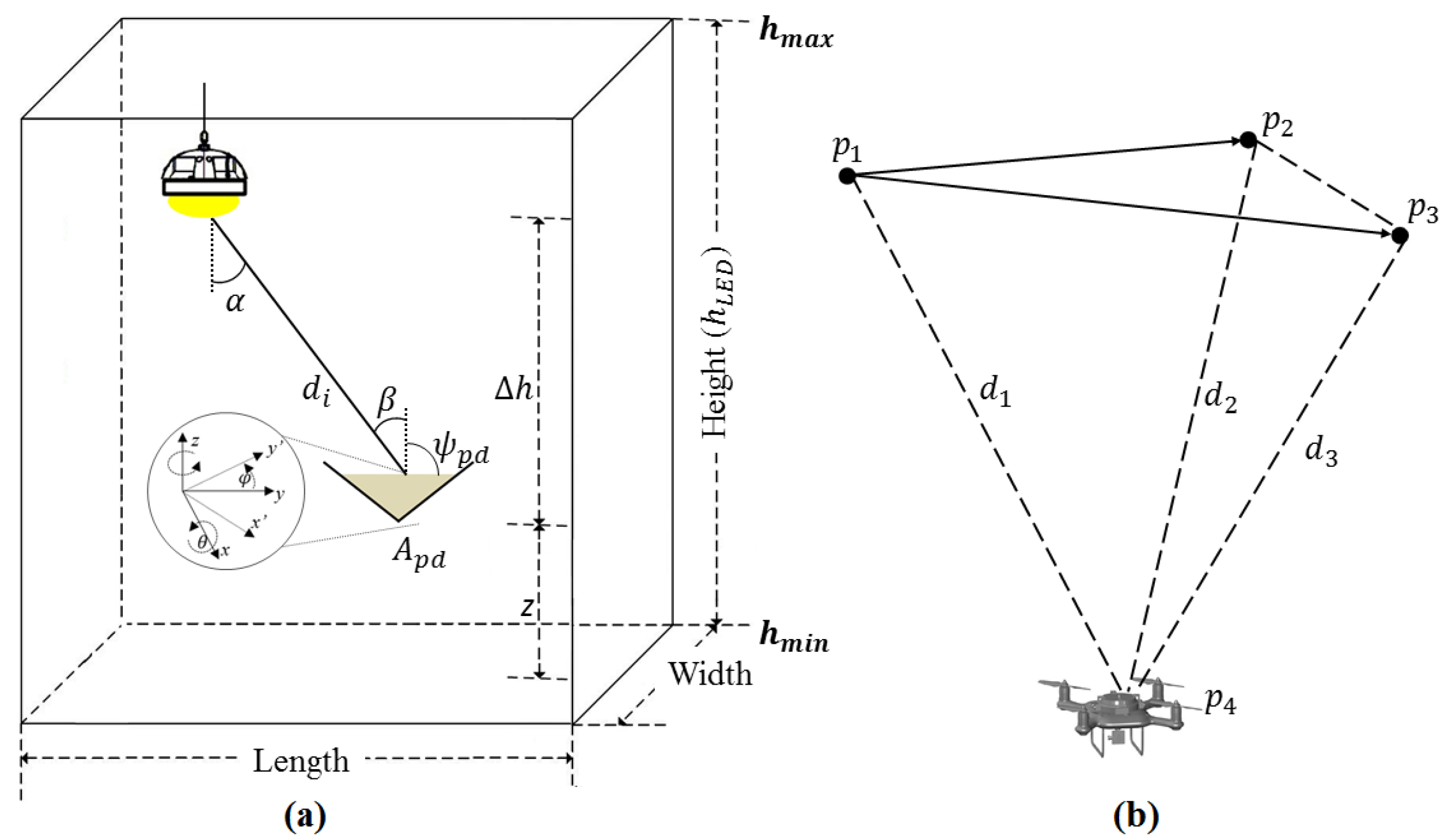
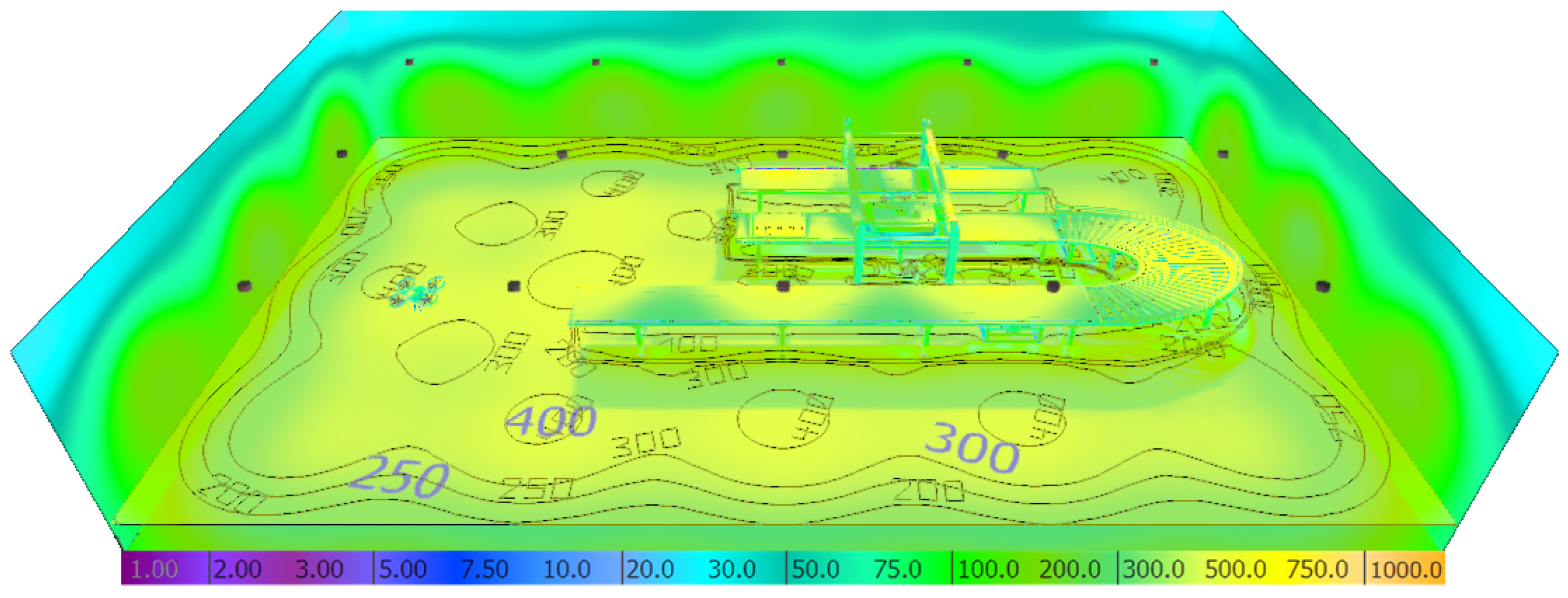
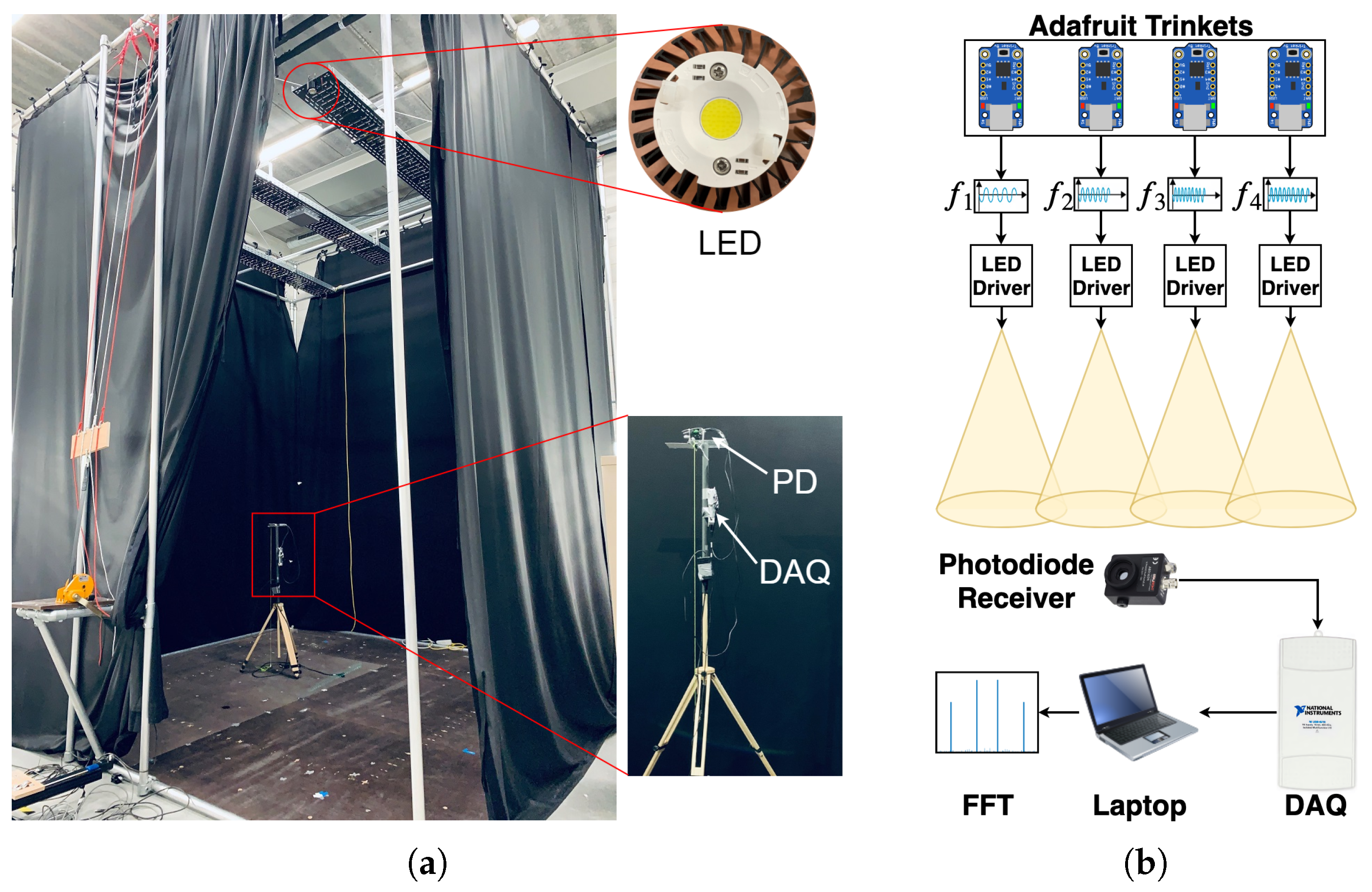
| Parameter | Value |
|---|---|
| Room Width × Length × Height | 25 m × 15 m × 5 m |
| Walls’ Reflectivity | 0.17 |
| Floor’s Reflectivity | 0.34 |
| Transmitter’s Power, | 80 W |
| Transmitter’s Semi-Angle, | |
| Receiver’s Height, z | 1.5–3.5 m |
| Photodetector Area, | 1 cm |
| Receiver’s FOV (Half Angle), | |
| Receiver’s Responsivity, | 0.54 A/W |
| Background Current, | 740 A |
| Bandwidth, B | 10 MHz |
| Positioning Error (cm) | LLS | CMD | ||||
|---|---|---|---|---|---|---|
| Simulation | 2.7 | 4.3 | 2.7 | 2.5 | 4.2 | 2.6 |
| Experimental | 11.4 | 25.3 | 12.9 | 10.5 | 23.5 | 12.2 |
| Simulation | 21.5 | 29.5 | 22.2 | 19.6 | 29.6 | 20.7 |
| Experimental | 26 | 36.8 | 25.4 | 21.6 | 35.9 | 23.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almadani, Y.; Ijaz, M.; Joseph, W.; Bastiaens, S.; Rajbhandari, S.; Adebisi, B.; Plets, D. A Novel 3D Visible Light Positioning Method Using Received Signal Strength for Industrial Applications. Electronics 2019, 8, 1311. https://doi.org/10.3390/electronics8111311
Almadani Y, Ijaz M, Joseph W, Bastiaens S, Rajbhandari S, Adebisi B, Plets D. A Novel 3D Visible Light Positioning Method Using Received Signal Strength for Industrial Applications. Electronics. 2019; 8(11):1311. https://doi.org/10.3390/electronics8111311
Chicago/Turabian StyleAlmadani, Yousef, Muhammad Ijaz, Wout Joseph, Sander Bastiaens, Sujan Rajbhandari, Bamidele Adebisi, and David Plets. 2019. "A Novel 3D Visible Light Positioning Method Using Received Signal Strength for Industrial Applications" Electronics 8, no. 11: 1311. https://doi.org/10.3390/electronics8111311
APA StyleAlmadani, Y., Ijaz, M., Joseph, W., Bastiaens, S., Rajbhandari, S., Adebisi, B., & Plets, D. (2019). A Novel 3D Visible Light Positioning Method Using Received Signal Strength for Industrial Applications. Electronics, 8(11), 1311. https://doi.org/10.3390/electronics8111311









