Identifying Near-Perfect Tunneling in Discrete Metamaterial Loaded Waveguides
Abstract
1. Introduction
2. Theoretical Background
3. Tunneling in Practical Microwave Metamaterials
4. Tunnel Identification Principle
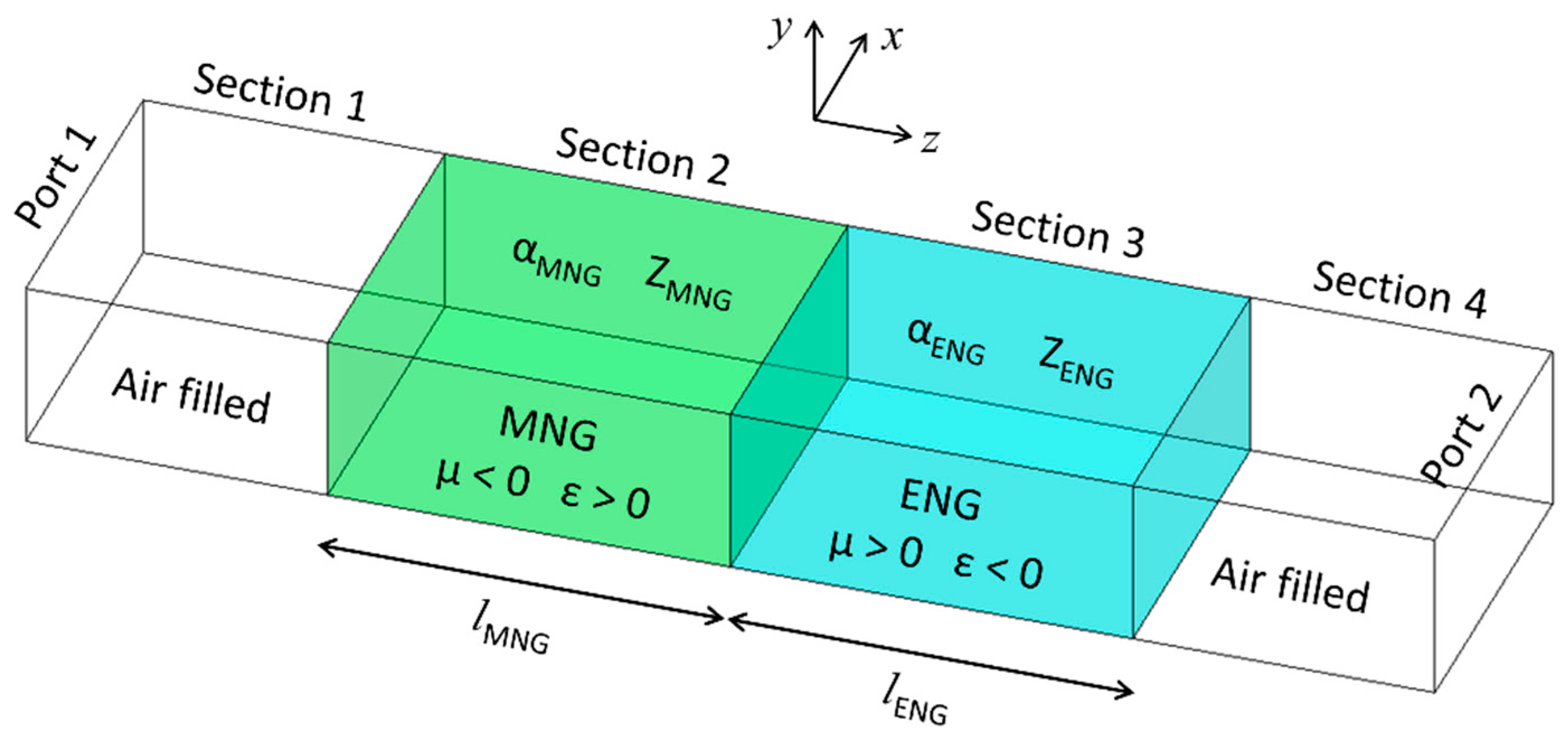
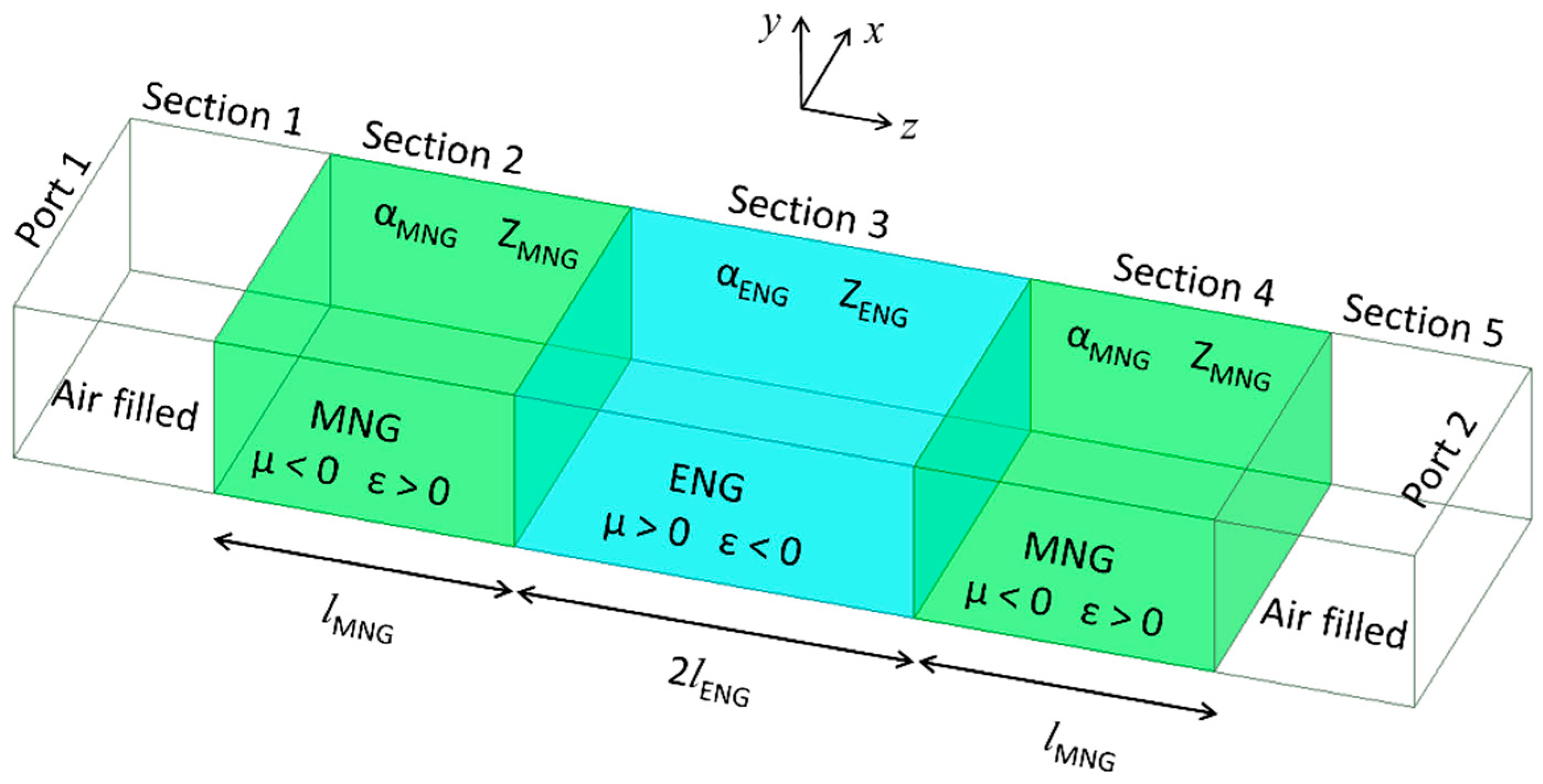
5. Description and Theoretical Analysis of Experimental Metamaterials
5.1. Description of Metamaterials
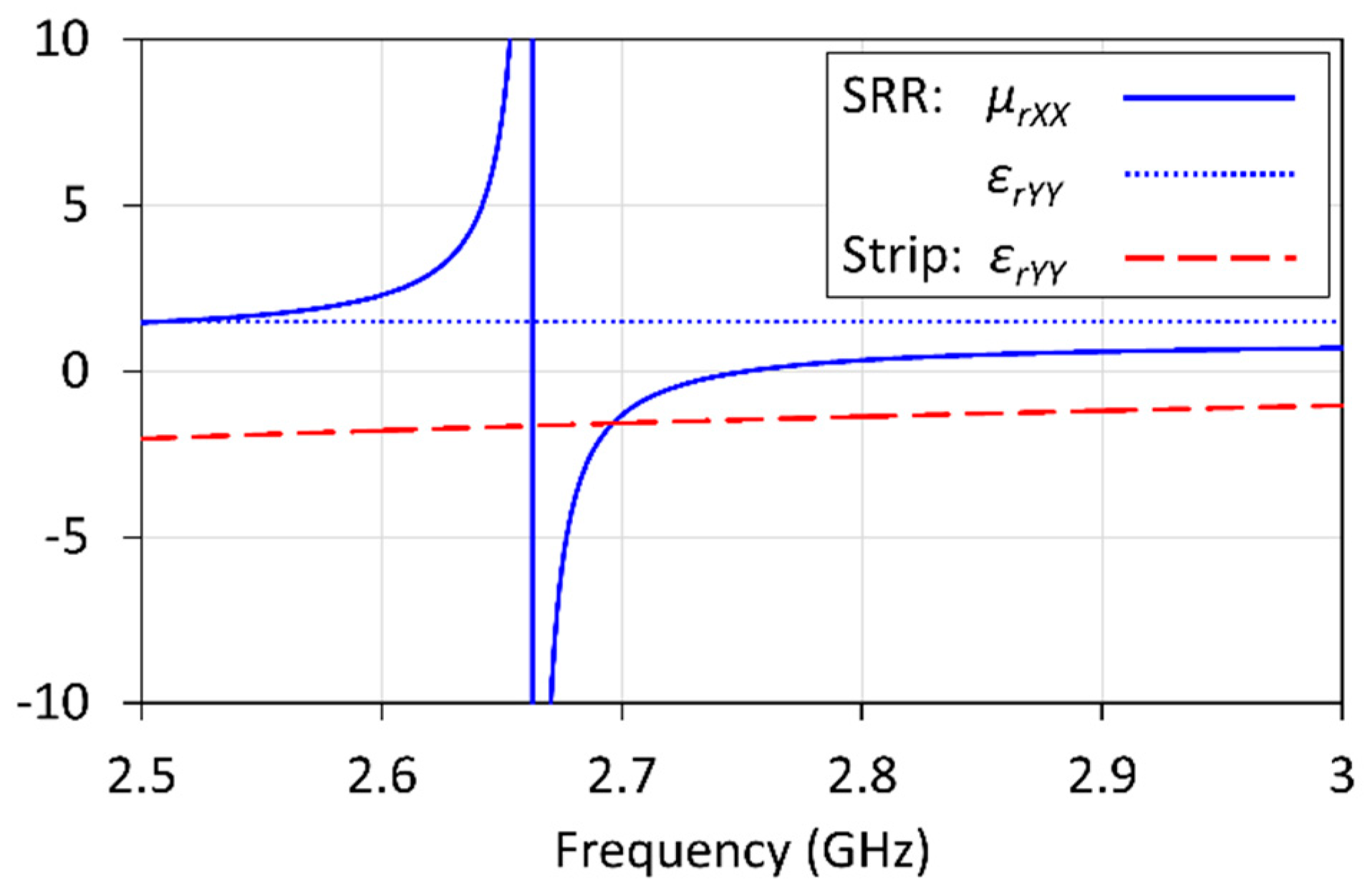
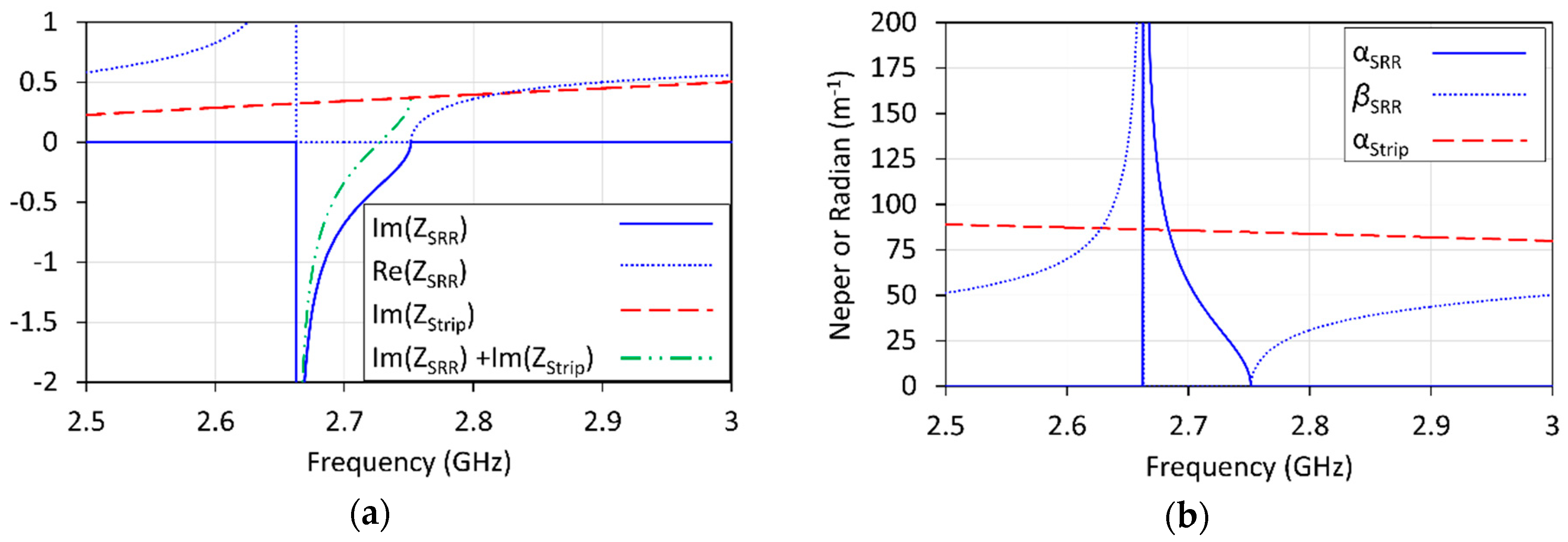
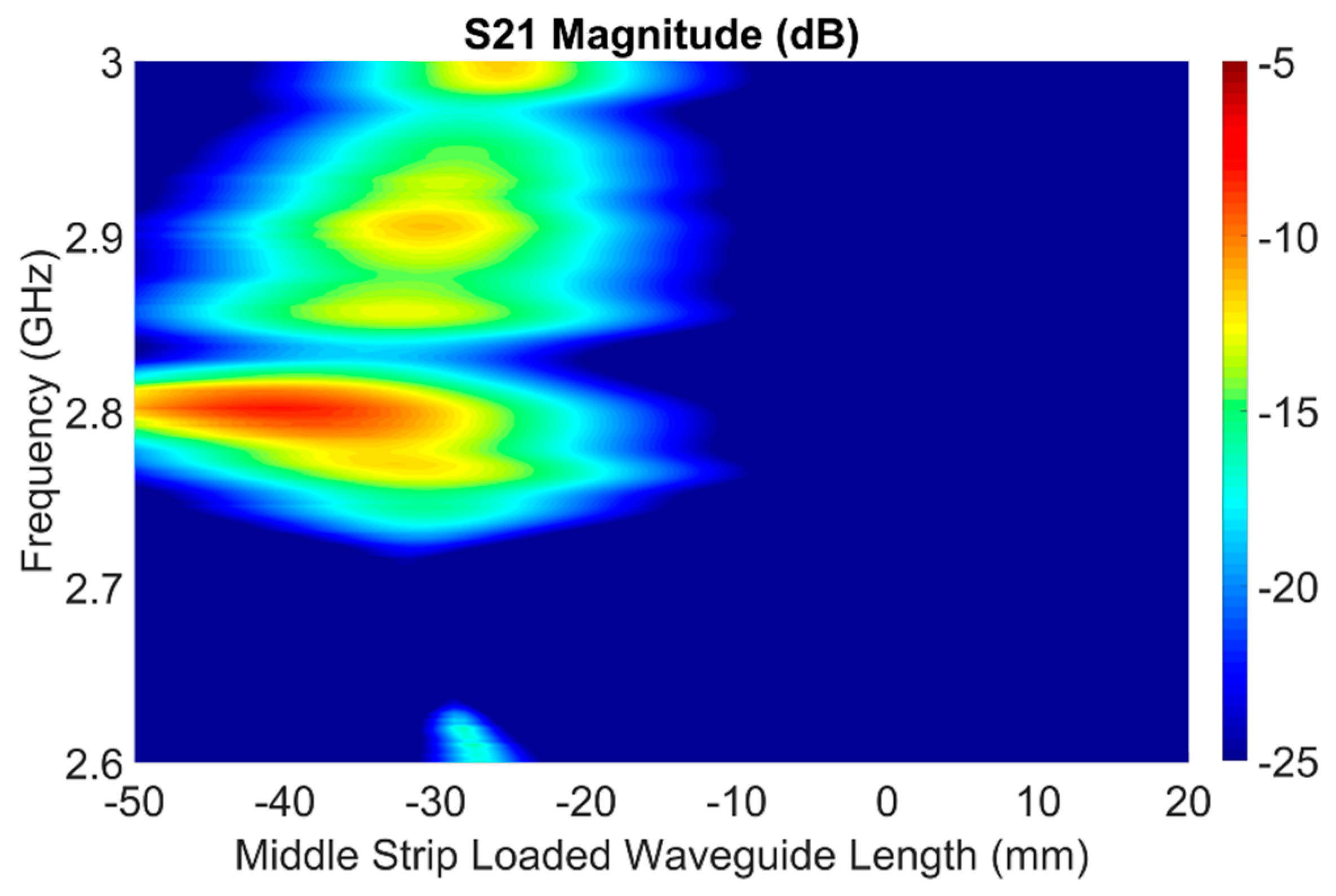
5.2. Theoretical Predictions
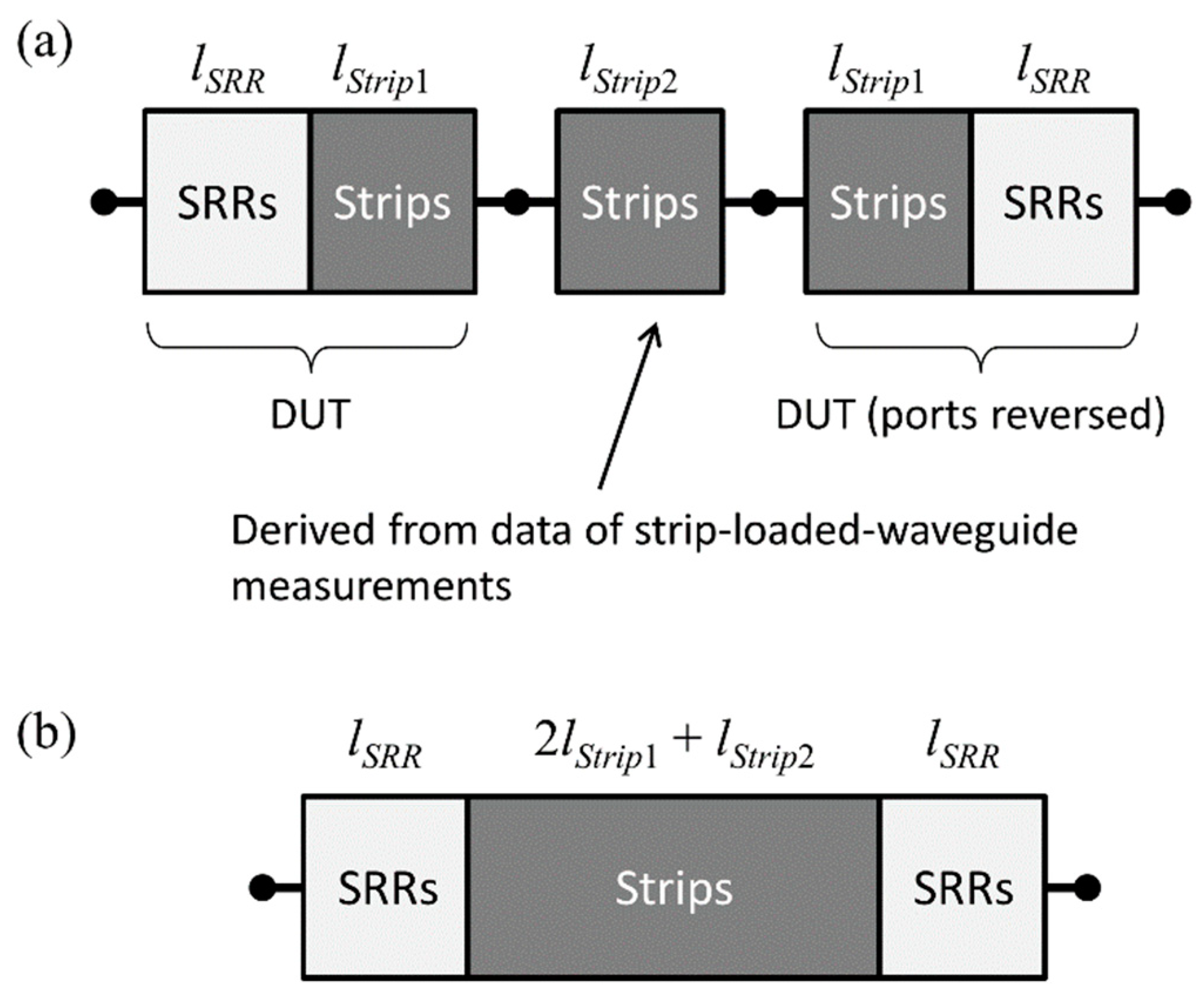
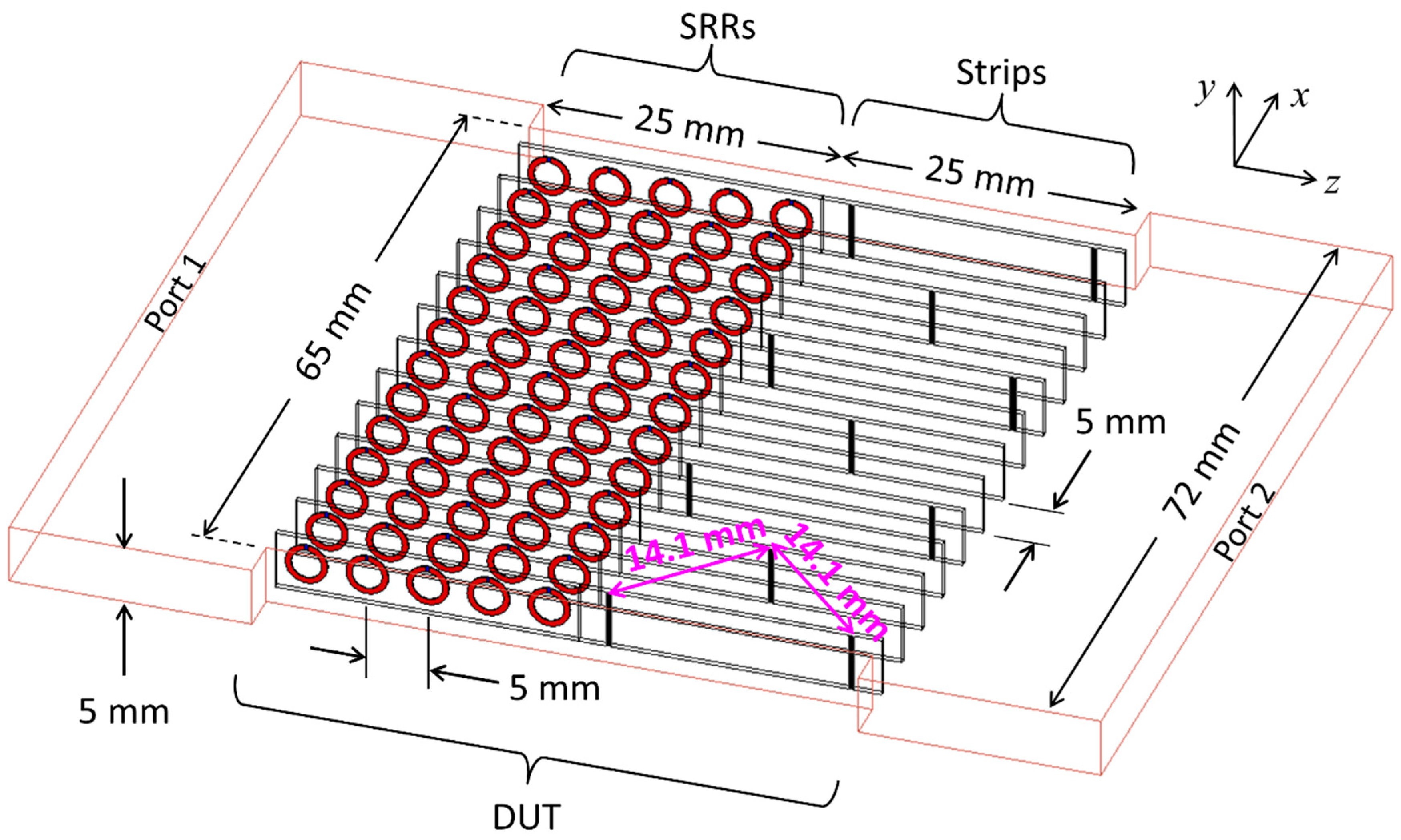
6. Experiment
6.1. Description of Metamaterials
6.2. Waveguide PCB Mount
6.3. Measurement Procedure
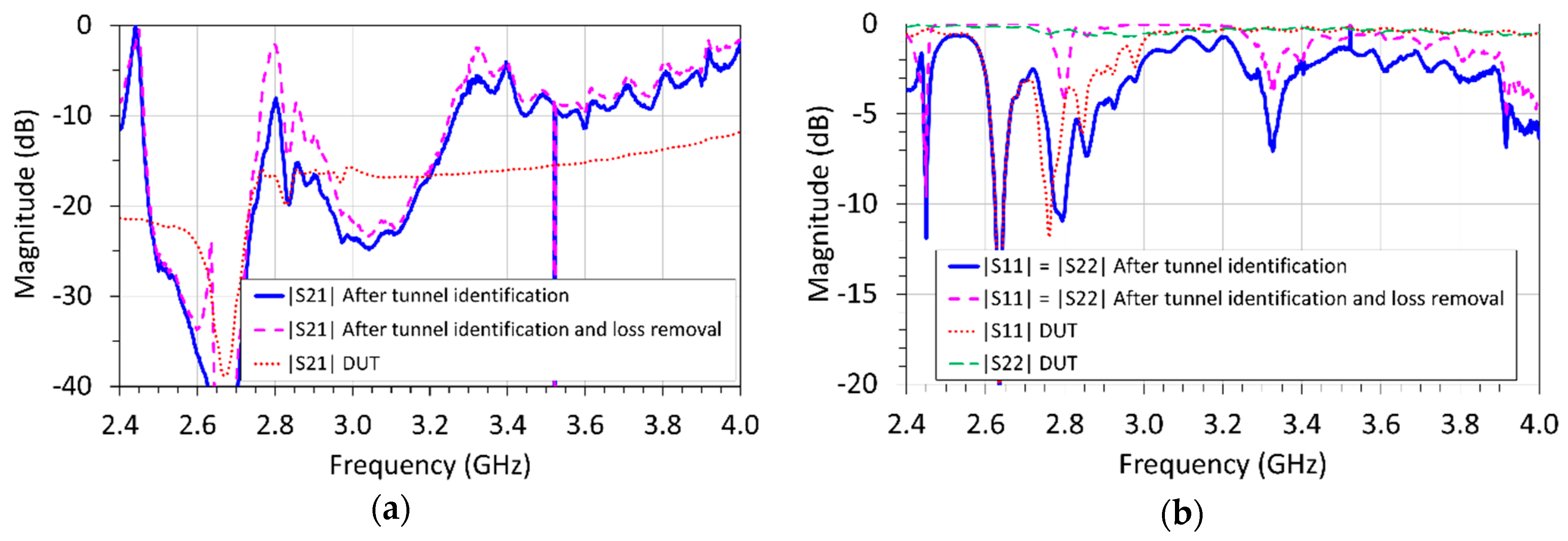
6.4. Strip and SRR Loaded Waveguide
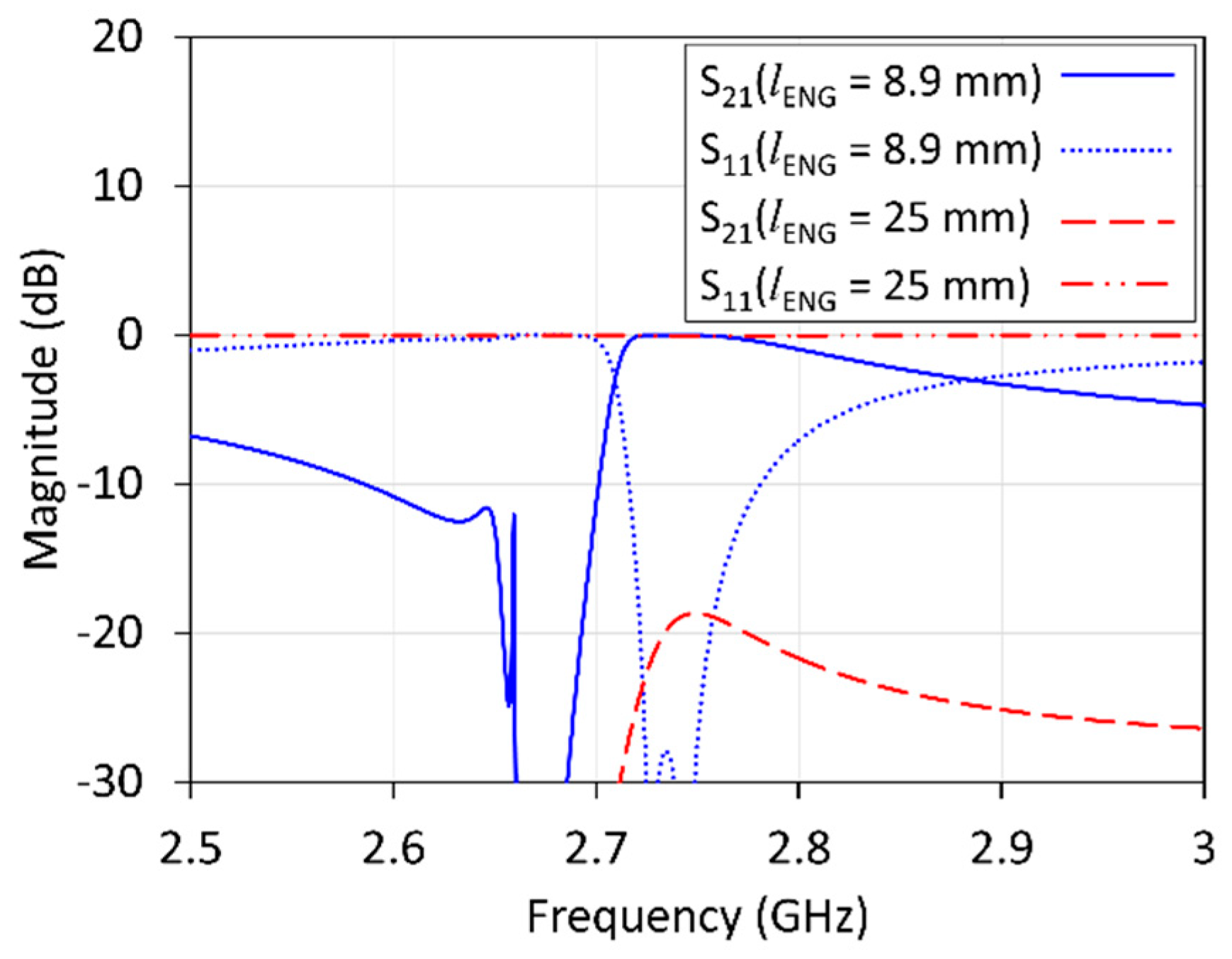
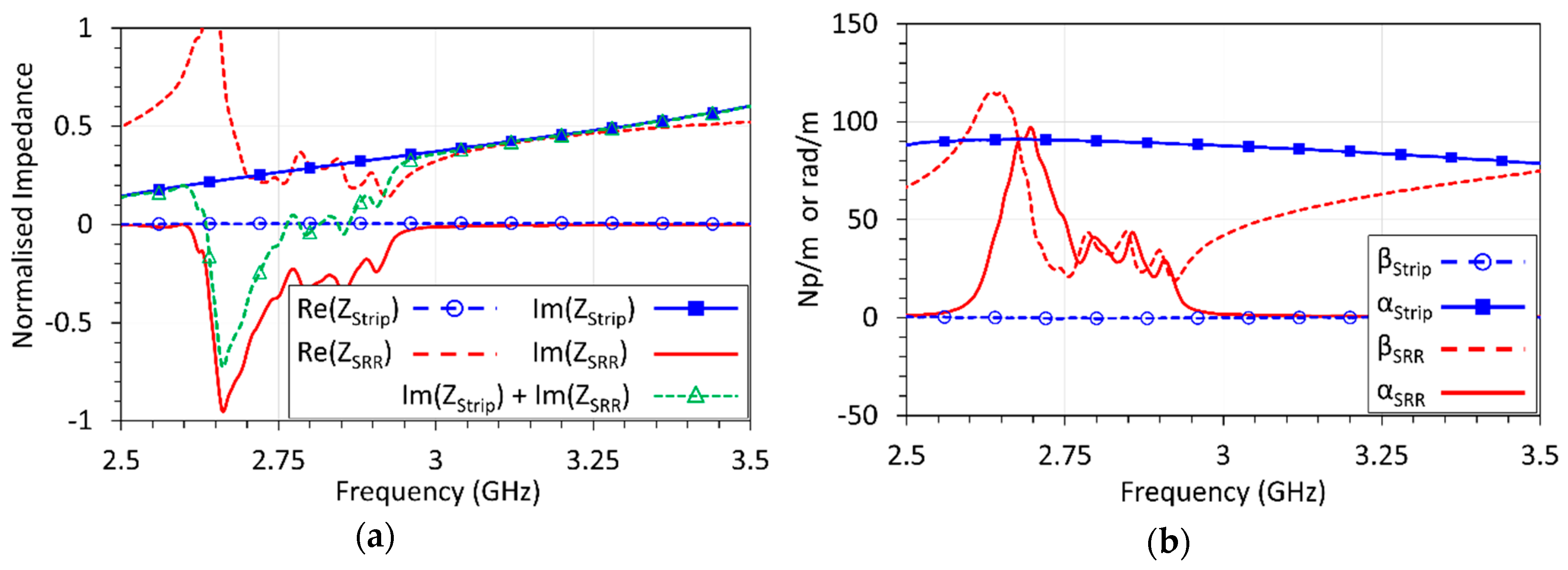
6.5. Tunnel Identification
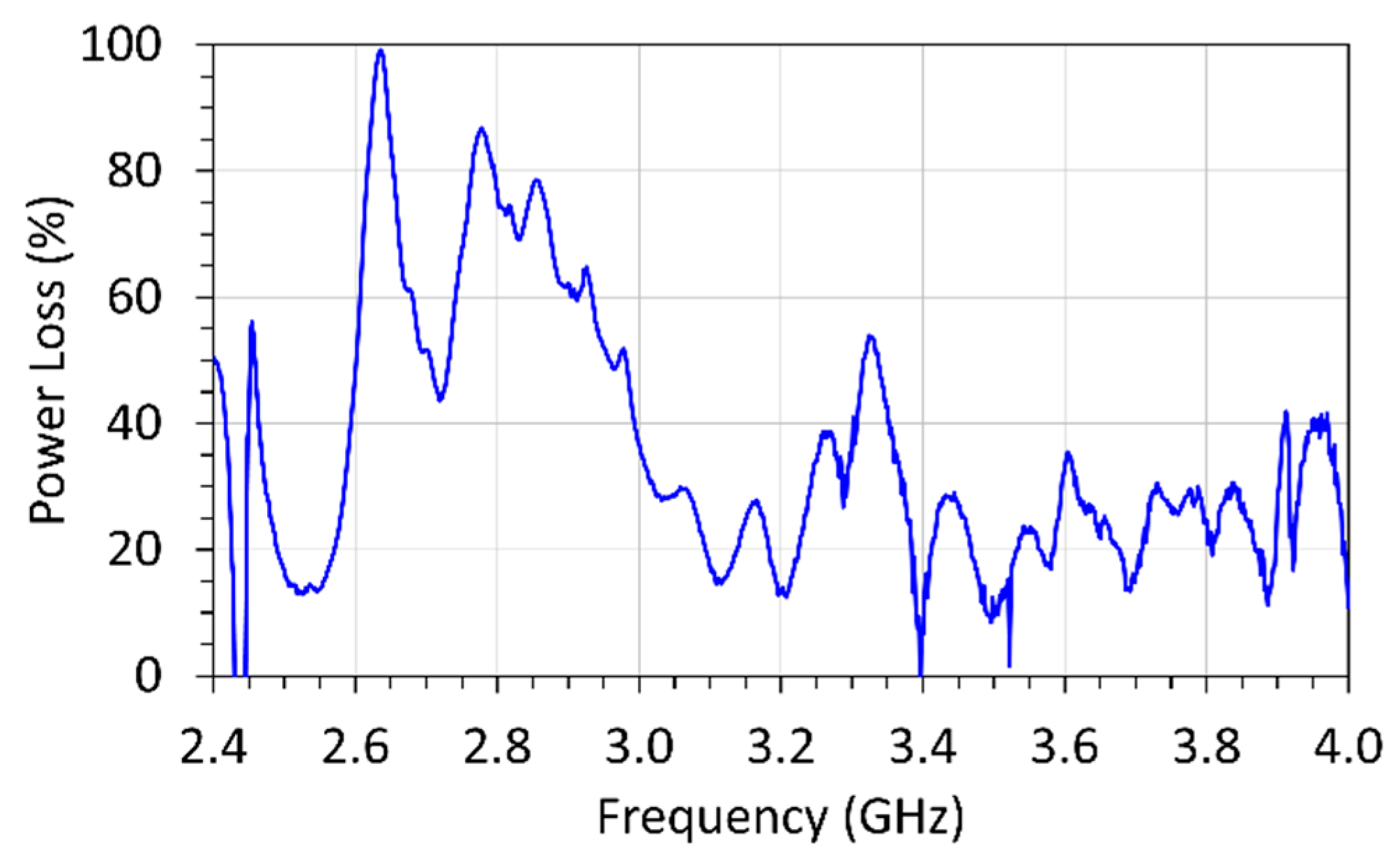
7. Other Observations
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
C.1. Anisotropic MNG
C.2. Anisotropic ENG
References
- Silveirinha, M.; Engheta, N. Tunneling of electromagnetic energy through subwavelength channels and bends using ε-near-zero materials. Phys. Rev. Lett. 2006, 97, 157403. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Cheng, Q.; Hand, T.; Mock, J.J.; Cui, T.J.; Cummer, S.A.; Smith, D.R. Experimental demonstration of electromagnetic tunneling through an epsilon-near-zero metamaterial at microwave frequencies. Phys. Rev. Lett. 2008, 100, 023903. [Google Scholar] [CrossRef] [PubMed]
- Edwards, B.; Alù, A.; Young, M.E.; Silveirinha, M.; Engheta, N. Experimental verification of epsilon-near-zero metamaterial coupling and energy squeezing using a microwave waveguide. Phys. Rev. Lett. 2008, 100, 033903. [Google Scholar] [CrossRef] [PubMed]
- Mitrovic, M.; Jokanovic, B.; Vojnovic, N. Wideband tuning of the tunneling frequency in a narrowed epsilon-near-zero channel. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 631–634. [Google Scholar] [CrossRef]
- Soric, J.C.; Alù, A. Longitudinally independent matching and arbitrary wave patterning using ε-near-zero channels. IEEE Trans. Microw. Theory Tech. 2015, 63, 3558–3567. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Pairing an epsilon-negative slab with a mu-negative slab: Resonance, tunneling and transparency. IEEE Trans. Antennas Propag. 2003, 51, 2558–2571. [Google Scholar] [CrossRef]
- Baena, J.D.; Jelinek, L.; Marqués, R.; Medina, F. Near-perfect tunneling and amplification of evanescent electromagnetic waves in a waveguide filled by a metamaterial: Theory and experiments. Phys. Rev. B 2005, 72, 075116. [Google Scholar] [CrossRef]
- Liu, R.; Zhao, B.; Lin, X.Q.; Cheng, Q.; Cui, T.J. Evanescent-wave amplification studied using a bilayer periodic circuit structure and its effective medium model. Phys. Rev. B 2007, 75, 125118. [Google Scholar] [CrossRef]
- Feng, Y.; Teng, X.; Wang, Z.; Zhao, J.; Jiang, T. Extraordinary transmission with evanescent wave enhancement in planar waveguide loaded with anisotropic metamaterials. In Proceedings of the 2008 Asia–Pacific Microwave Conference, Hong Kong/Macao, China, 16–20 December 2008; IEEE: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Feng, T.; Li, Y.; Jiang, H.; Sun, Y.; He, L.; Li, H.; Zhang, Y.; Shi, Y.; Chen, H. Electromagnetic tunneling in a sandwich structure containing single negative media. Phys. Rev. E 2009, 79, 026601. [Google Scholar] [CrossRef]
- Liu, C.H.; Behdad, N. Analysis of electromagnetic wave tunneling through stacked single-negative metamaterial slabs: A microwave filter theory approach. In Proceedings of the 2012 IEEE International Symposium on Antennas and Propagation, Chicago, IL, USA, 8–14 July 2012; IEEE: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; He, L.; Qiao, W.; Chen, L.; Wang, Q.; Zhao, Y. Tunneling time in a conjugate matched pair consisting of ε-negative and μ-negative materials. Physica B 2013, 431, 127–131. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Chen, X.; Liu, X.; Zhang, L.; Chen, H. Study on the tunneling mode in a sub-wavelength open-cavity resonator consisting of single negative materials. IEEE Trans. Antennas Propag. 2014, 62, 504–508. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Yu, X.; Li, Y.; He, L.; Fang, K. Electromagnetic tunneling through epsilon-negative waveguide paired with mu-negative waveguide. In Proceedings of the 2014 Asia-Pacific Conference on Antennas and Propagation, Harbin, China, 26–29 July 2014; IEEE: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, S.; Yan, X.; Shi, J. Electromagnetic tunneling through conjugated single-negative metamaterial pairs and double-positive layer with high-magnetic fields. Chin. Opt. Lett. 2014, 12, 101601. [Google Scholar] [CrossRef]
- Marques, R.; Martel, J.; Mesa, F.; Medina, F. Left-handed-media simulation and transmission of EM waves in subwavelength split-ring-resonator-loaded metallic waveguides. Phys. Rev. Lett. 2002, 89, 183901. [Google Scholar] [CrossRef]
- Hrabar, S.; Bartolic, J.; Sipus, Z. Waveguide miniaturization using uniaxial negative permeability metamaterial. IEEE Trans. Antennas Propag. 2005, 53, 110–119. [Google Scholar] [CrossRef]
- Odabasi, H.; Teixeira, F.L. Electric-field-coupled resonators as metamaterial loadings for waveguide miniaturization. J. Appl. Phys. 2013, 114, 214901. [Google Scholar] [CrossRef]
- Pollock, J.G.; Iyer, A.K. Below-cutoff propagation in metamaterial-lined circular waveguides. IEEE Trans. Microw. Theory Tech. 2013, 61, 3169–3178. [Google Scholar] [CrossRef]
- Esteban, J.; Camacho-Peñalosa, C.; Page, J.E.; Martín-Guerrero, T.M.; Márquez-Segura, E. Simulation of negative permittivity and negative permeability by means of evanescent waveguide modes—Theory and experiment. IEEE Trans. Microw. Theory Tech. 2005, 53, 1506–1514. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Low frequency plasmons in thin-wire structures. J. Phys. Condens. Matter 1998, 10, 4785–4809. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Ramo, S.; Whinnery, J.R.; van Duzer, T. Fields and Waves in Communication Electronics; John Wiley & Sons, Inc.: New York, NY, USA, 1994; ISBN 0-471-58551-34. [Google Scholar]
- Eccleston, K.W.; Platt, I.G. Printed NRI metamaterial based on broad-side-coupled SRRs and a thinned array of strips. In Proceedings of the 2016 Asia-Pacific Microwave Conference, New Delhi, India, 5–9 December 2016; IEEE: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005; ISBN 978-0-470-63155-3. [Google Scholar]
- Eberspächer, M.A.; Eibert, T.F. Extraction of embedded dispersion characteristics. In Proceedings of the 2011 Asia-Pacific Microwave Conferenc, Melbourne, Australia, 5–8 December 2011; IEEE: New York, NY, USA, 2011; pp. 801–804. [Google Scholar]
- Williams, D.F.; Jargon, J.; Arz, U.; Hale, P. Rectangular-waveguide impedance. In Proceedings of the 85th ARFTG Conference, Phoenix, AZ, USA, 22 May 2015; IEEE: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Marqués, R.; Mesa, F.; Martel, J.; Medina, F. Comparative analysis of edge-and broadside-coupled split ring resonators for metamaterial design-theory and experiments. IEEE Trans. Antennas Propag. 2003, 51, 2572–2581. [Google Scholar] [CrossRef]
- Eccleston, K.W. A new interpretation of through-line deembedding. IEEE Trans. Microw. Theory Tech. 2016, 64, 3887–3893. [Google Scholar] [CrossRef]
- Baskey, H.B.; Akhtar, M.J. An improved measurement technique for retrieval of effective constitutive properties of thin dielectric/magnetic and metamaterial samples. In Proceedings of the 83rd ARFTG Microwave Measurement Conference, Tampa, FL, USA, 6 June 2014; IEEE: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Hrabar, S.; Benic, L.; Bartolic, J. Simple experimental determination of complex permittivity or complex permeability of SNG metamaterials. In Proceedings of the 36th European Microwave Conference, Manchester, UK, 10–15 September 2006; IEEE: New York, NY, USA, 2006; pp. 1395–1398. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Bai, Y.; Luo, Y.; Ran, L.; Jiang, Q.; Kong, J.A. Experimental retrieval of the effective parameters of metamaterials based on a waveguide method. Opt. Express 2006, 14, 12944–12949. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kuester, E.F.; Holloway, C.L.; Scher, A.D.; Baker-Jarvis, J. Boundary effects on the determination of metamaterial parameters from normal incidence reflection and transmission measurements. IEEE Trans. Antennas Propag. 2011, 59, 2226–2240. [Google Scholar] [CrossRef]
- Arslanagić, S.; Hansen, T.V.; Mortensen, N.A.; Gregersen, A.H.; Sigmund, O.; Ziolkowski, R.W.; Breinbjerg, O. A review of the scattering-parameter extraction method with clarification of ambiguity issues in relation to metamaterial homogenization. IEEE Antennas Propag. Mag. 2013, 55, 91–106. [Google Scholar] [CrossRef]
- Machac, J.; Jelinek, L. Metamaterial made of BC-SRRs with randomly dispersed resonance frequencies. In Proceedings of the 2015 IEEE MTT-S International Microwave Symposium, Phoenix, AZ, USA, 17–22 May 2015; IEEE: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Gonzalez, G. Microwave Transistor Amplifiers—Analysis and Design, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1997; ISBN 0-13-254335-4. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eccleston, K.W.; Platt, I.G. Identifying Near-Perfect Tunneling in Discrete Metamaterial Loaded Waveguides. Electronics 2019, 8, 84. https://doi.org/10.3390/electronics8010084
Eccleston KW, Platt IG. Identifying Near-Perfect Tunneling in Discrete Metamaterial Loaded Waveguides. Electronics. 2019; 8(1):84. https://doi.org/10.3390/electronics8010084
Chicago/Turabian StyleEccleston, Kimberley W., and Ian G. Platt. 2019. "Identifying Near-Perfect Tunneling in Discrete Metamaterial Loaded Waveguides" Electronics 8, no. 1: 84. https://doi.org/10.3390/electronics8010084
APA StyleEccleston, K. W., & Platt, I. G. (2019). Identifying Near-Perfect Tunneling in Discrete Metamaterial Loaded Waveguides. Electronics, 8(1), 84. https://doi.org/10.3390/electronics8010084




