Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis
Abstract
1. Introduction
- (1)
- We present and investigate SP analysis of multisource PS EH relaying network in the HD mode over block Rayleigh-fading channel in both DLT and DTT modes.
- (2)
- The CF expressions of the OP for DLT mode and EC for DTT mode are proposed, analyzed and derived.
- (3)
- The CF for SER for DLT mode is analyzed and derived.
- (4)
- The influence of all primary system parameters on OP, EC, and SER is investigated and discussed.
- (5)
- All research results are demonstrated using the Monte Carlo simulation.
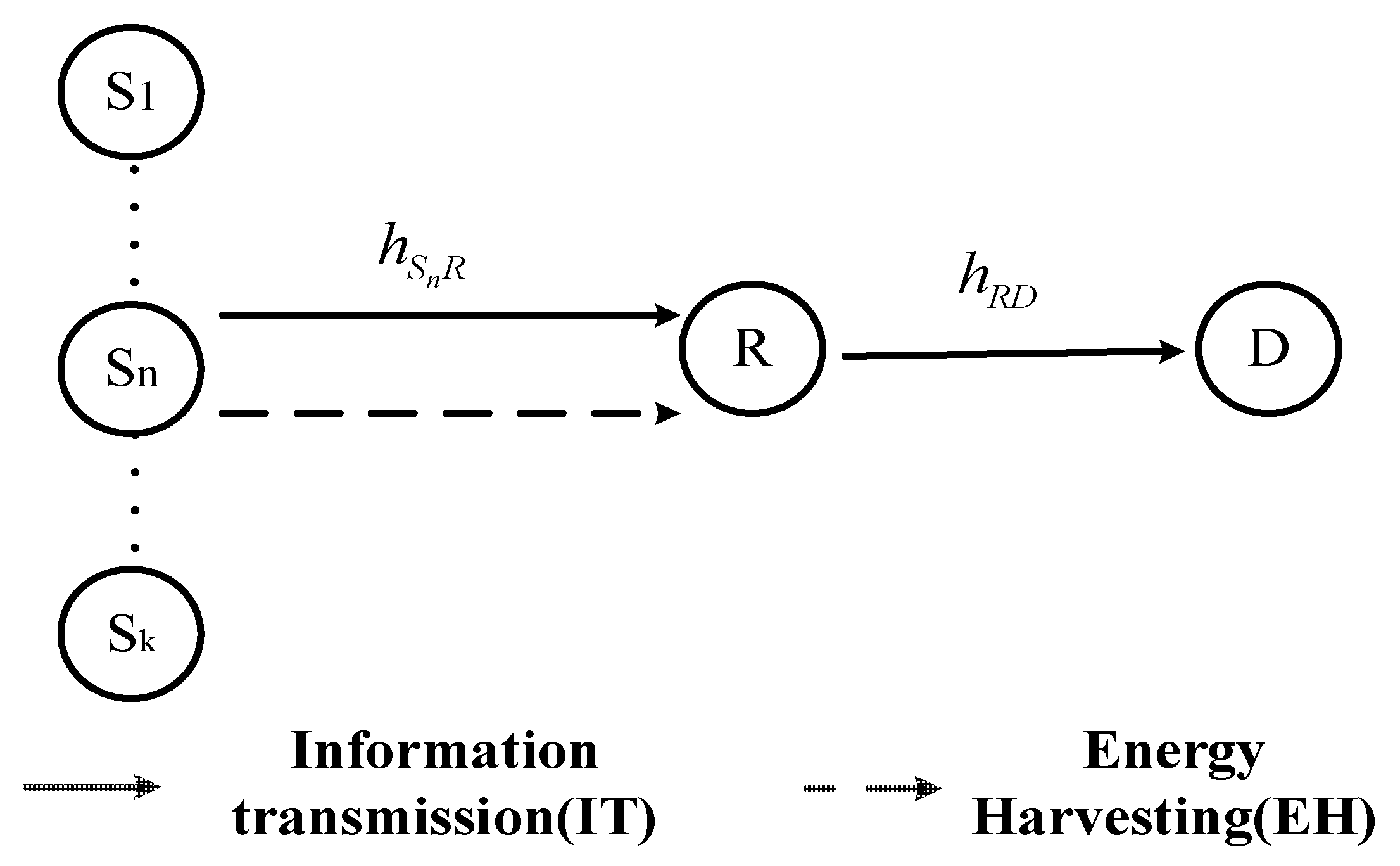
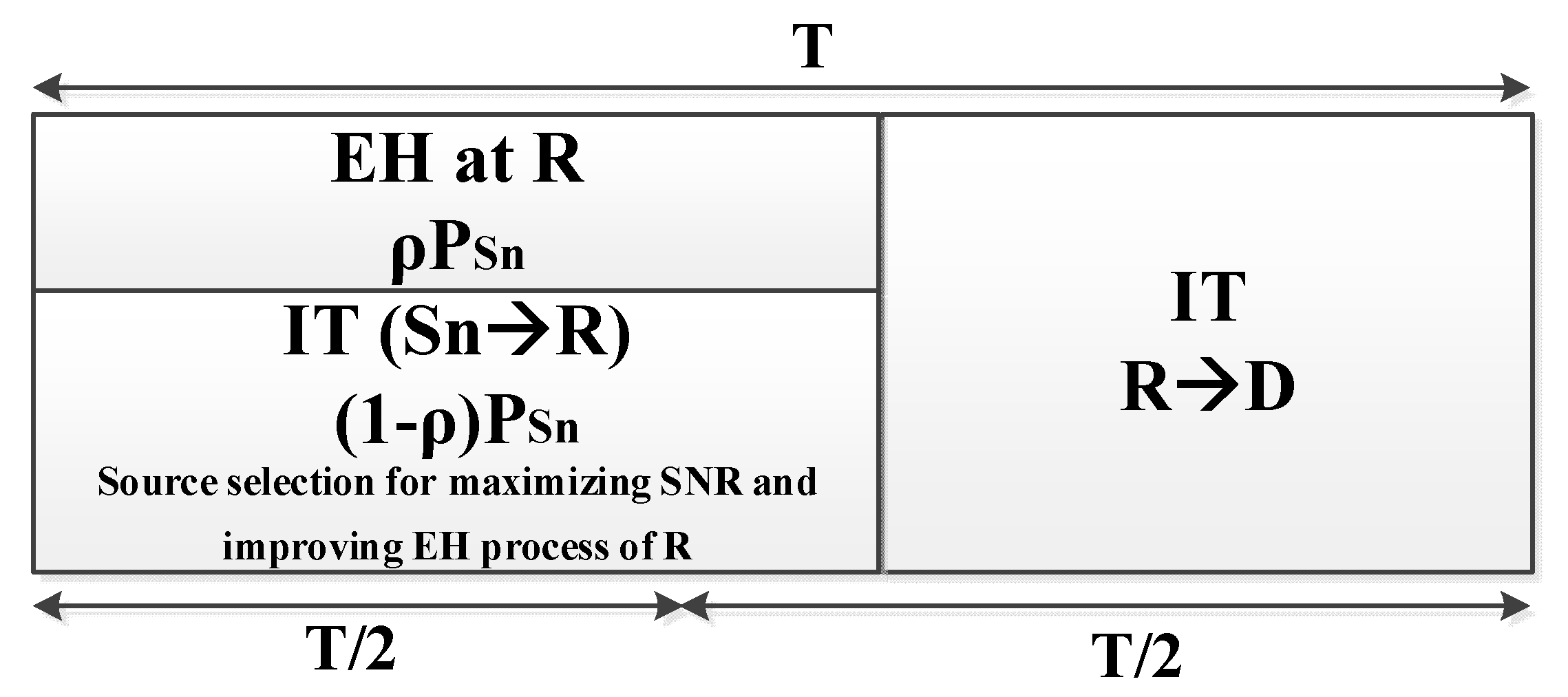
2. System Model
3. The System Performance
3.1. Delay-Limited Transmission (DLT) Mode
3.2. Delay-Tolerant Transmission (DTT) Mode
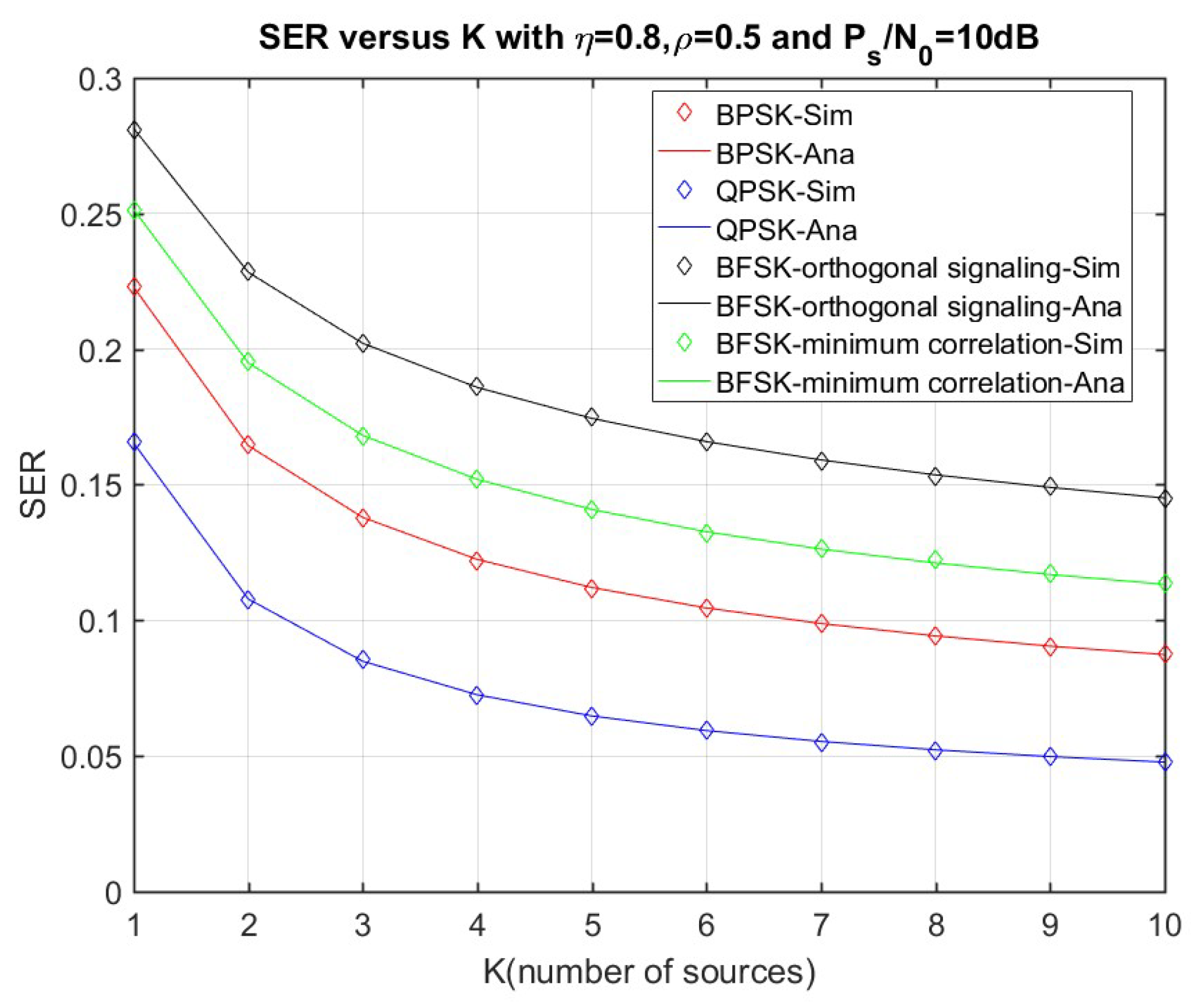
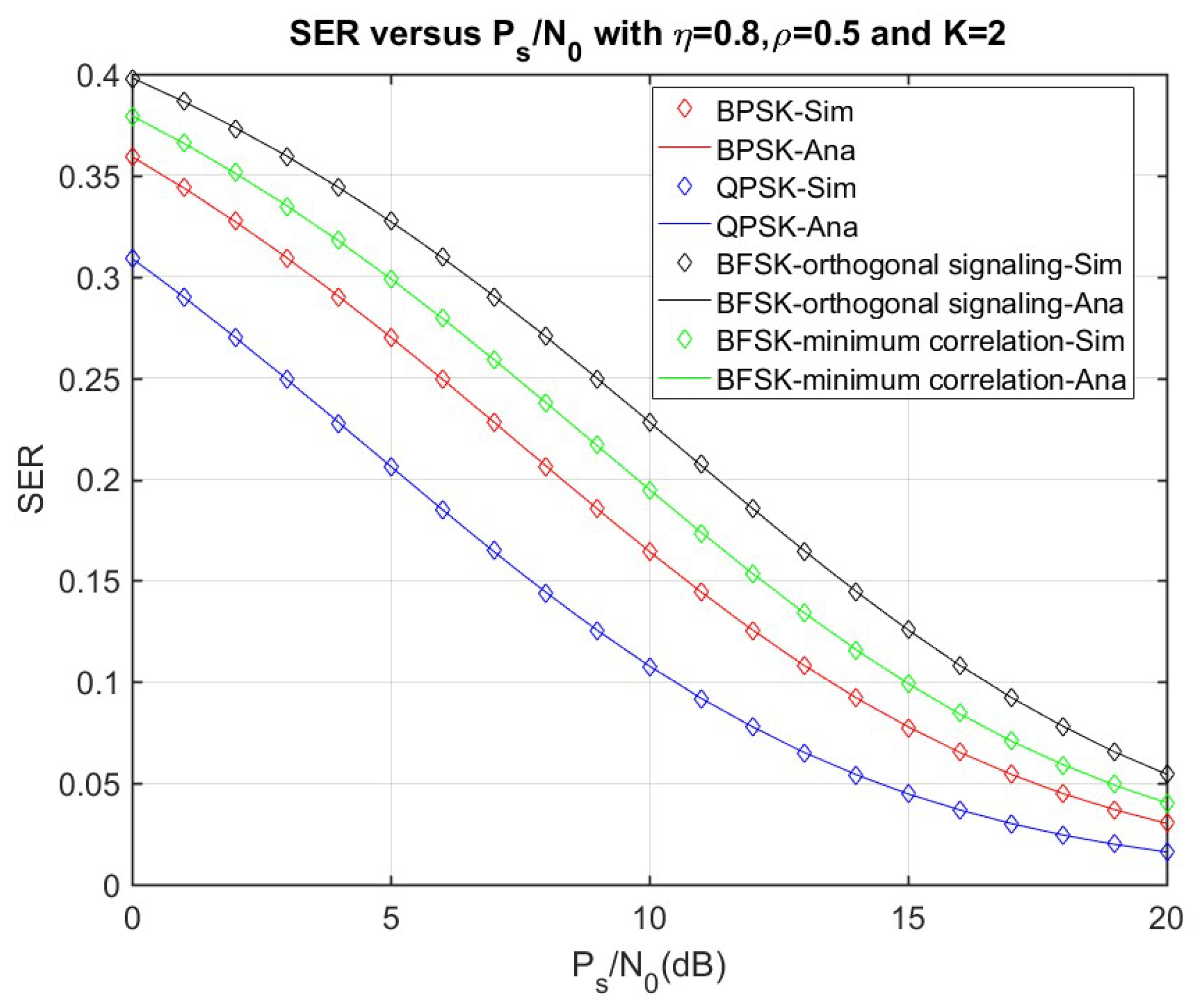
3.3. Symbol Error Ratio (SER) Analysis
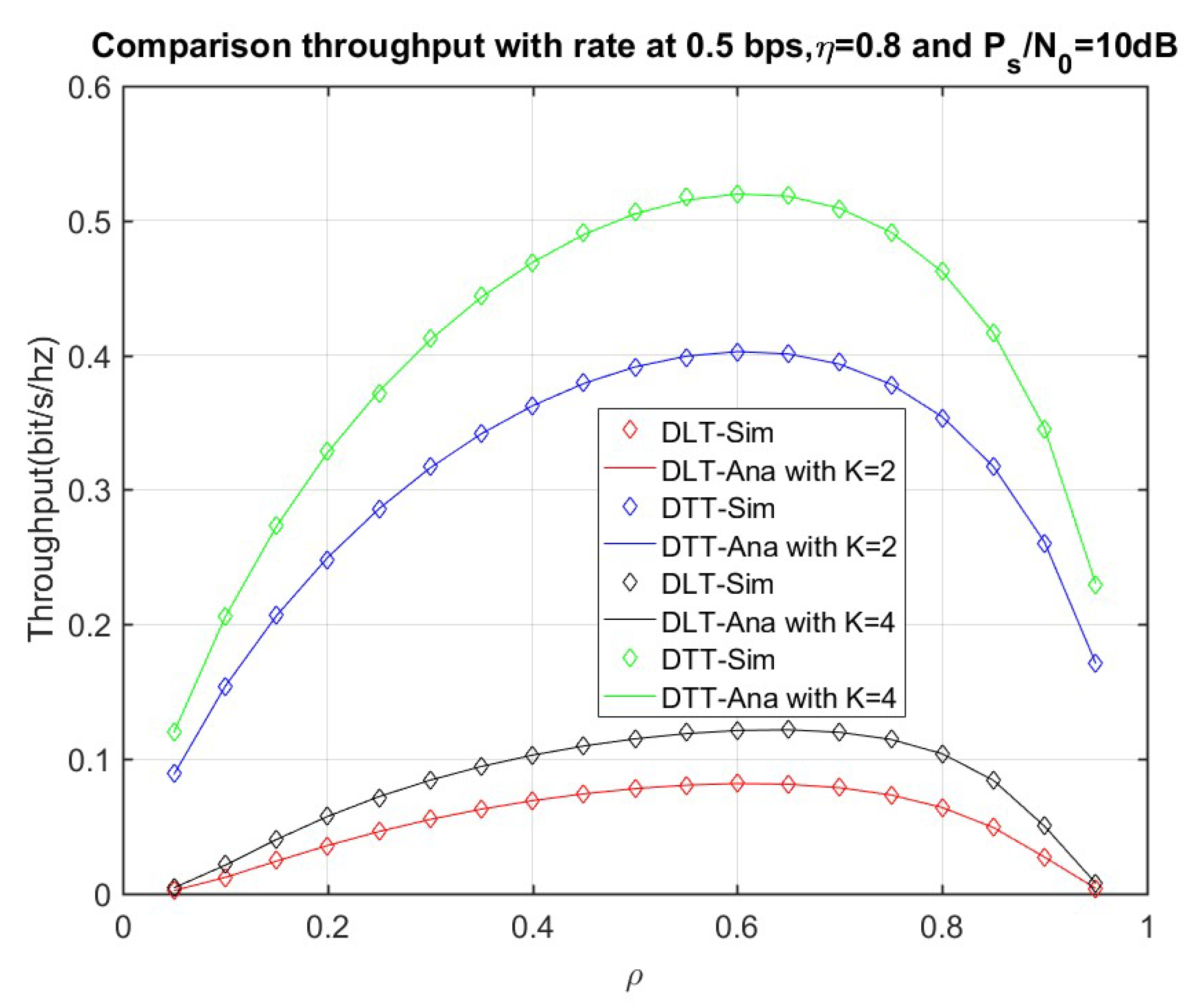
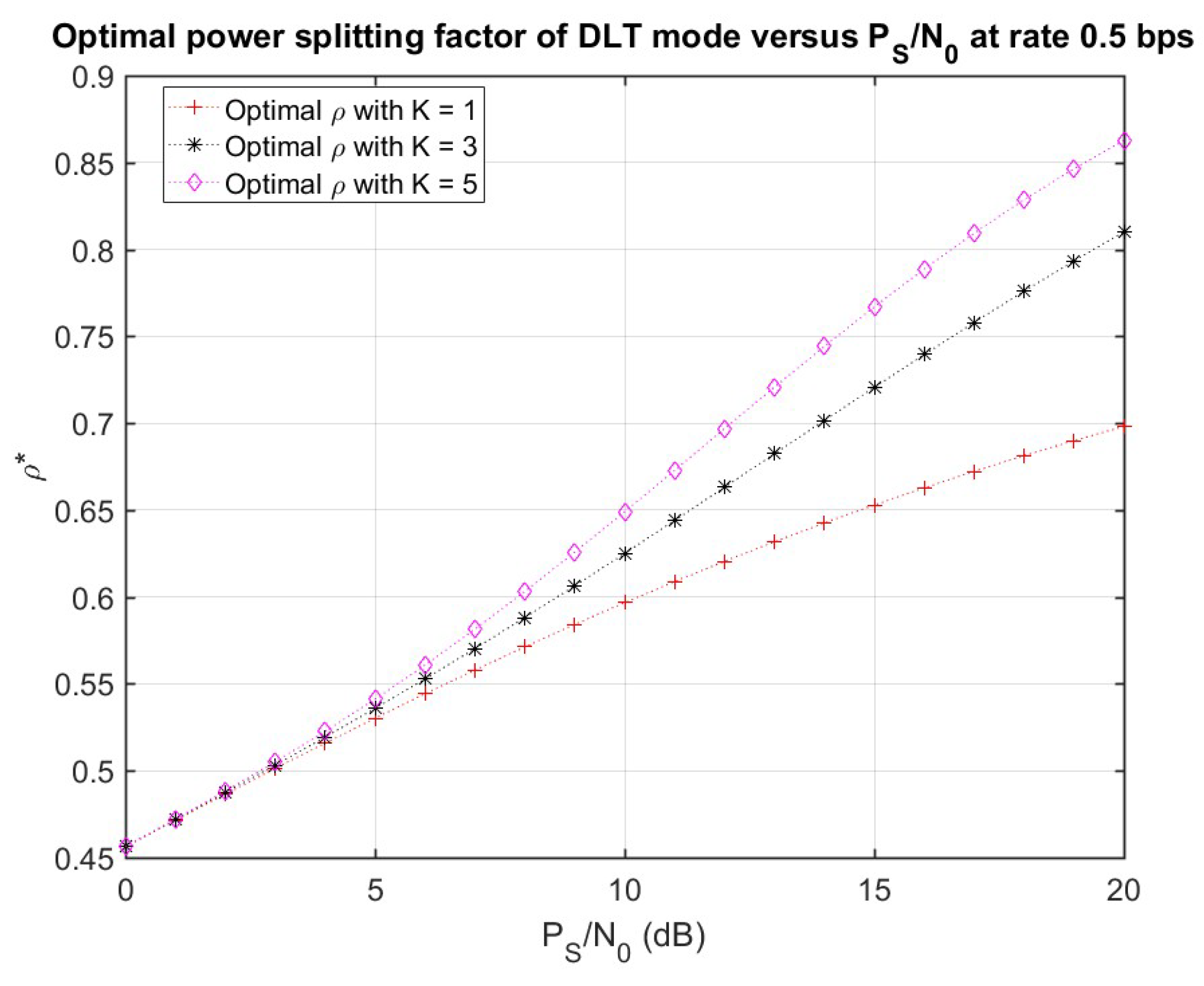
3.4. Optimal Power Splitting Factor
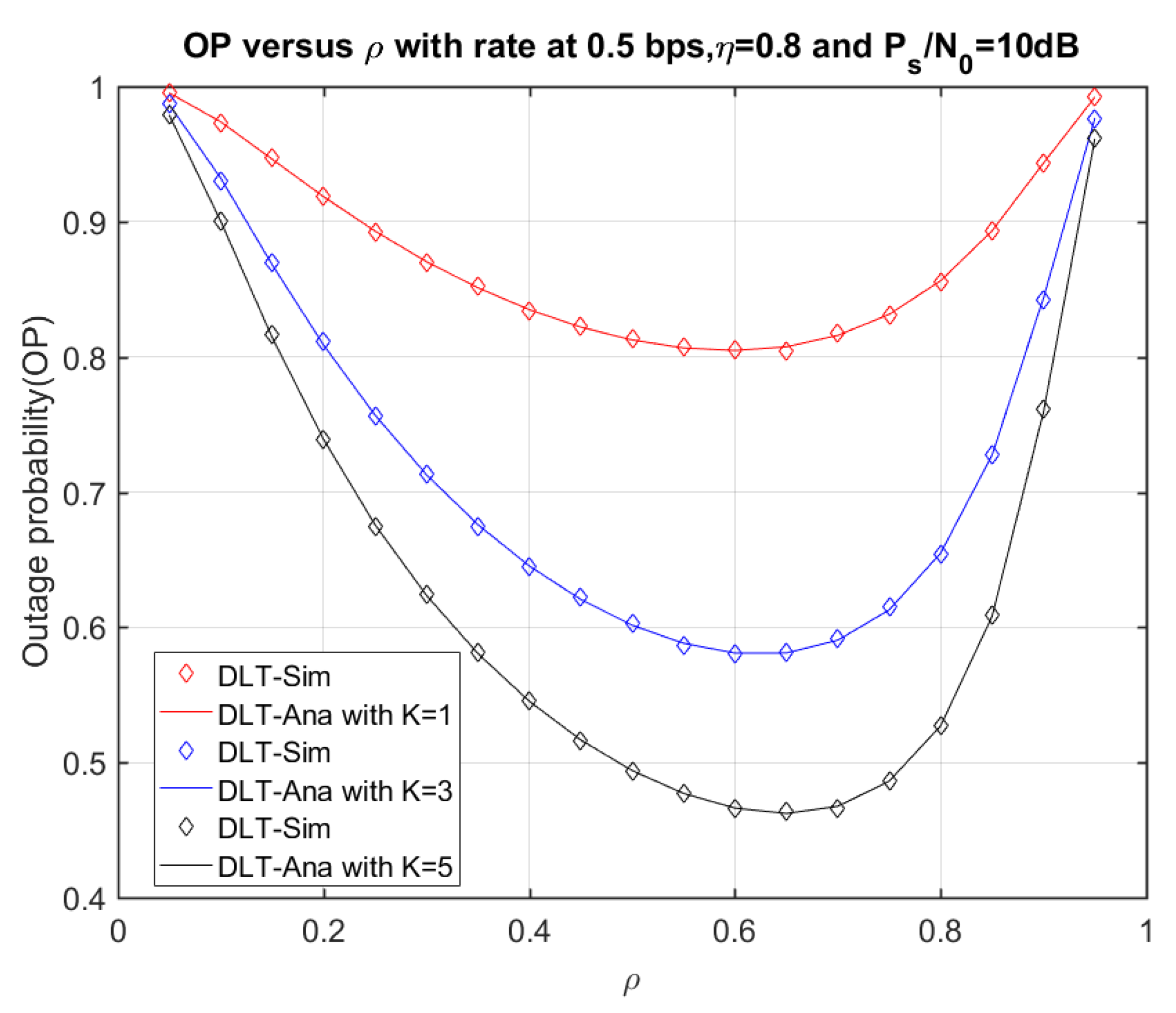
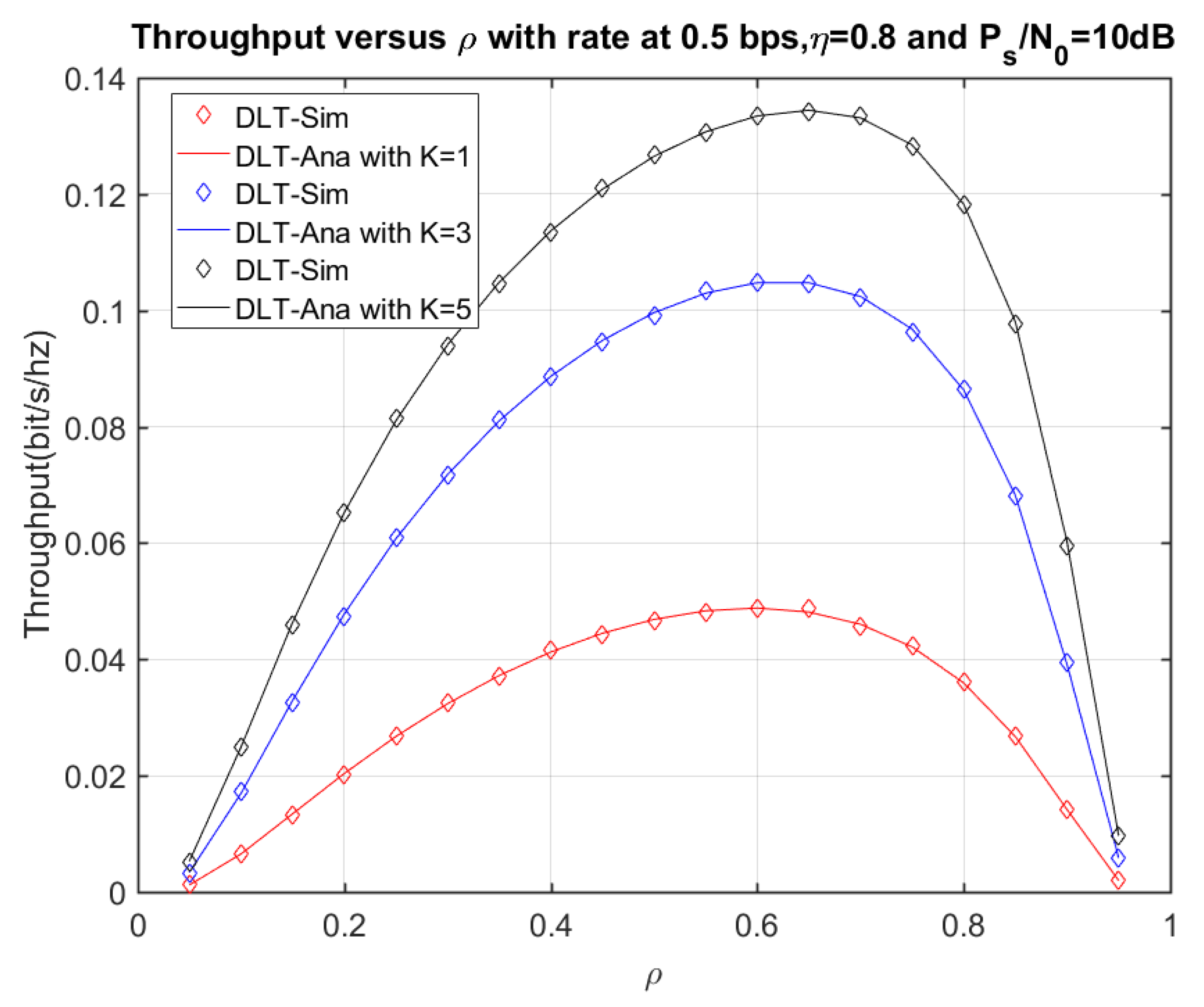
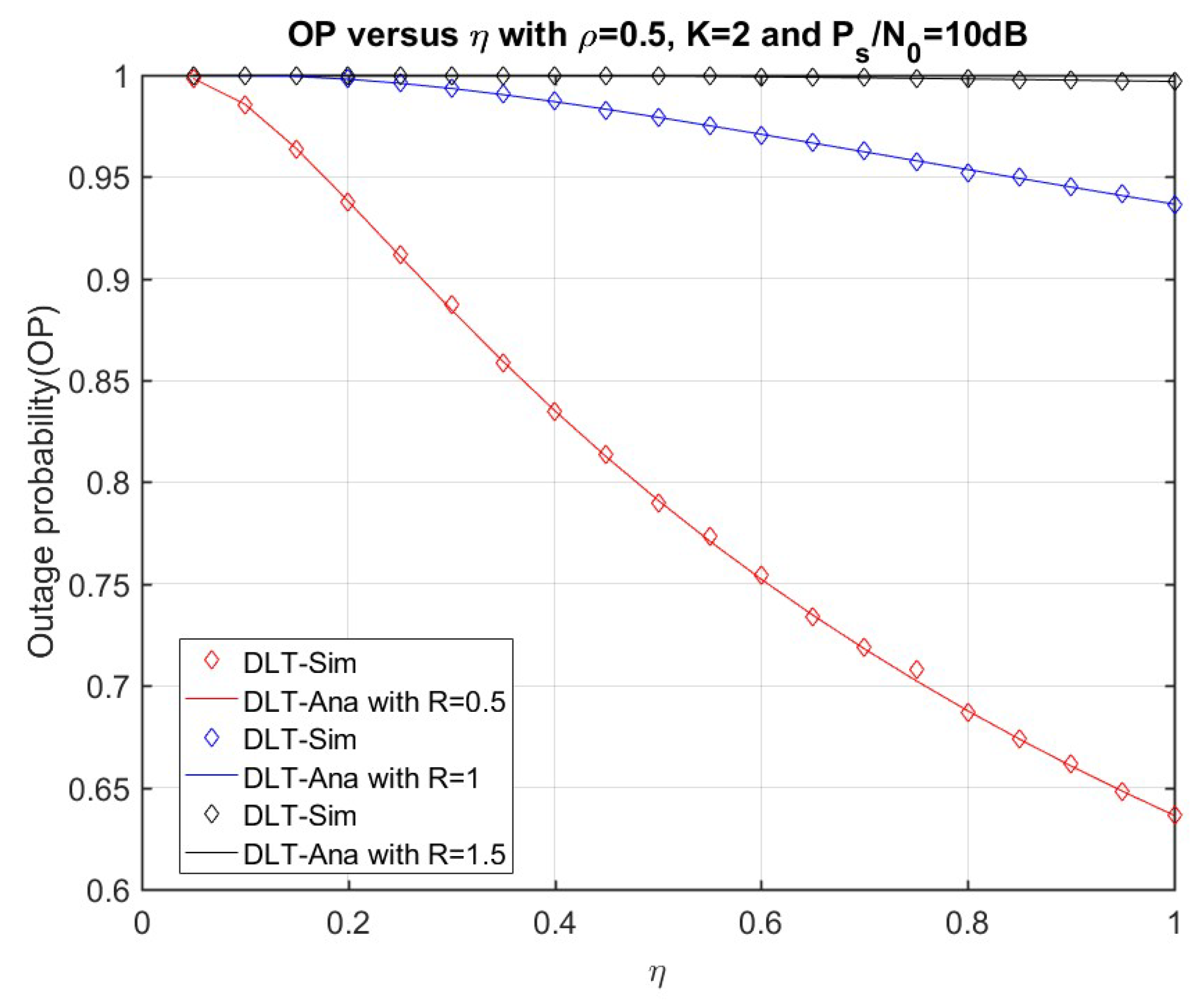
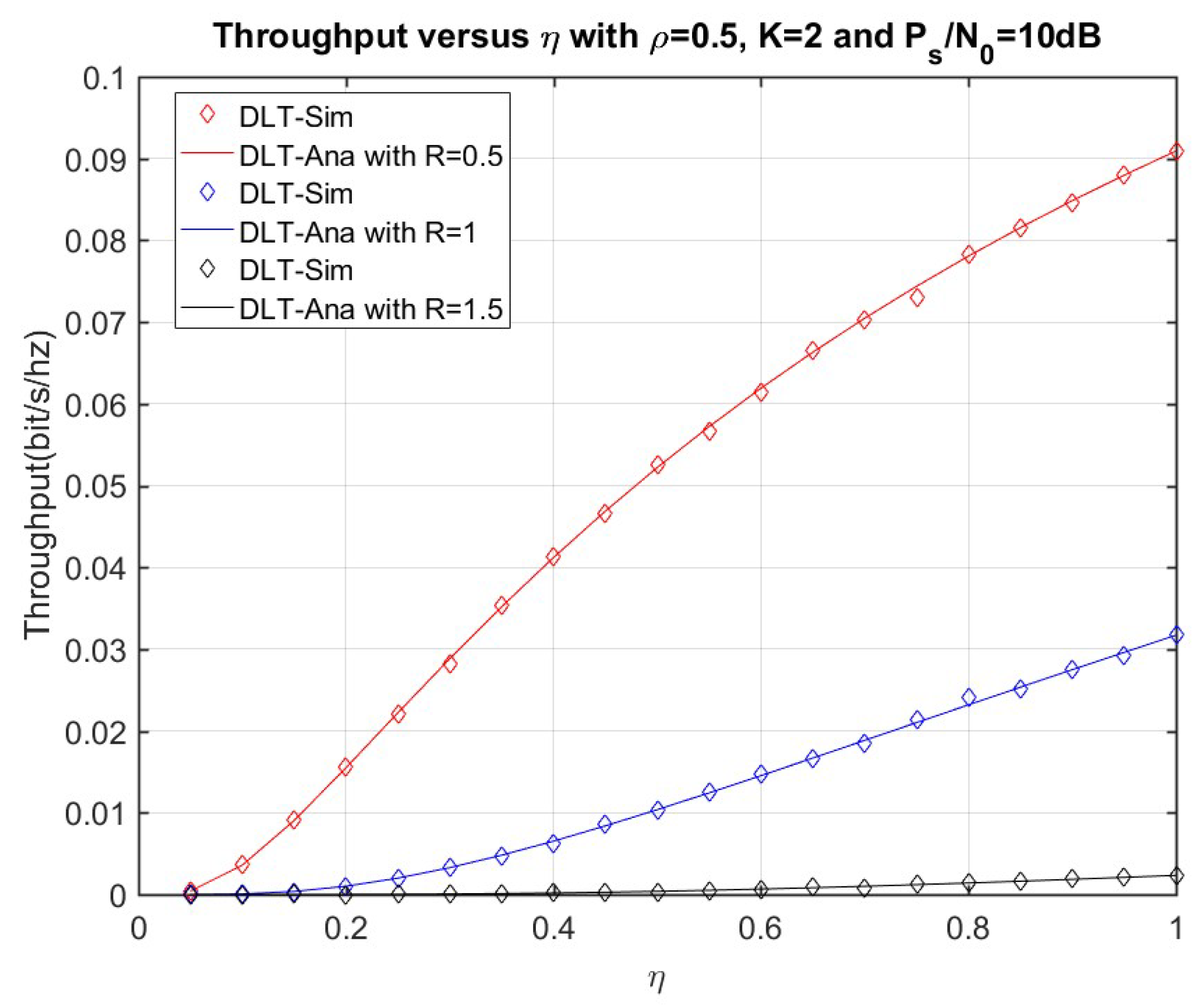
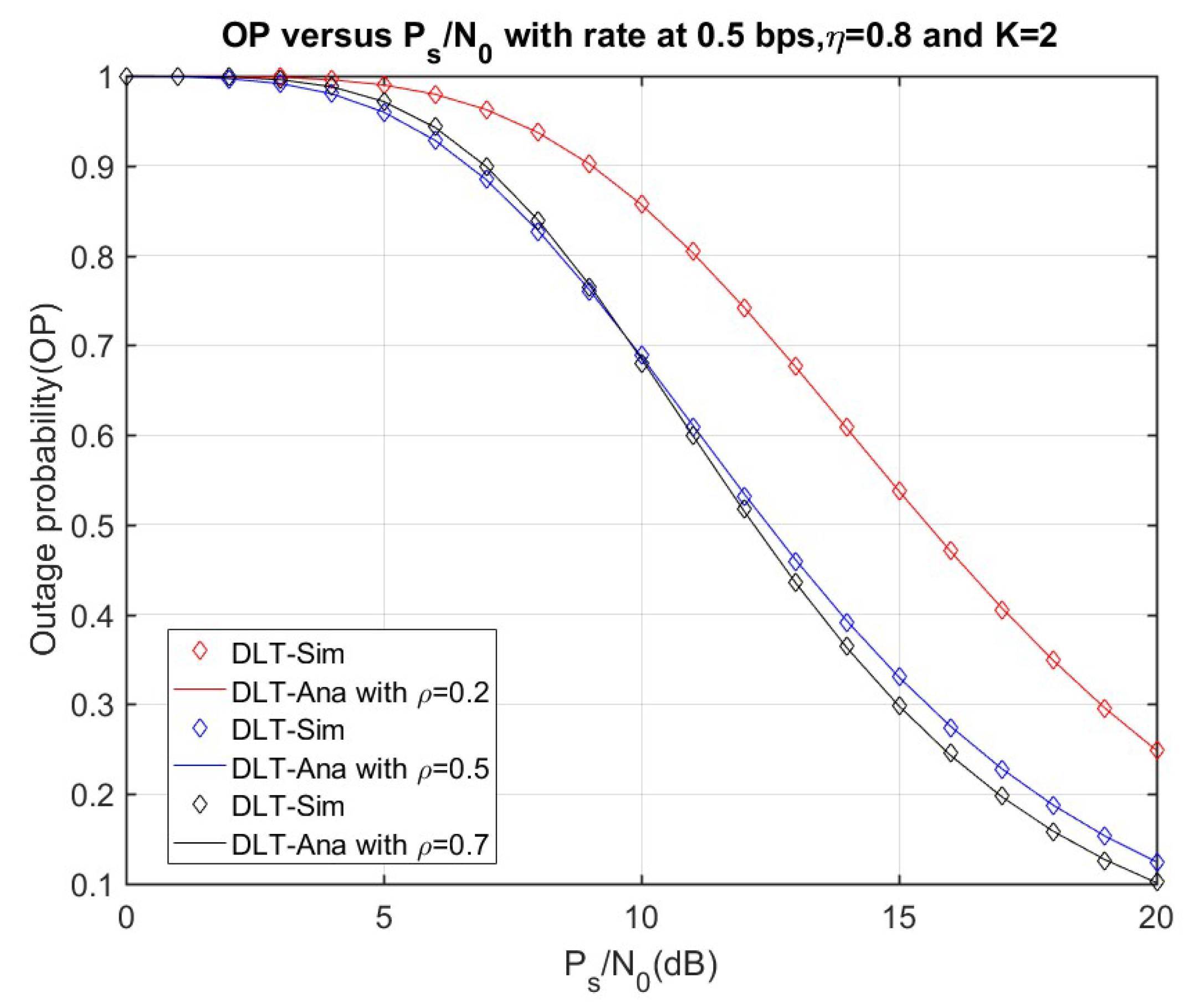
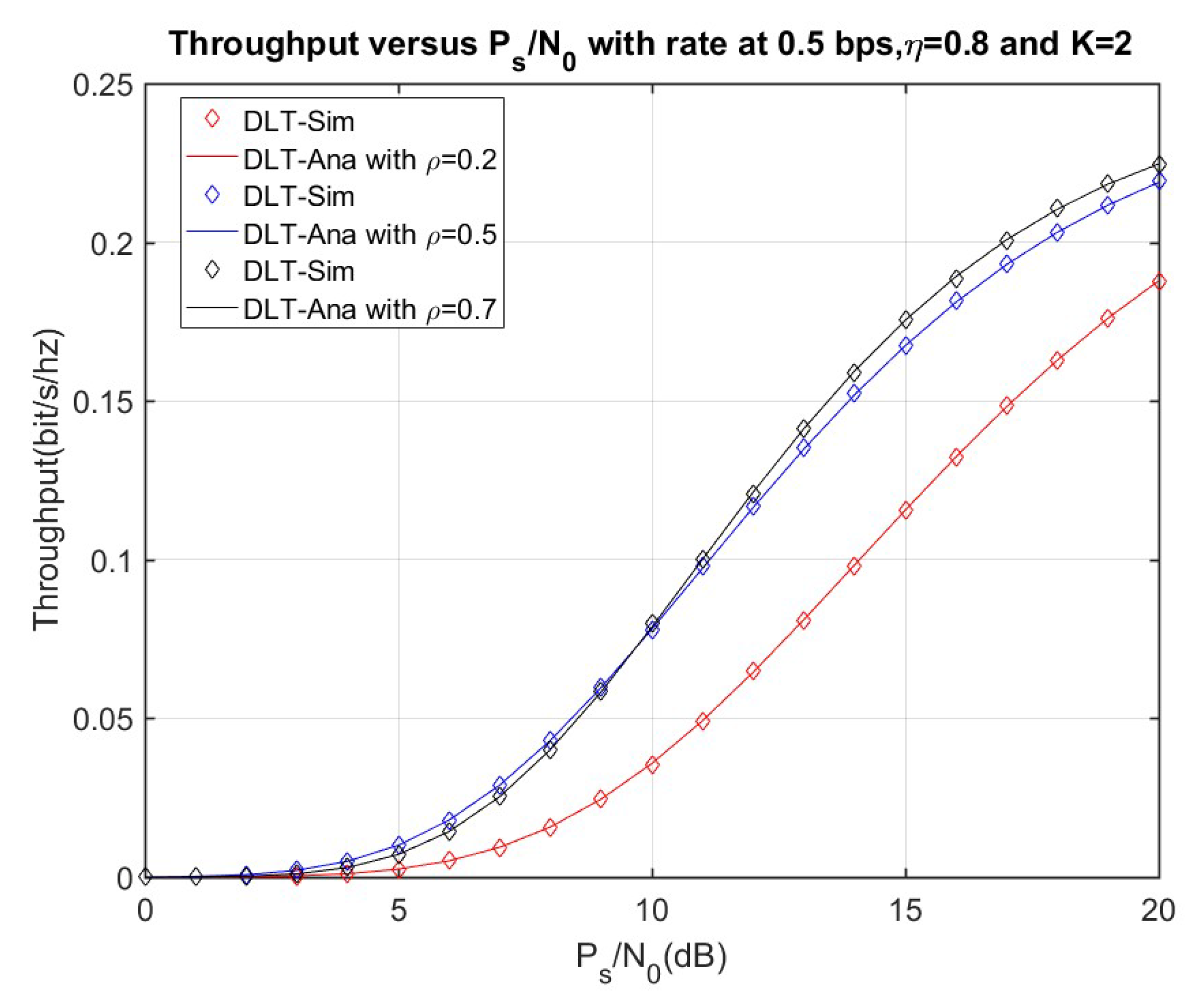
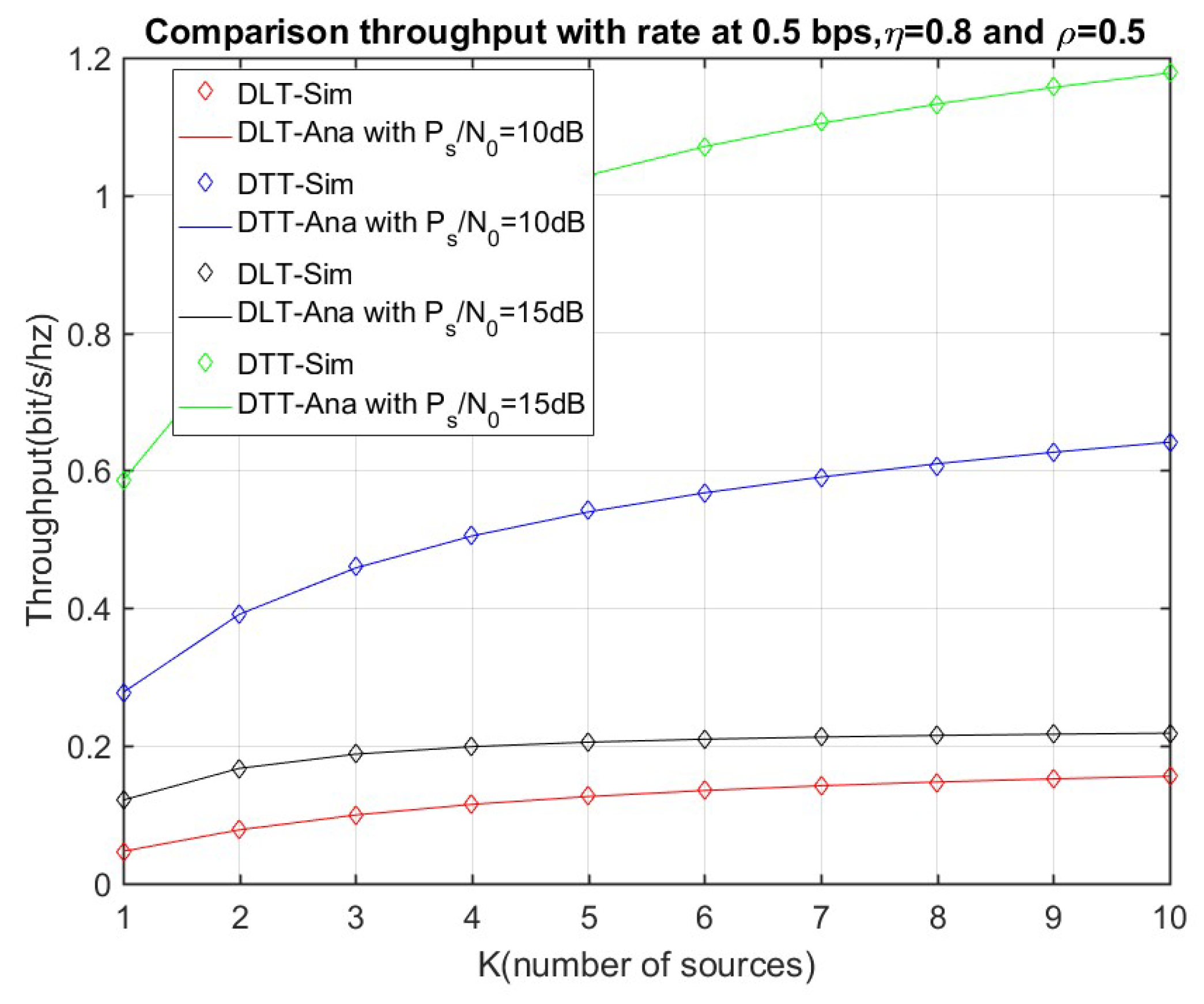
4. Numerical Results and Discussion
4.1. Delay-Limited Transmission (DLT) Analysis
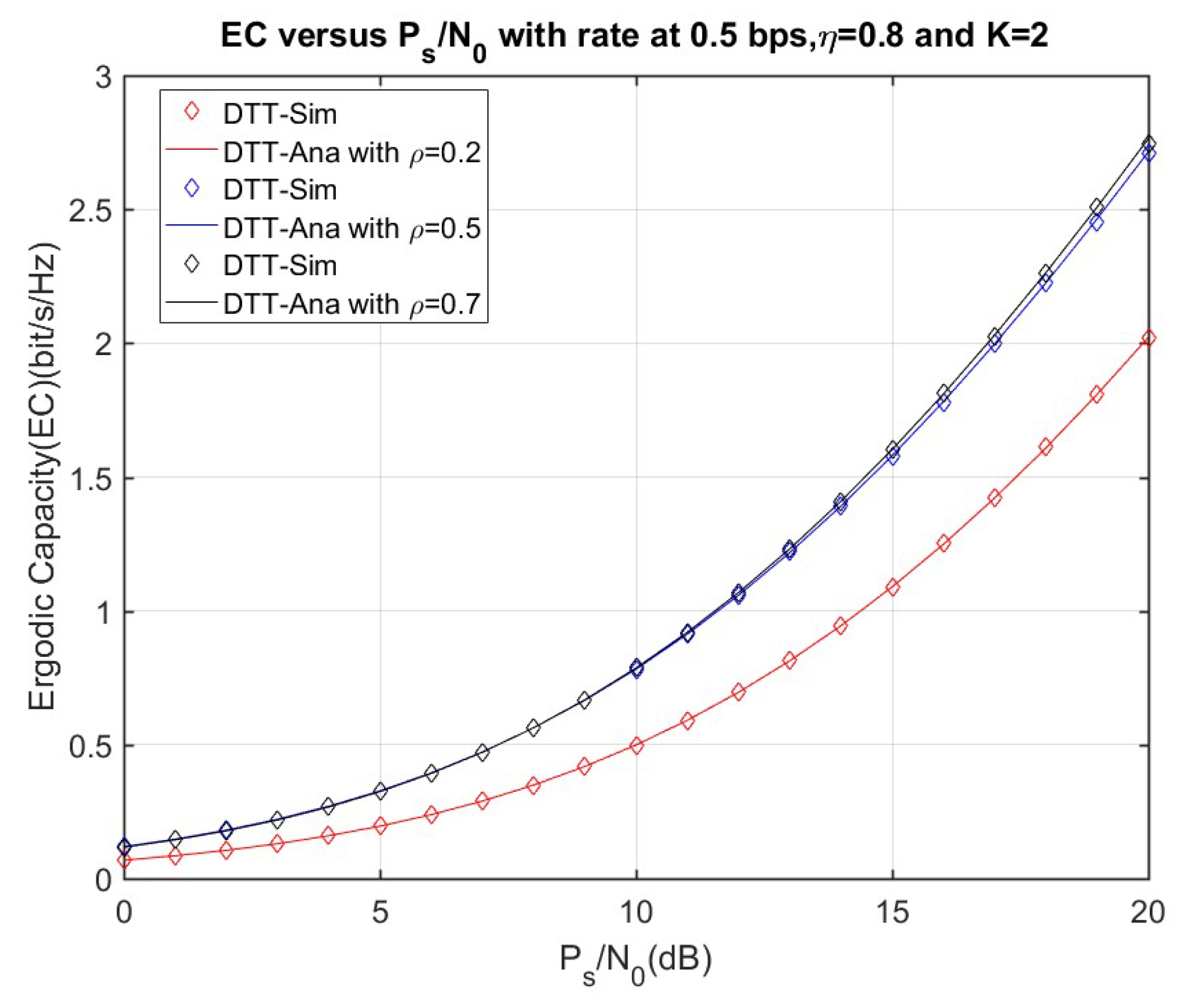
4.2. Delay-Tolerant Transmission (DTT) Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Niyato, D.; Kim, D.I.; Maso, M.; Han, Z. Wireless Powered Communication Networks: Research Directions and Technological Approaches. IEEE Wirel. Commun. 2017, 2–11. [Google Scholar] [CrossRef]
- Yu, H.; Lee, H.; Jeon, H. What is 5G? Emerging 5G Mobile Services and Network Requirements. Sustainability 2017, 9, 1848. [Google Scholar] [CrossRef]
- Rabie, K.M.; Salem, A.; Alsusa, E.; Alouini, M.S. Energy-harvesting in Cooperative AF Relaying Networks over Log-normal Fading Channels. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016. [Google Scholar]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Recent Advances in Joint Wireless Energy and Information Transfer. In Proceedings of the 2014 IEEE Information Theory Workshop (ITW2014), Hobart, Australia, 2–5 November 2014. [Google Scholar] [CrossRef]
- Kawabata, H.; Ishibashi, K. RF Energy Powered Feedback-aided Cooperation. In Proceedings of the 2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014. [Google Scholar] [CrossRef]
- Huang, K.; Lau, V.K. Enabling Wireless Power Transfer in Cellular Networks: Architecture, Modeling and Deployment. IEEE Trans. Wirel. Commun. 2014, 13, 902–912. [Google Scholar] [CrossRef]
- Medepally, B.; Mehta, N.B. Voluntary Energy Harvesting Relays and Selection in Cooperative Wireless Networks. IEEE Trans. Wirel. Commun. 2010, 9, 3543–3553. [Google Scholar] [CrossRef]
- De Rango, F.; Gerla, M.; Marano, S. A Scalable Routing Scheme with Group Motion Support in Large and Dense Wireless Ad Hoc Networks. Comput. Electr. Eng. 2006, 32, 224–240. [Google Scholar] [CrossRef]
- Zhou, B.; Lee, Y.Z.; Gerla, M.; De Rango, F. Geo-LANMAR: A Scalable Routing Protocol for Ad Hoc Networks with Group Motion. Wirel. Commun. Mob. Comput. 2006, 6, 989–1002. [Google Scholar] [CrossRef]
- Fazio, P.; De Rango, F.; Sottile, C.; Calafate, C. A New Channel Assignment Scheme for Interference-Aware Routing in Vehicular Networks. In Proceedings of the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), Budapest, Hungary, 15–18 May 2011. [Google Scholar] [CrossRef]
- Cassano, E.; Florio, F.; De Rango, F.; Marano, S. A Performance Comparison between ROC-RSSI and Trilateration Localization Techniques for WPAN Sensor Networks in a Real Outdoor Testbed. In Proceedings of the 2009 Wireless Telecommunications Symposium, Prague, Czech Republic, 22–24 April 2009. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-energy Tradeoff. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012. [Google Scholar] [CrossRef]
- Song, C.; Ling, C.; Park, J.; Clerckx, B. MIMO Broadcasting for Simultaneous Wireless Information and Power Transfer: Weighted MMSE Approaches. In Proceedings of the 2014 IEEE Globecom Workshops (GC Wkshps), Austin, TX, USA, 8–12 December 2014. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting Information and Energy Simultaneously. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008. [Google Scholar] [CrossRef]
- Salari, S.; Kim, I.M.; Kim, D.I.; Chan, F. Joint EH Time Allocation and Distributed Beamforming in Interference-Limited Two-Way Networks With EH-Based Relays. IEEE Trans. Wirel. Commun. 2017, 16, 6395–6408. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless Information and Power Transfer: A Dynamic Power Splitting Approach. IEEE Trans. Commun. 2013, 61, 3990–4001. [Google Scholar] [CrossRef]
- Jameel, F.; Wyne, S.; Ding, Z. Secure Communications in Three-Step Two-Way Energy Harvesting DF Relaying. IEEE Commun. Lett. 2018, 22, 308–311. [Google Scholar] [CrossRef]
- Chen, Y. Energy-Harvesting AF Relaying in the Presence of Interference and Nakagami-m Fading. IEEE Trans. Wirel. Commun. 2016, 15, 1008–1017. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Do, N.T.; Bao, V.N.; An, B. A Relay Selection Protocol for Wireless Energy Harvesting Relay Networks. In Proceedings of the 2015 International Conference on Advanced Technologies for Communications (ATC), Ho Chi Minh, Vietnam, 14–16 October 2015. [Google Scholar] [CrossRef]
- Nguyen, S.Q.; Kong, H.Y. Generalized Diversity Combining of Energy Harvesting Multiple Antenna Relay Networks: Outage and Throughput Performance Analysis. Ann. Telecommun. 2016, 71, 265–277. [Google Scholar] [CrossRef]
- Peng, C.; Li, F.; Liu, H. Optimal Power Splitting in Two-Way Decode-and-Forward Relay Networks. IEEE Commun. Lett. 2017, 21, 2009–2012. [Google Scholar] [CrossRef]
- Men, J.; Ge, J.; Zhang, C.; Li, J. Joint Optimal Power Allocation and Relay Selection Scheme in Energy Harvesting Asymmetric Two-way Relaying System. IET Commun. 2015, 9, 1421–1426. [Google Scholar] [CrossRef]
- Singh, S.; Modem, S.; Prakriya, S. Optimization of Cognitive Two-Way Networks with Energy Harvesting Relays. IEEE Commun. Lett. 2017, 21, 1381–1384. [Google Scholar] [CrossRef]
- Cai, G.; Fang, Y.; Han, G.; Xu, J.; Chen, G. Design and Analysis of Relay-Selection Strategies for Two-Way Relay Network-Coded DCSK Systems. IEEE Trans. Veh. Technol. 2018, 67, 1258–1271. [Google Scholar] [CrossRef]
- Kumar, N.; Bhatia, V. Outage Probability and Average Channel Capacity of Amplify-and-Forward in Conventional Cooperative Communication Networks over Rayleigh Fading Channels. Wirel. Pers. Commun. 2016, 88, 943–951. [Google Scholar] [CrossRef]
- Bhatnagar, M.R. On the Capacity of Decode-and-Forward Relaying over Rician Fading Channels. IEEE Commun. Lett. 2013, 17, 1100–1103. [Google Scholar] [CrossRef]
- Nguyen, T.; Quang Minh, T.; Tran, P.; Vozňák, M. Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors 2018, 18, 1781. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Minh, T.H.; Tran, P.T.; Vozňák, M. Adaptive Energy Harvesting Relaying Protocol for Two-Way Half Duplex System Network over Rician Fading Channel. Wirel. Commun. Mob. Comput. 2018. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Duy, T.T.; Luu, G.T.; Tran, P.T.; Vozňák, M. Energy Harvesting-based Spectrum Access with Incremental Cooperation, Relay Selection and Hardware Noises. Radioengineering 2017, 26, 240–250. [Google Scholar] [CrossRef]
- Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2015. [CrossRef]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions:With Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- McKay, M.R.; Grant, A.J.; Collings, I.B. Performance Analysis of MIMO-MRC in Double-Correlated Rayleigh Environments. IEEE Trans. Commun. 2007, 55, 497–507. [Google Scholar] [CrossRef]
- Duong, T.Q.; Duy, T.T.; Matthaiou, M.; Tsiftsis, T.; Karagiannidis, G.K. Cognitive Cooperative Networks in Dual-hop Asymmetric Fading Channels. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013. [Google Scholar] [CrossRef]
- Chong, E.K.; Zak, S.H. An Introduction to Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
| Symbol | Name | Values |
|---|---|---|
| Energy harvesting efficiency | 0.8 | |
| Mean of | 0.5 | |
| Mean of | 0.5 | |
| SNR threshold | 1 | |
| Ps/N0 | Source power to noise ratio | 0–20 dB |
| R | Source rate | 0.5 bit/s/Hz |
| K | Number of sources | 1–10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.N.; Tran, M.; Nguyen, T.-L.; Ha, D.-H.; Voznak, M. Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis. Electronics 2019, 8, 67. https://doi.org/10.3390/electronics8010067
Nguyen TN, Tran M, Nguyen T-L, Ha D-H, Voznak M. Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis. Electronics. 2019; 8(1):67. https://doi.org/10.3390/electronics8010067
Chicago/Turabian StyleNguyen, Tan N., Minh Tran, Thanh-Long Nguyen, Duy-Hung Ha, and Miroslav Voznak. 2019. "Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis" Electronics 8, no. 1: 67. https://doi.org/10.3390/electronics8010067
APA StyleNguyen, T. N., Tran, M., Nguyen, T.-L., Ha, D.-H., & Voznak, M. (2019). Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis. Electronics, 8(1), 67. https://doi.org/10.3390/electronics8010067







