Codebook-Aided DOA Estimation Algorithms for Massive MIMO System
Abstract
1. Introduction
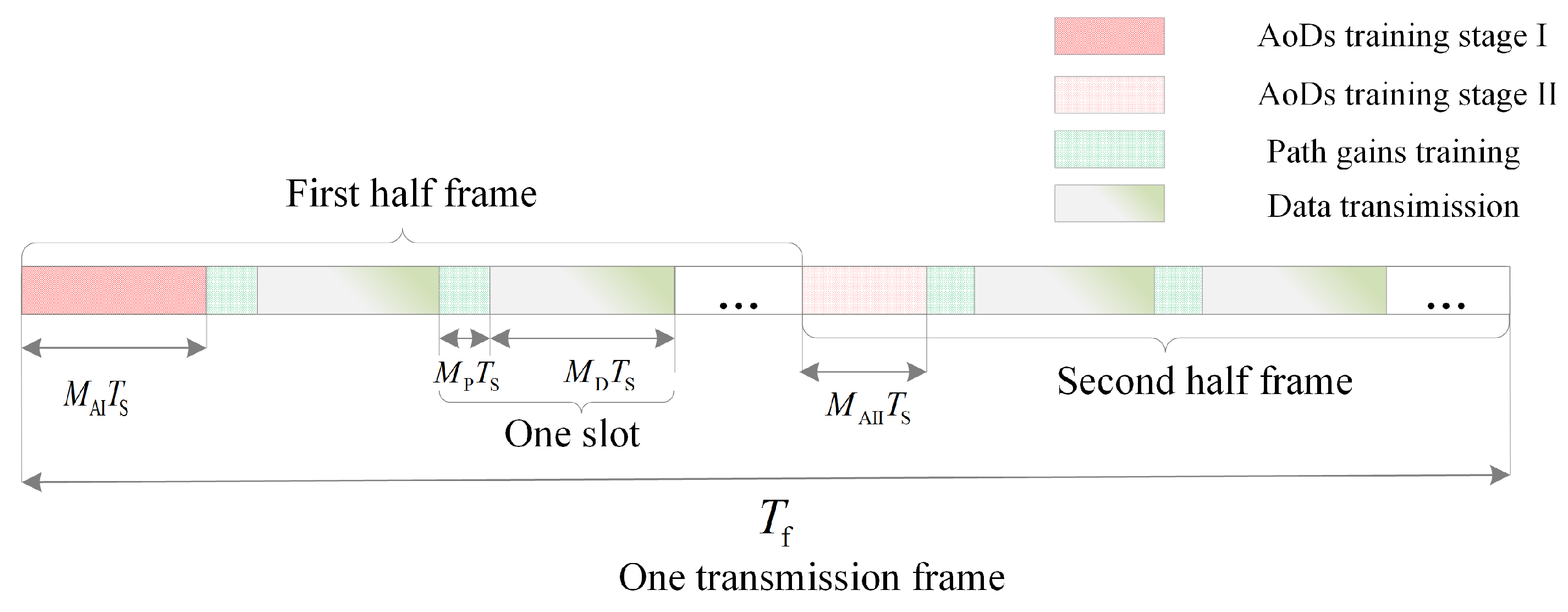
- New frame structure for downlink transmission: By leveraging the difference between variation of path AoDs and the path gains, we proposed a new frame structure for downlink transmission. (i) We theoretically prove the peculiarity of AoDs variation. (ii) We decouple AoD estimation of one frame into two separated stages. Within the first and the second half of transmission frame, the AoD estimation are performed in AoD training stage I and AoD training stage II respectively due to the property of AoDs variation.
- Low rank matrix recovery based DOA reconstruction: Apart from the classic MUSIC algorithm, we develop DOA reconstruction method based on low rank matrix recovery, which is referred to as convex optimization algorithm in this paper. We introduce the elastic regularization term to transform the covariance matrix reconstruction problem of the received signal into a semi-definite programming (SDP) problem, which can be effectively solved with polynomial-time complexity.
- Codebook-aided algorithms for DOA estimation: By separating the AoDs acquisition under the frame structure, we propose C-aided algorithms to reduce computational complexity, which includes the C-aided MUSIC algorithm and C-aided convex optimization algorithm. During the AoD training stage II, due to the small angle perturbation, we just focus on deterministic angle range rather with the help of channel codebook feedback and the AoDs obtained at AoD training stage I.
2. System Model
2.1. Data Model
2.2. AoDs Estimation Problem Formation
2.3. Codebook Channel Feedback
3. DOA Estimation Based on Codebook Feedback
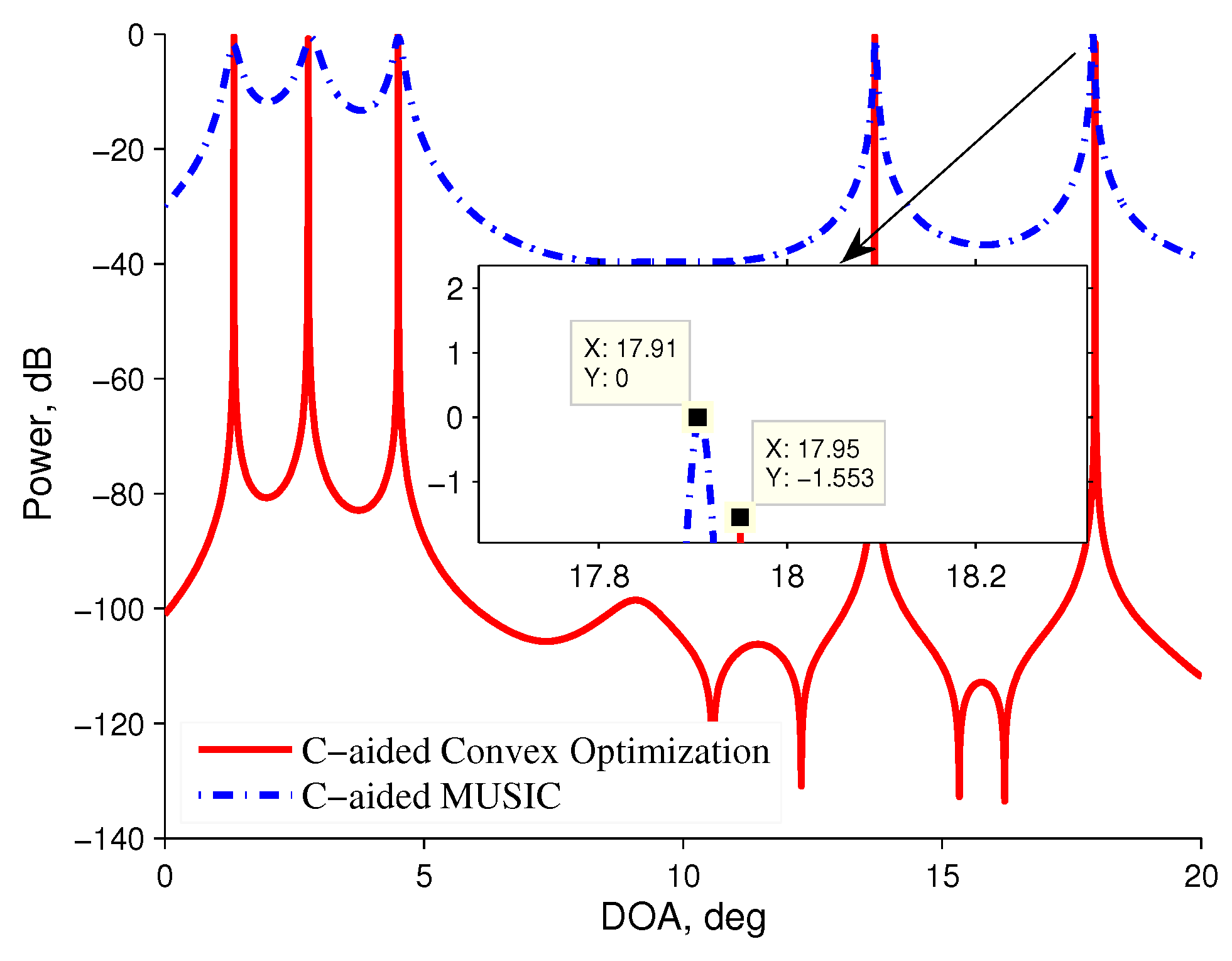
3.1. C-Aided MUSIC Algorithm
3.2. C-Aided Convex Optimization Algorithm
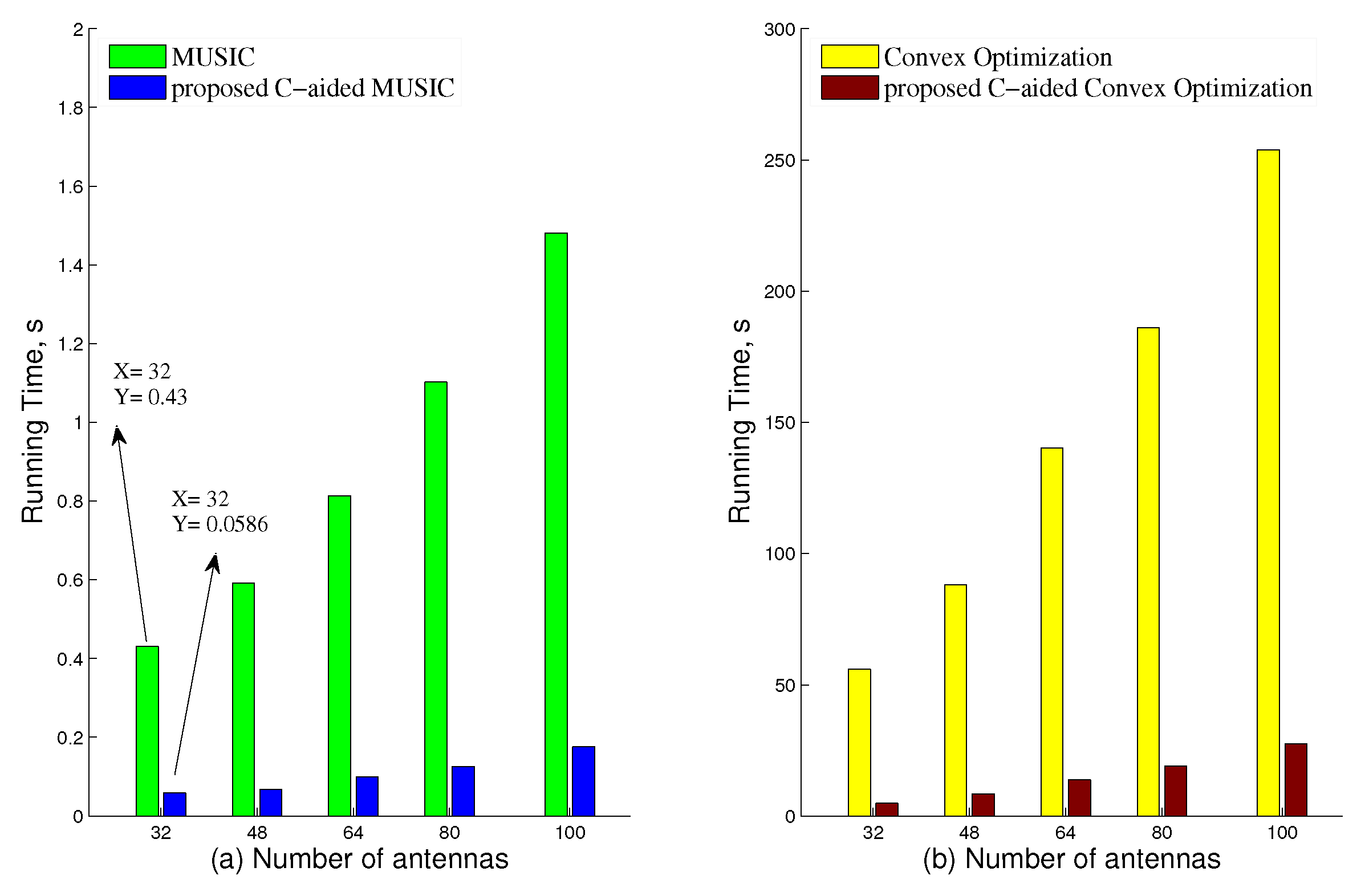
3.3. Computational Cost Comparison
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DOA | Direction of Arrival |
| CS | Compressed Sensing |
| MIMO | Multiple Input Multiple Output |
| BS | Base Station |
| CSI | Channel State Information |
| FDD | Frequency Division Duplex |
| MUSIC | Multiple Signal Classification |
| C-aided | Codebook aided |
| AoDs | Angles of Departure |
| Co-prime LAs | Co-prime Linear Arrays |
| UEs | User Equipments |
| ULAs | Uniform Linear Arrays |
| SDP | Semi-Definite Programming |
| RMSE | Root Mean Square Error |
| SNR | Signal-to-Noise Ratio |
Appendix A
- case 1: , where the AoDs are constant during one frame of transmission.
- case 2: is small, we have . When with denoting the resolution of AoDs, we consider the AoDs are relatively constant. As a consequence, we obtain the duration time of one frame .where v is the average moving speed of UE.
References
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Hassan, N.; Fernando, X. Massive MIMO wireless networks: An overview. Electronics 2017, 6, 63. [Google Scholar] [CrossRef]
- Matalatala, M.; Deruyck, M.; Tanghe, E.; Martens, L.; Joseph, W. Simulations of beamforming performance and energy efficiency for 5G mm-wave cellular networks. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Gandotra, P.; Jha, R.K.; Jain, S. Green Communication in Next Generation Cellular Networks: A Survey. IEEE Access 2017, 5, 11727–11758. [Google Scholar] [CrossRef]
- Mowla, M.M.; Ahmad, I.; Habibi, D.; Phung, Q.V. A Green Communication Model for 5G Systems. IEEE Trans. Green Commun. Netw. 2017, 1, 264–280. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Wang, Z.; Chen, S. Spatially Common Sparsity Based Adaptive Channel Estimation and Feedback for FDD Massive MIMO. IEEE Trans. Signal Process. 2015, 63, 6169–6183. [Google Scholar] [CrossRef]
- Shen, W.; Dai, L.; Shi, Y.; Shim, B.; Wang, Z. Joint Channel Training and Feedback for FDD Massive MIMO Systems. IEEE Trans. Veh. Technol. 2016, 65, 8762–8767. [Google Scholar] [CrossRef]
- Venieris, E.; Manikas, A. Near-far field multipath spatial-temporal localisation. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 1049–1054. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, Y.D.; Goodman, N.A. Optimized compressive sensing-based direction-of-arrival estimation in massive MIMO. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3181–3185. [Google Scholar] [CrossRef]
- Stöckle, C.; Munir, J.; Mezghani, A.; Nossek, J.A. 1-bit direction of arrival estimation based on Compressed Sensing. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 246–250. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Zhao, Y.; Shui, P.; Liu, H. Computationally Efficient DOA Estimation for MIMO Radar. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; pp. 1–3. [Google Scholar] [CrossRef]
- Sun, F.; Lan, P.; Gao, B. Partial spectral search-based DOA estimation method for co-prime linear arrays. Electron. Lett. 2015, 51, 2053–2055. [Google Scholar] [CrossRef]
- Shen, W.; Dai, L.; Zhang, Y.; Li, J.; Wang, Z. On the Performance of Channel-Statistics-Based Codebook for Massive MIMO Channel Feedback. IEEE Trans. Veh. Technol. 2017, 66, 7553–7557. [Google Scholar] [CrossRef]
- Tan, J.; Dai, L.; Li, J.; Jin, S. Angle-based codebook for low-resolution hybrid precoding in millimeter-wave massive MIMO systems. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Shen, W.; Dai, L.; Gui, G.; Wang, Z.; Heath, R.W.; Adachi, F. AoD-adaptive subspace codebook for channel feedback in an FDD massive MIMO systems. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, C. Pilot Decontamination in Wideband Massive MIMO Systems by Exploiting Channel Sparsity. IEEE Trans. Wirel. Commun. 2016, 15, 5087–5100. [Google Scholar] [CrossRef]
- Choi, J.; Lee, K.; Love, D.J.; Kim, T.; Heath, R.W. Advanced Limited Feedback Designs for FD-MIMO Using Uniform Planar Arrays. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. The Power of Convex Relaxation: Near-Optimal Matrix Completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, G.; Wang, X. Computationally efficient DOA estimation for monostatic MIMO radar based on covariance matrix reconstruction. Electron. Lett. 2017, 53, 111–113. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2008, 20, 1956–1982. [Google Scholar] [CrossRef]
- Horn, R.A. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]

| Parameter Name | Value |
|---|---|
| Array model at BS | ULAs |
| Number of BS antennas | 32 |
| Number of UEs K | 5 |
| Channel model | AWGN |
| Direction of independent narrowband signal | |
| Whole angle range | |
| Angle range with auxiliary codebook | |
| Searching step for MUSIC | |
| Error constant | 5 |
| Equilibrium regularization factor | 60 |
| Number of pilot for AoD training stage , | 500 |
| Number of Monte Carlo simulations L | 300 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wu, H.; Jin, L. Codebook-Aided DOA Estimation Algorithms for Massive MIMO System. Electronics 2019, 8, 26. https://doi.org/10.3390/electronics8010026
Li S, Wu H, Jin L. Codebook-Aided DOA Estimation Algorithms for Massive MIMO System. Electronics. 2019; 8(1):26. https://doi.org/10.3390/electronics8010026
Chicago/Turabian StyleLi, Shufeng, Hongda Wu, and Libiao Jin. 2019. "Codebook-Aided DOA Estimation Algorithms for Massive MIMO System" Electronics 8, no. 1: 26. https://doi.org/10.3390/electronics8010026
APA StyleLi, S., Wu, H., & Jin, L. (2019). Codebook-Aided DOA Estimation Algorithms for Massive MIMO System. Electronics, 8(1), 26. https://doi.org/10.3390/electronics8010026





