An Inverse Synthetic Aperture Ladar Imaging Algorithm of Maneuvering Target Based on Integral Cubic Phase Function-Fractional Fourier Transform
Abstract
1. Introduction
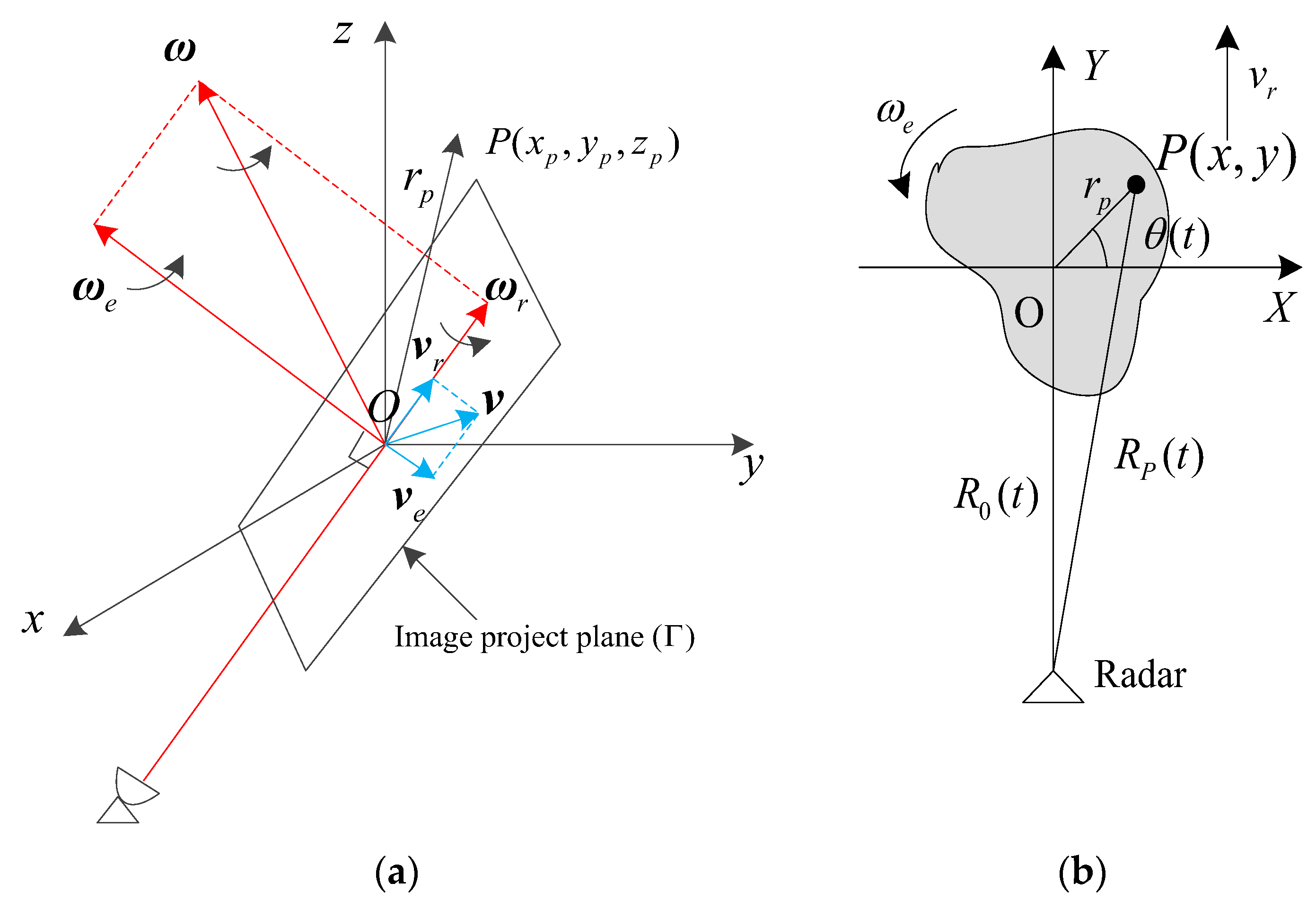
2. ISAL Signal Echo Model
3. Range Imaging Based on ICPF-FRFT
4. Azimuth Imaging Based on ICPF-FRFT
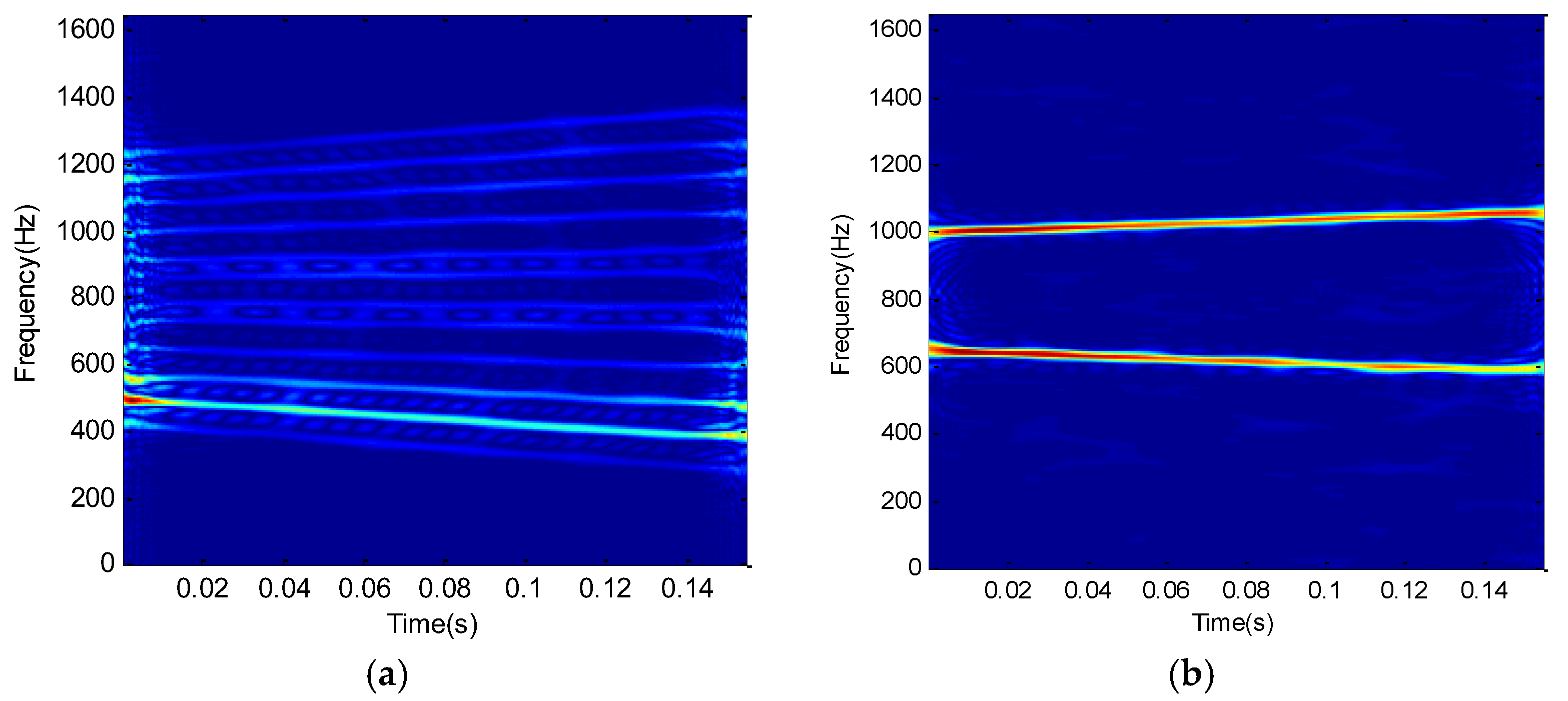
4.1. Feature of Azimuth Echo Signal
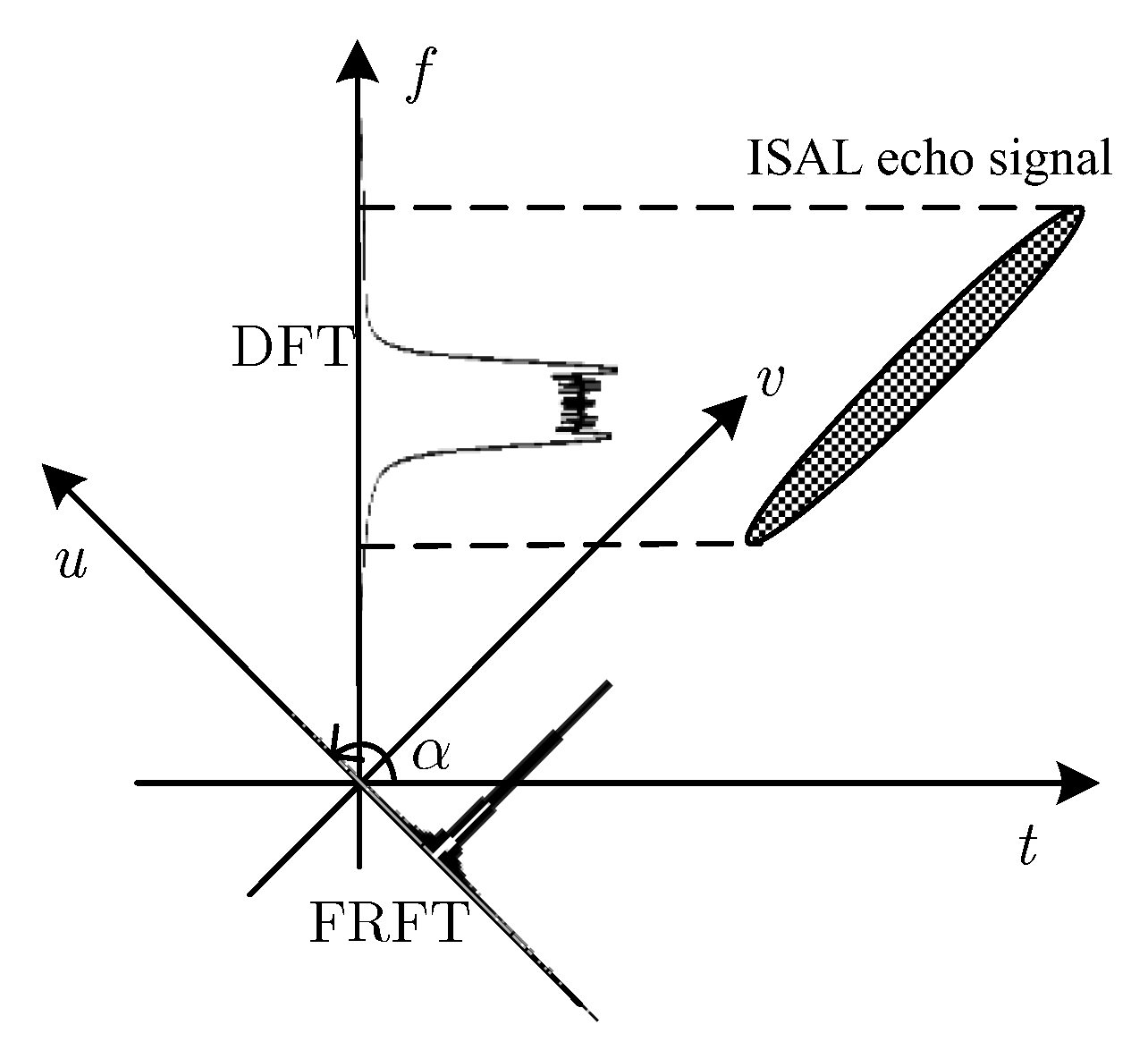
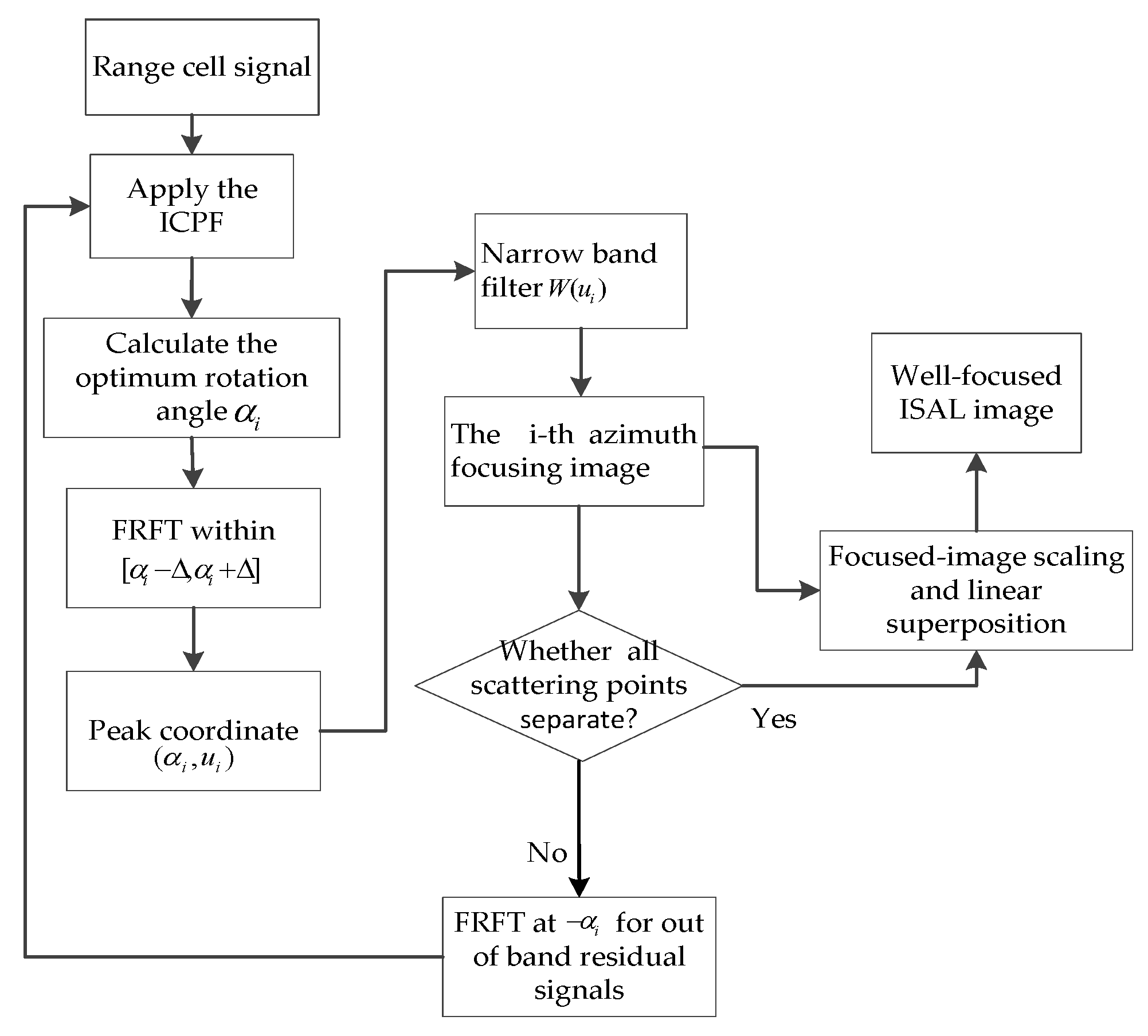
4.2. Azimuth Compression Based on ICPF-FRFT
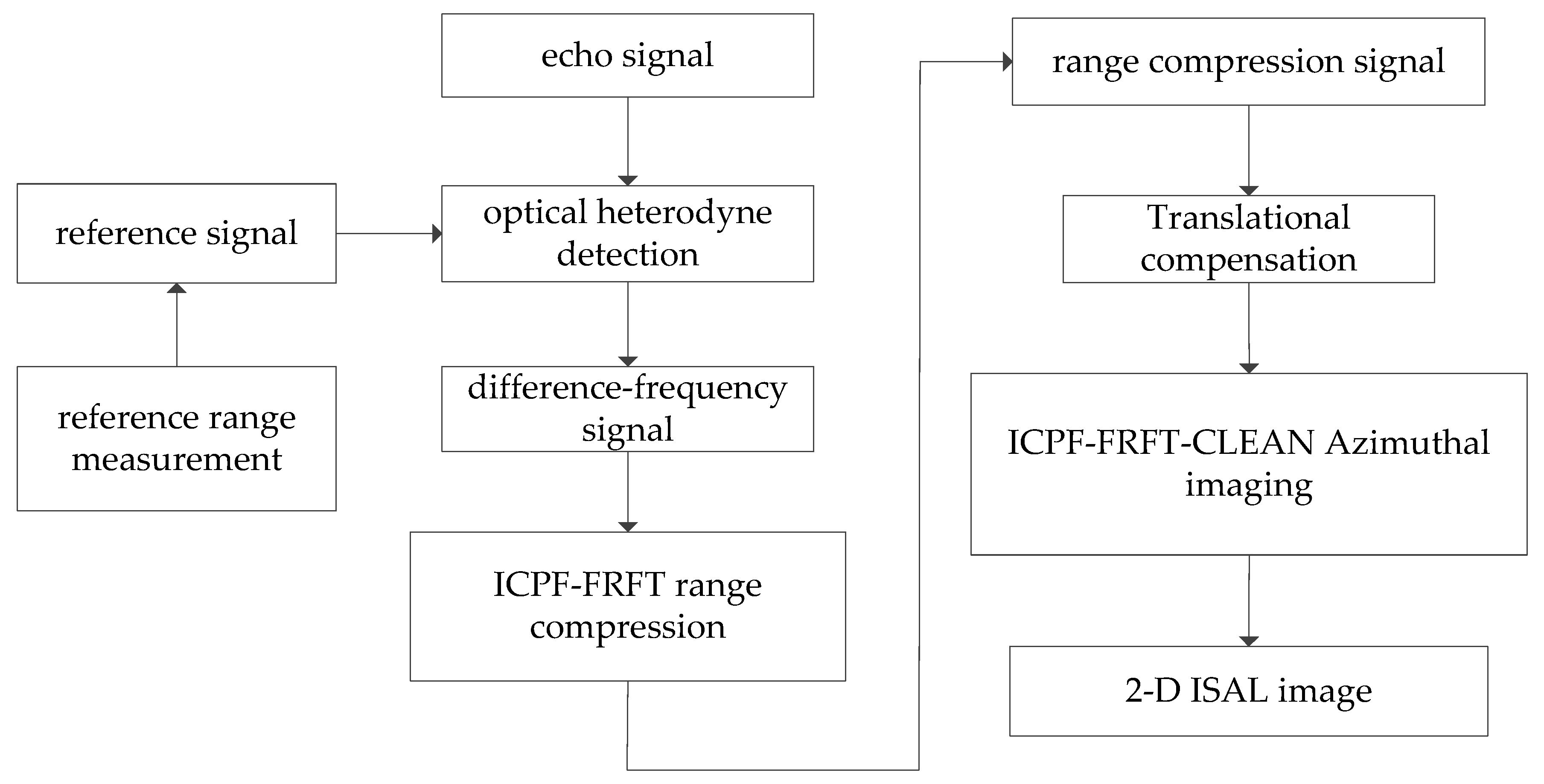
5. Imaging Procedure
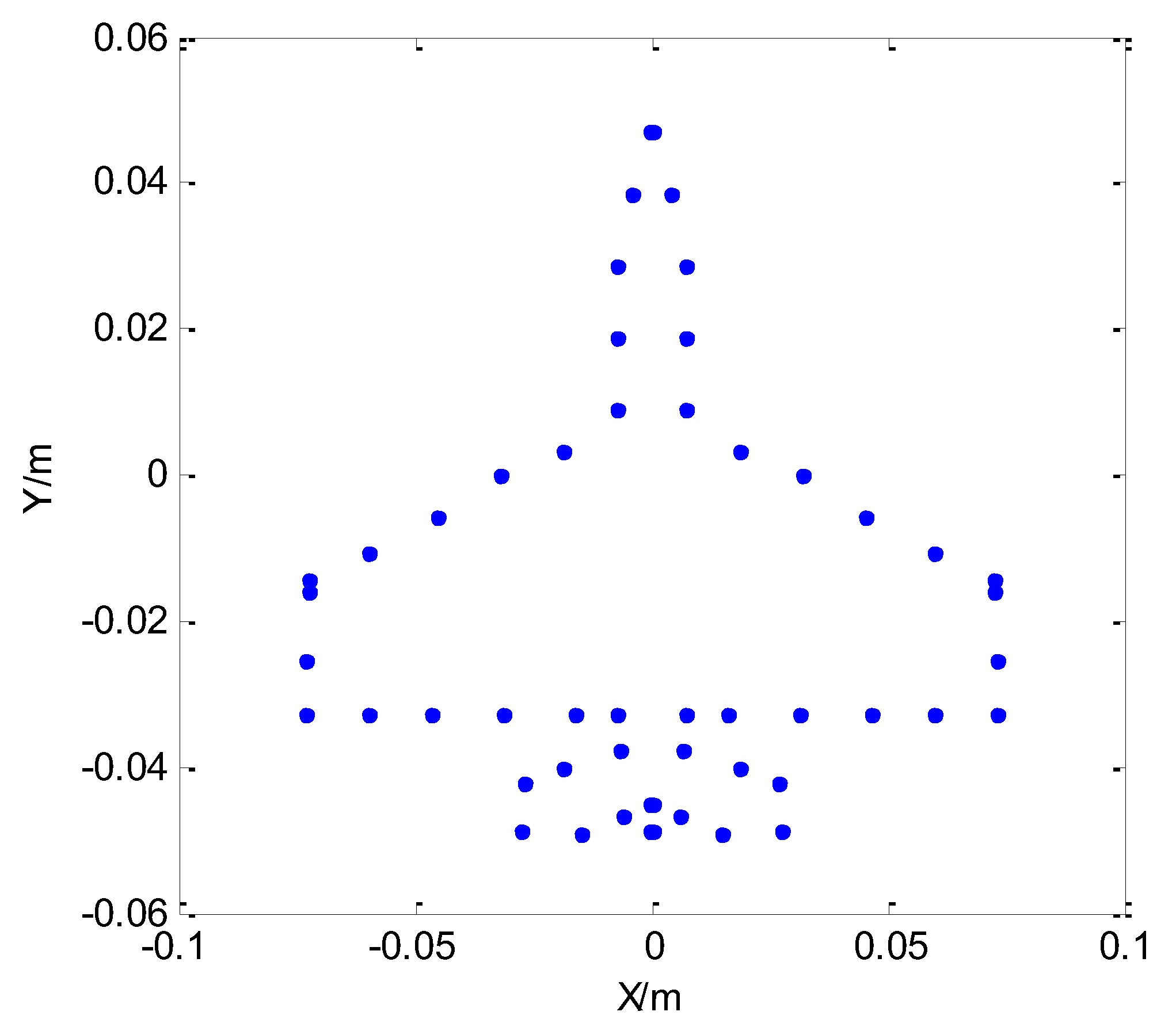
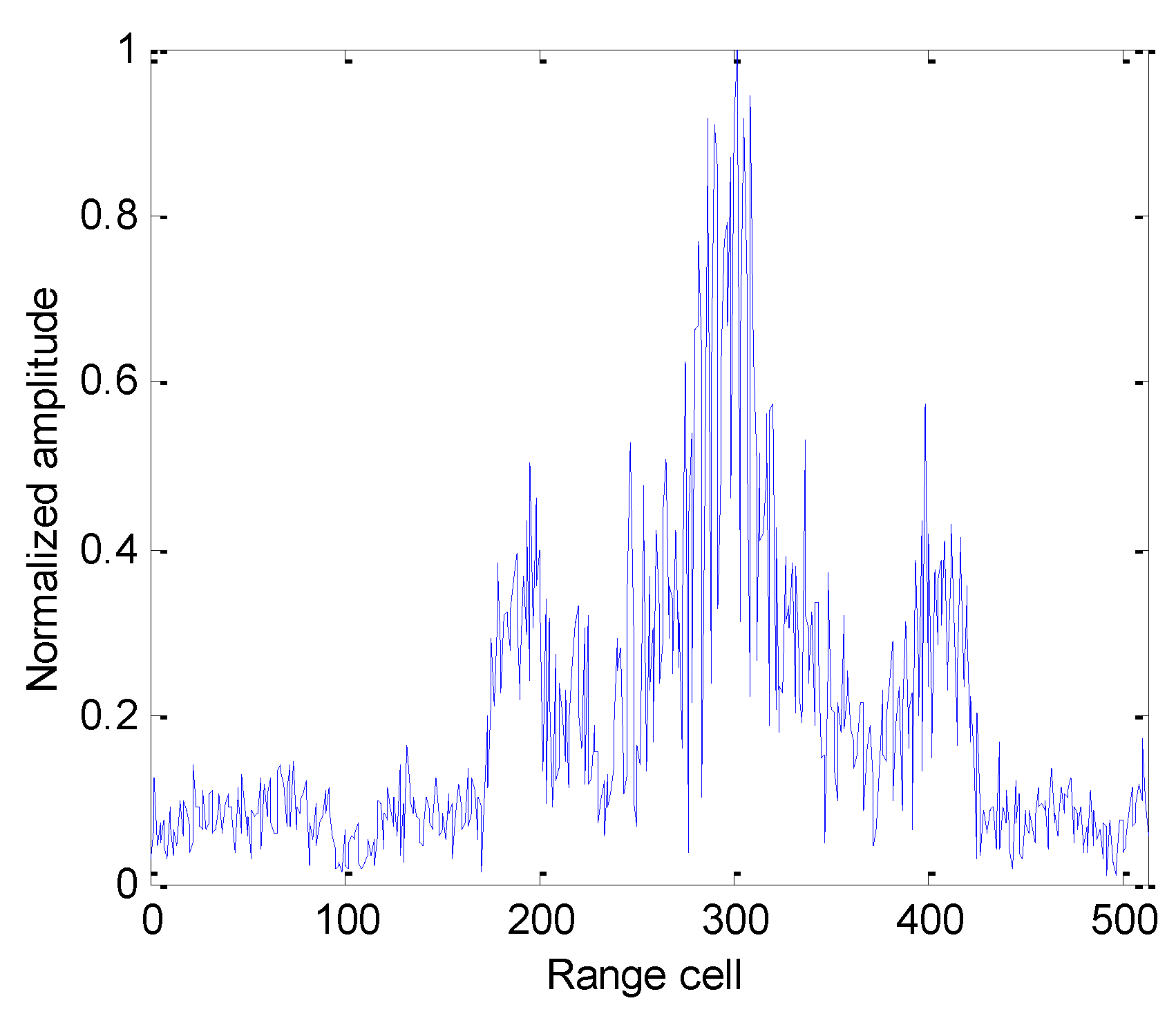
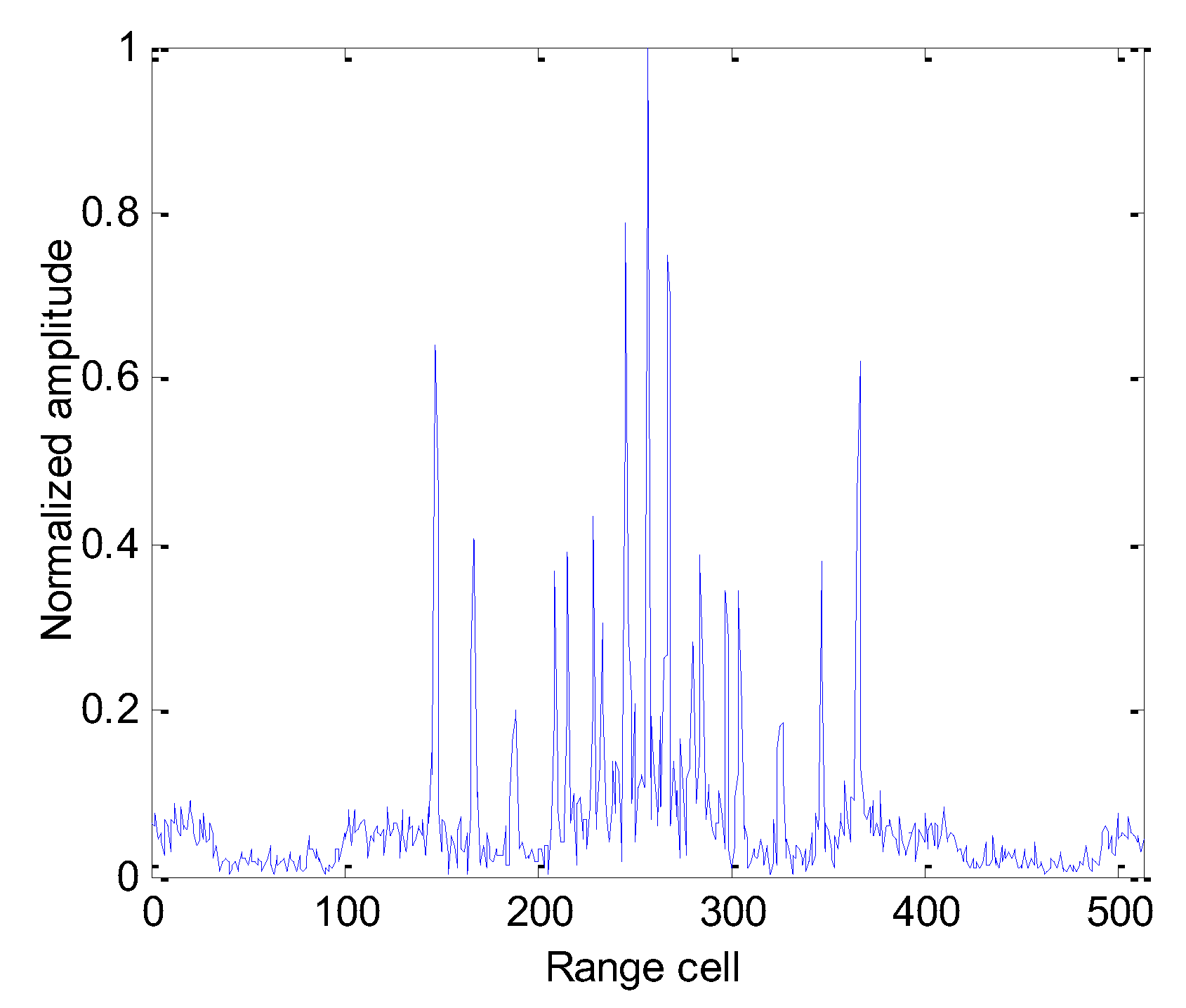
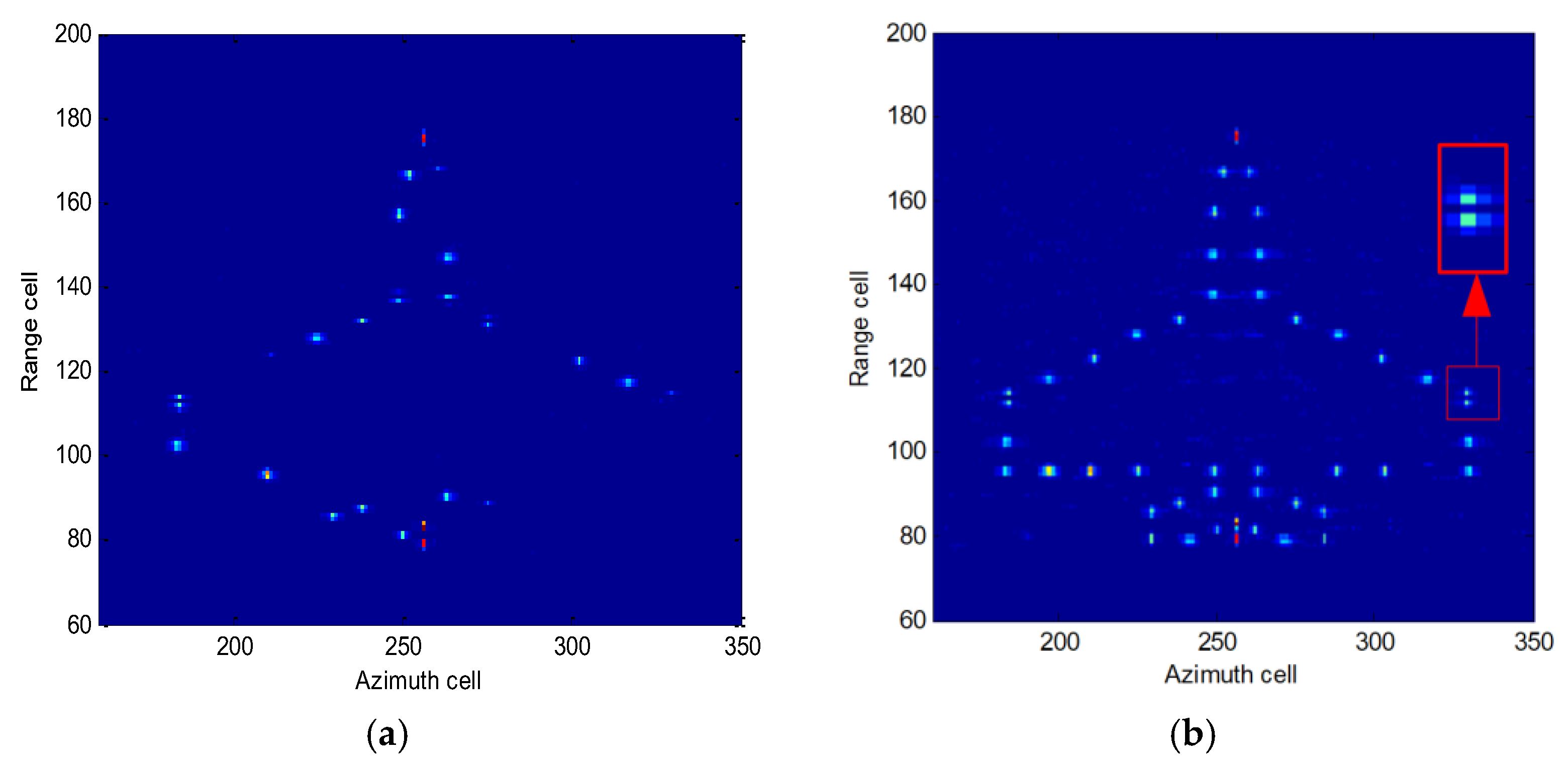
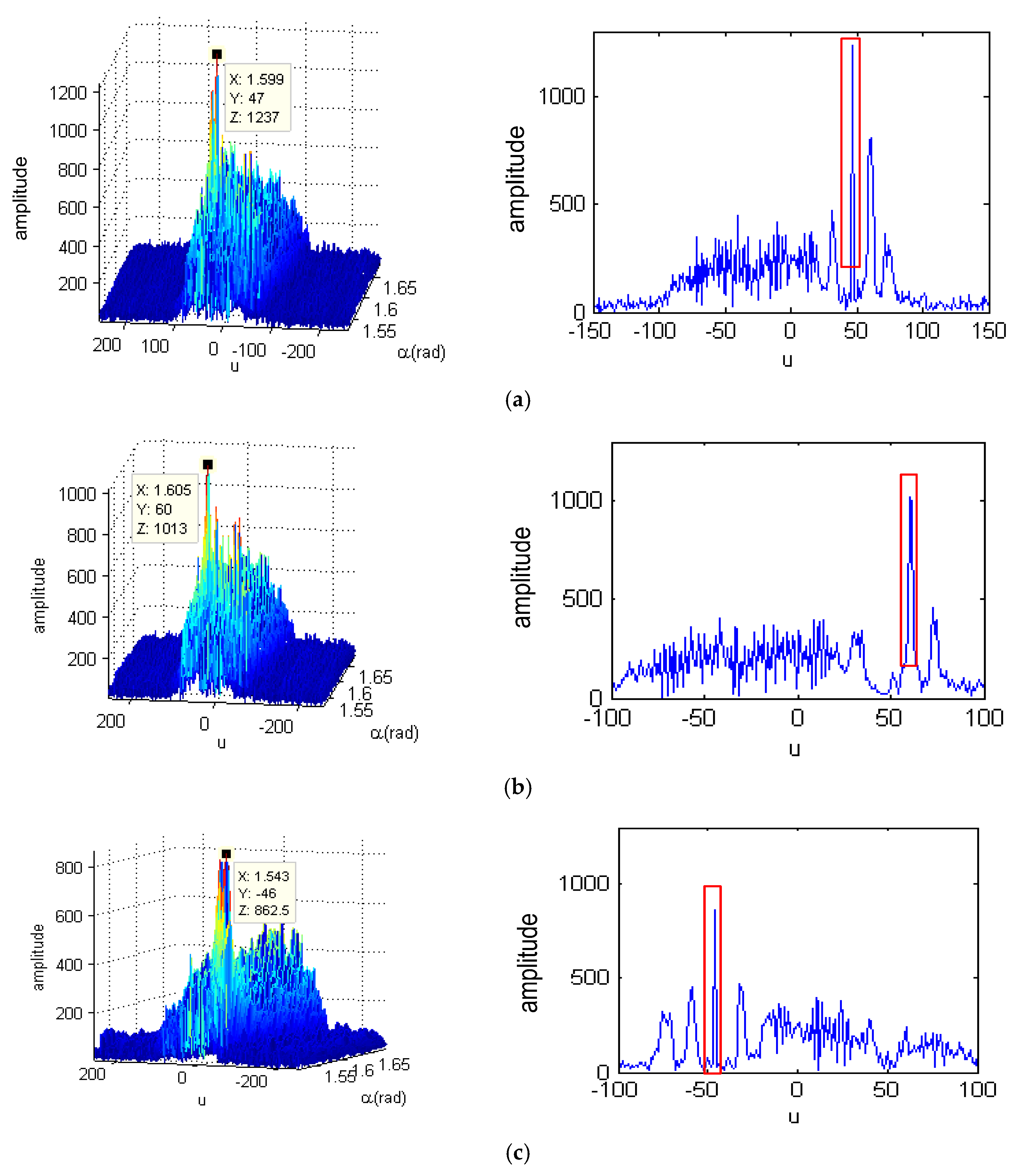
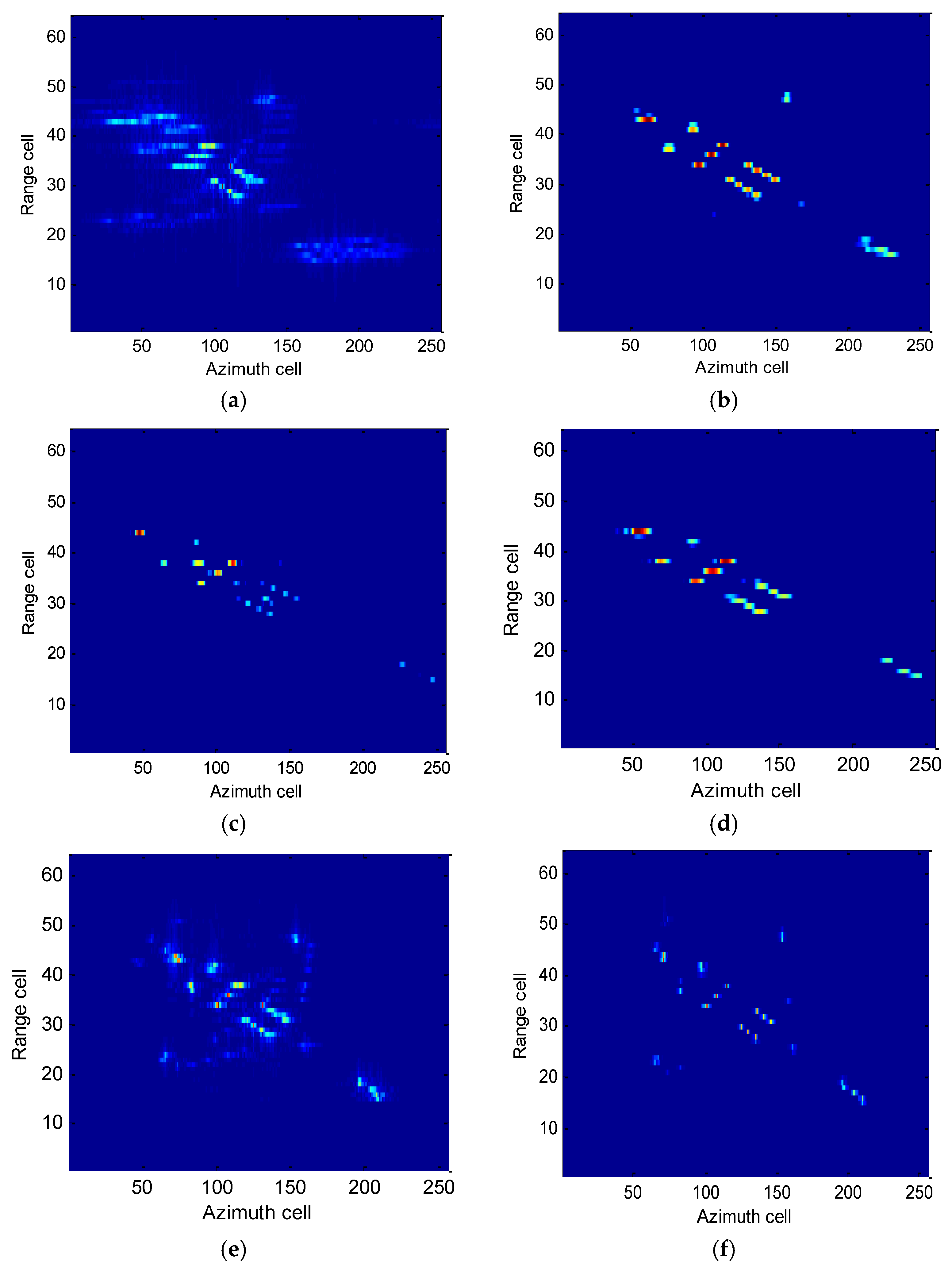
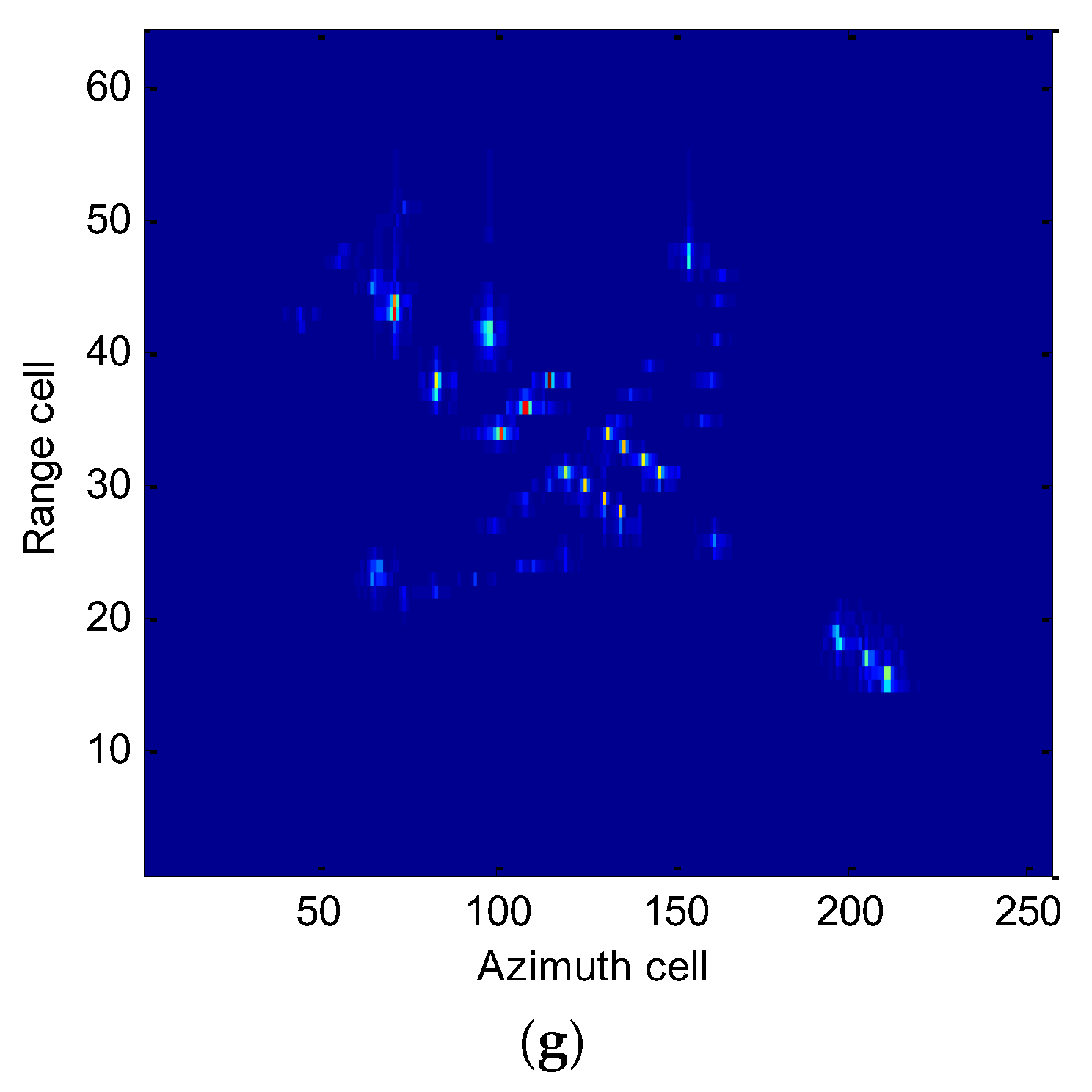
6. Experimental Results of Simulation and Real Data
6.1. Experimental Simulation Results
6.2. Experimental Results of Real Data
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, J.; Zhang, Q.; Yang, X.Y.; Luo, Y.; Zhu, X.P. High resolution imaging algorithm for inverse synthetic aperture imaging LADAR. Syst. Eng. Electron. 2011, 33, 1750–1755. [Google Scholar]
- Liu, L.R. Synthetic aperture laser imaging radar (I): Defocused and phase biased telescope for reception antenna. Acta Opt. Sin. 2008, 28, 997–1000. [Google Scholar]
- Beck, S.M.; Buck, J.R.; Buell, W.F.; Dickinson, R.P.; Kozlowski, D.A.; Marechal, N.J.; Wright, T.J. Synthetic-aperture imaging laser radar: Laboratory demonstration and signal processing. Appl. Opt. 2005, 44, 7621–7629. [Google Scholar] [CrossRef] [PubMed]
- Crouch, S.; Barber, Z.W. Laboratory demonstrations of interferometric and spotlight synthetic aperture ladar techniques. Opt. Express 2012, 20, 24237–24246. [Google Scholar] [CrossRef] [PubMed]
- Turbide, S.; Marchese, L.; Terroux, M.; Bergeron, A. Synthetic aperture ladar concept for infrastructure monitoring. In Electro-Optical Remote Sensing, Photonic Technologies and Applications VIII; and Military Applications in Hyperspectral Imaging and High Spatial Resolution Sensing II; International Society for Optics and Photonics: Bellingham, WA, USA, 2014. [Google Scholar]
- Barber, Z.W.; Dahl, J.R. Synthetic aperture ladar imaging demonstrations and information at very low return levels. Appl. Opt. 2014, 53, 5531–5537. [Google Scholar] [CrossRef] [PubMed]
- Trahan, R.; Nemati, B.; Zhou, H.; Shao, M.; Hann, I.; Schulze, W. Low-CNR inverse synthetic aperture LADAR imaging demonstration with atmospheric turbulence. In Long-Range Imaging; International Society for Optics and Photonics: Bellingham, WA, USA, 2016. [Google Scholar]
- Luan, Z.; Sun, J.; Zhou, Y.; Wang, L.; Yang, M.; Liu, L. Down-looking synthetic aperture imaging ladar demonstrator and its experiments over 1.2 km outdoor. Chin. Opt. Lett. 2014, 12, 111101. [Google Scholar] [CrossRef]
- Ikram, M.Z.; Abed-Meraim, K.; Hua, Y. Estimating the parameters of chirp signals: An iterative approach. IEEE Trans. Signal Process. 2002, 46, 3436–3441. [Google Scholar] [CrossRef]
- Barbarossa, S.; Scaglione, A.; Giannakis, G.B. Product high-order ambiguity function for multicomponent polynomial-phase signal modeling. IEEE Trans. Signal Process. 1998, 46, 691–708. [Google Scholar] [CrossRef]
- Xia, X.G. Discrete chirp-Fourier transform and its application to chirp rate estimation. IEEE Trans. Signal Process. 2000, 48, 3122–3133. [Google Scholar]
- Djurović, I.; Simeunović, M.; Wang, P. Cubic phase function: A simple solution to polynomial phase signal analysis. Signal Process. 2017, 135, 48–66. [Google Scholar] [CrossRef]
- Chen, V.C.; Miceli, W.J. Time-varying spectral analysis for radar imaging of maneuvering targets. IET Proc. Radar Sonar Navig. 1998, 145, 262–268. [Google Scholar] [CrossRef]
- Xing, M.D.; Wu, R.B.; Li, Y.C.; Bao, Z. New ISAR imaging algorithm based on modified Wigner Ville distribution. IET Proc. Radar Sonar Navig. 2009, 3, 70–80. [Google Scholar] [CrossRef]
- Trintinalia, L.; Ling, H. Joint time-frequency ISAR using adaptive processing. IEEE Trans. Antennas Propag. 1997, 45, 221–227. [Google Scholar] [CrossRef]
- Lao, G.; Yin, C.; Ye, W.; Sun, Y.; Li, G. A frequency domain extraction based adaptive joint time frequency decomposition method of the maneuvering target radar echo. Remote Sens. 2018, 10, 266. [Google Scholar] [CrossRef]
- Tao, R.; Deng, B.; Wang, Y. Research progress of the fractional Fourier transform in signal processing. Sci. China Inf. Sci. 2006, 49, 1–25. [Google Scholar] [CrossRef]
- Wang, B.; Xu, S.; Wu, W.; Hu, P.; Chen, Z. Adaptive ISAR imaging of maneuvering targets based on a modified Fourier transform. Sensors 2018, 18, 1370. [Google Scholar] [CrossRef] [PubMed]
- Attia, E.H. Data-adaptive motion compensation for synthetic aperture LADAR. In Proceedings of the 2004 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2004. [Google Scholar]
- Shapiro, J.H.; Capron, B.A.; Harney, R.C. Imaging and target detection with a heterodyne-reception optical radar. Appl. Opt. 1981, 20, 3292–3313. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Liu, Y.; Zhu, X. Parameters estimation of LFM signals by interpolation based on FRFT. Syst. Eng. Electron. 2011, 33, 2188–2193. [Google Scholar]
- O’Shea, P. A new technique for instantaneous frequency rate estimation. IEEE Signal Process. Lett. 2002, 9, 251–252. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Djurović, I.; Himed, B. Integrated cubic phase function for linear FM signal analysis. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 963–977. [Google Scholar] [CrossRef]
- Su, J.; Tao, H.; Xie, J.; Sun, Y.; Li, G. Imaging and Doppler parameter estimation for maneuvering target using axis mapping based coherently integrated cubic phase function. Digital Signal Process. 2018, 10, 266. [Google Scholar] [CrossRef]
- Li, H.; Qin, Y.L.; Li, Y.P.; Wang, H.Q.; Li, X. Analysis of multi-component LFM signals by the integrated quadratic phase function. J. Electron. Inf. Technol. 2012, 28, 926–931. [Google Scholar]
- Liu, Q.H.; Nguyen, N. An accurate algorithm for nonuniform fast Fourier transforms (NUFFT’s). IEEE Microw. Guided Wave Lett. 2002, 8, 18–20. [Google Scholar] [CrossRef]
- O’Shea, P. Improving polynomial phase parameter estimation by using nonuniformly spaced signal sample methods. IEEE Trans. Signal Process. 2012, 7, 3405–3414. [Google Scholar] [CrossRef]
- Xing, M.; Wu, R.; Lan, J.; Bao, Z. Migration through resolution cell compensation in ISAR imaging. IEEE Geosci. Remote Sens. Lett. 2004, 1, 141–144. [Google Scholar] [CrossRef]
- Simeunović, M.; Djurović, I. Non-uniform sampled cubic phase function. Signal Process. 2014, 101, 99–103. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Li, S.B. Inverse synthetic aperture radar imaging of ship targets with complex motion based on match Fourier transform for cubic chirps model. IET Radar Sonar Navig. 2013, 7, 994–1003. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Y. ISAR imaging of non-uniformly rotating target via range-instantaneous Doppler derivatives algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 167–176. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liu, Z.; Liu, Q.H. ISAR imaging of ship targets based on an integrated cubic phase bilinear autocorrelation function. Sensors 2017, 17, 498. [Google Scholar] [CrossRef] [PubMed]
- B727S.mat. Available online: https://www.mdpi.com/2072-4292/10/4/593/s1 (accessed on 12 April 2018).



| Radar Parameter | Value | Target Parameter | Value |
|---|---|---|---|
| Wavelength (μm) | 1.55 | Initial range (km) | 100 |
| bandwidth (Ghz) | 150 | Initial velocity (m/s) | 100 |
| Pulse width (μs) | 100 | Velocity acceleration (m/s2) | 30 |
| PRF () | 3.3 | Angular velocity (rad/s) | 0.005 |
| Range sampling number | 256 | Angular acceleration (rad/s2) | 0.01 |
| Pulse number | 512 | Angular acceleration rate (rad/s3) | 0.006 |
| Processing time (s) | 0.155 | - | - |
| Imaging Algorithm | RD | STFT | WVD | SPWVD | FRFT | No-CLEAN | ICPF-FRFT |
|---|---|---|---|---|---|---|---|
| Image entropy | 8.0546 | 9.2598 | 7.6822 | 6.0802 | 5.7540 | 4.1374 | 5.2629 |
| Contrast ratio | 1.6678 | 1.3632 | 3.4347 | 8.4177 | 10.8059 | 29.6294 | 13.0397 |
| Running time (s) | 0.2066 | 3.3042 | 4.9585 | 215.8427 | 77.0294 | 2.3453 | 3.8554 |
| Imaging Algorithm | RD | STFT | WVD | SPWVD | FRFT | No-CLEAN | ICPF-FRFT |
|---|---|---|---|---|---|---|---|
| Image entropy | 6.6428 | 6.1032 | 5.7609 | 4.8711 | 5.5242 | 3.9852 | 4.2940 |
| Contrast ratio | 2.3968 | 2.8949 | 3.6200 | 6.4915 | 4.8906 | 12.7516 | 7.5289 |
| Running time (s) | 0.0014 | 0.2350 | 0.4022 | 9.6358 | 24.0325 | 1.0412 | 1.2939 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Wu, Y.; Wang, H.; Qiu, L.; Jiang, J.; Sun, Y. An Inverse Synthetic Aperture Ladar Imaging Algorithm of Maneuvering Target Based on Integral Cubic Phase Function-Fractional Fourier Transform. Electronics 2018, 7, 148. https://doi.org/10.3390/electronics7080148
Lv Y, Wu Y, Wang H, Qiu L, Jiang J, Sun Y. An Inverse Synthetic Aperture Ladar Imaging Algorithm of Maneuvering Target Based on Integral Cubic Phase Function-Fractional Fourier Transform. Electronics. 2018; 7(8):148. https://doi.org/10.3390/electronics7080148
Chicago/Turabian StyleLv, Yakun, Yanhong Wu, Hongyan Wang, Lei Qiu, Jiawei Jiang, and Yang Sun. 2018. "An Inverse Synthetic Aperture Ladar Imaging Algorithm of Maneuvering Target Based on Integral Cubic Phase Function-Fractional Fourier Transform" Electronics 7, no. 8: 148. https://doi.org/10.3390/electronics7080148
APA StyleLv, Y., Wu, Y., Wang, H., Qiu, L., Jiang, J., & Sun, Y. (2018). An Inverse Synthetic Aperture Ladar Imaging Algorithm of Maneuvering Target Based on Integral Cubic Phase Function-Fractional Fourier Transform. Electronics, 7(8), 148. https://doi.org/10.3390/electronics7080148





