Precision Modeling: Application of Metaheuristics on Current–Voltage Curves of Superconducting Films
Abstract
1. Introduction
2. Related Work and Experimental Setup
2.1. Experimental Setup and Measurements Using PPMS
2.2. Approximation Using ANN
3. Problem Statement
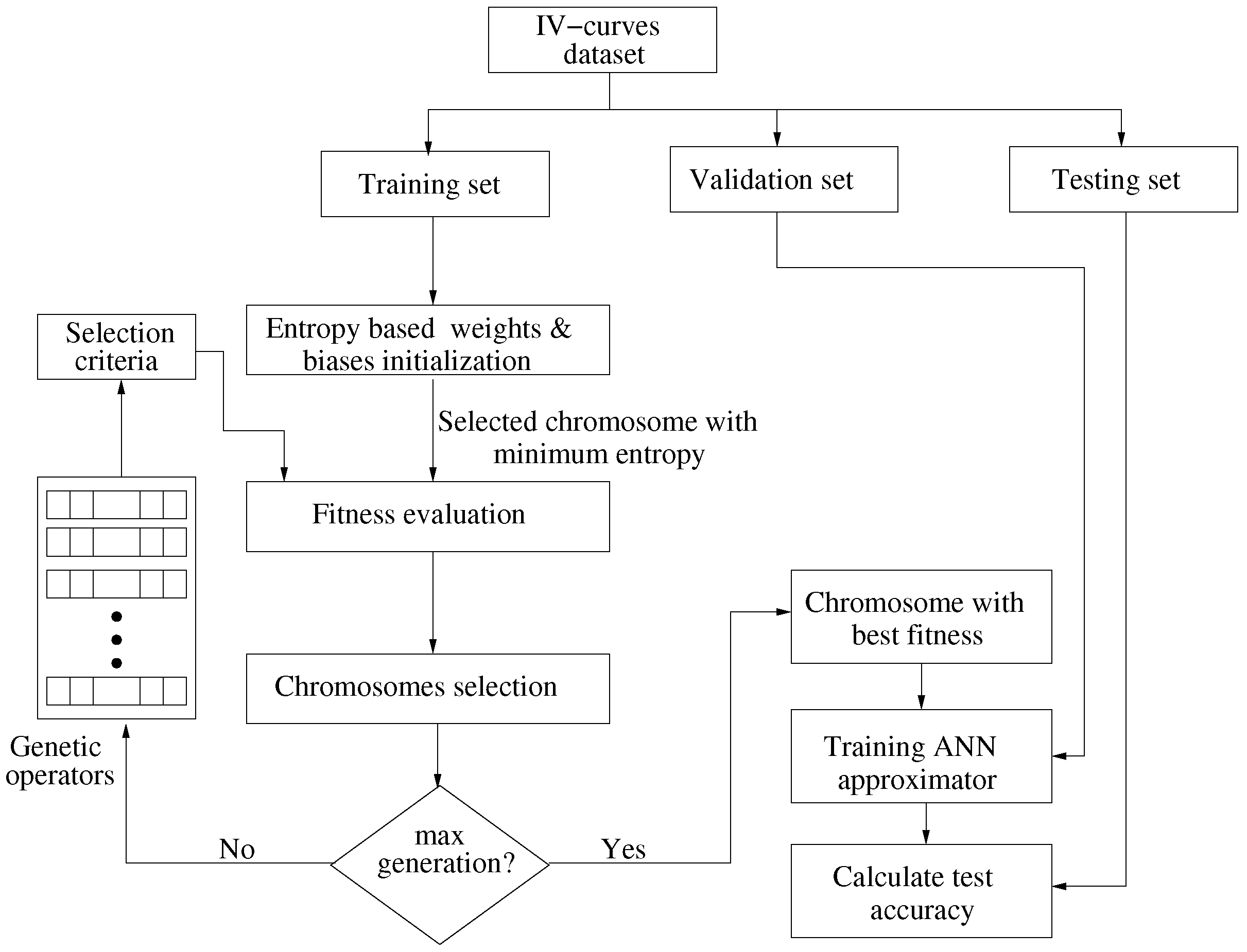
4. Proposed Optimization of ANN’s Coefficients
4.1. Genetic Algorithms
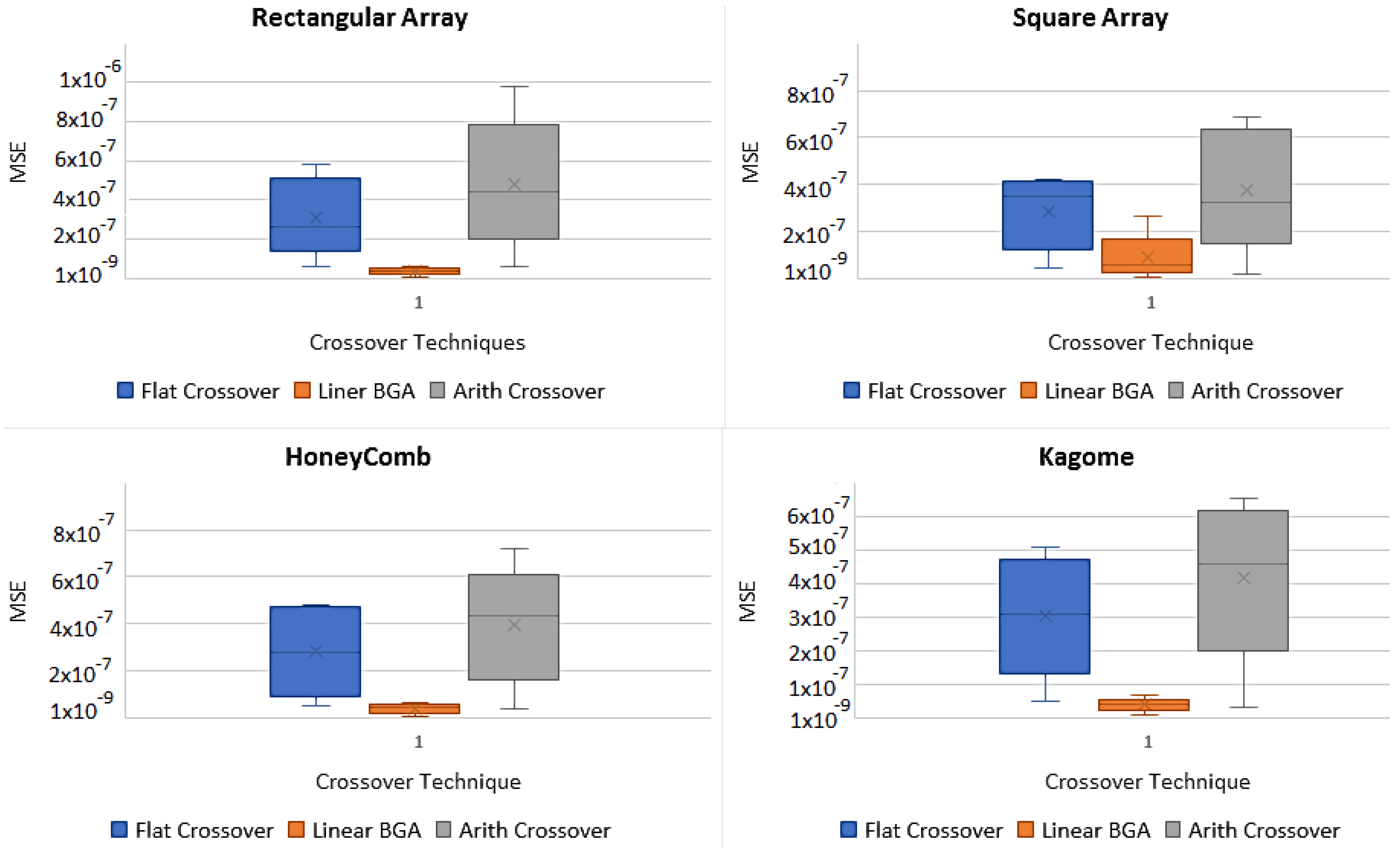
4.1.1. Crossover Operators
- Flat CrossoverAn offspring is generated where is a uniformly chosen random value from the intervalwhere m is the index for the number of genes and k is the index for the number of chromosomes.
- Linear Breeder Genetic Algorithm (BGA) CrossoverUnder the same consideration as above, let , where and . An is generated randomly with the probability of . Usually, and − sign is chosen with the probability of 0.8 [20].
- Arithmetic CrossoverIn arithmetic crossover, two Offsprings are generated, , where: and . Here, is a constant and user-defined value, which can vary with the number of generations.
4.1.2. Mutation Operator
4.1.3. Selection
4.1.4. Operation of a GA
- Create an initial population from a randomly generated weights and biases vector.
- Repeat until the best individuals are selected:
- Evaluate the fitness using MSE,
- Select the parents with best fitness level,
- Apply the selected crossover and mutation operators.
- Terminate upon convergence.
4.2. Entropy Based GA for Optimization
| Algorithm 1: Entropy based GA for weights and biases optimization |
 |
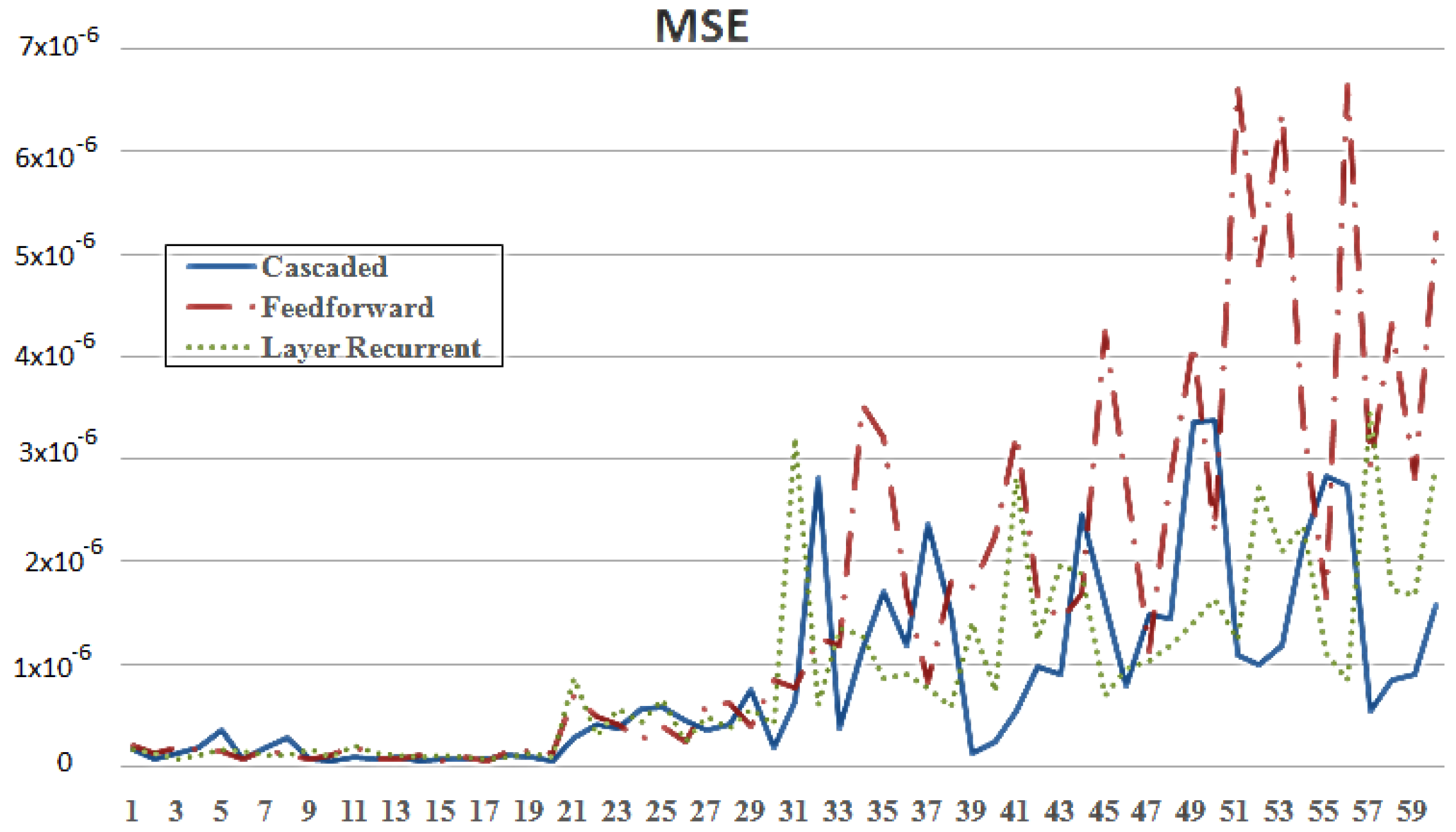
5. Simulation Results
5.1. Design Parameters
5.2. Results and Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| Set of real numbers | |
| Subset of features within | |
| Selected set of features | |
| Vector of predicted values | |
| Learning rate | |
| Step size | |
| Vector of weights and biases | |
| MSE constant | |
| Vector of entropy values | |
| Vector of optimized weights and biases | |
| Jacobian matrix | |
| I | Identity matrix |
| Error threshold | |
| Direction set variable | |
| Input vector | |
| Generated error | |
| Cost function based on mse | |
| Target vector | |
| Actual output vector | |
| Output layer transfer function | |
| Hidden layer transfer function | |
| Population size | |
| Offspring with maximum fitness | |
| kth chromosome | |
| kth gene | |
| Population selection rate | |
| Selected number of individuals in population |
References
- Acharya, S.; Bangera, K.V.; Shivakumar, G.K. Electrical characterization of vacuum-deposited p-CdTe/n-ZnSe heterojunctions. Appl. Nanosci. 2015, 5, 1003–1007. [Google Scholar] [CrossRef]
- Cleuziou, J.P.; Wernsdorfer, W.; Andergassen, S.; Florens, S.; Bouchiat, V.; Ondarçuhu, T.; Monthioux, M. Gate-tuned high frequency response of carbon nanotube Josephson junctions. Phys. Rev. Lett. 2007, 99, 117001. [Google Scholar] [CrossRef] [PubMed]
- Dinsmore, R.C., III; Bae, M.H.; Bezryadin, A. Fractional order Shapiro steps in superconducting nanowires. Appl. Phys. Lett. 2008, 93, 192505. [Google Scholar] [CrossRef]
- Mandal, S.; Naud, C.; Williams, O.A.; Bustarret, É.; Omnès, F.; Rodière, P.; Meunier, T.; Saminadayar, L.; Bäuerle, C. Detailed study of superconductivity in nanostructured nanocrystalline boron doped diamond thin films. Phys. Status Solidi 2010, 207, 2017–2022. [Google Scholar] [CrossRef]
- Kamran, M.; He, S.-K.; Zhang, W.-J.; Cao, W.-H.; Li, B.-H.; Kang, L.; Chen, J.; Wu, P.-H.; Qiu, X.-G. Matching effect in superconducting NbN thin film with a square lattice of holes. Chin. Phys. B 2009, 18, 4486. [Google Scholar] [CrossRef]
- Heiselberg, P. Shapiro steps in Josephson Junctions. Niels Bohr Institute, University of Copenhagen. 2013. Available online: https://cmt.nbi.ku.dk/student_projects/bsc/heiselberg.pdf (accessed on 13 July 2018).
- Sidorenko, A.; Zdravkov, V.; Ryazanov, V.; Horn, S.; Klimm, S.; Tidecks, R.; Wixforth, A.; Koch, T.; Schimmel, T. Thermally assisted flux flow in MgB2: Strong magnetic field dependence of the activation energy. Philos. Mag. 2005, 85, 1783–1790. [Google Scholar] [CrossRef]
- Fogel, N.Y.; Cherkasova, V.G.; Koretzkaya, O.A.; Sidorenko, A.S. Thermally assisted flux flow and melting transition for Mo/Si multilayers. Phys. Rev. B 1997, 55, 85. [Google Scholar] [CrossRef]
- Yu, C.C.; Chen, Y.T.; Wan, D.H.; Chen, H.L.; Ku, S.L.; Chou, Y.F. Using one-step, dual-side nanoimprint lithography to fabricate low-cost, highly flexible wave plates exhibiting broadband antireflection. J. Electrochem. Soc. 2011, 158, J195–J199. [Google Scholar] [CrossRef]
- Haider, S.A.; Naqvi, S.R.; Akram, T.; Kamran, M. Prediction of critical currents for a diluted square lattice using Artificial Neural Networks. Appl. Sci. 2017, 7, 238. [Google Scholar] [CrossRef]
- Haider, S.A.; Naqvi, S.R.; Akram, T.; Kamran, M.; Qadri, N.N. Modeling electrical properties for various geometries of antidots on a superconducting film. Appl. Nanosci. 2017, 7, 933–945. [Google Scholar] [CrossRef]
- Kamran, M.; Haider, S.A.; Akram, T.; Naqvi, S.R.; He, S.K. Prediction of IV curves for a superconducting thin film using artificial neural networks. Superlattices Microstruct. 2016, 95, 88–94. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Akram, T.; Haider, S.A.; Kamran, M. Artificial neural networks based dynamic priority arbitration for asynchronous flow control. Neural Comput. Appl. 2016, 29, 627–637. [Google Scholar] [CrossRef]
- Güçlü, U.; van Gerven, M.A. Deep neural networks reveal a gradient in the complexity of neural representations across the ventral stream. J. Neurosci. 2015, 35, 10005–10014. [Google Scholar] [CrossRef] [PubMed]
- Haykin, S. Neural Networks and Learning Machines; Pearson: Upper Saddle River, NJ, USA, 2009; Volume 3. [Google Scholar]
- Zermeño, V.; Sirois, F.; Takayasu, M.; Vojenciak, M.; Kario, A.; Grilli, F. A self-consistent model for estimating the critical current of superconducting devices. Supercond. Sci. Technol. 2015, 28, 085004. [Google Scholar] [CrossRef]
- Bonanno, F.; Capizzi, G.; Graditi, G.; Napoli, C.; Tina, G.M. A radial basis function neural network based approach for the electrical characteristics estimation of a photovoltaic module. Appl. Energy 2012, 97, 956–961. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Akram, T.; Iqbal, S.; Haider, S.A.; Kamran, M.; Muhammad, N. A dynamically reconfigurable logic cell: From artificial neural networks to quantum-dot cellular automata. Appl. Nanosci. 2018, 8, 89–103. [Google Scholar] [CrossRef]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; Wiley: New York, NY, USA, 1998; Volume 2. [Google Scholar]
- Herrera, F.; Lozano, M.; Sánchez, A.M. A taxonomy for the crossover operator for real-coded genetic algorithms: An experimental study. Int. J. Intell. Syst. 2003, 18, 309–338. [Google Scholar] [CrossRef]
- Razali, N.M.; Geraghty, J. Genetic algorithm performance with different selection strategies in solving TSP. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011; International Association of Engineers: Hong Kong, China, 2011; Volume 2, pp. 1134–1139. [Google Scholar]
- Mc Ginley, B.; Maher, J.; O’Riordan, C.; Morgan, F. Maintaining healthy population diversity using adaptive crossover, mutation, and selection. IEEE Trans. Evol. Comput. 2011, 15, 692–714. [Google Scholar] [CrossRef]



| Algo. | Crossover | Epochs | MSE | Crossover | Epochs | MSE | Crossover | Epochs | MSE |
|---|---|---|---|---|---|---|---|---|---|
| LM | Flat | 89 | 5.87 | Linear-BGA | 17 | 3.55 | Arithmetic | 136 | 5.87 |
| CGF | 205 | 4.41 | 292 | 3.16 | 181 | 3.42 | |||
| CGB | 784 | 2.12 | 210 | 4.79 | 331 | 9.80 | |||
| CGP | 93 | 2.60 | 394 | 6.08 | 139 | 4.41 | |||
| Bayesian | 49 | 5.84 | 42 | 7.50 | 107 | 6.24 | |||
| (a) Square Lattice | |||||||||
| LM | Flat | 79 | 4.11 | Linear-BGA | 39 | 2.67 | Arithmetic | 101 | 3.24 |
| CGF | 190 | 4.20 | 179 | 4.66 | 199 | 2.79 | |||
| CGB | 650 | 3.47 | 265 | 5.61 | 387 | 6.91 | |||
| CGP | 110 | 1.97 | 164 | 7.21 | 170 | 5.76 | |||
| Bayesian | 59 | 4.37 | 47 | 6.89 | 83 | 1.90 | |||
| (b) Rectangular Lattice | |||||||||
| LM | Flat | 94 | 4.74 | Linear-BGA | 25 | 3.21 | Arithmetic | 121 | 4.33 |
| CGF | 220 | 4.78 | 193 | 4.61 | 174 | 2.90 | |||
| CGB | 694 | 2.76 | 235 | 4.71 | 357 | 7.21 | |||
| CGP | 101 | 1.34 | 271 | 6.37 | 157 | 4.99 | |||
| Bayesian | 62 | 4.76 | 41 | 7.10 | 91 | 3.56 | |||
| (c) Honeycomb Lattice | |||||||||
| LM | Flat | 87 | 5.11 | Linear-BGA | 31 | 3.66 | Arithmetic | 132 | 5.81 |
| CGF | 187 | 4.36 | 216 | 4.12 | 177 | 3.66 | |||
| CGB | 733 | 3.08 | 213 | 4.53 | 358 | 6.54 | |||
| CGP | 113 | 2.11 | 308 | 6.88 | 151 | 4.61 | |||
| Bayesian | 54 | 4.89 | 36 | 8.87 | 83 | 3.11 | |||
| (d) Kagome Lattice | |||||||||
| Geometry | Training Algorithm | Epochs | MSE | ||||
|---|---|---|---|---|---|---|---|
| LM | CGF | CGB | CGP | BR | |||
| Square | ✓ | 30 | |||||
| ✓ | 591 | ||||||
| ✓ | 252 | ||||||
| ✓ | 322 | ||||||
| ✓ | 55 | ||||||
| Rectangular | ✓ | 39 | |||||
| ✓ | 478 | ||||||
| ✓ | 767 | ||||||
| ✓ | 388 | ||||||
| ✓ | 69 | ||||||
| HoneyComb | ✓ | 54 | |||||
| ✓ | 634 | ||||||
| ✓ | 276 | ||||||
| ✓ | 376 | ||||||
| ✓ | 67 | ||||||
| Kagome | ✓ | 43 | |||||
| ✓ | 476 | ||||||
| ✓ | 291 | ||||||
| ✓ | 463 | ||||||
| ✓ | 79 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naqvi, S.R.; Akram, T.; Haider, S.A.; Kamran, M.; Shahzad, A.; Khan, W.; Iqbal, T.; Umer, H.G. Precision Modeling: Application of Metaheuristics on Current–Voltage Curves of Superconducting Films. Electronics 2018, 7, 138. https://doi.org/10.3390/electronics7080138
Naqvi SR, Akram T, Haider SA, Kamran M, Shahzad A, Khan W, Iqbal T, Umer HG. Precision Modeling: Application of Metaheuristics on Current–Voltage Curves of Superconducting Films. Electronics. 2018; 7(8):138. https://doi.org/10.3390/electronics7080138
Chicago/Turabian StyleNaqvi, Syed Rameez, Tallha Akram, Sajjad Ali Haider, Muhammad Kamran, Aamir Shahzad, Wilayat Khan, Tassawar Iqbal, and Hafiz Gulfam Umer. 2018. "Precision Modeling: Application of Metaheuristics on Current–Voltage Curves of Superconducting Films" Electronics 7, no. 8: 138. https://doi.org/10.3390/electronics7080138
APA StyleNaqvi, S. R., Akram, T., Haider, S. A., Kamran, M., Shahzad, A., Khan, W., Iqbal, T., & Umer, H. G. (2018). Precision Modeling: Application of Metaheuristics on Current–Voltage Curves of Superconducting Films. Electronics, 7(8), 138. https://doi.org/10.3390/electronics7080138





