1. Introduction
Wind energy is recognized as one of the most promising technology for the effective implementation of modern sustainable energy policies. Unfortunately, the massive penetration of wind generators in existing electric grids caused several side-effects, which determines the need for improving the robustness of system control and protection functions, mitigating the impacts of the large uncertainties induced by the intermittent and not-programmable nature of the wind power profiles [
1]. To address this issue, the combination of effective wind forecasting tools and reliable generator models, implemented by knowledge discovering from experimental data streaming, represents one of the most promising enabling methodology, especially in assessing the impacts of wind power profiles on power system security and spinning reserve optimization [
2,
3], and in enhancing asset maintenance [
3] and optimal bidding in electrical markets [
4,
5].
The simplest solution methodology that could be adopted to solve these problems is based on the deployment of average models, which can be identified by curve-fitting of experimental data according to the procedure described in the IEC-61400-12 standard [
6]. These first-order models allow the assessment of wind power production as a function of a limited number of observable variables, mainly the wind speed, and are characterized by a low level of accuracy, since they are not able to take into account several important features characterizing the real generator operation. Hence, their application is typically restricted to a limited number of applications, which only require rough wind estimations, such as optimal sizing of wind farms and long-term wind energy assessment analysis [
7].
To improve the estimation accuracy, more sophisticated data-driven techniques, including deterministic, parametric, and probabilistic models, could be employed. Deterministic models subdivide the power curve of a wind generator in a proper number of wind speed classes, identifying, for each of them, a regressive model relating the measured power output and the corresponding wind speed. In particular, cubic regressive models parametrized on four wind speed classes, are typically employed for the analysis of large wind generators [
8]. Although these modeling approaches allows improving the modeling accuracy, they lack in describing the influence of several variables on the wind power profiles, such as air density and wind direction. These second-order effects can be taken into account by using parametric models, which are aimed at describing the impacts of a finite set of environmental variables on the generated power profiles by means of empirical equations, whose parameters are calibrated on the basis of measured data [
9]. Despite this adaptive feature, parametric models are not able to manage the intrinsic uncertainties affecting the measured variables, which can sensibly compromise the model performances, especially in the presence of severe environmental conditions.
To address this issue, probabilistic models, which aim at characterizing the stochastic nature of the measured data, can be adopted [
10,
11]. These modeling techniques, if integrated with multivariate regression algorithms relating the generated power to the wind turbine parameters [
9], could effectively support several important operation functions, such as on-line condition monitoring which allows monitoring the wind generators performances by detecting under-performance or faults [
12] and identifying the corresponding driving factors [
13].
Anyway, it is worth nothing that the modeling accuracy of data-driven techniques strictly depends by the consistency of the experimental data adopted to tune the models, which are collected by Supervisory Control And Data Acquisition systems, and could be affected by strong uncertainties, especially in harsh environmental condition [
7]. These uncertainties could sensibly compromise the model performances by generating incoherent or anomalous data, which mainly derive from sensor faults, measurement errors and electronic noise. In particular, the latter needs dedicates procedures for reducing the transmission error, such as done by authors of [
14] where intelligent segmentation techniques for reducing big data and reexamination of transmission protocols have been proposed.
Hence, in these operation scenarios, the probability of acquiring incorrect or anomalous data is notable and the development of advanced tools for removing these data from the ‘valid’ training set is strictly required.
To address this problem, the authors of [
15] propose an iterative technique for validity check, data scaling, missing data processing and lag removal steps of experimental wind data, which are then adopted to train an artificial neural network for on-line condition monitoring. Anyway, the application of this deterministic approach has been applied only to specific generator components data, i.e., relating to shaft and bearing, and its effectiveness in filtering other kinds of data, i.e., wind speed and power output, needs to be comprehensively assessed. This issue has been addressed in [
16], which proposes a deterministic filter technique for outliers detection in wind speed data, employing the obtained data for designing a wind power forecasting module based on a probabilistic neural network. Similarly, the detection of outliers can be addressed by using the ontology approach for managing information in big data as proposed by [
17], where this method allows management of the off shore wind farm data by building a hierarchical classification, from which it is possible to compute several derived quantities in order to make a comparison with the measured outliers by starting from the others available measured data through applying known mathematical relations.
Starting from these results, in [
18] an empirical methodology aimed at detecting anomalies in aggregate wind speed data has been proposed. Although this technique allows the detection and classification of local outlier factors, showing interesting results in several case studies [
19], its application is typically restricted to wind power forecasting since it does not allow to model the operation states of both the electrical grid (i.e., network congestions) and the wind turbine (i.e., derated/fault), which are required in on-line condition monitoring applications.
In trying to address this issue, the most promising enabling methodologies recently explored in the literature are based on probabilistic-based techniques, which aim at effectively detecting bad-data [
20], and data clustering analysis, which allows the exploration of data correlations by defining proper similarity measures [
21], confirm the well proved effectiveness of the applications clustering-based in wide and complex systems, such as the smart grids for acting policies of dynamic energy management as well summarized in [
22].
Although the application of these methodologies has been tested on several case studies, their large-scale deployment in real operation scenarios is still at its infancy, and more works should be done in order to improve their integration, and extensively validate their performance on real and complex case studies.
This paper intends to fill this gap by proposing a novel processing paradigm based on the integration of bad-data detection techniques and unsupervised clustering analysis for on-line detection of incoherent and anomalous data from a large database of wind data, and identification of a set of multivariate regression models relating the generated power to the measured variables. The main idea is to combine the robustness of adaptive filtering algorithms, which have proved their effectiveness in power system state estimation, with the data classification capability of fuzzy data clustering, which has been extensively applied in the task of solving complex multivariate modeling problems.
Detailed experimental results obtained on a real case study is presented and discussed in order to demonstrate the effectiveness of the proposed technique for on-line wind generators modeling.
2. Proposed Methodology
This paper proposes a processing technique for filtering experimental data by combining bad-data detection techniques with fuzzy cluster analysis, according to the processing architecture schematically depicted in
Figure 1.
By analyzing this figure it is worth nothing that the first module aims at identifying the set of data that are coherent with the properties of the rated power curve, described by the matrix
, with dimensions
, where I is the number of recorded measurements. Then, a polynomial regressive model is identified by fitting the rated wind generator data. This benchmark model is formalized in Equation (
1), where
,
,
are the cut-in, rated and cut-off speeds, respectively
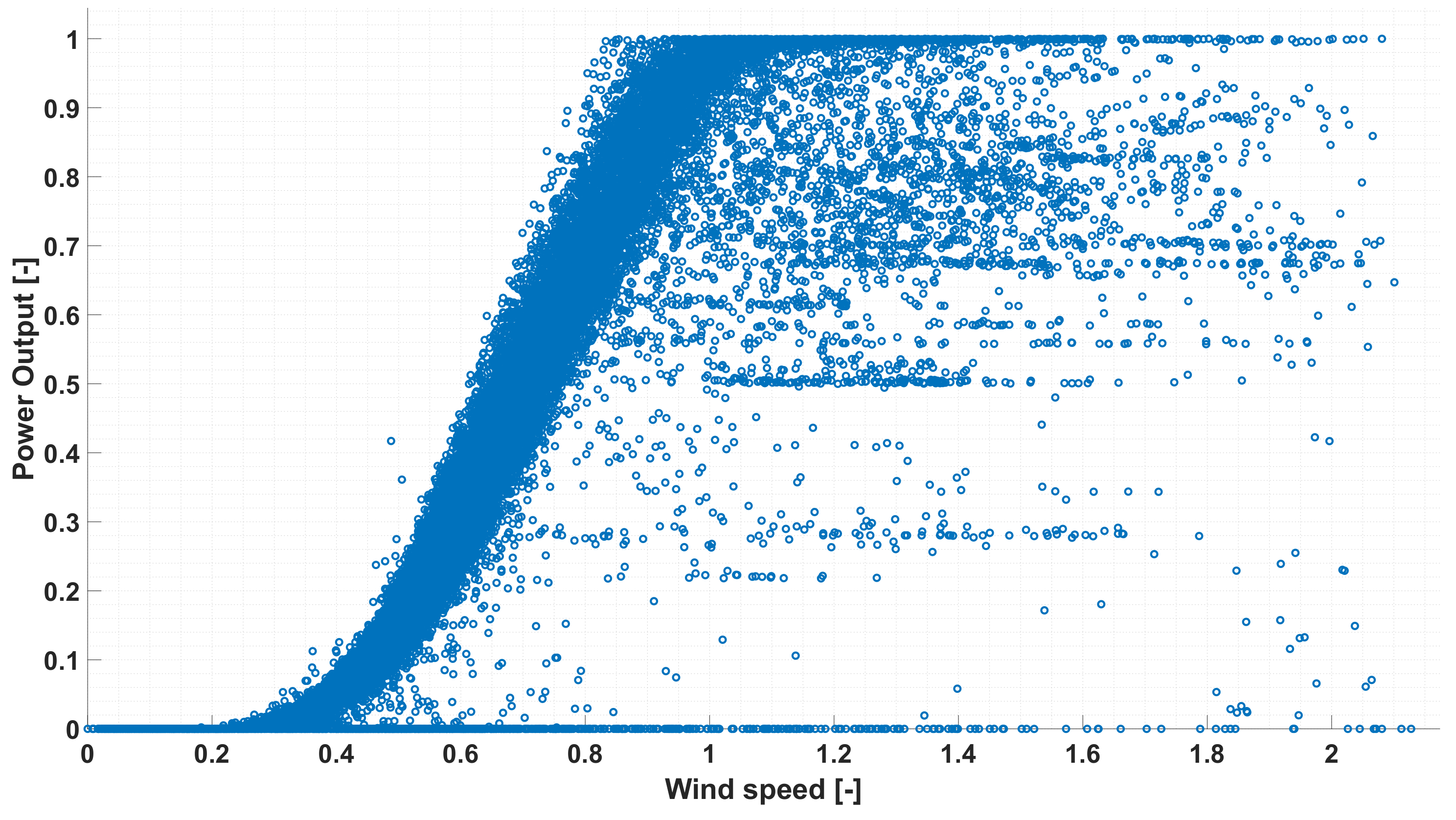
This regressive model allows filtering the elements of the matrix
, which are shown in
Figure 2, by detecting the measured data exceeding a fixed confidence interval. This interval has been identified by estimating, for each wind speed value included in the
matrix, the power computed by the model
1, considering the corresponding ratio between the rated and the estimated power, as shown in Equation (
2), where
is a heuristic coefficient identified by sensitivity analysis. After this process, the
matrix can be filtered as shown in Algorithm 1, hence obtaining the matrices
, whose dimensions are
with
, and
, whose dimensions are
with
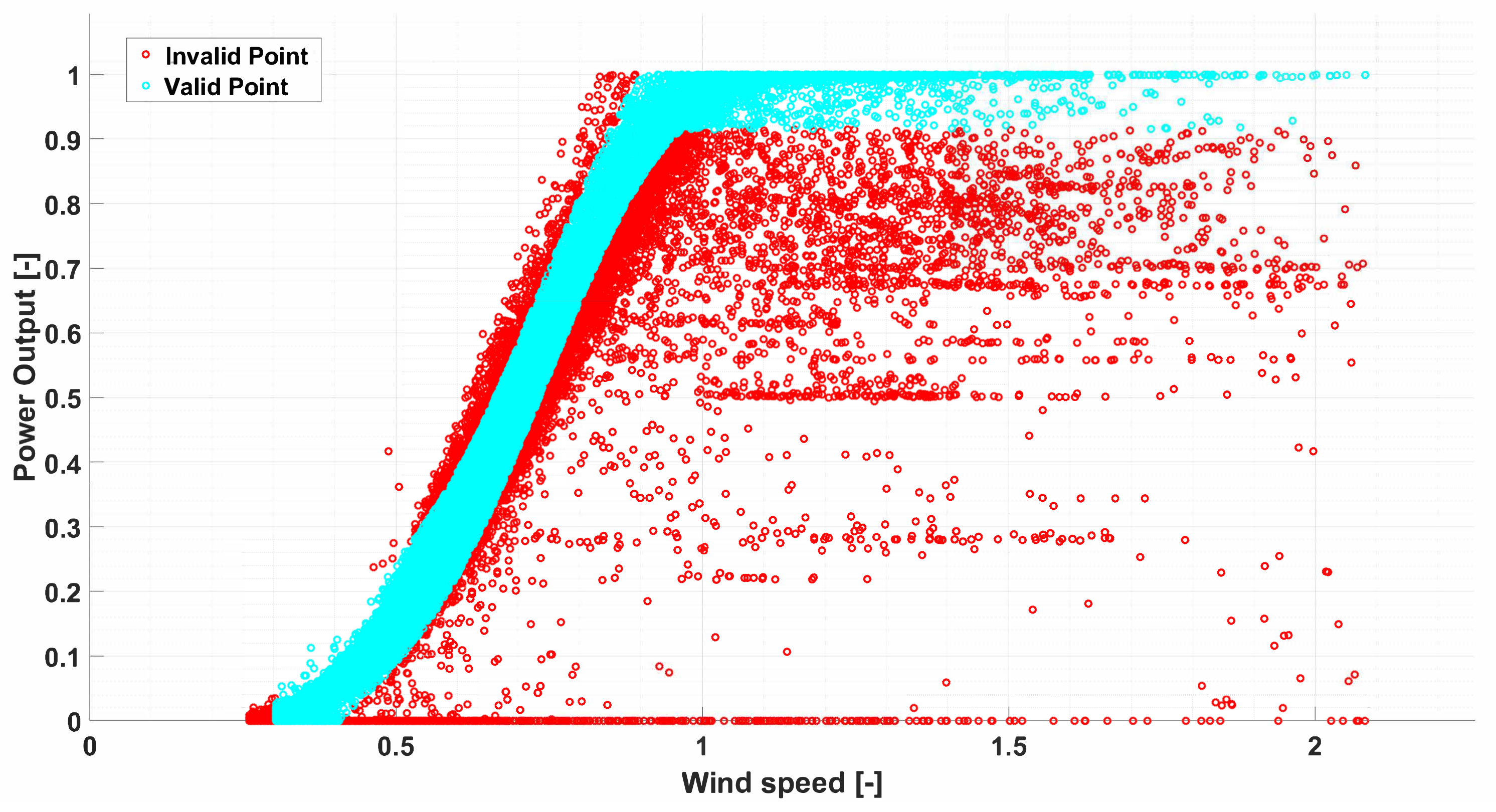
, which represent the matrices of the valid and invalid data, respectively, as shown in
Figure 3.
| Algorithm 1 Adding valid objects to |
| 1: | for , R do | |
| 2: | if then | |
| 3: | | ▹ is joined to |
| 4: | else | |
| 5: | | ▹ is joined to |
After this filtering process, the invalid data set is analyzed in order to detect operation data potentially referring to power derating states. This is obtained by deploying a fuzzy clustering technique [
23], which aims at classifying the data on the basis of their level of similarity.
More specifically, in order to identify the operation points corresponding to partial load operation, a Fuzzy C-Means (FCM) method-based has been employed to classify the matrix , with dimensions and a function of the measured wind speed and generated power. The main feature of FCM, which is particularly useful in solving this problem, is that it does not uniquely assign a member to a group, but a membership degree to each member for every groups between 0 and 1, which represents the corresponding probability to belong to each cluster.
Unfortunately, the technique does not compute the number of clusters, but this has been fixed by the Analyst. In this study the optimal number of partitions, whom number will be defined as
, has been calculated by applying the Calinski-Harabasz Criterion [
24] to the
matrix. According to this method, the optimal cluster numbers is identified by iteratively partitioning the elements of
minimizing the following objective function:
where
is the sum of squared error,
and
are the membership and cluster centers matrices, respectively, and
is the norm between the point
, which has components
and the center
of
sth cluster and
is the generic element of matrix
. Hence, the results of the application of the Fuzzy C-means method are the matrices
, where
s is the a
sth cluster of the
assigned as shown in
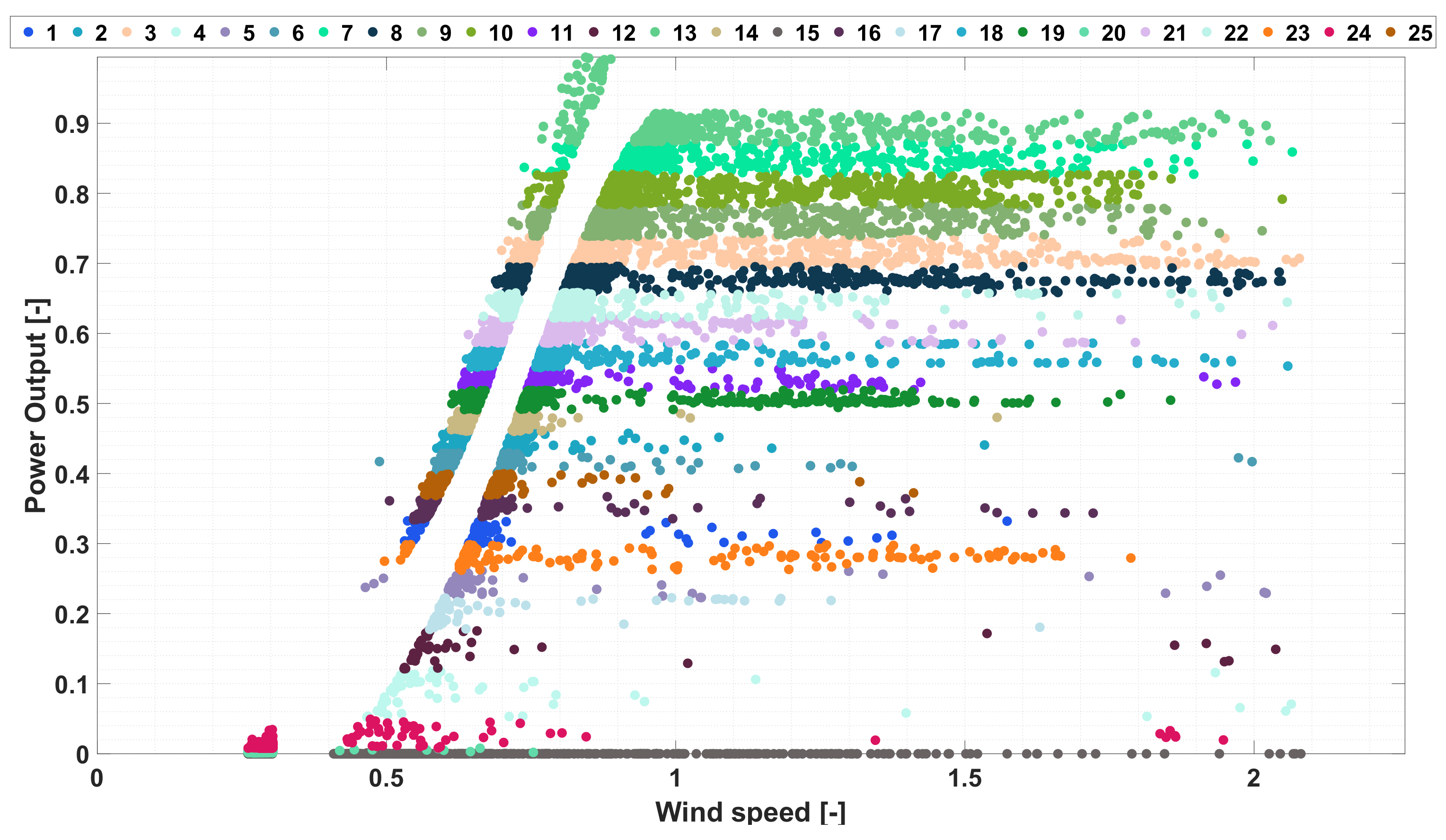
Figure 4 .
By observing the partitioning of the matrix
, and the distribution of the clustered points, several hidden properties can be identified as shown in
Figure 4, where an ensemble of a non-negligible number of points characterized by constant power output is observable in several regions of the identified classes. It is clear that these points can be classified as working points in derating operation conditions, which occur when the power output of the wind turbine is deliberately reduced by the system operator. Hence, to automatically detect these points an adaptive statistical algorithm has been designed. This algorithm allows the update of the set of the valid point
, and to identify a family of regressive models describing the generator power curve for different derating levels.
To address this issue, the first step is to identify, for each cluster, the set of operation points that are characterized by a constant power at different wind speed. This can be done by employing the following iteratuve algorithm:
where
is the power limit for the
sth cluster represented by the matrix
, whose dimensions depend on the number of elements of
which have been added to each cluster. The obtained
represents the limit of the derated power curve, and it allows to find the maximum power value at a certain derating level. This value can be used to select the elements of the valid data matrix
to adopt in identifying the corresponding regressive model, as described in Algorithm 2.
| Algorithm 2 |
| 1: | for , do | |
| 2: | for , k do | |
| 3: | if then | |
| 4: | | ▹ , is joined to matrix. |
| 5: | | |
In this algorithm the element of
, whose power output is lower than
, are added to
sth cluster. Then, for each
cluster, a derated power curve is identified by applying a 3th order least square regression method, as shown in Figure 7, where
is the lowest wind speed value for each
sth cluster, corresponding to the
value.
Finally, after identifying the power curves for each derating condition, proper acceptability bounds have been computed, and the elements of the matrix
have been processed in order to verify if they are coherent with these bounds, according to Algorithm 3. During this process not all derating power curves have been considered, but only those corresponding to statistically relevant sets, according to the number of elements of each
s-th cluster included in
before and after the algorithm application. The overall process is described in the following:
| Algorithm 3 Adding valid objects to |
| 1: | for , do |
| 2: | if then |
| 3: | for , do |
| 4: | if then |
| 5: | ↦ |
| 6: | |
Hence, the elements of
that respect these conditions are added to
, adjourning the matrix
, where
is the
object of
and
is:
and where
,
,
are coefficients that have been determined on the base of sensitive analysis, and
contains the number of elements for each cluster that has been obtained by the application of Fuzzy C-Means technique.
In particular, the optimal values of , and have been here identified in order to improve the expected classification accuracy of the proposed model. This is a complex issue, which is still an open problem in applying data clustering techniques because, if the filtering level is too high, a lack of information could be obtained, while, with lower filtering, the filtered data will contain too much invalid data, canceling out the effects of the proposed filtering data method. Then, the chosen of extreme parameters can in both cases reduce the accuracy of the developed model, causing the need to find the optimal compromise between these extreme cases.
3. Case Study
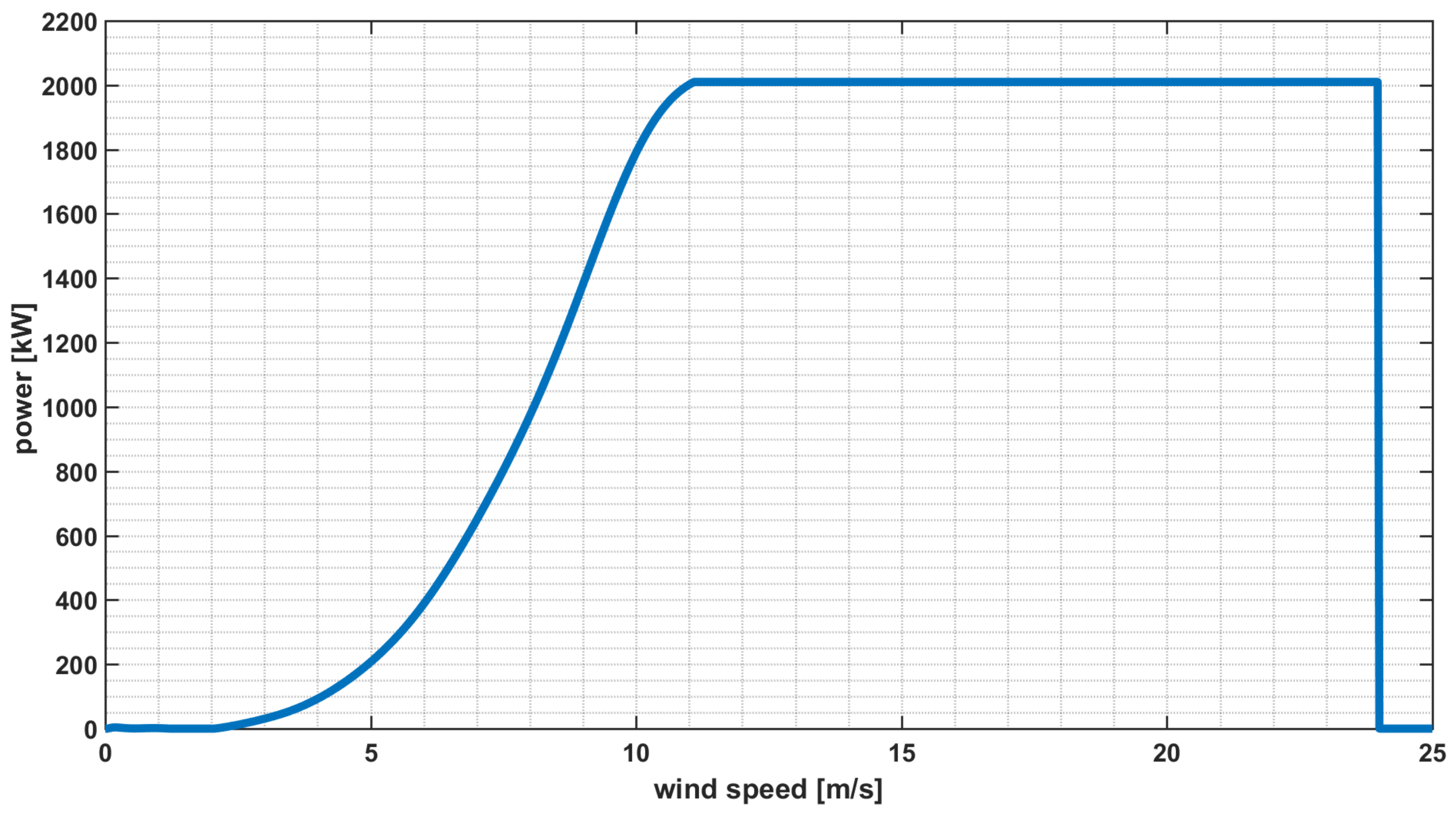
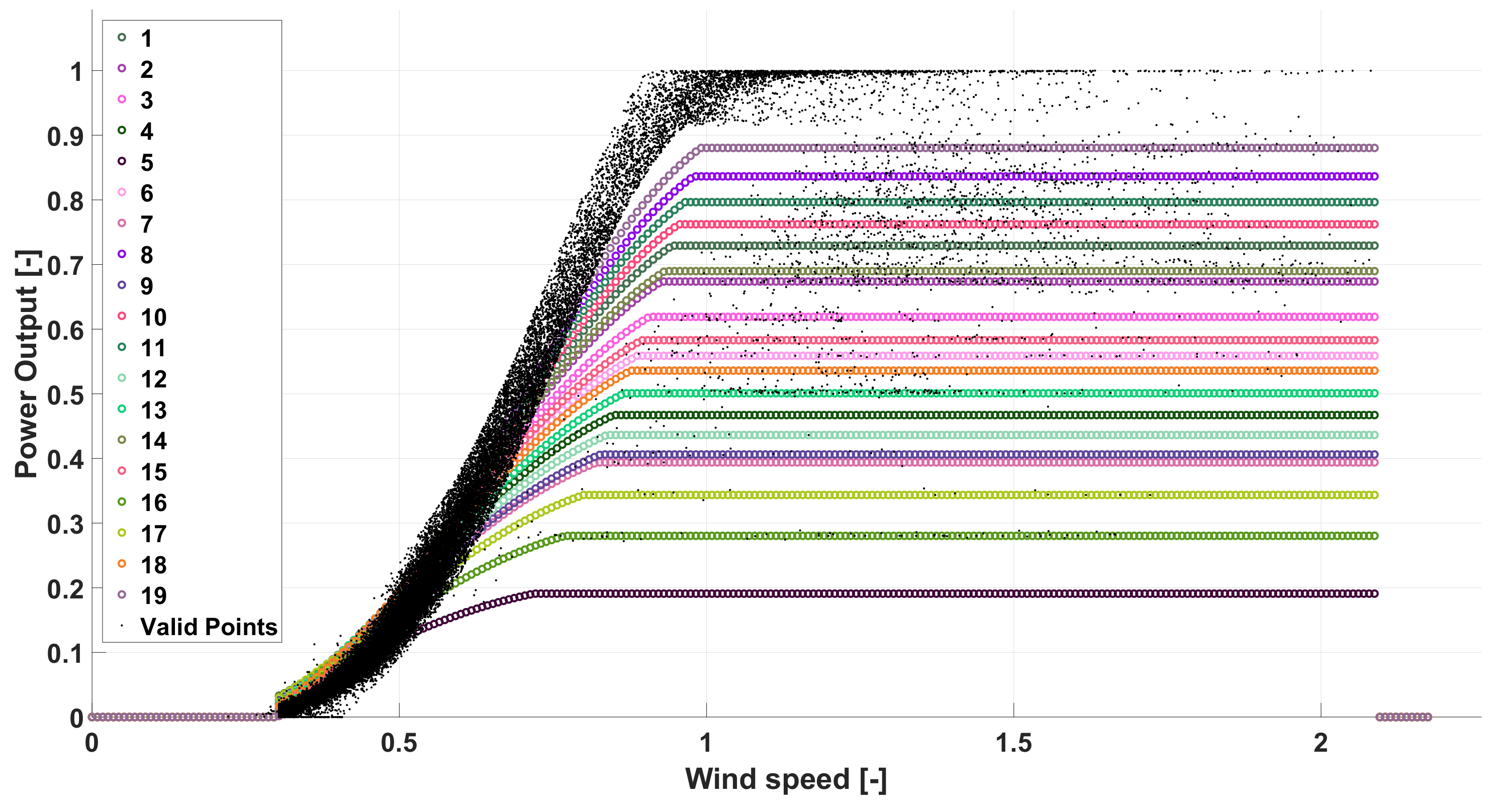
The described methodology has been applied to a real case study, which is based on a 38 MVA Wind Farm, composed by 19 generators characterized by the features shown in
Table 1 and in
Figure 5, where the corresponding power curve is reported. This wind farm is located in the South of Italy in an area characterized by a high penetration of wind generators, which is frequently congested in the transmission network. Consequently, the transmission system operator frequently imposes wind power curtailments, which result in derating power conditions for the analyzed generators.
The real data adopted in the experiments have been acquired from the SCADA system; they covered a time period of two years, include the wind speed, power output and pitch angle averaged on 10 min.
The input data are organized in the matrix
, which has dimensions
, where the first value is the number of measurements of wind speed and corresponding power output available, see
Figure 2. Assigning at
the values shown in
Table 2, the
has been partitioned in two matrices
and
by employing the Algorithm 1. The obtained matrices, which are depicted in
Figure 3, have dimensions of
and
, respectively.
After this preliminary phase,
has been processed by the Fuzzy C-means method, obtaining the results shown in
Figure 4, where the optimal number of partitions
has been calculated using the Calinski-Harabasz criteria.
Hence, the effected consideration are obviously mathematically defined as follows by using Algorithm 2, which is able to catch the constant part of the derated power curves also without a so evident shape of as shown in
Figure 6.
As it is shown in this figure, the application of CFM allows to define several groups of points, which are characterized by a horizontal stripe shape, where for the most part of the defined clusters the constant part of the derating power curves has been very clear highlighted, in particular for clusters 23, 18, 7, 8, 21, 10 and 20.
It is important remarking how the selection of the optimal number of clusters is a critical issue in applying data clustering techniques. In this study, FCM is applied in the task of subdividing the invalid data in many groups, triggering the identification procedure of the derating working points. Hence, the number of clusters is expected to influence the number of derating curves, requiring the adoption of a suitable tool for optimal selecting the class number. Moreover, other than searching the optimal number of clusters, there is the need of highlighting the desired features of data classified.
To address this complex issue, in this paper, after a comparative analysis of the most used solution techniques, the Calinsky-Harabasz criterion has been adopted. The application of this technique allows definition of groups of points characterized by a large span of wind speed while the corresponding power span is lower, hence obtaining a dense and well separated group, which are the best conditions for applying this method.
Furthermore, by considering the iterative nature of how this kind of criteria works, the Calinsky-Harabasz criterion allows the fast supply of the score, which is supplied for each trial in the searching of optimal number of clusters. Despite these benefits, a rigorous method for solving this problem is still an open problem, which needs more research efforts.
The obtained data classification is the prerequisite to detect the elements in
that correspond to derating operation points of the wind generators. To this aim, the clustering method first classifies the points of
in
power bands, then a subgroup of points characterized by constant power value for different wind speeds is identified for the defined clusters. This class of points represents the constant part of the derated power curves, where the corresponding values has been calculated using Equation (
6). Hence, by processing these data by the Algorithm 2, it is possible to obtain the derated power curves in
Figure 7, which have been employed to filter the points of
according to the procedure 3.
Hence, by observing this figure, the generated number of derated power curves is lower than the total number of defined clusters—this is caused by how the Algorithm 2 works. Indeed, the latter considers both the weight of each cluster population compared with the total number of points by statistical way and the percentage level of derated power to the rated one as filtering procedure.
In particular, assuming the values reported in
Table 2 for the coefficients
,
and
, the fitted curves shown in
Figure 6 have been obtained. In this figure, the elements of the matrix
classified as ’valid’ are represented by black dots. The described filtering algorithms rule their distribution as well shown, indeed the great part is distributed on the power curve at rate power, where points with too a large power deflection have been removed both for over and underestimation. In addition, the points that have been considered as derated power working points are distributed around the derated power curves, which have been used for filtering them. Furthermore, the proposed method allows the complete removal of the outliers that are characterized by too large uncorrelation between wind speed and the corresponding measured power value, such as in the bound included between
x axis and power curve 19 and at the right of the straight line that is parallel to
y axis passing for the cut-in speed value.
The valid data sets obtained have been adopted to identify a family of regressive models relating the wind speed, power output and the pitch angle for each derating condition. This is obtained by identifying the parameters of the following bi-variate polynomial function:
where
w is the wind speed, and
is the pitch angle.
In order to rigorously validate the accuracy of the obtained regressive models, the results obtained by applying different modeling techniques, including those based on the manufacturer data and those identified by applying local outliers factors, have been compared. The performances of the analyzed models have been evaluated over a one-year time horizon, which is characterized by the wind profile shown in
Figure 7.
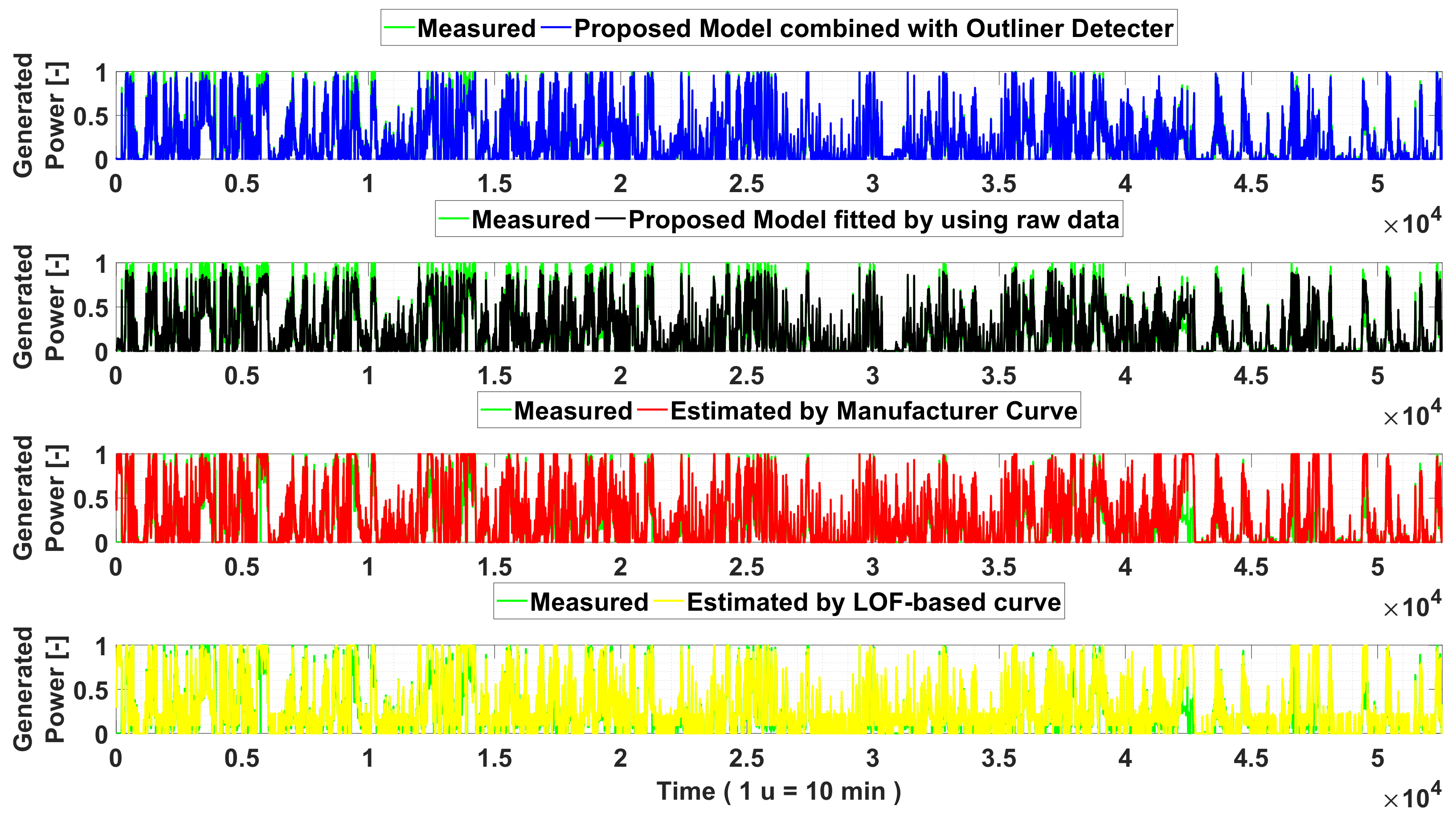
Starting from this data, the estimated generated power has been calculated for each of the analyzed method, obtaining the power profiles shown in
Figure 8.
By applying the described methodology and fitting the proposed models on both filtered and raw data the most relevant results are here discussed in order to prove the effectiveness of the proposal of the authors to increase the accuracy of the wind generators models addressed on-line monitoring or electric network control. Furthermore, in order to complete the analysis, the other model has been compared with the proposed ones, in particular the models have been compared with a model developed on the manufacturer data and applying the local outliner factor.
The performances of the models have been evaluated on a period of one year, whom wind profile is shown in
Figure 7, where is also possible appreciating the highlighted two central bounds that correspond to the areas where is possible producing wind power.
Then, by defining the following figure of merit:
where
is the measured power value, the corresponding error profiles have been computed, obtaining the profiles shown in
Figure 9.
By analyzing this figure, it appears clearly the benefits deriving by the application of the proposed filtering and classification algorithm, which is able to accurately assess the actual power profile, also in the presence of extremely changing operation scenario.
In particular, in
Figure 8 is shown the filtered data-based model that well characterize the behavior of the wind generator in the case of high wind speeds, which is included between the rate and cut-off values where the different values of pitch angles greatly influence the curtail of power, with respect to the other compared method.
Indeed, the power profile obtained by the raw data-based model has shown the worst accuracy for high power generation, which is caused by the huge number of miscorrelation between wind and the corresponding power values. This is evident when the raw data-based model estimates power for high speed values, observable with reference to the time window for the interval defined by units of time.
In addition, by observing power generation profiles of both manufacturer and LOF-based models it is evident their reduced ability to describe critical operation scenarios, which are characterized by derating operations where is clear the influence of pitch angle. All this finds evidence in
Figure 9, where for the considered time window is highlighted and this difference is expressed in per unit terms, and where the base value is the nominal active power of the wind generator.
All this is underlined in
Figure 9, which shows the worst accuracy of the latter two models for the large part of operation scenarios in characterizing wind generator behavior. Obviously, all these graphical considerations are mathematically summarized by using Equations (
11) and (
12).
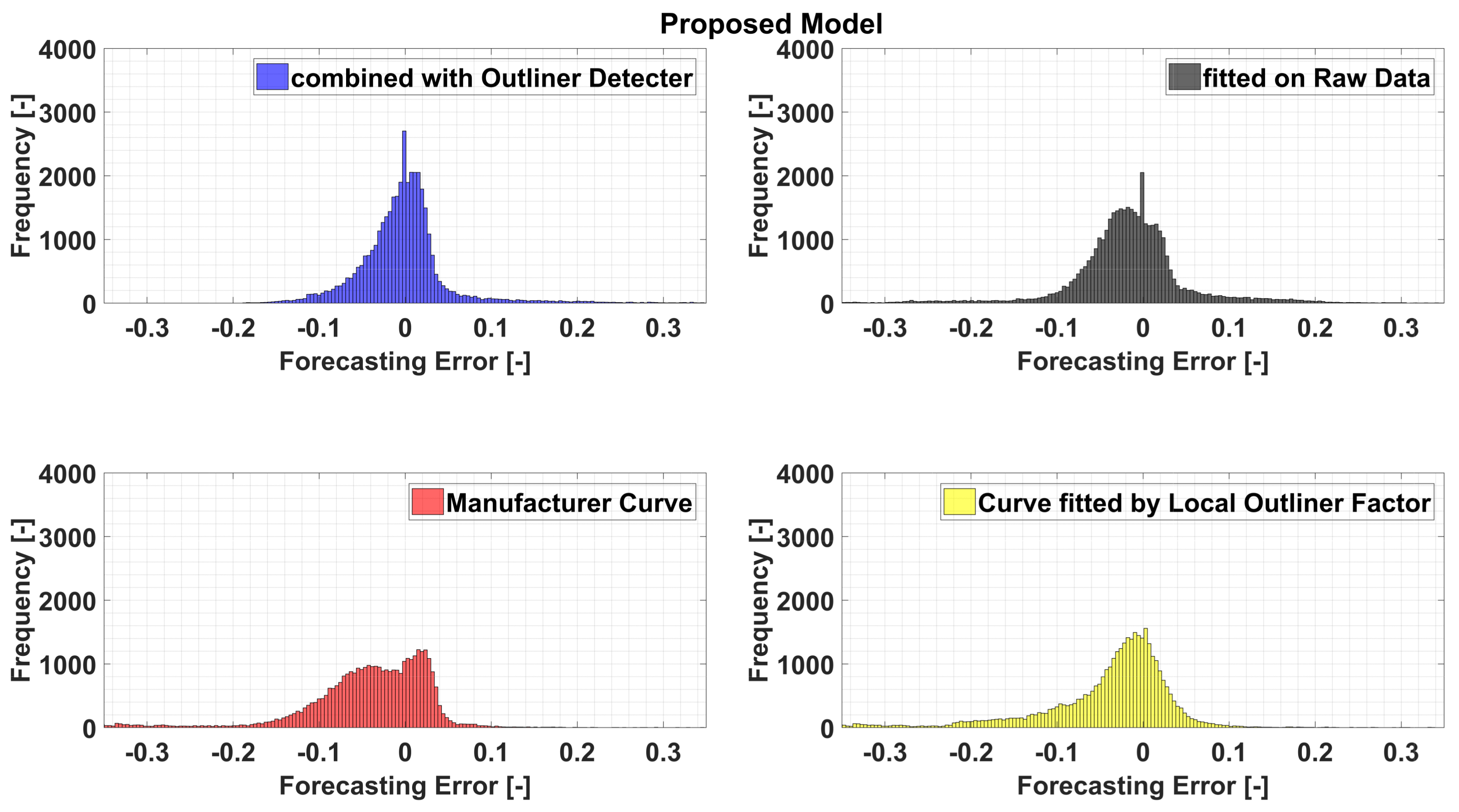
Furthermore, these features are confirmed by the distribution of the Root Mean Square Error depicted in
Figure 10, and the Normalized Root Mean Square error and the Normalized Mean Absolute error reported in
Table 3. The latter parameters have been computed as follows:
The model performances can be summarized in
Figure 10, where the higher stability of the filtered data-based model appears clear, while the raw data-based model shows a wider width of the error. As natural consequence of all this and as the manufacturer and LOF-based model shows, there is a clear lower accuracy as proved by their corresponding error distributions, where their widths is much greater than the first twice.
Hence, in order to assess the robustness of the proposed method, the obtained power curves have been applied in the task of modeling all the wind generators of the analyzed wind farm. The obtained results, which have been reported in
Table 4, confirmed the effectiveness of the proposed model in improving the modeling performance for all the wind generators.
Finally, the computational times required by the proposed methodology are shown in
Table 5, where the SCADA data extraction routine has shown to be the most time consuming process in the proposed methodology.
4. Conclusions
The high penetration of wind generators in modern electrical grids is pushing transmission system operators and energy producers to enhance critical operation functions with accurate and reliable wind generators models, designed and updated by processing experimental data. To deal with the anomalies and incoherence affecting measured data, this paper proposed a classification method based on bad-data detection and unsupervised clustering analysis for wind data filtering and data-driven generator modeling. The main idea was to combine the robustness of adaptive filtering algorithms with the data classification capability of fuzzy data clustering for on-line detection of a valid data-set, and identifying a set of multivariate regression models relating the generated power to the measured variables.
The experimental results obtained on a complex case study demonstrated the effectiveness of the proposed method in enhancing the generation modeling accuracy compared to other traditional solution algorithms.
In particular, power system operators frequently integrate simple and reliable models of wind generators in solving power system operation problems. Hence, the possibility of enhancing these models with advanced tools aimed at relating the actual derated power capability to the pitch angle represents a strategic tool for reducing renewable power curtailments and power system congestions.
Indeed, the proposed method allows managing huge data-sets by processing a large matrix of measured data with computational times compatible with the time constraints imposed by power system operation. Moreover, the developed wind generator model has shown to be highly adaptive, since it allows correctly describing the behavior of all the available generators.
Another important feature characterizing the proposed method is its capability in on-line detection of potential miscorrelation between the measured and the estimated power output, as a function of the available SCADA data. Thanks to this feature, the system operator can define effective policies for optimal reserve management, by taking into account the expected operating state of the available wind generators.
Finally, the proposed model, by explicitly taking into account the pitch angle, is particularly suitable for supporting condition monitoring applications, since it allows detection if a reduction of the generated power is related to a failure or due a voluntary power reduction imposed by the system operator for congestion management. This feature is particularly useful in accurately quantifying the wind power curtails that should be imposed in order to mitigate expected network congestion.