1. Introduction
Ships are an essential ocean target that play important roles both in the civil and military fields. Spaceborne synthetic aperture radar (SAR) has obvious advantages in ship target surveillance on the vast ocean, due to its all-time and all-weather active imaging abilities. However, with improved SAR resolution and increases to the synthetic period, the unique echo features of a moving ship lead to a series of adverse effects [
1]. Additionally, under normal sail, the ship’s motions have multiple periodicities and strong randomness, caused by the sea wind and waves, in three axes [
2]. The influences of these complex motions are mainly in three aspects: first, the motions generate high-order non-cooperative phase errors in the echo signal which cannot be accurately compensated. Second, ship rotation leads to different movement characteristics of its scattering points, and as a result the envelope migrations are different in different range cells. Third, the Doppler echo is periodic and random, which results in the frequency folding and wrapping in the azimuth dimension. Solving these three issues is the key to obtaining a precise image of moving ship targets.
To date, there are two methods of moving target imaging. Conventionally, a target is processed through three steps: moving target detection, moving parameters estimation and compensation, and azimuth imaging. To achieve a high-resolution and well-focused image, multichannel techniques are necessary, such as displaced phase center antenna (DPCA) imaging [
3], space-time adaptive processing (STAP) [
4], and along-track interference (ATI) [
5]. However, most current spaceborne SAR systems are single-channel and do not satisfy the multi-channel requirement; thus, these methods are not adaptively applied.
The second method, SAR–ISAR hybrid imaging, takes a secondary image by inverse SAR (ISAR), [
6,
7], and includes classical ISAR methods and time-frequency analysis methods. Due to the aforementioned problems caused by complex three-axis motions, the processing steps of envelope alignment and phase correction have few effects in the classical ISAR method. Nevertheless, time-frequency analysis can obtain clear two-dimensional images by analyzing the relationship between the scattering point location and the Doppler change in the echo phases, and there are three different means that can be adopted for imaging: polynomial phase compensation, range instantaneous Doppler (RID) imaging [
8] and extracting scattering points by using CLEAN technology [
9].
The high-resolution SAR echo of a moving ship can be expressed as a high-order multicomponent polynomial phase signal (mc-PPS) [
10], which may contain severe envelope migration and Doppler wrapping. Under these circumstances, the classical time frequency analysis method cannot satisfy the processing requirements of mc-PPS. To process mc-PPS effectively, two methods are popularly adopted. The first is the maximum likelihood (ML) method, which can obtain the optimal solution via parameter estimation [
11]. However, the application of the ML method is limited because of its multi-dimensional searching space and very large computation requirements. A modified quasi-ML (QML) method [
12] has been proposed, which offers several improvements and is widely applied in the PPS process. A detailed review of QML is presented in reference [
13]. The second generally adopted method is polynomial phase transformation (PPT) [
14], whether discrete polynomial phase transformation (DPT) [
15], high-order ambiguity function (HAF) [
16], or cubic phase function (CPF) [
17], etc., all of which can reduce the phase order based on phase differentiation (PD) and reduce the searching space to one dimension. These methods are influenced by the cross terms and their resolutions are limited by the PD process. Although many modified methods have been proposed to reduce the cross terms, such as the product forms of HAF (PAHF) [
18] and CPF (PCPF) [
19], these methods are also influenced by the cross terms of the mc-PPS, especially when numerous components are contained and the intensities of every component are similar. The PPT methods are reviewed in detail in Reference [
20].
The adaptive joint time frequency (AJTF) method [
21], as a modified ML method, is widely applied in ISAR imaging [
22], if parameterized, it can represent the signal by extracting the signal components piece by piece and offer good resolution without the influence of cross terms when processing high-order mc-PPS. However, the classical AJTF methods have very large computation requirements, are easily influenced by noise and estimation errors, and cannot fit the time window of the signal component correctly. In addition, classical AJTF application in ISAR imaging assumes only two-dimensional motions of the target, which is not the case for targets with complex three-dimensional motions [
23].
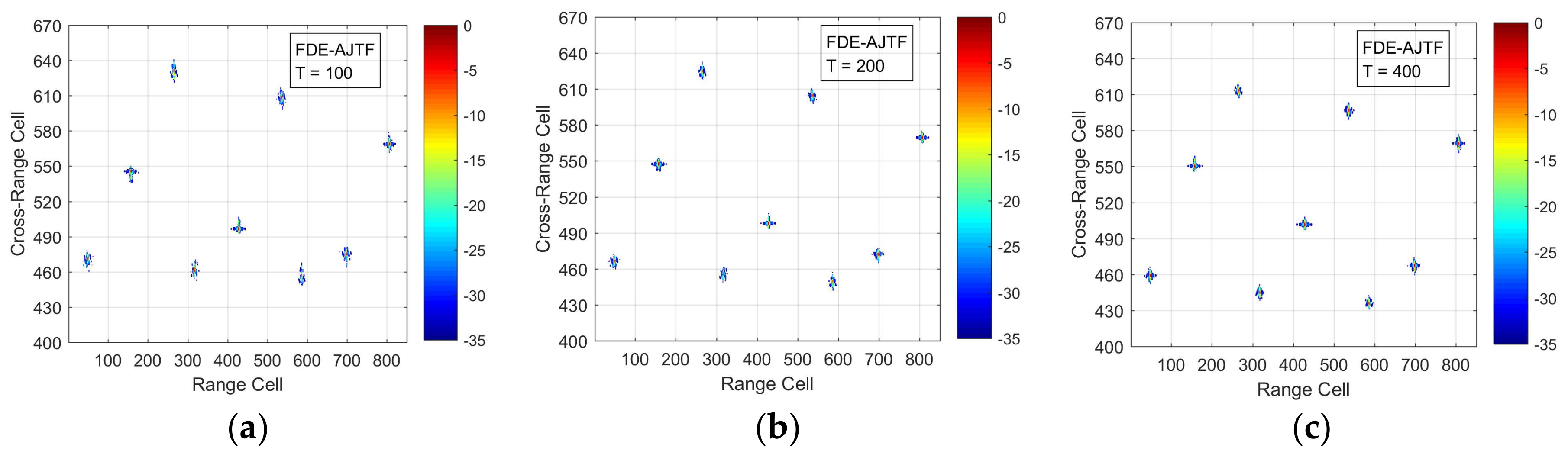
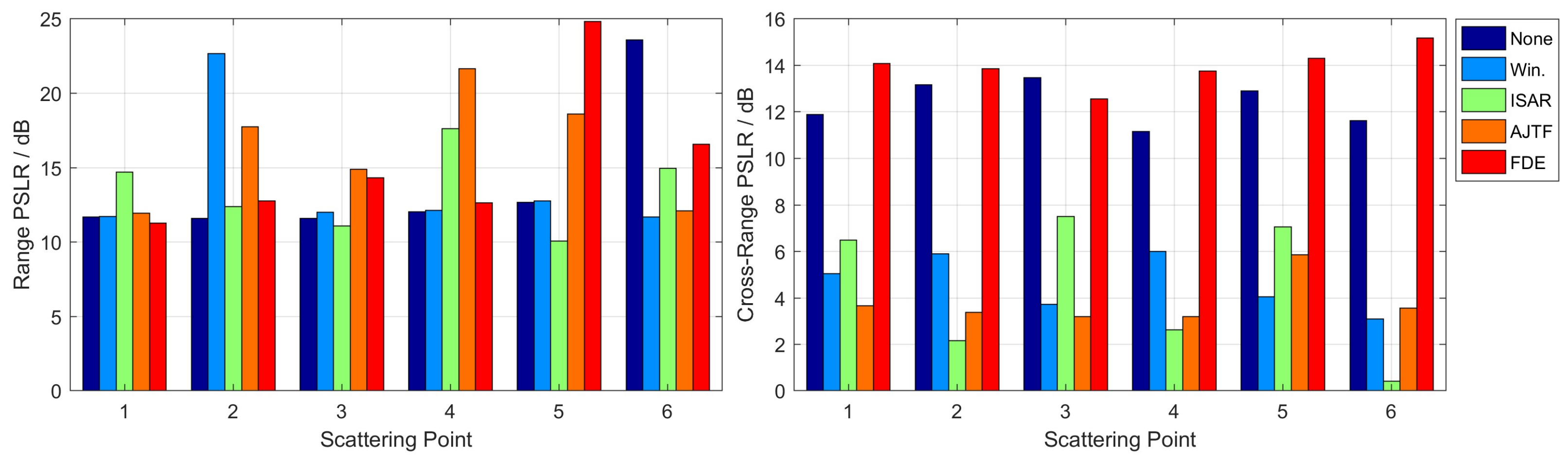
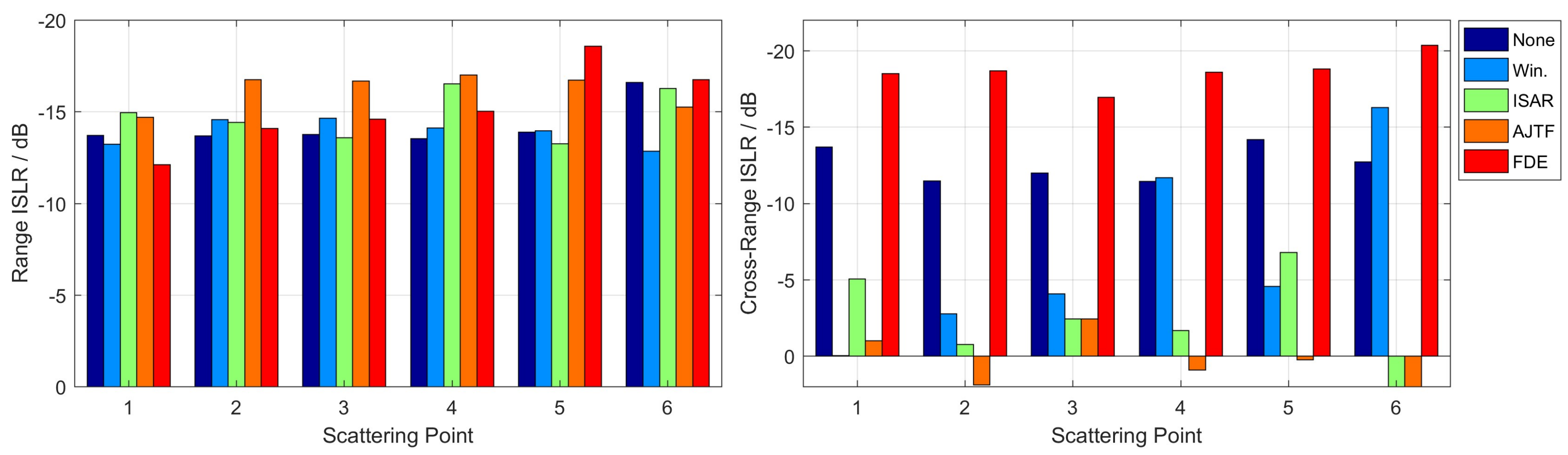
A frequency domain extraction-based AJTF (FDE–AJTF) decomposition method has been proposed, offering three improvements: estimation and extraction of the component in the frequency domain, the use of a time window on the basis function, and the adoption of CFAR detection in component extraction. These improvements increase the stability, speed, and accuracy of the components’ estimation and extraction [
24].
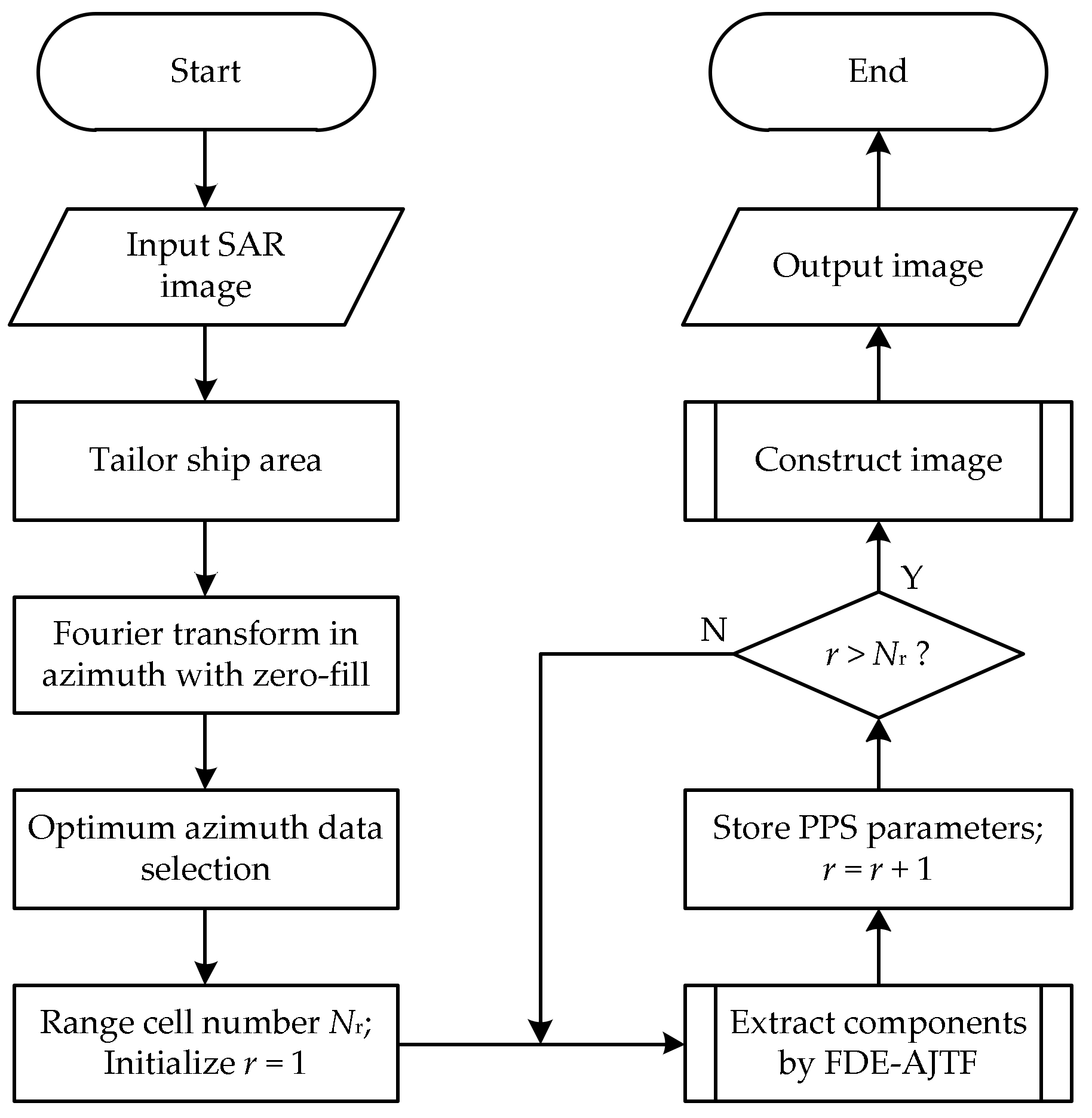
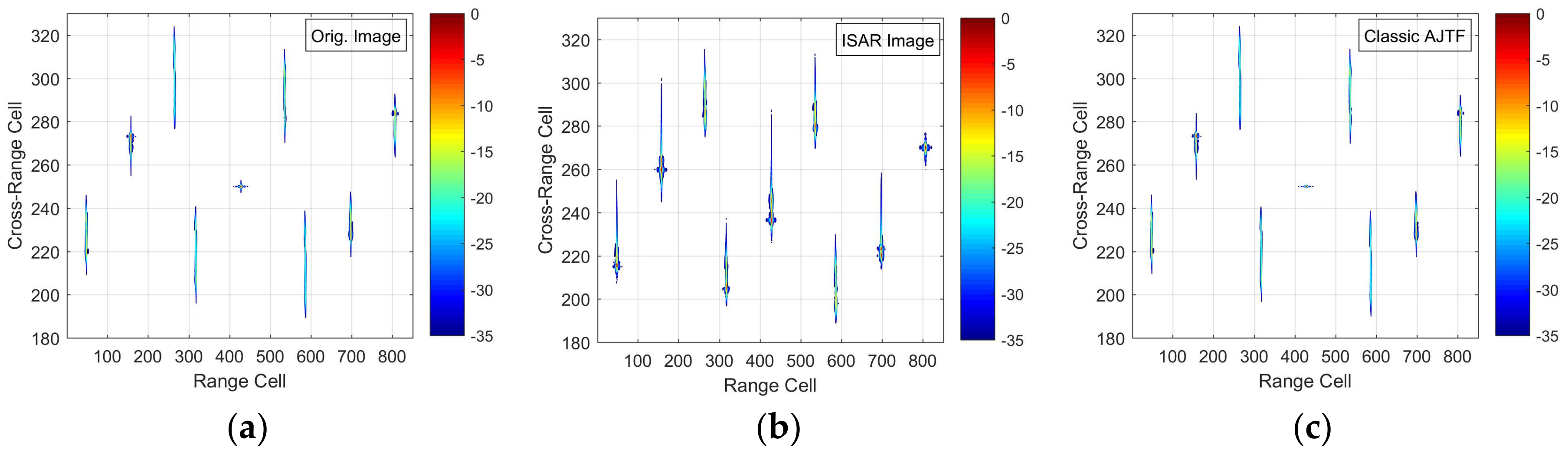
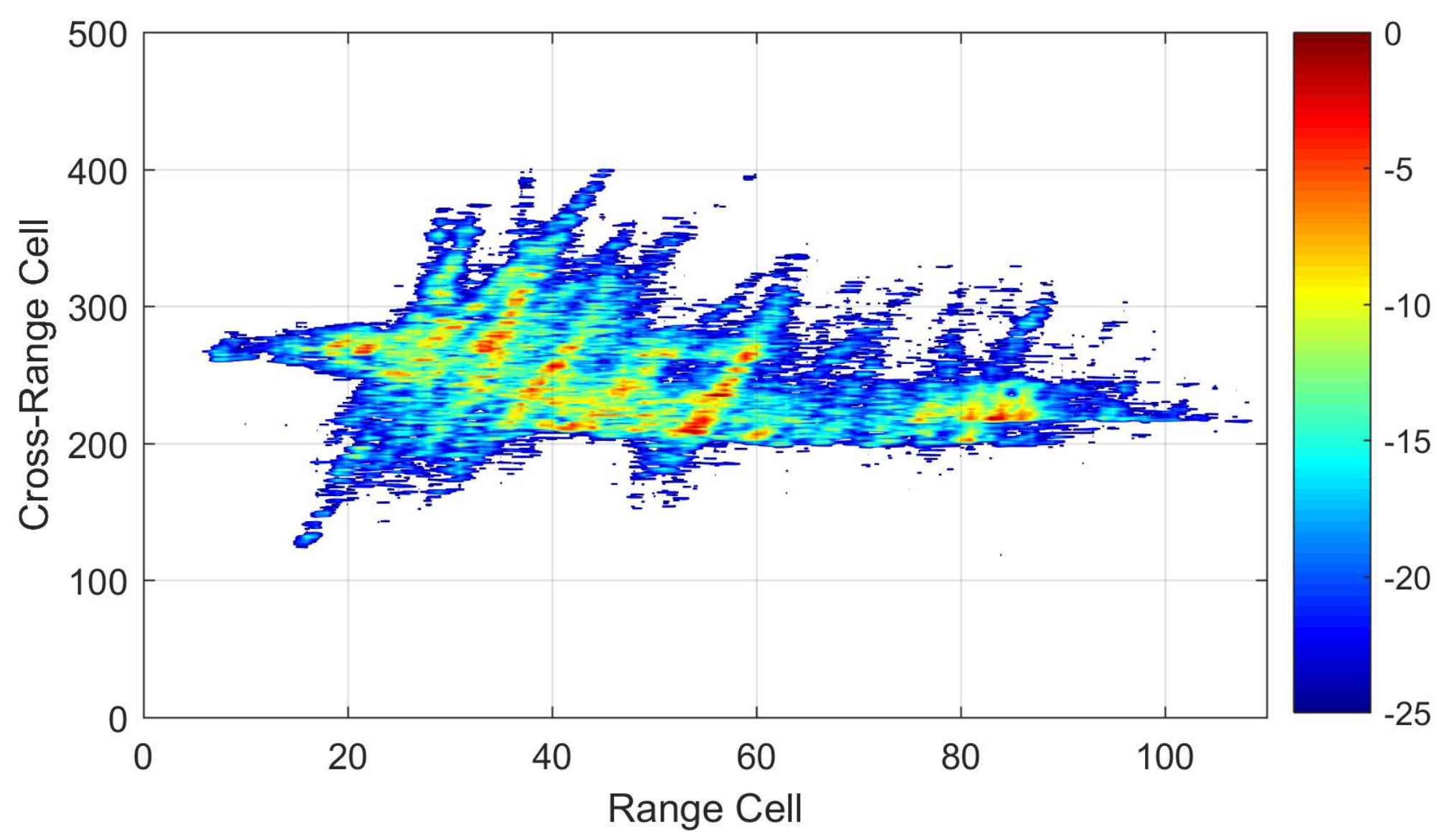
Based on FDE–AJTF decomposition, we propose a novel SAR–ISAR hybrid imaging method to solve the high-resolution imaging problems presented by a moving ship. In this method, the moving ship area on the complex SAR image data is initially tailored and translated to the range-Doppler domain by Fourier transformation; then, the optimum azimuth data with well-aligned envelopes is selected and decomposed to PPS components by the FDE–AJTF method; and finally, a two-dimensional RID image is constructed from these PPS components of all range cells.
2. SAR–ISAR Hybrid Imaging
2.1. Optimum Azimuth Data Selection Method
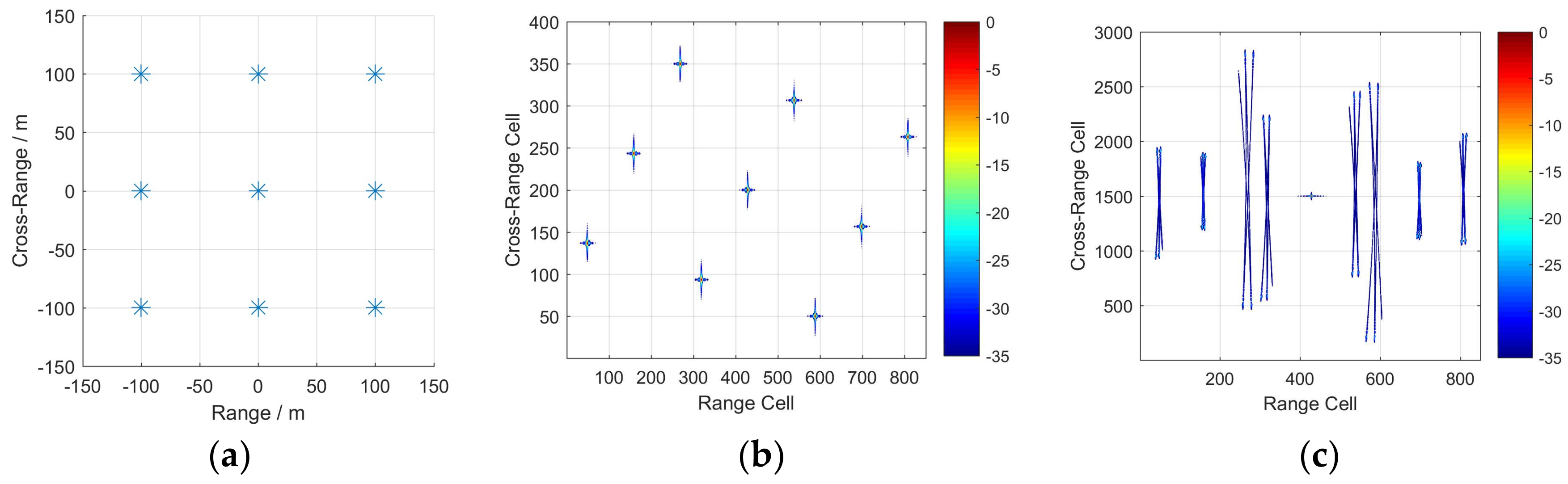
The imaging process in a spaceborne SAR system is mature and solidified, but cannot deal with single ship targets individually. However, the motion and scattering features of a target ship are wholly contained in the SAR complex image, which makes secondary ISAR imaging possible.
The imaging principles of SAR and ISAR are essentially the same. After SAR imaging is done, the phase errors caused by the motions of the SAR platform are compensated for, though the phase errors caused by the ship’s motions endure, causing a fuzzy and unfocused image. Fortunately, these remaining phase errors are in the azimuth dimension, and the ship target area on the SAR image is easily recognized to the clear background of the sea. After the image data of the ship target is tailored and transformed to the Doppler domain, the signal in each range cell can be regarded as a mc-PPS, and can be estimated and compensated by time frequency analysis.
The complex motions of a ship not only influence the echo phase in the azimuth dimension, but also lead to envelope migration in the range dimension. Thus, envelope alignment is the first step in single-ship targeting, whether using SAR or ISAR imaging. However, the scattering points of a complex three-axis moving ship have different motion characteristics, so that their envelopes migrate without a uniform rule for the different range cells, which makes it difficult to align all envelopes at once. This problem is particularly acute when the near points affect each other.
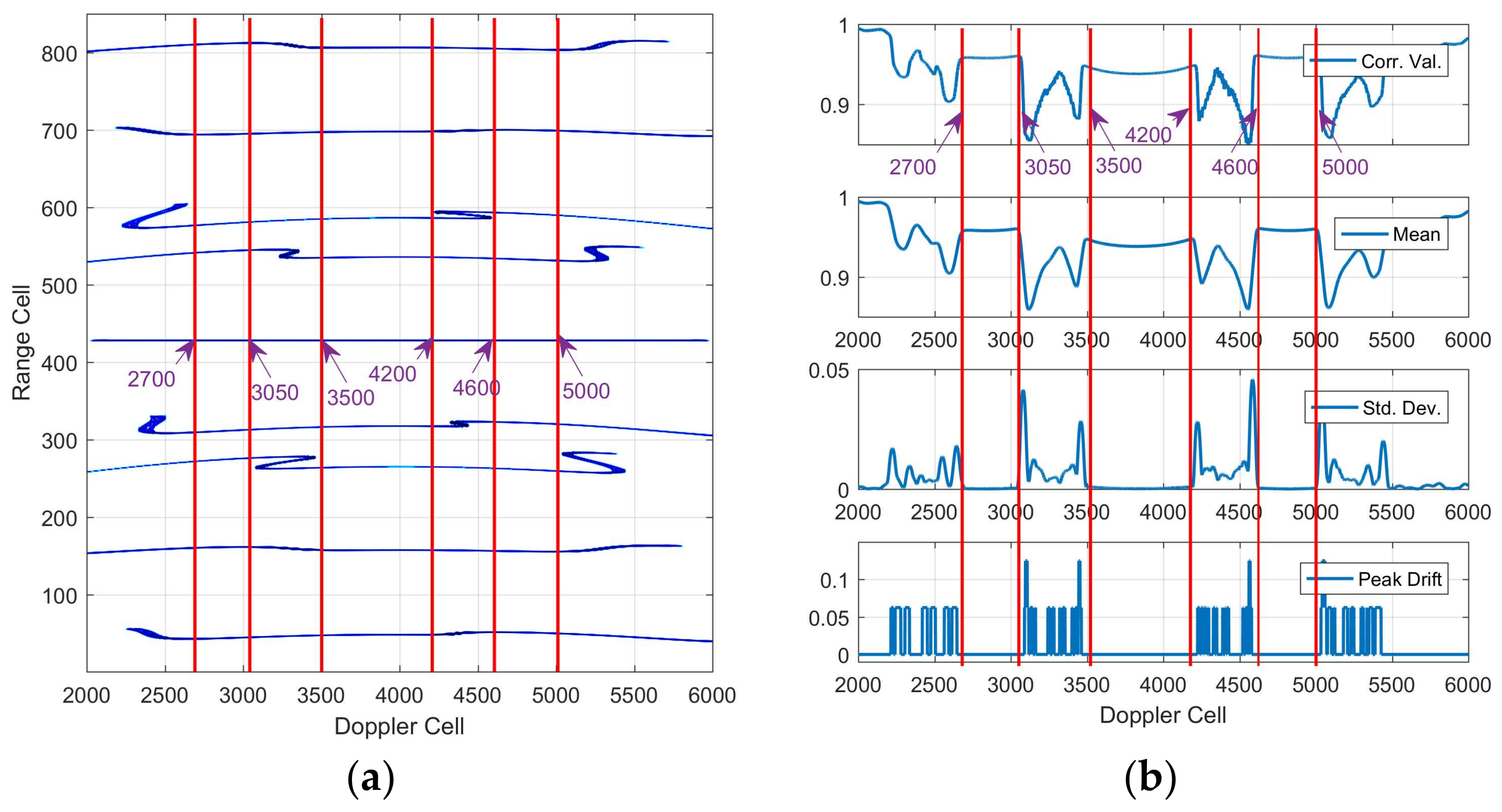
ISAR imaging by time frequency analysis provides a solution that does not require all the azimuth data, only an optimum section in which well-aligned envelopes are selected for processing. Hence, two benefits are brought: these envelopes are well-aligned in the optimum section, which reduces the negative effects of envelope migration; and the complexity of the Doppler in the section is lower, with a shortened azimuth time and easier, more accurate parameter estimation.
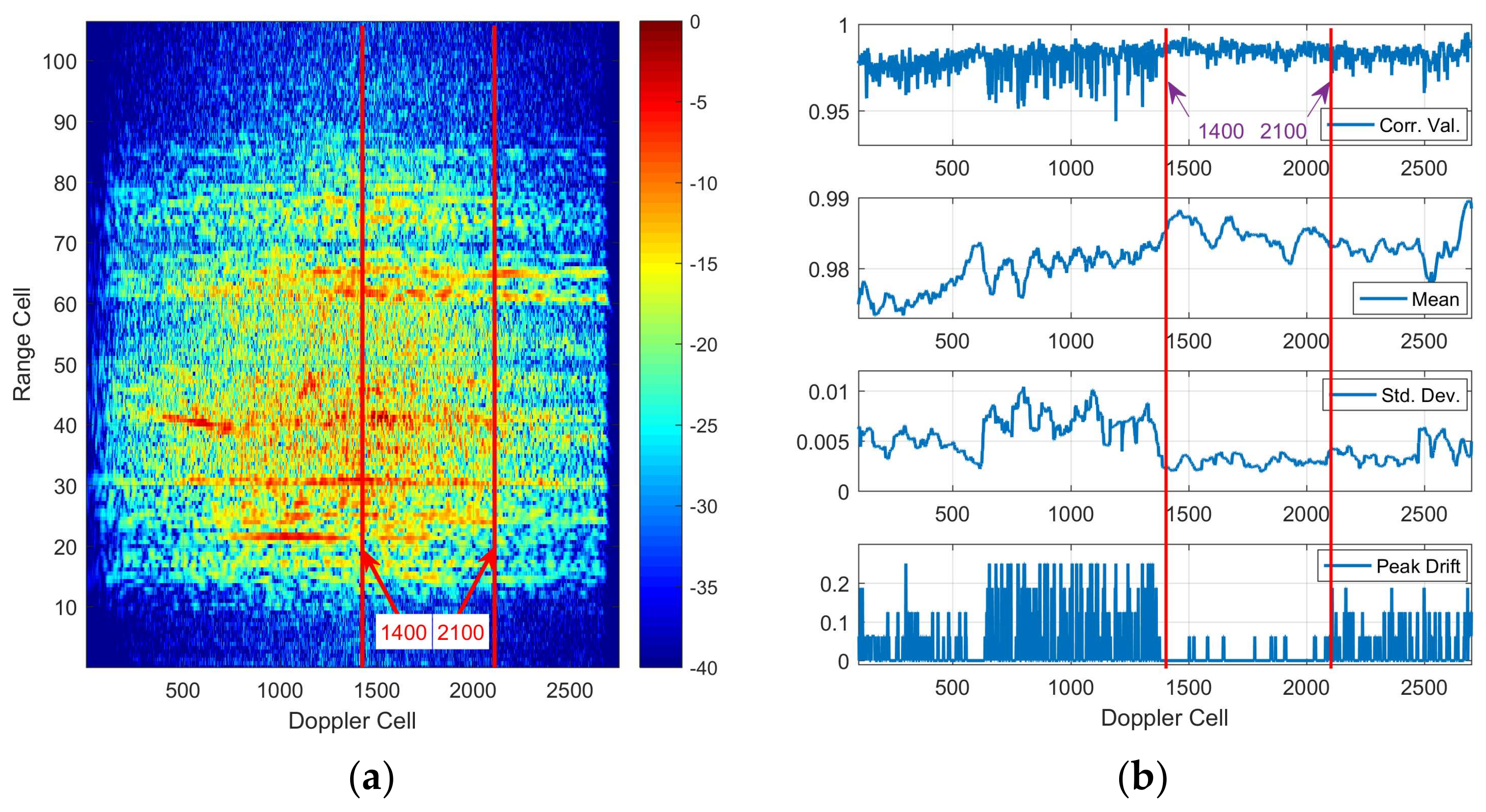
To select the optimum section, the correlation characteristics between the two adjacent range cells can be used as the basis for judgment. The correlation characteristics generally include four indices: the inner product, i.e., the correlation value at zero drift, the mean and standard deviations of the inner products within a certain range cell window, and the peak drift of the correlation.
Assuming the signal in the
rth range cell is
, then the correlation
of the
rth and (
r + 1)th range cells is as follows [
25]:
where
is the drift, and
is the signal length.
The normalized inner product
is the correlation value at zero drift, as follows:
The mean
and the standard deviation
of the inner products are as follows:
where
is the window width on the range cells, and
is the rectangular window.
The peak drift
is the maximum value position in the correlations:
where
gets the absolute value. To increase precision, interpolation is used in the calculation; here
may be a decimal.
These four indices should be comprehensively considered to select the optimum azimuth data section, in which these conditions are satisfied: the inner products are high and smooth with high mean and low standard deviations and the peak drifts of the correlations are small. Only after the optimum azimuth data is selected can the ISAR imaging be processed well.
However, there is another problem in optimum azimuth data selection: the point number of the Doppler transformation. Tailoring a ship area on a completed SAR image is essentially a windowing process in the time domain, while optimum azimuth data selection is also another windowing process after transforming to the Doppler domain. According to the features of discrete signal Fourier transformation, the resolution and frequency range are closely related to the point number of the transformation [
25]. The periodicity of the target ship’s three-axis motions generates a periodic Doppler in the echo, while the former two winnowing processes reduce the transform point number, which may result in Doppler folding and wrapping. To solve this problem, commonly the original complex image data is expanded by zero fill in the azimuth dimension before being transformed to the Doppler domain.
2.2. FDE–AJTF Decomposition Method
The echo signal for a range cell of a moving ship can be expressed as an mc-PPS, and one PPS component
in the whole signal is as follows [
24]:
where
is the component intensity;
is the rectangular time window of width
, and the center point is zero;
is a time-independent constant phase;
is the linear term of time
, which is related to the real position of the target scatter point; and
and the higher-order parameters are related to the target motion, which leads to the phase error and should be compensated in the imaging process.
To estimate the parameters, a basis function is needed. The basis function for the FDE–AJTF method is the compensation phase function
with a time window, as follows:
where
is the time window and
and
are the window’s center and width, respectively. The time window
is used to fit the real component time accurately. To simplify the analysis, the time window can be neglected.
The compensated signal
is obtained by following process:
where
is the basis function without a time window.
The image, that is, the frequency spectrum
, is obtained by Fourier transformation, as follows:
where,
is Fourier transformation. The maximum value of the spectrum is at
, which is the scattering point image as a
envelope function.
To get the best image, the fitness function is the maximum spectrum value
, as follows:
where
are the estimating parameters and
is the peak position
.
The spectrum peak is a
envelope function, and its main lobe is distributed in the neighborhood of
. The estimated component is extracted in the frequency domain by extracting the main lobe; meanwhile, the residual signal is updated by wiping off the main lobe as follows:
where
is the residual signal in the frequency domain and
is the neighborhood range. The minimum neighborhood is
; the robustness can be increased by extending the neighborhood range properly.
Then, the extracted component
can be represented as follows:
where
is the component intensity which is the main lobe energy of
.
The residual signal
in the time domain can be obtained by multiply the inverse Fourier transformation of
and the conjugate of the compensation phase function, as follows:
where
is the inverse Fourier transformation; the
is the conjugate of the compensation phase function with parameters
.
The other components can be extracted from the residual step by step, and finally the signal can be represented as follows:
where
is the component number and
is the residual after
components are extracted.
In the FDE–AJTF decomposition method, the optimization algorithms, such as the genetic algorithm (GA) [
26], particle swarm optimization (PSO) algorithm [
27], ant colony optimization (ACO) [
28], etc., are used to accelerate the parameter searching speed, and the constant false alarm ratio (CFAR) is applied in the component extraction to filter clutter and noise and to increase imaging effectiveness [
29]. As an example, in the simulation and experimental test of this paper, the PSO algorithm is used in the parameters searching.
2.3. Image Construction
Using RID imaging, after obtaining the time-frequency distributions (TFDs) at all azimuth times of all the range cells and distributing them across the three dimensions of time, frequency, and range, the two-dimensional RID image can be obtained by extracting a certain azimuth time slice of the TFDs of all the range cells [
8]. However, in this process we need to calculate the three-dimensional TFDs at all times of all ranges, resulting in a very large computation for which not all calculations are used. To reduce computation demands and improve efficiency, an image construction method is proposed to directly construct only the RID image at a particular time, by which method the display resolution and scale can be easily controlled.
The TFD of a single component signal converges to the instantaneous frequency curve with a probability of 1, whereas the phase of the PPS is continuously differentiable. Therefore, the instantaneous frequency of a single component can be calculated directly without any cross terms. According to Equation (12), the instantaneous frequency is calculated as follows:
where
are the estimated parameters. This instantaneous frequency is the basis of TFD.
The frequency and range scales to display should be determined first. In discrete signal time-frequency analysis the two scales are generally as follows:
where
is the signal length and
and
are the frequency and range scales, respectively.
Next, the axes of frequency and range can be determined as the requirements of the resolution and point number.
where
and
are the display resolutions of frequency and range, respectively, and
and
are the point numbers of frequency and range.
As shown by Equation (9), the frequency distribution of a scattering point is a
function, and according to the SAR imagery characteristics and the processing features of the limited discrete signal, the distribution of a scattering point in the range dimension is also a
function, so that the TFDs of a scattering point is a three-dimensional
function in the range, frequency and time dimensions. Based on the RID imagery principle, an RID image at a certain time is a slice of the TFDs, which is a two-dimensional
function in range and frequency dimensions, with its peak at the instantaneous frequency at the chosen time
. Furthermore, the two-dimensional
function can be expressed as a product of a
function in range dimension and another
function in frequency dimension. Assuming the instantaneous frequency at the time
of the
mth component of the
rth range cell is
, the instantaneous distribution in range and frequency dimensions
is as follows:
where
is the range and instantaneous Doppler (RID) image created by the component
and
is the chosen time. The first
function is in the range dimension, and the second one is in the frequency dimension. The two terms after the two
functions are used to control and suppress the side lobes, and
is the number of side lobes,
; and 0.886 is a factor of the 3 dB width of lobes in the
function.
Because of the linear characteristics of the components and their RID images, the entire image
is obtained by adding the
of all the components of all the ranges, as follows:
where
is the component number of the
rth range cell and
is the image at time
;
is the two dimensional image of the target at a certain time
with
as the axis of range dimension and
as the axis of cross-range dimension. The
axis is an alternative of the real range in azimuthal direction because of the linear relationship between the range and Doppler frequency of a scattering point. Furthermore, as a result of the time parameter
, a serial images can be obtained at different
, and the posture changing of the target is reflected through the image serials.
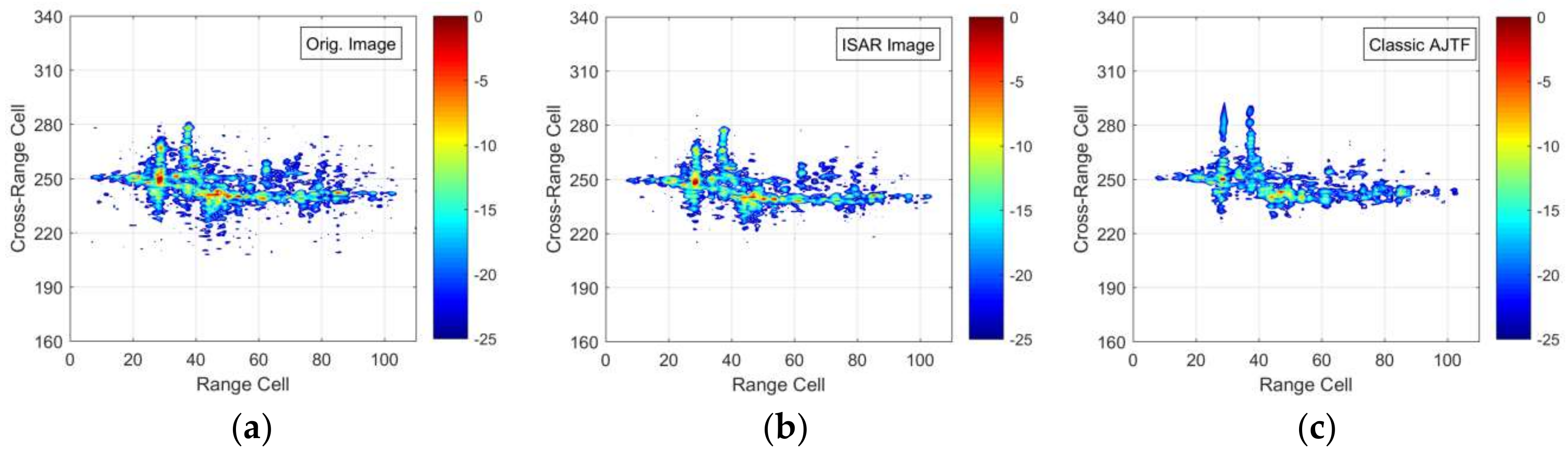
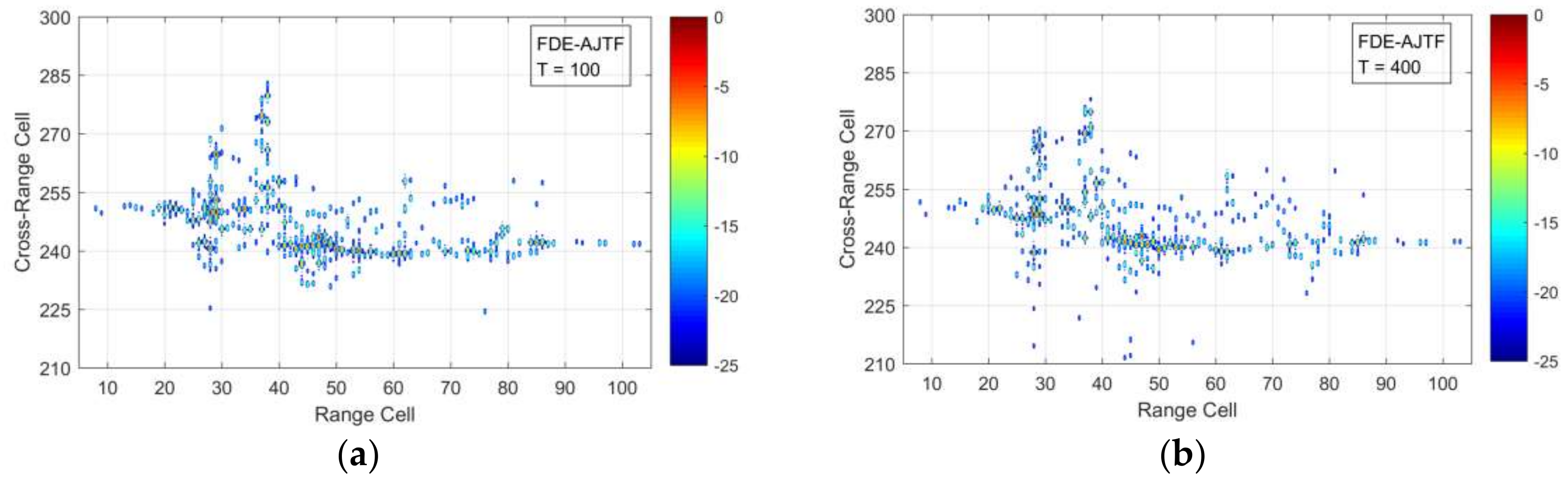
5. Conclusions
Ships are important types of ocean targets and have specific motion features caused by winds and waves. When imaged by high-resolution spaceborne SAR, however, these complex three-axis motions have a series of adverse effects, leading to fuzzy and unfocused imaging results. To address these problems, we propose a novel SAR–ISAR hybrid imaging method based on the FDE–AJTF decomposition method. This paper had four main parts. First, according to the correlation characteristics between every two adjacent range cells, a selecting method for optimum azimuth data was presented to reduce the influence of envelope migrations. Second, the FDE–AJTF decomposition method, which can estimate and extract the components in the echo signals, was presented. Third, an image construction method was proposed to reduce computation demands, allowing the display resolution and scale to be easily controlled. Finally, simulation and experimental tests were used to show and compare the imaging effects of different methods, verifying the feasibility and effectiveness of the proposed imaging method.