Compressed Sensing-Based DOA Estimation with Unknown Mutual Coupling Effect
Abstract
:1. Introduction
- The CS-based system model with unknown MC effect: A system model considering both the MC effect and the signal sparsity is proposed and converts the DOA estimation problem into a sparse reconstruction problem.
- The CS-based DOA estimation method with unknown MC coefficients: With the CS-based system model, a novel CS-based method (SDMC) is proposed and estimates both the DOA and the MC coefficient iteratively.
- The theoretical expressions of the gradient descent method: In the proposed SDMC method, the MC coefficients are estimated by the gradient descent method, and the corresponding expressions for the unknown parameters are derived theoretically.
2. ULA System for DOA Estimation with MC Effect
2.1. System Model without MC Effect
2.2. System Model with MC Effect
3. Sparse-Based DOA Estimation Method
3.1. Sparse System Model
3.2. DOA Estimation with Unknown MC Effect
| Algorithm 1 DOA estimation with unknown MC effect (SDMC algorithm). |
|
| Algorithm 2 MC effect estimation. |
|
4. Simulation Results
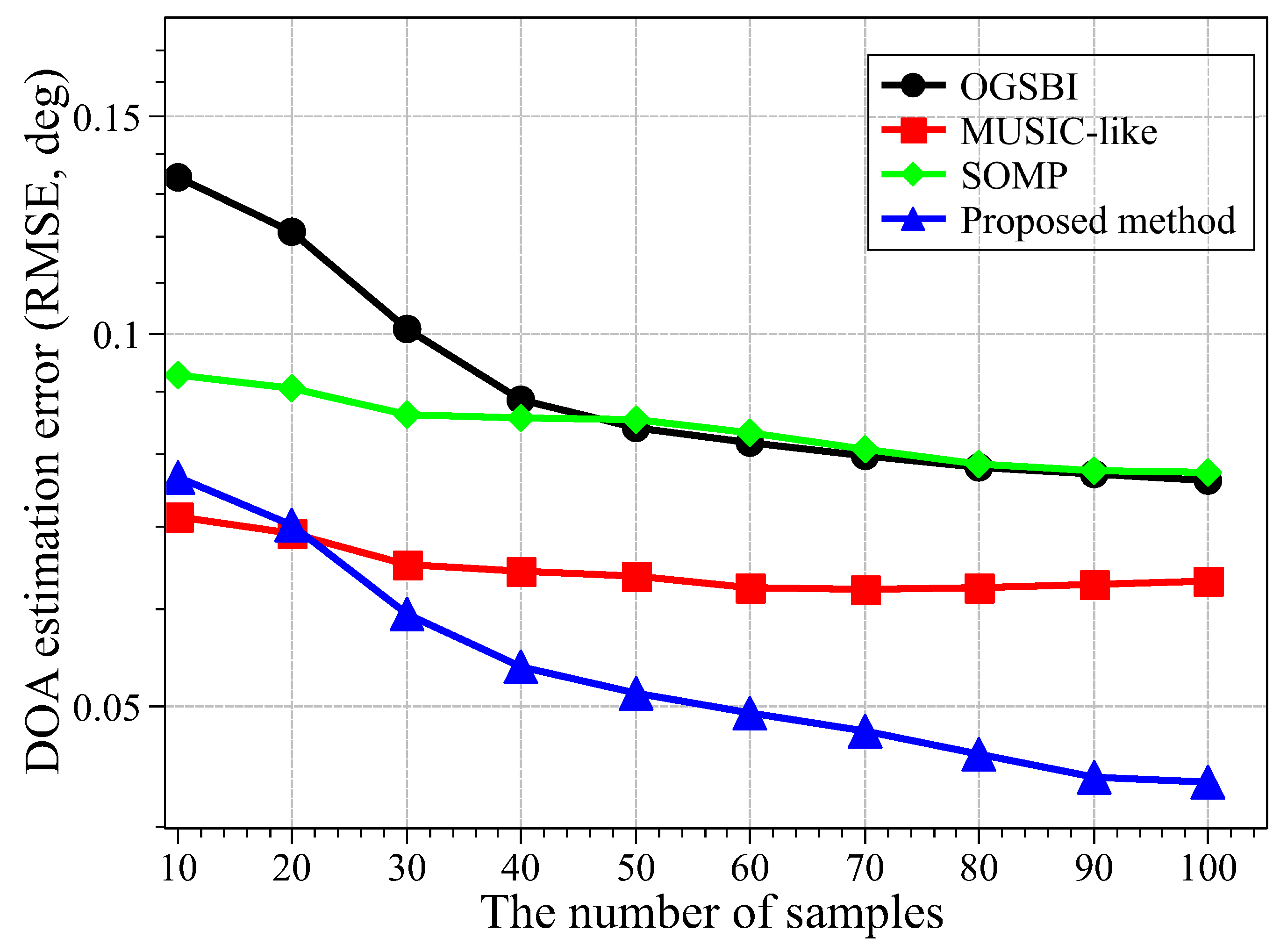
- MUSIC-like method proposed in [40] is a MUSIC-based method considering the MC effect.
- OGSBI method proposed in [31] is the method for DOA estimation based on the sparse Bayesian inference.
- SOMP method proposed in [44] is a sparse reconstruction method and can be used in the DOA estimation with multiple measurements.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 1
References
- Veen, B.D.V.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Chen, P.; Zheng, L.; Wang, X.; Li, H.; Wu, L. Moving target detection using colocated MIMO radar on multiple distributed moving platforms. IEEE Trans. Signal Process. 2017, 65, 4670–4683. [Google Scholar] [CrossRef]
- Lobos, T.; Leonowicz, Z.; Rezmer, J.; Schegner, P. High-resolution spectrum-estimation methods for signal analysis in power systems. IEEE Trans. Instrum. Meas. 2006, 55, 219–225. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Schmidt, R. A Signal Subspace Approach to Multiple Emitter Location Spectrum Estimation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1981. [Google Scholar]
- Chen, Z.; Wu, L.; Chen, P. Efficient modulation and demodulation methods for multi-carrier communication. IET Commun. 2016, 10, 567–576. [Google Scholar] [CrossRef]
- Zoltowski, M.; Kautz, G.; Silverstein, S. Beamspace Root-MUSIC. IEEE Trans. Signal Process. 1993, 41, 344–364. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Du, L.; Yardibi, T.; Li, J.; Stoica, P. Review of user parameter-free robust adaptive beamforming algorithms. Digit. Signal Process. 2009, 19, 567–582. [Google Scholar] [CrossRef]
- Cao, M.; Vorobyov, S.A.; Hassanien, A. Transmit array interpolation for DOA estimation via tensor decomposition in 2-D MIMO radar. IEEE Trans. Signal Process. 2017, 65, 5225–5239. [Google Scholar] [CrossRef]
- Khabbazibasmenj, A.; Hassanien, A.; Vorobyov, S.A.; Morency, M.W. Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar. IEEE Trans. Signal Process. 2014, 62, 1490–1500. [Google Scholar] [CrossRef]
- Hassanien, A.; Vorobyov, S.A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas. IEEE Trans. Signal Process. 2011, 59, 2669–2682. [Google Scholar] [CrossRef]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z.Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Stoica, P.; Wang, Z. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar]
- Beck, A.; Eldar, Y.C. Doubly Constrained Robust Capon Beamformer with Ellipsoidal Uncertainty Sets. IEEE Trans. Signal Process. 2007, 55, 753–758. [Google Scholar] [CrossRef]
- Aubry, A.; Maio, A.D.; Huang, Y.; Piezzo, M. Robust Design of Radar Doppler Filters. IEEE Trans. Signal Process. 2016, 64, 5848–5860. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. Doubly constrained robust Capon beamformer. IEEE Trans. Signal Process. 2004, 52, 2407–2423. [Google Scholar] [CrossRef]
- Kim, S.; Magnani, A.; Mutapcic, A.; Boyd, S.P.; Luo, Z. Robust Beamforming via Worst-Case SINR Maximization. IEEE Trans. Signal Process. 2008, 56, 1539–1547. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S. Underdetermined DOA estimation under the compressive sensing framework: A review. IEEE Access 2016, 4, 8865–8878. [Google Scholar] [CrossRef]
- Yu, Y.; Petropulu, A.P.; Poor, H.V. Measurement matrix design for compressive sensing-based MIMO radar. IEEE Trans. Signal Process. 2011, 59, 5338–5352. [Google Scholar] [CrossRef]
- Chen, P.; Qi, C.; Wu, L. Antenna placement optimisation for compressed-sensing-based distributed MIMO radar. IET Radar Sonar Navig. 2017, 11, 285–293. [Google Scholar] [CrossRef]
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F.; Massa, A. Directions-of-arrival estimation through Bayesian compressive sensing strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F.; Massa, A. Novel wideband DOA estimation based on sparse Bayesian learning with dirichlet process priors. IEEE Trans. Signal Process. 2016, 64, 275–289. [Google Scholar]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Spatial compressive sensing for MIMO radar. IEEE Trans. Signal Process. 2014, 62, 419–430. [Google Scholar] [CrossRef]
- Tan, Z.; Yang, P.; Nehorai, A. Joint sparse recovery method for compressed-sensing with structured dictionary mismatches. IEEE Trans. Signal Process. 2014, 62, 4997–5008. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L. Exact joint sparse frequency recovery via optimization methods. IEEE Trans. Signal Process. 2016, 64, 5145–5157. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L. Enhancing sparsity and resolution via reweighted atomic norm minimization. IEEE Trans. Signal Process. 2016, 64, 995–1006. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Chen, P.; Qi, C.; Wu, L.; Wang, X. Waveform design for Kalman filter-based target scattering coefficient estimation in adaptive radar system. IEEE Trans. Veh. Technol. 2018, 67, 1. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction-of-arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, J.; Zhang, J. Joint DOD and DOA estimation of bistatic MIMO radar in the presence of unknown mutual coupling. Signal Process. 2012, 92, 3039–3048. [Google Scholar] [CrossRef]
- Chen, P.; Wu, L.; Qi, C. Waveform Optimization for Target Scattering Coefficients Estimation Under Detection and Peak-to-Average Power Ratio Constraints in Cognitive Radar. Circuits Syst. Signal Process. 2016, 35, 163–184. [Google Scholar] [CrossRef]
- Clerckx, B.; Craeye, C.; Vanhoenacker-Janvier, D.; Oestges, C. Impact of Antenna Coupling on 2 × 2 MIMO Communications. IEEE Trans. Veh. Technol. 2007, 56, 1009–1018. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Lu, Y.; Ren, S.; Cao, S. Augmented nested arrays with enhanced DOF and reduced mutual coupling. IEEE Trans. Signal Process. 2017, 65, 5549–5563. [Google Scholar] [CrossRef]
- Rocca, P.; Hannan, M.A.; Salucci, M.; Massa, A. Single-snapshot DoA estimation in array antennas with mutual coupling through a multiscaling BCS strategy. IEEE Trans. Antennas Propag. 2017, 65, 3203–3213. [Google Scholar] [CrossRef]
- Hawes, M.; Mihaylova, L.; Septer, F.; Godsill, S. Bayesian compressive sensing approaches for direction-of-arrival estimation with mutual coupling effects. IEEE Trans. Antennas Propag. 2017, 65, 1357–1367. [Google Scholar] [CrossRef]
- Liao, B.; Zhang, Z.G.; Chan, S.C. DOA estimation and tracking of ULAs with mutual coupling. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 891–905. [Google Scholar] [CrossRef]
- Basikolo, T.; Ichige, K.; Arai, H. A novel mutual coupling compensation method for underdetermined direction-of-arrival estimation in nested sparse circular arrays. IEEE Trans. Antennas Propag. 2018, 66, 909–917. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, H.; Liao, B. Direction finding in MIMO radar with unknown mutual coupling. IEEE Access 2017, 5, 4439–4447. [Google Scholar] [CrossRef]
- Determe, J.; Louveaux, J.; Jacques, L.; Horlin, F. On the Noise Robustness of Simultaneous Orthogonal Matching Pursuit. IEEE Trans. Signal Process. 2017, 65, 864–875. [Google Scholar] [CrossRef]
- Determe, J.; Louveaux, J.; Jacques, L.; Horlin, F. On The Exact Recovery Condition of Simultaneous Orthogonal Matching Pursuit. IEEE Signal Process. Lett. 2016, 23, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Determe, J.; Louveaux, J.; Jacques, L.; Horlin, F. Improving the Correlation Lower Bound for Simultaneous Orthogonal Matching Pursuit. IEEE Signal Process. Lett. 2016, 23, 1642–1646. [Google Scholar] [CrossRef]
- Tsai, C.; Liu, Y.; Wu, A. Efficient Compressive Channel Estimation for Millimeter-Wave Large-Scale Antenna Systems. IEEE Trans. Signal Process. 2018, 66, 2414–2428. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| The signal-to-noise ratio (SNR) of received signal | 20 dB |
| The number of samples M | 100 |
| The number of antennas N | 25 |
| The number of antennas with MC effect N | 8 |
| The number of signals K | 3 |
| The space between antennas d | wavelength |
| The grid space | ° |
| The direction range | |
| The minimum DOA space between signals | 10° |
| Ground-Truth DOA | SOMP Method | Proposed Method | ||||
|---|---|---|---|---|---|---|
| Mean | Variance | Successful Ratio | Mean | Variance | Successful Ratio | |
| ° | ° | ° | ||||
| ° | ° | ° | ||||
| ° | ° | ° | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Cao, Z.; Chen, Z.; Liu, L.; Feng, M. Compressed Sensing-Based DOA Estimation with Unknown Mutual Coupling Effect. Electronics 2018, 7, 424. https://doi.org/10.3390/electronics7120424
Chen P, Cao Z, Chen Z, Liu L, Feng M. Compressed Sensing-Based DOA Estimation with Unknown Mutual Coupling Effect. Electronics. 2018; 7(12):424. https://doi.org/10.3390/electronics7120424
Chicago/Turabian StyleChen, Peng, Zhenxin Cao, Zhimin Chen, Linxi Liu, and Man Feng. 2018. "Compressed Sensing-Based DOA Estimation with Unknown Mutual Coupling Effect" Electronics 7, no. 12: 424. https://doi.org/10.3390/electronics7120424
APA StyleChen, P., Cao, Z., Chen, Z., Liu, L., & Feng, M. (2018). Compressed Sensing-Based DOA Estimation with Unknown Mutual Coupling Effect. Electronics, 7(12), 424. https://doi.org/10.3390/electronics7120424







