Abstract
The efficiency of autonomous systems that tackle tasks such as home cleaning, agriculture harvesting, and mineral mining depends heavily on the adopted area coverage strategy. Extensive navigation strategies have been studied and developed, but few focus on scenarios with reconfigurable robot agents. This paper proposes a navigation strategy that accomplishes complete path planning for a Tetris-inspired hinge-based self-reconfigurable robot (hTetro), which consists of two main phases. In the first phase, polyomino form-based tilesets are generated to cover the predefined area based on the tiling theory, which generates a series of unsequenced waypoints that guarantee complete coverage of the entire workspace. Each waypoint specifies the position of the robot and the robot morphology on the map. In the second phase, an energy consumption evaluation model is constructed in order to determine a valid strategy to generate the sequence of the waypoints. The cost value between waypoints is formulated under the consideration of the hTetro robot platform’s kinematic design, where we calculate the minimum sum of displacement of the four blocks in the hTetro robot. With the cost function determined, the waypoint sequencing problem is then formulated as a travelling salesman problem (TSP). In this paper, a genetic algorithm (GA) is proposed as a strong candidate to solve the TSP. The GA produces a viable navigation sequence for the hTetro robot to follow and to accomplish complete coverage tasks. We performed an analysis across several complete coverage algorithms including zigzag, spiral, and greedy search to demonstrate that TSP with GA is a valid and considerably consistent waypoint sequencing strategy that can be implemented in real-world hTetro robot navigations. The scalability of the proposed framework allows the algorithm to produce reliable results while navigating within larger workspaces in the real world, and the flexibility of the framework ensures easy implementation of the algorithm on other polynomial-based shape shifting robots.
1. Introduction
With the increasing pace of technology and robotic developments, our lifestyle has become more dependent on service robots, especially when it comes to the cleaning and maintenance of households. It is estimated that cleaning robots could reach a market value of USD 4.34 billion in 2023, of which floor-cleaning robots will hold a larger share [1]. The need for such applications has become imperative, as cleaning is considered by some as a dull, tedious, and mundane process. A key criterion while developing a cleaning robot is its capacity to demonstrate autonomous operation abilities. Having a consciousness of nearby obstacles is crucial while traversing autonomously in uncertain environments with complex settings. The overall efficacy of the robot is usually determined by the accuracy of the sensor module [2], the flexibility of control systems [3], and the intelligence of area coverage path planning strategies [4]. Among these autonomous aspects, the path planning strategy adopted determines whether the robot is capable of achieving effective area coverage while avoiding obstacles in a given environment. During the path planning phase, the shortest accessible route for smooth manoeuvring in the environment while preserving energy is strongly desired to amplify the performance of service robots. Coverage path planning is an interesting field of study for robotic scientists with numerous studies available in the research literature. Recently, various complete coverage-based path planning algorithms have been developed and implemented on robots to accomplish various objectives.
In a complete coverage path planning setup, grid-based coverage methods have been commonly used to create a workspace environment. In this type of setup, a captured map is treated as multiple areas, and each area contains a value that describes the target environment, stating whether an obstacle is present or whether there is an unoccupied space. There are numerous algorithms that realize a grid-based area coverage approach, such as hexagonal grid decomposition [5], wavefront algorithm [6], the neural network-based area coverage algorithm in Reference [3], and the spanning tree method [7]. A graph-based area coverage path planning approach was presented by Xu et al. in [8], where the mapped region is considered as a graph, and robot motion planning is applied to reach every point in the graph. Numerous 3D area coverage methods for service robots have been proposed and demonstrated in recent years. Jin et al. proposed a 3D area coverage technique for agricultural purposes [9]. Cheng et al. [10] presented the application of 3D area coverage for urban structure inspection. E Galceran et al. [11] presented a bathymetric 3D map to inspect ocean floors.
When it comes to area coverage by obstacle avoidance and non-overlapping of the covered region, cellular decomposition is the most preferred and frequently used path planning method [12,13,14]. In this method, the grid-based workspace environment is broken down into small uniformly-shaped cells of the same size with motion planning applied that helps to achieve area coverage. Past studies have developed different strategies to decompose the given area, like the trapezoidal decomposition method [15,16], boustrophedon decomposition [17], and Morse-based cellular decomposition [18]. Wong et al. [19] presented a topological area coverage method that uses the cloud point of landmarks as nodes to cover the area. Butler et al. [20] proposed an area coverage method based on sensors, where the sensed data are used to generate paths that allow the robot to navigate by achieving maximum area coverage. In [15], Timo et al. proposed a simple path planning method in agricultural applications using a trapezoidal decomposition method.
Among all coverage path planning techniques, the commonly used motion planning algorithms include spiral motion and boustrophedon motion (i.e., back and forth). Lie Tang et al. [9] propose a decomposition method where simple motion (e.g., zigzag) patterns are required to sweep and cover the whole cellular regions in order to cover the farming field using boustrophedon paths. Hameed et al. [21] utilized a boustrophedon path and presented a genetic algorithm for an area coverage path planning technique. In relation to spiral motion, Gabriel et al. used spiral motion in a cellular decomposition coverage technique [22]. In another work, a more energy- and time-efficient online coverage path planning technique is presented in [23], where they adopt a high-resolution grid map representation and utilize spiral path motion to perform efficient coverage. In works related to backtracking spiral motion, E. Gonzalez et al. utilized backtracking spiral motion in a cellular decomposition area coverage method [24]. Additionally, in order to consider the obstacles inside the grid space, they proposed an improvised spiral algorithm [25]. Generic reward-based algorithms are proposed in [26], which focused on autonomous shortest path planning while avoiding obstacles. Even though many studies have been done demonstrating the advantages of different motion techniques with respect to the context of coverage path planning, none of them have been applied to robots that have a reconfigurable capability. In particular, the hinged tetro (hTetro) robot requires a unique motion planning algorithm in order to achieve better performance. The research interest in reconfigurable robots has increased over the past two decades thanks to the evolution in electronic devices and information technologies. Reconfigurable robots are generally classified into inter-reconfigurable, intra-reconfigurable, and nested reconfigurable robots. In intra-reconfigurable robots, an individual robot changes its morphology by reconfiguration on its own. Scorpio [27], a bio-inspired robot, is an example where the robot has the capability of switching between rolling, wall climbing, and crawling forms. Another example of this is Robomods [28], a reconfigurable under-actuated legged robot which has the capability of generating distinct walking patterns. Inter-multiple reconfiguration robots come together to assemble and disassemble to form global morphologies. There are many precedencies, including CEBOT, M-TRAN, Molecube, CKBot, and ATRON. The third major category is nested reconfigurable robots where the robots have the ability to perform the functions of both inter- and intra-reconfigurable robots. hTetro (hinged tetro) [29] is an example of this, where the robot can change its morphology on its own and can also change its global morphology by attaching and detaching with a team of other hinged tetro robots [30]. With numerous studies that cover different aspects of reconfigurable robots, their application in the field of floor cleaning could become more meaningful. When it comes to area coverage and path planning strategies in reconfigurable robots, there are limited studies in this field. To accomplish this task, in our previous work, a novel coverage path planning strategy was proposed [31] for the hTetro robot based on the polyomino tiling theory. The method proposed here demonstrates the capability of the hTetro robot to generate a global tileset to cover the area where the robot is deployed. While assuming suitable morphology on each tile piece during navigation, the hTetro robot achieved maximum area coverage. In our previous works, the hTetro robot was controlled by a human operator during the process of area coverage where the robot changes its morphology at each tile piece without the implementation of any motion planning strategies.
In this paper, we investigate the crucial requirements of autonomous complete area coverage by understanding the generation of the tileset according to tiling theory [32], its applications in gaming [33], and computer graphics [34]. Then, the proposed complete path planning framework is derived from the analytical tiling methodology through the logical process into systems that are demonstrable on the real Tetris-mimicked reconfigurable floor cleaning robot. In this framework, after generating the tileset, a novel technique called tiling-based local motion planner for the considered robot platform is the core technology. Specifically, the proposed planner can autonomously create an optimal navigation route on the generated tileset with the objective of covering the unified area using the least energy. The order of the navigation sequence is modeled with respect to robot kinematic design and optimized by the generic algorithm of the traveling salesman problem (TSP) [35,36], which is well-known for finding the shortest route to connect predefined locations. Moreover, this paper concludes with experimental results that validate the efficacy of the approach through a systematically benchmarked performance evaluation compared with other conventional motion planning techniques (i.e., spiral and boustrophedon, greedy search) used in coverage path planning concerning total traveled distance and recovered areas. Based on the dynamics model and the inverse kinematics of robot configuration, the represented complete path planning framework with the proposed motion planner technique in this paper for the new class of reconfigurable robots has the capability of autonomously producing a global tileset, determining correlated local trajectories that are feasible, and generating appropriate motion signals to the motors.
2. Tiling-Based Complete Path Planing Framework for hTetro
The robot navigation and area coverage are directly proportional to its energy consumption. Thus, the desired algorithm satisfying the two criteria: firstly, maximum area coverage, and secondly minimum energy consumption, must be simultaneously applied in hTetro.
The motion planner framework for the hTetro robot over complete coverage tasks is shown in Figure 1. Note that the choices of the global tileset, the feasible local trajectory, and the mechanism morphology of the robot are critical for achieving the area covering targets. It allows a customized robot to evaluate the geometry of the environment, compute desired body morphology as a global plan, select associated local optimal trajectories, and generate appropriate motor primitives. The process of the proposed tiling motion planner is divided into a set of different stages. The first stage is the planning stage where the high-level global coverage planning will be based on the tiling theory. The second set is the execution stage which produces the trajectory based on TSP (i.e., motion planning) to complete the tileset and then generates the control commands making the robot navigate for optimal locations with appropriate morphologies.
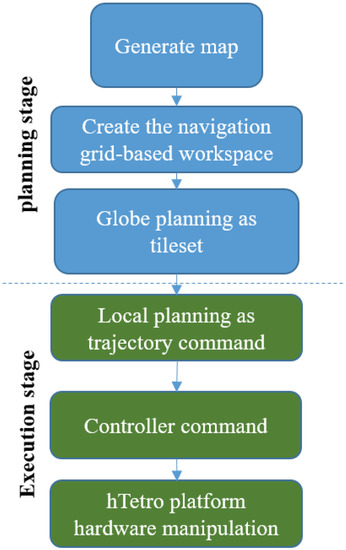
Figure 1.
The proposed tiling-based motion planning framework for hTetro: hinged tetro robot.
Specifically, The tiling theory [32] used to create patterns of polyominoes such as dominos, triminos, and tetrominoes assists in completely covering a given workspace. The hTetro platform in this paper can change its morphology to seven tetrominoes and adapt into particular tileset plans. However, this tiling-based generated set can have the flexibility of random ordering. Thus, the navigation algorithm applied with the class of shape-shifting robot must select the shortest route with the least energy to visit each waypoint defined at the location of the tileset precisely once. Typically, we use the TSP to model this class of problem. By following the solution of the TSP, less energy with the shortest Euclidean distance is achieved. Note that in this paper, the TSP cost functions are derived with respect to hTetro kinematic design during shapeshifting and navigation inside the testbed with all predefined tiling patterns. The main difficulty of the TSP is the immense number of possible trajectory options: for n waypoints. There are numerous algorithms to solve the TSP aiming the shortest path and runtime optimization, such as zigzag, spiral, and greedy search [37]. However, real-time path planning and control logic on decisions made dynamically for the shortest distance in the prescribed path is highly required. Thus, to speed up the processing time for deriving the optimal solution, the genetic algorithm (GA) [36] is a feasible solution.
3. The GA for the TSP-Based Local Motion Planner
3.1. hTetro in a Workspace
To create the local path planner from the global tileset, the robot footprint inside the workspace should be defined by considering the robot’s kinematic design. The hTetro hardware architecture is shown in Figure 2, while Figure 3 represents hTetro’s location in the workspace and one example of shapeshifting to an O shape. Specifically, the hTetro consists of four blocks named a, b, c, and d in world frame w. Each block of hTetro is provided with DC motors for its stable and balanced locomotion. Three high-torque servo motors present at the hinge position are responsible for shapeshifting. Each DC motor and servomotor (at hinge positions) operate at 7.4 V and 14.8 V, respectively. The hTetro robot consists of navigational components in each block, which benefit smooth locomotion. Since the robot base is reconfigurable, achieving differential movement is very challenging. Hence, we developed linear locomotive gaits and made the robot traverse forward, backward, leftward, and rightward directions. In order to achieve the mentioned motion capability, we established omnidirectional wheels in each block of the hTetro robot.
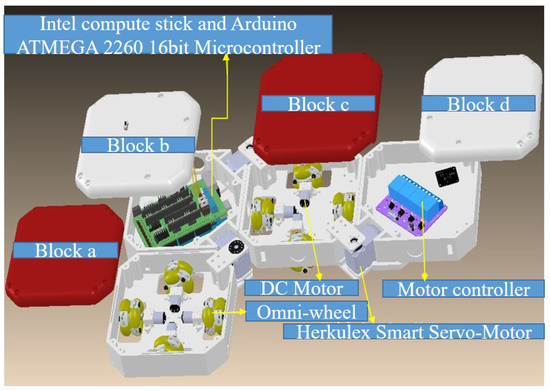
Figure 2.
hTetro platform with hardware component setting.
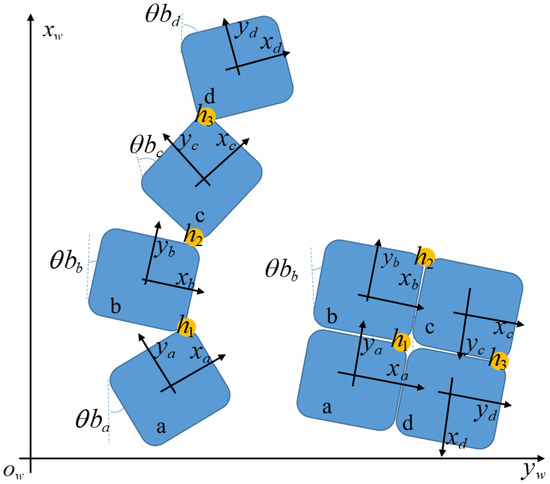
Figure 3.
hTetro platform location on workspace and shifting mechanism to O shape.
The servomotors hold the four blocks together and assist in reconfiguration by adjusting the rotating angles () with respect to the workspace frame. The possible rotational angles that can be achieved by each block locally are . However, the angle will be constant whereas the block b acts as a foothold for the hTetro platform. As a result, block b is typically the center of focus, and it helps to maintain stability by holding two of the three servomotors. By changing the rotating angles, hTetro can changed into seven morphologies (i.e., O, Z, L, T, J, S, I) as in Figure 4. One example of a tileset with tetromino patterns where hTetro fits inside the tileset of an 8 × 8 workspace is shown in Figure 5b,c. Specifically, tiling theory [32] with several lemmas that provide the suggestion of what tiling patterns should be used to completely tile the predefined workspace. If the size of the coverage area is not a multiple of hTetro blocks, we can segment this workspace into two partially overlapping sub-workspaces and both can be tiled by tiling theory. Figure 5d–f provide an example of how to tile a workspace with the size of 6 × 7, which is not a multiple of the hTetro blocks. The appropriate location and orientation inside the workspace of the selected tile among suggested tiling patterns is determined by the backtracking algorithm [38]. After the considered tile is identified, the algorithm tries to tile the rest of the tileset in the workspace. If the next tile cannot be located by the algorithm, then the other possible placements are tried. Even after trying all possible placements, when the algorithm departs from tile combinations, then it backtracks to the previous tiling pattern and executes the same procedure with the new tiling pattern among the tileset. The same process continues until the fully tiled defied workspace is obtained. Note that using this approach, we can make sure that the defined workspace can be tiled completely without any revisited areas by using several tileset options.
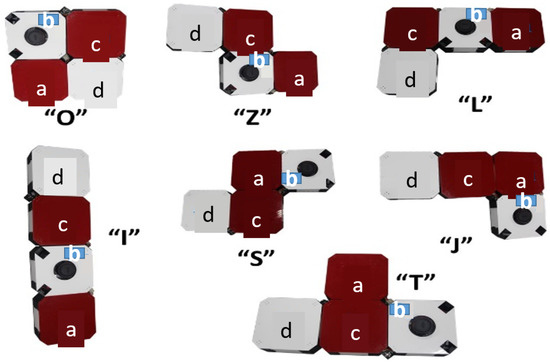
Figure 4.
hTetro platform with seven configurations.
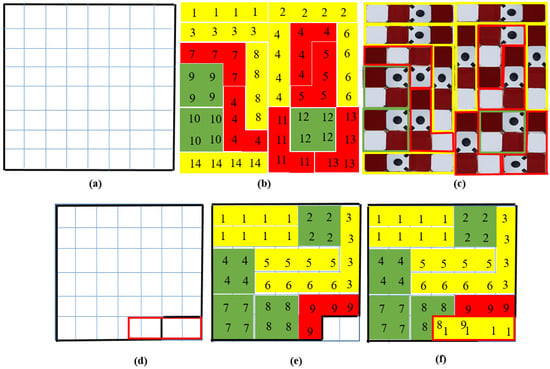
Figure 5.
Tilesets by tiling theory and hTetro morphologies fitting inside the tilesets. (a) 8 × 8 workspace; (b) tileset; (c) hTetro morphologies fit in platform; (d) partially overlapped sub-workspaces of 6 × 7 workspace; (e) tileset for sub-workspace; (f) tileset for 6 × 7 workspace with overlapped cells.
The proposed block diagram in Figure 6 describes the steps to give the order of navigation to cover the entire surface by applying tiling theory. To fit the morphologies inside one specific tileset, firstly, the navigation sequence for this tileset is generated by the proposed local planner of the complete path planning framework. At each waypoint location, hTetro assumes its shape according to the tileset plan by rotating the servo motors at the hinges connecting blocks, then hTetro travels to the next defined waypoints by the locomotion modules in the four blocks. When block b arrives at the desired location, the same process is repeated until all the patterns of the workplace tileset are visited.

Figure 6.
Block diagram of proposed local motion planing strategy for tiling-based complete path planning. TSP: traveling salesman problem.
Typically, in order to accomplish this sequence of planning and navigation, the robot must know the location on the map where it needs to move in real-time. In most grid-based coverage path planning techniques, each cell represents the full robot (i.e., each cell is robot-sized). So, the path planning scheme needs to pass the grid coordinates to achieve the full coverage. Since the hTetro platform is unique in its reconfiguration ability, the hTetro’s four blocks occupy a single cell in the grid at any point in time. To know the road map, the path planning technique should generate reference coordinates as waypoints. These coordinates will act as waypoints for the robot that aid it in achieving full coverage. Thus, block b is chosen as a reference on the 2D map and the other blocks will determine its relative position with respect to block b. The generated coordinates will be tagged with block b for all seven of hTetro’s configurations. The algorithm undergoes row-wise search to account the reference block b for each generated tileset.
Figure 7 and Figure 8 show the locations of blocks a, c, and d with respect to block b for different shapes. For asymmetrical morphologies T, J, and L, as a result of the kinematic design constraints of hinges, each tiling pattern has only one possible option of block locations, as seen in Figure 7. On the other hand, for the symmetrical morphologies (i.e., O, I, S, Z), the options of block locations are provided as in Figure 8. Because of the symmetrical characteristics, there are two options for block location associated with I, S, and Z tiling pattern, and there are four options for the O tiling pattern. Furthermore, to locate the block locations for one morphology, the robot orientation in the grid-based workspace is also considered. Figure 9 provides an example of blocks’ locations with respect to the orientations of the T morphology.
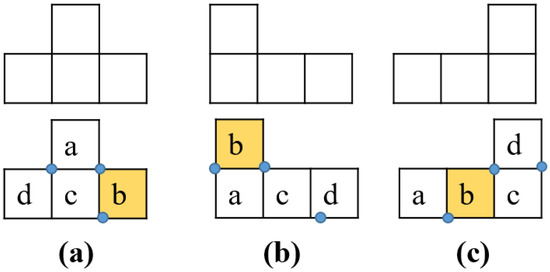
Figure 7.
The tiling pattern and corresponding other blocks’ locations considering block b as a reference point for hTetro asymmetric mythologies. (a) T shape; (b) J shape; (c) L shape.
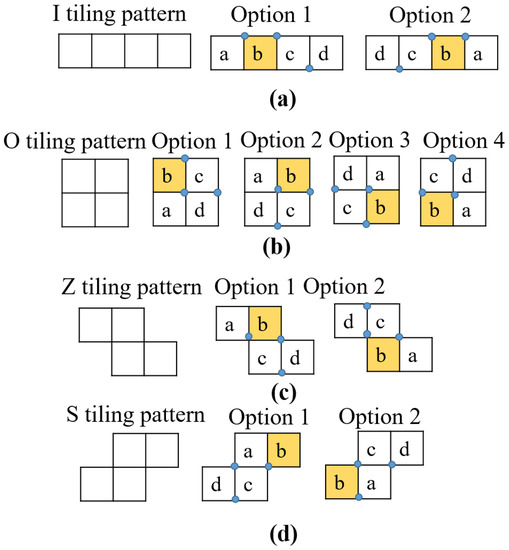
Figure 8.
The tiling pattern and corresponding other blocks’ locations considering block b as a reference point for hTetro symmetrical morphologies. (a) I shape; (b) O shape; (c) Z shape; (d) S shape.
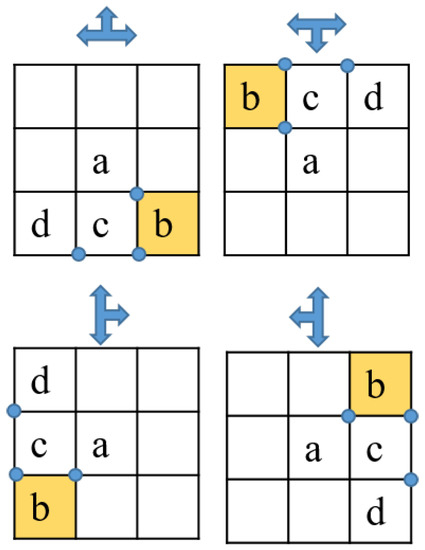
Figure 9.
Unique shape matrix with respect to hTetro orientation.
Given one waypoint , the 2D locations of blocks a, b, c, and d in the global frame are marked as , respectively. Using this hTetro location definition, the displacement between two corresponding blocks l where of two tiling patterns is modeled as Euclidean distance and is found as in (1). As shown in Figure 10, in order to find the cost weight associated with moving the robot from waypoint to another waypoint , the block displacement as the summation of Euclidean distances of all four hTetro blocks are considered. Specifically, the cost function of pair and (i.e., ) is calculated as in (2), where k ranging from 1 to n − 1 represents the pair order of n waypoints and the coefficients (whose summation is always 1) are used to adjust the role of each block displacement to the associated cost. Based on the importance of each block, we can assign the corresponding coefficients. The higher the coefficient, the more importance associated to the considered block. If the four blocks of hTetro are considered as having the same weight, the coefficients are set equal to 0.25. The proposed cost function represents the total displacement between the positions of any two tiling combinations in the workspace.
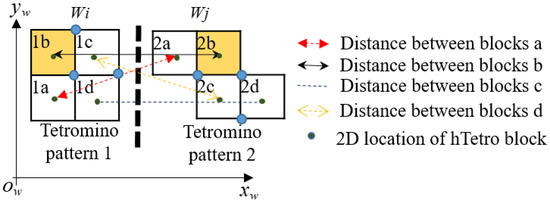
Figure 10.
Finding block location for the symmetrical morphology O.
Algorithm 1 is used to find the block locations and orientations for any predefined workspace ws with size and completely filled with the appropriate tileset. Specifically, the algorithm undergoes row-wise search in order to visit all the tilesets. At each tiling pattern p, if it is of the asymmetric type, the locations of each block as in Figure 6 are assigned to this tiling pattern. On the other hand, if the visited tiling pattern p is of the symmetric type, the morphological orientation as in Figure 8 having the block locations yield the nearest Euclidean distance as per Equation (3) with all blocks of the previous waypoint is selected. In detail, given the orientation options of one symmetric morphology , Equation (2) is used to locate the blocks of . Figure 11 gives an example of filling the block locations of tiling pattern O given the block locations of the previous symmetrical tiling pattern S. As one can see, the block locations of the O morphology as in Figure 11b yielded the nearest distance with previous tiling pattern S. As a result, this option was selected for the block location of O in this case.
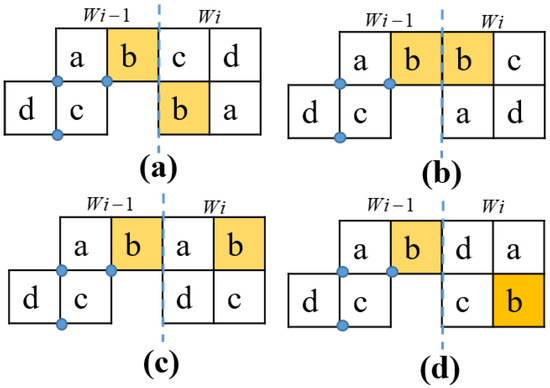
Figure 11.
The distance between each block of two sample shapes of hTetro.(a) option 1; (b) option 2; (c) option 3; (d) option 4.
| Algorithm 1: Assigning block locations for each tiling pattern |
| 1 Function BLOCK LOCATIONS{workspace, tileset}: |
| 2 workspace{} |
| 3x ←0, j ←0, y ←0, p ←0 |
| 4 for all x, x ←0, to do |
| 5 for all y, y ←0, to do |
| 6 if is the location of tiling pattern p then |
| 7 if tiling pattern p is asymmetrical morphology then |
| 8 Assign: blocks locations: according to Figure 7 |
| 9 elseif tiling pattern p is symmetrical morphology then |
| 10 Search: for tiling pattern as in Figure 8 having blocks yield the nearest distance with blocks of pattern with |
| 11 Assign: block locations: according to Figure 8 |
| 12 end |
| 13 end |
| 14 end |
| End Function |
4. Trajectory Generation
In the case of n tiling patterns generated to cover the workspace completely, after locating the blocks of hTetro inside the workspace, the desired path is the set of n − 1 segments where each segment connects a pair . The objective function of the path searching problem is formulated as in (4) given as a list of tiling patterns, locations, and the cost weights between each pair of waypoints with respect to block b, the shortest possible route where each waypoint is visited exactly only one time is obtained. To get the output value of (4), the GA of TSP is applied. Reference [36] explains the GA of TSP in detail. GAs are suitable for dealing with big searching candidates and autonomously finding the optimal solution.
Specifically, the GA as in Algorithm 2 for tiling motion sequence generation starts with a set of trajectories within the defined workspace, called the population. Since there is a high chance that the new population will be more suitable than the previous one, the temporal route from one population is considered to create a new population. Solutions are selected according to their fitness by producing and mutating the processes to form new solutions called children of parents—the lower their weights, the more chances they have to reproduce. The best children are added to the final route. If the termination condition as the improvement of the current best solution is satisfied, this process is stopped, and the best order of individual waypoints is output. The population size defines the GA’s convergence speed. If the size of populations is large, then the GA slows down [36].
During the GA construction process, we chose 60 chromosomes as the initial population since a population size of 50–100 is commonly used in normal GA problems and this population size provides a decent diversity in chromosome genes and it is a considerably small size, which speeds up the computational process.
Currently, the setup of chromosomes in our GA is straight-forward. Since all the waypoints have already been labelled, each chromosome consists of a sequence of the indices of the waypoints that the robot is going to visit. In this scenario, performing a single locus gene change for the mutation process will result in a waypoint being visited twice while another waypoint is unvisited. Therefore, we perform a mutation swap similar to a 2-opt algorithm during the GA process. This process produces an offspring that inherits most of its parent’s genes but with two random waypoints swapped. During the GA process of our proposed scenario, crossover is not included in the pseudocode due to a similar waypoint re-visiting issue.
Moreover, the cost weight between waypoints affects the decision for selecting the best children. The proposed cost function as per Equation (2) is feasible to model our hTetro platform. As a result, the GA with TSP works well with all dynamic environments, and is applicable in reconfigurable robots with specific angular movements.
| Algorithm 2: Genetic Algorithm |
| 1 Function GENETIC ALGORITHM {tileset, tiling waypoints locations}: |
| 2Define the location of the reference block |
| 3Define the cost function between two waypoints. |
| 4Initialize the random waypoints of the population. |
| 5 While (Stop condition is not satisfied) DO |
| 6 Select parents: possible trajectories to connect all waypoints from the population. |
| 7 Produce children: from the parent trajectories which are selected. |
| 8 Mutate: perform swap mutation between two random waypoints |
| 9 Extend: the population size by adding the best children to the population. |
| 10 Reduce: the population extension. |
| 11 end |
| 12Output the optimal order of each waypoint. |
| End Function |
5. Experimental Results
To evaluate the performance of the proposed motion planning framework to cover the predefined areas given the generated tilesets, the experimental workspaces on the simulated environment were partitioned as grids. The workspaces without obstacles had the column × row sizes 10 × 10, 8 × 7, and 6 × 6, and the workspace with obstacles presented as the number −1 had the size of 11 × 11. Specifically, the proposed technique was benchmarked with three conventional motion planning techniques used in complete path planning: zigzag, spiral, and greedy search. The comparison criteria included efficient path generation, time, and re-covering workspace to complete the generated paths. The simulations were conducted using MATLAB Simulink.
In part one of the experiments, we evaluated the path generation for each test, and the generated tiling patterns for workspaces are shown in Figure 12. Depending on the workspace size, the tiling theory can select the appropriate tiling shapes and orientations, that is, in Figure 12a the 9 tilesets of L, Z, J, O, and in Figure 12b the 25 tilesets of Z and T were used. Furthermore, considering the workspace with obstacles as in Figure 12d, the tileset was generated by selecting the appropriate tetromino types to cover all of the cells without obstacles. As a result of the row-wise search in Algorithm 1, in order to number the reference block b for each generated tileset as in Figure 13, each block location (a, b, c, d) on the workspaces is clearly visible. After four blocks of hTetro are located for each tiling pattern, the optimal path searching algorithm (GA for TSP) can generate the robot’s navigation trajectory to connect all the b blocks in each tiling pattern. The total associated costs and generated trajectory (directions) for each testbed are shown in Figure 13. Note that the cost weights as per Equation (2) with coefficients were applied to all the testbeds.
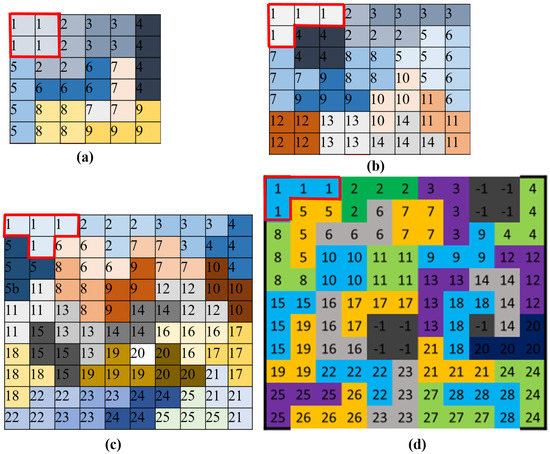
Figure 12.
Generated tileset for tested workspaces. (a) 6 × 6 workspace; (b) 8 × 7 workspace; (c) 10 × 10 workspace; (d) 11 × 11 workspace with obstacles.
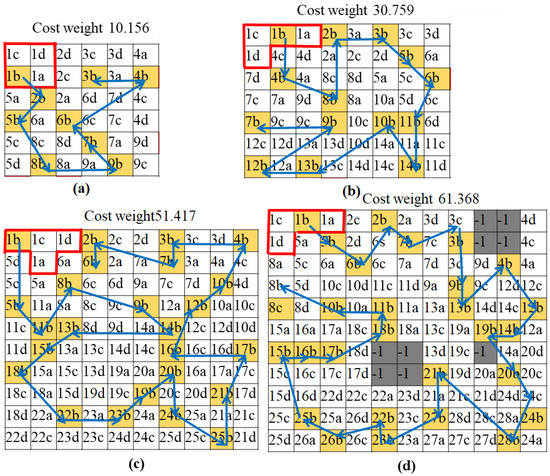
Figure 13.
Path generated for the different workspaces with different shapes. (a) Optimal path for 6 × 6; (b) Optimal path for 8 × 7; (c) Optimal path for 10 × 10; (d) Optimal path for 11 × 11.
Figure 14 shows the trajectories, and Table 1 provides the cost weights and running time generated by zigzag scanning, spiral scanning, and the greedy search method with 10,000 iterations and the proposed method for an 11 × 11 workspace grid with 28 waypoints, respectively. Note that the zigzag scanning method connects the waypoints by the one-row or two-rows-wise nearest searching. The spiral scanning methods connect waypoints from out-to-in by one-row (or column) and two-rows (or columns) based nearest searching. Zigzag and spiral are being mentioned and evaluated because they are the most prominent algorithms implemented in current mobile floor cleaning robots (especially the zigzag pattern algorithm). Demonstrating a different approach that has the potential to outperform existing robot navigation models is crucial for our future implementation. The greedy search provides only the choices for random trajectories from the initial waypoint and continuously searches for the next nearest reference waypoint to connect all the waypoints and selects the path with the lowest associated cost. As a result, the proposed method required a slightly longer running time than zigzag or spiral scanning and had a significantly lower running time than the greedy search. Regarding cost weight, the proposed method could generate the path with the lowest value.
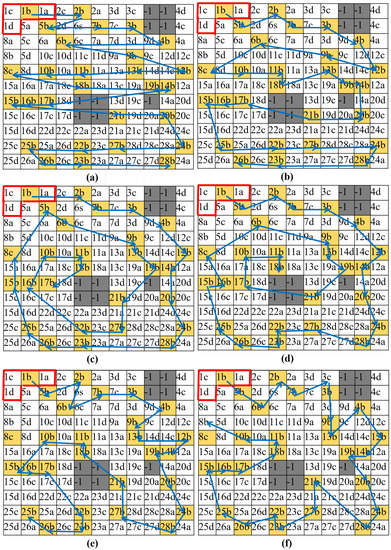
Figure 14.
Comparison results between methods for an 11 × 11 workspace. (a) Zigzag scanning 1 row order; (b) Zigzag scanning 2 row order; (c) Spiral scanning 1 row order; (d) Spiral scanning 2 row order; (e) Greedy search; (f) Proposed method.

Table 1.
Comparison results of path planning strategies.
Although the zigzag and spiral scanning methods could give the solution to tile the predefined area almost instantly, they produced the longest travel path regarding the hTetro block movement. As a result, to finish the generated trajectory of these methods, time spent to travel was significantly high. Besides, the greedy search took the most time to create a path connecting all waypoints and its generated cost weight was also higher than the proposed method. Although taking a slightly longer time than zigzag and spiral scanning to generate the path as a results of optimization processes, the proposed method yielded the lowest cost function and it could considerably reduce the time and energy consumed when robot traveled to cover the workspace. It can be said that the proposed method gives a compromise solution between time spent to generate the traveling sequence and time spent to complete the plan. This proves that the TSP in combination with GA is feasible and suitable to generate navigation trajectories for this reconfigurable robot.
The effects of changing the coefficient values in cost function (2) were considered. Figure 15 and Table 2 show the results of different coefficient settings. As one can see, the different paths with corresponding associated costs were generated for different coefficient values. Figure 15a where value was set to one and others (i.e., ) were set to zero shows that if we consider one given optimal path generated with the cost function of only b, the cost weight considering four blocks of this path is considerably higher. Furthermore, considering one workspace size, tiling theory worked well to generate different tiling patterns. Figure 16a,b show the two tilesets with their optimal path planning and corresponding costs required to cover the grid space by tiling theory, and Figure 16c is the tileset for only the O configuration. Given the tiling pattern O and the workspace as in Figure 12, the O configuration could completely tile Figure 12a by the path in Figure 16c without re-visited areas, yielding lower cost weight than paths with several tiling patterns generated by the tiling theory in Figure 16a,b. Hoverer, the O configuration could only completely tile Figure 12b,c with several revisited areas, and failed to completely tile Figure 12d with obstacles. In this paper, we suggest the tiling theory as the autonomous framework to ensure complete tiling of the workspace without revisiting grid cells since these are two of the most important aspects of cleaning robots. Table 3 gives the results of cost weights for two possibilities of tileset for each tested workspace. Based on the available options of tiling patterns suggested by the tiling theory, several of the optimal navigation sequences associated with the minimum of the defined cost weight for different tilesets were acquired by proposed trajectory generation. Then, the robot could choose the appropriate tileset considering the minimization the sum of each block displacements and according to our preferences in terms of time efficiency and energy efficiency to cover the predefined workspace.
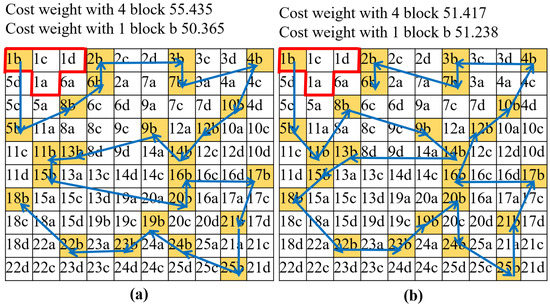
Figure 15.
Paths generation for hTetro. (a) Path considering only block b; (b) Path considering all four blocks.

Table 2.
Cost weight comparision between cost function of blocks for 10 × 10 workspace.
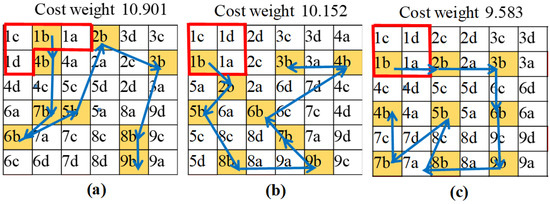
Figure 16.
Paths generation for different tilesets with the same 6 × 6 workspace. (a) Optimal path consisting of L, S, J, O, Z; (b) Optimal path consisting of O, I J, L; (c) Optimal path consisting of only O.

Table 3.
Cost weight comparison between different tilesets for the same workspace.
In part two of the experiments, the simulator initiated the robot’s navigation right after applying the specific path planning technique to complete the predefined tileset. The testbed square area was converted into an 11 × 11 grid with the obstacles set similarly to the arrangement in Figure 13d. Since the workspace cell was equal to a 25 × 25 cm hTetro block, the dimension of the workspace was 275 × 275 cm. The performance of the strategies was evaluated based on two criteria, including the total distance traveled and the average grid coverage time of each algorithm. Figure 17 shows the simulation workspace environment, the waypoints are marked as red dots, and robot’s navigation path to clear the waypoints one-by-one were tracked. The paths generated by all test methods are shown in Figure 14. The total distance traveled was determined based on the trajectories of all four hTetro blocks throughout the navigation process and calculated by averaging the final values of the trajectories once the navigation terminated. To calculate the average grid coverage time of a navigation strategy, we assumed that each grid in the workspace required at least 1 s to be covered by an hTetro block. Since the robot moved at a constant speed during the simulation, the Simulink could calculate the total time spent by hTetro blocks on an individual grid, and the average grid coverage time accordingly. The average grid coverage time is an important criterion which determines the efficiency of the proposed path planning algorithm in terms of area re-covered.
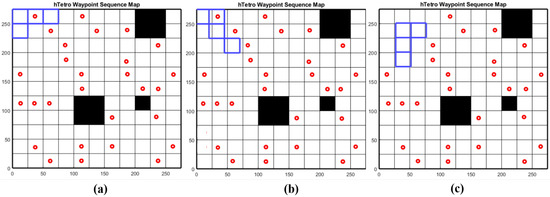
Figure 17.
Simulation workspace environment. (a) Robot at first waypoint; (b) Robot transformation on workspace; (c) Robot navigate to clear the next waypoint.
During the robot’s navigation, the simulator generated a grid coverage heat map. The robot coverage heat map includes the areas that were covered by the hTetro robot and are represented in a color spectrum between green to red and normalized to the range from 0 to 255. The intensity of the red increases when more time is spent by the robot to cover the area, indicating that the corresponding grid is being visited several times throughout the entire navigation process. The coverage heat maps generated for all tested variants (i.e., zigzag, spiral, greedy search navigation technique, and the proposed method) are shown in Figure 18. The numerical results of grid traveling distance and the grid coverage time are provided in Table 4. According to the results demonstrated in Table 4, our proposed path planning strategy had an advantage compared to the other coverage algorithms, with the smallest average grid coverage time, and the shortest distance traveled. In order to have the additional information from the heat map of Figure 18, Figure 19 illustrates the recovered area traveled versus all four algorithms by plotting the color values in Figure 18 which were larger than 100 and 150. Note that the 11 × 11 workspace consisted of 121 cells, and the average pixel values of cells were considered to determine the re-covered areas. Since the intensity value of cells increased if the robot spent time to stay or re-visited the cells during navigation and transformation, the greater the number of cells in Figure 19, the more re-covered areas in the considered method. We added the results in Table 5 to summarize the re-covered grid cells in percentage format for the 11 × 11 workspace with obstacles. It was observed that the re-covered distance traveled in the proposed method yielded the lowest value of re-coverage percentage. The re-covered distance traveled of the proposed method was approximately 5% less than greedy search and approximately 12% less than zigzag and spiral methods.
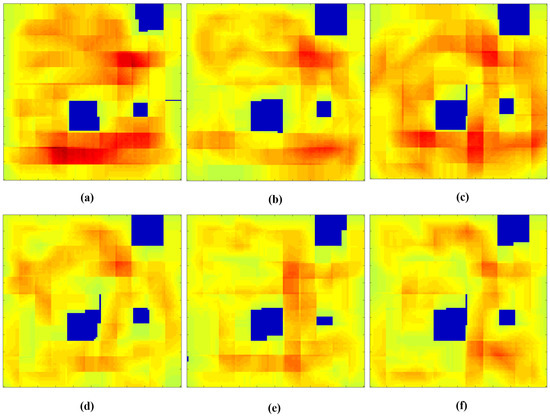
Figure 18.
Heat map output of each considered algorithm for 11 × 11 workspace. (a) Zigzag scanning 1 row order; (b) Zigzag scanning 2 row order; (c) Spiral scanning 1 row order; (d) Spiral scanning 2 row order; (e) Greedy search; (f) Proposed method.

Table 4.
Path planning performance of navigation simulation.
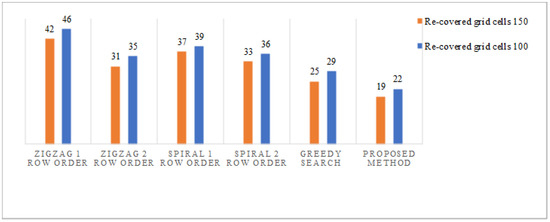
Figure 19.
The area re-covered comparison.

Table 5.
Comparison results of percentage re-covered area from the heat-map, with different simulation environment thresholds.
6. Discussion and Future Works
In the present paper, we would like to address that the proposed shape-shifting robot could accomplish complete area coverage through tiling theory together with waypoint sequencing that connects the Tetris patterns. Our contribution is that we modeled the navigation sequence generation for our special Tetris-inspired reconfigurable floor-cleaning robot to complete tilesets by tetromino tiling theory as a TSP problem. Note that in our previous work, the benchmark outperformed hTetro with fixed-form robots in terms of the percentage of area coverage. The present work is the first time we considered the efficiency of navigation distance to completely cover a given workspace. Our main focus was to present a reliable and scalable framework that is capable of achieving these goals and is applicable to other reconfigurable robots in order to achieve maximum area coverage tasks while minimizing energy consumption. GA fills in the missing link between the unsequenced waypoint series to a full path for robot navigation since it is one of the fastest approaches to reach the solution for the TSP, and is scalable.
For real-time deployment, besides using GA as one of the fastest algorithms to solve the TSP, we suggest that cellular decomposition as in [9] can be applied to segment large and complicated workspaces to several simple grid-based sub-workspaces before applying the proposed path planning framework. Furthermore, to balance the cost weight and path generating time, a running time threshold can be set for drawing the GA’s solution to a given sub-workspace. We can deploy the trial-and-error approach within our hTetro platform system configuration to find the optimal path generation time for each workspace size.
Moving forward, we have identified the efficiency optimization of the entire process as a definite priority for future works. Since the proposed complete path planning framework is essentially a two-step process (i.e., waypoint generating and waypoint sequencing), consider the following example: the waypoint generator can tile a square-shaped area using all O-shaped morphology, all L-shaped morphology, and a combination of several morphologies. The path planning strategy has to ensure the maximization of area coverage while limiting the revisited areas, and it is one of the most important tasks of a cleaning robot. However, it is apparent that the fewer times the robot changes its morphology during the navigation process, the total cost of the entire process is lower. The current tiling strategy based on tiling theory that we implemented herein is unable to identify this, since it simply focuses on the generation of a tileset that covers the area completely, which makes the search for an optimal algorithm with ideal parameters for pure waypoint sequencing a priority for further research in the future. The formulation of this entire efficiency optimization problem is interesting, and will be the within scope of another paper. Once the model is constructed, genetic algorithms with different mutation rates and crossover rate settings will be considered, and other evolutionary algorithms such as ant colony algorithms will be evaluated to identify the best optimization technique that yields the ideal results.
7. Conclusions
Tiling theory in combination with GA and the TSP is applied in robotics as a feasible method for complete path planning, and is utilized during the shifting mechanism of the Tetris-inspired self-reconfigurable robot hTetro in this paper. The proposed tiling motion planning algorithm exploiting robot kinematic design had the shortest distance traveled and shortest grid coverage time compared to the other algorithms tested in most scenarios during navigation without revisiting the same grid twice. With the reliable and consistent outcome of the proposed algorithm in this simulation, we can safely conclude that this is currently a feasible algorithm that can be adapted into physical robots for integration and real-world experiments. The proposed framework can extend to other polyomino-based robot platforms. Future research will focus on developing cost functions considering the obstacles in between pairs of waypoints, effects of friction, motor type, robot mass, and the real-time testing of hTetro with these considerations.
Author Contributions
Conceptualization, A.V.L.; Data curation, A.V.L. and P.-C.K.; Formal analysis, A.V.L. and M.A.; Investigation, A.V.L. and P.V.; Methodology, A.V.L., P.V., and P.-C.K.; Project administration, R.E.M.; Supervision, R.E.M.; Validation, R.E.M.; Writing—original draft, A.V.L. and V.S.; Writing—review & editing, M.A., T.H.Q.M., V.S. and R.E.M.
Funding
This research was funded by the National Robotics R&D Program Office, Singapore, under Grant No. RGAST102, the Singapore University of Technology and Design (SUTD) which are gratefully acknowledged to conduct this research work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marketsandmarkets. Cleaning Robot Market by Type, Product (Floor-Cleaning Robot, Lawn-Cleaning Robot, Pool-Cleaning Robot, Window-Cleaning Robot), Application (Residential, Commercial, Industrial, Healthcare), and Geography—Global Forecast to 2023. 2018. Available online: https://www.marketsandmarkets.com/Market-Reports/cleaning-robot-market-22726569.html (accessed on 5 October 2018).
- Gao, X.; Li, K.; Wang, Y.; Men, G.; Zhou, D.; Kikuchi, K. A floor cleaning robot using Swedish wheels. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO 2007), Sanya, China, 15–18 December 2007; pp. 2069–2073. [Google Scholar]
- Yang, S.X.; Luo, C. A neural network approach to complete coverage path planning. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 718–724. [Google Scholar] [CrossRef]
- Fink, J.; Bauwens, V.; Kaplan, F.; Dillenbourg, P. Living with a vacuum cleaning robot. Int. J. Soc. Robot. 2013, 5, 389–408. [Google Scholar] [CrossRef]
- Luo, C.; Yang, S.X. A real-time cooperative sweeping strategy for multiple cleaning robots. In Proceedings of the 2002 IEEE International Symposium on Intelligent Control, Vancouver, BC, Canada, 30 October 2002; pp. 660–665. [Google Scholar]
- Zelinsky, A.; Jarvis, R.A.; Byrne, J.; Yuta, S. Planning paths of complete coverage of an unstructured environment by a mobile robot. In Proceedings of the International Conference on Advanced Robotics, Tokyo, Japan, 8–9 November 1993; Volume 13, pp. 533–538. [Google Scholar]
- Gabriely, Y.; Rimon, E. Spanning-tree based coverage of continuous areas by a mobile robot. Ann. Math. Artif. Intell. 2001, 31, 77–98. [Google Scholar] [CrossRef]
- Xu, L. Graph Planning for Environmental Coverage. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2011. [Google Scholar]
- Jin, J.; Tang, L. Coverage path planning on three-dimensional terrain for arable farming. J. Field Robot. 2011, 28, 424–440. [Google Scholar] [CrossRef]
- Cheng, P.; Keller, J.; Kumar, V. Time-optimal UAV trajectory planning for 3D urban structure coverage. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2008), Nice, France, 22–26 September 2008; pp. 2750–2757. [Google Scholar]
- Galceran, E.; Carreras, M. Planning coverage paths on bathymetric maps for in-detail inspection of the ocean floor. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 4159–4164. [Google Scholar]
- Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decomposition. In Field and Service Robotics; Springer: Berlin, Germany, 1998; pp. 203–209. [Google Scholar]
- Acar, E.U.; Choset, H.; Rizzi, A.A.; Atkar, P.N.; Hull, D. Morse decompositions for coverage tasks. Int. J. Robot. Res. 2002, 21, 331–344. [Google Scholar] [CrossRef]
- Lumelsky, V.J.; Mukhopadhyay, S.; Sun, K. Dynamic path planning in sensor-based terrain acquisition. IEEE Trans. Robot. Autom. 1990, 6, 462–472. [Google Scholar] [CrossRef]
- Oksanen, T.; Visala, A. Coverage path planning algorithms for agricultural field machines. J. Field Robot. 2009, 26, 651–668. [Google Scholar] [CrossRef]
- Choset, H.; Burdick, J. Sensor-based exploration: The hierarchical generalized voronoi graph. Int. J. Robot. Res. 2000, 19, 96–125. [Google Scholar] [CrossRef]
- Acar, E.U.; Choset, H. Robust sensor-based coverage of unstructured environments. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 61–68. [Google Scholar]
- Acar, E.U.; Choset, H. Sensor-based coverage of unknown environments: Incremental construction of morse decompositions. Int. J. Robot. Res. 2002, 21, 345–366. [Google Scholar] [CrossRef]
- Wong, S.C.; MacDonald, B.A. A topological coverage algorithm for mobile robots. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; Volume 2, pp. 1685–1690. [Google Scholar]
- Butler, Z.J.; Rizzi, A.A.; Hollis, R.L. Contact sensor-based coverage of rectilinear environments. In Proceedings of the 1999 IEEE International Symposium on Intelligent Control/Intelligent Systems and Semiotics, Cambridge, MA, USA, 17 September 1999; pp. 266–271. [Google Scholar]
- Hameed, I.; Bochtis, D.; Sorensen, C. Driving angle and track sequence optimization for operational path planning using genetic algorithms. Appl. Eng. Agric. 2011, 27, 1077–1086. [Google Scholar] [CrossRef]
- Gabriely, Y.; Rimon, E. Spiral-stc: An on-line coverage algorithm of grid environments by a mobile robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’02), Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 954–960. [Google Scholar]
- Hsu, P.M.; Lin, C.L.; Yang, M.Y. On the complete coverage path planning for mobile robots. J. Intell. Robot. Syst. 2014, 74, 945–963. [Google Scholar] [CrossRef]
- Gonzalez, E.; Alarcon, M.; Aristizabal, P.; Parra, C. BSA: A coverage algorithm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; Volume 2, pp. 1679–1684. [Google Scholar]
- Gonzalez, E.; Alvarez, O.; Diaz, Y.; Parra, C.; Bustacara, C. BSA: A complete coverage algorithm. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation (ICRA 2005), Barcelona, Spain, 18–22 April 2005; pp. 2040–2044. [Google Scholar]
- Lee, H.Y.; Shin, H.; Chae, J. Path Planning for Mobile Agents Using a Genetic Algorithm with a Direction Guided Factor. Electronics 2018, 7, 212. [Google Scholar] [CrossRef]
- Tan, N.; Mohan, R.E.; Elangovan, K. Scorpio: A biomimetic reconfigurable rolling–crawling robot. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416658180. [Google Scholar] [CrossRef]
- Nansai, S.; Rojas, N.; Elara, M.R.; Sosa, R. Exploration of adaptive gait patterns with a reconfigurable linkage mechanism. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 4661–4668. [Google Scholar]
- Veerajagadheswar, P.; Elara, M.R.; Pathmakumar, T.; Ayyalusami, V. A Tiling-Theoretic Approach to Efficient Area Coverage in a Tetris-Inspired Floor Cleaning Robot. IEEE Access 2018, 6, 35260–35271. [Google Scholar] [CrossRef]
- Kee, V.; Rojas, N.; Elara, M.R.; Sosa, R. Hinged-Tetro: A self-reconfigurable module for nested reconfiguration. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Besacon, France, 8–11 July 2014; pp. 1539–1546. [Google Scholar]
- Le, A.; Prabakaran, V.; Sivanantham, V.; Mohan, R. Modified A-Star Algorithm for Efficient Coverage Path Planning in Tetris Inspired Self-Reconfigurable Robot with Integrated Laser Sensor. Sensors 2018, 18, 2585. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.H.; Lagarias, J.C. Tiling with polyominoes and combinatorial group theory. J. Comb. Theory Ser. A 1990, 53, 183–208. [Google Scholar] [CrossRef]
- Jho, C.W.; Lee, W.H. Video Puzzle Game Application of Polyomino Re-tiling. In Embedded and Multimedia Computing Technology and Service; Springer: Berlin, Germany, 2012; pp. 363–369. [Google Scholar]
- Lo, K.Y.; Fu, C.W.; Li, H. 3D polyomino puzzle. ACM Trans. Graph. 2009, 28, 157. [Google Scholar] [CrossRef]
- Lin, S.; Kernighan, B.W. An effective heuristic algorithm for the traveling-salesman problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef]
- Larranaga, P.; Kuijpers, C.M.H.; Murga, R.H.; Inza, I.; Dizdarevic, S. Genetic algorithms for the travelling salesman problem: A review of representations and operators. Artif. Intell. Rev. 1999, 13, 129–170. [Google Scholar] [CrossRef]
- Geng, X.; Chen, Z.; Yang, W.; Shi, D.; Zhao, K. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search. Appl. Soft Comput. 2011, 11, 3680–3689. [Google Scholar] [CrossRef]
- Backtracking. A Polyomino Tiling Algorithm. 2018. Available online: https://gfredericks.com/gfrlog/99 (accessed on 28 October 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).