Reliability of Variable Speed Pumped-Storage Plant
Abstract
:1. Introduction
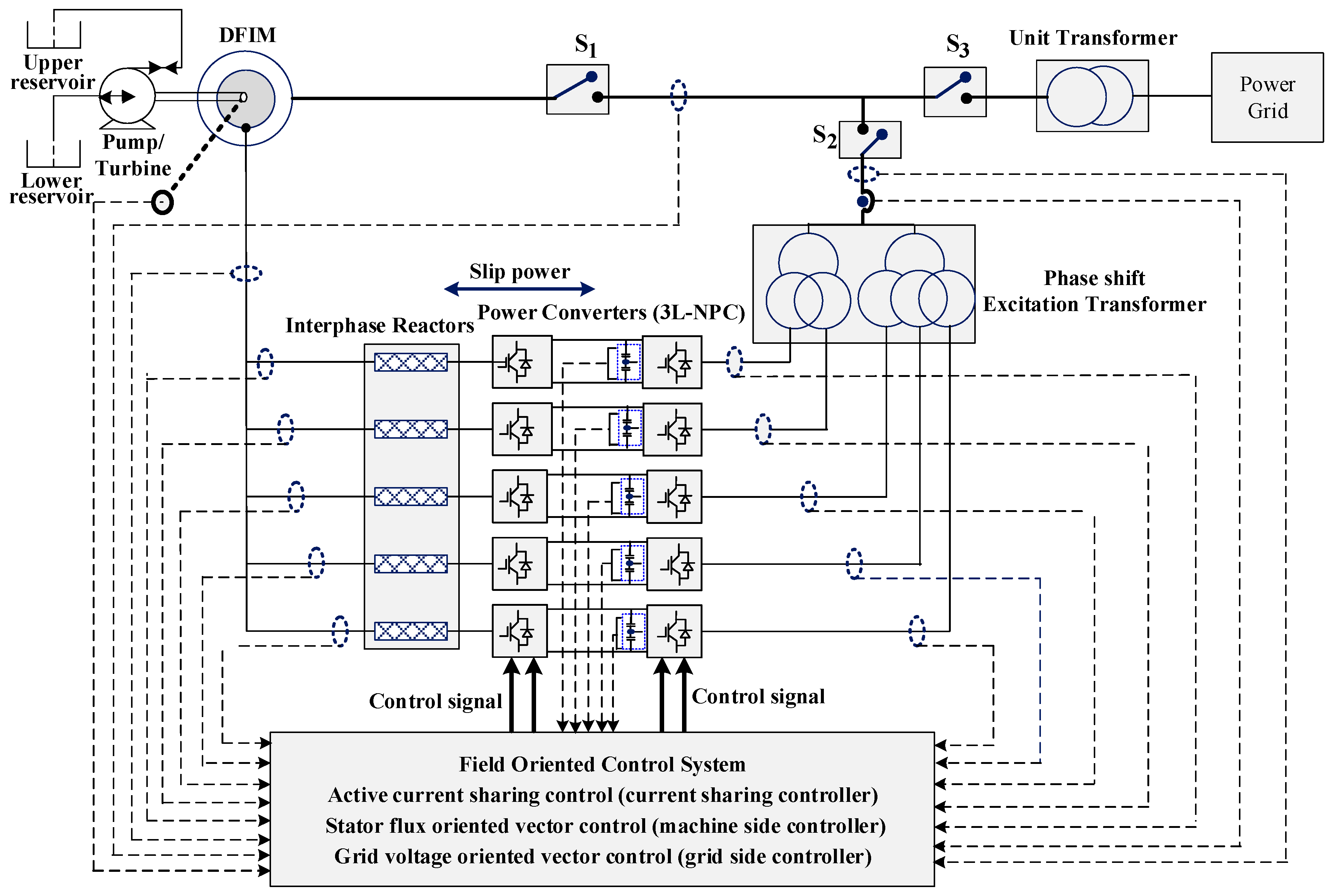
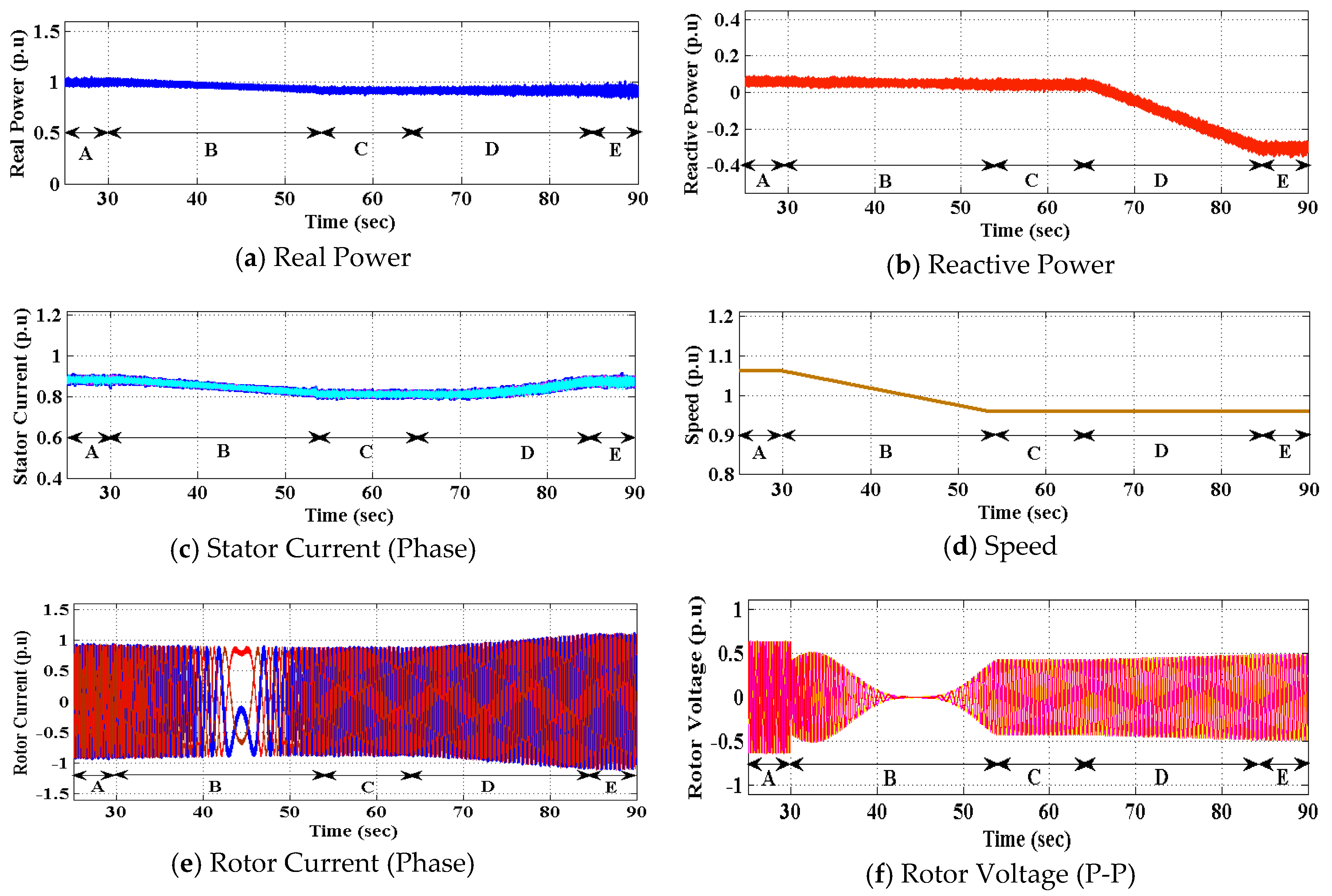
2. Survivability Analysis of a 250-MW Variable-Speed Unit
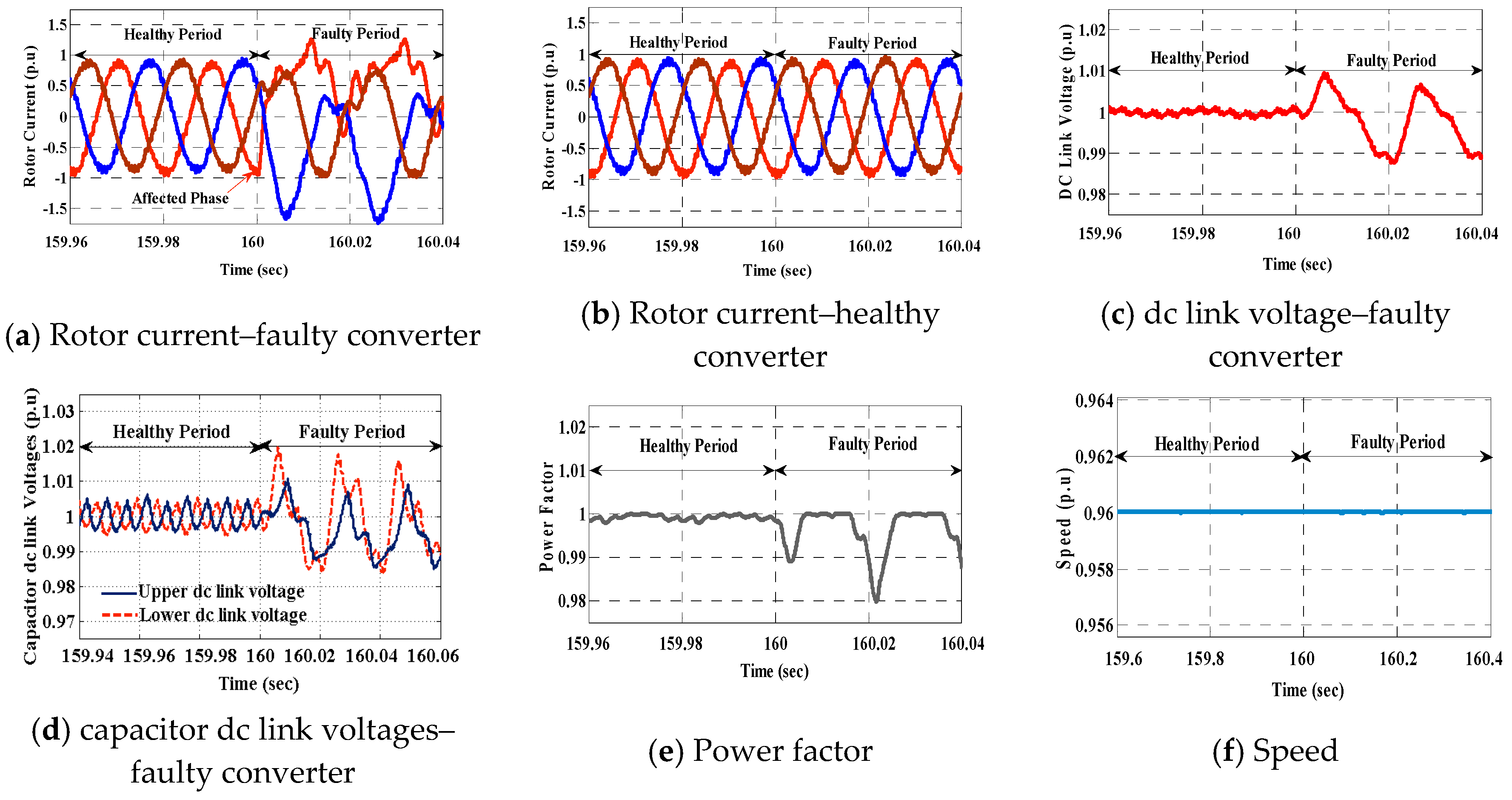
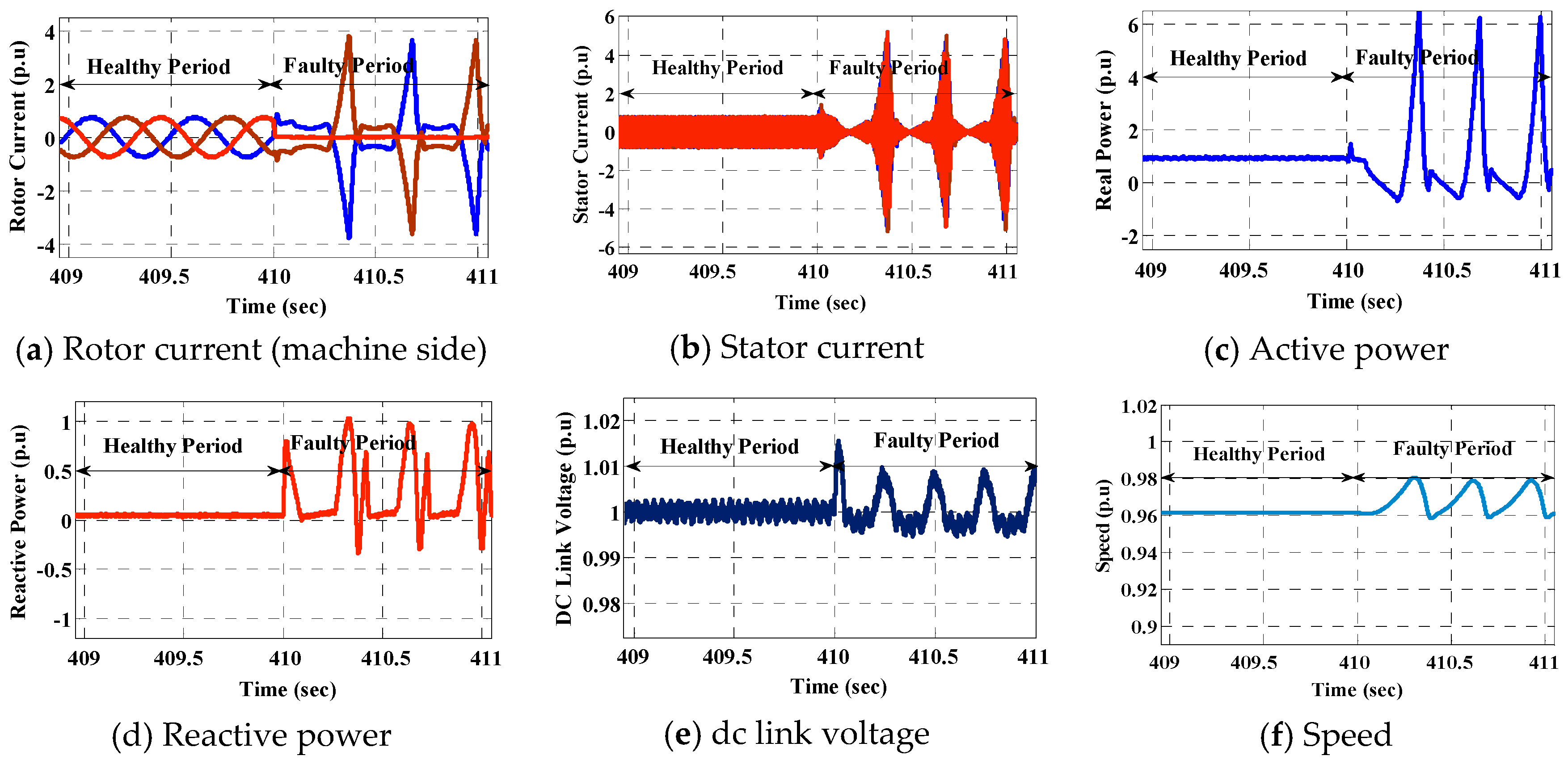
2.1. Converter Faults
2.2. Sensor Faults
2.3. Rotor Winding Faults
3. Markov Reliability Model
4. Reliability Calculation of a 250-MW DFIM Variable-Speed Unit
4.1. Power Converter Modelling
4.2. Sensor Modelling
4.3. Converter Control System
4.4. Transformer
4.5. Doubly Fed Induction Machine
4.6. Interphase Reactors
4.7. Circuit Breakers
4.8. Cooling System
4.9. Cabling
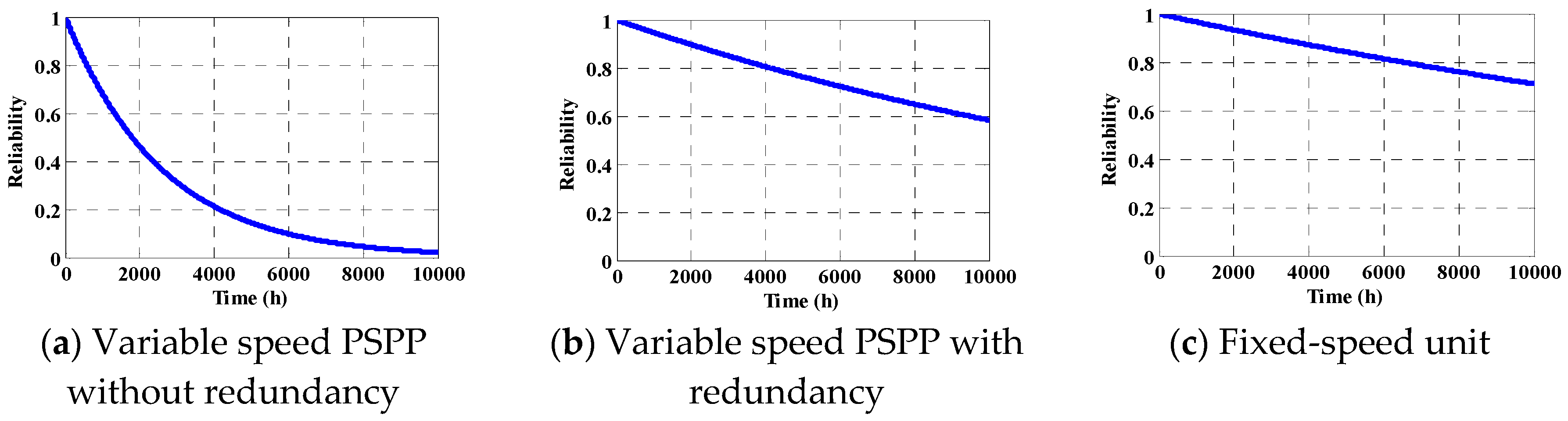
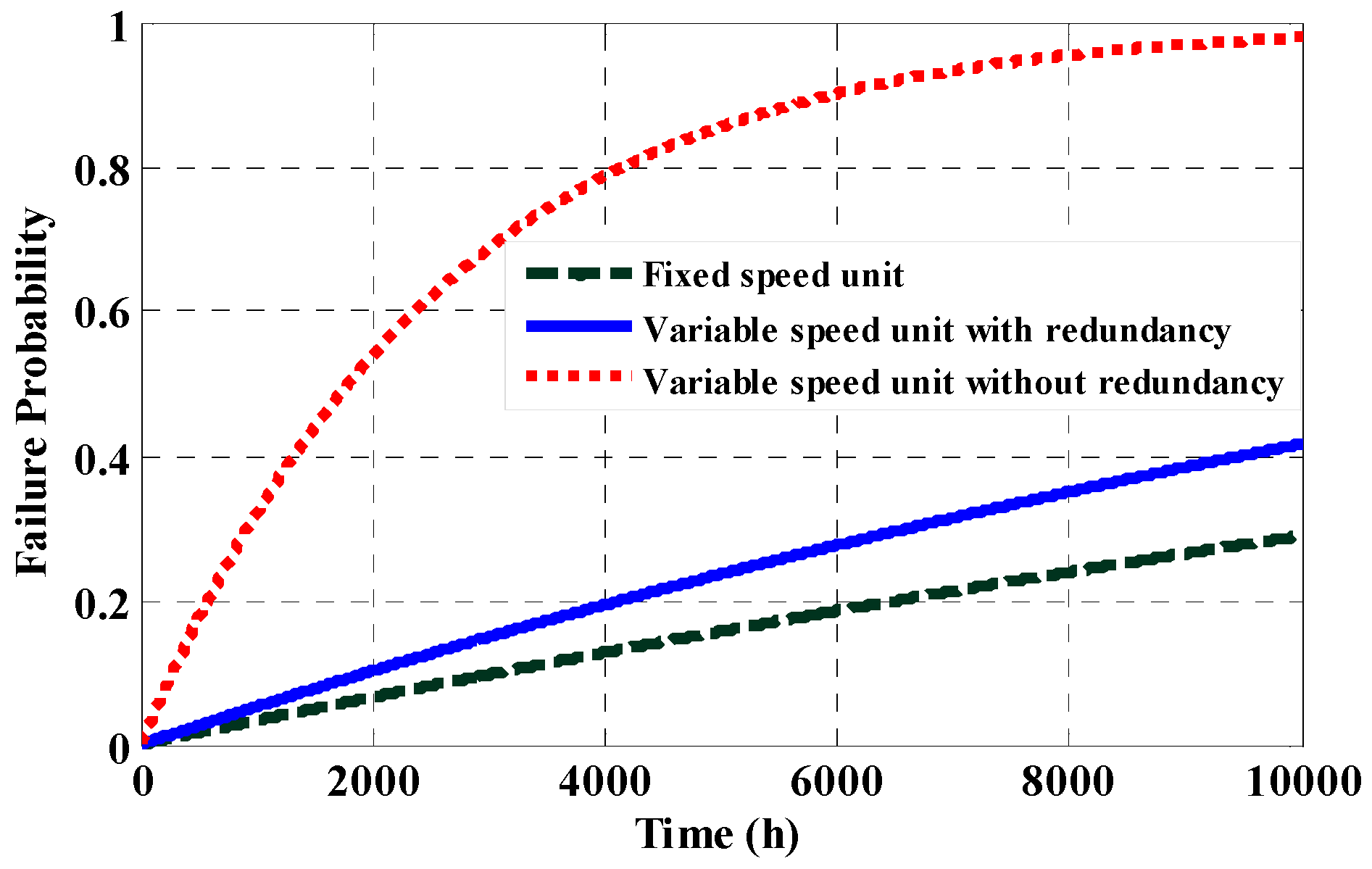
5. Reliability Estimation of a 250-MW DFIM Variable-Speed Unit
5.1. Reliability Calculation with Power and Control Redundancy
5.2. Reliability Calculation for Fixed-Speed Unit
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pérez-Diaz, I.; Chazarra, M.; González, J.G.; Cavazzini, G.; Stoppato, A. Trends and challenges in the operation of pumped-storage hydropower plants. J. Renew. Sustain Energy Rev. 2015, 44, 767–784. [Google Scholar] [CrossRef]
- Cavazzini, G.; Pérez-Diaz, J.I. Technological Developments for Pumped Hydro Energy Storage; Technic Report; European Energy Research Alliance: Brussels, Belgium, 2014; pp. 1–128. [Google Scholar]
- Energy Storage Association. Variable Speed Pumped Hydroelectric Storage; Technic Report; Energy Storage Association: Washington, DC, USA, 2018. [Google Scholar]
- United States Department of Energy Global Energy Storage Database. Pumped Storage Plant; Technic Report; United States Department of Energy Global Energy Storage Database: Washington, DC, USA, February 2017. [Google Scholar]
- Toshiba Energy Systems & Solutions. Adjustable Speed Pumped Storage Plant—Advantages of Adjustable Speed and Quick Response; Technic Report; Toshiba Energy Systems & Solutions: Kanagawa, Japan, 2018; pp. 1–24. [Google Scholar]
- Lefebvre, N.; Tabarin, M.; Teller, O. A solution to intermittent renewables using pumped hydropower. Renew. Energy World Mag. May 2015, 3, 50–53. [Google Scholar]
- Schlunegger, H.; Oberhasli, A.T. 100 MW Full-Size Converter in the Grimsel 2 Pumped-Storage Plant; Technic Report; Oberhasli Hydroelectric Power Company: Innertkirchen, Switzerland, 2013. [Google Scholar]
- Lung, K.L.; Hung, Y.; Lu, W.; Kao, W.S. Modeling and dynamic simulations of doubly fed adjustable-speed pumped storage units. IEEE Trans. Energy Convers. 2007, 22, 250–258. [Google Scholar] [CrossRef]
- Kuwabara, T.S.; Furuta, A.; Kita, H.; Mitsuhashi, E. Design and dynamic response characteristics of 400MW adjustable speed pumped storage unit for Ohkawachi power station. IEEE Trans. Energy Convers. 1996, 11, 376–384. [Google Scholar] [CrossRef]
- Joseph, A.; Chelliah, T.R. A Review of Power Electronic Converters for Variable Speed Pumped Storage Plants: Configurations, Operational Challenges and Future Scopes. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 103–119. [Google Scholar] [CrossRef]
- An, C.; Lloyd, G.J.; Smith, B.; Zou, L.; Girardot, E.; Schwery, A.; Wechsler, A.; Perugini, G.; Kawkabani, B. Design and testing of a new protection relay for variable speed DFI motor generators. In Proceedings of the 12th IET International Conference Developments in Power System Protection, Copenhagen, Denmark, 31 March–3 April 2014; pp. 1–6. [Google Scholar]
- Dujic, D. Pumped Hydro Storage Power Plants Emulation Platform. Power Electronics Laboratory-News, 19 January 2018. [Google Scholar]
- Joseph, A.; Desingu, K.; Semwal, R.R.; Chelliah, T.R.; Khare, D. Dynamic performance of pumping mode of 250 MW variable speed hydro-generating unit subjected to power and control circuit faults. IEEE Trans. Energy Convers. 2018, 33, 430–441. [Google Scholar] [CrossRef]
- Central Electricity Authority of India. Technical Standards for Connectivity to the Grid—Hydropower Plant; Technic Report; Central Electricity Authority of India: New Delhi, India, 2007. [Google Scholar]
- Jou, S.-T.; Lee, S.-B.; Park, Y.B.; Lee, K.-B. Direct power control of a DFIG in wind turbines to improve dynamic responses. J. Power Electron. 2009, 9, 781–790. [Google Scholar]
- Chwa, D.; Lee, K.-B. Variable structure control of the active and reactive powers for a DFIG in wind turbines. IEEE Trans. Ind. Appl. 2010, 46, 2545–2555. [Google Scholar] [CrossRef]
- Giaourakis, D.G.; Safacas, A.N. Effect of short-circuit faults in the back-to-back power electronic converter and rotor terminals on the operational behavior of the doubly-fed induction generator wind energy conversion system. J. Mach. 2015, 5, 2–26. [Google Scholar] [CrossRef]
- Saleh, S.A.; Aljankawey, A.S.; Abu-Khaizaran, M.S.; Alsayid, B. Influences of power electronic converters on voltage–current behaviors during faults in DGUs—Part I: Wind energy conversion systems. IEEE Trans. Ind. Appl. 2015, 51, 2819–2831. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, K.B.; Blaabjerg, F. Open-switch fault detection method of a back-to-back converter using NPC topology for wind turbine systems. IEEE Trans. Ind. Appl. 2015, 51, 325–335. [Google Scholar] [CrossRef]
- Shevchuk, V.P. Investigations of the operation reliability increase of the alternating current electric machines in diamond extractive industries. In Proceedings of the 8th International Scientific and Practical Conference of Students, Post-graduates and Young Scientists Modern Technique and Technologies, Tomsk, Russia, 12 April 2002; pp. 103–104. [Google Scholar]
- Lopez, J.; Sanchis, P.; Roboam, X.; Marroyo, L. Dynamic behavior of the doubly fed induction generator during three-phase voltage dips. IEEE Trans. Energy Convers. 2007, 22, 709–717. [Google Scholar] [CrossRef]
- Hu, S.; Lin, X.; Kang, Y.; Zou, X. An improved low-voltage ride-through control strategy of doubly fed induction generator during grid faults. IEEE Trans. Power Electron. 2011, 26, 3653–3665. [Google Scholar] [CrossRef]
- Lee, S.B.; Lee, K.-B.; Lee, D.-C.; Kim, J.M. An improved control method for a DFIG in a wind turbine under an unbalanced grid voltage condition. J. Electr. Eng. Technol. 2010, 5, 614–622. [Google Scholar] [CrossRef]
- Oliver, J.A.; Poteet, D. High-speed, high-horsepower electric motors for pipeline compressors: Available ASD technology, reliability, harmonic control. IEEE Trans. Energy Convers. 1995, 3, 470–476. [Google Scholar] [CrossRef]
- Bozzo, R.; Fazio, V.; Savio, S. Power electronics reliability and stochastic performances of innovative ac traction drives: A comparative analysis. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 1–7. [Google Scholar]
- Klug, R.D.; Griggs, M. Reliability and availability of megawatt drive concepts. In Proceedings of the 2004 International Conference on Power System Technology, Singapore, 21–24 November 2004; pp. 665–671. [Google Scholar]
- Wikstrom, P.; Terens, L.A.; Kobi, H. Reliability, availability, and maintainability of high-power variable-speed drive systems. IEEE Trans. Ind. Appl. 2000, 36, 231–241. [Google Scholar] [CrossRef]
- Rausand, M.; Høyland, A. System Reliability Theory: Models, Statistical Methods, and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Joseph, A.; Selvaraj, R.; Chelliah, T.R.; Sarma, A. Starting and Braking of a Large Variable Speed Hydro- Generating Unit Subjected to Converter and Sensor Faults. IEEE Trans. Ind. Appl. 2018, 54, 3372–3382. [Google Scholar] [CrossRef]
- Friedli, T.; Kolar, J.; Rodriguez, J.; Patrick, W. Comparative evaluation of three-phase AC-AC matrix converter and voltage dc-link back-to-back converter systems. IEEE Trans. Ind. Electron. 2012, 59, 4487–4510. [Google Scholar] [CrossRef]
- Xie, K.; Jiang, Z.; Li, W. Effect of wind speed on wind turbine power converter reliability. IEEE Trans. Energy Convers. 2012, 27, 96–104. [Google Scholar] [CrossRef]
- Carroll, J.; McDonald, A.; McMillan, D. Failure rate, repair time and unscheduled O&M cost analysis of offshore wind turbines. Wind Energy 2016, 19, 1107–1119. [Google Scholar]
- Al Mamun, M.; Yoshizawa, D.; Mukunoki, M. Performance evaluation of a large capacity 3-level IEGT inverter. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, VIC, Australia, 3–6 June 2013; pp. 201–207. [Google Scholar]
- Bazzi, A.M.; Dominguez-Garcia, A.; Krein, P.T. Markov reliability modeling for induction motor drives under field-oriented control. IEEE Trans. Power Electron. 2012, 27, 534–546. [Google Scholar] [CrossRef]
- Molaei, M.; Oraee, H.; Fotuhi-Firuzabad, M. Markov model of drive motor systems for reliability calculation. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; pp. 2286–2291. [Google Scholar]
- Sodha, N.S. Power Transformers Failure Modes, Investigation & Prevention Techniques; Technic Report; Power Grid: Gurgaon, India, 2016. [Google Scholar]
- Siemens. Phase Shifting Transformer—Quality and Reliability; Technic Report; Siemens: Munich, Germany, 2018; pp. 1–10. [Google Scholar]

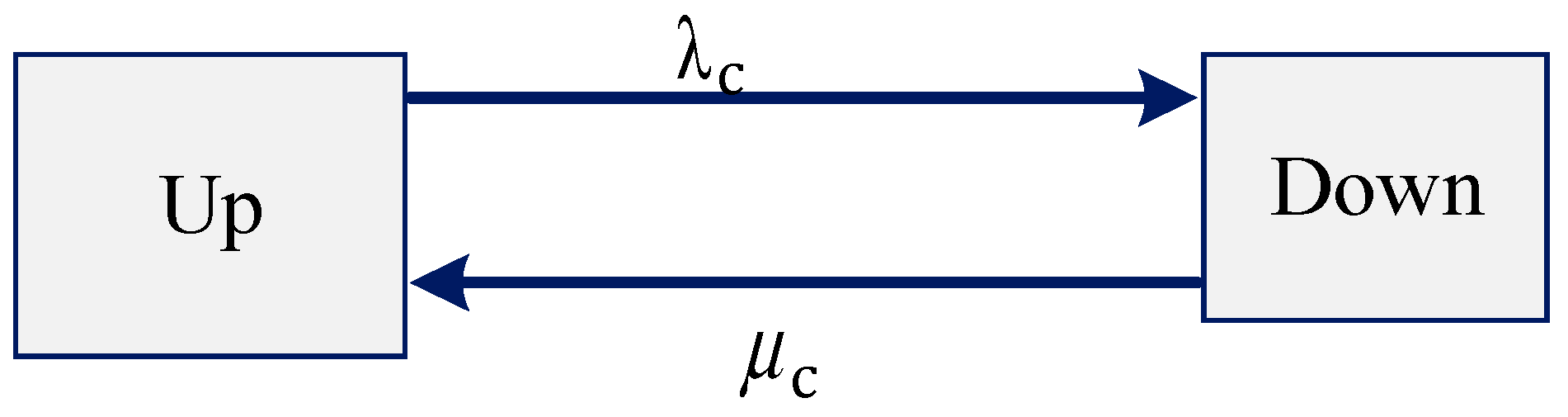
| System | Faults | Fault Status | |
|---|---|---|---|
| Power Converter | Machine side converter | Single Device/Leg Open Circuit Fault | F |
| Single Device/Leg Short Circuit Fault | F | ||
| Grid side converter | Single Device/Leg Open Circuit Fault | S | |
| Single Device/Leg Short Circuit Fault | F | ||
| DC Link | Open circuit/Short circuit | F | |
| System | Faults | Fault Status | |
|---|---|---|---|
| Sensors | Omission/saturation | Speed sensor | F |
| DC link voltage sensor | F | ||
| Reactive power signal | F | ||
| Single rotor Current Sensor | S | ||
| Single grid current sensor | S | ||
| Single grid voltage sensor | F | ||
| Gain/Bias | Speed sensor | F | |
| DC link voltage sensor | F | ||
| Reactive power signal | S | ||
| Single rotor Current Sensor | S | ||
| Single grid current sensor | F | ||
| Single grid voltage sensor | S | ||
| S.No | Components | Failure Rate (1 FIT = 1 Failure over 109 h) |
|---|---|---|
| 1 | Power IEGT | 100 FIT |
| 2 | Power Diode | 80 FIT |
| 3 | DC-Link Capacitance | 300 FIT |
| 4 | DC-Link | 45 FIT |
| S.No | Components | Failure Rate (1 FIT = 1 Failure over 109 h) |
|---|---|---|
| 1 | Grid Side Converter | 5562 FIT |
| 2 | Machine Side Converter | 46,040 FIT |
| S.No | Sensor | Type of Fault | Failure Rate (1 FIT = 1 Failure over 109 h) |
|---|---|---|---|
| 1 | Speed encoder | Omission | 740 |
| Gain | 190 | ||
| Bias | 420 | ||
| Constant | 190 | ||
| Noise | 190 | ||
| 2 | Current sensor | Omission/Gain/Bias/Constant/Noise | 100 |
| 3 | Voltage sensor | Omission/Gain/Bias/Constant/Noise | 160 |
| S.No | Components | Failure Rate (1 FIT = 1 Failure over 109 h) |
|---|---|---|
| 1 | Control power supply | 800 FIT |
| 2 | Binary I/O | 800 FIT |
| 3 | Main processing board | 800 FIT |
| 4 | Pulse processing board | 400 FIT |
| 5 | Communication board | 200 FIT |
| 6 | Operator panel | 400 FIT |
| 7 | Internal I/O board | 400 FIT |
| 8 | External I/O board | 800 FIT |
| S.No | Components | Fixed Speed PSPP (Single Channel Power Converter ****) | Variable Speed PSPP (Five Channel Power Converter ****) | ||||
|---|---|---|---|---|---|---|---|
| Without Redundancy | With Redundancy | ||||||
| Failure Rate | Reliability Chain | Failure Rate | Reliability Chain | Failure Rate | Reliability Chain | ||
| 1 | Power Converters | 4267 | Parallel * | 277,135 | Series | 36,950 | Parallel *** |
| 2 | Converter Control System | 3200 | Parallel * | 27,600 | Series | 3680 | Parallel *** |
| 3 | Sensors | 1620 | Parallel | 27,630 | Series/parallel ** | 27,630 | Series/Parallel ** |
| 4 | Machine | 8300 | Series | 14,040 | Series | 14,040 | Series |
| 5 | Power Transformer | 5940 | Series | 5940 | Series | 5940 | Series |
| 6 | Excitation Transformer | 5940 | Series | 20,790 | Series | 20,790 | Series |
| 7 | Interphase Reactors/Filters | 950 | Series | 4750 | Series | 4750 | Series |
| 8 | Circuit Breakers | 1920 | Series | 1920 | Series | 1920 | Series |
| 9 | Cooling System | 3200 | Series | 3200 | Series | 3200 | Series |
| 10 | Cabling | 800 | Series | 4000 | Series | 4000 | Series |
| S.No | Particulars | Pumped-Storage Power Plant Unit (250 MW) | ||
|---|---|---|---|---|
| Variable-Speed Unit | Fixed-Speed Unit | |||
| Without Redundancy | With Redundancy | |||
| 1 | MTTF (years) | 0.295 | 0.934 | 2.63 |
| 2 | Availability | 0.9775 | 0.9916 | 0.9964 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joseph, A.; Chelliah, T.R.; Lee, S.S.; Lee, K.-B. Reliability of Variable Speed Pumped-Storage Plant. Electronics 2018, 7, 265. https://doi.org/10.3390/electronics7100265
Joseph A, Chelliah TR, Lee SS, Lee K-B. Reliability of Variable Speed Pumped-Storage Plant. Electronics. 2018; 7(10):265. https://doi.org/10.3390/electronics7100265
Chicago/Turabian StyleJoseph, Anto, Thanga Raj Chelliah, Sze Sing Lee, and Kyo-Beum Lee. 2018. "Reliability of Variable Speed Pumped-Storage Plant" Electronics 7, no. 10: 265. https://doi.org/10.3390/electronics7100265
APA StyleJoseph, A., Chelliah, T. R., Lee, S. S., & Lee, K.-B. (2018). Reliability of Variable Speed Pumped-Storage Plant. Electronics, 7(10), 265. https://doi.org/10.3390/electronics7100265






