Free-Space Materials Characterization by Reflection and Transmission Measurements using Frequency-by-Frequency and Multi-Frequency Algorithms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Slab Scattering Model
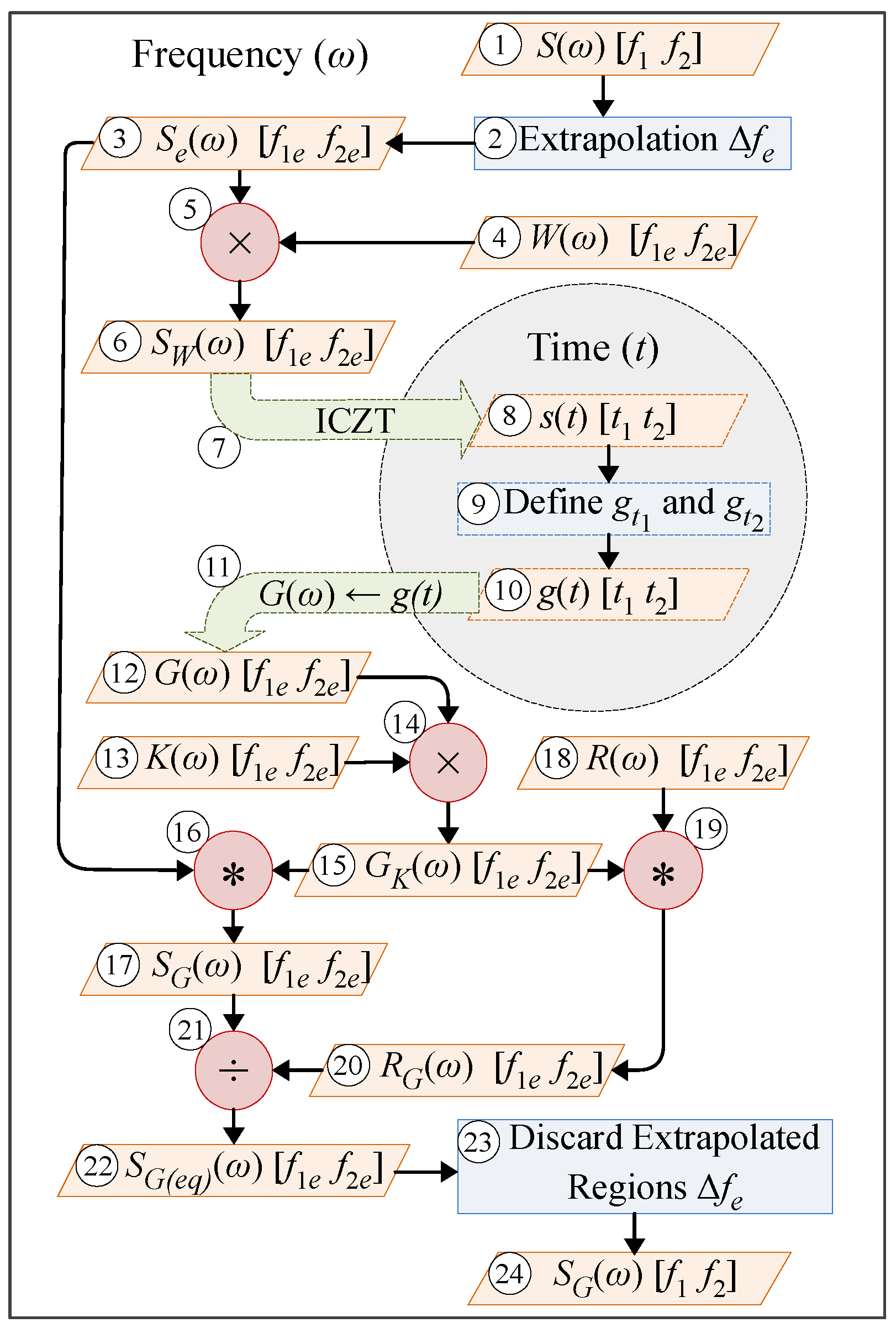
2.2. Multi-Frequency Extraction
2.3. Frequency-by-Frequency Extraction
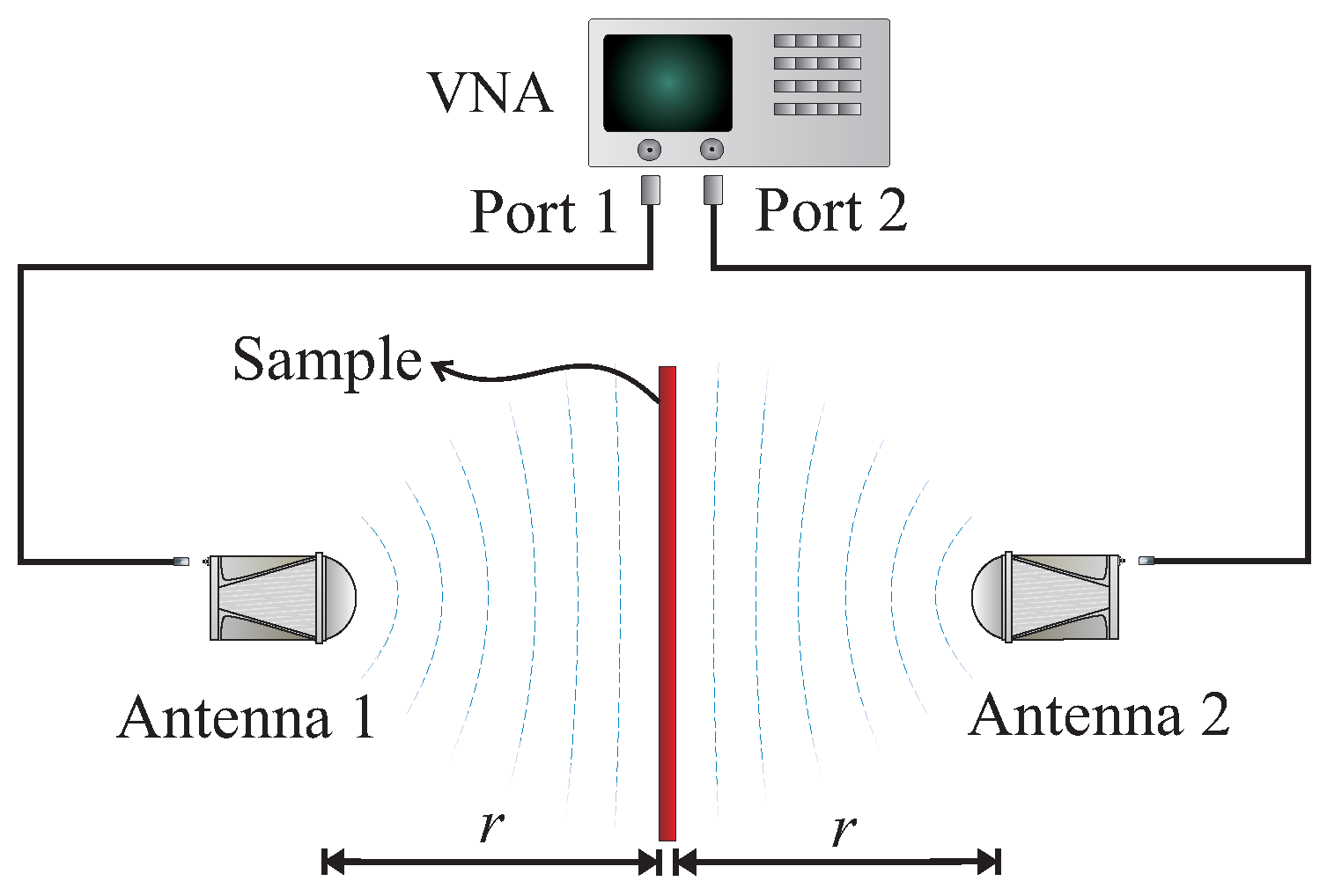
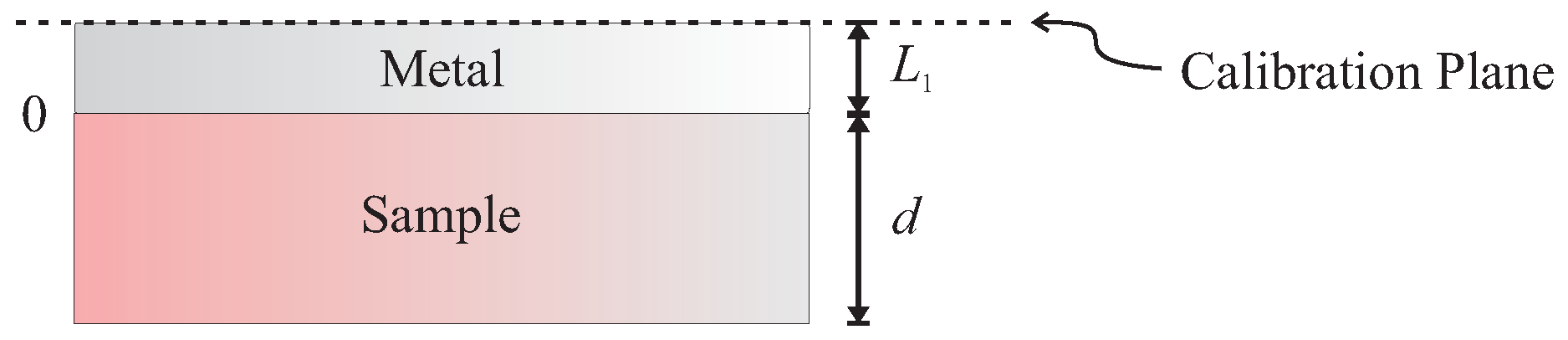
2.4. Experimental Setup
2.5. Calibration
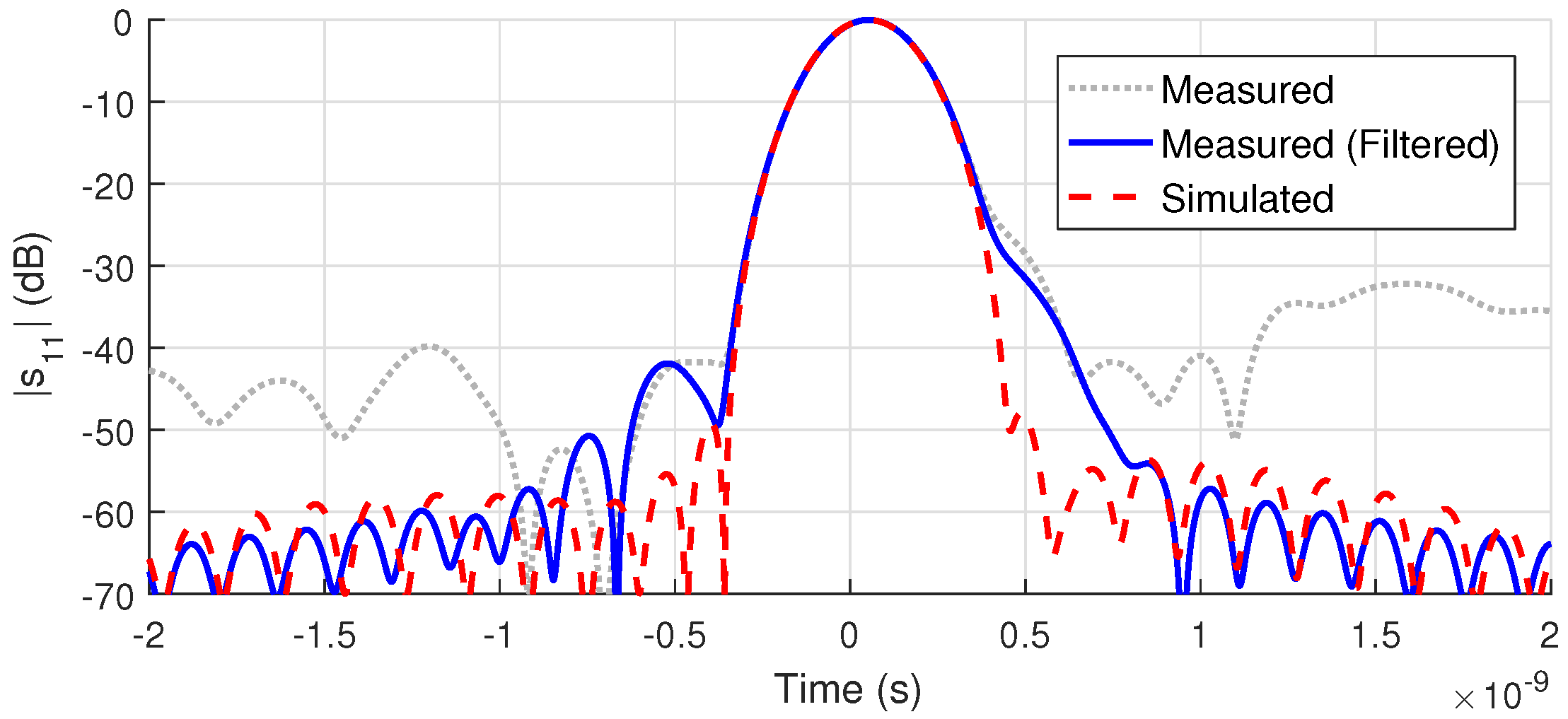
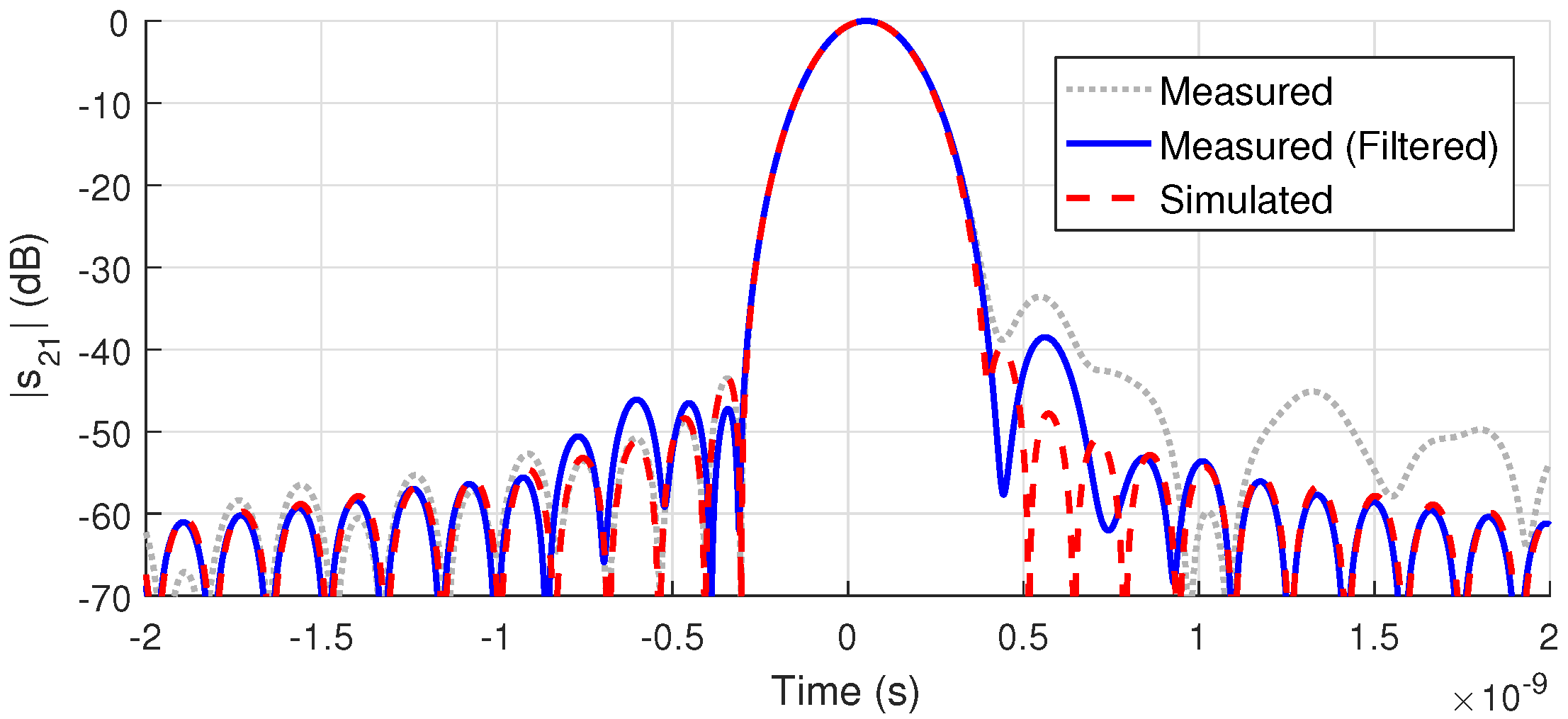
2.6. Filtering the S-Parameters
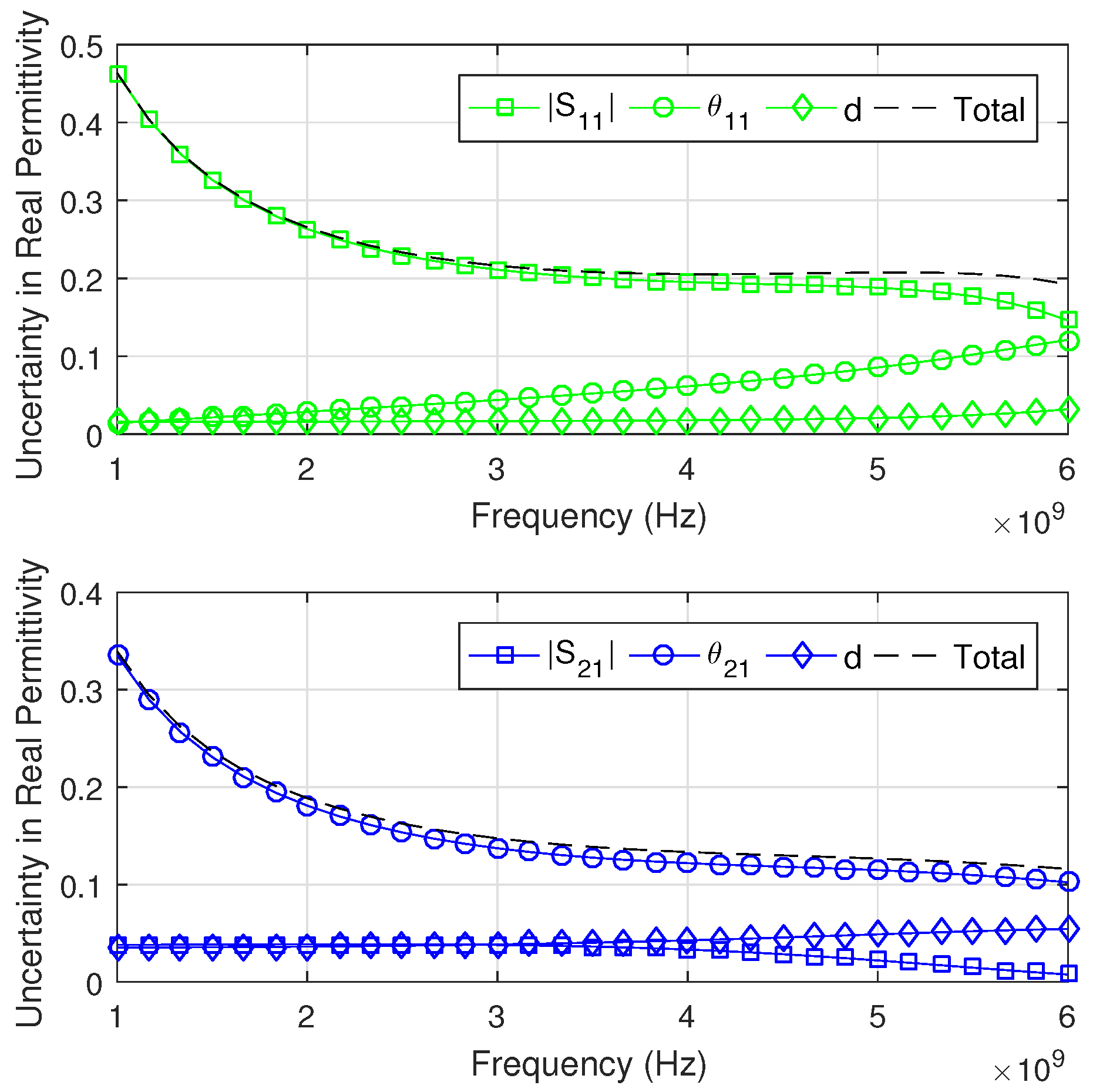
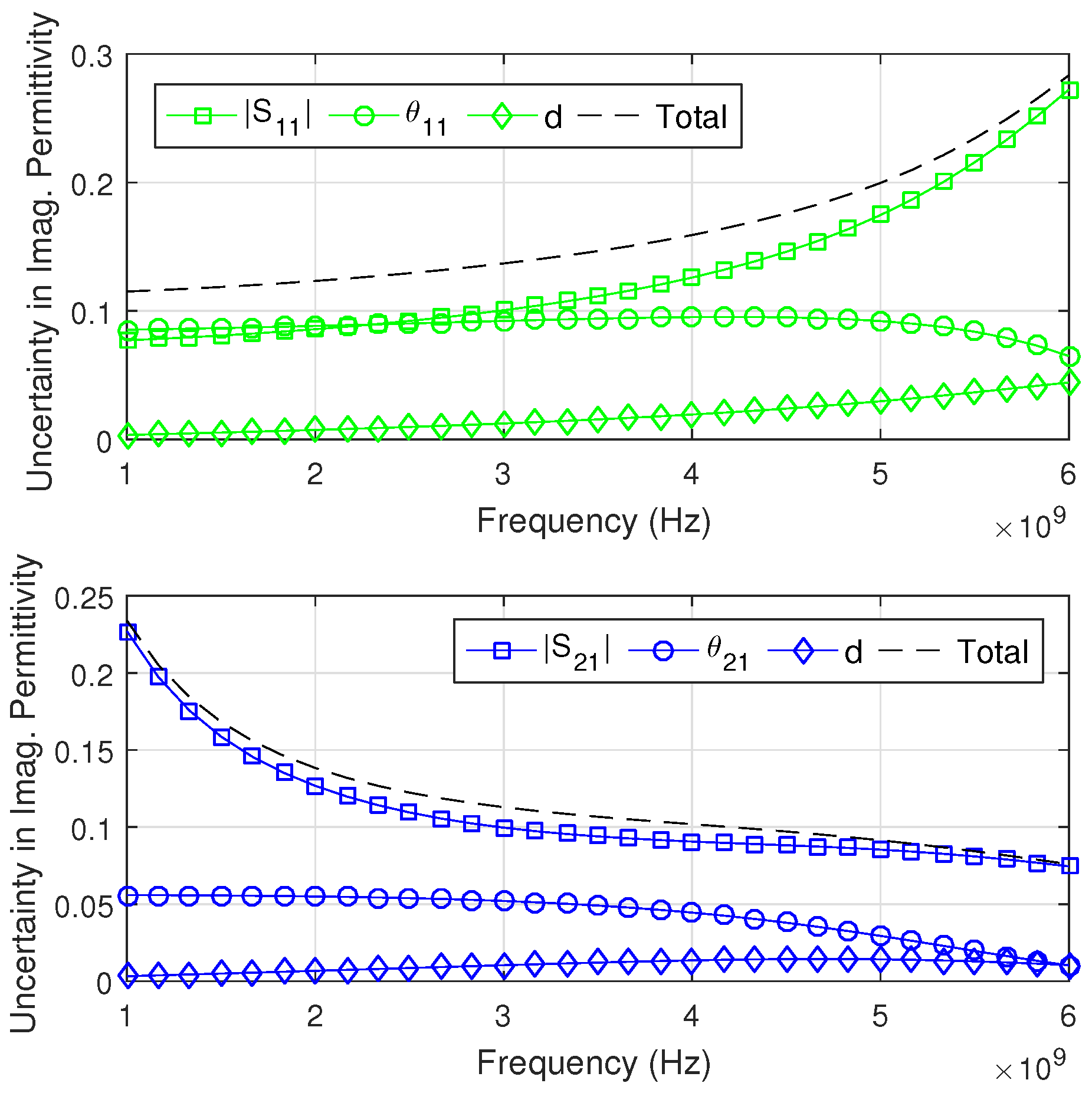
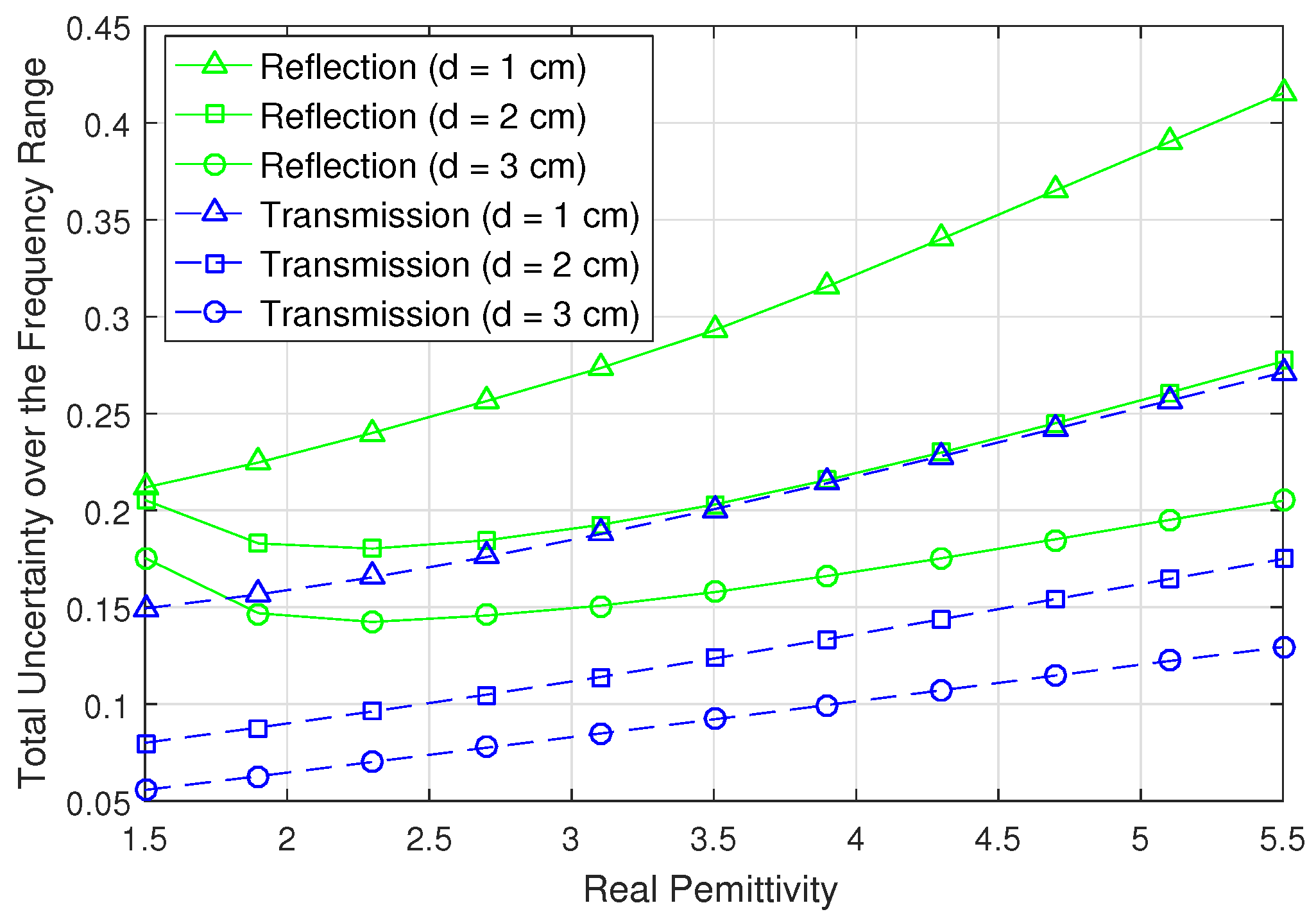
3. Analysis of the Uncertainties in the Model
3.1. Individual Contributions on the Total Uncertainty
3.2. Uncertainty for Different Materials and Thicknesses
4. Results and Discussion
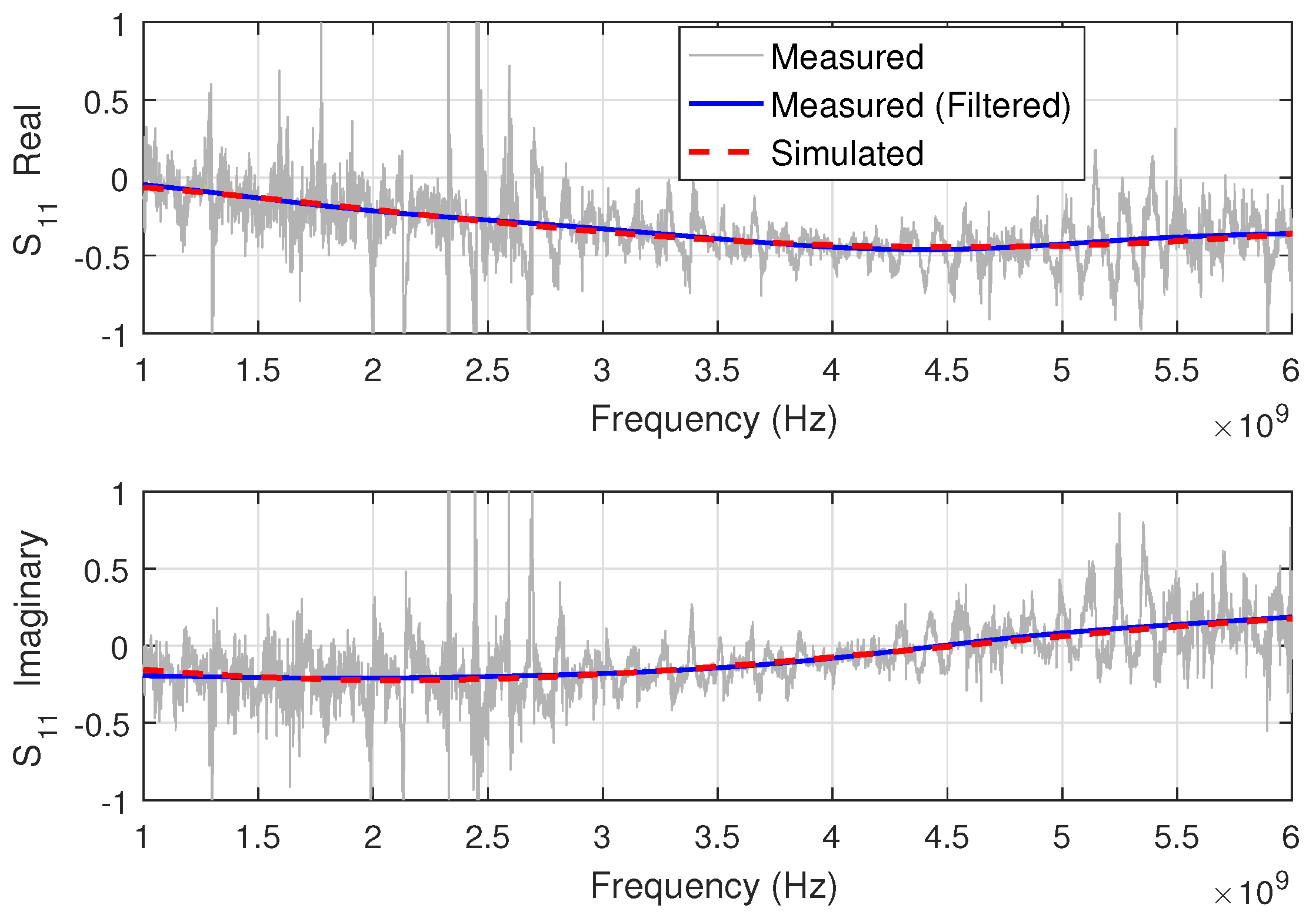
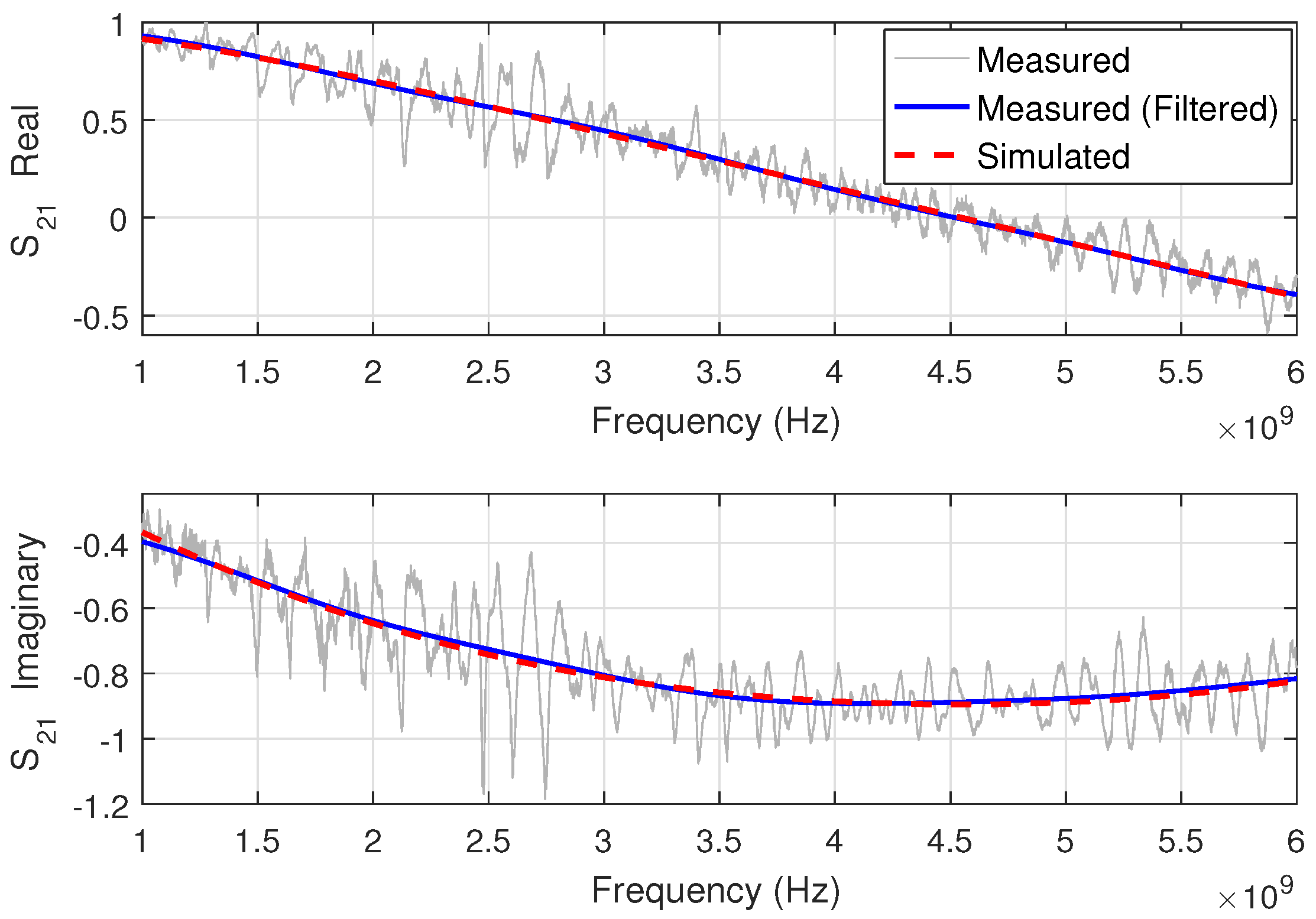
4.1. Frequency-by-Frequency with Simulated Data
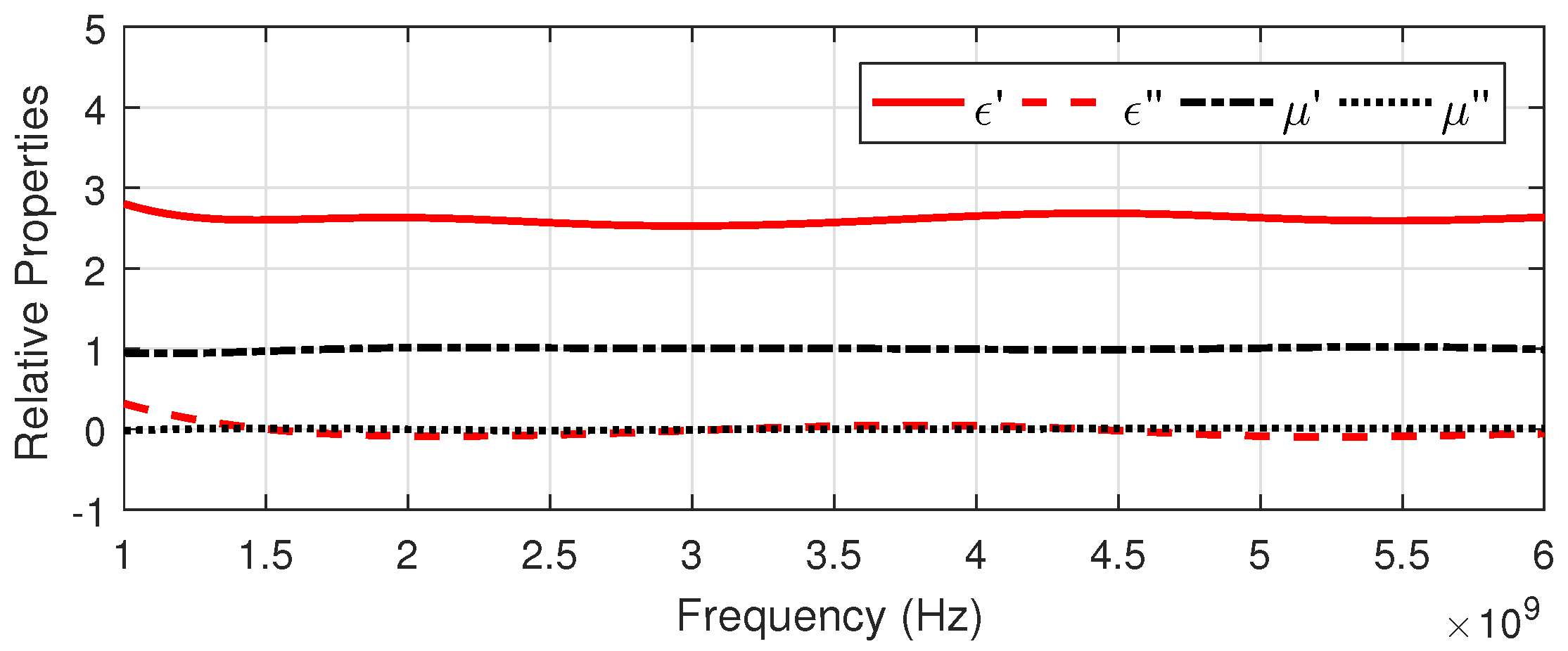
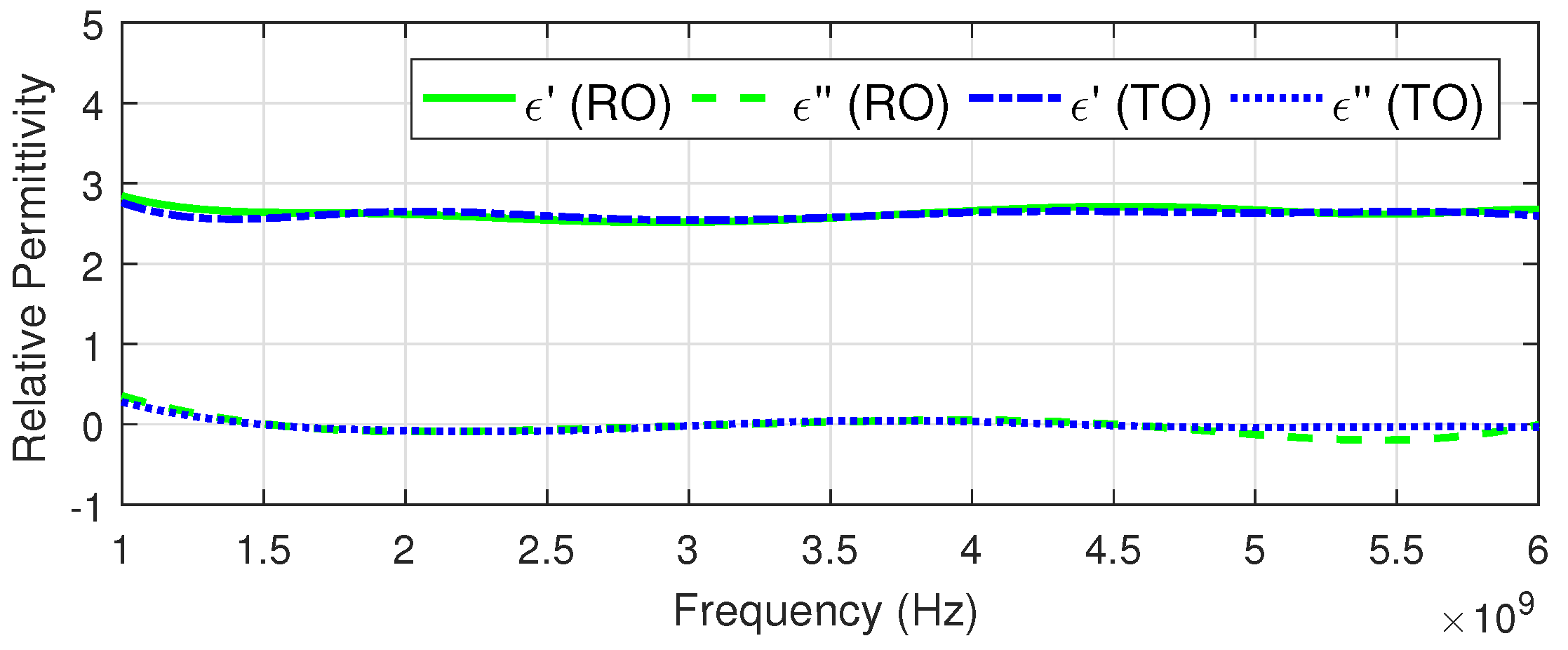
4.2. Frequency-by-Frequency with Experimental Data
4.3. Multi-Frequency Reconstruction with Simulated Data
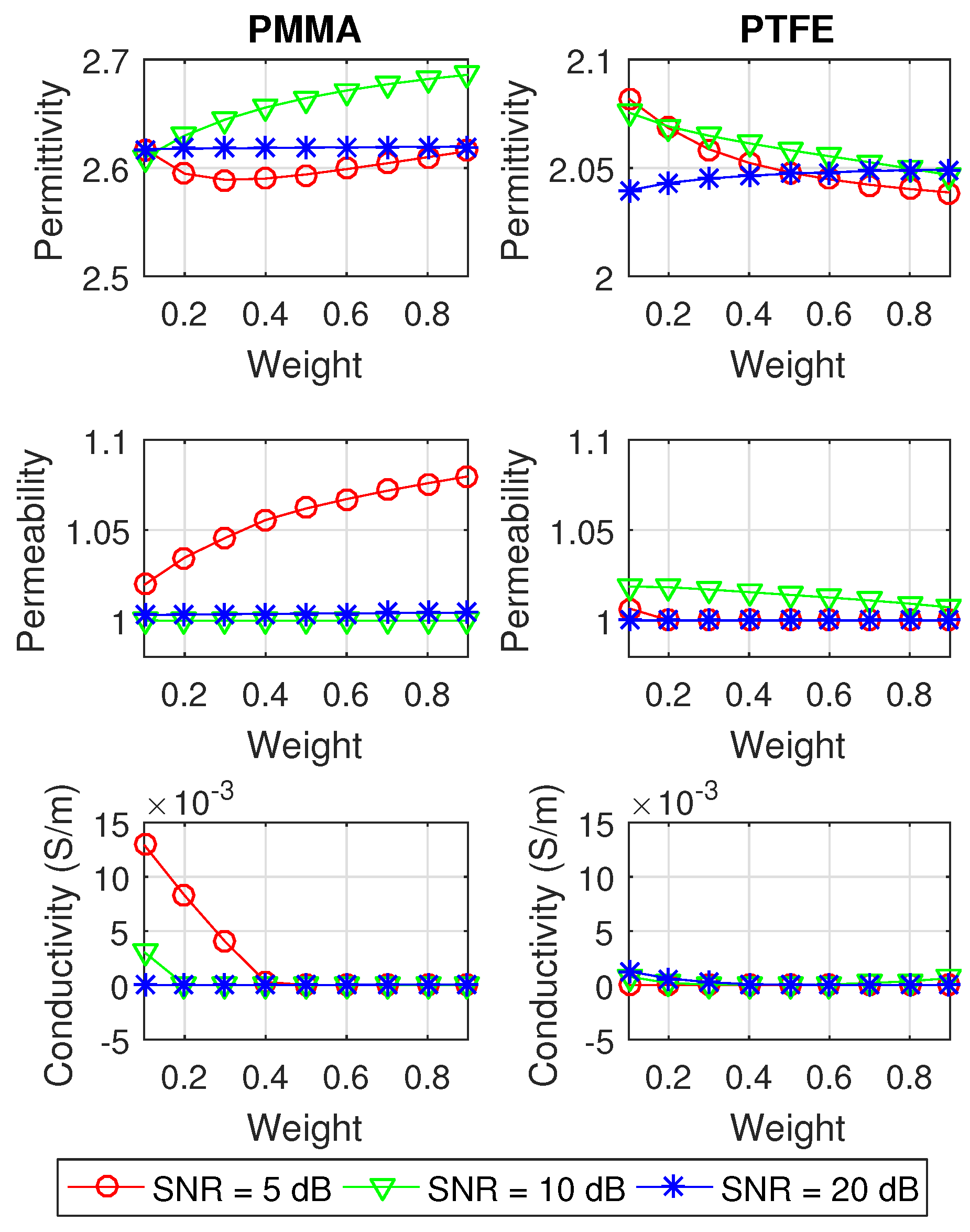
4.4. Multi-Frequency Reconstruction with Experimental Data
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
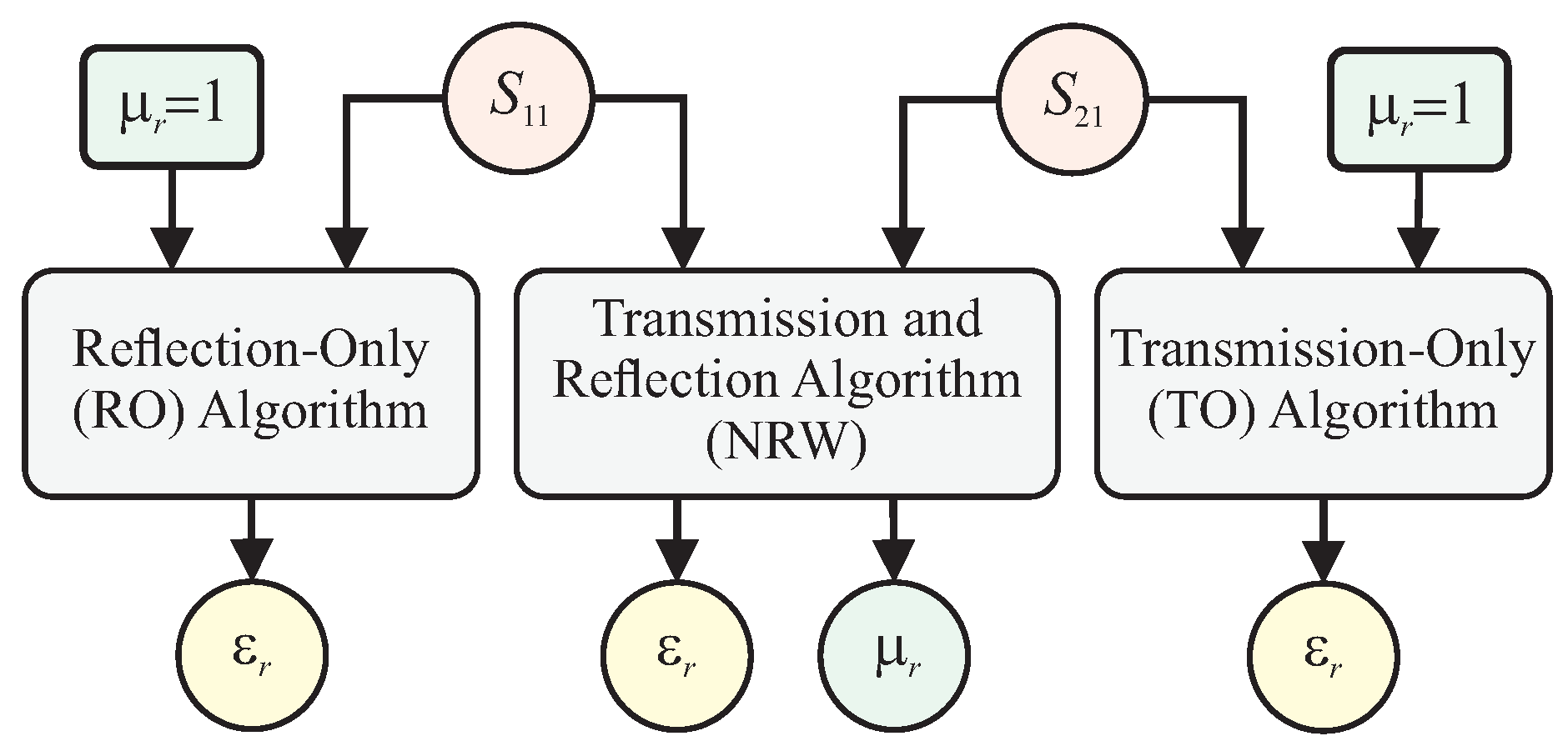
Appendix A. The Nicolson-Ross-Weir (NRW) Algorithm
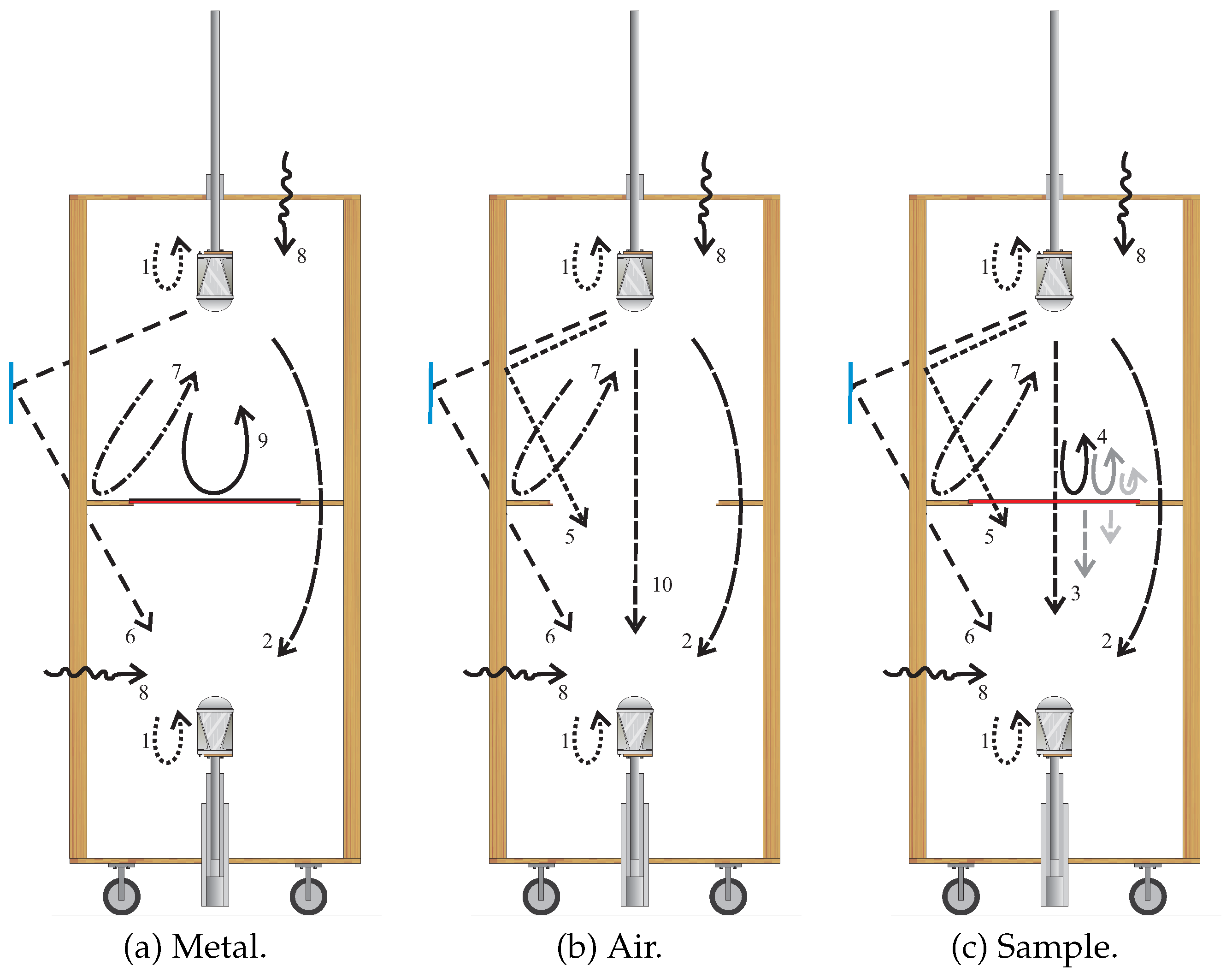
Appendix B. Filtering the S-Parameters with the Time-Domain Gating
References
- Chen, L.; Ong, C.; Neo, C.; Varadan, V.V.; Varadan, V.K. Microwave Electronics—Measurement and Materials Characterization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Balanis, C.A. Advanced Engineering Electromagnetics, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hiebel, M. Fundamentals of Vector Network Analysis, 5th ed.; Rohde & Schwarz: Munich, Germany, 2011. [Google Scholar]
- Costa, F.; Borgese, M.; Degiorgi, M.; Monorchio, A. Electromagnetic Characterisation of Materials by Using Transmission/Reflection (T/R) Devices. Electronics 2017, 6, 95. [Google Scholar] [CrossRef]
- Ghodgaonkar, D.K.; Varadan, V.V.; Varadan, V.K. A Free-space Method for Measurement of Dielectric Constants and Loss Tangents at Microwave Frequencies. IEEE Trans. Instrum. Meas. 1989, 37, 789–793. [Google Scholar] [CrossRef]
- William, S.W.; Alberto, S. Measurement of Dielectric Material Properties—Application Note; Rohde & Schwarz: Munich, Germany, 2006. [Google Scholar]
- Varadan, V.V.; Hollinger, R.D.; Ghodgaonkar, D.K.; Varadan, V.K. Free-space, broadband measurements of high-temperature, complex dielectric properties at microwave frequencies. IEEE Trans. Instrum. Meas. 1991, 40, 842–846. [Google Scholar] [CrossRef]
- Jose, K.A.; Varadan, V.K.; Varadan, V.V. Wideband and noncontact characterization of the complex permittivity of liquids. Microw. Opt. Technol. Lett. 2001, 30, 75–79. [Google Scholar] [CrossRef]
- Brancaccio, A.; D’Alterio, G.; Stefano, E.D.; Guida, L.D.; Feo, M.; Luce, S. A free-space method for microwave characterization of materials in aerospace application. In Proceedings of the MetroAeroSpace 2014, Benevento, Italy, 29–30 May 2014. [Google Scholar]
- Zaki, F.M.; Awang, Z.; Baba, N.H.; Zoolfakar, A.S.; Bakar, R.A.; Zolkapli, M.; Fadzlina, N. A free-space method for measurement of complex permittivity of double-layer dielectric materials at microwave frequencies. In Proceedings of the 2010 IEEE Student Conference on Research and Development (SCOReD), Putrajaya, Malaysia, 13–14 December 2010. [Google Scholar] [CrossRef]
- Ozbay, E.; Aydin, K.; Cubukcu, E.; Bayindir, M. Transmission and Reflection Properties of Composite Double Negative Metamaterials in Free Space. IEEE Trans. Antennas Propag. 2003, 51, 2592–2595. [Google Scholar] [CrossRef]
- Seo, I.S.; Chin, W.S.; Lee, D.G. Characterization of electromagnetic properties of polymeric composite materials with free space method. Compos. Struct. 2004, 66, 533–542. [Google Scholar] [CrossRef]
- Chung, J.Y. Broadband Characterization Techniques for RF Materials and Engineered Composites. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2010. [Google Scholar]
- Hock, K.M. Error correction for diffraction and multiple scattering in free-space microwave measurement of materials. IEEE Trans. Microw. Theory Technol. 2006, 54, 648–659. [Google Scholar] [CrossRef]
- Cuinas, I.; Sanchez, M.G. Building material characterization from complex transmissivity measurements at 5.8 GHz. IEEE Trans. Antennas Propag. 2000, 48, 1269–1271. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, X.; Huang, K.; Li, X.; Zhang, S. A Practical Evaluation Method of Building Penetration Loss at 3.5 GHz for IMT Application. In Proceedings of the 2017 9th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 14–15 January 2017; pp. 150–153. [Google Scholar] [CrossRef]
- Hasar, U. Non-destructive testing of hardened cement specimens at microwave frequencies using a simple free-space method. NDT E Int. 2009, 42, 550–557. [Google Scholar] [CrossRef]
- Solimene, R.; Napoli, R.D.; Soldovieri, F.; Pierri, R. TWI for an unknown symmetric lossless wall. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2876–2886. [Google Scholar] [CrossRef]
- Brancaccio, A.; Soldovieri, F.; Leone, G.; Sglavo, D.; Pierri, R. Microwave characterization of materials in civil engineering. Proc. EUMA 2006, 2, 128–135. [Google Scholar]
- Arunachalam, K.; Melapudi, V.; Udpa, L.; Udpa, S. Microwave NDT of cement-based materials using far-field reflection coefficients. NDT E Int. 2006, 39, 585–593. [Google Scholar] [CrossRef]
- Denoth, A. Structural phase changes of the liquid water component in Alpine snow. Cold Reg. Sci. Technol. 2003, 37, 227–232. [Google Scholar] [CrossRef]
- Trabelsi, S.; Nelson, S.O. Free-Space Measurement of Dielectric Properties of Cereal Grain and Oilseed as Microwave Frequencies. IOP Meas. Sci. Technol. 2003, 14, 589–600. [Google Scholar] [CrossRef]
- Friedsam, G.L.; Biebl, E.M. A broadband free-space dielectric properties measurement system at millimeter wavelengths. IEEE Trans. Instrum. Meas. 1997, 46, 515–518. [Google Scholar] [CrossRef]
- Suzuki, H.; Nishikata, A.; Higashida, Y.; Takahashi, T.; Hashimoto, O. Free space method with parallel electromagnetic wave beam by using dielectric lenses and horn antennas for reflectivity of electromagnetic absorbers in millimeter waves. In Proceedings of the 2005 IEEE International Workshop on Measurement Systems for Homeland Security, Contraband Detection and Personal Safety Workshop, Orlando, FL, USA, 29–30 March 2005; pp. 63–69. [Google Scholar] [CrossRef]
- Hassan, A.M.; Obrzut, J.; Garboczi, E.J. A Q-Band Free-Space Characterization of Carbon Nanotube Composites. IEEE Trans. Microw. Theory Technol. 2016, 64, 3807–3819. [Google Scholar] [CrossRef] [PubMed]
- Collier, R.; Skinner, D. (Eds.) Microwave Measurements, 3rd ed.; IET Electrical Measurement Series; The Institution of Engineering and Technology: Stevenage, UK, 2007. [Google Scholar]
- Amiet, A. Free Space Permittivity and Permeability Measurements at Microwave Frequencies. Ph.D. Thesis, Monash Univercity, Melbourne, Australia, 2003. [Google Scholar]
- Time Domain Analysis Using a Network Analyzer—Application Note 1287-12; Agilent Technologies: Santa Clara, CA, USA, 2012.
- Time Domain Measurements Using Vector Network Analyzers—Application Note No. 11410-00206, Rev. D; Anritsu: Kanagawa Prefecture, Japan, 2009.
- Condori-Arapa, C. Antenna Elements Matching—Time Domain Analysis. Master’s Thesis, Gävle University College, Gävle, Sweden, 2010. [Google Scholar]
- Gonçalves, F.J.F.; Mesquita, R.C.; Silva, E.J. Implementing a Time-Domain Filter for Extracting the Electromagnetic Constitutive Properties. In Proceedings of the MOMAG, João Pessoa, Brazil, 5–8 August 2012. [Google Scholar]
- Baker-Jarvis, J.; Geyer, R.G.; Domich, P.D. A nonlinear least-squares solution with causality constraints applied to transmission line permittivity and permeability determination. IEEE Trans. Instrum. Meas. 1992, 41, 646–652. [Google Scholar] [CrossRef]
- Nicolson, A.M.; Ross, G.F. Measurement of the Intrinsic Properties of Materials by Time-Domain Techniques. IEEE Trans. Instrum. Meas. 1970, 19, 377–382. [Google Scholar] [CrossRef]
- Weir, W.B. Automatic Measurement of Complex Dielectric Constant and Permeability at Microwave Frequencies. Proc. IEEE 1974, 62, 33–36. [Google Scholar] [CrossRef]
- Baker-Jarvis, J.; Janezic, M.D.; Riddle, B.F.; Johnk, R.T.; Kabos, P.; Holloway, C.L.; Geyer, R.G.; Grosvenor, C.A. Measuring the Permittivity and Permeability of Lossy Materials: Solids, Liquids, Metals, Building Materials, and Negative-Index Materials; Technical Note 1536; NIST—National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005. Available online: https://www.nist.gov/publications/measuring-permittivity-and-permeability-lossy-materials-solids-liquids-metals-and (accessed on 12 September 2018).
- Boughriet, A.H.; Legrand, C.; Chapoton, A. Noniterative Stable Transmission/Reflection Method for Low-Loss Material Complex Permittivity Determination. IEEE Trans. Microw. Theory Technol. 1997, 45, 52–57. [Google Scholar] [CrossRef]
- Balanis, C.A. Anntena Theory—Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Dhondt, G.; Zutter, D.D.; Martens, L. An improved free-space technique modelling for measuring dielectric properties of materials. In Proceedings of the 1996 Digest IEEE Antennas and Propagation Society International Symposium, Baltimore, MD, USA, 21–26 July 1996. [Google Scholar]
- Bartley, P.G.; Begley, S.B. Improved Free-Space S-Parameter Calibration. In Proceedings of the 2005 IEEE Instrumentationand Measurement Technology Conference, Ottawa, ON, Canada, 16–19 May 2005. [Google Scholar]
- Bartley, P.G.; Begley, S.B. A new free-space calibration technique for materials measurement. In Proceedings of the Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012; pp. 47–51. [Google Scholar] [CrossRef]
- Baker-Jarvis, J.; Vanzura, E.J.; Kissick, W.A. Improved Technique for Determining Complex Permittivity with the Transmission/Reflection Method. IEEE Trans. Microw. Theory Technol. 1990, 38, 1096–1102. [Google Scholar] [CrossRef]
- Jebbor, N.; Bri, S.; Sánchez, A.; Chaibi, M. A fast calibration-independent method for complex permittivity determination at microwave frequencies. Measurement 2013, 46, 2206–2209. [Google Scholar] [CrossRef]
- Hasar, U.C. Thickness-Invariant Complex Permittivity Retrieval from Calibration-Independent Measurements. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 201–203. [Google Scholar] [CrossRef]
- Hasar, U.C. Determination of Complex Permittivity of Low-Loss Samples From Position-Invariant Transmission and Shorted-Reflection Measurements. IEEE Trans. Microw. Theory Technol. 2018, 66, 1090–1098. [Google Scholar] [CrossRef]
- Akhter, Z.; Akhtar, M.J. Free-Space Time Domain Position Insensitive Technique for Simultaneous Measurement of Complex Permittivity and Thickness of Lossy Dielectric Samples. IEEE Trans. Instrum. Meas. 2016, 65, 2394–2405. [Google Scholar] [CrossRef]
- Deng, L.; Chen, X.L.; Li, Y. S-parameters extraction of a desired network with time-domain gates. Progress Electromagn. Res. Lett. 2016, 61, 91–97. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Schafer, R.W.; Rader, C.M. The Chirp Z-Transform Algorithm and Its Application. Bell Syst. Tech. J. 1969, 1249–1292. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Pearson: London, UK, 2010. [Google Scholar]
- Smith, S.W. Digital Signal Processing—A Practical Guide for Engineers and Scientists; Newnes: Wolgan Valley, NSW, Australia, 2003. [Google Scholar]
- I Yagüe, R.D.P.D.; Ibars, A.B.; Martínez, L.F. Analysis and Reduction of the Distortions Induced by Time-Domain Filtering Techniques in Network Analyzers. IEEE Trans. Instrum. Meas. 1998, 47, 930–934. [Google Scholar] [CrossRef]
- Silov, G. Analisi Matematica—Funzioni di più Variabili Reali, 1st ed.; Edizioni MIR: Moscow, Russia, 1979. [Google Scholar]
- R&S ZVL Vector Network Analyzer Specifications PD 5213.8150.22, Version 10.00; Technical Report; Rohde & Schwarz: Munich, Germany, 2017.
- Lu, K.; Brazil, T.J. A systematic error analysis of HP 8510 time-domain gating techniques with experimental verification. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 14–18 June1993; pp. 1259–1262. [Google Scholar] [CrossRef]
- Harris, F.J. On the Use of Windows for Hamonic Analysis with the Discrete Fourier Transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]

| PTFE (NRW) | ||||
| SNR (dB) | ||||
| 5 | 2.05 ± 0.04 | −0.01 ± 0.07 | 1.00 ± 0.02 | −0.01 ± 0.02 |
| 10 | 2.04 ± 0.02 | 0.01 ± 0.03 | 0.99 ± 0.03 | 0.01 ± 0.01 |
| 20 | 2.04 ± 0.04 | 0.00 ± 0.02 | 0.99 ± 0.02 | 0.00 ± 0.01 |
| PTFE (Reflection) PTFE (Transmission) | ||||
| SNR (dB) | ||||
| 5 | 2.05 ± 0.07 | 0.00 ± 0.07 | 2.05 ± 0.03 | −0.02 ± 0.08 |
| 10 | 2.05 ± 0.03 | 0.00 ± 0.04 | 2.03 ± 0.06 | 0.02 ± 0.04 |
| 20 | 2.04 ± 0.02 | 0.00 ± 0.03 | 2.03 ± 0.06 | −0.01 ± 0.02 |
| PMMA (NRW) | ||||
| SNR (dB) | ||||
| 5 | 2.61 ± 0.08 | 0.03 ± 0.1 | 0.99 ± 0.03 | −0.03 ± 0.03 |
| 10 | 2.60 ± 0.04 | −0.01 ± 0.04 | 0.98 ± 0.02 | −0.02 ± 0.03 |
| 20 | 2.60 ± 0.04 | 0.01 ± 0.04 | 1.00 ± 0.01 | 0.00 ± 0.01 |
| PMMA (Reflection) PMMA (Transmission) | ||||
| SNR (dB) | ||||
| 5 | 2.58 ± 0.11 | 0.06 ± 0.12 | 2.62 ± 0.06 | −0.01 ± 0.07 |
| 10 | 2.61 ± 0.06 | 0.02 ± 0.07 | 2.60 ± 0.05 | −0.03 ± 0.03 |
| 20 | 2.60 ± 0.04 | 0.01 ± 0.05 | 2.60 ± 0.05 | 0.00 ± 0.04 |
| PTFE (NRW) | ||||
| r | ||||
| 48 cm | 2.04 ± 0.03 | 0.01 ± 0.05 | 0.98 ± 0.02 | 0.00 ± 0.01 |
| 30 cm | 2.04 ± 0.03 | −0.03 ± 0.03 | 0.99 ± 0.02 | 0.03 ± 0.02 |
| PTFE (Reflection) PTFE (Transmission) | ||||
| r | ||||
| 48 cm | 2.06 ± 0.04 | 0.03 ± 0.06 | 2.01 ± 0.03 | 0.00 ± 0.04 |
| 30 cm | 2.08 ± 0.06 | −0.06 ± 0.04 | 2.02 ± 0.04 | 0.01 ± 0.03 |
| PMMA (NRW) | ||||
| r | ||||
| 48 cm | 2.61 ± 0.05 | −0.02 ± 0.07 | 1.00 ± 0.02 | 0.00 ± 0.01 |
| 30 cm | 2.64 ± 0.07 | −0.03 ± 0.04 | 1.01 ± 0.03 | 0.01 ± 0.01 |
| PMMA (Reflection) PMMA (Transmission) | ||||
| r | ||||
| 48 cm | 2.62 ± 0.07 | −0.03 ± 0.1 | 2.61 ± 0.04 | −0.01 ± 0.06 |
| 30 cm | 2.66 ± 0.09 | −0.06 ± 0.07 | 2.64 ± 0.06 | 0.01 ± 0.04 |
| PTFE (without Gating) PTFE (with Gating) | |||||||
| w | (S/m) | w | (S/m) | ||||
| 0.1 | 2.03 | 1.00 | 0.00 | 0.1 | 2.02 | 1.00 | 0.00 |
| 0.2 | 2.03 | 1.00 | 0.00 | 0.2 | 2.03 | 1.00 | 0.00 |
| 0.3 | 2.03 | 1.00 | 0.00 | 0.3 | 2.03 | 1.00 | 0.00 |
| 0.4 | 2.03 | 1.00 | 0.00 | 0.4 | 2.03 | 1.00 | 0.00 |
| 0.5 | 2.03 | 1.00 | 0.00 | 0.5 | 2.03 | 1.00 | 0.00 |
| 0.6 | 2.03 | 1.00 | 0.00 | 0.6 | 2.03 | 1.00 | 0.00 |
| 0.7 | 2.04 | 1.00 | 0.00 | 0.7 | 2.03 | 1.00 | 0.00 |
| 0.8 | 2.04 | 1.00 | 0.00 | 0.8 | 2.04 | 1.00 | 0.00 |
| 0.9 | 5.00 | 2.10 | 0.00 | 0.9 | 4.98 | 2.44 | 0.05 |
| PMMA (without Gating) PMMA (with Gating) | |||||||
| w | (S/m) | w | (S/m) | ||||
| 0.1 | 2.61 | 1.00 | 0.00 | 0.1 | 2.59 | 1.01 | 0.01 |
| 0.2 | 2.61 | 1.00 | 0.00 | 0.2 | 2.59 | 1.01 | 0.01 |
| 0.3 | 2.61 | 1.00 | 0.00 | 0.3 | 2.59 | 1.01 | 0.01 |
| 0.4 | 2.61 | 1.00 | 0.00 | 0.4 | 2.59 | 1.01 | 0.01 |
| 0.5 | 2.61 | 1.00 | 0.00 | 0.5 | 2.59 | 1.01 | 0.01 |
| 0.6 | 2.61 | 1.00 | 0.00 | 0.6 | 2.59 | 1.01 | 0.01 |
| 0.7 | 2.61 | 1.00 | 0.00 | 0.7 | 2.59 | 1.01 | 0.01 |
| 0.8 | 2.61 | 1.00 | 0.00 | 0.8 | 2.59 | 1.01 | 0.01 |
| 0.9 | 2.61 | 1.00 | 0.00 | 0.9 | 5.00 | 1.72 | 0.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves, F.J.F.; Pinto, A.G.M.; Mesquita, R.C.; Silva, E.J.; Brancaccio, A. Free-Space Materials Characterization by Reflection and Transmission Measurements using Frequency-by-Frequency and Multi-Frequency Algorithms. Electronics 2018, 7, 260. https://doi.org/10.3390/electronics7100260
Gonçalves FJF, Pinto AGM, Mesquita RC, Silva EJ, Brancaccio A. Free-Space Materials Characterization by Reflection and Transmission Measurements using Frequency-by-Frequency and Multi-Frequency Algorithms. Electronics. 2018; 7(10):260. https://doi.org/10.3390/electronics7100260
Chicago/Turabian StyleGonçalves, Fábio Júlio F., Alfred G. M. Pinto, Renato C. Mesquita, Elson J. Silva, and Adriana Brancaccio. 2018. "Free-Space Materials Characterization by Reflection and Transmission Measurements using Frequency-by-Frequency and Multi-Frequency Algorithms" Electronics 7, no. 10: 260. https://doi.org/10.3390/electronics7100260
APA StyleGonçalves, F. J. F., Pinto, A. G. M., Mesquita, R. C., Silva, E. J., & Brancaccio, A. (2018). Free-Space Materials Characterization by Reflection and Transmission Measurements using Frequency-by-Frequency and Multi-Frequency Algorithms. Electronics, 7(10), 260. https://doi.org/10.3390/electronics7100260






