Coupled-Region Visual Tracking Formulation Based on a Discriminative Correlation Filter Bank

Abstract

The visual tracking algorithm based on discriminative correlation filter (DCF) has shown excellent performance in recent years, especially as the higher tracking speed meets the real-time requirement of object tracking. However, when the target is partially occluded, the traditional single discriminative correlation filter will not be able to effectively learn information reliability, resulting in tracker drift and even failure. To address this issue, this paper proposes a novel tracking-by-detection framework, which uses multiple discriminative correlation filters called discriminative correlation filter bank (DCFB), corresponding to different target sub-regions and global region patches to combine and optimize the final correlation output in the frequency domain. In tracking, the sub-region patches are zero-padded to the same size as the global target region, which can effectively avoid noise aliasing during correlation operation, thereby improving the robustness of the discriminative correlation filter. Considering that the sub-region target motion model is constrained by the global target region, adding the global region appearance model to our framework will completely preserve the intrinsic structure of the target, thus effectively utilizing the discriminative information of the visible sub-region to mitigate tracker drift when partial occlusion occurs. In addition, an adaptive scale estimation scheme is incorporated into our algorithm to make the tracker more robust against potential challenging attributes. The experimental results from the OTB-2015 and VOT-2015 datasets demonstrate that our method performs favorably compared with several state-of-the-art trackers.

1. Introduction

Visual tracking plays an important role in computer vision, with numerous applications in areas such as robotics, human behavior analysis, intelligent traffic monitoring, and many more [1]. In recent years, numerous excellent tracking algorithms have emerged, but there are still some challenges that need to be addressed due to the practical complex background, such as illumination variation, scale variation, and occlusion. To solve the troubles caused by these challenges, the proposed trackers are generally divided into two categories: generative and discriminative methods. Generative trackers [2,3,4] perform tracking by searching for patches most similar to the target. Conversely, discriminative trackers [5,6,7,8,9] perform tracking by separating the target from the background.

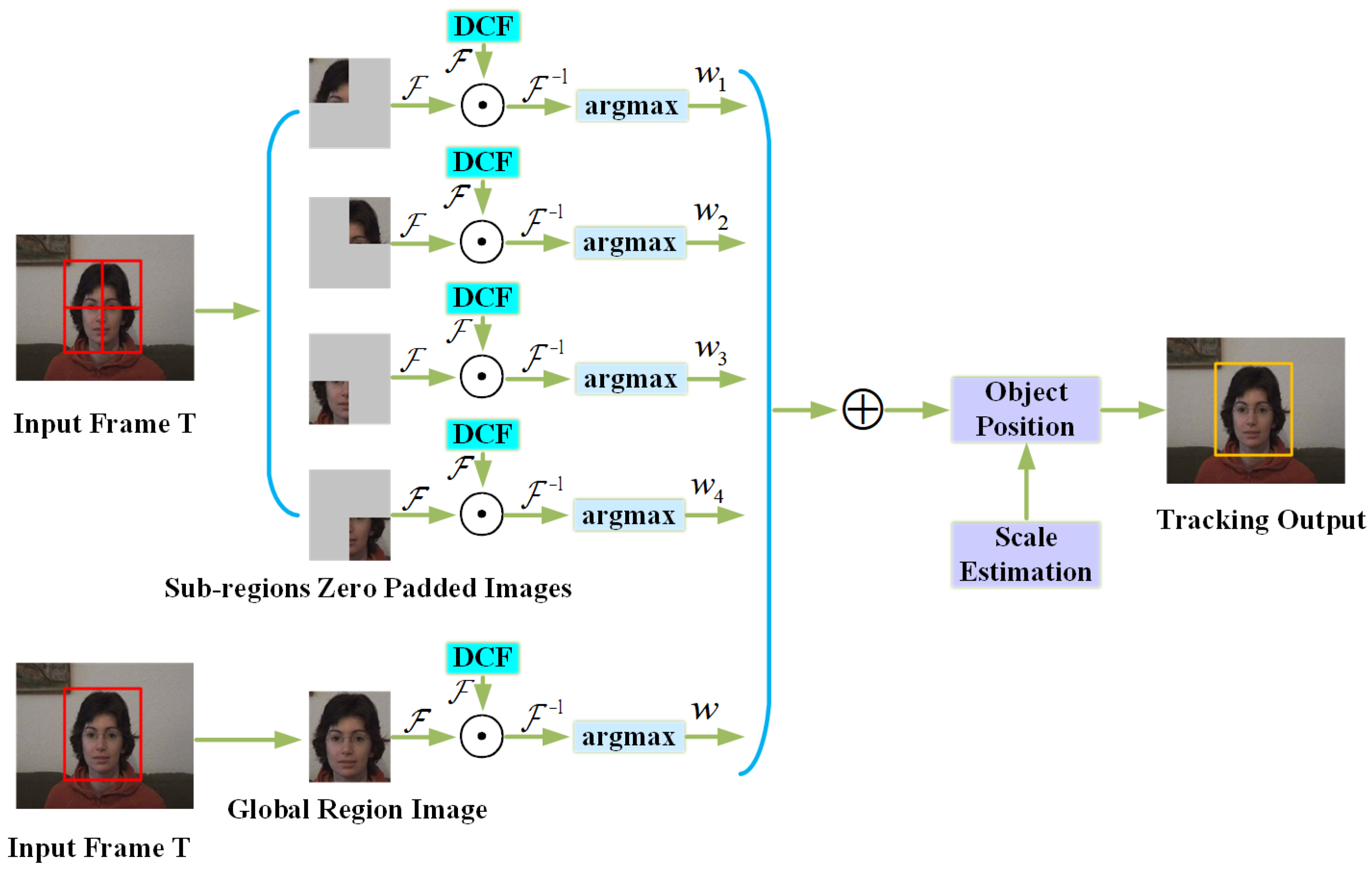
Recently, the existing correlation filter tracking algorithms [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] have demonstrated superior performance in terms of speed and robustness. The main idea of the correlation filter-based tracking method is that the correlation output of each interested target is a correlation peak in the image sequence, while other background regions have a low correlation response, and thus the target is positioned in a new frame by the coordinates of the maximum correlation peak. According to the convolution theorem, the correlation in the time domain corresponds to the element-wise multiplication in the frequency domain. Therefore, the essential idea of the high-speed correlation filter calculation is that it can be effectively calculated by fast Fourier transformation (FFT) and pointwise operations in the frequency domain. Thus, the time-consuming process of the convolution operation is effectively avoided. Based on this principle, the correlation filter tracking framework can meet the requirements of real-time tracking. Nevertheless, empirical experiments show that the sensitivity of the correlation filter when encountering challenging occlusion scenarios and the appearance of the target changes irregularly in tracking, which are easy to cause tracker drift. To deal with these issues, in this work, we formulate multiple discriminative correlation filters called discriminative correlation filter bank (DCFB) for visual tracking to solve the drifting problem caused by occlusion. Figure 1 demonstrates the overview of our formulation.

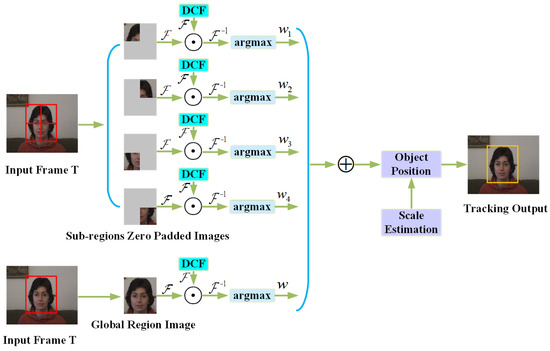
Figure 1. Overview of our algorithm. In the t-th frame, the sliding window obtains the sub-region and global region images, and the sub-region images are zero-padded to the same size as the global image. Subsequently, the correlation operation is performed with the trained DCFB in the frequency domain, and the position corresponding to the maximum correlation response is weighted to make the joint optimization the final target position. In addition, accurate scale estimation makes the tracking process more robust.

Our method combines the appearance models of multiple sub-regions and the global target region for the motion model, and not only takes the differences between sub-regions into account, but also effectively utilizes the constraint relationship between sub-regions and the global region to preserve the overall structure of the target. During tracking, the motion model of sub-regions and the global target region are basically consistent, and the sub-region patches are zero-padded to the same size as the global target region, which can effectively avoid noise aliasing during correlation operation, thereby improved the robustness of the discriminative correlation filter. Noise aliasing is an error that occurs when signal reconstruction, that is to say, information from high frequency is disguised as low frequency content. The advantage of the proposed DCFB tracking method is that the effective appearance of the remaining visible sub-region patches can still provide reliable cues for tracking when the target is partially occluded, since we can formulate multiple correlation filters corresponding to different sub-region patches simultaneously. Extensive experiments on the OTB-2015 [31] and VOT-2015 [32] datasets evidence the effectiveness of the proposed framework compared with several state-of-the-art trackers.

The contributions of this work are as follows. First, we formulate multiple discriminative correlation filters corresponding to different sub-region and global region patches simultaneously to combine and optimize the final tracking result. Second, we ensure that sub-region patches are zero-padded to the same size as the global target region to avoid noise aliasing during correlation operation, thereby improved the robustness of the discriminative correlation filter. Third, our proposed model not only exploits the constraint relationship between sub-regions and the global target region to learn multiple discriminative correlation filters jointly, but also preserves the overall structure of the target. Fourth, we validate our tracker by demonstrating that it performs favorably against state-of-the-art trackers, using the OTB-2015 [31] and VOT-2015 [32] as two benchmark datasets.

The remainder of the paper is arranged as follows. In Section 2, we review work related to ours. In Section 3, we describe the proposed tracking algorithm in detail. The experimental evaluations and analysis are reported in Section 4. Finally, we summarize this paper and point out the research direction of future work in Section 5.

2. Related Works

As a result of the annual visual object tracking (VOT) challenge, many excellent visual tracking algorithms have emerged one after another. To review these algorithms, readers can refer to References [32,33,34,35] for more details. In this section, we mainly review the literature related to our work, including correlation filter-based and part-based correlation filter tracking algorithms.

2.1. Correlation Filter Visual Tracking

The potential of correlation filters for visual tracking has attracted widespread attention, mainly because the correlation operation reduces the overhead time through fast Fourier transformation (FFT) in the frequency domain. Bolme et al. [10] the first used correlation filter to build a tracking framework by learning a minimum output sum of squared error (MOSSE) for appearance model. Its speed is several hundred frames per second, meeting the requirements of real-time tracking. The correlation filter of the circulant structure with kernel (CSK) [14] uses the kernel trick to learn the appearance model and further improve tracking performance. The KCF tracker [15] is an upgraded version of CSK. It uses the histogram of oriented gradients (HOG) feature instead of the original grayscale feature to represent the target, and shows an amazing speed on the OTB2013 dataset [36], but cannot achieve online scale estimation. The discriminative scale space tracking (DSST) [11] method consists of a translation correlation filter and a scale correlation filter to achieve target localization and target scale detection, respectively. The scale adaptive with multiple features (SAMF) [12] tracker solves online scale detection using KCF as a baseline. The fast DSST (fDSST) method [37] is an accelerated version of DSST. In addition to increasing speed, it is more accurate in scale estimation and tracking is more robust.

Recently, the strategy of reducing the boundary effects [25,26,38] has been integrated into the correlation filter model, which has greatly improved the quality of the tracking model. In Reference [21,27,28,29], the authors used depth features instead of hand-crafted features for visual tracking, which further enhances the robustness and accuracy of the tracker. The continuous convolution operators (C-COT) tracking algorithm [21] presents the best performance in VOT2016 [34], but it is a very complex model that cannot achieve real-time tracking. The efficient convolution operators (ECO) tracker [29] solved the speed problem of C-COT by optimizing model size, sample set size, and update strategy. In this work, we construct a robust discriminative correlation filter bank tracking framework to solve the tracker drift caused by occlusion scenarios, which is different from the existing correlation filter trackers.

2.2. Part-Based Correlation Filter Tracking Algorithm

The part-based strategy using a correlation filter effectively solves the occlusion problem for visual tracking owing to the fact that visible parts are still used when occlusion occurs. Liu et al. [39] proposed using a discriminative part selection strategy to filtrate the most discriminative information parts from several candidate parts, and each part corresponds to a correlation output. Subsequently, all of the correlation outputs are combined to estimate the position of the target. In Reference [17], the authors proposed a reliable patch tracking algorithm to achieve target tracking by using reliable patches that can be effectively tracked throughout the tracking video. These reliable patches are calculated and selected by the trackable confidence function, and the trackable confidence and motion information are incorporated into the particle filter framework in order to estimate the position and scale of the target. In Reference [40], the authors proposed coupling interactions between local and global correlation filters for handling partial occlusion during tracking. First, using the local parts to estimate the initial position of the target based on the deformable model. Once a part is occluded or the appearance changes severely, the reliable parts provides new information to estimate a coarse prediction; then, the coarse result defines the search neighborhood, the final position of the target is estimated in conjunction with global filter; finally, the new prediction is provided to the part filters as the new reference position that is used in the deformable model to again estimate the position of the next frame target. Liu et al. [30] proposed to use the spatial constraints among local parts to preserve the structure of the target for the motion model that not only allows most parts to have similar motion, but also tolerate outlier parts of different motion directions. During tracking, the state of the part is predicted based on the maximum correlation response value of each part, and the location of the target is ultimately estimated by weighting average the state of all parts. Fan et al. [41] introduced a local-global correlation filter (LGCF) tracking method to solve the occlusion issue, which not only takes into account the constrained relationship of the local parts and global target, but also integrates the temporal consistencies of the local parts and global target to mitigate model drift, and then uses an occlusion detection model to exclude the occluded part to accurately estimate the location of the target. Wang et al. [42] developed a novel structured correlation filter model based on coupled interactions between a static model and a dynamic model to handle partial occlusion in tracking. The static model uses the star graph to model the spatial structure among parts to capture the spatial information of the parts and achieve the initial prediction of the target. The dynamic model uses this coarse initial prediction as a reference to estimate the final state of the target through Bayesian inference, and then the new target location is provided to the static model in order to update. However, the target response adaptive change tracking algorithm [24] exhibits superior performance when dealing with occlusion problems in scenarios, which utilizes the idea that the target response changes with frame changes. In Reference [23], the authors first considered the quality problem of the training samples in a joint optimization framework. The joint optimization function—consisting of the appearance model and the training sample weights—is used to purify the training sample set, thereby improving the tracking accuracy to counter occlusion challenges in a scene.

More relevant to our work is [41]. However, our method is different from [41] reflecting the following three aspects. First, we do not use the circulant structure of the training sample to learn correlation filters, empirical experiments show that these cyclic shift patches are only approximations of the actual samples, and are thus unreliable in the actual tracking occlusion scene. Second, in our method, the sub-region patches used for training the correlation filter are zero-padded to the same size as the global target region to avoid noise aliasing during the correlation operation. Third, we formulate multiple discriminative correlation filters instead of kernelized correlation filters corresponding to different sub-region and global region patches simultaneously to combine and optimize the final tracking output.

3. Our Tracking Framework

In this section, we describe the proposed tracking framework in detail. Starting with discussing the employed baseline tracker, we then introduce the proposed tracking framework. Finally, the proposed tracking algorithm is presented.

3.1. Baseline Approach

We adopted the DSST algorithm [11] as our baseline tracker. The DSST algorithm is a discriminative correlation filter tracker, which learns an appearance model on a single sample f, centered around the target with a d-dimension feature vector for calculation during tracking. $f^l$ is used to represent the d-dimension feature vector of sample f, and $l\in \{1,2,\cdots ,d\}$. The correlation filter h, consisting of one filter $h^l$ per feature dimension, is optimized by minimizing the following objective function:

$$\epsilon ={∥{\displaystyle \sum _{l=1}^d}{h}^l\ast f^l-g∥}^2+\lambda {\displaystyle \sum _{l=1}^d}{∥h^l∥}^2,$$

(1)

where g is the Gaussian function label, f is the training example, $\lambda$ is the regularization term coefficient, and $\ast$ denotes circular correlation. The closed form expression of Equation (1) is as follows:

$$H^l=\frac{\overline{G}{F}^l}{{\displaystyle \sum _{k=1}^d}\overline{F^k}{F}^k+\lambda },l=1,2,\cdots ,d,$$

(2)

where $F,H$ and G denote the Fourier transforms of $f,h$ and g, respectively. $\overline{H}$ is the complex conjugate of H.

The updated plan is as follows:

$$\begin{array}{c}{A}_t^l=(1-\eta )A_{t-1}^l+\eta \overline{G_t}{F}_t^l\hfill \\ B_t=(1-\eta )B_{t-1}+\eta {\displaystyle \sum _{k=1}^d}\overline{F_t^k}{F}_t^k,\hfill \end{array}$$

(3)

where $\eta$ is a learning rate parameter. $A_t^l$ and $B_t$ are the numerator and denominator of the filter $H_t^l$.

We then estimated the new location of the target according to the maximum correlation score $y_t$ on the candidate patch $z_t$ in a new frame t. The maximum correlation score $y_t$ is computed as:

$$y_t={\mathcal{F}}^{-1}\left(\frac{{\displaystyle \sum _{l=1}^d}\overline{A_{t-1}^l}{Z}_t^l}{B_{t-1}+\lambda }\right).$$

(4)

Readers may refer to Reference [11] for more details.

3.2. The Proposed Tracking Model

Based on the baseline tracker’s objective function Equation (1), we obtained the objective function of the sub-region and global model; see Equations (5) and (6), respectively.

$$\underset{{\{h_s\}}_{s=1}^N}{argmin}{\displaystyle \sum _{s=1}^N}\left({∥{\displaystyle \sum _{l=1}^d}{h}_s^l\ast f_s^l-g_s∥}^2+\lambda {{\displaystyle \sum _{l=1}^d}∥h_s^l∥}^2\right)$$

(5)

$$\underset{{}_{h_g}}{argmin}\left({∥{\displaystyle \sum _{l=1}^d}{h}_g^l\ast f_g^l-g_g∥}^2+\lambda {{\displaystyle \sum _{l=1}^d}∥h_g^l∥}^2\right).$$

(6)

Here, N indicates that the target is divided into N sub-regions. Each sub-region is zero-padded to the same size as the global image and corresponds to a discriminative correlation filter.

In tracking, the sub-regions and global model of the target are difficult to keep consistent because of the target self-deformation and the interference of the occlusion scenarios. In order to preserve the overall structure of the target among the sub-regions and global region to mitigate the drift risk and tolerate the outliers of the sub-regions model, the constraint between the sub-regions and the global model should be added and sparse. The constraint model [41] is represented by Equation (7):

$$h_s=h_g+{\nu }_s,$$

(7)

where $h_s$ and $h_g$ represent motion match models of the sub-region and global region, respectively, and ${\nu }_s$ denotes the constraint between $h_s$ and $h_g$.

In object tracking sequence, the target and background between consecutive frames are basically similar, so the target matching model $h^{t-1}$ is consistent with $h^t$. This phenomenon is called temporal consistency [41]. Its mathematical model is shown as follows:

$$\begin{array}{c}\underset{h_s}{argmin}{\displaystyle \sum _{s=1}^N}{∥h_s^{t-1}-h_s^t∥}^2\hfill \\ \underset{h_g}{argmin}{∥h_g^{t-1}-h_g^t∥}^2.\hfill \end{array}$$

(8)

By combining the above points to construct our tracking model, it can effectively learn the correlation filter models of the sub-regions and global region through the following optimization:

$$\begin{array}{c}\underset{{\left\{h_s^t\right\}}_{s=1}^N,h_g^t}{argmin}\left\{{\displaystyle \sum _{s=1}^N}\left({∥h_s^t\ast f_s^t-g_s^t∥}^2+\lambda {∥h_s^t∥}^2\right)+\left({∥h_g^t\ast f_g^t-g_g^t∥}^2+\lambda {∥h_g^t∥}^2\right)+\gamma {\displaystyle \sum _{s=1}^N}{∥{\nu }_s^t∥}_1+\frac{\xi }{2}{∥h_g^t-h_g^{t-1}∥}^2+\frac{\beta }{2}{\displaystyle \sum _{s=1}^N}{∥h_s^t-h_s^{t-1}∥}^2\right\}\hfill \\ s.t.h_s^t=h_g^t+{\nu }_s^t,\hfill \end{array}$$

(9)

where $\xi$ and $\beta$ denote trade-off coefficients, $\gamma$ is the regularization term coefficient. The trade-off coefficients are used to control the strength of the regularization term and prevent it from becoming larger during the optimization process. In fact, the motion models between consecutive frames are basically similar, so the regularization terms formed by the differences of their motion models can’t be too strong. Otherwise, if the target is occluded during the tracking process, it will lead to tracking failure or tracker drift, that is to say, the trade-off coefficients act as a role in guaranteeing the similarity of the motion models between consecutive frames.

3.3. Optimization Tracking Model

The optimization of Equation (9) is solved by constructing a Lagrangian function, which is an objective function formed by the augmented Lagrange multipliers being incorporated into the constraint condition. Then, the alternating direction method of multipliers (ADMM) [43] is used to implement an iterative update through a series of simple closed form operations. For details of the designed Lagrangian function, see Equation (10).

$$\begin{array}{cc}\hfill L(h_g^t,{\{h_s^t,{\nu }_s^t,{\epsilon }_s^t,{\tau }_s^t\}}_{s=1}^N)& ={\displaystyle \sum _{s=1}^N}\left({∥h_s^t\ast f_s^t-g_s^t∥}^2+\lambda {∥h_s^t∥}^2\right)+\left({∥h_g^t\ast f_g^t-g_g^t∥}^2+\lambda {∥h_g^t∥}^2\right)\hfill \\ & +\gamma {\displaystyle \sum _{s=1}^N}{∥{\nu }_s^t∥}_1+\frac{\xi }{2}{∥h_g^t-h_g^{t-1}∥}^2+\frac{\beta }{2}{\displaystyle \sum _{s=1}^N}{∥h_s^t-h_s^{t-1}∥}^2\hfill \\ & +{\displaystyle \sum _{s=1}^N}\left\{{({\epsilon }_s^t)}^T(h_s^t-h_g^t-{\nu }_s^t)+\frac{{\tau }_s^t}{2}{∥h_s^t-h_g^t-{\nu }_s^t∥}^2\right\}.\hfill \end{array}$$

(10)

Here, ${\epsilon }_s^t$ and ${\tau }_s^t$ are the Lagrange multiplier and penalty parameter, respectively. However, the new objective function becomes Equation (11).

$$\underset{h_g^t,{\{h_s^t,{\nu }_s^t,{\epsilon }_s^t,{\tau }_s^t\}}_{s=1}^N}{argmin}L(h_g^t,{\{h_s^t,{\nu }_s^t,{\epsilon }_s^t,{\tau }_s^t\}}_{s=1}^N).$$

(11)

Next, each parameter is iteratively updated using the ADMM by minimizing Equation (11). When one of the parameters is updated, the other parameters remain fixed. The procedure for updating each parameter variable is as follows.

Update$h_g^t$: The $h_g^t$ is updated by solving Equation (12) with the closed form solution, while the other parameters are fixed.

$$h_g^t=\underset{h_g^t}{argmin}\left\{\left({∥h_g^t\ast f_g^t-g_g^t∥}^2+\lambda {∥h_g^t∥}^2\right)+\frac{\xi }{2}{∥h_g^t-h_g^{t-1}∥}^2+{\displaystyle \sum _{s=1}^N}\left\{-{({\epsilon }_s^t)}^T{h}_g^t+\frac{{\tau }_s^t}{2}{∥h_s^t-h_g^t-{\nu }_s^t∥}^2\right\}\right\},$$

(12)

its closed solution gives Equation (13).

$$h_g^t={\mathcal{F}}^{-1}\left(\frac{F_g^t\overline{G_g^t}+\frac{\xi }{2}{H}_g^{t-1}+{\displaystyle \sum _{s=1}^N}\left\{{\left({\epsilon }_s^t\right)}^T+\frac{{\tau }_s^t}{2}\left(H_s^t-{\nu }_s^t\right)\right\}}{F_g^t\overline{F_g^t}+\left(\lambda +\frac{\xi }{2}+{\displaystyle \sum _{s=1}^N}\frac{{\tau }_s^t}{2}\right)I}\right),$$

(13)

where $F,H,G$ and $\nu$ denote the discrete Fourier transforms (DFTs) of $f,h,g$ and $\nu$, respectively. I is the identity matrix. The bar $\overline{G_g^t}$ denotes a complex conjugation.

Update$h_s^t$: The $s^{th}$ independent sub-problem $h_s^t$ is updated by solving Equation (14) with the closed form solution, while the other parameters are fixed.

$$h_s^t=\underset{h_s^t}{argmin}\left\{{∥h_s^t\ast f_s^t-g_s^t∥}^2+\lambda {∥h_s^t∥}^2+\frac{\beta }{2}{∥h_s^t-h_s^{t-1}∥}^2+{\left({\epsilon }_s^t\right)}^T{h}_s^t+\frac{{\tau }_s^t}{2}{∥h_s^t-h_g^t-{\nu }_s^t∥}^2\right\},$$

(14)

its closed solution gives Equation (15).

$$h_s^t={\mathcal{F}}^{-1}\left(\frac{\overline{G_s^t}{F}_s^t+\frac{\beta }{2}{H}_s^{t-1}+\frac{{\tau }_s^t}{2}\left(H_g^t+{\nu }_s^t\right)-{\left({\epsilon }_s^t\right)}^T}{\overline{F_s^t}{F}_s^t+\left(\lambda +\frac{\beta }{2}+\frac{{\tau }_s^t}{2}\right)I}\right).$$

(15)

Update${\nu }_s^t$: The $s^{th}$ independent sub-problem ${\nu }_s^t$ is updated by solving Equation (16) with the closed form solution, while the other parameters are fixed.

$${\nu }_s^t=\underset{{\nu }_s^t}{argmin}\left\{\gamma {∥{\nu }_s^t∥}_1-{({\epsilon }_s^t)}^T{\nu }_s^t+\frac{{\tau }_s^t}{2}{∥h_s^t-h_g^t-{\nu }_s^t∥}^2\right\}.$$

(16)

The solution of Equation (16) can be converted to the solution of Equation (17) according to Reference [43], and its closed solution gives Equation (18).

$${\nu }_s^t=\underset{{\nu }_s^t}{argmin}\left\{\frac{\gamma }{{\tau }_s^t}{∥{\nu }_s^t∥}_1+\frac{1}{2}{∥{\nu }_s^t-\left(h_s^t+\frac{{\epsilon }_s^t}{{\tau }_s^t}-h_g^t\right)∥}^2\right\},$$

(17)

$${\nu }_s^t=S_{\frac{\gamma }{{\tau }_s^t}}\left(h_s^t+\frac{{\epsilon }_s^t}{{\tau }_s^t}-h_g^t\right).$$

(18)

Here,

$$S_{\theta }\left({\mathrm{x}}_i\right)=\mathrm{sign}\left({\mathrm{x}}_i\right)max\left(0,\left|{\mathrm{x}}_i\right|-\theta \right)$$

(19)

represents the soft threshold function of the vector $\mathrm{x}$.

Update${\epsilon }_s^t$ and ${\tau }_s^t$: The Lagrange multiplier ${\epsilon }_s^t$ and penalty parameter ${\tau }_s^t$ are updated as in Equation (20).

$${\epsilon }_s^t={\epsilon }_s^t+{\tau }_s^t\left(h_s^t-h_g^t-{\nu }_s^t\right),{\tau }_s^t=\phi {\tau }_s^t$$

(20)

The solution of the objective function Equation (11) obtained through ADMM optimization is shown in Algorithm 1.

Algorithm 1: ADMM optimization for Equation (11).

3.4. Tracking

3.4.1. Position Estimation

In a new frame t, a sample patch $z_t$ is extracted from the region centered around the previous frame target position. The HOG feature vector is then used to represent the sample patch $z_t$. Using the obtained sub-region and global region correlation filters, we can obtain the correlation responses of the sub-regions and global region in the frequency domain.

The correlation response $y_g^t$ of global region is computed by:

$$y_g^t={\mathcal{F}}^{-1}\left(\overline{H_g^{t-1}}\odot Z_g^t\right),$$

(21)

the correlation response $y_s^t$ of the $s^{th}$ sub-region is computed by:

$$y_s^t={\mathcal{F}}^{-1}\left(\overline{H_s^{t-1}}\odot Z_s^t\right),$$

(22)

where the operator ⊙ is the Hadamard product, while $H_g^{t-1}$ and $H_s^{t-1}$ are the updated correlation filters of the global region and sub-regions in the previous frame, respectively.

The maximum correlation response value corresponds to the coordinate that indicates the location of the target, that is to say, the position $p_g$ of the global region target is obtained by finding the maximum correlation response $y_g^t$, and the position $p_s$ of the $s^{th}$ sub-region target is obtained by finding the maximum correlation response $y_s^t$. The final target position P estimation depends on the global region target position $p_g$ and the sub-region target position $p_s$, as follows:

$$P={\omega }_g{p}_g+{\displaystyle \sum _{s=1}^N}{\omega }_s\left(p_s+{\Delta }_s\right),$$

(23)

where ${\omega }_g$ and ${\omega }_s$ denote the weights of the global region target position and the sub-regions target position, respectively. ${\Delta }_s$ is the deformation vector [44] between the $s^{th}$ sub-region and the object center. These weights are calculated based on their corresponding correlation response maximum values, as in Reference [45].

$${\omega }_g=\frac{f\left(max\left(y_g\right)\right)}{f\left(max\left(y_g\right)\right)+{\displaystyle \sum _{s=1}^N}f\left(max\left(y_s\right)\right)}$$

(24)

$${\omega }_s=\frac{f\left(max\left(y_s\right)\right)}{f\left(max\left(y_g\right)\right)+{\displaystyle \sum _{s=1}^N}f\left(max\left(y_s\right)\right)},$$

(25)

where $f\left(x\right)=\frac{1}{1+exp\left(-x\right)}$.

3.4.2. Scale Estimation

Resolving the scale change of the target is an important issue for visual tracking, and can make the tracking process more accurate. Existing correlation filter trackers [11,12,19,37] exhibit superior performance in estimating target scale change. These algorithms estimate the target’s scale by constructing a target pyramid, which is a different scale pool sampled around the estimated current target position and then correlated with the updated discriminative correlation filter. The maximum correlation response value corresponding to the scale level is the current target size. However, the scale of these filters does not change adaptively as the target scale changes, which leads to the inaccurate estimation of the target scale. Using the idea that the relative distance among the sub-regions and the target scale change is proportional, the filter scale can be adaptively changed to accurately estimate the target’s scale. This approach is described in References [40,41,45]. In this work, we use existing heuristics to estimate the target’s scale according to the method presented in Reference [45]. Specifically, we calculate the target’s scale in the t-frame as follows:

$$\left({\mathrm{w}}_t,{\mathrm{h}}_t\right)=\left({\mathrm{w}}_{t-1},{\mathrm{h}}_{t-1}\right)\times \frac{1}{N\left(N-1\right)}{\displaystyle \sum _{i=1,j=1}^N}\frac{∥p_i^t-p_j^t∥}{∥p_i^{t-1}-p_j^{t-1}∥}\begin{array}{ccc}& s.t.& i\ne j,\end{array}$$

(26)

where ${\mathrm{w}}_t$ and ${\mathrm{h}}_t$ denote the width and height of the target in the t-frame, respectively. $∥·∥$ stands for the Euclidean metric. $p_i^t$ indicates the position of the i-th sub-region in the t-th frame.

3.4.3. Model Update

During online tracking, the appearance model of the target may undergo severe changes. In order to solve these situations, after predicting a new target position in each frame, we have to update the sub-regions and global region correlation filters. To obtain a relatively good approximation, we used dynamic averaging to update the sub-regions and global region correlation filters as follows:

$$H_g^t=\eta H_g^t+\left(1-\eta \right)H_g^{t-1}$$

(27)

$$H_s^t=\eta H_s^t+\left(1-\eta \right)H_s^{t-1},$$

(28)

where t and $\eta$ denote the frame index and learning rate, respectively. The global region correlation filter $h_g^t={\mathcal{F}}^{-1}\left(H_g^t\right)$, and the sub-regions correlation filter $h_s^t={\mathcal{F}}^{-1}\left(H_s^t\right)$.

3.5. Proposed Tracking Algorithm

An overview of the proposed tracking algorithm is listed in Algorithm 2.

Algorithm 2: The proposed tracking algorithm.

4. Experiment

In this section, the effectiveness of the proposed tracking algorithm is confirmed by comparing it with state-of-the-art trackers on two popular datasets: the OTB-2015 [31] and VOT-2015 [32] visual tracking benchmark datasets. In addition, we present the details of implementation and the ablation analysis in Section 4.1 and Section 4.2, respectively. The experimental results are shown in Section 4.3, and the experimental analysis is reported in Section 4.4.

4.1. Implementation Details

Our tracker was implemented using the MATLAB R2017a software platform. We set the same parameters during tracking, and ran at around 1.5 fps. The regularization term coefficient $\lambda$ and the learning rate $\eta$ were set to 0.01 and 0.025, respectively. The parameters $\gamma ,\xi$ and $\beta$ were all set to 0.01. We found that setting the number of sub-regions N to 4 was more suitable for the experiment. This is because too many sub-regions cause a low target resolution, resulting in less feature information for identifying the target, while too few sub-regions will reduce the feature information of the visual parts due to occlusion. We used the HOG feature for target representation.

4.2. Ablation Analysis

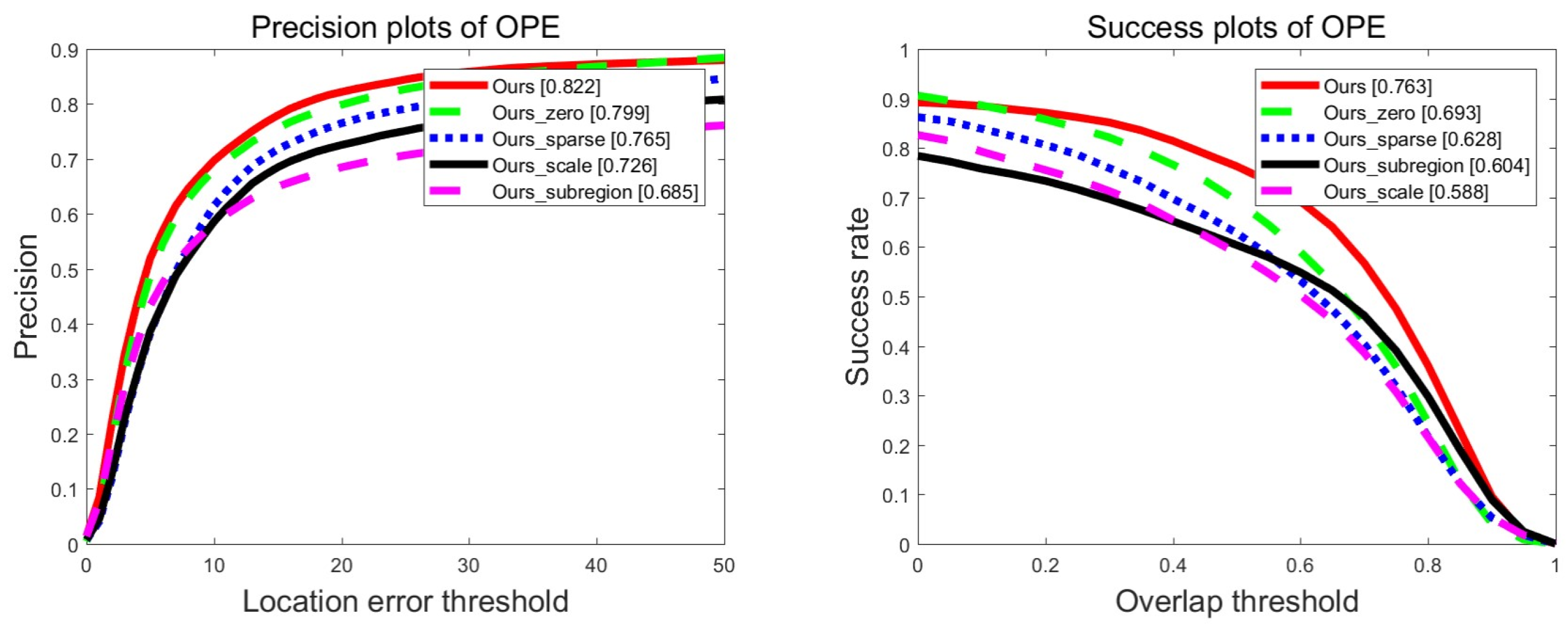
Our algorithm consists of four important components including zero-padding, scale estimation, sub-regions, and sparse constraint. In order to evaluate the effectiveness of each component in our tracking framework, we conduct ablation study on the OTB-2015 dataset by disabling each component one by one. The comparison results of the distance and overlap precision are shown in Figure 2.

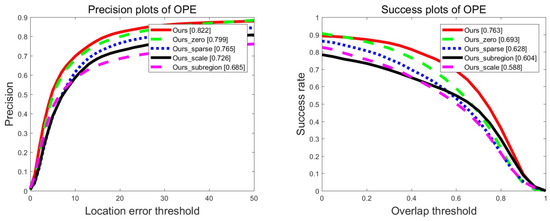
Figure 2. Precision and success plots of disabling component tracker on the OTB-2015 dataset for the ablation analysis. In this plot, Ours_subregion denotes Ours without using the subregion, and likewise Ours_scale, Ours_zero, and Ours_sparse denotes Ours without using scale estimation, zero-padding, and sparse constraint, respectively.

As shown in Figure 2, without the zero-padding component, the tracking results are relatively good due to the accurate scale estimation, the coupling and constraints between the sub-regions and the global region, all of which are attributed to our coupled-region tracking formulation. Without the sparse constraint component, in complex scenarios, due to the inability to tolerate the outliers of the subregion, our tracking model is difficult to completely preserve the internal structure of the target, which may cause the risk of tracker drift. Therefore, the scores of the distance and overlap precision are not the result of the promising. The scale estimation is an important role in our tracking framework. To evaluate the performance of our tracker, we disable the scale estimation component for tracking. Figure 2 shows that the value of the overlap precision is low. The main reason is that the tracker cannot adaptively change the scale through scale variation sequence.

Extensive evaluations demonstrate that coupling subregion tracking formulation is an effective strategy to solve occlusion problem. However, we disable the sub-region component for tracking, which is similar to the baseline tracker, while the baseline tracker does not solve the occlusion problem, so it is lower than the proposed tracker in terms of the value of the distance and overlap precision. In general, each component plays an important role in our tracking framework, and by jointly optimizing them, we receive the promised tracking performance.

4.3. Experimental Results

We performed comprehensive experiments on the OTB-2015 [31] and VOT-2015 [32] benchmark datasets to evaluate the performance of our tracker.

4.3.1. Experiment on the OTB-2015 Dataset

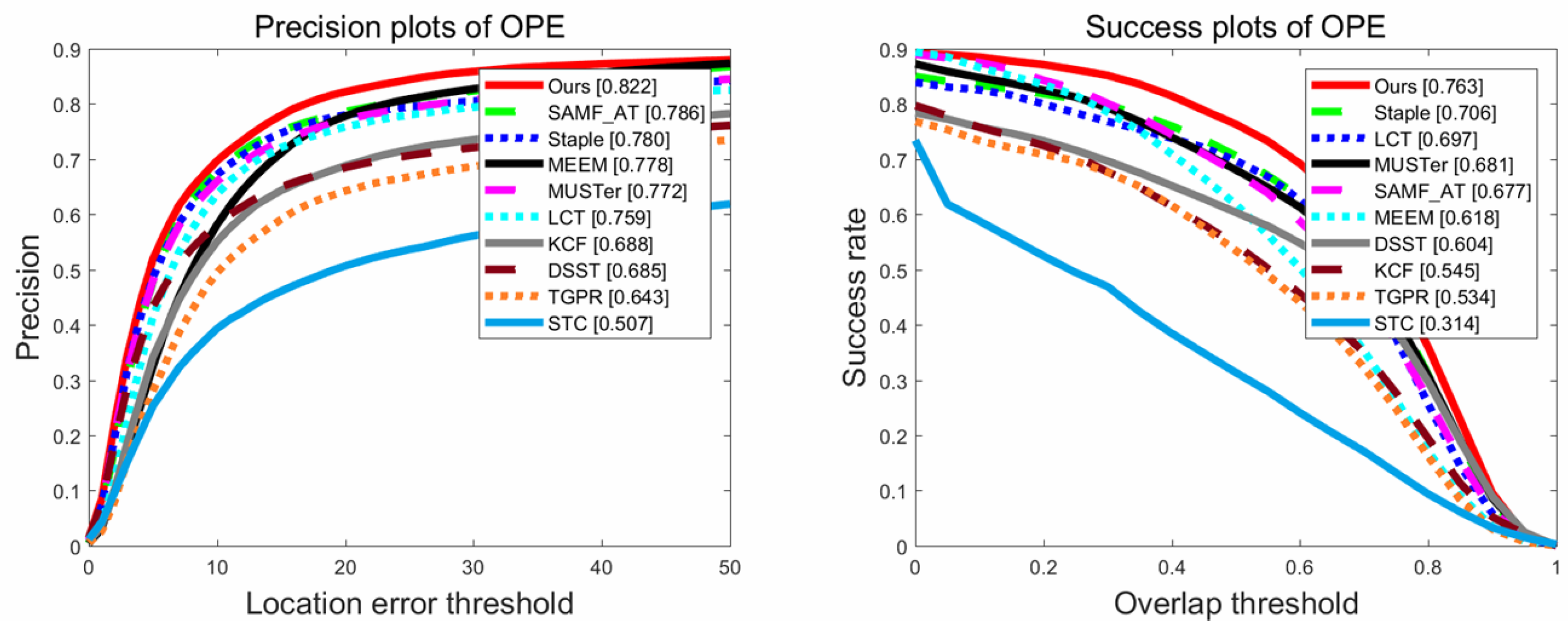
The OTB-2015 benchmark dataset contains 100 fully annotated video sequences, which are divided into 11 different attributes such as: Illumination Variation (IV), Scale Variation (SV), Occlusion (OCC), Deformation (DEF), Motion Blur (MB), Fast Motion (FM), In-Plane Rotation (IPR), Out-of-Plane Rotation (OPR), Out-of-View (OV), Background Clutters (BC), and Low Resolution (LR). These attributes represent different challenging scenarios for visual tracking. Using this dataset to test the performance of our algorithm by comparing it with the other nine excellent trackers: TGPR [46], SAMF_AT [24], STC [20], MUSTer [16], Staple [47], LCT [19], KCF [15], MEEM [7], DSST [11], and BACF [38]. We reported the comparison results through the one-pass evaluation (OPE) with precision and success plots. The precision plot shows the percentage of frames in which the center position error is smaller than a certain threshold; we used a threshold of 20 pixels for all comparison trackers. The success plot presents the percentage of successful frames where the overlap score between the tracking bounding box and the ground-truth bounding box was more than one threshold. The overlap score is defined as $\frac{area(B_T\cap B_G)}{area(B_T\cup B_G)}$, where $B_T$ and $B_G$ are the tracking bounding box and the ground-truth bounding box, respectively. We used a threshold of 0.5 to rank all comparison trackers in the success plots. The precision and success plots demonstrate the mean results over the OTB-2015 dataset.

As shown in Figure 3, the comparison results of the precision and success plots show that our tracking algorithm outperforms other state-of-the-art trackers in terms of distance precision and overlap precision. We can see that our tracker achieved the ranking scores of 0.822 and 0.763 in distance precision and overlap precision, respectively. However, the distance precision and overlap precision ranking scores of the baseline tracker DSST [11] were 0.693 and 0.535, respectively. Obviously, our tracking algorithm was greatly improved in terms of distance and overlap precision. There are two main reasons. First, the motion model of the proposed method is completely different from the DSST. We use the idea of optimization and constraint to retain the internal structure of the target, while DSST has no optimization model. Second, the scale estimation method is different. We use the strategy of proportional to relative distance among sub-regions, whereas DSST uses the strategy of constructing target scale pyramid to estimate scale.

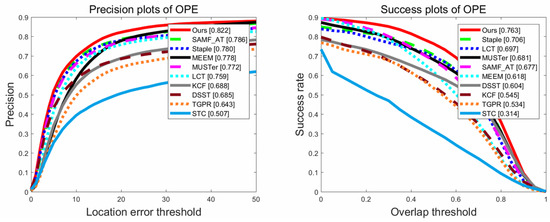
Figure 3. Precision and success plots of different trackers on the OTB-2015 dataset. Our tracker is better than other trackers.

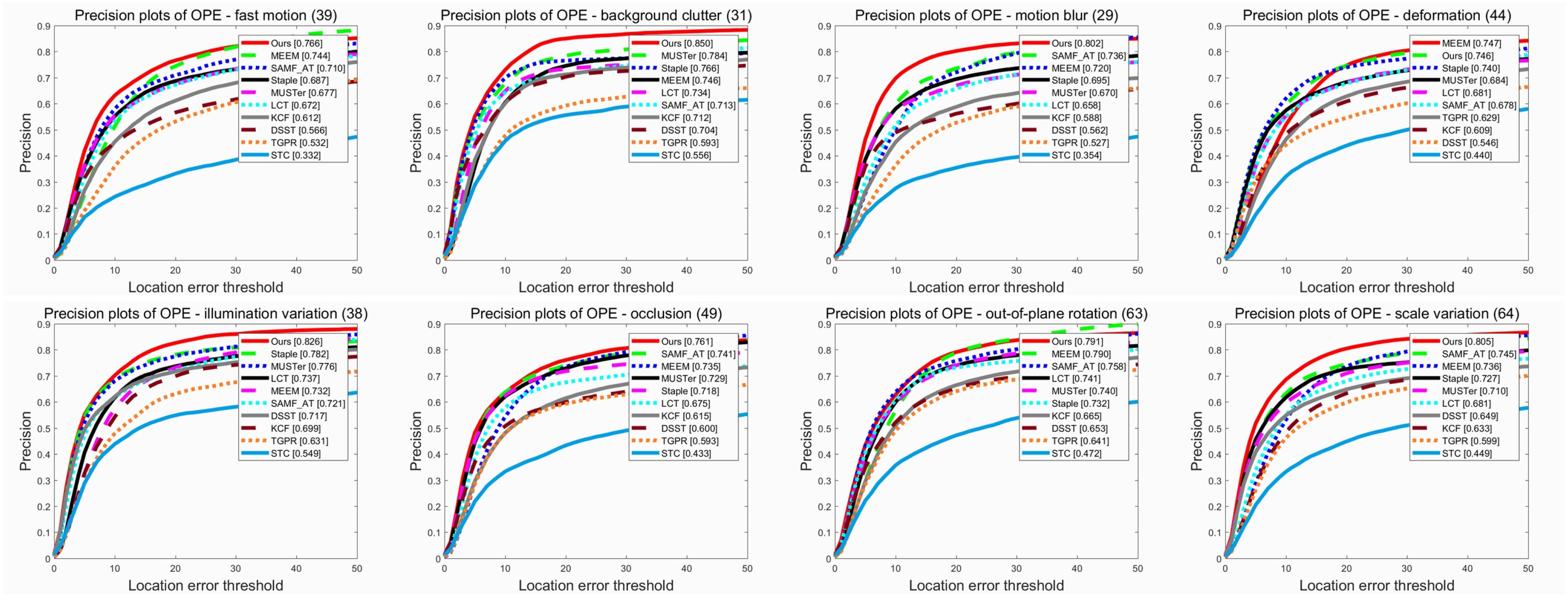
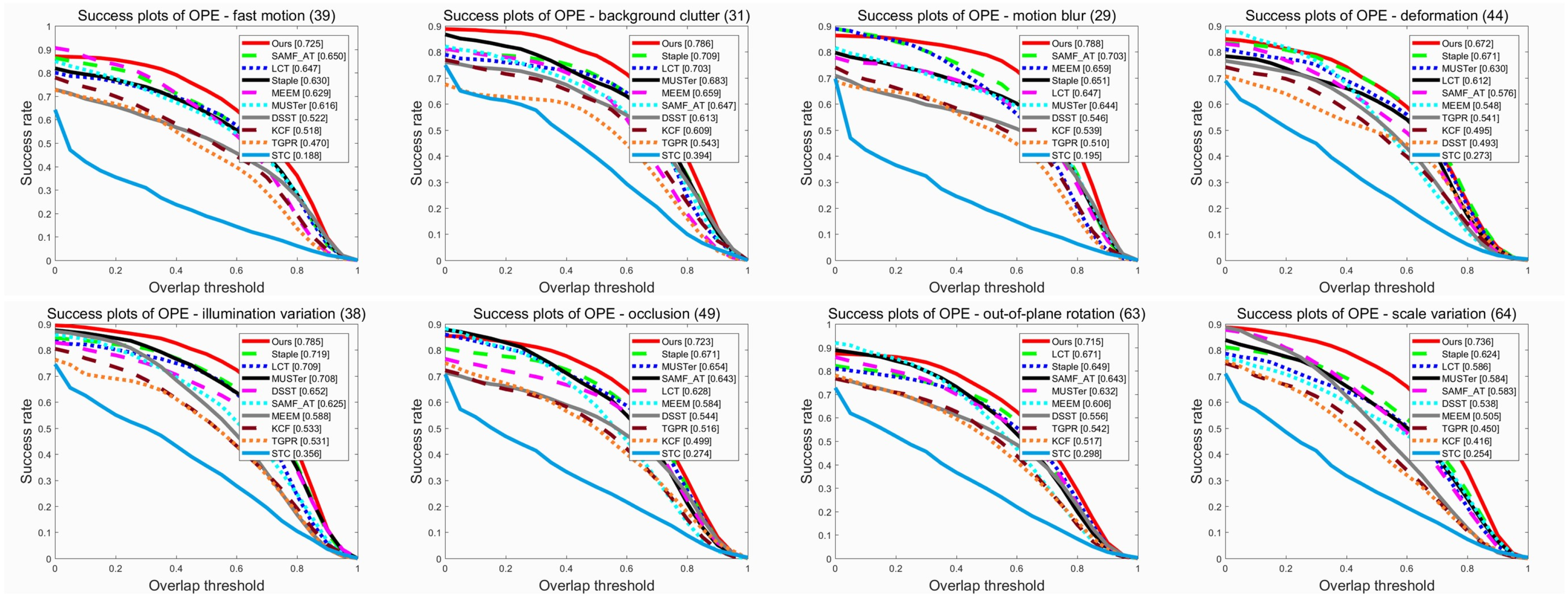
To demonstrate the robustness of our tracker when faced with different challenging attributes, we present the comparison results of eight attributes (IV, SV, OCC, DEF, MB, FM, OPR and BC) in terms of distance and overlap precision. See Figure 4 and Figure 5 for details. The results show that our tracker ranks second and first in the precision and success plot for sequences with deformation, respectively, while it ranks first in the precision and success plots for the other seven scenarios with challenging attributes. These results confirm that our approach has a very promising performance in dealing with such challenges, especially in scenarios with occlusion.

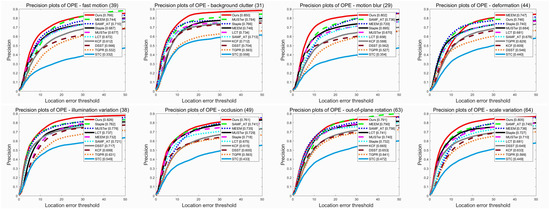
Figure 4. Performance evaluation of distance precision on eight challenging attributes (FM, BC, MB, DEF, IV, OCC, OPR and SV) of the OTB-2015 dataset.

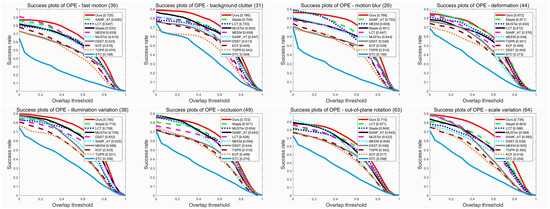
Figure 5. Performance evaluation of overlap precision on eight challenging attributes (FM, BC, MB, DEF, IV, OCC, OPR and SV) of the OTB-2015 dataset.

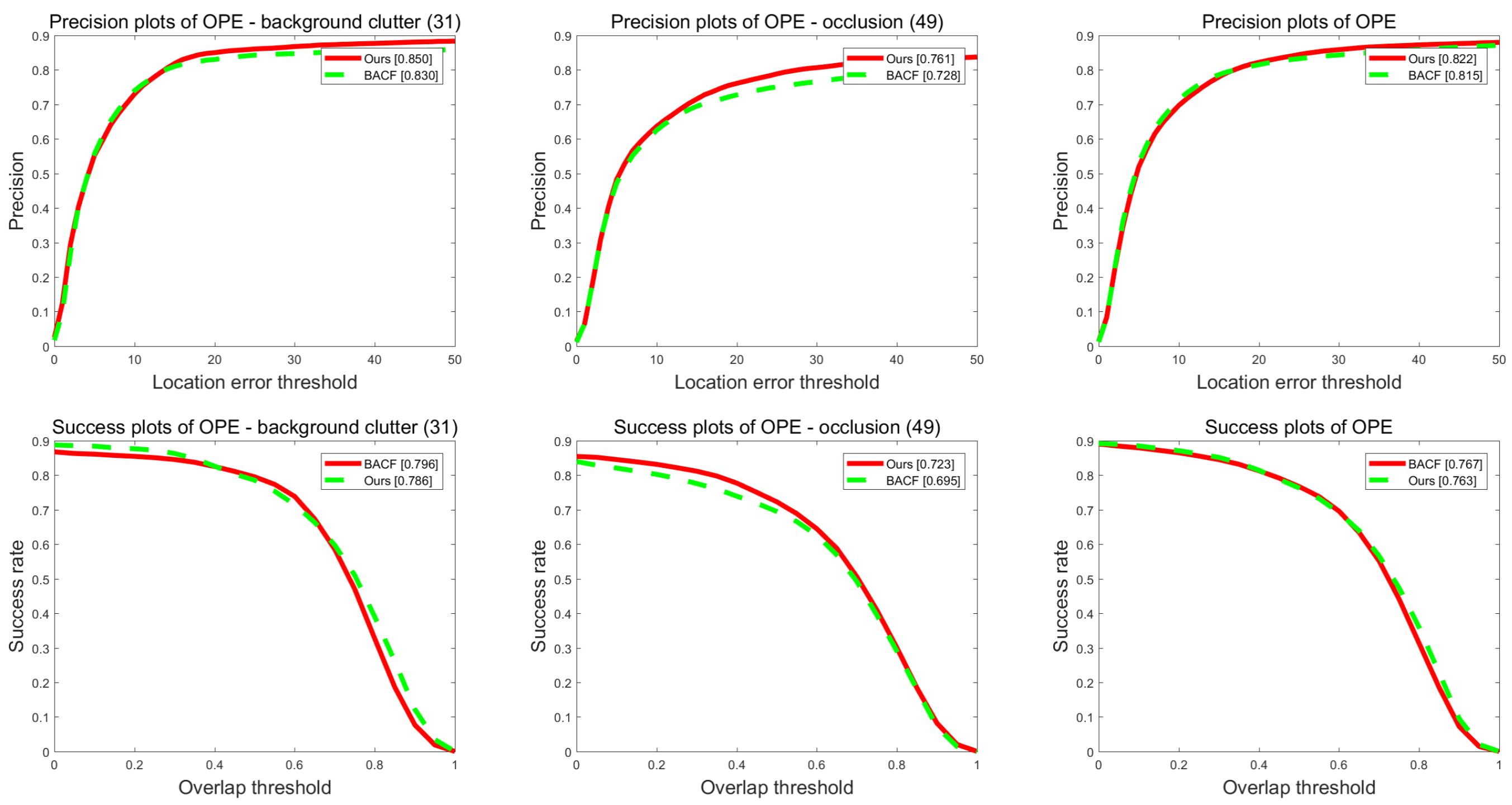
Both our algorithm and the BACF [38] tracker use the idea of zero-padding and ADMM iterative optimization, and both use the dynamic average strategy formulation for model update. Figure 6 shows the performance comparison of our method and BACF on the OTB-2015 dataset in terms of background clutters, occlusion and all sequences challenging attributes.

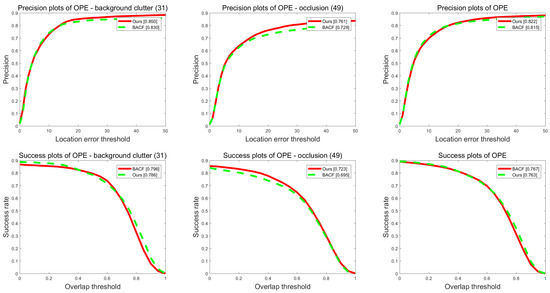
Figure 6. Performance evaluation of our method and BACF on the OTB-2015 dataset.

In the sequence of background clutters attribute, the results in Figure 6 show that our method and BACF are 0.85 and 0.83 in terms of distance precision, respectively, and the overlap precision is 0.786 and 0.796 respectively. In the sequence of occlusion, our approach outperforms BACF in terms of distance and overlap precision, this is the advantage of our coupled-region visual tracking formulation in solving occlusion problems. In all sequences, our approach outperforms BACF in terms of distance precision, whereas our method is slightly behind BACF in terms of overlap precision. In general, our approach and BACF have their own merits in performing tracking.

In order to more intuitively demonstrate the superior performance of our algorithm, we plotted the experimental results of 11 different challenge attribute sequences in OTB-2015 into Table 1 and Table 2. By comparing distance and overlap precision with other state-of-the-art trackers, it can be seen at a glance that our tracker is superior to the other trackers apart from BACF in terms of overlap precision. However, in terms of distance precision, our tracker achieved the best results in six of the 11 attributes. In the remaining attribute sequences (DEF, IPR, OV, FM, and LR), the BACF [38] and MEEM [7] performs better. Based on the results of Table 1 and Table 2, we analyze the reasons for the advantages of our method in terms of partial challenging attributes.

Table 1. Comparison of our tracker with other state-of-the-art trackers on 11 different attributes of the OTB-2015 dataset. Average precision scores (%) at a threshold of 20 pixels are presented. The optimal results are highlighted in bold.

Attribute	Ours	BACF	TGPR	SAMF_AT	STC	MUSTer	Staple	LCT	KCF	MEEM	DSST
IV	82.6	80.8	63.1	72.1	54.9	77.6	78.2	73.7	69.9	73.2	71.7
SV	80.5	77.4	59.9	74.5	44.9	71	72.7	68.1	63.3	73.6	64.9
OCC	76.1	72.8	59.3	74.1	43.3	72.9	71.8	67.5	61.5	73.5	60
DEF	74.6	75.8	62.9	67.8	44	68.4	74	68.1	60.9	74.7	54.6
MB	80.2	73.6	52.7	73.6	35.4	67	69.5	65.8	58.8	72	56.2
FM	76.6	78.6	53.2	71	33.2	67.7	68.7	67.2	61.2	74.4	56.6
IPR	77	77.8	65.8	77.5	47.6	76.8	76.3	77.5	68.6	78.8	69.4
OPR	79.1	77.3	64.1	75.8	47.2	74	73.2	74.1	66.5	79	65.3
OV	64.1	76.5	49.3	65	35	59.1	66.1	59.2	49.8	68.5	47.8
BC	85	83	59.3	71.3	55.6	78.4	76.6	73.4	71.2	74.6	70.4
LR	74.7	79.5	62.6	78.8	48.9	74.7	69.5	69.9	67.1	80.8	68.4
Overall	82.2	81.5	64.3	78.6	50.7	77.2	78	75.9	68.8	77.8	68.5

Table 2. Comparison of our tracker with other state-of-the-art trackers on 11 different attributes of the OTB-2015 dataset. Average success scores (%) at a threshold of 0.5 are presented. The optimal results are highlighted in bold.

Attribute	Ours	BACF	TGPR	SAMF_AT	STC	MUSTer	Staple	LCT	KCF	MEEM	DSST
IV	78.5	78.4	53.1	62.5	35.6	70.8	71.9	70.9	53.3	58.8	65.2
SV	73.6	70.4	45	58.3	25.4	58.4	62.4	58.6	41.6	50.5	53.8
OCC	72.3	69.5	51.6	64.3	27.4	65.4	67.1	62.8	49.9	58.4	54.4
DEF	67.2	69.2	54.1	57.6	27.3	63	67.1	61.2	49.5	54.8	49.3
MB	78.8	71.2	51	70.3	19.5	64.4	65.1	64.7	53.9	65.9	54.6
FM	72.5	74.4	47	65	18.8	61.6	63	64.7	51.8	62.9	52.2
IPR	69.2	69.7	55.4	64	30.8	64.3	66.7	68.7	54	61.9	58.9
OPR	71.5	70.8	54.2	64.3	29.8	63.2	64.9	67.1	51.7	60.6	55.6
OV	64.1	69.4	45.2	61	22.5	54.1	56	53.1	45.7	56.8	44.2
BC	78.6	79.6	54.3	64.7	39.4	68.3	70.9	70.3	60.9	65.9	61.3
LR	67.9	65	38.1	56.7	22.6	44.2	45.9	48.4	25.1	33	41.9
Overall	76.3	76.7	53.4	67.7	31.4	68.1	70.6	69.7	54.5	61.8	60.4

In the scene of the illumination variation(IV) attribute, the target appearance model will be seriously affected, often causing the tracker to drift. In our tracking framework, the HOG feature was used to represent the target and to some extent suppress the illumination variation. Together with our accurate scale estimation scheme, the tracker is more robust. In the actual tracking scene, the occlusion is usually accompanied by the occurrence of background clutters (BC). Our method solves the occlusion problem, which is naturally equivalent to solving the background clutters problem, which is attributed to the coupling formulation between the sub-regions and the global region. The internal structure of the target is preserved, and the outliers of the sub-region can be tolerated. In the out-of-plane rotation (OPR)scenarios, we use the idea that the relative distance among the sub-regions and the target scale change is proportional and the filter scale can be adaptively changed to accurately estimate the target’s scale, thereby lowering the risk of drift and tracking failure. In the low resolution (LR) sequences, our tracker does not perform as well as MEEM in terms of distance precision, because MEEM tracks the target with multiple appearance models. While in our tracking framework, the parts are small in size and low in resolution, and cannot contain enough target feature information, so that our algorithm does not perform well in low-resolution scenes. However, in the range of successful frames tracked, since the scale of our correlation filter can be adaptively changed to accurately estimate the target’s scale, our tracker performs well in terms of overlap precision.

Next, the qualitative evaluation and analysis were carried out to further demonstrate that the performance of the proposed tracker is superior to other state-of-the-art trackers on the OTB-2015 [31] image sequence. Figure 7 shows the qualitative comparison results of our algorithm with nine state-of-the-art trackers (TGPR [46], SAMF_AT [24], STC [20], MUSTer [16], Staple [47], LCT [19], KCF [15], MEEM [7], and DSST [11]) on seven sequences (Shaking, Dog1, Jogging1, BlurCar3, Surfer, Skater2 and Football1). In Shaking, illumination variation is the most representative challenging attribute. The SAMF_AT, Staple, and KCF trackers performed poorly due to noise image gradient effects. In our tracking framework, the HOG feature was used to represent the target and to some extent suppress the illumination variation. Compared to other trackers, our tracker showed better tracking results. In Dog1, scale variation is the most representative challenging attribute. Although there are significant scale variations between different frames, our tracking algorithm could accurately estimate the scale and position of the target. However, the MEEM, KCF, and TGPR trackers failed to address the challenges of scale variations. In the Jogging1 sequence, occlusion is the most representative challenging attribute. When the target experienced partial and full occlusion, the proposed algorithm performed more robustly during the tracking process. This is because the remaining visible sub-region patches can still provide reliable cues for tracking. However, the tracking bounding box of these trackers (DSST, STC, Staple, TGPR, and KCF) lost the target when the occlusion occurred, eventually resulting in tracking failure. In other sequences (BlurCar3, Surfer, Skater2 and Football1), our tracker performed well in terms of scale and position estimation. However, the STC tracker did not perform well during the tracking process. The main reason for this was attributed to two aspects: first, the STC tracker uses image intensity as features to represent the appearance model of the target context. Second, the estimated scale depends on the response map of a single filter.

Figure 7. Qualitative evaluation of our algorithm and nine other state-of-the-art trackers on seven sequences (from top to bottom: Shaking, Dog1, Jogging1, BlurCar3, Surfer, Skater2 and Football1). These sequences correspond to the attributes IV, SV, OCC, MB, FM, OPR and BC, respectively.

4.3.2. Experiment on the VOT-2015 Dataset

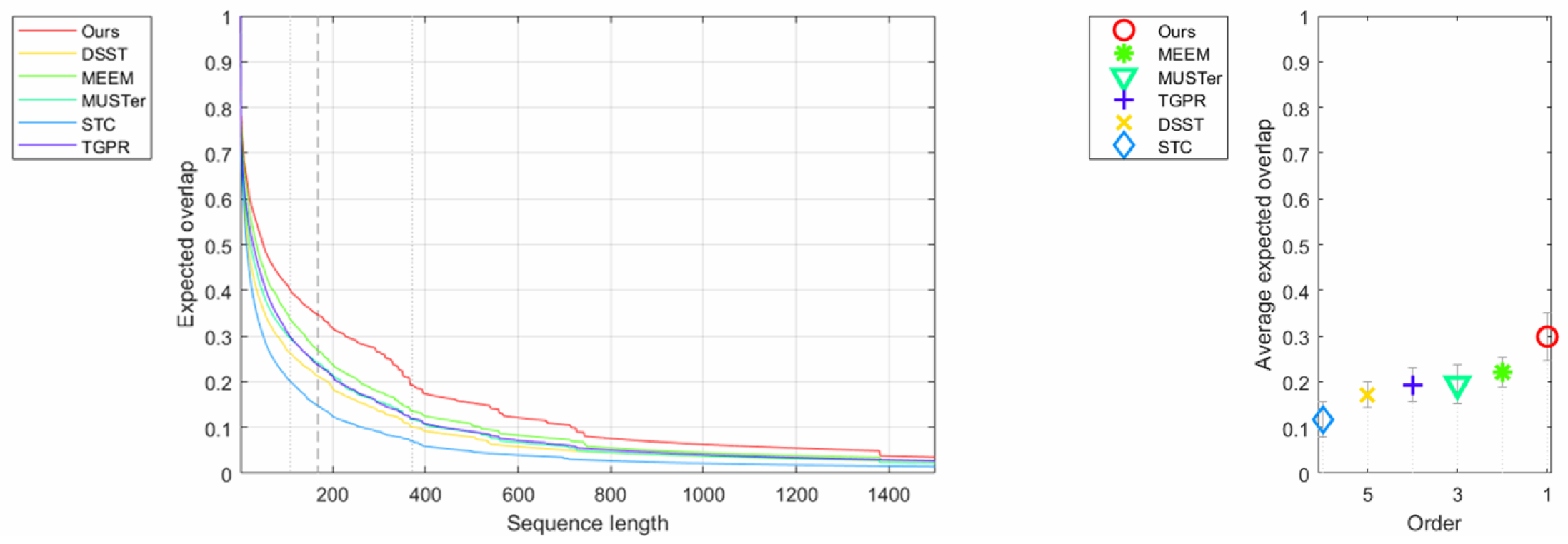
The VOT-2015 dataset [32] includes 60 video sequences. Using this dataset to test the performance of our algorithm by comparing it with the other five excellent trackers: TGPR [46], STC [20], MUSTer [16], MEEM [7], and DSST [11]. We reported the comparison results of average accuracy, robustness, and expected average overlap (EAO) to evaluate these trackers. Accuracy and robustness measures were based on the overlap ratio during successful tracking and the number of tracking failures per sequence, respectively. While the expected average overlap (EAO) is the new evaluation indicator for VOT-2015, this measure is based on empirical estimations of short-term sequence lengths. Table 3 presents the comparison results on the VOT-2015 in terms of accuracy, robustness, and expected average overlap. Our approach demonstrated a promising performance.

Table 3. Average ranks of accuracy, robustness, and expected average overlap under baseline experiments on the VOT-2015 dataset. The best three scores are highlighted in red, blue, and green, respectively.

Tracker	Acc. Rank	Rob. Rank	EAO
Ours	1.35	1.43	0.2987
MEEM	1.85	2.37	0.2212
MUSTer	1.67	2.20	0.1950
TGPR	2.12	2.67	0.1938
DSST	1.83	2.97	0.1719
STC	3.97	4.03	0.1179

To further demonstrate that the performance of our tracker is superior to the five other state-of-the-art trackers on the VOT-2015 dataset, Figure 8 shows more intuitive comparison.

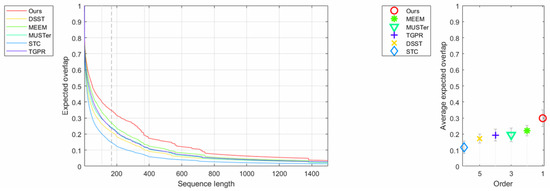
Figure 8. Expected average overlap curves and scores for the experiment baseline on the VOT-2015 dataset.

4.4. Experimental Analysis

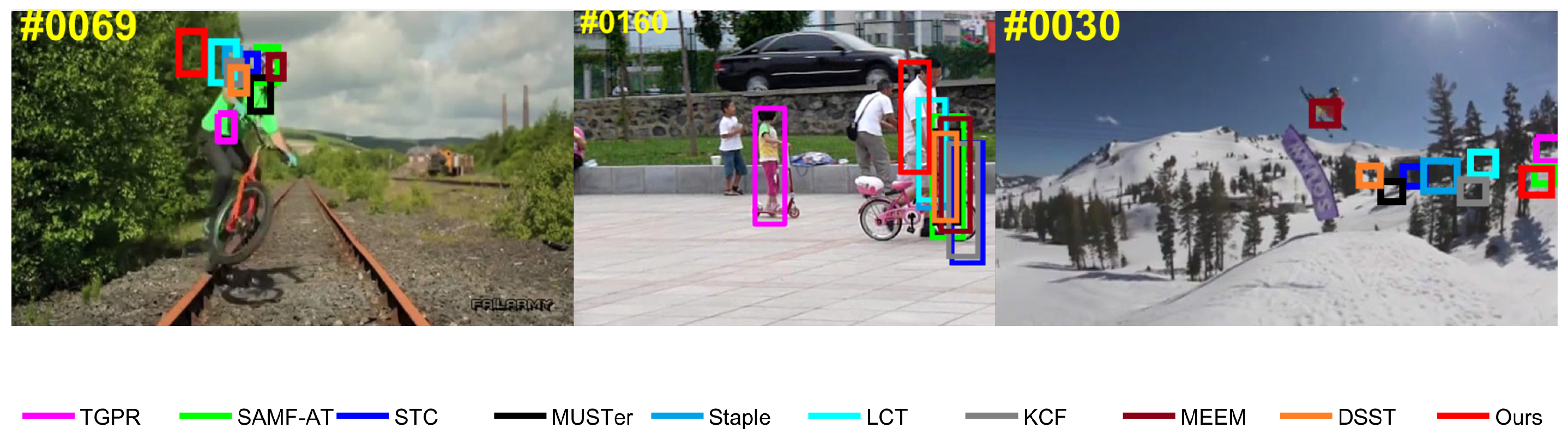
Our tracker achieved amazing results in many challenging scenarios. Especially in scenes where the target is partially occluded, the effective appearance of the remaining visible parts can still provide reliable cues for tracking. According to the coupling between the sub-regions and the global region, the complete structure of the target can be retained, and the outliers of the occluded sub-regions can be tolerated. This strategy can achieve effective tracking for solving the occlusion problem. However, the proposed algorithm did not perform well when faced with certain challenging attribute sequences (IPR, LR, and OV). In addition, when the sub-regions are completely occluded for long-term, our tracking framework did not effectively activate the tracker. The sampling frames for tracking failure are shown in Figure 9. There are three reasons for the flaws in our tracker. First, our algorithm does not solve the rotation problem of the target, so it cannot generate the rotated tracking bounding boxes for the IPR challenging attribute. Second, our framework lacks an occlusion re-identification scheme; therefore, when long-term occlusion occurs, the tracker cannot be active for a long time, causing the tracking to fail. The occlusion re-identification scheme incorporated into the tracking framework causes the tracker to skip the current occluded frame and calculate the tracking result from the next frame, which increases the adaptability of the discriminative correlation filter bank. Third, when a target in a low-resolution sequence is divided into multiple sub-regions, these sub-regions lack sufficient target feature information to train the robust discriminant correlation filter bank. Eventually, the tracking bounding boxes will not be able to effectively identify the target.

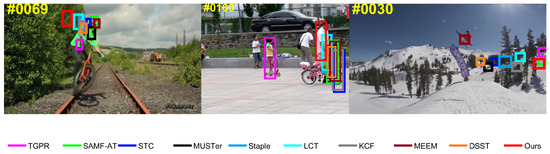
Figure 9. Failure cases on the OTB-2015 (from left to right: Biker, Girl2, and Skiing). In the Biker sequence, OV and LR are the most representative challenging attributes. The Girl2 sequence contains long-term occlusion tracking challenges. In the Skiing sequence, the target undergoes LR and IPR during tracking.

5. Conclusions

In this paper, the discriminative correlation filter bank model is formed by combining multiple optimized correlation filters. We formulated multiple discriminative correlation filters corresponding to different sub-region and global patches simultaneously to achieve a robust tracking performance. By this means, the visible sub-regions can alleviate tracker drift when partial occlusion occurs. In addition, the sub-region patches used to train the correlation filters are zero-padded to the same size as the global target region to avoid noise aliasing during the correlation operation. Moreover, we used the ADMM optimization approach to iteratively train our correlation filters over time; this strategy will greatly improve the robustness of the tracker. Finally, we demonstrated the competitive accuracy and superior tracking performance of our method compared to state-of-the-art methods using the OTB-2015 and VOT-2015 datasets. In future work, we will study an effective occlusion detection model and incorporate this model into our tracking framework. When long-term occlusion occurs, the tracker can adaptively skip the occluded frame and calculate the tracking result from the next frame during the tracking process. Furthermore, the online adaptive update strategy will also be the focus of future work, because a real-time update tracker can greatly improve the accuracy of tracking for complex appearance changes.