Automatic EMI Filter Design for Power Electronic Converters Oriented to High Power Density
Abstract
:1. Introduction
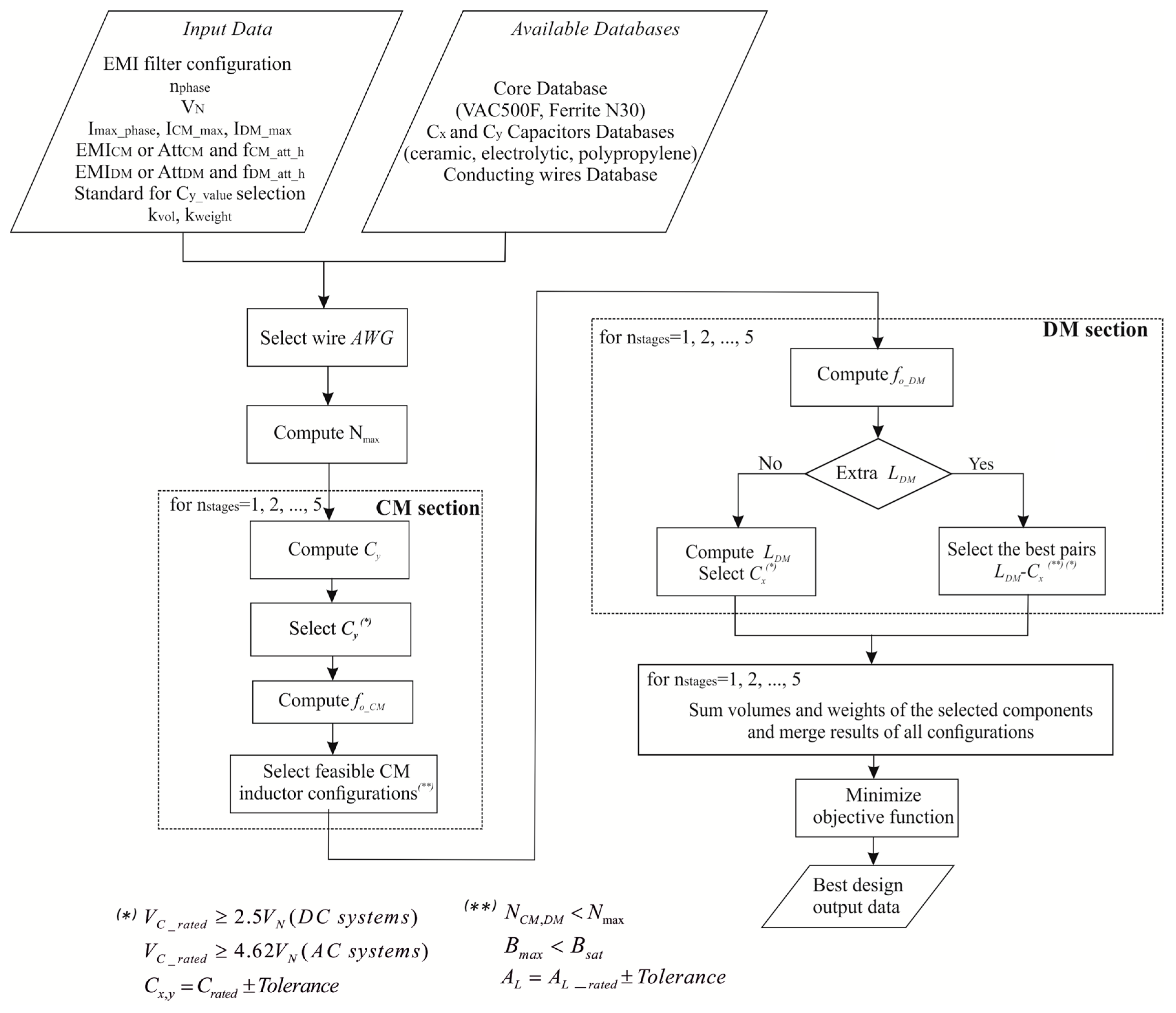
2. The Rule-Based Computer-Aided EMI Filter Design Procedure
- EMI filter topology (e.g., Γ, Π, T);
- nphase: number of AC phases or DC lines of the power electronic system;
- VN: rated voltage of the power converter;
- Imax_phase: maximum operating current;
- ICM_max, IDM_max: maximum value of the CM and DM currents;
- Standard for Cy_value selection: the CM capacitance value limits the ground current and thus it is related to safety issues. Either the SAE AES 1831 standard or the maximum ground leakage current are taken into consideration to define the capacitance value;
- kvol, kweight: coefficients provided by the designer which allow one to obtain the best design, assuming any linear combination of volume and weight as the objective function;
- filter design can be performed either on the basis of the measured CM/DM spectra (EMICM, EMIDM), or by explicitly giving the required CM/DM attenuations (AttCM, AttDM) and the CM/DM component frequencies to be attenuated (fCM_att_h and fDM_att_h). In the first case, the algorithm identifies the crucial point among the more relevant peaks at the lowest frequencies on the EMI spectra. Then, it computes the required attenuations for the CM and DM noise as expressed in (1) and (2), respectively:
- core material and model;
- geometric dimensions and weight;
- inductance factor AL (µH/1 turn) at 10 kHz and the value of flux density saturation;
- AL tolerance.
- brand, material, series, model, and package;
- rated capacitance and voltage;
- capacitance tolerance;
- geometric dimensions and weight.
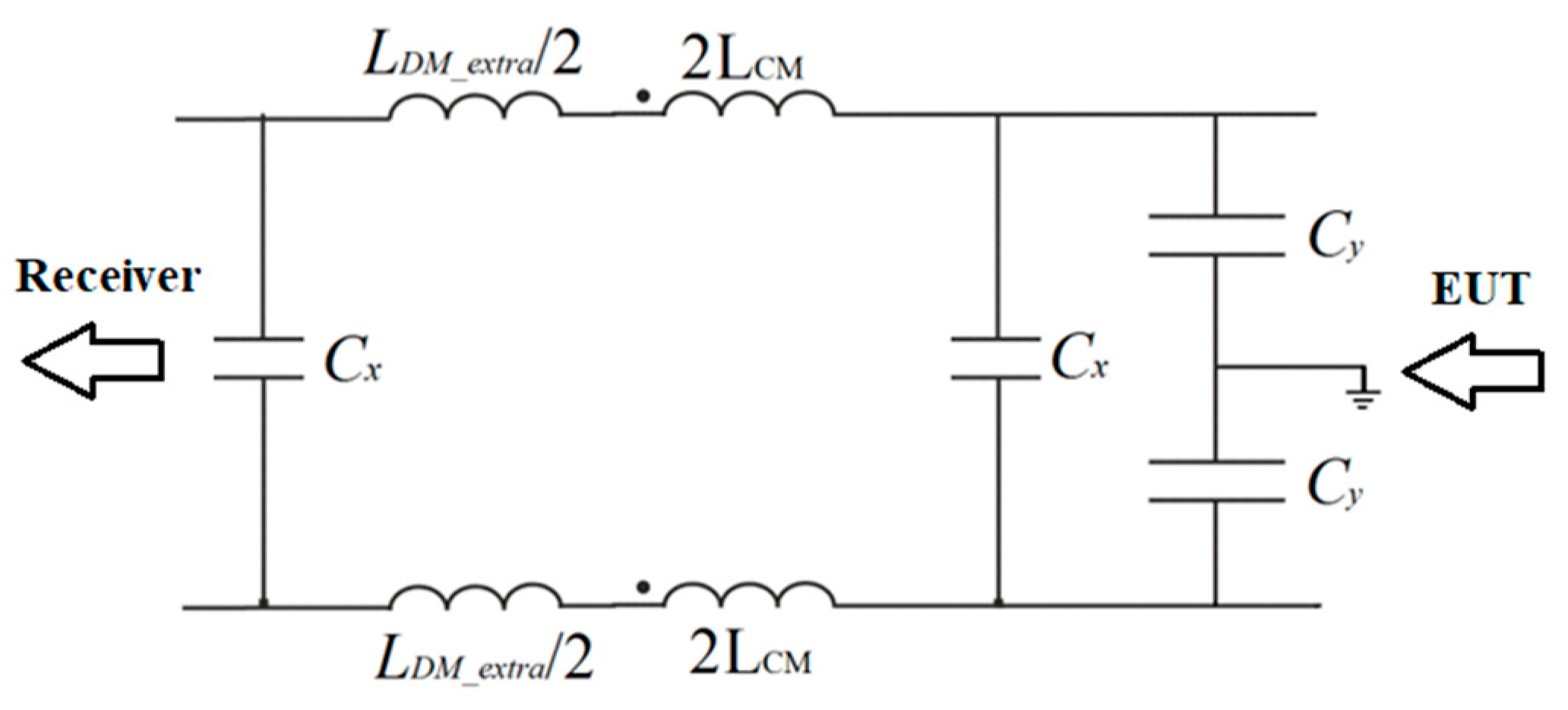
2.1. CM Section Design
2.2. DM Section Design
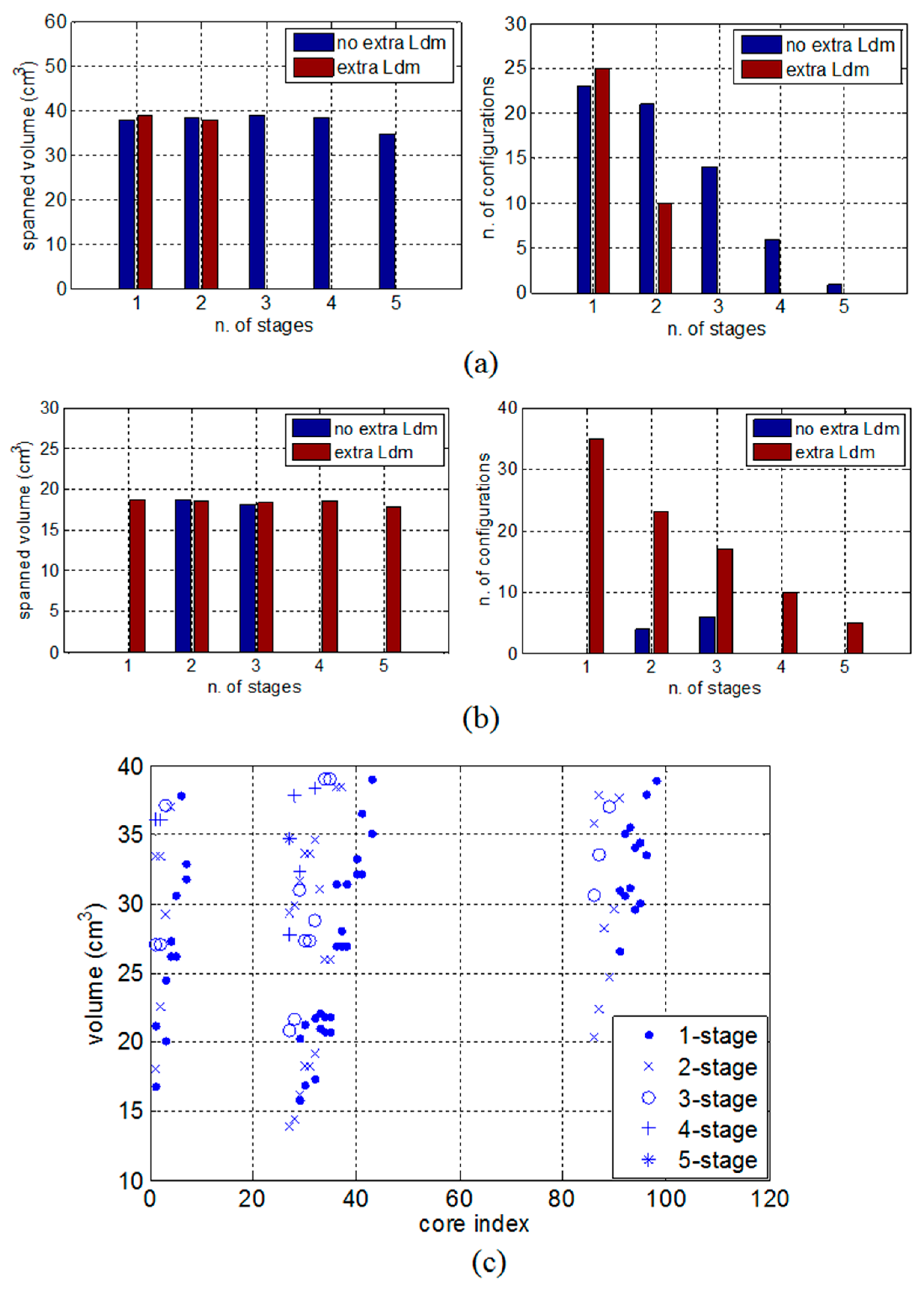
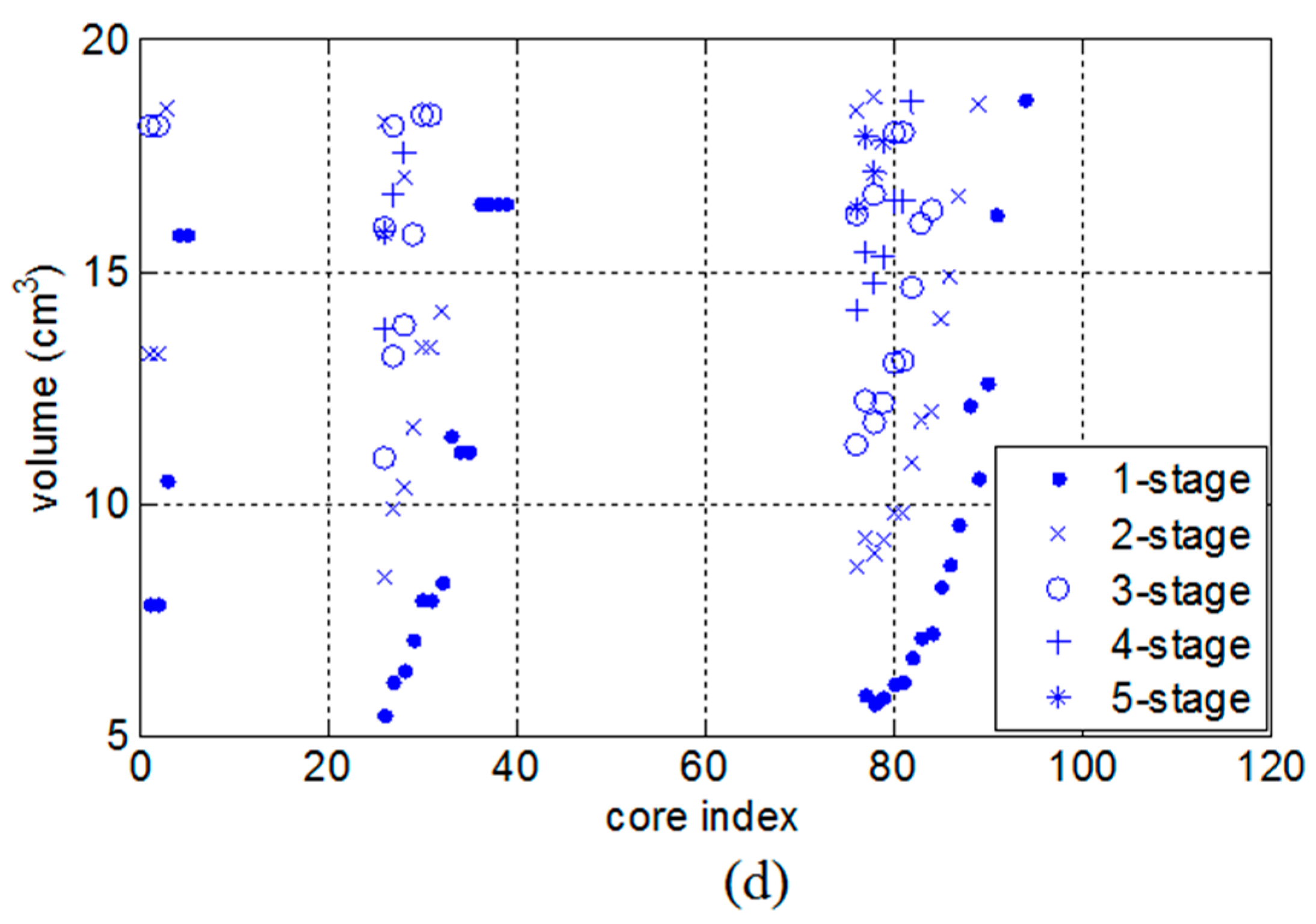
- the “No extra LDM” procedure computes, for nstages = 1, …, 5, the leakage inductance of the feasible CM chokes and the corresponding computed value for the DM capacitance.After the computation of the CDM capacitance, the algorithm selects the capacitor with the minimum volume, according to the design constraint
- in the “Extra LDM” procedure, for nstages = 1, …, 5, the DM inductance candidate values are obtained on the basis of the X-capacitors values (ranging between 10 nF and 330 µF). For each DM core, the number of turns is then computed as follows:
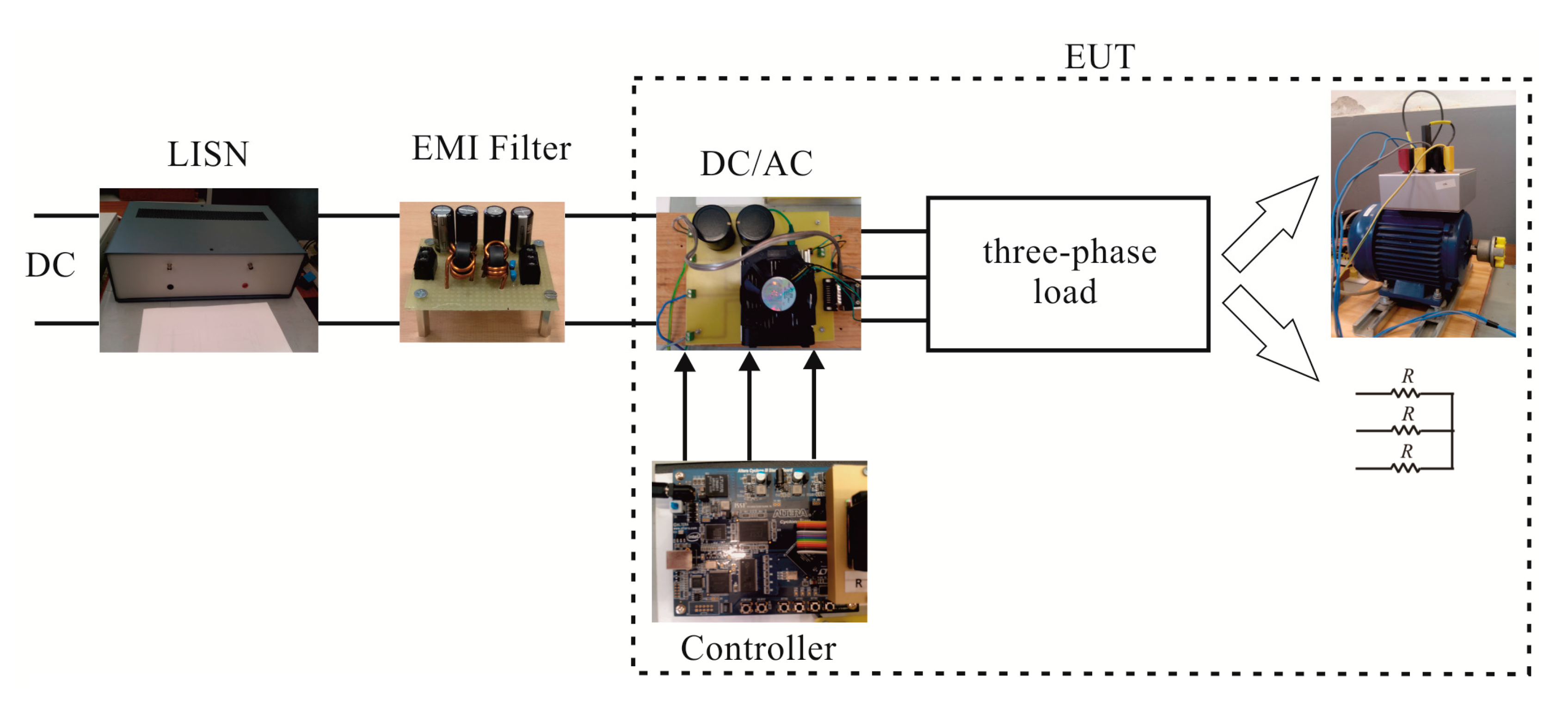
3. Experimental Setup
- Case study #2: a symmetric resistive load with low-power (7.2 W).
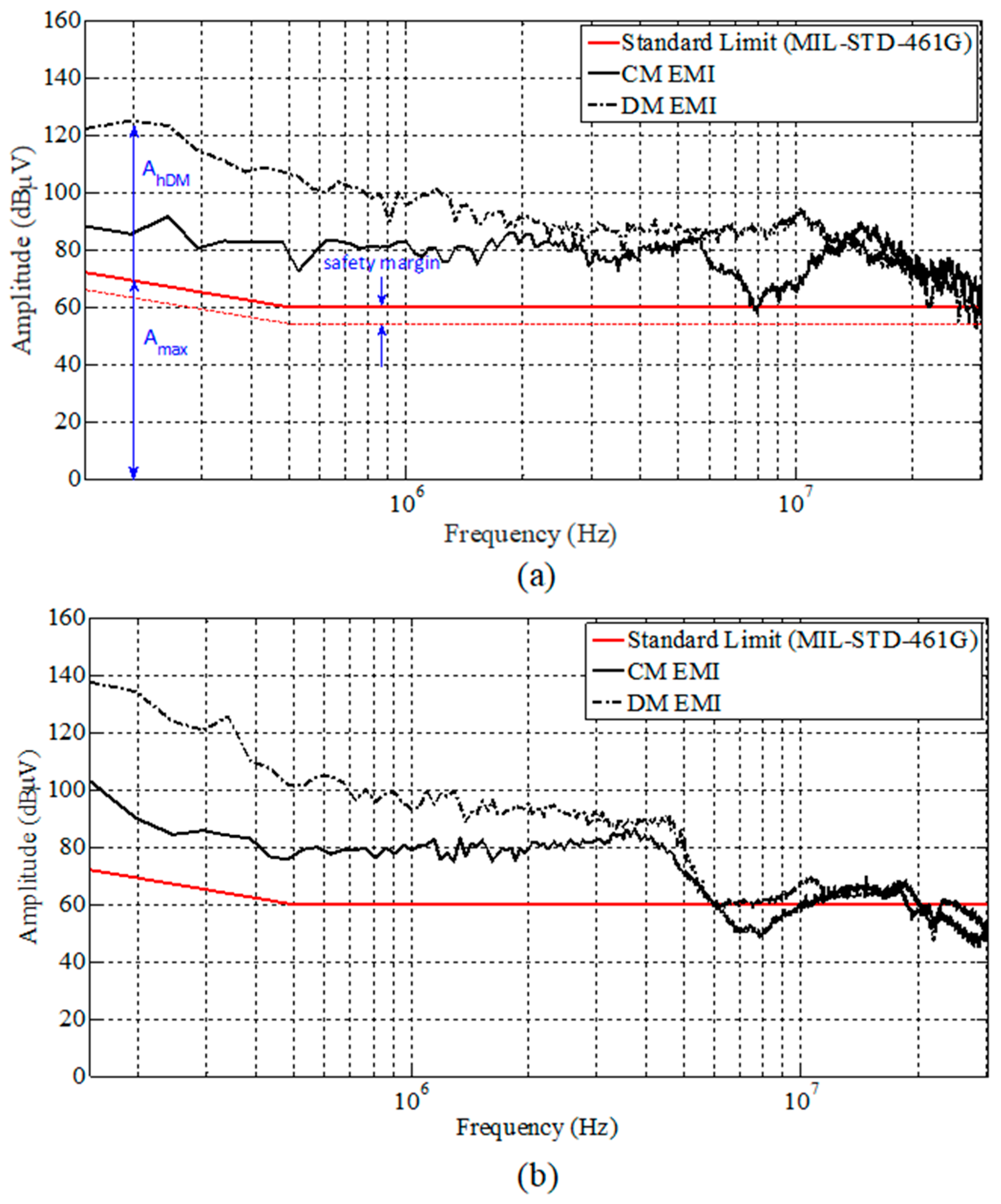
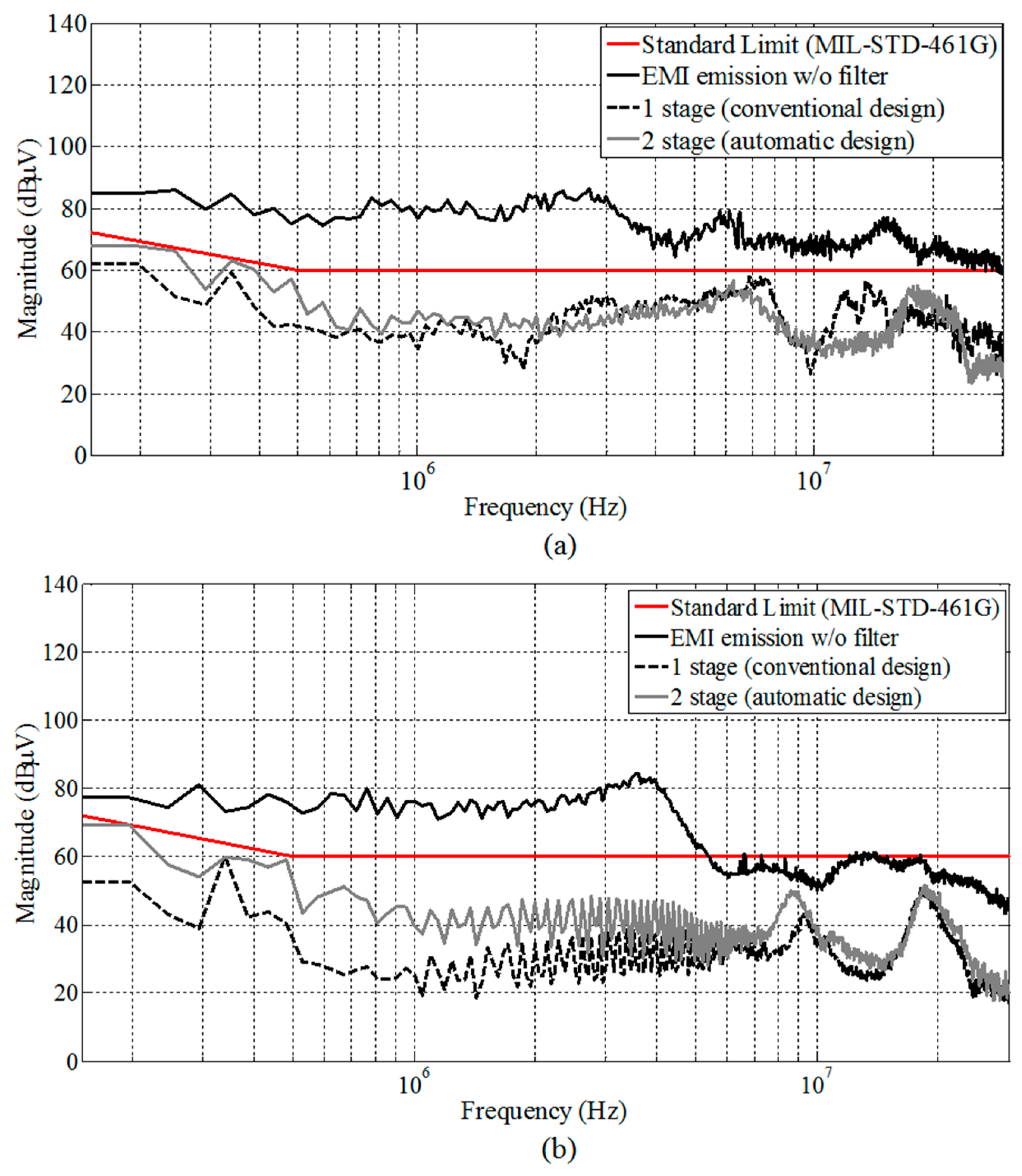
4. Experimental Validation and Discussion
- -
- AttCM = 30 dBμV@150 kHz;
- -
- -AttDM = 60 dBμV@170 kHz.
- -
- AttCM = 25 dBμV@150 kHz;
- -
- AttDM = 60 dBμV@150 kHz.
- -
- [30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56] dBμV in case study #1;
- -
- [25, 30, 35, 40, 45, 50, 55, 60, 65] dBμV in case study #2;
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Kolar, J.W.; Drofenik, U.; Biela, J.; Heldwein, M.L.; Ertl, H.; Friedli, T.; Round, S.D. PWM Converter Power Density Barriers. In Proceedings of the Power Conversion Conference (PCC ’07), Nagoya, Japan, 2–5 April 2007; pp. 9–29. [Google Scholar]
- Ahmed, H.F.; Cha, H.; Kim, S.-H.; Kim, D.-H.; Kim, H.-G. Wide Load Range Efficiency Improvement of a High-Power-Density Bidirectional DC–DC Converter Using an MR Fluid-Gap Inductor. IEEE Trans. Ind. Appl. 2015, 51, 3216–3226. [Google Scholar] [CrossRef]
- Grobler, I.; Gitau, M.N. Modelling and measurement of high-frequency conducted electromagnetic interference in DC–DC converters. IET Sci. Meas. Technol. 2017, 11, 495–503. [Google Scholar] [CrossRef]
- Grobler, I.; Gitau, M.N. Analysis, modelling and measurement of the effects of aluminum and polymer heatsinks on conducted electromagnetic compatibility in DC–DC converters. IET Sci. Meas. Technol. 2017, 11, 414–422. [Google Scholar] [CrossRef]
- Hu, B.; Tarateeraseth, V.; See, K.Y.; Zhao, Y. Assessment of electromagnetic interference suppression performance of ferrite core loaded power cord. IET Sci. Meas. Technol. 2010, 4, 229–236. [Google Scholar] [CrossRef]
- Sun, J.; Chen, W.; Yang, X. EMI Prediction and Filter Design for MHz GaN Based LLC Half-Bridge Converter. In Proceedings of the IEEE 8th International Power Electronics and Motion Control Conference (IPEMC 2016-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 297–304. [Google Scholar]
- Kotny, J.L.; Duquesne, T.; Idir, N. Filter design method for GaN-Buck converter taking into account of the common-mode propagation paths. In Proceedings of the IEEE 20th Workshop on Signal and Power Integrity (SPI 2016), Turin, Italy, 8–11 May 2016; pp. 1–4. [Google Scholar]
- Liu, Y.; Peng, J.; Wang, G.; Wang, H.; See, K.Y. THD and EMI performance study of foil-wound inductor of LCL filter for high power density converter. In Proceedings of the IEEE 8th International Power Electronics and Motion Control Conference (IPEMC 2016-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3467–3471. [Google Scholar]
- Mallik, A.; Ding, W.; Khaligh, A. A Comprehensive Design Approach to an EMI Filter for a 6-kW Three-Phase Boost Power Factor Correction Rectifier in Avionics Vehicular Systems. IEEE Trans. Veh. Technol. 2017, 66, 2942–2951. [Google Scholar] [CrossRef]
- Silva, M.; Hensgens, N.; Oliver, J.; Alou, P. New considerations in the input filter design of a three-phase buck-type PWM rectifier for aircraft applications. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE 2011), Phoenix, AZ, USA, 17–22 September 2011; pp. 4087–4092. [Google Scholar]
- Danilovic, M.; Luo, F.; Xue, L.; Wang, R.; Mattavelli, P.; Boroyevich, D. Size and weight dependence of the single stage input EMI filter on switching frequency for low voltage bus aircraft applications. In Proceedings of the 15th International Power Electronics and Motion Control Conference (PEMC 2012), Novi Sad, Serbia, 4–6 September 2012; pp. LS4a.41–LS4a.47. [Google Scholar]
- Di Piazza, M.C.; Ragusa, A.; Vitale, G. An optimized feedback common mode active filter for vehicular induction motor drives. IEEE Trans. Power Electron. 2011, 26, 3153–3162. [Google Scholar] [CrossRef]
- Kahoul, R.; Azzouz, Y.; Ravelo, B.; Mazari, B. New Behavioral Modeling of EMI for DC Motors Applied to EMC Characterization. IEEE Trans. Ind. Electron. 2013, 60, 5482–5496. [Google Scholar] [CrossRef]
- Ala, G.; Di Piazza, M.C.; Giaconia, G.C.; Giglia, G.; Vitale, G. Design and performance evaluation of a high power density EMI filter for PWM inverter-fed induction motor drives. In Proceedings of the IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC 2015), Rome, Italy, 10–13 June 2015; pp. 1573–1579. [Google Scholar]
- Ala, G.; Di Piazza, M.C.; Giaconia, G.C.; Giglia, G.; Vitale, G. Design and performance evaluation of a high power density EMI filter for PWM inverter-fed induction motor drives. IEEE Trans. Ind. Appl. 2016, 52, 2397–2404. [Google Scholar] [CrossRef]
- Maillet, Y.; Lai, R.; Wang, S.; Wang, F.; Burgos, R.; Boroyevich, D. High-Density EMI Filter Design for DC-Fed Motor Drives. IEEE Trans. Power Electron. 2010, 25, 1163–1172. [Google Scholar] [CrossRef]
- Luo, F.; Dong, D.; Boroyevich, D.; Mattavelli, P.; Wang, S. Improving high-frequency performance of an input common mode EMI filter using an impedance-mismatching filter. IEEE Trans. Power Electron. 2014, 29, 5111–5115. [Google Scholar] [CrossRef]
- Wang, F.; Shen, W.; Boroyevich, D.; Ragon, S.; Stefanovic, V.; Arpilliere, M. Design Optimization of Industrial Motor Drive Power Stage Using Genetic Algorithms. In Proceedings of the IEEE Industry Applications Conference, Tampa, FL, USA, 8–12 October 2006; pp. 2581–2586. [Google Scholar]
- Narayanasamy, B.; Jalanbo, H.; Luo, F. Development of Software to Design Passive Filters for EMI Suppression in SiC DC Fed Motor Drives. In Proceedings of the IEEE 3rd Workshop on Wide Bandgap Power Devices and Applications (WiPDA 2015), Blacksburg, VA, USA, 2–4 November 2015; pp. 230–235. [Google Scholar]
- Raggl, K.; Nussbaumer, T.; Kolar, J.W. Guideline for a Simplified Differential-Mode EMI Filter Design. IEEE Trans. Ind. Electron. 2010, 57, 1031–1040. [Google Scholar] [CrossRef]
- Raggl, K.; Nussbaumer, T.; Kolar, J.W. Model Based Optimization of EMC Input Filters. In Proceedings of the IEEE 11th Workshop on Control and Modeling for Power Electronics (COMPEL 2008), Zurich, Switzerland, 17–20 August 2008; pp. 1–6. [Google Scholar]
- Boillat, D.O.; Krismer, F.; Kolar, J.W. EMI Filter Volume Minimization of a Three-Phase, Three-Level T-Type PWM Converter System. IEEE Trans. Power Electron. 2017, 32, 2473–2480. [Google Scholar] [CrossRef]
- Ala, G.; Di Piazza, M.C.; Giaconia, G.C.; Giglia, G.; Luna, M.; Vitale, G.; Zanchetta, P. Computer Aided Optimal Design of High Power Density EMI Filters. In Proceedings of the IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC 2016), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Ozenbaugh, R.L.; Pullen, T.M. EMI Filter Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781439844755. [Google Scholar]
- Di Piazza, M.C.; Ragusa, A.; Vitale, G. Common Mode EMI Propagation in High Voltage DC supplied Induction Motor Drives for Electric Vehicles Application. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC 2009), Miami, FL, USA, 3–6 May 2009; pp. 647–652. [Google Scholar]
- Anand, S.; Fernandez, B.G. Optimal voltage level for DC microgrids. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society (IECON 2010), Glendale, AZ, USA, 7–10 November 2010; pp. 3034–3039. [Google Scholar]
- Kakigano, H.; Nomura, N.; Ise, T. Loss evaluation of DC distribution for residential houses compared with AC system. In Proceedings of the International Power Electronics Conference (IPEC), Sapporo, Japan, 21–24 June 2010; pp. 480–486. [Google Scholar]
- Department of Defense. Military Standard 461G: Requirements for the Control of Electromagnetic Interference Characteristics of Subsystems and Equipment; AMSC: Devens, MA, USA, 2015. [Google Scholar]
- Kumar, M.; Agarwal, V. Power line filter design for conducted electromagnetic interference using time-domain measurements. IEEE Trans. Electromagn. Compat. 2006, 48, 178–186. [Google Scholar] [CrossRef]
| System Type | DC System |
|---|---|
| VN | 48 V |
| Imax_phase | 5 A |
| Icm_max | 32 mA |
| Idm_max | 150 mA |
| kvol | 100% |
| kweight | 0% |
| System Type | DC System |
|---|---|
| VN | 48 V |
| Imax_phase | 150 mA |
| Icm_max | 45 mA |
| Idm_max | 60 mA |
| kvol | 100% |
| kweight | 0% |
| Conventional Design | Automatic Design | |
|---|---|---|
| Number of Stages | 1 | 2 |
| LCM@10 kHz | 0.8 mH | 126 µH (each stage) |
| CM inductor core dimensions (mm × mm × mm) | 27.9 × 13.6 × 12.5 | 12 × 8.0 × 4.5 (each stage) |
| CM core AL@10 kHz | 65.5 µH (Vitroperm 500F, model T60006-L2025-W380) | 28 µH (Vitroperm 500F, model T60006-L2012-W902) (each stage) |
| Number of turns per CM winding | 5 | 3 (each stage) |
| CCM | 200 nF | 100 nF (each stage) |
| Cy | 100 nF, ceramic, 250 V, (Murata RDER72E104K2) | 47 nF, ceramic, 250 V, (Murata RDER72E473K2) (each stage) |
| LDM@10 kHz | 1.6 µH (Lleakage = 0.2% LCM) | 252 nH (Lleakage = 0.2% LCM) (each stage) |
| CDM | 47 µF, electrolytic, 400 V, (Panasonic EEUEE2G470) | 33 µF, electrolytic, 160 V, (Kemet ESG336M160AH4) (each stage) |
| Wire size | 15 AWG | 15 AWG |
| Volume | 25.87 cm3 | 13.88 cm3 (all stages) |
| Weight | 44 g | 19.12 g (all stages) |
| Conventional Design | Automatic Design | |
|---|---|---|
| Number of Stages | 1 | 2 |
| LCM@10 kHz | 0.8 mH | 56 µH (each stage) |
| CM inductor core dimensions (mm × mm × mm) | 27.9 × 13.6 × 12.5 | 14.1 × 6.6 × 6.3 (each stage) |
| CM core AL@10 kHz | 65.5 µH (Vitroperm 500F, model T60006-L2025-W380) | 28 µH (Vitroperm 500F, model T60006-L2012-W902) (each stage) |
| Number of turns per CM winding | 5 | 2 (each stage) |
| CCM | 200 nF | 100 nF (each stage) |
| Cy | 100 nF, ceramic, 250 V, (Murata RDER72E104K2) | 47 nF, ceramic, 250 V, (Murata RDER72E473K2) (each stage) |
| LDM@10 kHz | 1.6 µH (Lleakage = 0.2% LCM) | 459 µH (Extra LDM) (each stage) |
| DM inductor core dimensions (mm × mm × mm) | n.a. | 11.2 × 5.1 × 5.8 (two for each stage) |
| DM core AL@10 kHz | n.a. | 25.5 µH (Vitroperm 500F, model T60006-L2009-W914) (2 for each stage) |
| Number of turns per DM winding | n.a. | 3 (each stage) |
| CDM | 47 µF, electrolytic, 400 V, (Panasonic EEUEE2G470) | 33 nF, polypropylene, 560 V, (Kemet 46KF23301P02) (each stage) |
| Wire size | 15 AWG | 21 AWG |
| Volume | 25.87 cm3 | 9.88 cm3 (all stages) |
| Weight | 44 g | 14.42 g (all stages) |
| CM Attenuation (dBµV) | Number of Stages | Volume (cm3) |
|---|---|---|
| 30 | 2 | 13.88 |
| 32 | 2 | 13.88 |
| 34 | 2 | 13.88 |
| 36 | 2 | 13.88 |
| 38 | 2 | 13.88 |
| 40 | 2 | 13.88 |
| 42 | 1 | 15.8 |
| 44 | 1 | 15.8 |
| 46 | 2 | 16.2 |
| 48 | 2 | 16.2 |
| 50 | 2 | 16.2 |
| 52 | 2 | 18.1 |
| 54 | 2 | 18.1 |
| 56 | 2 | 18.3 |
| CM Attenuation (dBµV) | Number of Stages | Volume (cm3) |
|---|---|---|
| 25 | 1 | 5.46 |
| 30 | 1 | 5.46 |
| 35 | 1 | 5.46 |
| 40 | 1 | 6.19 |
| 45 | 1 | 6.94 |
| 50 | 1 | 7.79 |
| 55 | 2 | 8.43 |
| 60 | 2 | 8.43 |
| 65 | 2 | 9.88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giglia, G.; Ala, G.; Di Piazza, M.C.; Giaconia, G.C.; Luna, M.; Vitale, G.; Zanchetta, P. Automatic EMI Filter Design for Power Electronic Converters Oriented to High Power Density. Electronics 2018, 7, 9. https://doi.org/10.3390/electronics7010009
Giglia G, Ala G, Di Piazza MC, Giaconia GC, Luna M, Vitale G, Zanchetta P. Automatic EMI Filter Design for Power Electronic Converters Oriented to High Power Density. Electronics. 2018; 7(1):9. https://doi.org/10.3390/electronics7010009
Chicago/Turabian StyleGiglia, Graziella, Guido Ala, Maria Carmela Di Piazza, Giuseppe Costantino Giaconia, Massimiliano Luna, Gianpaolo Vitale, and Pericle Zanchetta. 2018. "Automatic EMI Filter Design for Power Electronic Converters Oriented to High Power Density" Electronics 7, no. 1: 9. https://doi.org/10.3390/electronics7010009
APA StyleGiglia, G., Ala, G., Di Piazza, M. C., Giaconia, G. C., Luna, M., Vitale, G., & Zanchetta, P. (2018). Automatic EMI Filter Design for Power Electronic Converters Oriented to High Power Density. Electronics, 7(1), 9. https://doi.org/10.3390/electronics7010009









