Study of the Contributions of Donor and Acceptor Photoexcitations to Open Circuit Voltage in Bulk Heterojunction Organic Solar Cells
Abstract
1. Introduction
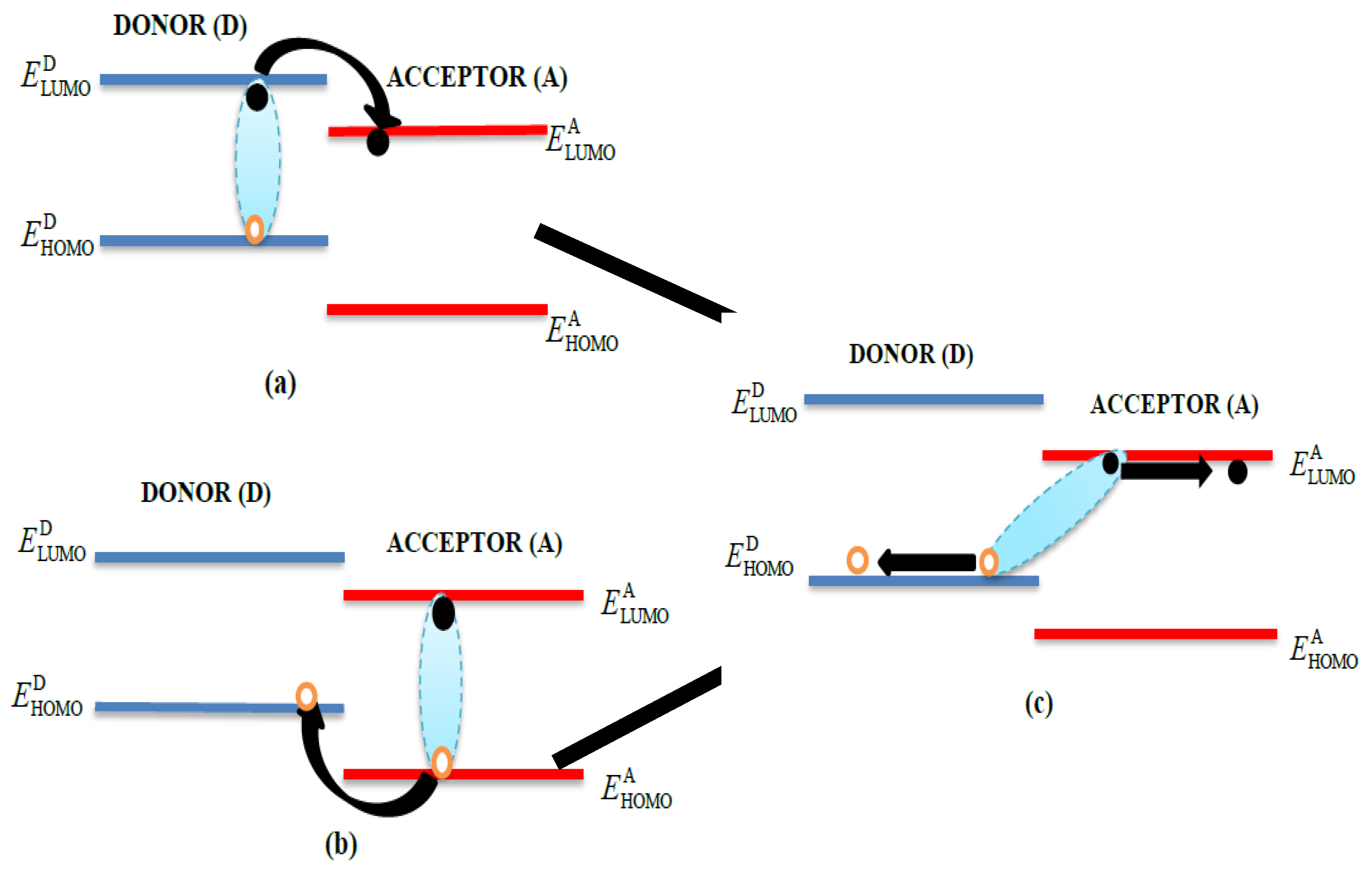
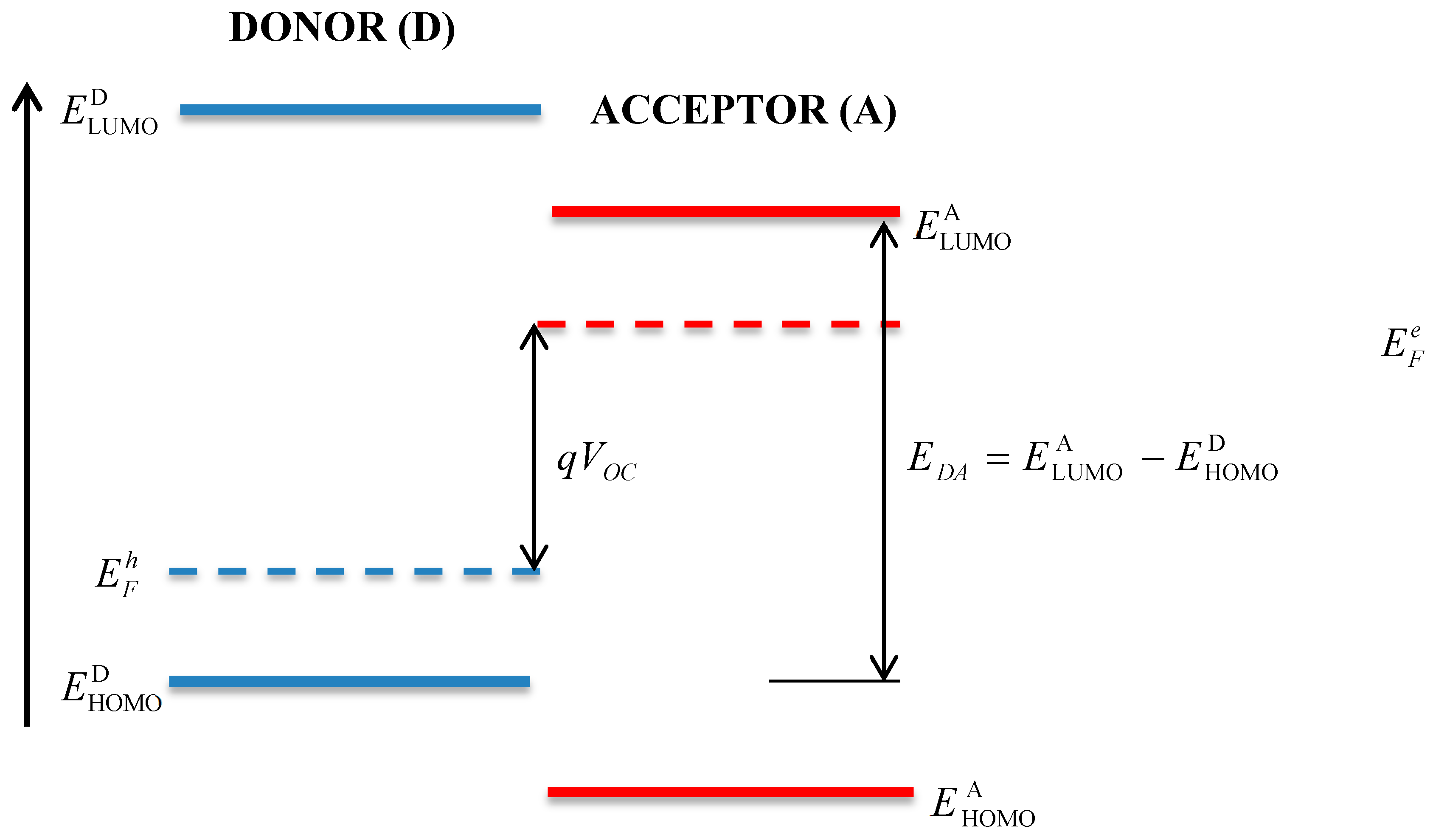
2. Theoretical Formalism
2.1. Photoexcitation of the Donor
2.2. Photoexcitation of the Acceptor
2.3. Simultaneous Photoexcitation of the Donor and Acceptor
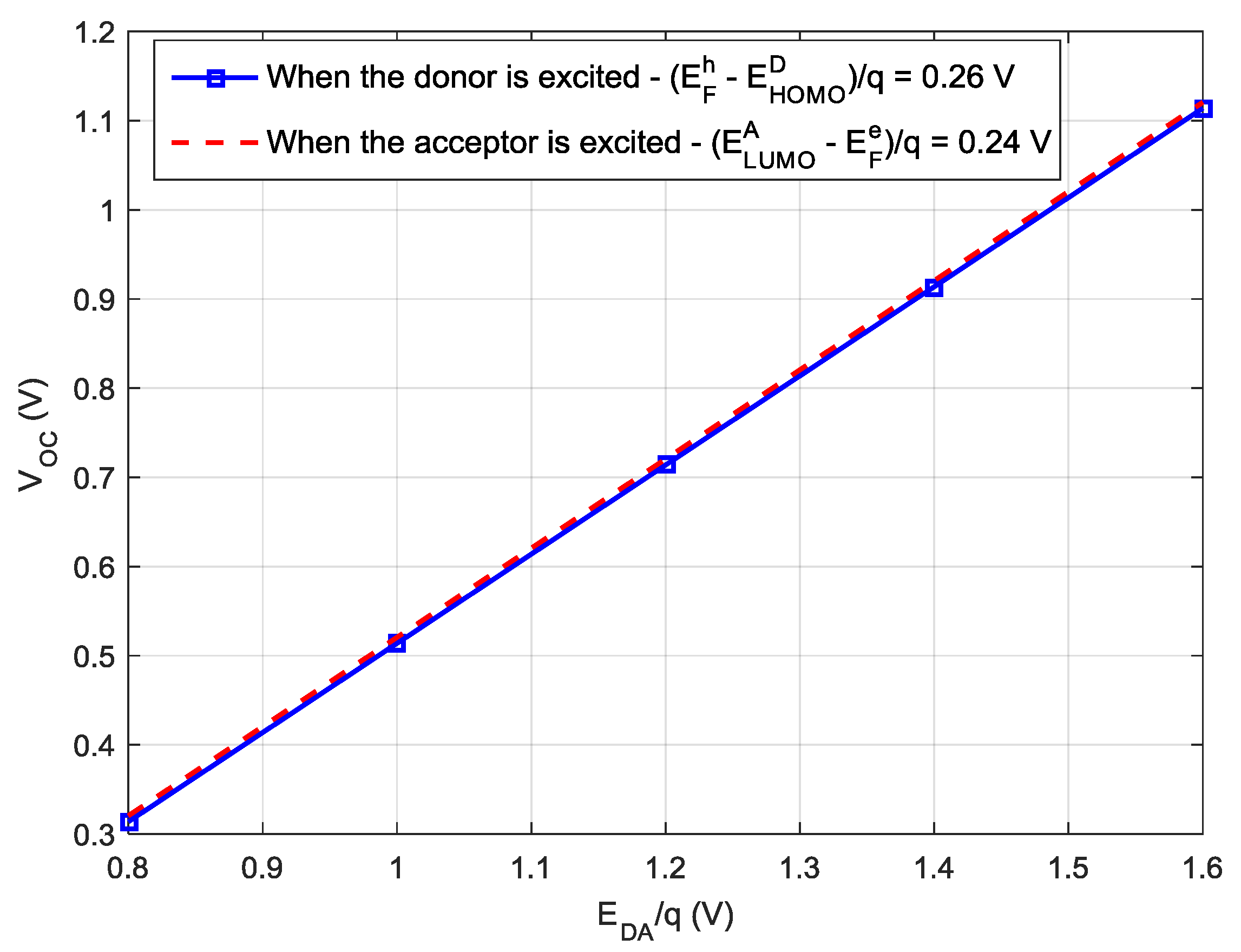
3. Results
4. Discussions
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Inche Ibrahim, M.L.; Ahmad, Z.; Sulaiman, K.; Muniandy, S.V. Combined influence of carrier mobility and dielectric constant on the performance of organic bulk heterojunction solar cells. AIP Adv. 2014, 4, 057133. [Google Scholar] [CrossRef]
- Zhong, Y.; Tada, A.; Izawa, S.; Hashimoto, K.; Tajima, K. Enhancement of without loss of in organic solar cells by modification of donor/acceptor interfaces. Adv. Energy Mater. 2014, 4, 1301332. [Google Scholar] [CrossRef]
- Chen, C.-C.; Chang, W.-H.; Yoshimura, K.; Ohya, K.; You, J.; Gao, J.; Hong, Z.; Yang, Y. An efficient triple-junction polymer solar cell having a power conversion efficiency exceeding 11%. Adv. Mater. 2014, 26, 5670–5677. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Li, Y.; Yang, G.; Jiang, K.; Lin, H.; Ade, H.; Ma, W.; Yan, H. Efficient organic solar cells processed from hydrocarbon solvents. Nat. Energy 2016, 1, 15027. [Google Scholar] [CrossRef]
- Zhang, S.; Ye, L.; Hou, J. Breaking the 10% efficiency barrier in organic photovoltaics: Morphology and device optimization of well-known PBDTTT polymers. Adv. Energy Mater. 2016, 6, 1502529. [Google Scholar] [CrossRef]
- Gan, Q.; Bartoli, F.J.; Kafafi, Z.H. Plasmonic-enhanced organic photovoltaics: Breaking the 10% efficiency barrier. Adv. Mater. 2013, 25, 2385–2396. [Google Scholar] [CrossRef] [PubMed]
- Deibel, C.; Wagenpfahl, A.; Dyakonov, V. Influence of charge carrier mobility on the performance of organic solar cells. Phys. Status Solidi 2008, 2, 175–177. [Google Scholar] [CrossRef]
- Narayan, R.M.; Singh, J. Study of the mechanism and rate of exciton dissociation at the donor-acceptor interface in bulk-heterojunction organic solar cells. J. Appl. Phys. 2013, 114. [Google Scholar] [CrossRef]
- Ompong, D.; Singh, J. Diffusion length and Langevin recombination of singlet and triplet excitons in organic heterojunction solar cells. ChemPhysChem 2015, 16, 1281–1285. [Google Scholar] [CrossRef] [PubMed]
- Scharber, M.C.; Muhlbacher, D.; Koppe, M.; Denk, P.; Waldauf, C.; Heeger, A.J.; Brabec, C.J. Design rules for donors in bulk-heterojunction solar cells—Towards 10% energy-conversion efficiency. Adv. Mater. 2006, 18, 789–794. [Google Scholar] [CrossRef]
- Kietzke, T.; Egbe, D.A.M.; Hörhold, H.-H.; Neher, D. Comparative study of M3EH−PPV-based bilayer photovoltaic devices. Macromolecules 2006, 39, 4018–4022. [Google Scholar] [CrossRef]
- Mihailetchi, V.D.; Blom, P.W.M.; Hummelen, J.C.; Rispens, M.T. Cathode dependence of the open-circuit voltage of polymer:fullerene bulk heterojunction solar cells. J. Appl. Phys. 2003, 94, 6849–6854. [Google Scholar] [CrossRef]
- Ross, R.B.; Cardona, C.M.; Guldi, D.M.; Sankaranarayanan, S.G.; Reese, M.O.; Kopidakis, N.; Peet, J.; Walker, B.; Bazan, G.C.; van Keuren, E.; et al. Endohedral fullerenes for organic photovoltaic devices. Nat. Mater. 2009, 8, 208–212. [Google Scholar] [CrossRef] [PubMed]
- Lenes, M.; Wetzelaer, G.; Kooistra, F.B.; Veenstra, S.C.; Hummelen, J.C.; Blom, P.W.M. Fullerene bisadducts for enhanced open-circuit voltages and efficiencies in polymer solar cells. Adv. Mater. 2008, 20, 2116–2119. [Google Scholar] [CrossRef]
- Fengling, Z.; Bijleveld, J.; Perzon, E.; Tvingstedt, K.; Barrau, S.; Inganäs, O.; Andersson, M.R. High photovoltage achieved in low band gap polymer solar cells by adjusting energy levels of a polymer with the LUMOs of fullerene derivatives. J. Mater. Chem. 2008, 18, 5468–5474. [Google Scholar] [CrossRef]
- Rand, B.; Burk, D.; Forrest, S. Offset energies at organic semiconductor heterojunctions and their influence on the open-circuit voltage of thin-film solar cells. Phys. Rev. B 2007, 75, 115327. [Google Scholar] [CrossRef]
- Koster, L.J.A.; Mihailetchi, V.D.; Ramaker, R.; Blom, P.W.M. Light intensity dependence of open-circuit voltage of polymer:fullerene solar cells. Appl. Phys. Lett. 2005, 86, 123509. [Google Scholar] [CrossRef]
- Riede, M.; Mueller, T.; Tress, W.; Schueppel, R.; Leo, K. Small-molecule solar cells-status and perspectives. Nanotechnology 2008, 19, 424001. [Google Scholar] [CrossRef] [PubMed]
- Brabec, C.J.; Cravino, A.; Meissner, D.; Sariciftci, N.S.; Fromherz, T.; Rispens, M.T.; Sanchez, L.; Hummelen, J.C. Origin of the open circuit voltage of plastic solar cells. Adv. Funct. Mater. 2001, 11, 374–380. [Google Scholar] [CrossRef]
- Yang, Q.-D.; Li, H.-W.; Cheng, Y.; Guan, Z.; Liu, T.; Ng, T.-W.; Lee, C.-S.; Tsang, S.-W. Probing the energy level alignment and the correlation with open-circuit voltage in solution-processed polymeric bulk heterojunction photovoltaic devices. ACS Appl. Mater. Interfaces 2016, 8, 7283–7290. [Google Scholar] [CrossRef] [PubMed]
- Cho, N.; Schlenker, C.W.; Knesting, K.M.; Koelsch, P.; Yip, H.-Y.; Ginger, D.S.; Jen, A.K.-Y. High dielectric constant side-chain polymers show reduced non-geminate recombination in heterojunction. Adv. Energy Mater. 2014, 4, 1301857. [Google Scholar] [CrossRef]
- Chen, S.; Tsang, S.W.; Lai, T.H.; Reynolds, J.R.; So, F. Dielectric effect on the photovoltage loss in organic photovoltaic cells. Adv. Mater. 2014, 26, 6125–6131. [Google Scholar] [CrossRef] [PubMed]
- Koster, L.J.A.; Mihailetchi, V.D.; Blom, P.W.M. Bimolecular recombination in polymer/fullerene bulk heterojunction solar cells. Appl. Phys. Lett. 2006, 88, 052104. [Google Scholar] [CrossRef]
- Cowan, S.R.C.; Roy, A.; Heeger, A.J. Recombination in polymer-fullerene bulk heterojunction solar cells. Phys. Rev. B 2010, 82, 245207. [Google Scholar] [CrossRef]
- Vandewal, K.; Tvingstedt, K.; Gadisa, A.; Inganas, O.; Manca, J.V. On the origin of the open-circuit voltage of polymer-fullerene solar cells. Nat. Mater. 2009, 8, 904–909. [Google Scholar] [CrossRef] [PubMed]
- Shuttle, C.G.; O’Regan, B.; Ballantyne, A.M.; Nelson, J.; Bradley, D.D.C.; Durrant, J.R. Bimolecular recombination losses in polythiophene: Fullerene solar cells. Phys. Rev. B 2008, 78, 113201. [Google Scholar] [CrossRef]
- Maurano, A.; Hamilton, R.; Shuttle, C.G.; Ballantyne, A.M.; Nelson, J.; O’Regan, B.; Zhang, W.; McCulloch, I.; Azimi, H.; Morana, M.; et al. Recombination dynamics as a key determinant of open circuit voltage in organic bulk heterojunction solar cells: A comparison of four different donor polymers. Adv. Mater. 2010, 22, 4987–4992. [Google Scholar] [CrossRef] [PubMed]
- Lange, I.; Kniepert, J.; Pingel, P.; Dumsch, I.; Allard, S.; Janietz, S.; Scherf, U.; Neher, D. Correlation between the open-circuit voltage and the energetics of organic bulk heterojunction solar cells. J. Phys. Chem. Lett. 2013, 4, 3865–3871. [Google Scholar] [CrossRef]
- Garcia-Belmonte, G.; Boix, P.P.; Bisquert, J.; Lenes, M.; Bolink, H.J.; La Rosa, A.; Filippone, S.; Martín, N. Influence of the intermediate density-of-states occupancy on open-circuit voltage of bulk heterojunction solar cells with different fullerene acceptors. J. Phys. Chem. Lett. 2010, 1, 2566–2571. [Google Scholar] [CrossRef]
- Garcia-Belmonte, G.; Juan Bisquert, J. Open-circuit voltage limit caused by recombination through tail states in bulk heterojunction polymer-fullerene solar cells. Appl. Phys. Lett. 2010, 96, 113301. [Google Scholar] [CrossRef]
- Blakesley, J.C.; Greenham, N.C. Charge transfer at polymer-electrode interfaces: The effect of energetic disorder and thermal injection on band bending and open-circuit voltage. J. Appl. Phys. 2009, 106, 034507. [Google Scholar] [CrossRef]
- Credgington, D.; Durrant, J.R. Insights from transient optoelectronic analyses on the open-circuit voltage of organic solar cells. J. Phys. Chem. Lett. 2012, 3, 1465–1478. [Google Scholar] [CrossRef] [PubMed]
- Vandewal, K.; Gadisa, A.; Oosterbaan, W.D.; Bertho, S.; Banishoeib, F.; Van Severen, I.; Lutsen, L.; Cleij, T.J.; Vanderzande, D.; Manca, J.V. The relation between open-circuit voltage and the onset of photocurrent generation by charge-transfer absorption in polymer: Fullerene bulk heterojunction solar cells. Adv. Funct. Mater. 2008, 18, 2064–2070. [Google Scholar] [CrossRef]
- Vandewal, K.; Tvingstedt, K.; Gadisa, A.; Inganäs, O.; Manca, J.V. Relating the open-circuit voltage to interface molecular properties of donor:acceptor bulk heterojunction solar cells. Phys. Rev. B 2010, 81, 125204. [Google Scholar] [CrossRef]
- Piersimoni, F.; Chambon, S.; Vandewal, K.; Mens, R.; Boonen, T.; Gadisa, A.; Izquierdo, M.; Filippone, S.; Ruttens, B.; D’Haen, J.; et al. Influence of fullerene ordering on the energy of the charge-transfer state and open-circuit voltage in polymer:fullerene solar cells. J. Phys. Chem. C 2011, 115, 10873–10880. [Google Scholar] [CrossRef]
- Giebink, N.C.; Wiederrecht, G.P.; Wasielewski, M.R.; Forrest, S.R. Ideal diode equation for organic heterojunctions. I. Derivation and application. Phys. Rev. B 2010, 82, 155305. [Google Scholar] [CrossRef]
- Hendriks, K.H.; Wijpkema, A.S.G.; van Franeker, J.J.; Wienk, M.M.; Janssen, R.A.J. Dichotomous role of exciting the donor or the acceptor on charge generation in organic solar cells. J. Am. Chem. Soc. 2016, 138, 10026–10031. [Google Scholar] [CrossRef] [PubMed]
- Cook, S.; Katoh, R.; Furube, A. Ultrafast studies of charge generation in PCBM:P3HT blend films following excitation of the fullerene PCBM. J. Phys. Chem. C 2009, 113, 2547–2552. [Google Scholar] [CrossRef]
- Bakulin, A.A.; Hummelen, J.C.; Pshenichnikov, M.S.; van Loosdrecht, P.H.M. Ultrafast hole-transfer dynamics in polymer/PCBM bulk heterojunctions. Adv. Funct. Mater. 2010, 20, 1653–1660. [Google Scholar] [CrossRef]
- Ren, G.; Schlenker, C.W.; Ahmed, E.; Subramaniyan, S.; Olthof, S.; Kahn, A.; Ginger, D.S.; Jenekhe, S.A. Photoinduced hole transfer becomes suppressed with diminished driving force in polymer-fullerene solar cells while electron transfer remains active. Adv. Funct. Mater. 2013, 23, 1238–1249. [Google Scholar] [CrossRef]
- Armin, A.; Kassal, I.; Shaw, P.E.; Hambsch, M.; Stolterfoht, M.; Lyons, D.M.; Li, J.; Shi, Z.; Burn, P.L.; Meredith, P.J. Spectral dependence of the internal quantum efficiency of organic solar cells: Effect of charge generation pathways. Am. Chem. Soc. 2014, 136, 11465–11472. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Hendriks, K.H.; Furlan, A.; Roelofs, W.S.C.; Wienk, M.M.; Janssen, R.A.J.J. Efficient tandem and triple-junction polymer solar cells. Am. Chem. Soc. 2013, 135, 18942–18948. [Google Scholar] [CrossRef] [PubMed]
- Bakulin, A.A.; Dimitrov, S.D.; Rao, A.; Philip, C.Y.; Chow, P.C.Y.; Christian, B.; Nielsen, C.B.; Bob, C.; Schroeder, B.C.; Iain McCulloch, J.; et al. Charge-transfer state dynamics following hole and electron transfer in organic photovoltaic devices. J. Phys. Chem. Lett. 2013, 4, 209–215. [Google Scholar] [CrossRef] [PubMed]
- Yeboah, D.; Singh, J. Dependence of exciton diffusion length and diffusion coefficient on photophysical parameters in bulk heterojunction organic solar cells. J. Electron. Mater. 2017. [Google Scholar] [CrossRef]
- Narayan, M.; Singh, J. Photovoltaic contribution of photo-generated excitons in acceptor material of organic solar cells. J. Mater. Sci. Mater. Electron. 2017, 28, 7070–7076. [Google Scholar] [CrossRef]
- Singh, J.; Narayan, M.; Ompong, D. Comparative contributions of singlet and triplet excitons in the performance of organic devices. Phys. Status Solidi C 2016, 13, 77–80. [Google Scholar] [CrossRef]
- Gregg, B.A. Excitonic Solar Cells. J. Phys. Chem. B 2003, 107, 4688–4698. [Google Scholar] [CrossRef]
- Singh, J.; Narayan, M.; Ompong, D.; Zhu, F. Dissociation of charge transfer excitons at the donor-acceptor interface in bulk heterojunction organic solar cells. J. Mater. Sci. Mater. Electron. 2017, 28, 7095–7099. [Google Scholar] [CrossRef]
- Wagenpfahl, A.; Rauh, D.; Binder, M.; Deibel, C.; Dyakonov, V. S-shaped current-voltage characteristics of organic solar devices. Phys. Rev. B 2010, 82, 115306. [Google Scholar] [CrossRef]
- Koster, L.J.A.; van Strien, W.J.; Beek, W.J.E.; Blom, P.W.M. Device operation of conjugated polymer/zinc oxide bulk heterojunction solar cells. Adv. Funct. Mater. 2007, 17, 1297–1302. [Google Scholar] [CrossRef]
- Qia, B.; Wang, J. Open-circuit voltage in organic solar cells. J. Mater. Chem. 2012, 22, 24315–24325. [Google Scholar] [CrossRef]
- Cowan, S.R.; Leong, W.L.; Banerji, N.; Dennler, G.; Heeger, A.J. Identifying a threshold impurity level for organic solar cells: Enhanced first-order recombination via well-defined PC84BM traps in organic bulk heterojunction solar cells. Adv. Funct. Mater. 2011, 21, 3083–3092. [Google Scholar] [CrossRef]
- Meijer, E.J.; de Leeuw, D.M.; Setayesh, S.; van veenendaal, E.; Huisman, B.-H.; Blom, P.W.M.; Hummelen, J.C.; Scherf, U.; Klapwijk, T.M. Solution-processed ambipolar organic field-effect transistors and inverters. Nat. Mater. 2003, 2, 678–682. [Google Scholar] [CrossRef]
- Ebenhoch, B.; Thomson, S.A.J.; Genevicius, K.; Juška, G.; Samuel, I.D.W. Charge carrier mobility of the organic photovoltaic materials PTB7 and PC71BM and its influence on device performance. Org. Electron. 2015, 22, 62–68. [Google Scholar] [CrossRef]
- Lin, J.D.A.; Liu, J.; Kim, C.; Tamayo, A.B.; Proctor, C.M.; Nguyen, T.-Q. Effect of structural variation on photovoltaic characteristics of phenyl substituted diketopyrrolopyrroles. RSC Adv. 2014, 4, 14101–14108. [Google Scholar] [CrossRef]
- Walker, B.; Tamayo, A.B.; Dang, X.; Zalar, P.; Seo, J.H.; Garcia, A.; Tantiwiwat, M.; Nguyen, T. Nanoscale phase separation and high photovoltaic efficiency in solution-processed, small-molecule bulk heterojunction solar cells. Adv. Funct. Mater. 2009, 19, 3063–3069. [Google Scholar] [CrossRef]
- Mandoc, M.M.; Koster, L.J.A.; Blom, P.W.M. Optimum charge carrier mobility inorganic solar cells. Appl. Phys. Lett. 2007, 90, 133504. [Google Scholar] [CrossRef]
- Philippa, B.; Stolterfoht, M.; Burn, P.L.; Juŝka, G.; Meredith, P.; Whitel, R.D.; Pivrikas, A. The impact of hot charge carrier mobility on photocurrent losses in polymer-based solar cells. Sci. Rep. 2014, 4, 5695. [Google Scholar] [CrossRef] [PubMed]
- Koster, L.J.A.; Smits, E.C.P.; Mihailetchi, V.D.; Blom, P.W.M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 2005, 72, 085205. [Google Scholar] [CrossRef]
- Würfel, U.; Neher, D.; Spies, A.; Albrecht, S. Impact of charge transport on current voltage characteristics and power-conversion efficiency of organic solar cells. Nat. Commun. 2011, 6, 6951. [Google Scholar] [CrossRef] [PubMed]
- Proctor, C.M.; Kim, C.; Neher, D.; Nguyen, T.Q. Nongeminate recombination and charge transport limitations in diketopyrrolopyrrole-based solution-processed small molecule solar cells. Adv. Funct. Mater. 2013, 23, 3584–3594. [Google Scholar] [CrossRef]
- Oosterhout, D.S.; Ferguson, A.J.; Larson, B.W.; Olson, D.C.; Kopidakis, N. Modeling the free carrier recombination kinetics in PTB7:PCBM organic photovoltaics. J. Phys. Chem. C 2016, 120, 24597–24604. [Google Scholar] [CrossRef]
- Collins, S.A.; Proctor, C.M.; Ran, N.A.; Nguyen, T.-Q. Understanding open-circuit voltage loss through the density of states in organic bulk heterojunction solar cells. Adv. Energy Mater. 2016, 6, 1501721. [Google Scholar] [CrossRef]
- Cravino, A. Origin of the open circuit voltage of donor-acceptor solar cells: Do polaronic energy levels play a role? Appl. Phys. Phys. Lett. 2007, 91, 243502. [Google Scholar] [CrossRef]
- Sun, Y.; Takacs, C.J.; Cowan, S.R.; Seo, J.H.; Gong, X.; Roy, A.; Heeger, A.J. Efficient, air-stable bulk heterojunction polymer solar cells using MoO(x) as the anode interfacial layer. Adv. Mater. 2011, 23, 2226–2230. [Google Scholar] [CrossRef] [PubMed]
- Orlowski, B.A.; Pieniazek, A.; Goscinski, K.; Kopalko, K. Quasi Fermi levels in semiconductor photovoltaic heterojunction. Acta Phys. Pol. A 2016, 129. [Google Scholar] [CrossRef]
- Tuladhar, S.M.; Azzouzi, M.; Delval, F.; Yao, J.; Guilbert, A.A.Y.; Kirchartz, T.; Montcada, N.F.; Dominguez, R.; Langa, F.; Palomares, E.; et al. Low open-circuit voltage loss in solution-processed small-molecule organic solar cells. ACS Energy Lett. 2016, 1, 302–308. [Google Scholar] [CrossRef]
- Baran, D.; Vezie, M.S.; Gasparini, N.; Deledalle, F.; Yao, J.; Schroeder, B.C.; Bronstein, H.; Ameri, T.; Kirchartz, T.; McCulloch, I.; et al. Role of polymer fractionation in energetic losses and charge carrier lifetimes of polymer: Fullerene solar cells. J. Phys. Chem. C 2015, 119, 19668–19673. [Google Scholar] [CrossRef]
- Yao, J.; Kirchartz, T.; Vezie, M.S.; Faist, M.A.; Gong, W.; He, Z.; Wu, H.; Troughton, J.; Watson, T.; Bryant, D.; et al. Quantifying losses in open-circuit voltage in solution-processable solar cells. Phys. Rev. Appl. 2015, 4, 014020. [Google Scholar] [CrossRef]
- Bartynski, A.N.; Gruber, M.; Das, S.; Rangan, S.; Mollinger, S.; Trinh, C.; Bradforth, S.E.; Vandewal, K.; Salleo, A.; Bartynski, R.A.; et al. Symmetry-breaking charge transfer in a zinc chlorodipyrrin acceptor for high open circuit voltage organic photovoltaics. J. Am. Chem. Soc. 2015, 137, 5397–5405. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Liu, B.; Melianas, A.; Bergqvist, J.; Tress, W.; Bao, Q.; Qian, D.; Inganäs, O.; Zhang, F. A new fullerene-free bulk-heterojunction system for efficient high-voltage and high-fill factor solution-processed organic photovoltaics. Adv. Mater. 2015, 27, 1900–1907. [Google Scholar] [CrossRef] [PubMed]
- Ran, N.A.; Kuik, M.; Love, J.A.; Proctor, C.M.; Nagao, I.; Bazan, G.C.; Nguyen, T.-Q. Understanding the charge-transfer state and singlet exciton emission from solution-processed small-molecule organic solar cells. Adv. Mater. 2014, 26, 7405–7412. [Google Scholar] [CrossRef] [PubMed]
| Active Layer Blend | (V) | (1027m−3s−1) | (10−17 m3s−1) | (m2V−1s−1) | (m2V−1s−1) | |
|---|---|---|---|---|---|---|
| MDMO-PPV:PC61BM | 1.30 1 | 2.7 8 | 5.73 | 2 × 10−7 8 | 2 × 10−8 8 | 3.4 8 |
| P3HT:PC60BM | 1.00 2 | 6.25 2 | 7.08 | 1 × 10−7 2 | 1 × 10−8 2 | 3.4 2 |
| PCDTBT:PC71BM | 1.20 3 | 1.0 9 | 0.1 | 2.9 × 10−7 9 | 3.0 × 10−9 9 | 3.4 9 |
| OC1C10-PPV:PC61BM | 1.30 4 | 2.7 10 | 7.30 | 2.5 × 10−7 10 | 3.0 × 10−8 10 | 3.4 10 |
| PTB7:PC71BM | 1.09 5 | 10 11 | 5.91 | 1 × 10−7 11 | 2.0 × 10−8 11 | 3.5 11 |
| mono-DPP:PC71BM | 1.16 6 | 4.99 13 | 5.3 | 1 × 10−7 12 | 2.0 × 10−9 12 | 4.0 12 |
| bis-DPP:PC71BM | 1.20 7 | 4.12 14 | 2.6 | 1.5 × 10−7 12 | 3.4 × 10−8 12 | 4.0 12 |
| Active Layer Blend | (V) | (m−3) | (V) | (V) | (V) |
|---|---|---|---|---|---|
| MDMO-PPV:PC61BM | 0.20 | 1.80 × 1022 | 0.95 | 0.35 | 0.83 [64] |
| P3HT:PC60BM | 0.26 | 1.80 × 1022 | 0.51 | 0.49 | 0.63 [51] |
| PCDTBT:PC71BM | 0.22 | 1.80 × 1022 | 0.73 | 0.47 | 0.85 [65] |
| OC1C10-PPV:PC61BM | 0.20 | 1.80 × 1022 | 0.96 | 0.34 | 0.85 [59] |
| PTB7:PC71BM | 0.18 | 1.90 × 1022 | 0.75 | 0.34 | 0.75 [54] |
| mono-DPP:PC71BM | 0.20 | 2.50 × 1022 | 0.81 | 0.35 | 0.78 [61] |
| bis-DPP:PC71BM | 0.17 | 1.00 × 1022 | 0.85 | 0.35 | 0.52 [61] |
| Active Layer Blend | (V) | (m−3) | (V) | (V) | (V) |
|---|---|---|---|---|---|
| MDMO-PPV:PCBM | 0.18 | 0.95 × 1022 | 0.93 | 0.37 | 0.83 [64] |
| P3HT:PC60BM | 0.24 | 0.95 × 1022 | 0.52 | 0.48 | 0.63 [51] |
| PCDTBT:PC71BM | 0.20 | 0.95 × 1022 | 0.73 | 0.47 | 0.85 [65] |
| OC1C10-PPV:PC61BM | 0.19 | 0.95 × 1022 | 0.94 | 0.36 | 0.85 [59] |
| PTB7:PC71BM | 0.16 | 0.89 × 1022 | 0.75 | 0.34 | 0.75 [54] |
| mono-DPP:PC71BM | 0.16 | 0.38 × 1022 | 0.79 | 0.37 | 0.78 [61] |
| bis-DPP:PC71BM | 0.18 | 1.58 × 1022 | 0.85 | 0.35 | 0.52 [61] |
| Active Layer Blend | (V) | (V) | (V) |
|---|---|---|---|
| MDMO-PPV:PC61BM | 0.91 | 0.39 | 0.83 [64] |
| P3HT:PC60BM | 0.50 | 0.50 | 0.63 [51] |
| PCDTBT:PC71BM | 0.77 | 0.43 | 0.85 [65] |
| OC1C10-PPV:PC61BM | 0.91 | 0.39 | 0.85 [59] |
| PTB7:PC71BM | 0.74 | 0.35 | 0.75 [54] |
| mono-DPP:PC71BM | 0.79 | 0.37 | 0.78 [61] |
| bis-DPP:PC71BM | 0.85 | 0.35 | 0.52 [61] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeboah, D.; Singh, J. Study of the Contributions of Donor and Acceptor Photoexcitations to Open Circuit Voltage in Bulk Heterojunction Organic Solar Cells. Electronics 2017, 6, 75. https://doi.org/10.3390/electronics6040075
Yeboah D, Singh J. Study of the Contributions of Donor and Acceptor Photoexcitations to Open Circuit Voltage in Bulk Heterojunction Organic Solar Cells. Electronics. 2017; 6(4):75. https://doi.org/10.3390/electronics6040075
Chicago/Turabian StyleYeboah, Douglas, and Jai Singh. 2017. "Study of the Contributions of Donor and Acceptor Photoexcitations to Open Circuit Voltage in Bulk Heterojunction Organic Solar Cells" Electronics 6, no. 4: 75. https://doi.org/10.3390/electronics6040075
APA StyleYeboah, D., & Singh, J. (2017). Study of the Contributions of Donor and Acceptor Photoexcitations to Open Circuit Voltage in Bulk Heterojunction Organic Solar Cells. Electronics, 6(4), 75. https://doi.org/10.3390/electronics6040075






