1. Introduction
Renewable energy resources play a major role in the current world’s energy generation. To interconnect renewable energy resources, grid connected three-phase VSIs are widely utilized [
1]. However, the increased number of connections between the VSIs and the grid should never degrade the power quality, particularly at the point of common coupling (PCC), while the total harmonic distortion (THD) should never go beyond a specific limit to prevent harmonics related problems. It is possible to reduce the THD with the switching frequency (
fsw) being increased. However, when the
fsw is increased, the switching losses are likewise increased and, therefore, this can result in a reduction in the inverter’s efficiency as well. Consequently,
fsw is typically, but not optimally, chosen as a trade-off between the output power quality and the efficiency at a specific loading condition. Since the operating conditions of the VSI are continuously varying, the variable switching frequency (VSF) enables the inverter switching losses to be decreased in regions where the harmonic content is insignificant, and, in the same sense, the harmonic content can be reduced in the regions where the inverter losses are highly insignificant.
The performance of the three-phase grid connected VSIs is highly dependent on the selected
fsw. Therefore, literature has proposed numerous algorithms of the VSF to enhance the inverter’s efficiency [
2,
3], inverter’s transient response [
4], and the acoustic noise of induction motor [
5]. Switching frequency is varied either within the fundamental period [
6,
7,
8,
9], or based on the operating conditions [
10,
11,
12], such that the switching losses or the THD are minimized. In [
6], the proposed algorithm is formulated based on the current-ripple analysis of the three-phase inverters in a time-domain. The idea was geared toward the reduction of
fsw, while maintaining the peak current ripple under a certain limit; consequently, there is a reduction in the average
fsw, and thus a reduction in switching losses. Application of the above algorithm can be found in [
7,
8] as well. In [
9], the switching frequency trajectory was derived using calculus of variations and based on the current ripples analysis relative to the single-phase inverters in time-domain, in order to reduce the switching losses while meeting certain THD requirements. This method suffers from computational complexity and requires heavy offline calculations. In [
10], the efficiency of single-phase inverter is incrementally enhanced, while satisfying standard THD; the result of the algorithm was an increase in the efficiency of the inverter in comparison with the conventional sinusoidal pulse-width modulation (SPWM) as well as the space-vector pulse-width modulation (SVPWM). In any case, the aim of the aforementioned methods was to enhance the efficiency of the inverter, while ensuring that the THD is continuously positioned to the highest allowable limit. An offline technique was proposed by the authors of [
11] for the minimization of the losses of VSIs based on multi-objective optimization, where the proposed algorithm was used to control synchronous motors. Meanwhile, the target is characterized based on the weighted combination of the peak-to-peak ripple of electromagnetic torque and switching losses, in a way that a fair balance is achieved. In [
12], an optimization process was applied on the electric and hybrid vehicle motor drive, in which
fsw was varied with different modulation indices or input voltages. Concurrent switching losses minimization and dead-time compensation study was presented in [
13] under various power levels and different power factors. Compared with discrete pulse width modulation techniques, switching losses were reduced by 15%.
The switching losses were reduced at high current-levels in [
14] by proposing new SVPWM strategies in which the number of switch commutations of the quasi-Z-source inverter is reduced. In [
15], a lower number of commutations is achieved by the proposed optimization. The variable switching frequency reduces about 19% of the switching losses compared with constant switching frequency for similar output current quality. Analytical variable switching frequency is presented in [
16] according to the modulation index and a predefined current ripple band. The switching frequency varies within the fundamental cycle (sub-fundamental) to reduce the switching losses of two level inverter traction drive system. In [
17], the switching loss is analyzed under different discontinuous SVPWM techniques for balanced two-phase load fed by a three-leg inverter. The algorithm tried to balance the switching losses of each phase-leg at lower current ripple. In [
18], 3D-SVPWM of four-leg VSI was presented to reduce the switching losses of the proposed shunt compensator by 33%. The efficiency of a grid-tied full bridge inverter is improved in [
19] using the variable switching frequency scheme. The authors minimize the switching losses at predefined THD using a bipolar modulation scheme. Variable switching frequency was used in [
20] to reduce switching losses and electromagnetic interference (EMI) noise of a common voltage oriented SPWM rectifier considering the restrictions on voltage ripple at the direct current (DC) link.
The THD and the maximum torque ripple of the permanent magnet synchronous machine are optimized in [
21]. For this target, the authors presented a finite control set model based on a predictive control scheme. A new behavioral model for losses in power semiconductors was proposed in [
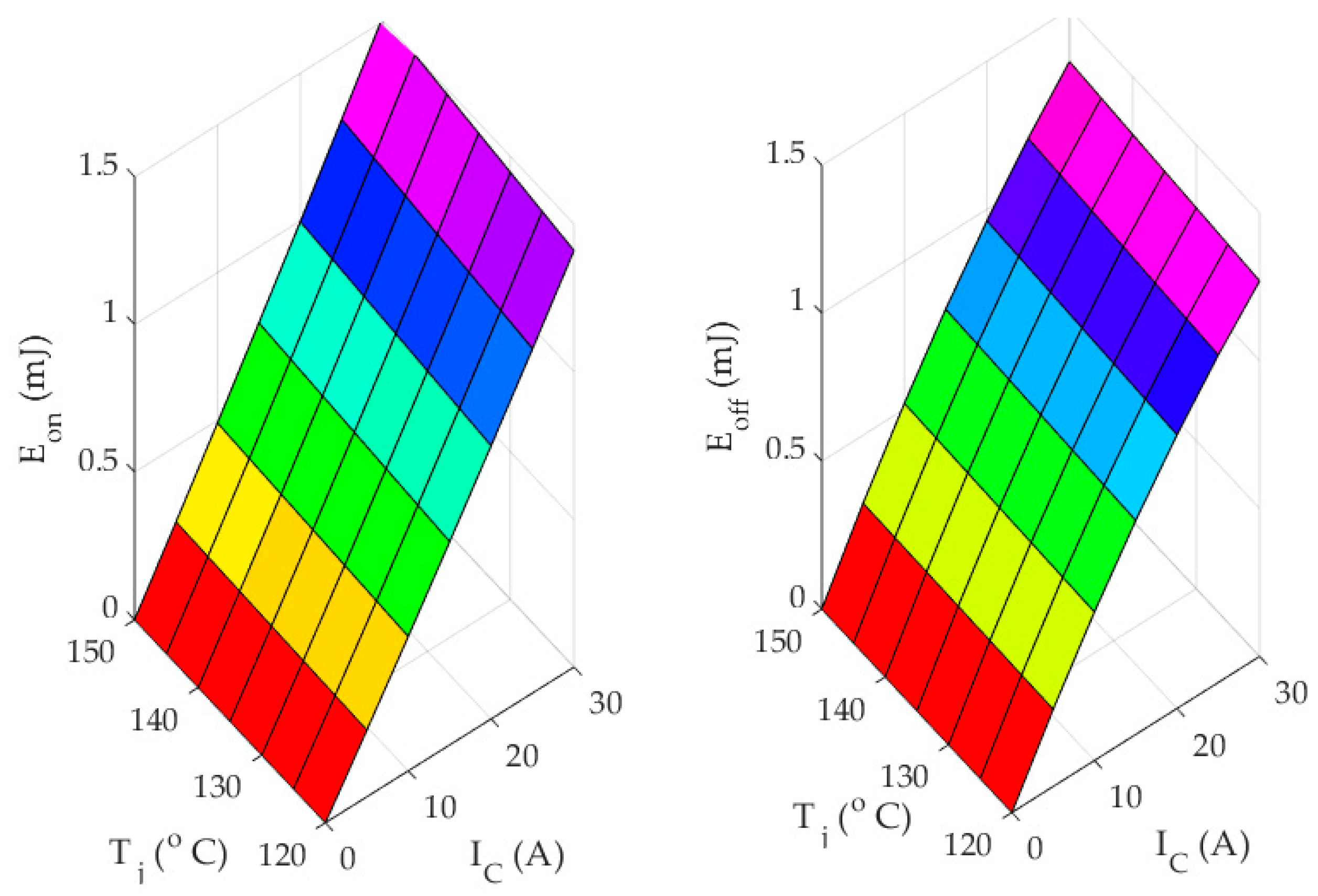
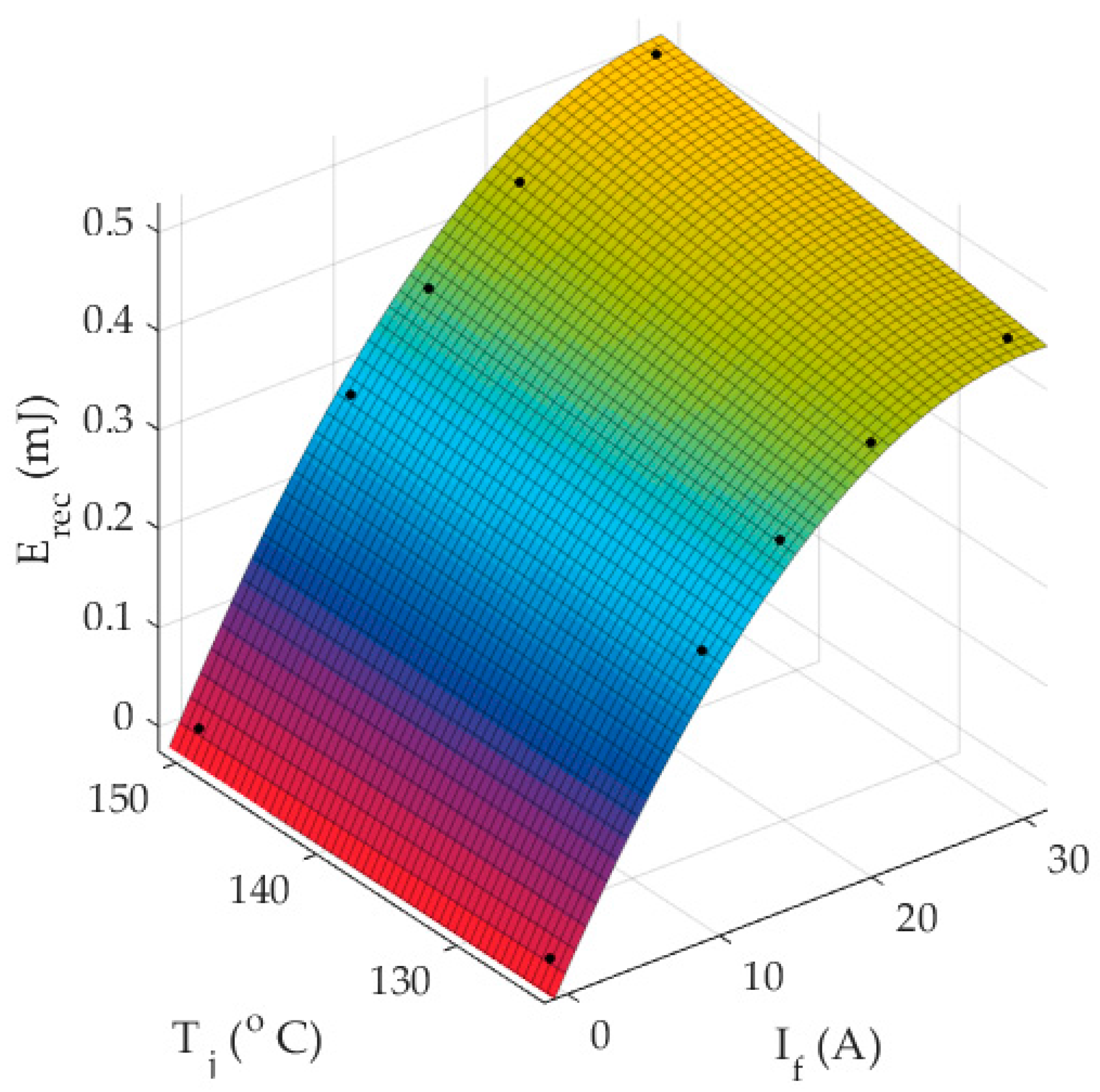
22] where the impacts of gate resistance and gate voltage are considered. A summary of the several behavioral models existing in literature and industry was listed.
The major contribution this paper puts in place is the proposition of an efficient and practically sound VSF algorithm whereby there is an online variation of fsw at various loading conditions, including the ambient temperature effect. The intensive calculations that are typically required with the exiting fsw variation-laws are avoided in the proposed algorithm. Moreover, the benefits of the proposed algorithm include the improvement of the inverters’ switching devices and packaging reliability by reducing the variations in the junction temperature, which has a direct effect on the lifetime of the inverter. The attractiveness of this algorithm lies in its simplicity, in which the online computation of the optimal switching frequency can be easily done. Most of the algorithms that have been introduced in the literature suffer from computational complexity that makes them lack practical sound. The advantages of this new proposed algorithms can be summarized in four main points: (1) easy to be implemented using micro-controllers; and (2) the proposed procedure can be generalized for any power converter that includes multi-level inverters regardless of the control mode and the used technology of the power device. However, the proposed mathematical derivations are discussed on an IGBT power module of Infineon® FP50R06KE3 (Neubiberg, Germany). The same procedures are valid for different technologies that have different power loss analysis. (3) The proposed procedure does not require offline computations and lookup tables; and, (4) since the temperature is considered in the proposed algorithm, the algorithm can reduce the thermal stress on the inverter during high ambient temperature by reducing the switching frequency. Conversely, if the energy loss parameters are not directly given from the manufacturer datasheets, the parameters can be experimentally characterized.
The remaining parts of this study are organized as follows. Short summary of the architecture and the control mode of operations of VSIs are presented in
Section 2.
Section 3 presents the estimation of power losses.
Section 4 presents the thermal modeling of the IGBT power module.
Section 5 presents the time-domain current ripple analysis.
Section 6 presents the proposed variable switching algorithm.
Section 7 presents a discussion of the experimental validation. Finally,
Section 8 concludes the paper.
2. Voltage Source Inverters
VSIs are crucial components in the alternating current (AC) microgrids and modern power systems. To ensure power system reliability, integrating distribution generators (DGs) with existing power systems has some technical and practical constraints. One of these main limitations is power system stability. Voltage stability becomes more important if the microgrid is off-grid (i.e., isolated microgrid) or if connected with a relatively weak power system. The controllability of the VSIs and the DGs adds effective and supportive actions that can improve the performance of the power systems and microgrids in steady state and transient modes of operation [
23].
VSIs can be categorized into three main modes of operation and control schemes. The first one is usually named as a grid-forming power converter in which the VSI is working as a conventional AC source. The voltage and the frequency are controlled and stabilized; however, the output current is load dependent. The uninterruptible power supply (UPS) is an appropriate example of grid-forming VSI. The UPS delivers certain voltage and frequency, where the input of the UPS is also considered as a DC, regardless of being from isolated batteries or converted from an online AC power supply.
The second category is known as grid-feeding power converters. Under this mode of operation, the voltage control is not targeted in the control scheme of the VSI. Moreover, the VSI is working as a current source to supply the desired real and reactive powers. Feeding an energized power system adds more restrictions to the VSI and synchronizing the voltage at PCC is crucially important to track the desired real and reactive power set points. In the previous two modes of operation, either the voltage or the current is controlled. For power system stability, it is occasionally important to control both the output voltage and current. This category is known as grid-supporting power converters and can be classified into two modes: (1) besides supplying the demanded active and reactive powers, it must contribute to stabilizing the voltage and/or the frequency of the grid-connected systems; and (2) the supplied active and reactive powers are subjected to the output voltage magnitude. The voltage magnitude and frequency have higher priority in the second mode than the first mode, and, hence, they can be implemented either in islanded or grid connected microgrids [
23].
The proposed algorithm is not limited to one topology or control mode from the aforementioned architectures. However, for the sake of discussion and clarity, the grid-forming scheme is taken as an example in this paper.
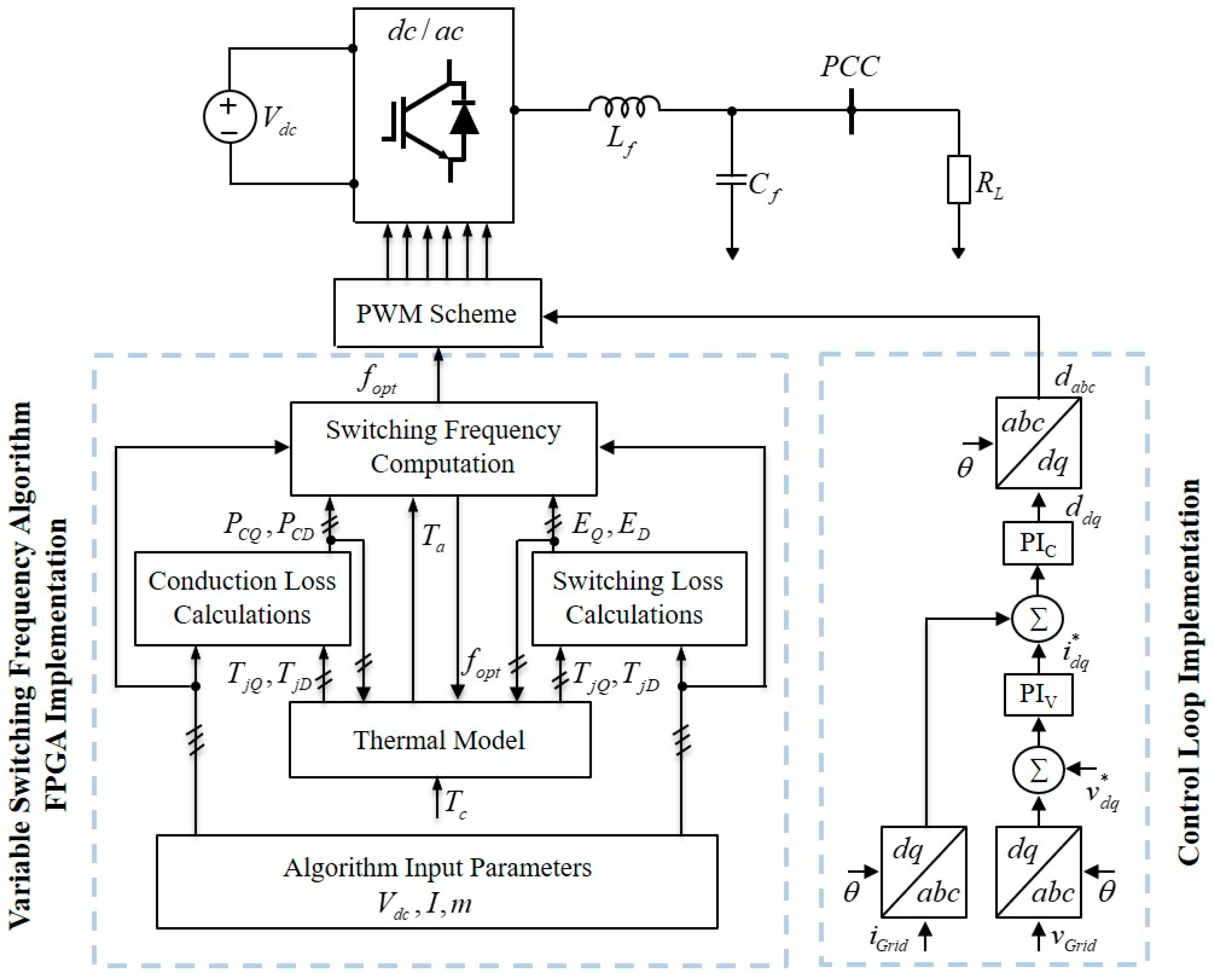
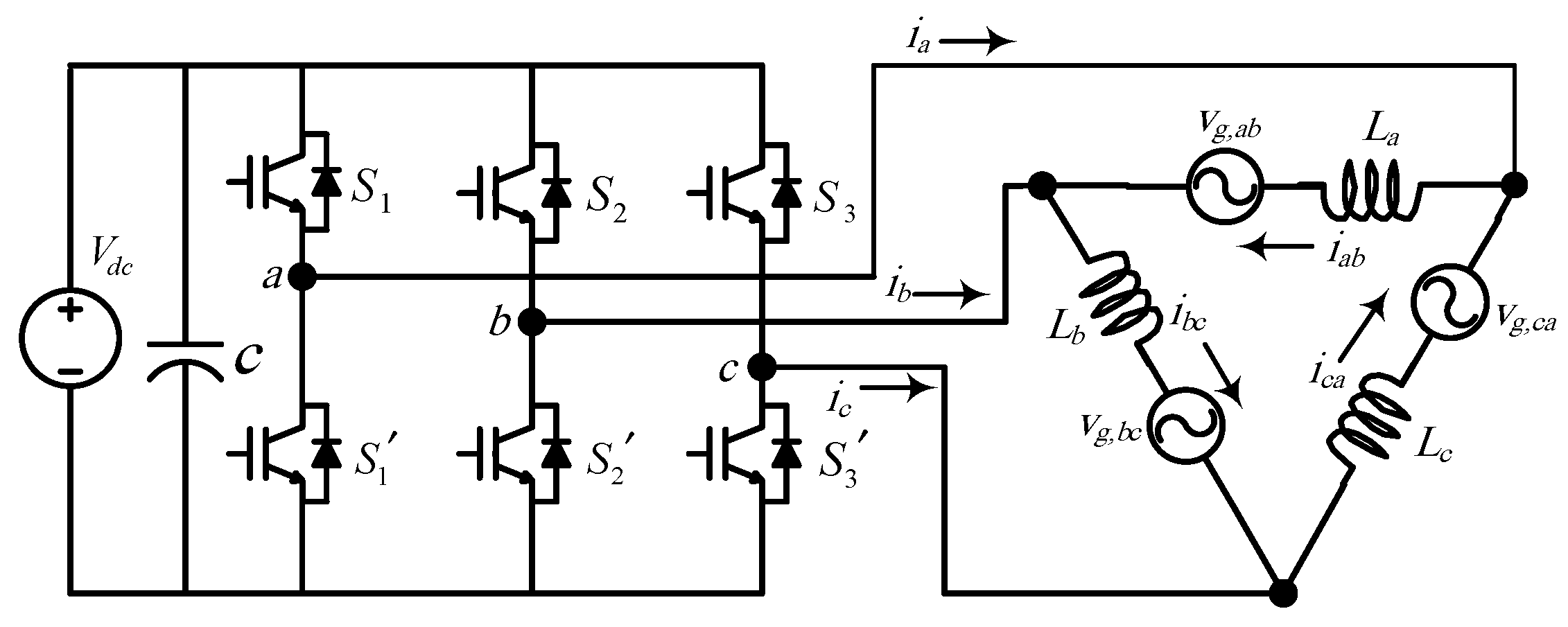
Figure 1 shows the grid-forming scheme associated with the proposed algorithm, as executed in the FPGA, which will be discussed in detail throughout the paper. To this end, any control scheme ends by generating the power reference to the pulse width modulator. The second and the important side for the modulator is generating the carrier signal and the switching frequency that are related to the proposed work. The inputs of the VSF algorithm are the loading measurements and the measured temperature.
4. Thermal Modeling of the IGBT Power Module
Power losses that occur in a semiconductor switch are the main cause of rise of its junction temperature; therefore, a thermal model that estimates the junction temperature from the power losses has to be constructed. Thermal models can be steady-state models such as thermal resistance networks in which only the steady-state temperatures can be estimated, or dynamic models such as the well-known Foster and Cauer models that can estimate the transient behavior of the temperature when it changes from one steady-state point to another [
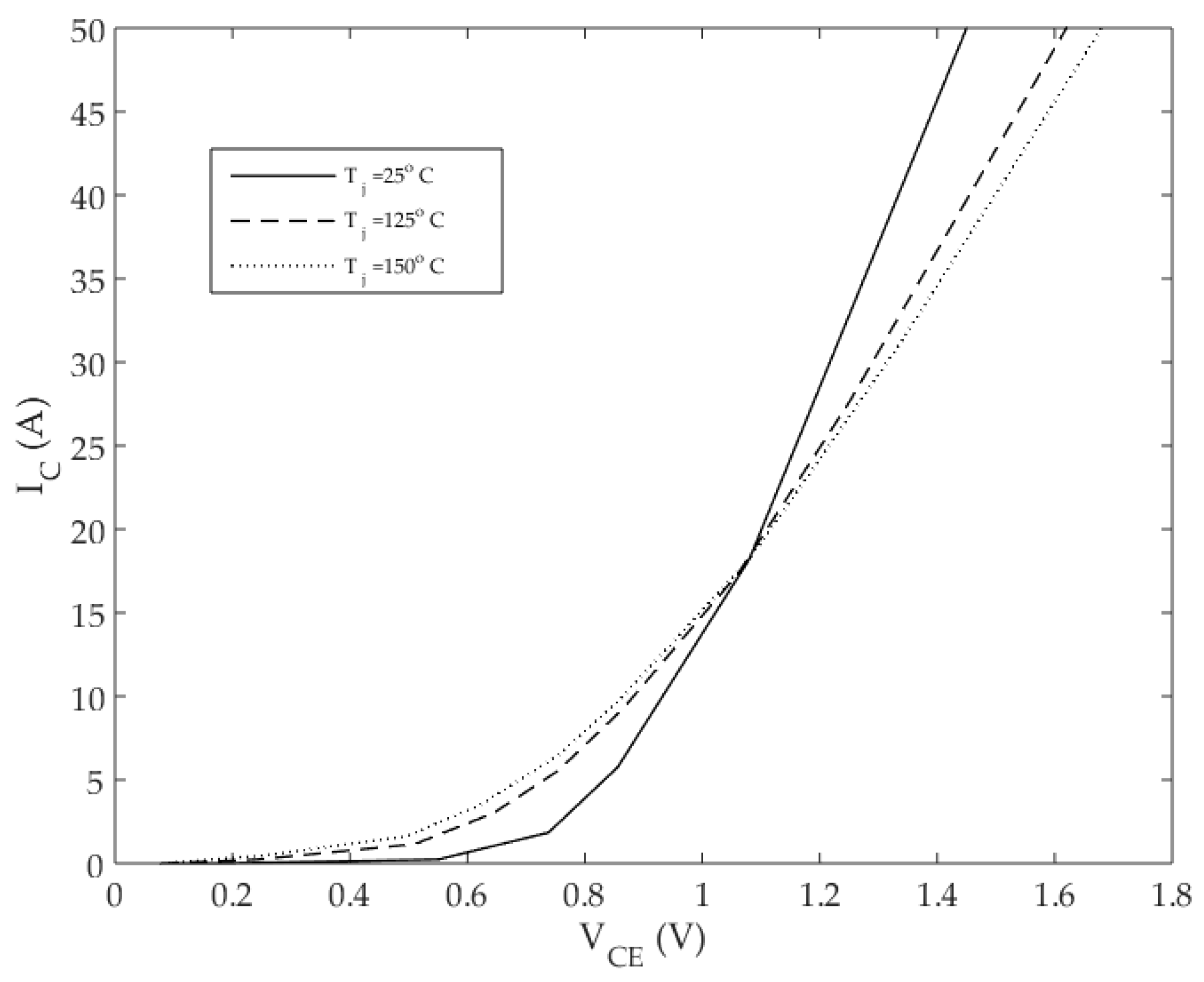
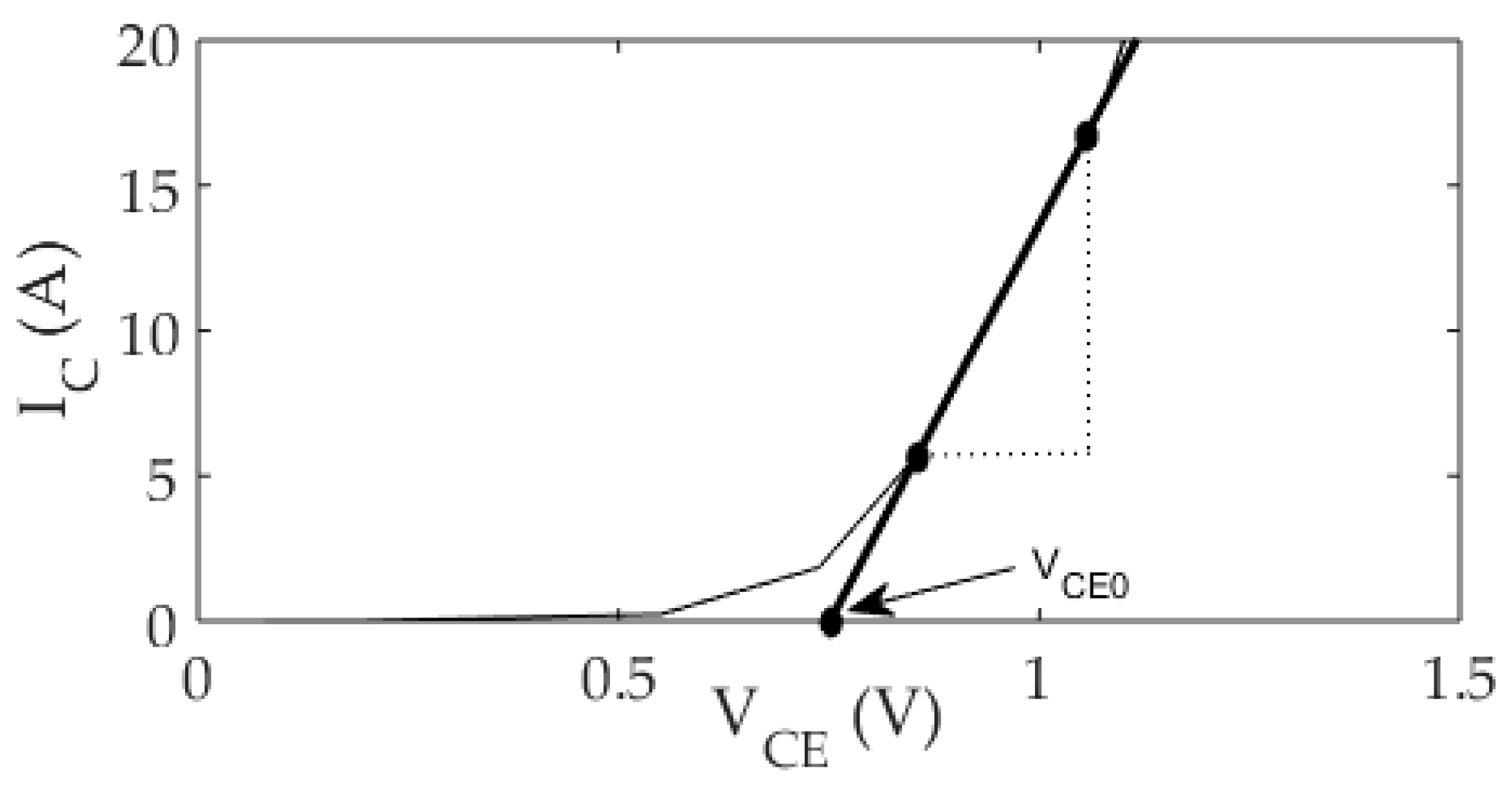
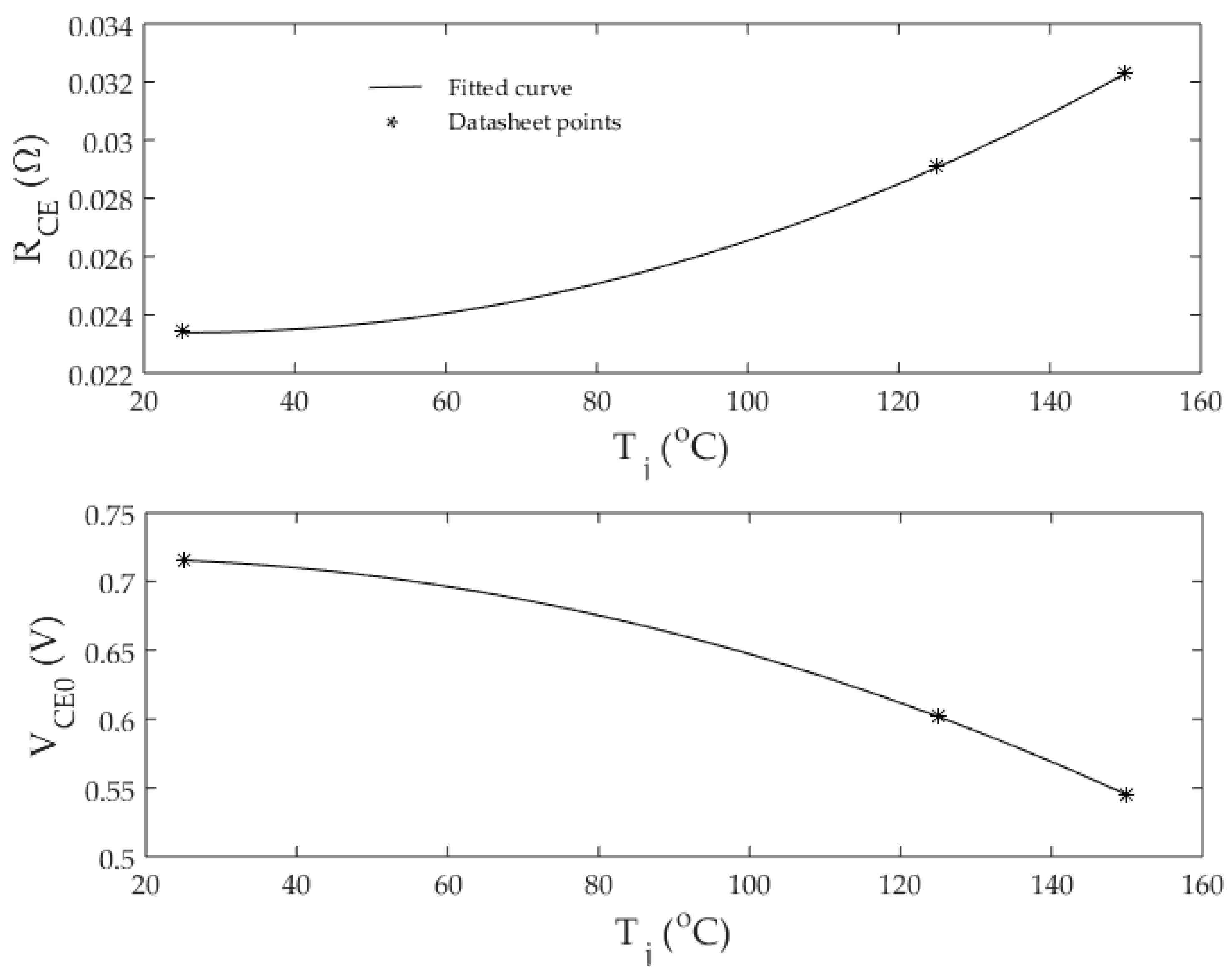
31]. For gird-tied inverters, the time interval between two consecutive active-power set-points is much larger than the time constant of the thermal model in general. Since the aim of this study is to develop an algorithm that changes the switching frequency with the change in the steady-state operating conditions (mainly the active-power) as will be described later, thermal transients can be ignored. Hence, a steady-state thermal model is adopted in this study. In steady-state operating conditions, a specific IGBT conducts for a half-cycle, whereas its anti-parallel diode conducts for the other half, which causes the junction temperature to increase during the half-cycle of conduction and decrease during the other one; this causes a junction temperature ripple that the steady-state thermal model cannot estimate. However, for 50–60 Hz operation, the junction temperature ripple is much smaller than the average value of the junction temperature; therefore, a steady-state thermal model can be used. To account for the rise of the instantaneous junction temperature above its average value, the maximum junction temperature that corresponds to the maximum power dissipation is set to a value lower than the maximum operating junction temperature defined in the datasheet of the semiconductor device; this practice is a norm when it comes to the design of cooling systems of semiconductors.
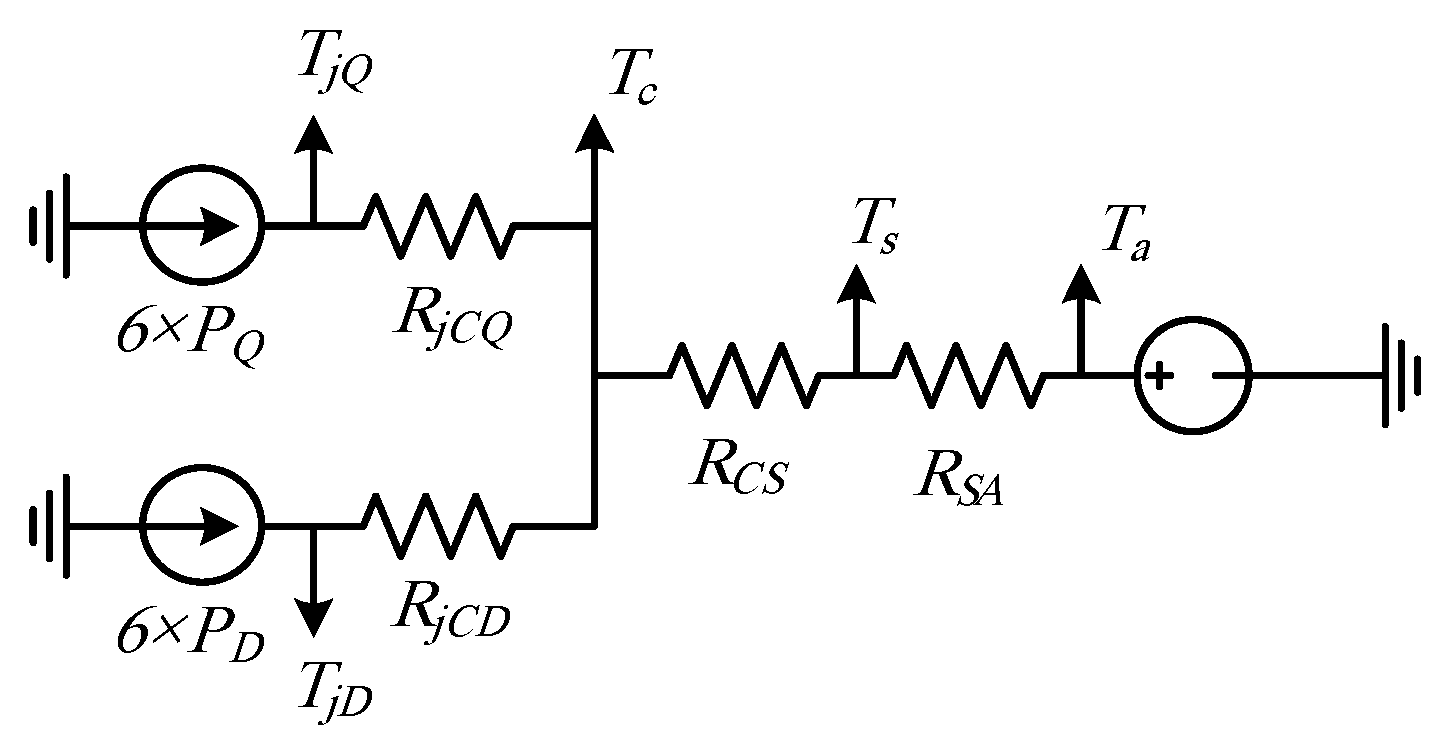
Using the analogy between the electrical and thermal systems, it becomes possible to construct a thermal network whereby each resistor represents the thermal resistance regarding a particular material or path, while each current source represents a source of power loss. Moreover, the temperature difference across a particular material is represented by the voltage difference across the resistor [
32].
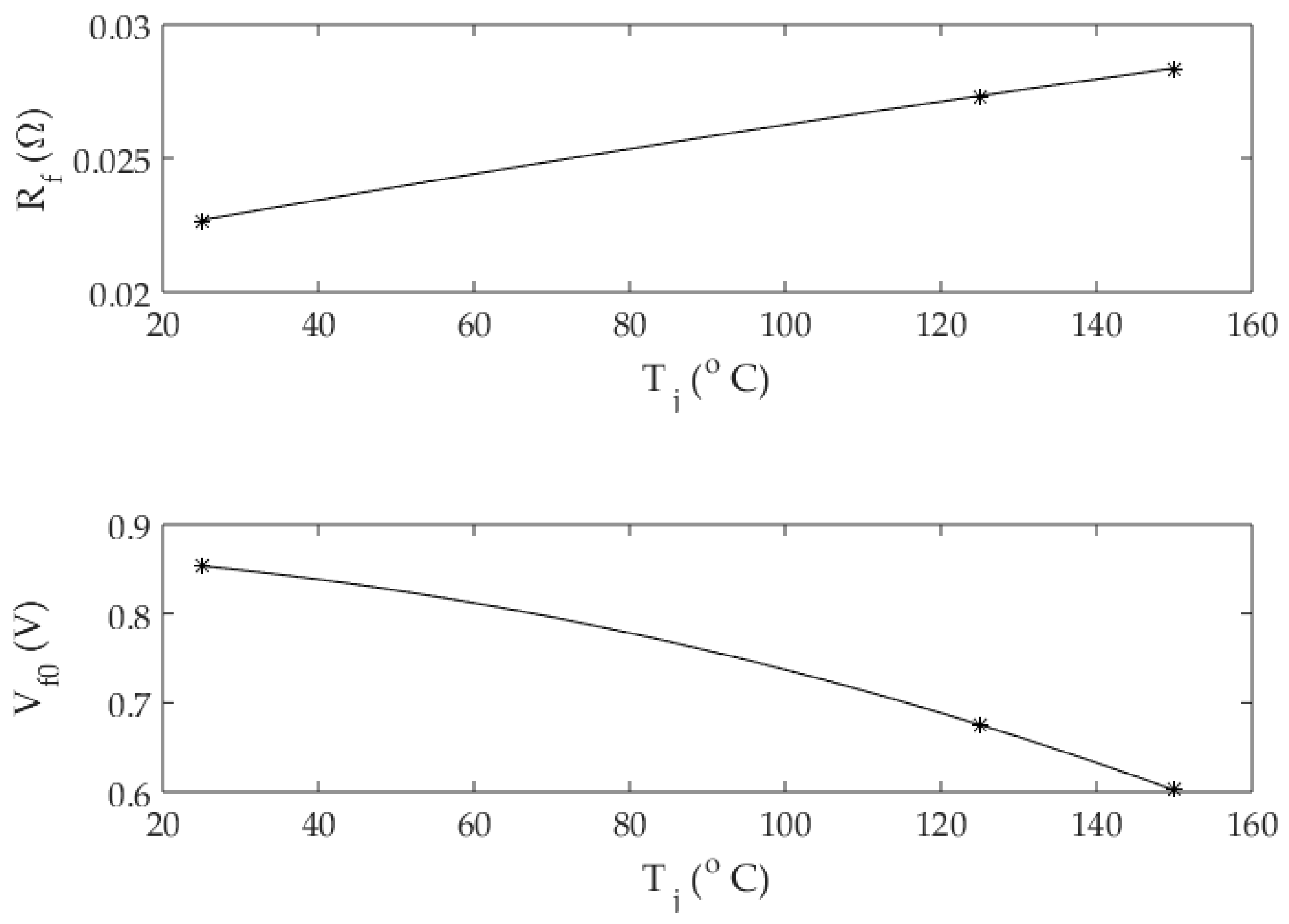
The thermal resistance of a material in °C/W is defined as its resistance to heat flow across a temperature gradient. In the datasheet of the IGBT modules, the thermal resistances (
Rx) of the major heat flow paths are provided, the notation ‘
x’ can be {
j,
C,
S,
A} to denote the junction, case, sink and ambient, respectively. In addition, the zero-order thermal resistance network [
26] of the IGBT module shown in
Figure 8, is adopted in this study. This thermal model matches the fast-computational time associated with the proposed online variable switching frequency algorithms. The thermal resistance of the heat sink is denoted as (
). Based on
Figure 8, the following relations can be deduced:
where
is the heat sink temperature,
is the ambient temperature,
is the case (or base-plates),
is the IGBT’s junction temperature, and
is the diode’s junction temperature. All the temperatures are in °C.
5. Time Domain Current Ripple Analysis
Figure 9 shows the circuit diagram of the grid connected inverter, which includes an inductor (
) to represent the grid-inductance in series with a sinusoidal voltage source (
) for the grid to be represented. This representation is valid for any inverter that supplies motor loads and/or grids [
33].
Before proceeding with the current-ripple analysis based on time domain, the following assumptions are made:
The input voltage is ripple-free.
fsw is relatively higher compared to the fundamental frequency.
The modulating signals during each Tsw remain constant.
The impact of dead-time is neglected.
From the circuit diagram of
Figure 9, the voltage between phases
a and
b can be written as
where
is the inverter’s output line-line voltage,
is the phase-current, and
is the line-line grid voltage.
As mentioned earlier, the load current consists of the ripple component and the fundamental-frequency component. Therefore,
can be written as
where
is the load current fundamental component and
is the load current ripple component. Substituting Equation (30) in Equation (29), yields Equation (31), and then the load current ripple component can be expressed as in Equation (32):
The term
doesn’t appear in Equation (32) because of the assumption that the fundamental component is constant within
Tsw. The inductor resistance can be neglected, and since
fsw is much greater compared to the fundamental frequency, the current ripple component is placed under the assumption of rising and falling in a linear manner around the fundamental value. Using linear approximation, each segment of the current ripple is given as
where
is the current ripple segment over the interval of time
,
is the voltage at time
and
is the voltage at time
.
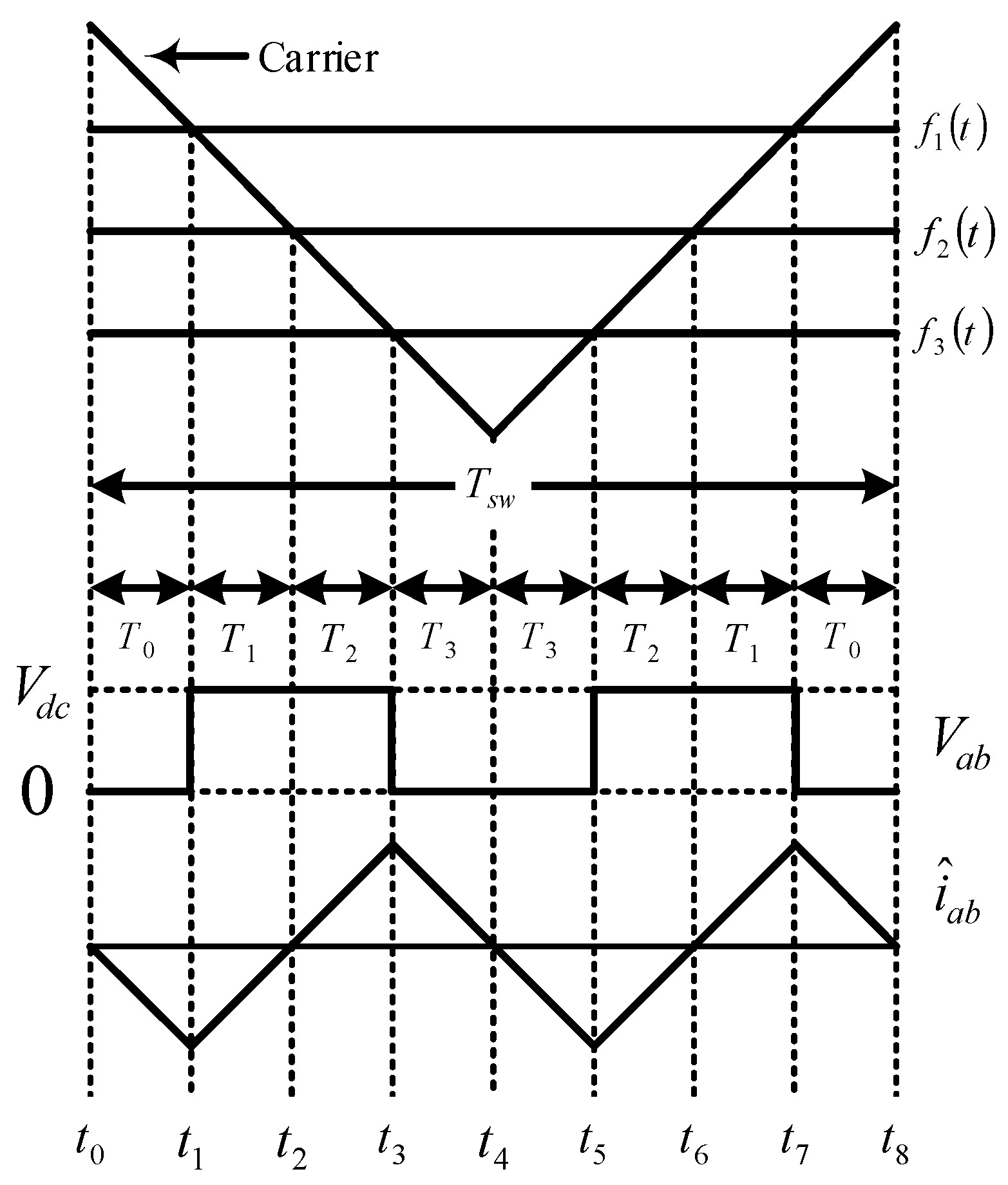
The ripple component and the output line-line voltage of the load current at
Tsw are shown in
Figure 10. The ripple of the load current can be given as
The ripple current mean square value over
Tsw (i.e.,
) can be expressed as
The time intervals
,
,
and
can be related to
as
Substituting Equation (43) in Equations (40), (41), and (42) yields
To find the current ripple root mean square (
rms) value over a fundamental period (
), Equation (44) is integrated over the fundamental period as in Equation (45):
It should be noted that the integration was conducted over the period
and the symmetry justifies integration over a half period. Substituting Equation (44) in Equation (45) gives
If it is a Y-connected load, Equation (46) yields
The THD in the inductor current
is given as
where
is the fundamental current’s
rms value.
6. The Proposed VSF Algorithm
Generally, the manufacturers of grid-tied inverters specify the PWM switching frequency
fsw as a design value with respect to the rated operating conditions. Increasing
fsw reduces the
rms value of the current ripple and therefore the total demand distortion
TDD is reduced as well. However, the value of
fsw is limited by the heat dissipation capability of the semiconductor power switches and their associated cooling system. When the operating point of the inverter is below the rated conditions, the cooling system appears to be oversized since it is possible to increase the switching frequency and hence enhance the quality of the output current. Using the aforementioned premise, each operating condition can be considered as a design problem; however, the switching frequency is the only degree of freedom that is available in the problem design. Therefore, an algorithm that is able to improve the output power quality of the grid-tied inverter without changing the physical structure of the system is significant from an industrial point of view [
34].
Increasing
fsw will increase the power losses and hence reduce the efficiency. However, the output power quality is improved. Since increasing or decreasing
fsw will improve one feature of the system and degrade the other, this means that a conflict between two desired objectives is met, which is a typical multi-objective optimization problem. In such problems, there is no unique optimal solution but rather a set (maybe infinite) of optimal solutions. The selection of one solution among the set of solutions is a degree of freedom left to the preference of the designer [
35,
36].
To obtain an optimal solution with a reduced computational complexity that is strictly required for an algorithm that can determine the optimal
fsw online (i.e., without heavy offline calculations that are stored in lookup tables), a weighted-sum objective function is defined as follows:
where
is the optimization cost function to be minimized.
fsw is bounded by the upper and the lower permissible bounds,
fsw,l and
fsw,u, respectively.
is the trade-off factor. To this end, since each individual goal has distinct value, it is advisable to normalize both objectives in order to avoid misleading solutions as
where
is the normalized cost function,
is the
TDD at
,
is the
TDD at
,
is the least expected switching losses, and
is the highest acceptable switching losses.
Furthermore, the optimal value of
fsw (
) can be found by equating the first order derivative of Equation (50) to zero, that is:
Rearranging Equation (51) yields
As the operation and the loading conditions are varying, there is a change in the energy losses. Therefore,
changes. In other words, for every new condition that emerges, a new optimization problem is solved. The maximum allowable switching frequency (
) can be expressed based on switching energy losses given in Equation (53). However,
is restricted by the highest allowable
, which is assumed to be 5%. The minimum allowable switching frequency can be expressed as in Equation (54):
Making use of Equations (53) and (54), (52) can be rewritten as
The highest permissible losses are limited by the highest allowable
TJQ and
TJD. This value has to be evaluated for each new ambient temperature. Based on the thermal layout in
Figure 8, the highest permissible total losses for each diode (
) at a given ambient temperature can be given as in Equation (56) and the highest permissible losses for each IGBT (
) can be related to Equation (56) as shown in Equation (57):
From Equations (56) and (57), the highest permissible losses (
) can be evaluated with a consideration of just the switching loss aspect as follows:
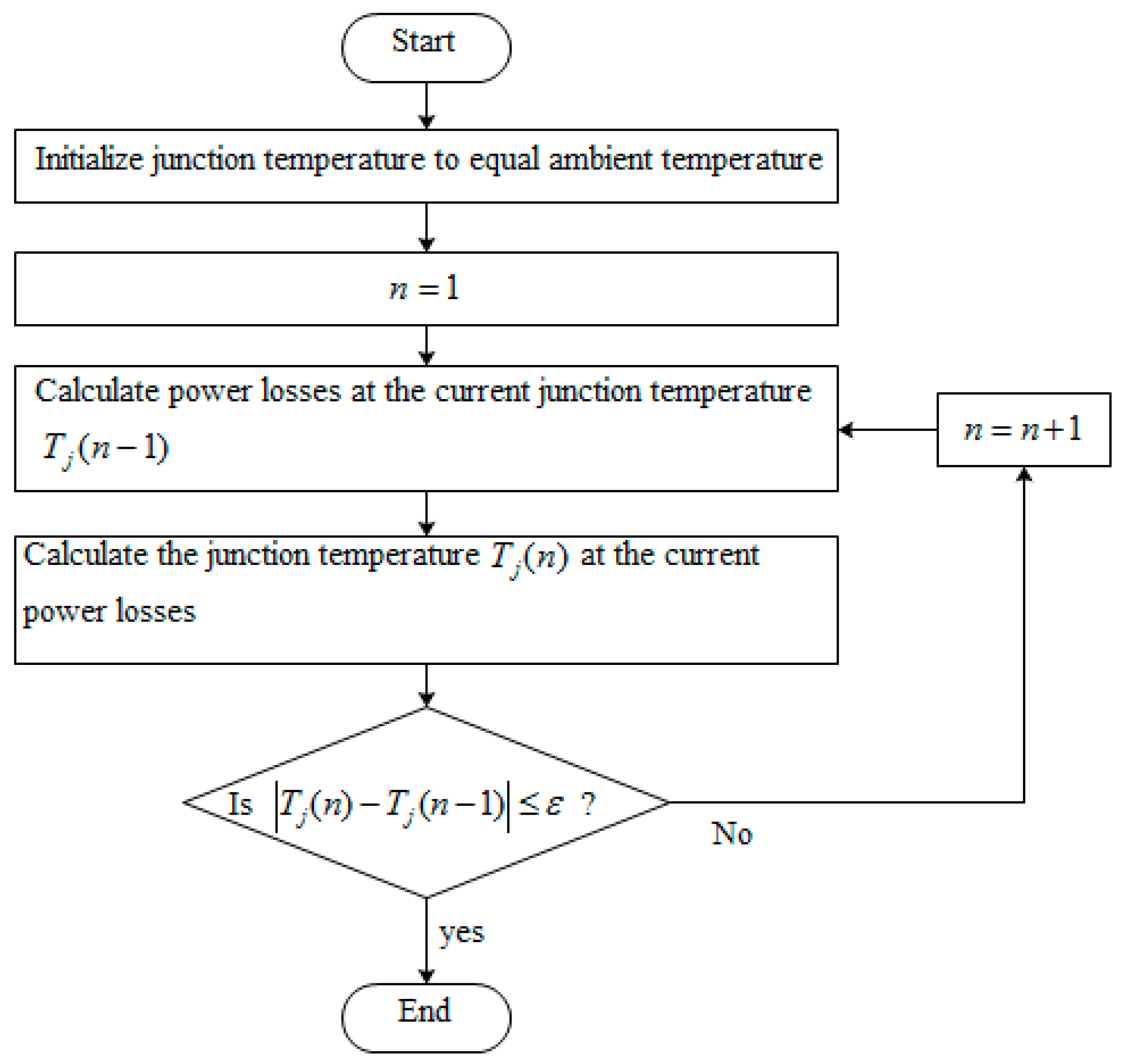
Figure 1 shows the implementation of the proposed algorithm in the FPGA platform. The operating conditions including the modulation index, the DC-link voltage, and grid current, and the power factor are used to estimate the conductions losses utilizing Equations (10) and (14) and the energy switching losses evaluating Equations (17), (18) and (22). From the power and energy losses’ estimates, the optimal switching frequency is computed from Equation (55). Since the junction temperatures and power losses are mutually dependent, an iterative solution must be used as in
Figure 11. It should be mentioned that the effect of the ambient temperature is taken into consideration as feedback from the case temperature, since the IGBT power module includes a thermistor that can be measured as in
Figure 1.
7. The Experimental Results
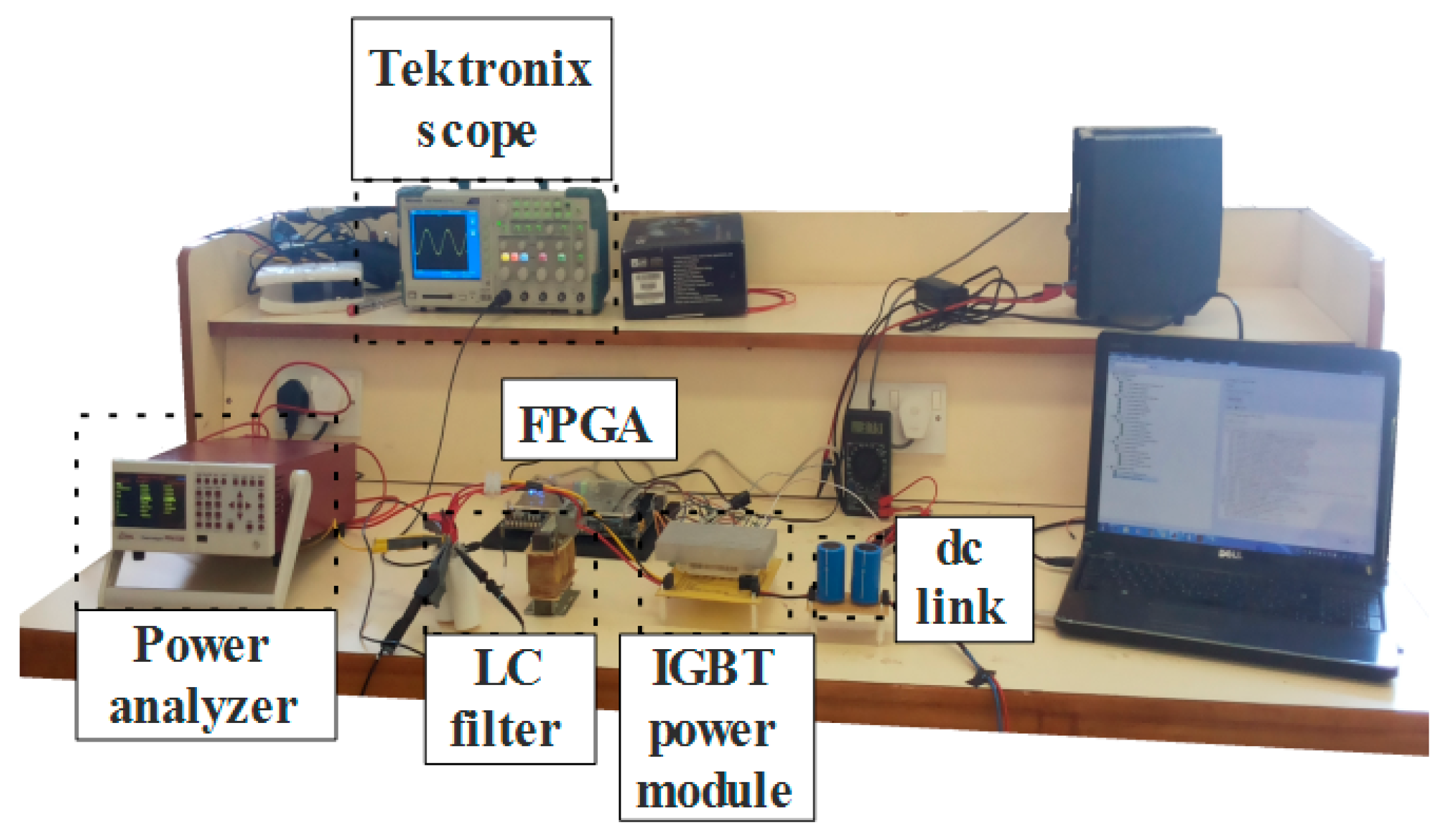
Validating the significance of this proposed algorithm requires the setup of an experiment as in
Figure 12. The experimental tests were performed on three-phase IGBT power module (Part Number: FP50R06KE3) cascaded with passive low pass inductor and capacitor (LC) filter output and supplying a Y-connected resistive load.
Table 1 illustrates the system parameters and
Table 2 depicts the optimal switching frequency at different loading conditions alongside total switching losses,
TDD, and case temperature assuming a weighting factor of 0.6. As is evident, the proposed algorithm varies
fsw to obtain the best balance between the
TDD and the switching losses based on inverter’s loading conditions including the ambient temperature. When this system is at heavy loads, switching losses are high; therefore, the algorithm reduces
fsw, while keeping the
TDD below the 5% limit (IEEE standard 519-2014). However, at light loads, the switching losses becomes low; hence, the algorithm increases the switching frequency for the output current quality to be enhanced.
The measurement of the
TDD was carried out by measuring the total harmonic distortion of the output current (
) at certain loading conditions using the harmonic analysis functionality provided by a Tektronix oscilloscope (Model Number: TPS2024B). According to IEEE-519
TDD is defined as “
the total root-sum-square harmonic current distortion, in percent of the maximum demand load current”. The calculated
TDD is obtained from
, the
rms value of load current (
) and the
rms value of the rated current (
) as in Equation (59)
The measurement of the switching losses is initiated by measuring the steady-state case temperature at each operating condition by which the total power losses can be estimated. To extract the switching losses component, the experiment is performed again with fixed switching frequency while keeping other operating conditions unchanged, and, as a result, the conduction losses are unchanged as well. Since the switching losses are almost linearly related to the switching frequency, the switching losses can be deduced.
The following steps describe the experimental procedure in which switching losses are extracted:
- (1)
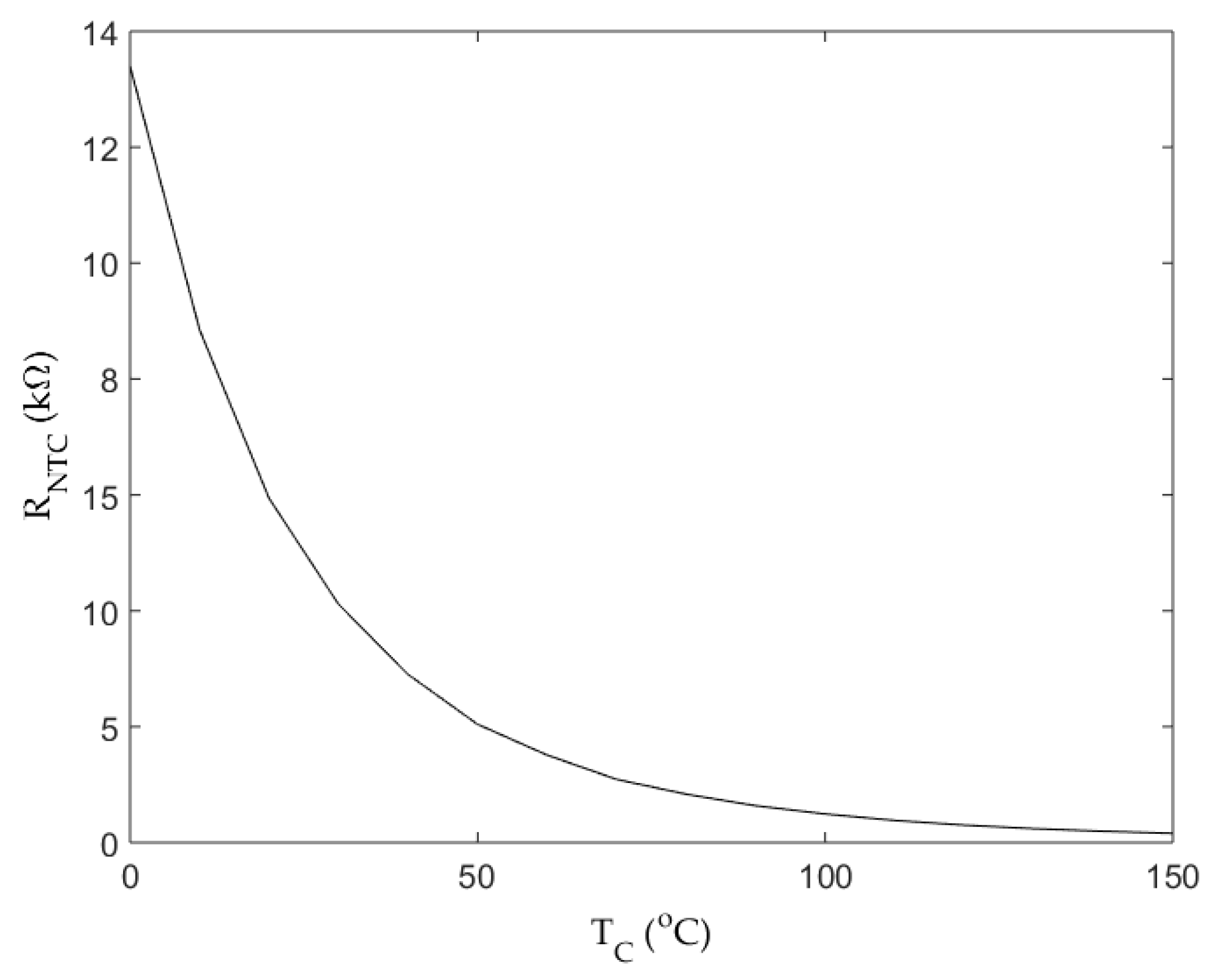
Measure the case (base plate) temperature by the solid state temperature sensors (negative temperature coefficient (NTC) thermistor)
RNTC. The temperature characteristic of this thermistor is shown in
Figure 13 and Equation (60):
- (2)
From the measured case temperature and based on re-arranging of Equations (24)–(28), the total power losses is determined by Equation (61)
- (3)
Under the same loading conditions, the switching frequency is varied, case temperature is measured, and losses are calculated.
- (4)
Based on the calculated power losses, the following set of Equations (62)–(65) can be computed:
where
is the switching frequency of interest and
is the second switching frequency.
Validating how effective the proposed algorithm requires the experimental system to be tested with a fixed
fsw while constantly keeping the
TDD at 2.5%.
fsw is selected as 25 kHz, which is approximately the middle point relative to the variable frequency range, with the system being tested under the same load conditions.
Table 3 summarizes the performance of the inverter. Comparing the results from
Table 3 and
Table 4, there is a reduction of the switching power losses at full load by about 51.6% using the proposed VSF algorithm, while the
TDD is below the 5% limit. The decrease in the switching losses with the use of the proposed VSF algorithm is justified by the fact that the weight of 0.6 automatically leads the algorithm to favor the reduction of the switching power losses.
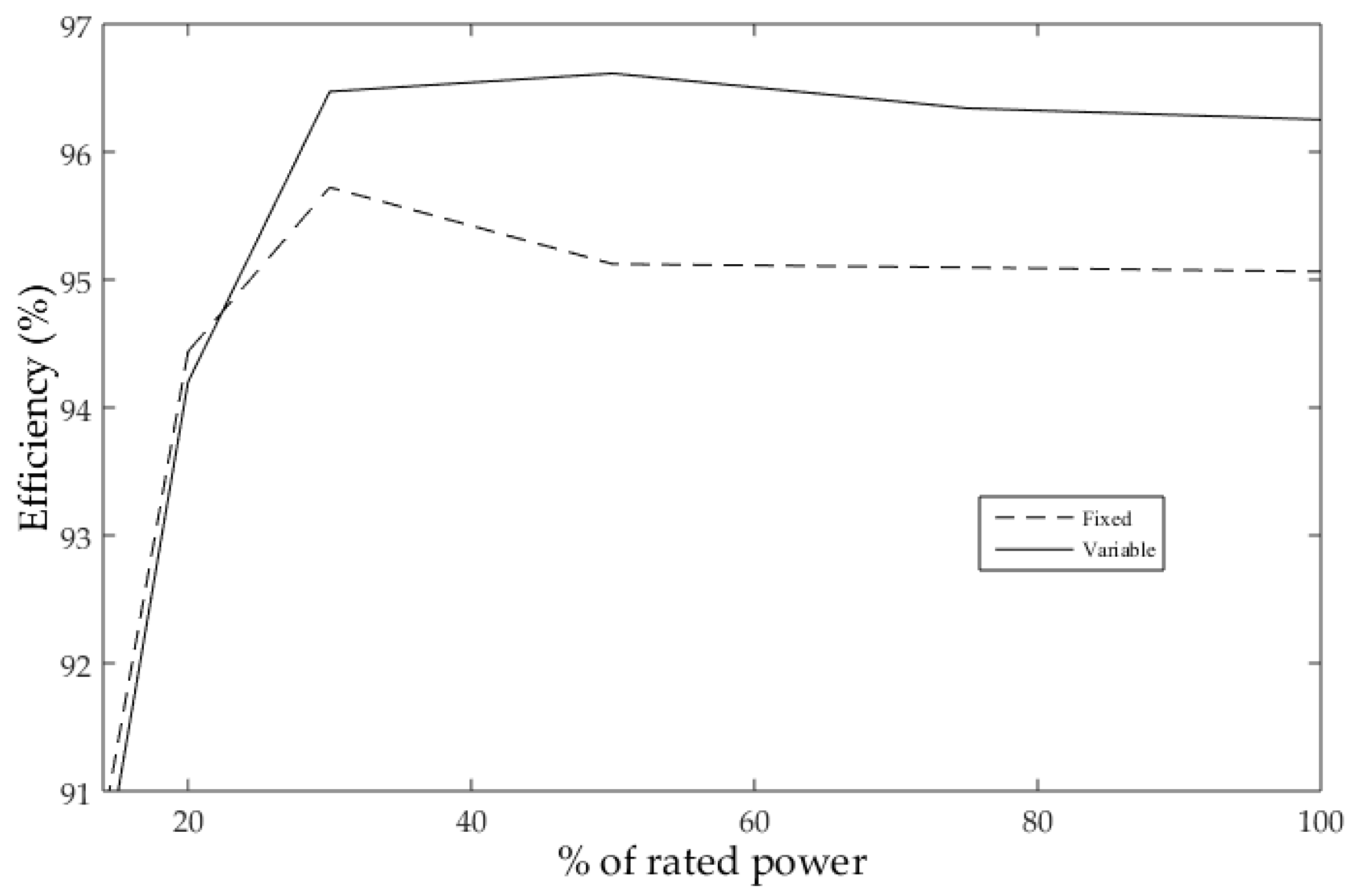
Figure 14 gives the measured efficiency curves, which is for the whole inverter system alongside the fixed and VSF algorithms. It is obvious that the inverter efficiency is enhanced for a large array of load conditions.
Table 4 indicates a comparison between the calculated and experimental results. It can be shown that the power losses and
TDD models are highly accurate.
To further highlight the significance of the proposed algorithm, the California Energy Commission (CEC) efficiency of the inverter is measured under the fixed and VSF algorithms, the CEC efficiency is 97.3% using the proposed VSF algorithm, and 96.39% with the fixed fsw. Therefore, it can be deduced from comparing the efficiencies of both algorithms that fsw can be increased without degrading the efficiency of the inverter.
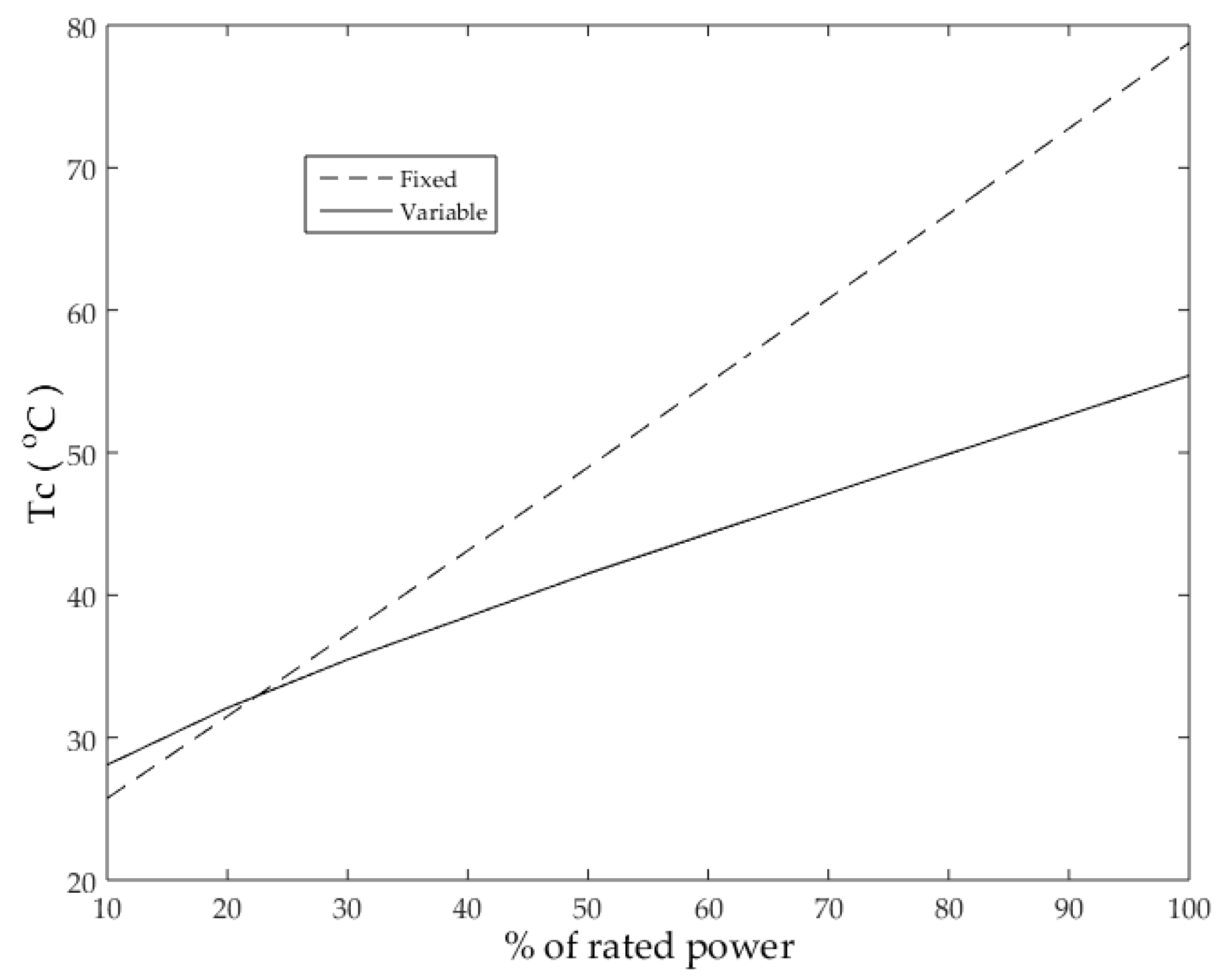
An interesting property related to the proposed VSF algorithm is the fact that the junction temperature variation under different load conditions tends to be lower than that one under fixed
fsw. As can be shown in
Figure 15, the case temperature rate of change with the VSF algorithm is less than that of the fixed
fsw. This property holds even if more weight is given to the
TDD. In other words, regardless of the selected weighting factor, the temperature profile when using the proposed algorithm will always have a slope that is under the one when using the fixed switching frequency. The importance of this property comes from the fact that the lifetime of the inverter is inversely proportional to the junction temperature difference [
37,
38,
39].