1. Introduction
According to CISCO, an american multinational technology company, by 2020, more people (5.4 B) will have mobile phones than have electricity (5.3 B), running water (3.5 B) and cars (2.8 B). In addition, 75% of the mobile data traffic will be bandwidth-hungry video. Users will expect wireline quality in wireless services and higher bit rates and more reliable connections will be mandatory. While conventional techniques struggling to provide these bit rates, massive multiple-input-multiple-output (MIMO) systems promise 10 s of Gbps data rates to support real-time wireless multimedia services without occupying much additional spectrum [
1].
Massive MIMO technology has got much attraction lately as it promises truly broadband wireless networks [
2]. Massive MIMO systems use base station (BS) antenna arrays, with few hundred elements, simultaneously serving many tens of active terminals (users) using the same time and frequency resources.
1.1. Background
It is well known that, in classical MIMO, multiple antennas at both ends exploit wireless channel diversity to provide more reliable high-speed connections. Massive MIMO (also known as Large-Scale Antenna Systems, Very Large MIMO, Hyper MIMO, and Full-Dimension MIMO) makes a bold development from current practice using a very large number of service antennas (e.g., hundreds or thousands) that are operated fully coherently and adaptively.
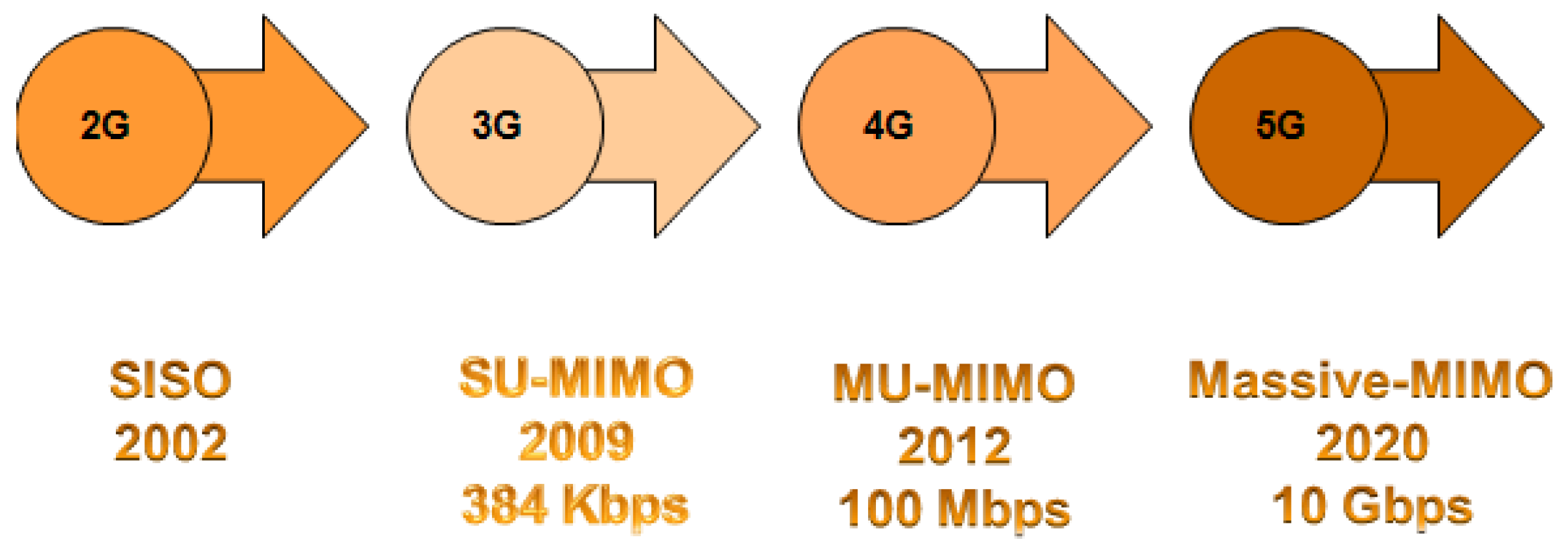
Figure 1 shows the speed improvement of wireless networks over the years starting from single-input-single-output (SISO) systems, single user (SU) and multiple users (MU) MIMO networks. MU-MIMO systems already provide significant advantages over earlier systems. Massive MIMO aims to further enhance this (to 10 Gbps and more) using hundreds of antennas exploiting advances in parallel digital signal processing and high-speed electronics. Extra antennas help with focusing the transmission and reception of signal energy into ever-smaller regions of space. This brings huge improvements in throughput and energy efficiency, in particular when combined with simultaneous scheduling of numerous user terminals (e.g., tens or hundreds).
The more the BS antennas used, the more the data streams can be released to serve more terminals, reducing the radiated power, while boosting the data rate. This will also improve link reliability through spatial diversity and, provide more degrees of freedom in the spatial domain, and improve the performance irrespective of the noisiness of the measurements. In addition, because massive MIMO systems have a broad range of states of freedom, and greater selectivity in transmitting and receiving the data streams, interference cancellation is enhanced. BSs can relatively easily avert transmission into undesired directions to alleviate harmful interference which, leads to low latency as well. In addition, massive MIMO makes a proper use of beamforming techniques to reduce fading drops; this further boosts signal-to-noise-ratio (SNR), bit rate and reduces latency [
3].
Furthermore, increasing the number of BS antennas above the number of active users leads to higher throughput [
1]. Channel estimation quality per antenna also improves with the number of BS antennas especially in the presence of high correlation among the antennas which is very typical [
4]. In addition, the eigenvalue histogram of a single implementation converges to the average asymptotic eigenvalue distribution [
5]. This leads to the possibility of employing simple low complexity detection techniques while preserving an excellent performance. In addition, the channel becomes more predestined and random detectors matrices are readily solved.
Aggressive spatial multiplexing in massive MIMO systems leads to an impressive improvement in the network capacity by minimizing multiuser interference by steering the signal accurately in the right direction. Massive MIMO systems concentrate the released energy into small user centric zones, which dramatically increases the throughput and the energy efficiency [
1]. Since all of the users can take part in the multiplexing gain, costly antenna array deployments are only necessary on the BS side, which saves on costs by sharing. This also leaves the user equipment less complex, often with a single antenna. A higher number of BS antennas revokes the effects of uncorrelated noise and small-scale fading, and lowers the required transmitted energy per bit [
6]. The propagation medium minimally affects the performance of a massive MIMO system because of multi-user diversity.
Due to the advantages and popularity of massive MIMO, recently there has been an increase in papers written on this area.
Table 1 describes some of these.
1.2. Networked MIMO and Massive MIMO
MIMO systems can be cooperative or non-cooperative. Cooperating systems are often called
Networked MIMO, where a certain user is served by all BSs within its range of operation. The typical massive MIMO BSs do not cooperate in this sense [
13]. Both systems mitigate interferences of multi cellular wireless networks in separate ways and are not to be confused with each other [
14]. Networked MIMO emulates distributed antenna arrays by creating clusters of connected BSs. Note that each BS has a relatively small number of antennas only. Channel state information (CSI) as well as data are shared among the collaborating BSs through backhaul links. This contributes to interference cancellation, and then data is passed to the scheduled downlink users cooperatively from the BSs (sometimes using beamforming) [
15]. In contrary, massive MIMO systems have substantial (
M) number of antennas per BS, simultaneously serving a much smaller (
K) number of users [
8].
Table 2 compares cooperating network MIMO and conventional massive MIMO approaches.
1.3. Massive MIMO in Wireless Sensor Networks
Wireless sensor networks (WSN) are special kinds of monitoring networks, aiming at detecting, measuring, monitoring certain physical phenomena, such as temperature, humidity, pressure, vibration, etc. Each device in the WSN is termed as a node that exchanges information with its neighbour. Typically nodes have limited connectivity and energy resources. All data will be poured into a BS node, or a sink, which in turn relays the information to an outside user, or a server to process it. WSN nodes are small in size, cheap in cost, and do not employ complicated processing units, except the sink node. WSN may be composed of hundreds or thousands of nodes to provide coverage on a large scale basis.
Recently, several research efforts have been addressed to discuss the benefit of introducing a massive number of antennas at the BS, or the sink node. Multiple antennas at the BS improve the detection performance, the estimation performance, and energy efficiency, even when using simpler algorithms, and linear receivers with partial CSI knowledge.
In [
16], the authors studied the detection, and estimation performances of a Gaussian signal communicating over a coherent multiple access channel in a WSN having a massive MIMO BS, or fusion center (FC). The Neyman–Pearson detectors and the linear minimum mean squared error (LMMSE) estimation detectors that require full CSI were studied. Significant performance gains were achieved at low sensor transmit power levels. However, the energy detector shows improvement in gain under both low and high sensor power assumptions.
In addition, in [
17], the authors compared the performance of a low cost energy detector to that of an expensive complex optimal detector, in a WSN having multiple antennas at the FC, both analytically and by simulation.
Finally, the authors in [
18] optimized the transmission power at each node of a WSN having multiple antennas at the FC, using two different scenarios—in correlated and in uncorrelated fading channels with noise. The authors proved that the total power consumption at the nodes is saved as the number of antennas increases.
2. Homogeneous MIMO (Single Tier Systems)
Conventional MIMO systems are composed of randomly distributed multiple antenna BSs, where each BS is serving a certain number of users. All BSs are working with the same access methods, diversity techniques, and type of transmission. The average transmit power per unit service area is also often the same (subjected to power control algorithms).
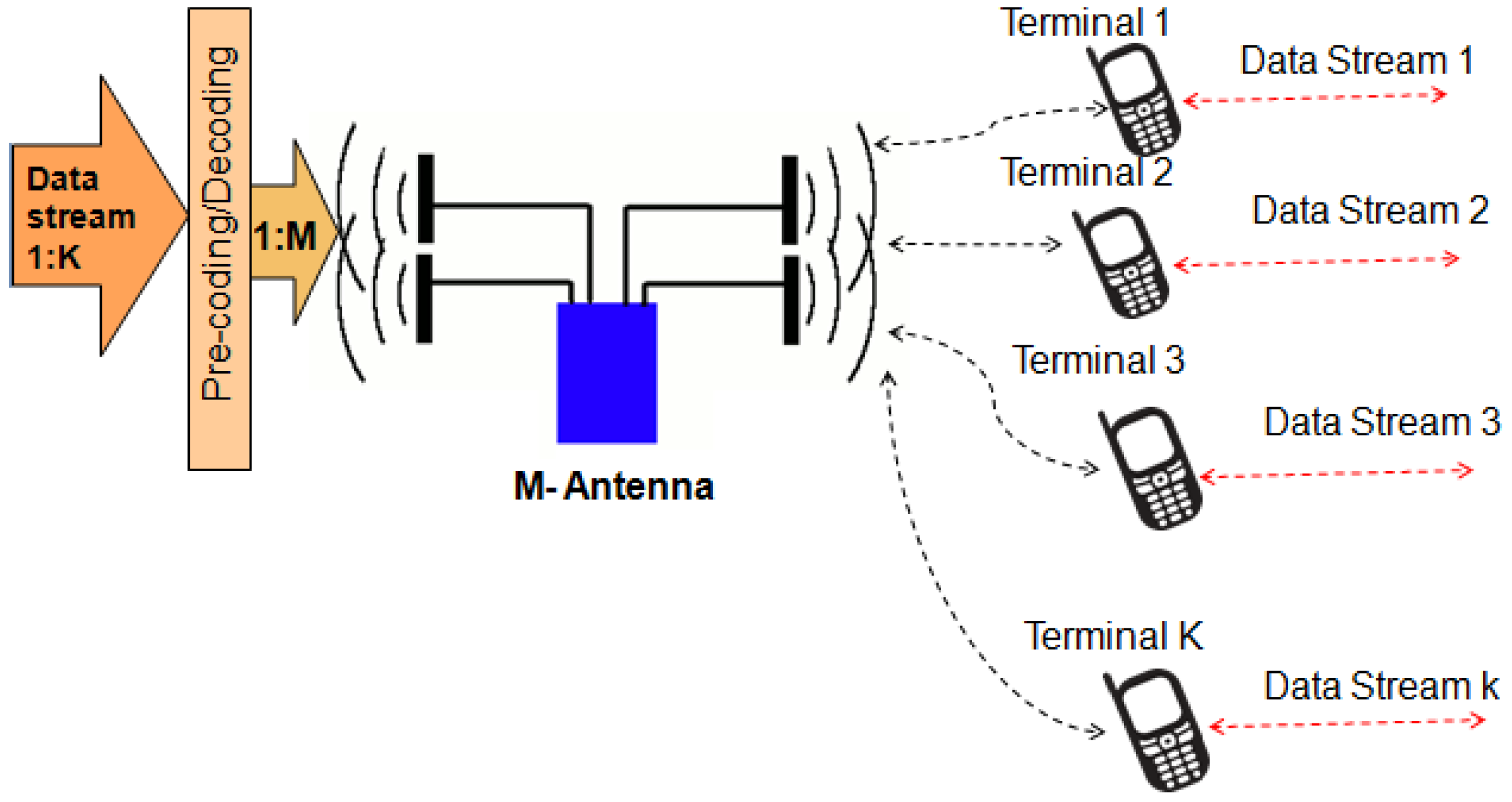
Figure 2 shows the uplink and the downlink of a massive MIMO single cell system. As shown in
Figure 2, the BS is composed of a few hundred service antennas serving a few hundred users each, usually with only one antenna.
The steps of the uplink operation are as follows [
7]:
Encoding is employed to prepare data for transmission.
Pilot sequences and uplink data sequences are transmitted at the same time and over the same frequencies from each user to the BS.
The BS receives the sum of data streams from all the users, and estimates the channel.
Decoding and detection operations produce individual data streams by utilizing the estimated CSI.
The steps of the downlink process are as follows:
Beamforming: Data streams are transmitted from the BSs to only the intended users by means of beamforming, where the different data streams may occupy the same frequencies at the same time (space division multiplexing).
Precoding: The previous operation is carried out knowing the frequency response of the propagation channels (or CSI) between each of its elements and each user and precoding the signals accordingly.
Linear decoding or demultiplexing is employed on the uplink, while linear precoding or multiplexing is employed on the downlink.
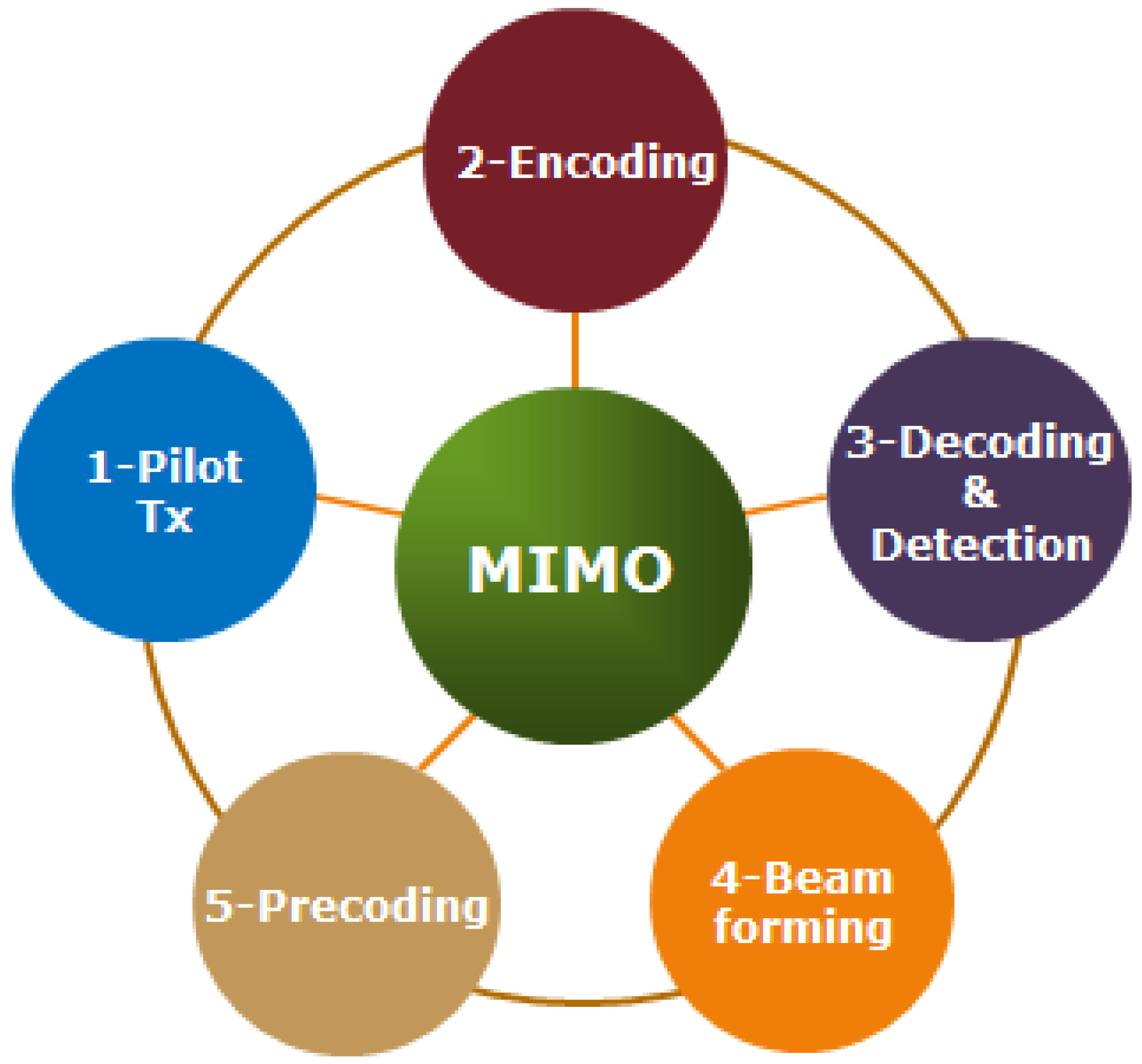
Figure 3 shows major elements of a massive MIMO system.
Linear precoding techniques at the downlink aim to focus each signal at its desired terminal and mitigate interference towards other terminals [
1]. Meanwhile, receive combining is used in the uplink for differentiation between signals sent from different terminals. The more the antennas used, the finer the spatial focusing can be. Low-complexity precoding methods are mandatory and critical to minimize the computational complexity of the precoder [
19].
Unlike the conventional MIMO, massive MIMO uses linear precoders, such as maximum ratio combining (MRC), matched filtering, conjugate beamforming, minimum mean squared error (MMSE) receive combining, and zero-forcing (ZF) [
4].
2.1. Pilot Transmission
When a signal propagates from the transmitter to the receiver, it experiences the effect of shadowing, scattering, fading, and path loss. Knowing the CSI in both forward and reverse links is crucial for accomplishing successful transmission under various channel conditions. Training sequences are often designed to optimize an equalizer at the receiver by providing CSI. In massive MIMO systems, the pilot sequence is used to estimate the CSI in both directions. For downlink transmission, the pilot sequences’ sample period should be longer than the number of transmitting BS antennas. For uplink transmission, the pilot sequence sample period should be longer than the number of users (K), so that the BS would learn the uplink channel matrix.
Pilot contamination is a crucial problem in massive MIMO, which is caused by non-orthogonality of pilot sequences used in adjacent cells. Usually, reusing pilots in multiple cells is the main cause of the problem. In this case, the estimated channel vector in any cell is the summation of all the channel vectors of users from the neighboring cells (in addition to the original cell). As the number of interfering cells increase, the problem exponentially grows and eventually causes system malfunction.
Various solutions were introduced to solve this problem, which are:
Channel Estimation Methods: These are based on some channel estimation algorithm to detect the CSI by picking up the strongest channel impulse responses, often done with less number of pilots than users.
Time-Shifted Pilot Based Methods: These are based on insertion of shifted pilot locations in slots (or a shifted frame structure).
Optimum Pilot Reuse Factor Methods: These are based on choosing a reuse factor greater than unity optimized in some sense. In addition, please note there are significant performance gaps that exist among different reuse patterns.
Pilot Sequence Hopping Methods: These schemes switch users randomly to a new pilot between time slots, which provides randomization in the pilot contamination.
Cooperative Methods: Here, each BS tries to find unique optimum pilots that are also suitable for other BSs.
Cell Sectoring based Pilot Assignment: These schemes are based on sectioning the cells into a center and edge regions. Users in neighboring border areas partly reuse sounding sequences. This improves the quality of service by reducing the number of serviced users. However, by significantly reducing serviceable users, it degrades the system capacity.
Angle of Arrival (AOA) based methods: Use the fact that non-overlapping user terminals reusing the pilots would have different AOA. However, this needs a way to detect AOA such as directional antennas.
2.2. Encoding Techniques
MIMO encoding is all about converting data into symbols appropriate for transmission over multiple transmit antennas. Space multiplexing and space-time coding are the commonly used encoding techniques, as they do not require knowledge of the CSI at the transmitter.
Table 3 compares Spatial Multiplexing, Space–Time Coding, and Spatial Modulation. MIMO encoding using known CSI at the transmitter is known as precoding [
5].
2.3. Channel Estimation Methods: (TDD or FDD?)
A non-stationary wireless channel needs to be re-estimated after every coherence time lap. Massive MIMO systems were originally envisioned for time division duplex (TDD) operation, in which the channel is periodically estimated in one direction and compensation can be applied in both directions assuming reciprocity.
TDD systems have the following features:
In TDD systems, multi-user precoding in the downlink and detection in the uplink require CSI knowledge at the BS. The resource, time or frequency needed for channel estimation is proportional to the number of the transmit antennas.
In frequency division duplexing (FDD), uplink and downlink use different frequency bands (different CSI in both links). The uplink channel estimation at the BS is done by letting all users send different pilot sequences. To get the CSI for the downlink channel, the BS transmits pilot symbols to all users. The users respond by the estimated CSI for the downlink channels [
4].
CSI can be estimated at the receiver side only, or at both at the transmitter and the receiver. Estimation at both sides has some advantages. The CSI does not have to be transmitted, which yields low latency and high capacity. In addition, more power can be allocated to the (OFDM) subchannels with higher channel gain. Schemes with estimation at the receiver side only experience higher outage probability with fast fading channels but have lower complexity.
As the number of BS antennas goes up, the time required to transmit the downlink pilot symbols increases. In addition, as the number of BS antennas grows, FDD channel estimation becomes almost impossible and a TDD approach can resolve this issue. In TDD systems, due to channel reciprocity, only CSI for the uplink needs to be estimated. In addition, linear MMSE based channel estimation can provide near-optimal performance with low complexity [
20].
Table 4 compares various channel estimation techniques of massive MIMO systems.
2.4. Detection of Encoded Signals (an Open Area of Research)
We will explain the detection techniques of encoded signals in more detail. In addition,
Table 5 shows the different detection techniques in MIMO systems.
Signal detection implies accurate estimation of the transmit vector knowing the received vector and (sometimes) the channel. Detection of MIMO encoded signals is very demanding and probably the most important task, since the received signal is subjected to noise, fading, shadowing as well as spatial interference. Advanced signal processing methods are required for accurate detection. Since the elements of the transmitted vector belong to a predefined discrete alphabet, detection is harder when the alphabet is bigger. Some detection algorithms produce soft values of the estimate of the transmitted symbols while the others produce hard values [
5]. The estimated soft values are fed into the channel decoders in coded systems. Hard outputs like search-based algorithms test a set of discrete valued vectors and then choose the best one among them as the output. In general, the soft fed values give a better performance compared to hard inputs. The general trend has been to consider optimization algorithms and artificial intelligence to achieve superior detection performance.
Detection can be done using linear or nonlinear algorithms. Linear detection generally generates soft estimates of the transmitted vectors [
5]. Linear detection has less complexity but yields lower performance and limited spectral efficiency. The performance of linear detectors deteriorates rapidly as the number of transmitting antennas increases.
Lattice Reduction (LR) based linear detection has better performance than ordinary linear detection. However, instead of applying the linear transformation to the received signal model, they apply it to an equivalent system model obtained using LR-techniques. The new channel matrix is more orthogonal than the old one. Slicing is done on the data vector instead of the transmitted vector.
Interference cancelation detectors are nonlinear, which perform estimation and removal of interference in multiple stages. Popular schemes are successive and parallel interference cancelation detectors.
There are optimal detectors such as Maximum Likelihood Detectors. Local search detectors also seek for optimal solution. However, these methods have an issue of huge problem size, as well as the lack of knowledge of the problem structure. The good thing about local search is its neighborhood function that guides the search to a right solution. Another popular technique is the polynomial time approximation algorithm, but it gives an inferior solution.
Tabu search is a mathematical optimization method that is used to solve combinatorial optimization problems. It is effective when the problem size gets very large. It has the ability of quickly find near-optimal solutions [
5].
Low-complexity MIMO uses detection based on probabilistic data association. Remote sensing applications have been using this detection method for target tracking for some time. Since signals coming from the targets are weak, the detection threshold is lower. However, this leads to detection of additional unwanted signals and noise. Data association means to specify which measurements are the most suitable to be used in tracking filters. This technique’s principal aim is to track targets where there is uncertainty in their data association [
5].
2.5. Beamforming
Beamforming is a technique that enables focusing the signal from multiple antennas into one strong beam, minimizing energy in side lobes at the transmitter end. At the receiver, beamforming refers to a kind of spatial multiplexing that combines the received signals to add up in a certain direction, and rejecting the signals coming from any other direction, and considering them as interference. The direction control of the signal is done by adjusting the weights of the signal phase amplitudes of multiple antennas. Beamforming techniques are categorized into:
Fixed beamformers that employ fixed weights and phases to combine the signals without considering the properties of the received signals.
Adaptive beamformers that may steer the direction of the main lobe in the desired direction, adaptively minimizing interference.
Table 6 describes the different beamforming techniques recently discussed in the literature for multiple user MIMO.
MIMO Beamforming Configurations can be categorized into:
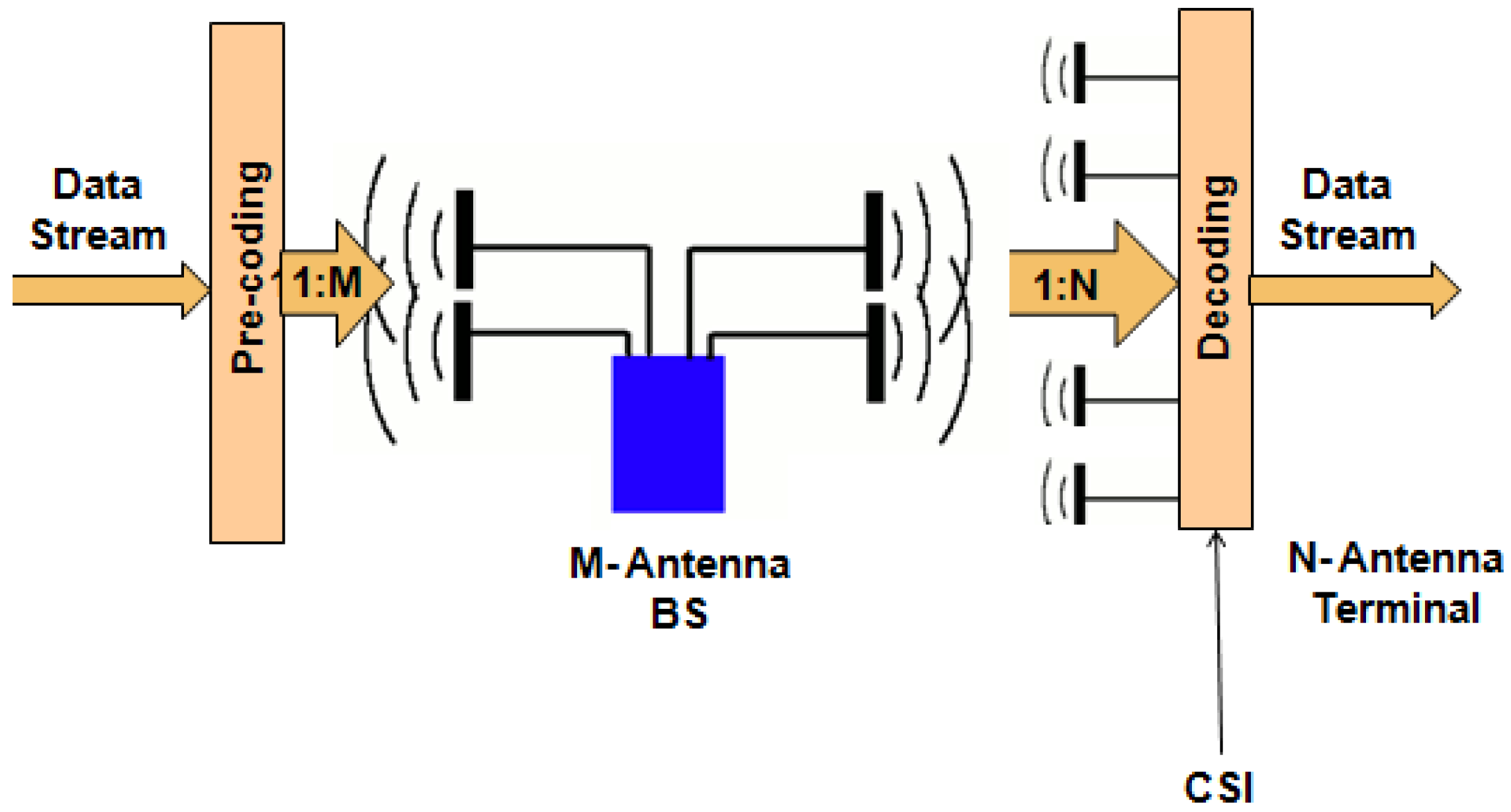
Figure 4 shows a PTP MIMO system. The BS has
M antennas, and it transmits data (a vector-valued signal) to a user having
K antennas. This transmitted vector is multiplied by the channel matrix to produce the received signal vector. Different users are served over different time/frequency blocks by time division/frequency division multiplexing.
An extensive discussion on PTP MIMO is presented in the following papers:
The authors in [
136] studied Array Beamforming Synthesis and related areas. The existing beamforming techniques for PTP MIMO lack providing efficient beamformers especially in certain situations such as under different power constraints or array sizes, certain types of channels, and with random initializations. To solve this problem, they proposed an iterative algorithm that specifies transmit and receive beamformers based on various channel information available to the transmitter and the receiver.
In [
137], the authors introduced an optimum linear precoder imposed on both sum-power and maximum eigenvalue power. In [
138], the authors discussed the most spectral-efficient power allocation strategy and specified whether it is energy efficient or not. The proposed approach in [
139] optimally switches between beamforming and Orthogonal Space–Time Block Coding by varying the periodicity of feedback intervals and varying the amounts of channel state information for mobile users to determine the optimum diversity feedback. The approach in [
140] proposed a new adaptive symbol mapping scheme for PTP MIMO by disordering the transmitted symbols in a frame using dynamic mapping (either by changing the allocation order of the symbols on the antennas or by applying a scrambling process that reverses the symbols sign). The aim of doing this was to increase the symbols’ received power and to reduce the interference between the symbols.
Table 7 compares PTP and MU-MIMO, regarding implementation and precoding complexity, error rate, rate gain and, operation flexibility [
4].
PTP MIMO is not very suitable for massive MIMO due to the following reasons:
Training time is related to the number of antennas and becomes too high as the number of antennas grows.
Independent electronics chains are required for each antenna; hence, as the number of antennas increases, the system becomes very complicated and expensive.
Multiplexing gains fall near the edge of the cell.
Line-of-sight conditions for compact arrays permits only one data stream [
1].
MU-MIMO alleviates some of the pernicious effects of PTP MIMO.
2.6. Precoding Techniques (Linear or Nonlinear?)
It is well known that MIMO effectively utilizes multiple channels between the BS and users by using appropriate (space-time) coding to increase system throughput.
On the other hand, the massive MIMO system works by space division multiplexing by knowing the CSI of every link connecting the BS to a user.
Precoding in massive MIMO systems is essentially a beamforming approach that enables multi-streams transmission. On the other hand, linear decoding techniques aim to accurately detect signal from the desired terminal and mitigate interference from other terminals [
1]. Both linear precoding (or multiplexing) that is employed in the downlink, and linear decoding (or demultiplexing) that is employed in the uplink can approach the Shannon’s limit with substantial number of antennas.
Consider
Table 9, which compares different precoding techniques introduced in literature for massive MIMO networks.
Received signals from different terminals are combined in the uplink using appropriate decoding. The more the antennas are used, the finer the spatial focusing can be so that a large array is built in practice. The use of nonlinear but power efficient RF front-end amplifiers are preferred to minimize power consumption in this high bit rate scenario (Note that energy per bit will decrease in proportion to the square bit rate. Hence, the transmit power has to be very high at Gigabit data rates.) Therefore, to avoid signal distortion at nonlinear amplifiers, often the transmit signal is required to have a low peak-to-average-power-ratio (PAPR), which is difficult to achieve, especially in orthogonal frequency-division multiplexing (OFDM) environments. Several PAPR reduction techniques and precoding can hence be fruitful. Furthermore, precoding with such power-efficient amplifier constraints leads to improvement in the power efficiency of the entire system.
Low-complexity precoding methods are mandatory and critical to minimize the computational complexity of the precoder [
19]. A recent study mentions that single-carrier modulation (SCM) can, in theory, fulfill near-optimal sum rate performance in massive MIMO systems operating at low-transmit-power-to-receiver-noise-power ratios, distinct from the channel power delay profile and with an equalization-free receiver [
141]. In SCM, the PAPR performance is also optimally maintaining a constant envelope.
For conventional MIMO systems, both nonlinear precoding and linear precoding techniques are used without preferences, although nonlinear methods, such as dirty-paper-coding (DPC) and lattice-aided methods, have better performance with higher implementation complexity. Unlike the conventional MIMO, massive MIMO systems use linear precoders, such as maximal ratio combining (MRC), matched filtering, conjugate beamforming, minimum mean squared error (MMSE) and zero-forcing (ZF) [
4].
Table 10 makes a comparison between MRC, MMSE, and ZF precoding techniques.
In addition,
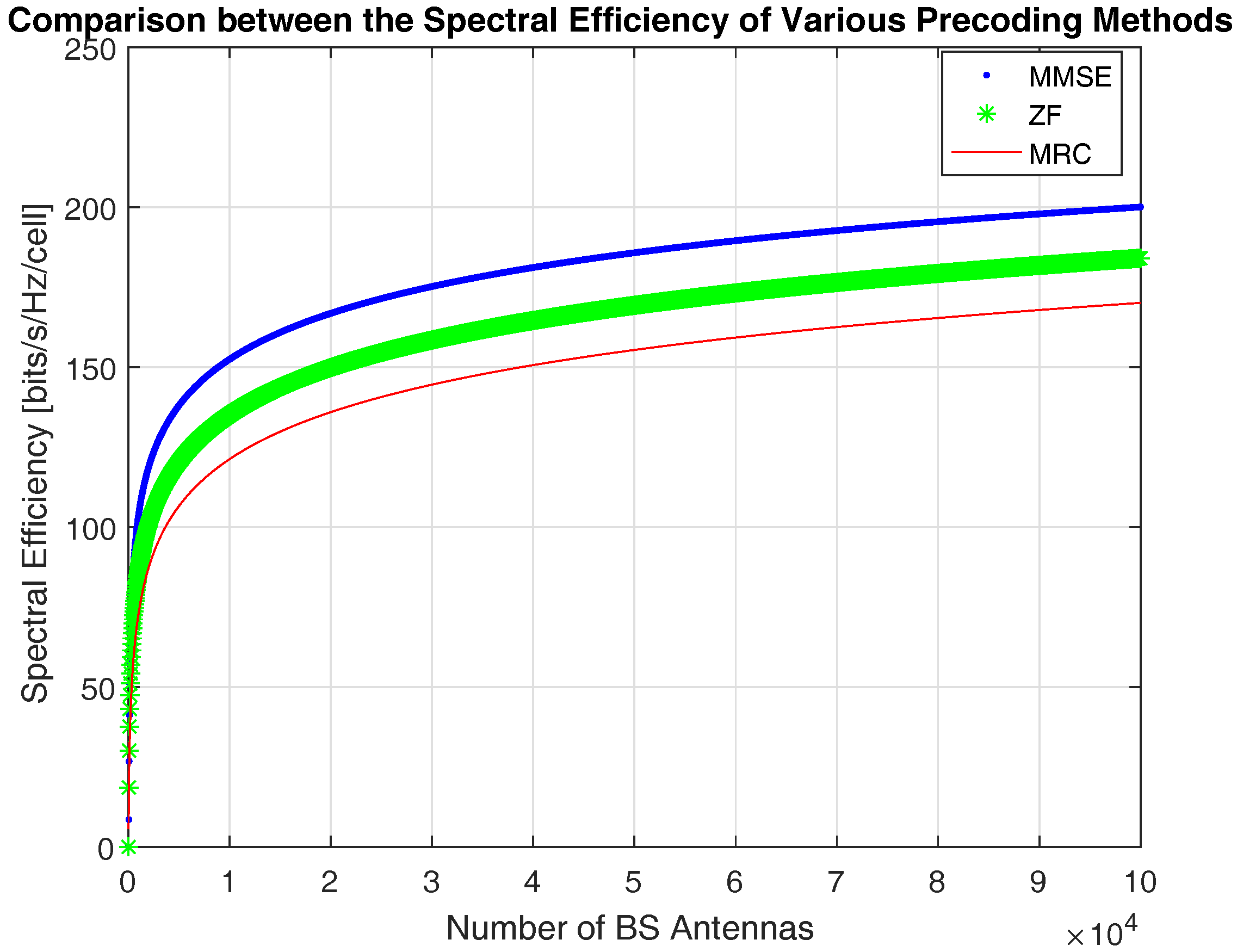
Figure 5 shows a comparison between MMSE, ZF, and MRC precoding techniques vs. the number of BS antennas.
In MRC, the multiple antenna transmitter uses the channel estimate of a terminal to maximize the strength of that terminal’s signal by adding the signal components coherently. MRC precoding maximizes the SNR and works well in the massive MIMO system, since the base station radiates low signal power to the users on average.
ZF precoding is a method of spatial signal processing by which the transmitter can null out multiuser interference signals. In general, ZF precoder performs well under high SNR conditions.
The ZF precoder outperforms MRC, as shown in
Figure 5 in performance as well as in computational complexity. It also suppresses inter-cell interference at the cost of reducing the array gain [
6]. It is noted that spectral efficiency increases as the number of BS antennas grows. In addition, the figure shows the superiority of the performance of MMSE, especially in massive MIMO.
MMSE precoding is the optimal linear precoding in a massive MIMO downlink system. This technique uses the mean square error (MSE). The Lagrangian technique is used to optimize this precoder, using the average power of each transmitting antenna as the constraint.
Advantages of MMSE are [
163]:
Its combining receiver creates one scalar channel per terminal, thus balancing between amplifying the signals and suppressing the interference.
The remaining interference is treated as extra additive noise; thus, conventional single-user detection algorithms can be applied.
Performance improves by adding more BS antennas.
Small-scale fading averages out over the array.
Other widely used linear precoding and decoding schemes are matched filtering (MF) and conjugate beamforming (CB). Advantages of these techniques are:
There are new precoding techniques introduced in the literature for millimeter-wave massive MIMO. In [
165], the authors proposed a hybrid precoding scheme combining both analog and digital precoding to overcome the high signal attenuation that happens at mmWave frequencies using a non-complex sub array. This work reiterated the benefit of hybrid analog/digital precoding work that optimizes the achievable capacity of each antenna array by employing the concept of consecutive interference cancellation.
3. Multi-Tier Networks Very Promising for the Next Century?
All the systems that we have described in the previous sections were about homogeneous MIMO cellular networks, where the system has a single network, with a number of BSs—either cooperating or non-cooperating to serve a number of simultaneous homogeneous users. Typically, in those systems, the BSs were identical in terms of average transmit power per unit area, access techniques, number of antennas, modulation and estimation schemes.
The new trend in wireless communications to meet the growing demand is the introduction of low power nodes (Femto-cell, Pico-cells, Wi-Fi access points, distributed antennas, etc.) with heterogeneous users. In these MIMO heterogeneous networks (HetNets), where there are multiple tiers working together at the same time, the capacity increases tremendously.
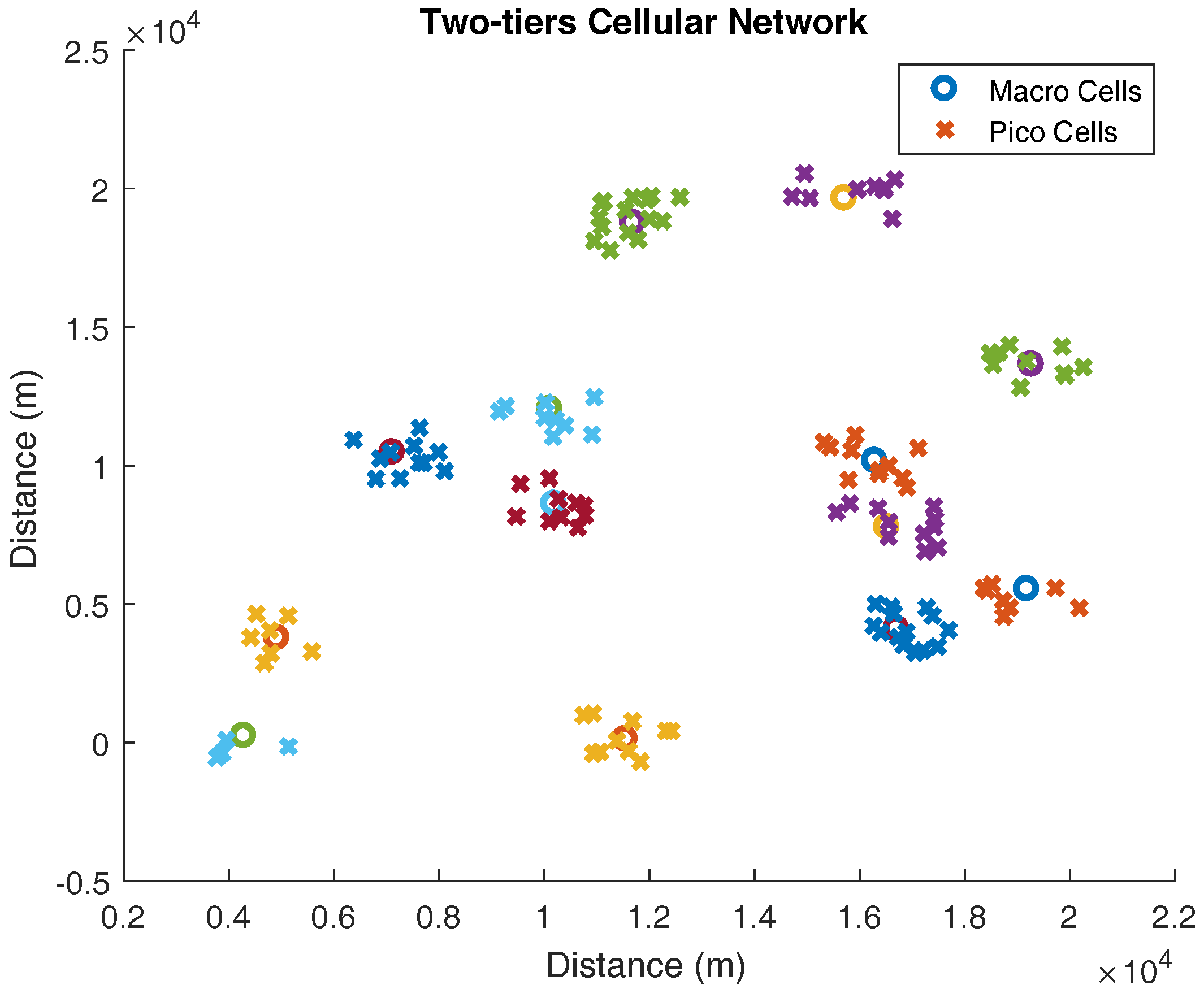
Figure 6 shows a Poisson point process (PPP)-based two-tier cellular network with a 20 km × 20 km area, consisting of femto-cells (crosses) and macrocells (dots). With the aid of stochastic geometry, the BS locations in each tier were modeled using a dependent or independent PPP to distribute the BSs randomly in different locations. The users associated with those BSs were modeled using a dependent PPP (using a parent–child relationship).
HetNets can either be open access or closed access. In open access HetNets, the users can work under any BS in any tier, whereas in closed access networks, the user has limited access to certain tiers only, or has access to only the BSs in its own tier.
Table 11 highlights the differences between homogeneous and heterogeneous networks.
Authors in [
166] modeled the MIMO HetNets in a fixed cell size (allocation of users to BSs is based on fixed distances). Inter-cell and inter-tier interference were considered in this model approximating the interference distribution using a Gamma function. Outage probability and per user capacity (as a function of the distance to the cell center) were studied. Performances of single and multi-tier cases were compared. One limitation of this paper is the assumption of a fixed cell size. In turn, the users are associated with the BSs based on fixed distances, which may not be realistic. In addition, the numerical integrals need to be computed.
Authors of [
167] studied multi antenna HetNets with zero-forcing precoding. They compared the coverage probability and rate per user for both open access (where users are allowed to access any BS in any tier) and closed access networks (where users are granted access to certain BSs in restricted tiers). The authors used a cell association criterion based on the maximum Signal to Interference Plus Noise Ratio (SINR). In addition, the authors compared the performance with various combinations of multiple antenna techniques. The performance when the BS is serving a single user in each resource block (by SISO or single user beamforming (SU-BF) is compared with MIMO configuration serving multiple blocks (by space division multiple access (SDMA)). However, the approximations need more characterizations. In addition, the numerical integrals need extra computational tools to obtain the results.
In [
168], the authors introduced the fractional frequency reuse (FFR) technique to manage the cross-tier interference (strict FFR and soft frequency reuse). In addition, the authors derived the coverage probability for open-access and closed-access networks (different association policies) and the average rate for the cell edge users. Finally, the authors compared the performance of different FFR and access cases under the full SDMA and SU-BF.
In [
169], the energy efficiency of different MIMO diversity schemes and antenna configurations using adaptive modulation of a two-tier network is studied to ensure a minimum quality of service (QoS). Energy is saved while obtaining the same throughput by using femto-cells with sleeping mode capabilities, where only a few of the available antennas are used. This paper identifies that the diversity schemes that provide the highest throughput is different than the ones that achieve the highest energy efficiency.
Finally, in [
170], the authors derived general and asymptotic success probability expressions for multi-user HetNets with ZF precoding, using a novel Toeplitz matrix representation. In addition, they showed the effect of the BS density on the success probability and derived an optimal BS density for obtaining the maximum area spectral efficiency (ASE) while guaranteeing a certain link reliability. This paper is straightforward with a simple system model. More sophisticated system models should be investigated.
In addition, the advantages of introducing mmWave frequency operation in HetNets is discussed in [
171]. The authors discussed the potentials and challenges of the 5G HetNet wireless networks, which merge mmWave technologies into a massive MIMO approach. First, they discussed the extended requirements for 5G wireless networks with an enormous number of devices that demand more concealment, data rate, better energy and cost efficiency. Then, they discussed the difficulties including traffic arrangement, radio resource management, mobility management, and low-cost beamforming. In the end, they presented some design and case studies to illustrate how to address some of the challenges in 5G MIMO HetNet.
4. Conclusions
Massive MIMO is an innovative technology that helps in the achievement of higher system throughput and reliable transmission for 5G and beyond wireless networks.
In this paper, we discussed major elements of massive MIMO networks, namely pilot usage, precoding, encoding, detection, and beamforming. We provided a detailed overview of some of the research efforts done in this area so far. We observe that fast booming HetNets would be more promising to improve data rates and provide flexibility in user-BS association.
There are many interconnected design issues that need to be properly understood and solved before widespread deployment of the massive MIMO technology. Several open research challenges are still facing the progress and development of this emerging technology.
More research is needed to introduce new adaptive beamforming techniques to achieve higher received symbol power and less interference. In addition, introducing efficient beamformers for PTP networks to work under different constraints and with different types of channels would be beneficial for enabling PTP widespread application in massive MIMO systems.
As detection becomes harder when the number of BS antennas increases, more advanced signal processing methods are required for better detection and are associated with introducing low complexity optimum and nonlinear detectors, and precoders to improve the performance and reduce the computational complexity.
Introducing new techniques to reduce the training time, especially when the number of antennas increases is needed, will, in turn, improve the performance of FDD systems in massive MIMO to improve channel gain, capacity, received power, and reduce latency.
As the number of interfering cells increases, pilot contamination exponentially grows up, and prevents proper system function. Introduced methods to reduce pilot contamination are very limited and aim to reduce the effect of the problem, but do not provide a final solution.
The benefits and issues of using the mmWave frequency band, and its application on beamforming, channel estimation, and precoding techniques in homogeneous and heterogeneous systems, need better research studies. They are thought to increase user bandwidth, reduce form factor, limit inter cell interference, and allow greater frequency reuse.
In WSNs, more research is needed on the optimum low cost, less complex detectors to improve gain, and boosting energy efficiency.
Finally, in HetNets, more traffic management, radio resource management, network planning, and inter-tier interference management are required, as those networks are more complicated, have more dense cells, and any user can access any BS in any tier. In addition, more research efforts should be directed to study various performance metrics in HetNets in the massive MIMO context.