1. Introduction
Space-time adaptive processing (STAP) is a technique used in airborne radar to significantly improve detection performance by suppressing strong clutter returns emanating from stationary scatterers on the Earth’s surface [
1,
2]. STAP dynamically adjusts its response by estimating the null-hypothesis covariance matrix on a coherent processing interval (CPI) basis. The STAP output is
, where
is the STAP weight vector and
is the space-time snapshot whose elements are the voltages collected for
pulses and
spatial channels at range bin
. Specifically,
, where
is an arbitrary scalar,
is the null-hypothesis covariance matrix estimate, and
is the hypothesized target space-time steering vector. A maximum likelihood estimate (MLE) for the unknown, null-hypothesis covariance matrix, described in [
3], follows by averaging training data taken over the range swath within the current CPI,
where
is the training data set. The formulation leading to Equation (1) assumes that each space-time snapshot in the training data set is independent and identically distributed (iid) with respect to the null-hypothesis condition of the cell under test (CUT). The STAP implementation that follows by incorporating the inverse of Equation (1) in the weight calculation is called sample matrix inversion (SMI).
Accurate covariance estimation is critical to successful STAP implementation. When the space-time data are homogeneous, the iid assumption is met and it is seen that the SMI solution attains, on average, a 3 dB loss in signal-to-interference-plus-noise ratio (SINR) relative to the optimal when approximately
training samples are available [
3]. The solution asymptotically converges to the optimal case as the sample size increases. However, heterogeneous clutter is commonly encountered in airborne radar STAP scenarios, violating the iid condition, thus leading to covariance matrix estimation error and consequent loss in detection performance [
4]. Spatially-varying clutter radar cross section (RCS), manmade objects such as buildings and parked vehicles, inhomogeneous variation in clutter spectral spread due to clutter type and wind pattern, moving vehicles on highways, and shadowing effects resulting from obscuration due to variable terrain height lead to a heterogeneous clutter response [
4]. With the use of high resolution waveforms in modern radar systems, heterogeneous clutter effects are even more pronounced as inconsistencies in terrain type lead to spiky clutter responses (e.g., in mountainous terrain, semi-urban regions, and forested terrain). The compound clutter model is of interest in such cases, and matches the underlying, heterogeneous phenomenology by modulating two distributions [
5]. Of the various cases of compound clutter models, we are interested in the K-distribution model, which shows good empirical fit to real data and presents a relatively simple parameterization [
5,
6]. In this paper, the modulating component is represented with a gamma random variable that shapes the envelope of the returns. Specifically, based on the compound clutter model, we have developed the cell-based clutter model (CCM) to simulate K-distributed clutter. The CCM allows us to compare STAP algorithm performance in spiky, heterogeneous environments.
Previous studies have assessed theoretical limits of STAP in K-distributed clutter [
7,
8], demonstrating the deficiencies of standard algorithms. Several detectors have been proposed to combat K-distributed clutter, including general log-likelihood ratio tests [
9,
10]. However, these algorithms presume that the background clutter is perfectly parameterized by the K-distribution, an impractical assumption for real data. In this paper, we demonstrate the efficacy of knowledge-aided parametric covariance estimation (KAPE) [
11,
12] in estimating covariance matrices of K-distributed clutter generated with the CCM. Rather than estimate the
-by-
covariance matrix and deal with complications due to clutter heterogeneity, KAPE efficiently estimates a few parameters of a physics-based covariance model while depending on a priori knowledge, including platform and radar state vectors provided by the aircraft navigation system. By tailoring KAPE to estimate complex clutter gains over angle solely using the CUT, the processor is able to adapt to spiky clutter returns and improve detection rates over traditional STAP implementation.
The remainder of the paper is organized as follows. In
Section 2, we propose the CCM based on the compound clutter model essential to assess STAP performance in heterogeneous, spiky clutter environments.
Section 3 describes KAPE and its application to spiky clutter. Numerical analysis characterizing the impact of spiky clutter on traditional STAP implementation and the benefits of KAPE in such circumstances is given in
Section 4; as a reference, we include a comparison to STAP in homogenous clutter environments. We provide a summary in
Section 5.
2. Spiky Clutter Model
The K-distribution is a special case of compound clutter models that assume clutter returns are products of two independent random variables: the slow varying and fast varying components [
5,
6,
7]. For our purposes, a non-Gaussian random texture, chosen to be gamma distributed, modulates a Gaussian variate (Rayleigh complex envelope) representing random scattering from a rough surface. This model captures spiky, spatially-varying RCS variation via the non-Gaussian term. The proposed compound probability density model, used herein, is then given as
where
is the Rayleigh probability density function,
and
is the gamma density function,
with shape and scale parameters
and
, respectively.
is the gamma function. For modeling purposes, we introduce the gamma ratio,
, to describe the state of the scene [
4]: smaller values of the ratio simulate spiky clutter scenes, as they correspond to larger standard deviations of the gamma density function, whereas as the variance of the gamma random variable goes to zero, the gamma ratio,
, increases and the scene converges to the homogeneous case.
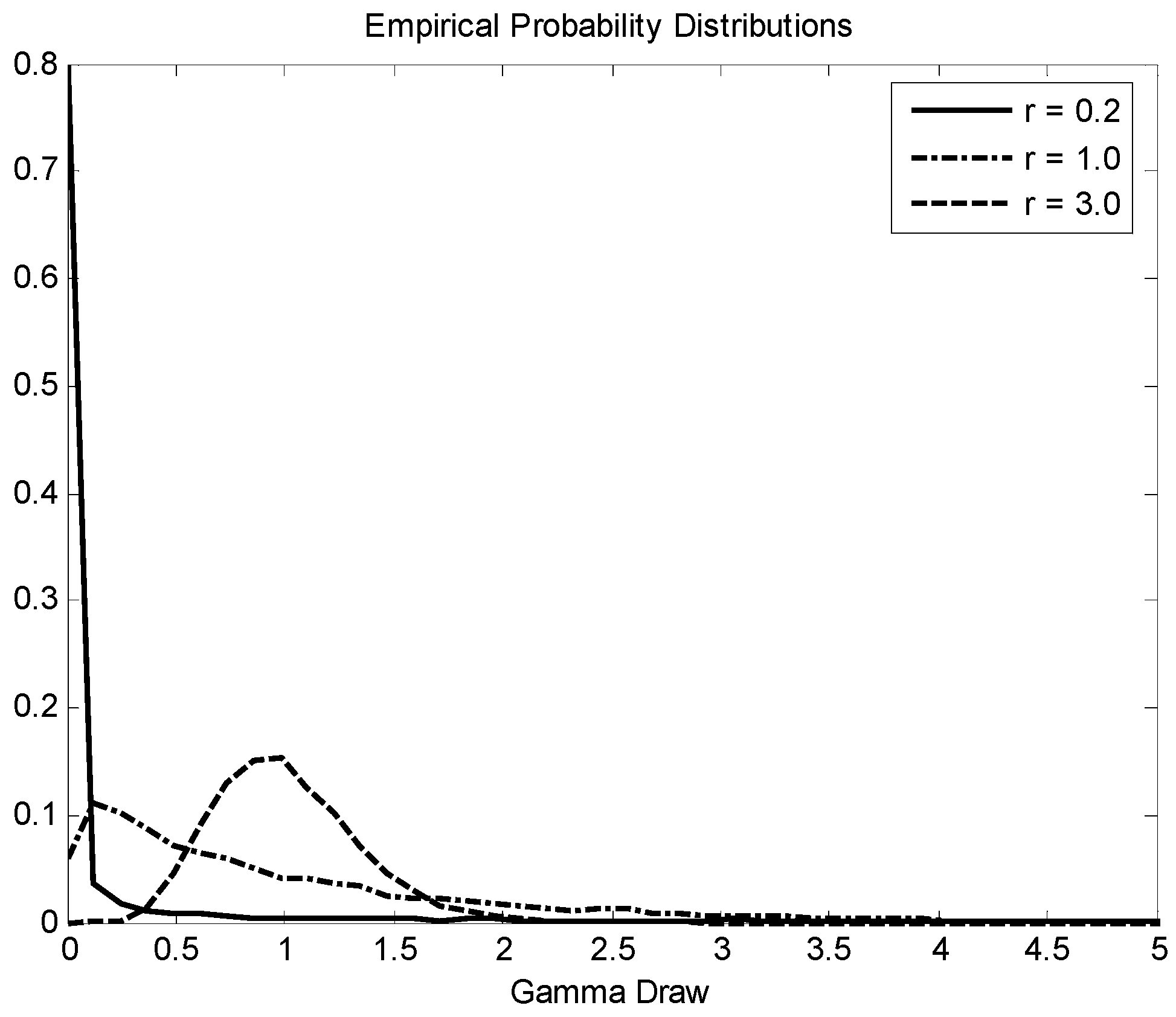
Figure 1 plots several empirically-derived, K-distributed density functions for selected gamma ratio values with the mean fixed at 1. We observe that the distributions trend toward spikier scenes with decreasing
.
To simulate clutter backgrounds of interest, the gamma parameters of the K-distribution model can be estimated with samples of real data. However, such estimates are affected by radar parameters, including the radar resolution and the grazing angle. This implies that a new data set is required if the radar configuration is modified. To avoid this situation, and related complications, we instead propose to directly model the reflectivity for the scene of interest. Upon generating a simulated scene, we have the flexibility of computing the backscatter returns for any desired radar mode. This is the motivation behind the cell-based clutter model, viz., decoupling the simulation dependencies between the spatial scene and the radar system of interest.
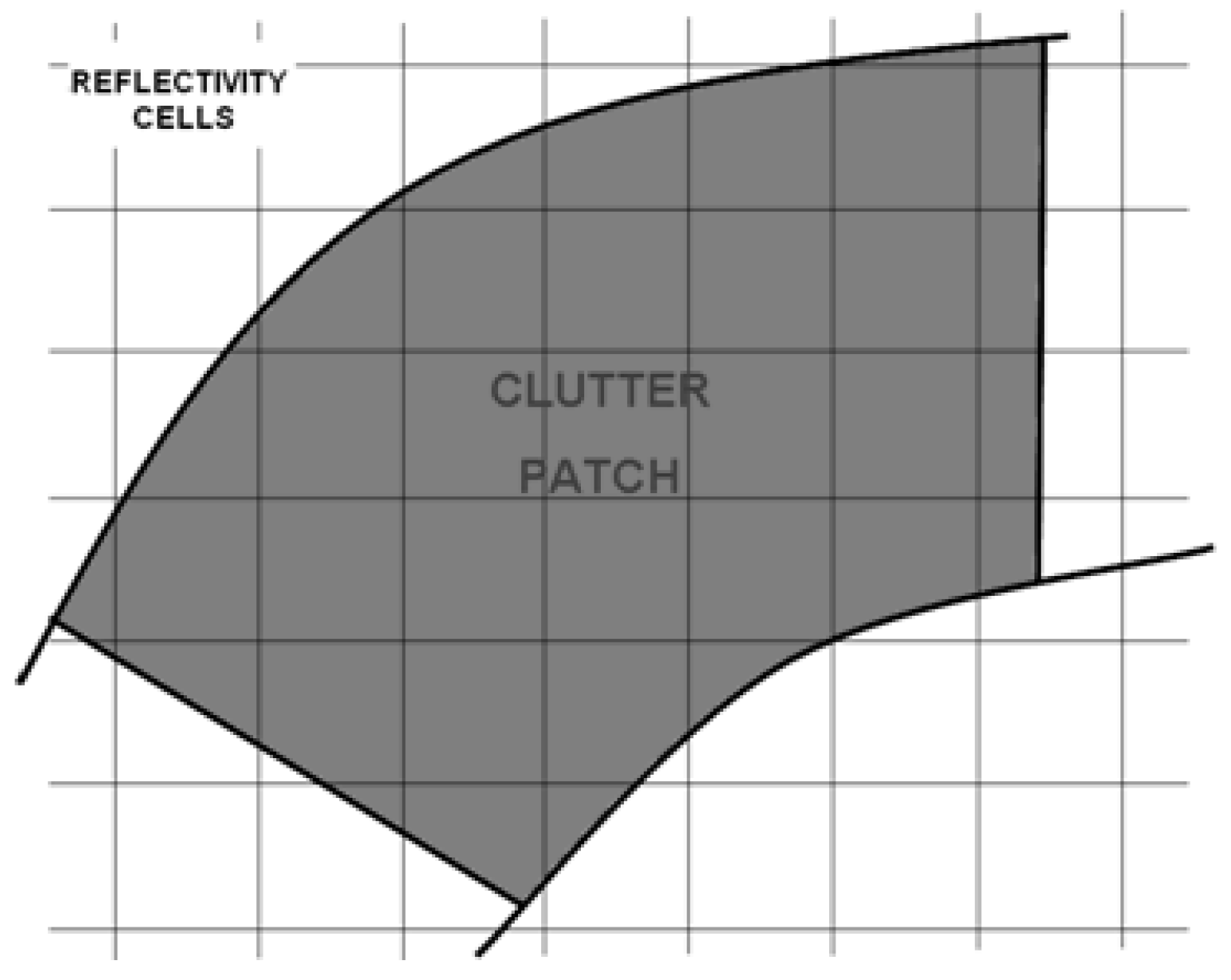
The CCM is based on the concept of modeling clutter reflectivity as the modulation of two independent processes. From Equations (2) and (3), the Rayleigh random variable is generated by taking the magnitude of a zero-mean, unit-variance, complex Gaussian random variable, resulting in a unit-mean, unit-variance process [
13]. Hence, we see that the parameters of the gamma distribution solely determine the statistics of the compound distribution. With this in mind, the CCM divides the scene of interest into cells of sufficiently fine size relative to the high radar range resolution condition, thus being capable of delineating disparate clutter regions. A new simulation is initiated by assigning each cell a reflectivity drawn from the gamma distribution with a gamma ratio that aptly describes the clutter roughness. The radar voltage return at range
is approximated as the sum of the contributions from
clutter patches that divide the iso-range ring,
where
and
are the complex voltage and space-time steering vector of the
clutter patch, respectively [
1,
2]. The gamma-drawn patch reflectivity,
, corresponding to the
patch is refined by averaging the intersecting scene cells as illustrated in
Figure 2. The RCS per area is determined by adapting the constant gamma model,
where
is the grazing angle [
14]. The
complex gain is then calculated as
In this instance, , is the area of the clutter patch, and is a normalized beamformer voltage gain factor incorporating the remaining elements of the radar range equation.
The sum of independent gamma random variables with a common scale parameter is also gamma distributed [
13]. This is precisely the case with the CCM. The CCM can also generate homogeneous clutter by assigning a constant value,
, to each cell, implying that all patch reflectivity values,
,
,…,
, will be equivalent. Referring to Equations (2) and (3) for a compound distribution, this reduces the model to a modulation multiplication between a Rayleigh distribution and a constant. The resulting distribution is a scaled Rayleigh, which describes a homogeneous scene.
One immediate advantage of the CCM is that the scene parameters, i.e., the gamma distribution parameters, need only to be generated once. This grants the flexibility to simulate returns from multiple radar systems, e.g., systems of varying range resolutions, aircraft velocities, and array configurations. The scene parameters may be estimated a priori from an existing data base, supporting knowledge-aided techniques. The cell sizes can be set based on terrain variation. Moreover, we find the returns from the CCM agree with expectation, given the radar configuration. In low-resolution radar systems, each clutter patch will intersect with many cells of the cell-map. By the central limit theorem, the average of many identically distributed and independently drawn gamma random variables will converge to a Gaussian random variable. This resembles homogeneous clutter, which is what has been observed for such systems [
1,
2]. Conversely, high-resolution radar generates smaller clutter patches, and hence intersects with less cells. As a result, the received distribution maintains the spikiness of the original scene [
5,
7].
3. Knowledge-Aided Parametric Covariance Matrix Estimation (KAPE)
STAP is an important element of airborne radar systems. It cancels ground clutter returns by adapting the space-time filter response to null along the clutter ridge coupled in angle and Doppler [
1,
2]. Successful STAP application hinges on accurate estimates of clutter-plus-noise covariance matrices. The dominant approach for covariance estimation is given by the calculation in Equation (1). This approach converges to the average behavior of space-time data composing the training set, falling short of yielding effective performance when heterogeneous clutter is present [
4]. SMI STAP cannot provide the instantaneous response required to adapt to spiky clutter returns. If not properly accounted, spiky clutter simultaneously increases false alarm occurrences while masking targets. Unfortunately, this type of spiky heterogeneity is evidenced in practical radar operating scenarios.
The KAPE algorithm is a parametric approach that addresses the shortcomings of the SMI method [
11,
12]. KAPE is able to adapt solely using information from the CUT, which is effective against clutter discretes and targets in secondary data (TSD) [
11]. We will show that it is also effective in spiky, K-distributed clutter.
KAPE models the clutter ridge of the scene of interest by dividing the iso-range ring into
patches, where each patch represents a constant azimuth interval. Let
denote the ideal,
NM-dimensional space-time steering vector corresponding to the
patch. The precise space-time steering vector for the
patch is
, where
is an
N-by-one vector of ones,
are the antenna channel errors relative to the ideal condition,
denotes the Hadamard product, and
is the Kronecker product. KAPE utilizes information on the array manifold to account for deviations in the spatial steering vectors due to tilting and other hardware errors. These adjustments are given by the estimated error vector,
, giving the calibrated space-time steering vectors,
In the absence of clutter spread, and by assuming negligible contributions from range ambiguities, the return of the CUT can be represented as
The complex gains for each resolvable clutter patch are given as
,
,…,
; KAPE estimates unknown parameters directly from the space-time data as given in [
11,
12]. Next, denoting
as the matrix whose columns are the steering vectors in Equation (9), the KAPE clutter covariance matrix follows as
with
This approach parameterizes the initial clutter covariance estimation problem into that of estimating the power gains in the direction of the modeled steering vectors. (In [
11,
12], we consider the challenges of compensating array errors, clutter spectral spread, and array pointing.) An effective method to estimate the magnitude-squared of the gains,
,
,…,
, involves exploiting the redundancies of the pulse returns for a given range bin. Let
be the received spatial data corresponding to the
range bin and
pulse return and
be the corrected spatial steering vector corresponding to the
patch. Then the power of the
clutter patch is estimated as
which averages over the pulses of the CUT. Multiple range bins may be used to improve the estimation, provided that they are statistically consistent. Other methods, such as pseudo-matrix inversions, have been explored, but resulted in inferior estimates.
KAPE adapts to spurious spikes in heterogeneous clutter by estimating parameters of the clutter covariance matrix model using a single range bin, namely the CUT. Conversely, the SMI covariance matrix estimate is an average of the clutter statistics within the range swath. Consequently, clutter spikes are under-nulled, leading to an increase in false alarms.
4. Numerical Analysis
Using the CCM, we analyze SMI STAP and KAPE in heterogeneous, spiky, K-distributed clutter. SMI represents the traditional approach to STAP implementation. The main performance metric is the receiver-operating characteristic (ROC), a plot detailing the achievable probability of detection,
, given an achievable probability of false alarm,
. We test each Doppler bin to within the radar’s minimum detectable velocity (MDV), which is set to −15 dB SINR loss for the simulations [
15]. We seed 0 dB Swerling 1 targets into the data [
16]. The detection statistic is calculated by applying the Extended Factored Algorithm (EFA) for dimension-reduction [
1,
2,
17], followed by an adaptive matched filter (AMF) normalization [
18]. Dimension reduction can be applied directly within the KAPE model by using an appropriate linear transformation [
12]. The false alarms are calculated by tallying the number of samples exceeding the fixed thresholds applied to the clutter-plus-noise-only data. Similarly, detection probabilities are calculated using thresholds applied to the clutter-plus-noise-plus-target data.
To simulate heterogeneous clutter, we incorporate the CCM with a gamma ratio of 0.1 into the well-known and commonly used space-time clutter model given in [
2] and described by Equation (5). As demonstrated in
Figure 1, this corresponds to a large variance, and hence spiky data. The radar system is a sidelooking uniform linear array (ULA) with
pulses per CPI and
element-level channels [
2].
Table 1 lists other key radar parameters for the simulation. Note that we only have access to
samples for covariance matrix estimation, where
is the number of adaptively combined Doppler filters used in the EFA implementation
; this training size is much less than the
samples needed in the full space-time case. The limited range swath size was selected to better match realistic scenarios since large spans of approximately homogeneous data are not typically available.
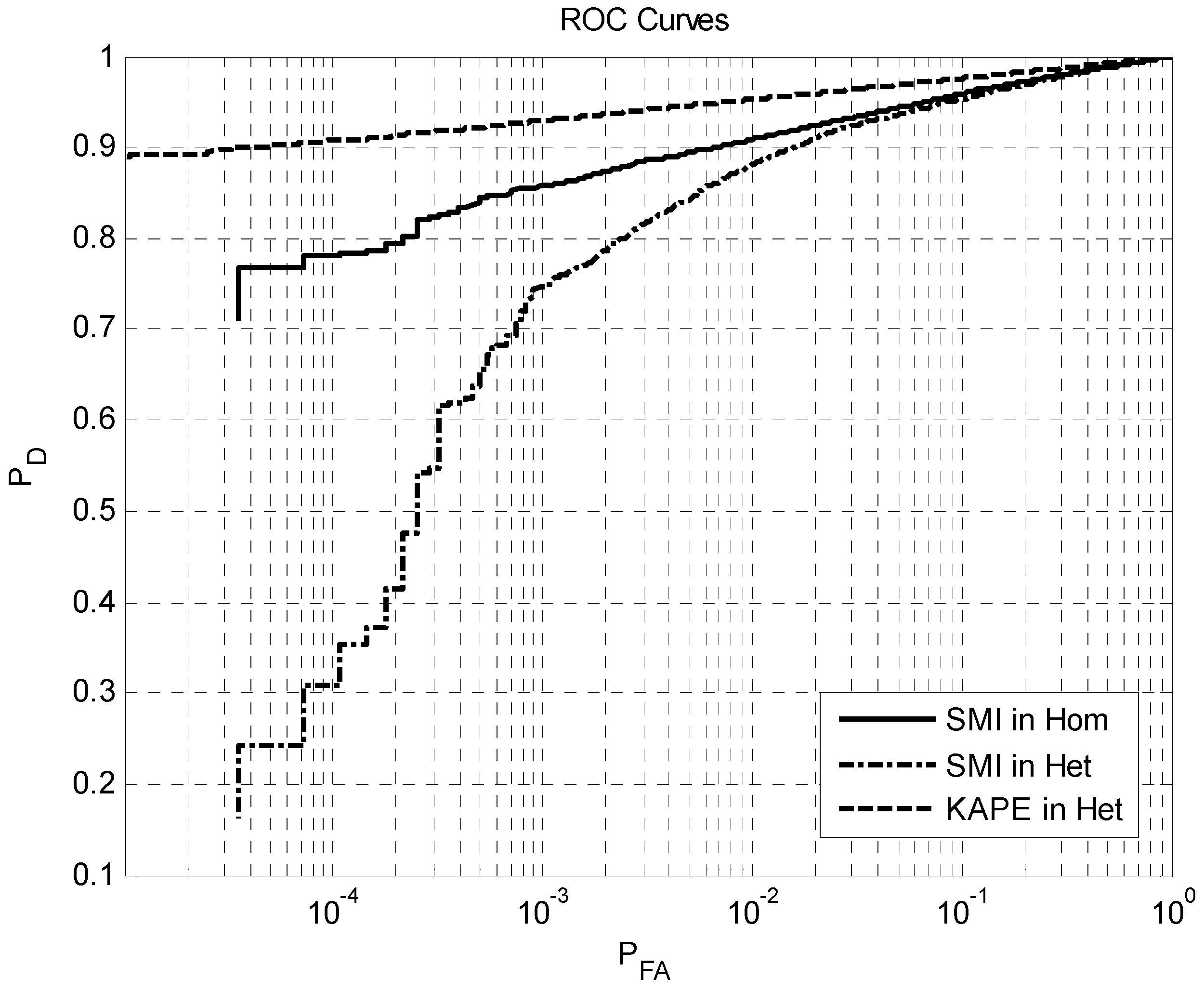
Figure 3 compares the ROC curves for simulations corresponding to several implementation cases of interest: SMI STAP and KAPE applied to spiky, K-distributed, heterogeneous clutter data; and, SMI STAP applied to homogeneous clutter, generated using the same simulation model with very high gamma ratio, to show the deleterious impact of spiky clutter on SMI STAP and the effectiveness of KAPE. The solid line demonstrates that the SMI STAP using EFA performs well in homogeneous (“Hom”) clutter. For example, we approximately attain a
of 0.84 at a
of
. However, the dash–dot curve illustrates severe degradation for SMI STAP in the presence of spiky, heterogeneous (“Het”) clutter. Performance loss results from spiky clutter residue as a result of insufficiently deep adaptive nulls due to covariance matrix estimation error. For a
of
,
diminishes to approximately 0.64, which is unacceptable in practice. KAPE performance in spiky heterogeneous clutter, shown by the dashed line, substantially exceeds SMI STAP performance for operation in both heterogeneous and homogeneous clutter; e.g., at a
of
, the KAPE
is roughly 0.92.
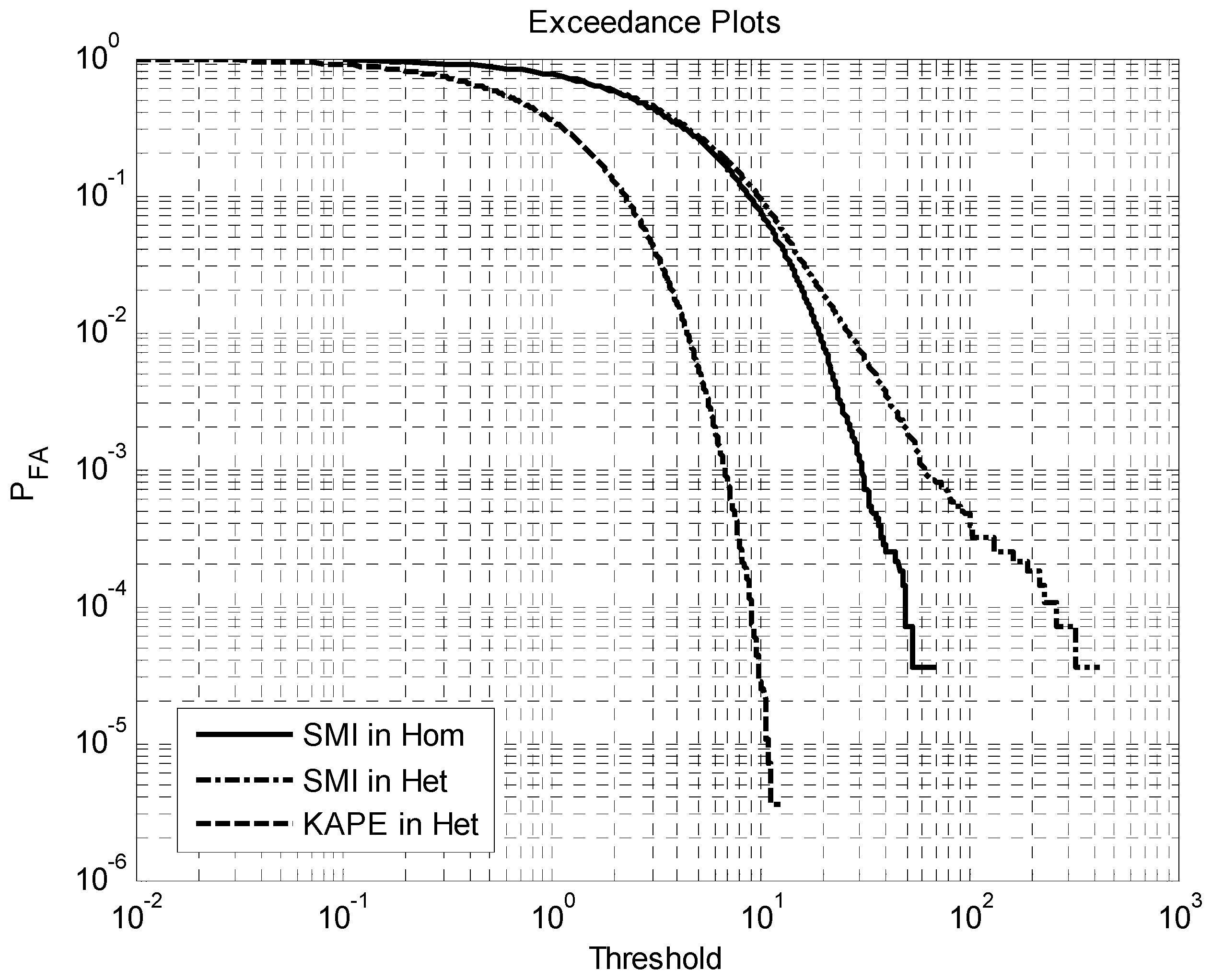
The exceedance plots in
Figure 4—showing
versus threshold—further illustrate the effects of spiky clutter. The heavy tail corresponding to the exceedance of the SMI method in heterogeneous clutter is the result of strong, spiky clutter left unsuppressed by the STAP filter. To mitigate clutter residue, the threshold must be increased at the expense of reduced target detection performance, thus degrading the overall ROC performance of SMI. In contrast, the short exceedance tail obtained using KAPE indicate its ability to generate sufficiently deep nulls by matching the varying clutter power for the CUT. KAPE outperforms SMI in the homogeneous case, as well, because the corresponding model error is less than the SMI covariance matrix estimation error [
3].