1. Introduction
The study of lock-in techniques to detect and measure very small signals, usually buried deeply in high level noise, has been investigated since the late 1940s [
1,
2]. Quite soon it was clear that the method possessed significant potential, irrespective of the frequency range in which it found application. Lock-in amplification is mainly a phase-sensitive detection technique capable of isolating a segment of the signal at a specific reference frequency and phase. Even if this signal is buried in noise sources many times larger, the system cuts down and strongly rejects the noise signals at frequencies other than a reference “locked-in” frequency, so that they do not affect the signal measurement.
For a long time lock-in techniques were strongly based on analog electronics components. Since the advent of powerful digital systems, namely DSP (digital signal processing), 32-bit microprocessors with internal DSP capabilities, ASICs (application specific integrated circuits) and PLDs (programmable logic devices) or field programmable gate arrays, progressively replaced analog models by outperforming them in every aspect, such as the allowable frequency range, the level of input noise and the stability—all of them directly related to the sampling speed of the front-end ADCs—in addition to the available digital computing power.
Many applications have profited from lock-in systems, spanning across very different fields. Some researchers successfully used the method for low-frequency photothermal detecting systems [
3] where multiple demodulating channels, implemented within a unique FPGA, allowed compact, yet simultaneous, analysis of the signal of interest with multiple different frequencies. Another interesting study has been carried out for portable pulse-oximeter applications [
4] where a single CMOS chip was designed with an integrated LIA in order to reach very low power consumption.
Advantages of FPGA based LIA systems were also investigated in [
5], where emphasis was given to their compactness and low-cost implementation caused by the FPGA’s flexibility in fulfilling more than a single digital task at the same time.
Within the e-health field, remarkable importance has been given to brain studies and recent investigations on neurology and brain–computer interfaces (BCI) have proved the benefits of functional near-infrared spectroscopy (fNIRS) acquisition systems, especially when combined with simultaneous EEG, for better understanding the spectroscopy results. Various commercial products and research prototypes have been proposed in the literature so far [
6,
7,
8,
9,
10] and this work also aims to contribute to this interesting research subject. In particular, the system in [
10] is based on double-wavelength LEDs injecting infrared light into the scalp and recovering back the light, partially diffused and partially scattered, from the same surface but at a few centimeters away from the optical source, using a lock-in technique. At a proper source-detector distance, usually ranging between 2 cm and 3 cm, it is possible to detect brain activities related to suitable stimuli, in the form of oxygenation variations. Of course higher number of source-detector couples (called fNIRS channels) lead to better volume resolution on the whole head, eventually ending up with a complete brain oxygenation mapping capability.
Since the human scalp presents quite high attenuation values in the infrared region and it is not possible to increase the amount of impinging light for safety reasons, the choice of very sensitive detectors, capable of fully reaching single photon counting performance, is of great importance. Silicon photomultipliers (SiPM) have been then adopted since they fulfill these stringent requirements [
11,
12,
13,
14] and the rest of this paper will describe the system architecture that has been realized and the experimental results that evaluate the obtained performances in terms of fidelity on the detecting action and the related computational loads.
The main goal of this work is to explore the possibilities of a digital implementation of LIA systems to improve fNIRS system performance and to evaluate its impact on the final signal detection and noise rejection capability.
Moreover, are the secondary goals, such as the exploitation of FPGA flexibility by investigating the overall latitude of the method, with particular emphasis on playing with the LIA digital filter parameters; and to predict the possibility to implement, for a limited number of channels, these algorithms on a general-purpose microcontroller.
2. System Architecture
In order to reach the described goals, a system able to accomplish the desired tasks and to assure rapid prototyping has been designed, capable of leaving the highest possible freedom degrees for further investigations and optimization of performances based on parameter elaboration.
The implementation of the lock-in amplifier used is the well-known dual-phase LIA [
5]. It takes the input signal, modulated at a predefined and fixed frequency, and multiplies it by generated sine and cosine reference signals, running at the same frequency of the modulated signal. The outputs are low-pass filtered with a properly-designed digital filter in order to reject noise and unwanted frequency components. The obtained filtered signals from each branch represent the convolutions of the input signal and the sine and cosine reference signals. In order to find the channel output amplitude, these convolutions are then squared and summed together, and finally the square root is calculated. Signal phase is, meanwhile, neglected because it is not adding significant information in our investigations.
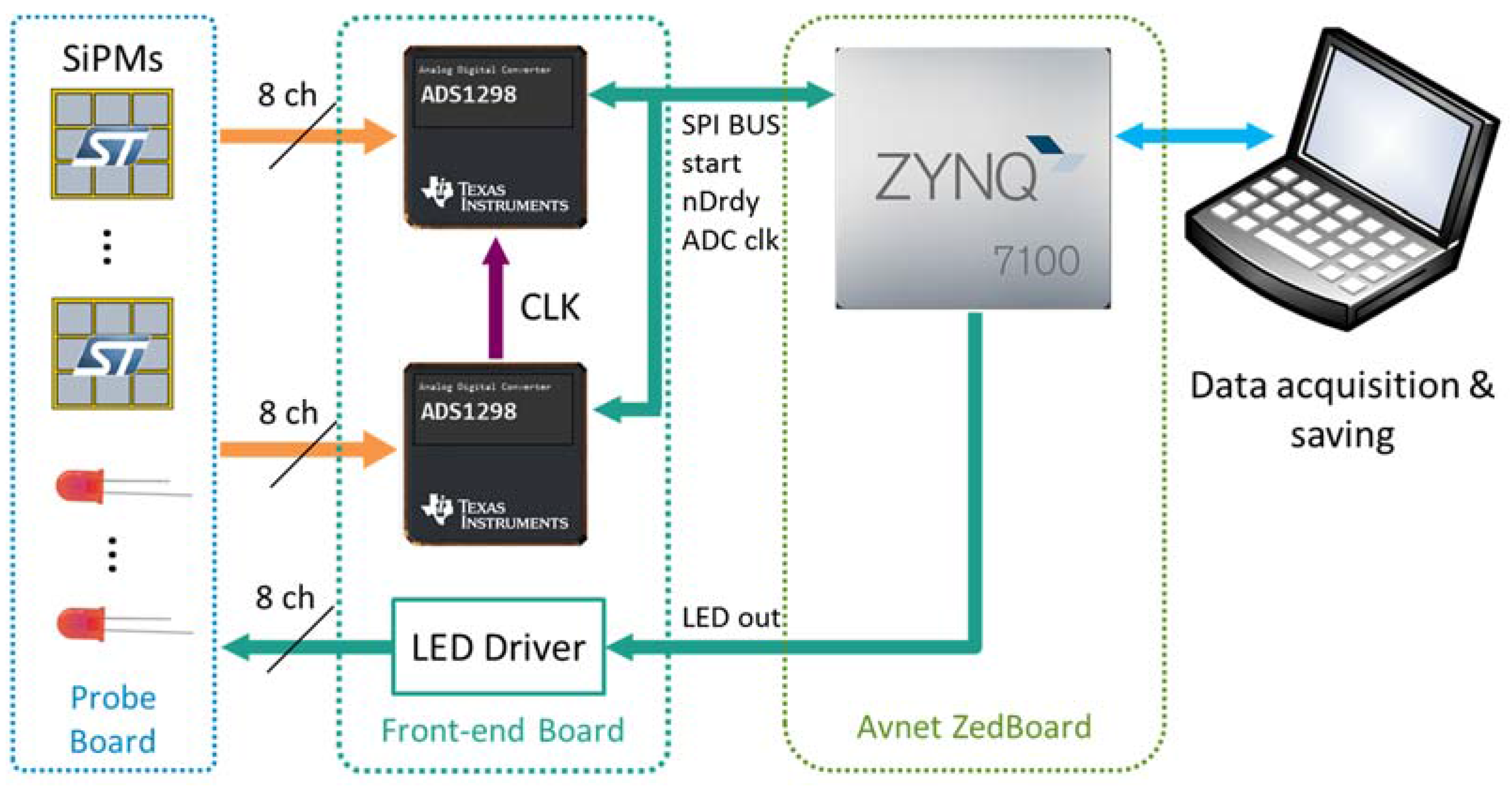
Thus, as depicted in
Figure 1, a system consisting of a probe board, a front end board, an FPGA board that in our case is a ZedBoard™ by Avnet (Phoenix, Arizona, USA), and a PC for programming, data retrieval, and tests has been designed.
2.1. Probe Board
The probe board contains 16 silicon photomultipliers (SiPMs) and four dual-wavelength LEDs (850 and 735 nm). It is implemented on a flexible PCB (made of Kapton™), capable of being easily adapted, as in typical fNIRS application of brain oxygenation monitoring, to the different shapes of the subject under test. A deeper description of these probe boards can be found in [
11].
2.2. Front-End Board
The front-end board is responsible for analog to digital data conversion and uses two ADS1298 analog-digital converters (ADCs), connected in a daisy-chain in order to acquire a total of 16 output signals coming from the probe board. The ADS1298 is a low power analog front-end (AFE) optimized for medical instrumentation systems, manufactured by Texas Instruments (Dallas, Texas, USA) [
15]. It performs a true simultaneous sampling of eight channels with 24-bit delta-sigma (ΔΣ) ADCs, each containing a built-in programmable gain amplifier (PGAs). It can operate, in free run, with data rate capabilities ranging from 250 SPS up to 32 kSPS; even at the fastest 16–32 kSPS sampling speed, resolution is limited to 16 bits. These devices can be cascaded in a daisy-chain configuration; thus, by sharing the same reference clock and using an external start pulse, it is possible to run potentially very large numbers of simultaneous channels. Within the presented work, our system was limited only to 16 channels, but it can be easily upgraded to 128 channels by simply cascading eight front-end boards.
In addition, the front-end board also have some suitable circuitry needed to drive LEDs, as visible in
Figure 1. For the purpose of this work a fixed value of current (about 1 mA) was necessary, hence a simple circuit has been used to drive the LEDs when the corresponding digital input is high.
2.3. Avnet Zedboard
The core of the system has been realized on an Avnet ZedBoard™ [
16], a development board based on the Xilinx (San Jose, California, USA) Zynq®-7000. The programmable SoC (System-on-a-chip) Zynq®-7000 implements a dual ARM Cortex-A9 based processing subsystem, with a large series of peripherals (Ethernet, USB, SD card, etc.), and has a large programmable logic block section, connected to other peripherals. Internal communication between the inner parts of the FPGA is assured by high-speed AXI bus. This configuration allows the realization of very fast performance of low-level entities, and due to the presence of the internal ARM microcontroller, to easily interface the board and data with external systems. The board has been programmed using XILINX Vivado® EDA software.
Programmable logic blocks of the FPGA has been extensively used to control the front-end board and to implement most of the entities needed to realize the lock-in amplifier; whereas some less-demanding functions run in the above-mentioned ARM processors.
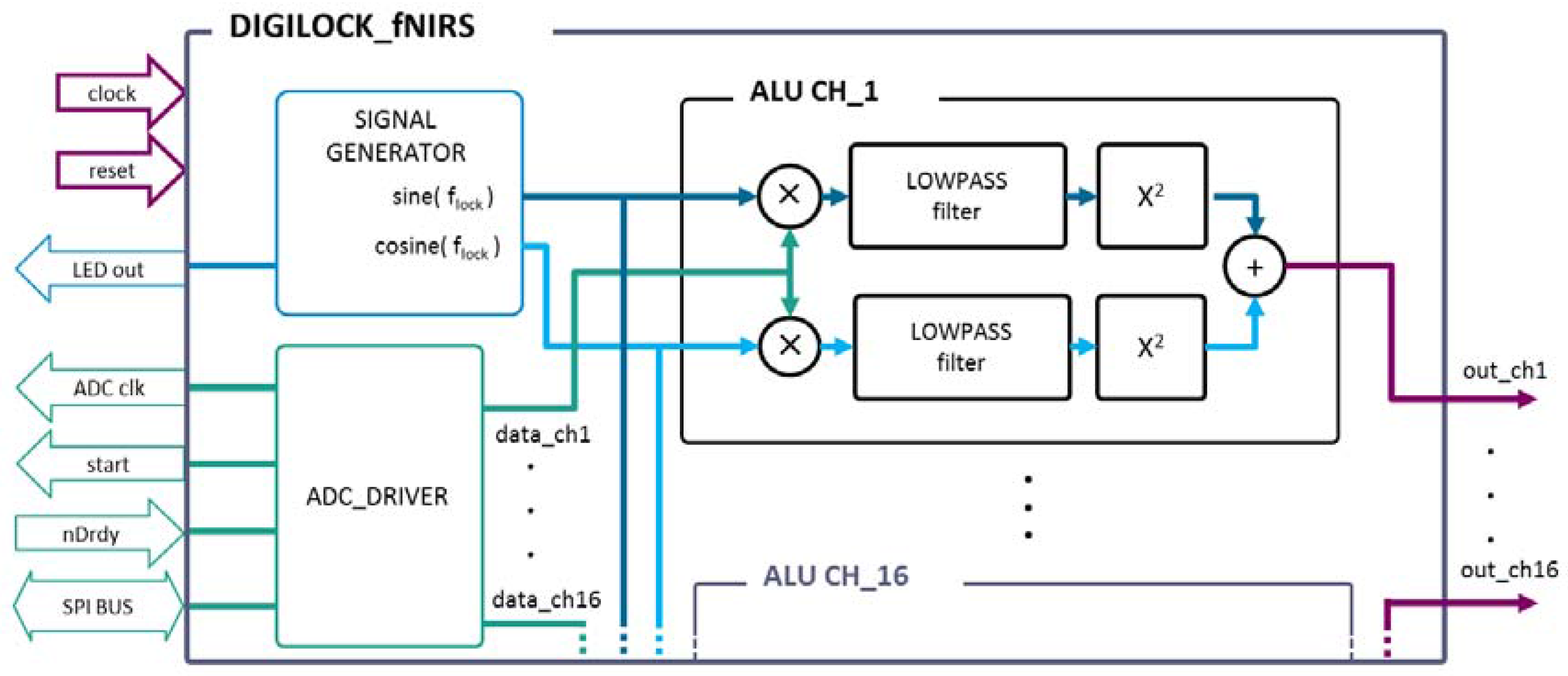
The implemented programmable logic entities, repeated for each channel (see
Figure 2) are: an ADC driver, a signal generator, and the tailored ALU.
The ADC driver communicates with daisy-chained ADCs using the SPI protocol, providing same ADC clock and Start conversion signals. When the signal nDrdy is asserted, a new set of data samples are ready to be collected. The entity parses the received packet and gives an output signal for each channel. The SPI frequency is 16 MHz with a sampling rate of 16 kSPS.
The signal generator is mainly a look-up table working as a function generator and it also creates a coherent square-wave digital signal at the lock-in frequency named LED out, used to properly synchronize the probe’s LEDs. The lock-in frequency is generated by dividing the sampling frequency by integer factors (8, 10, 16, or 20) selectable with switches on the FPGA board. Sine and cosine outputs are shared among all ALU entities.
The ALU implements the core part of the lock-in amplifier. It performs multiplications of the input signal by reference signals, the low-pass filtering, and the square and the sum of the obtained signals. These output values are then stored in the internal dual-port block RAM.
Within the lock-in algorithm, a final square root operation is needed and it was decided to execute it using the ARM processor of the FPGA, mainly because it was the easiest solution, even if the design of an optimized programmable logic entity executing the square root would have required only slightly extra effort.
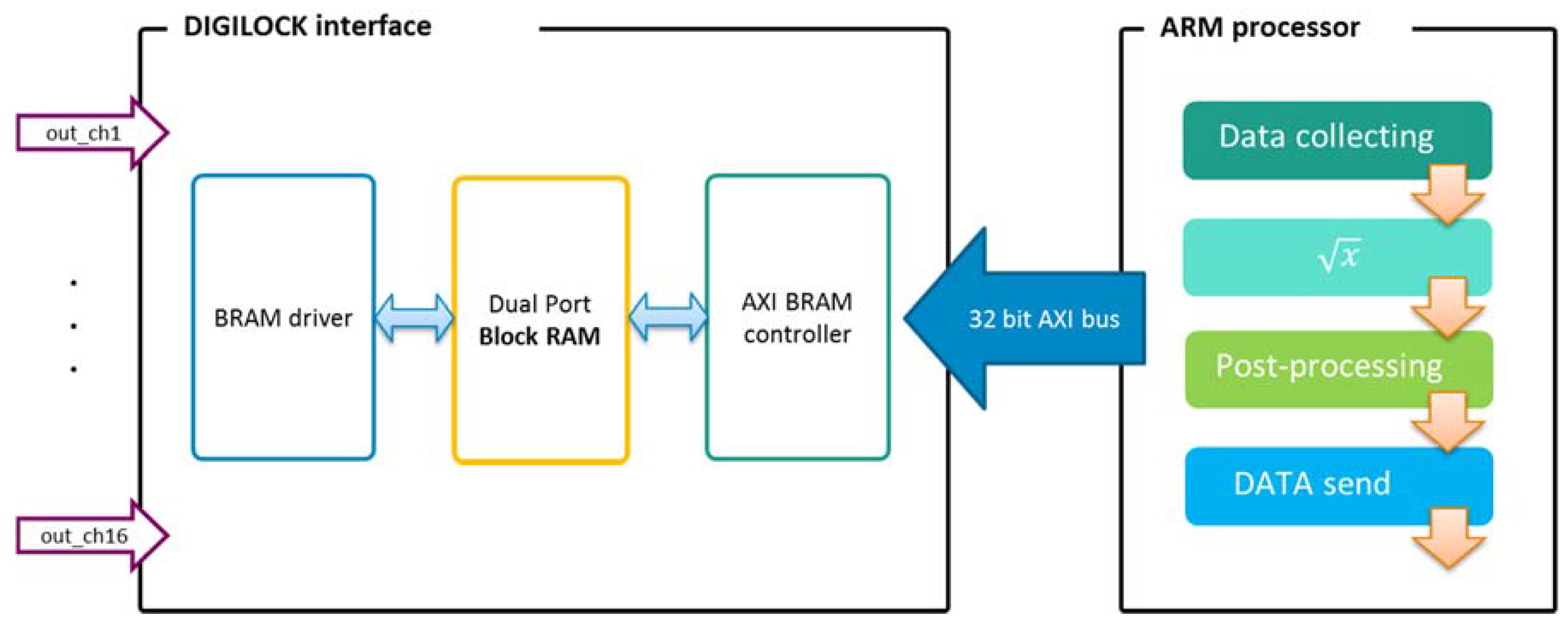
Data sharing between the programmable logic (PL) side and the internal ARM processor goes through a dual-port block RAM. This memory resides on programmable logic and is transparently mapped into the ARM memory space through the AXI block RAM controller (see
Figure 3).
The PL interrupts the ARM processor every time a new set of data samples, raw input, and lock-in data output for each channel are ready. Square root operations and needed signal post-processing to adjust the voltage scale are performed by the ARM processor before sending data to the PC for subsequent evaluation.
The ZedBoard™ is linked to a host PC through a gigabit Ethernet connection, capable of transmitting a TCP packet every dataset with negligible delay. This mechanism ensures that all data samples are promptly delivered to host PC.
2.4. Filter Design
The key component of the lock-in chain is the way the low-pass filter is designed and implemented, because it has a deep impact on the reconstruction of the original input signal. Signals coming out from the optical sensors have a typical bandwidth ranging from DC up to 8 Hz, while the attenuation must be high enough to reject unwanted noise near the designed lock-in frequency. These constraints must be satisfied by the filter’s transfer function. In order to investigate the behavior of different filter architectures on output signals, some FIR and IIR filters have been designed and instantiated within the FPGA hardware; they have also been experimentally tested by being provided with the same input data samples in order to highlight the differences.
The pass-band frequency of the filter was set slightly larger than the maximum frequency component of the fNIRS signal, and has been chosen as 10 Hz. Additionally, the roll-off of the transition band was chosen as a compromise between filter complexity and response characteristics.
The FIR filter has been designed as a two-stage cascading FIR filter, using MathWorks (Natick, Massachusetts, USA) MATLAB® Filter Designer tools. The first stage has a 10 Hz pass frequency and 100 Hz stop frequency, while the imposed slope provides about 80 dB of attenuation at the stop frequency. It uses an equiripple filter configuration which involves 724 taps [
17]. The first stage has been internally divided into twelve parts, running in parallel with results summed together, each with a 64 serial tap block in order to properly balance the computational load, using zeros coefficient padding to obtain an integer multiple of 64. The second stage has been added to eliminate the residual signal outside the band of interest. It is a 64-coefficient equiripple FIR filter, and has a 150 Hz pass frequency and an 1800 Hz stop frequency with an attenuation of 100 dB. Taps’ coefficients are represented with signed 16-bit integers.
The designed IIR filter is a Fourth-order filter implemented as cascade of two identical stages of direct form II biquad architecture. The selected architecture, for the IIR filter, is the well-known biquad implementation (second-order filter with one stage), mainly for its low phase distortion and remarkable stability to truncation errors. IIR filter coefficients have been designed using a MATLAB
® script, as described in [
18]. Each stage has a 3 dB frequency located at 10 Hz and an attenuation of 40 dB at 100 Hz. Since Zynq® FPGA does not implement an internal floating point unit in hardware, the hardware arithmetic of the filter uses 32-bit integer numbers but, to achieve a correct computation, a 2.30 fixed point coefficient representation (two digits for the integer part and 30 for the decimal part) has been used. The overall IIR filter has characteristics similar to FIR, but it only requires 10 multiplications and 12 sums per sample [
19].
3. Experimental Results
The measurement setup equipment, used to prove and verify system functionality, includes an arbitrary wave generator (AWG) the AFG3102 by Tektronix™ (Beaverton, Oregon, USA), in addition to the hardware previously described.
In order to test the goodness of the implemented system, it was very useful to simulate an input signal having properties suitable to be realistic enough as a bio-signal and with clearly observable temporal and spectral behavior. A sinc(t) waveform has been selected to be the modulating signal for its spectral property and shape. The flexibility of easily selecting the lock-in frequency divider has been exploited to find the optimal frequency for noise rejection. The highest possible lock-in frequency () has been selected for all tests.
A simple modulator has been used to generate the test signals using the reference square wave, provided by the FPGA at lock-in frequency, while the modulating signal was created by the AWG.
On the PC side a virtual instrument, created with LabVIEW software, reads signal data from a TCP connection and presents the waveforms through some generated user-friendly charts.
3.1. IIR-FIR Comparison
In order to properly evaluate LIA performance, comparing the results coming from the FIR and IIR filters and their fidelity level, several tests with some
sinc(
t) signals of suitable frequency were carried out by feeding them into the ADC input, one at a time: first a
sinc(
t) with a frequency bandwidth of 3.5 Hz, falling completely within the LIA’s pass band; after that a second test used a
sinc(
t) with an extended bandwidth of 15 Hz. The equivalent formula of signal
m(
t), used in the described measurements, was:
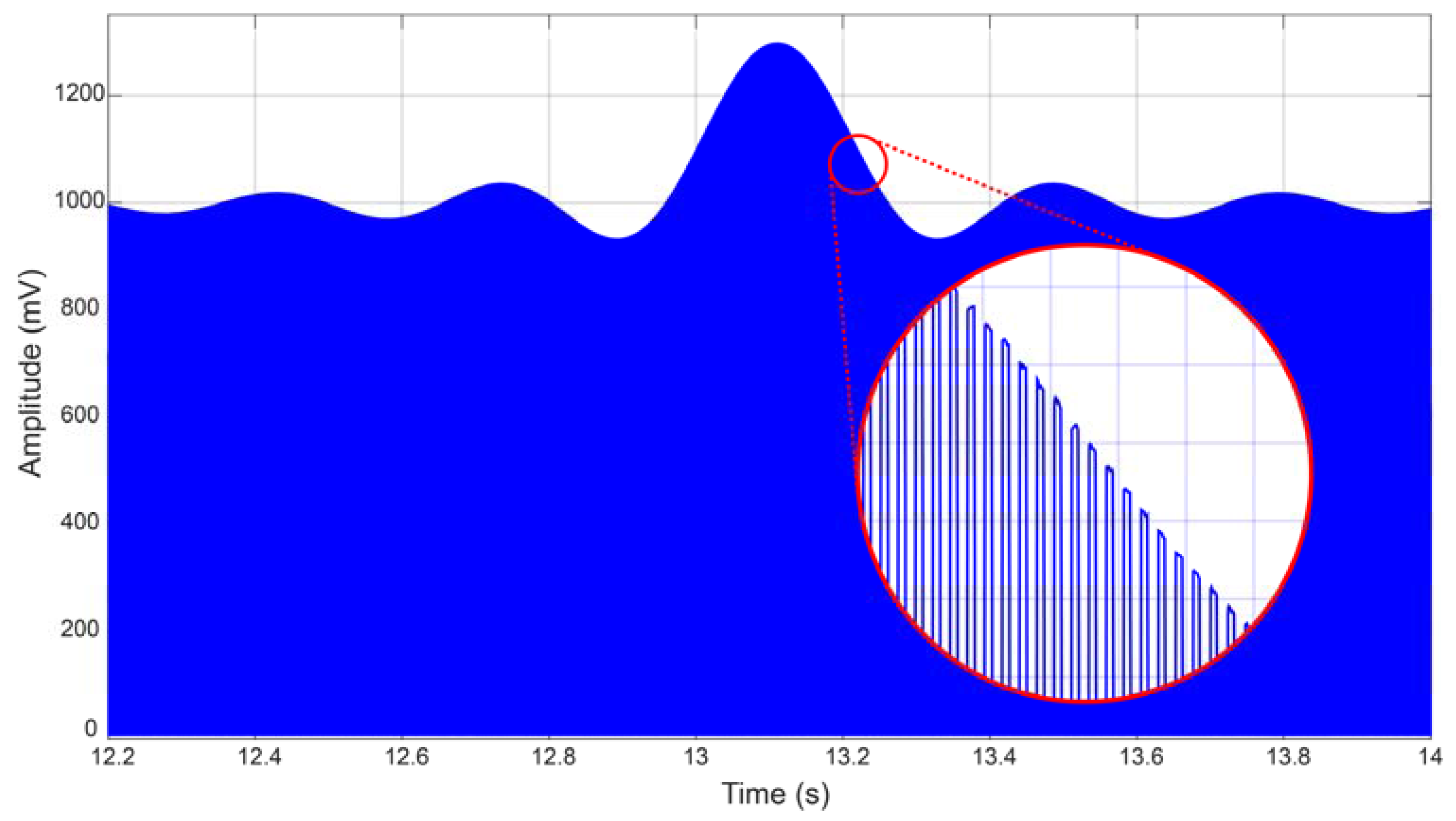
The
Figure 4 shows an example of the modulated signal, used as test signal and acquired by the system.
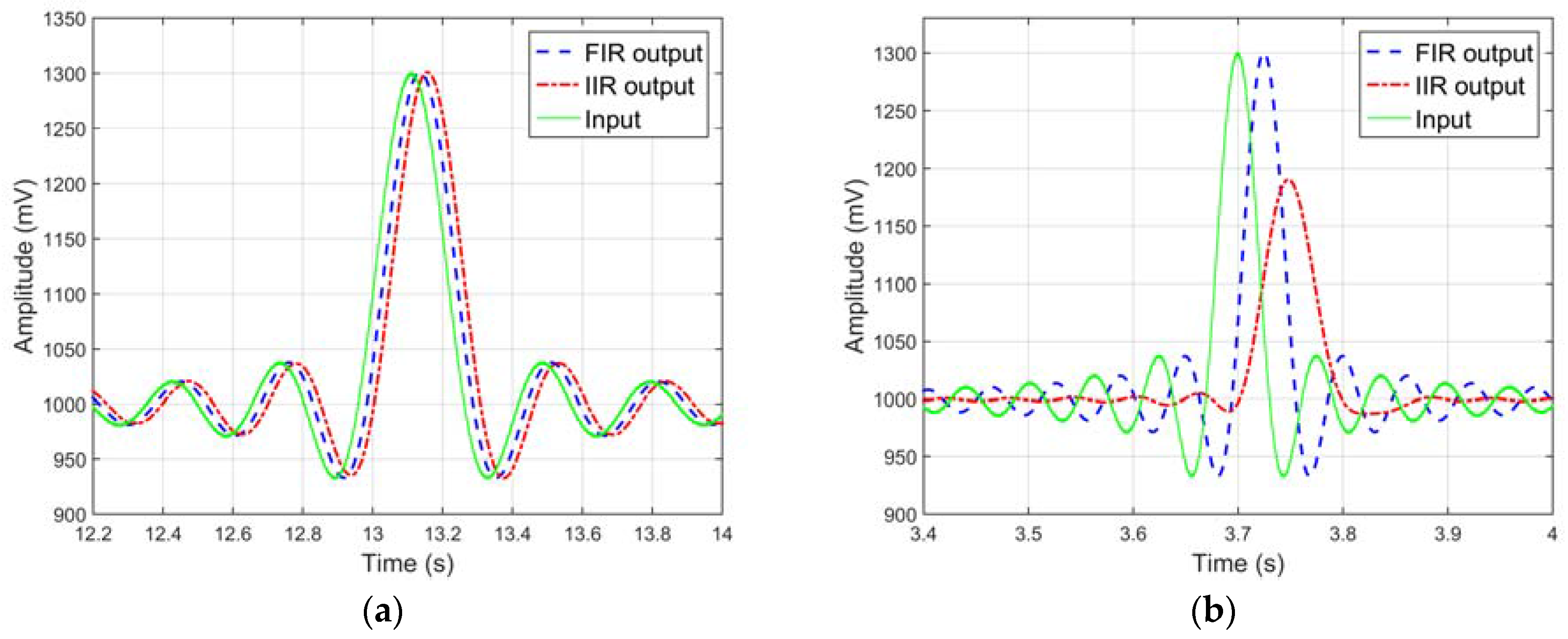
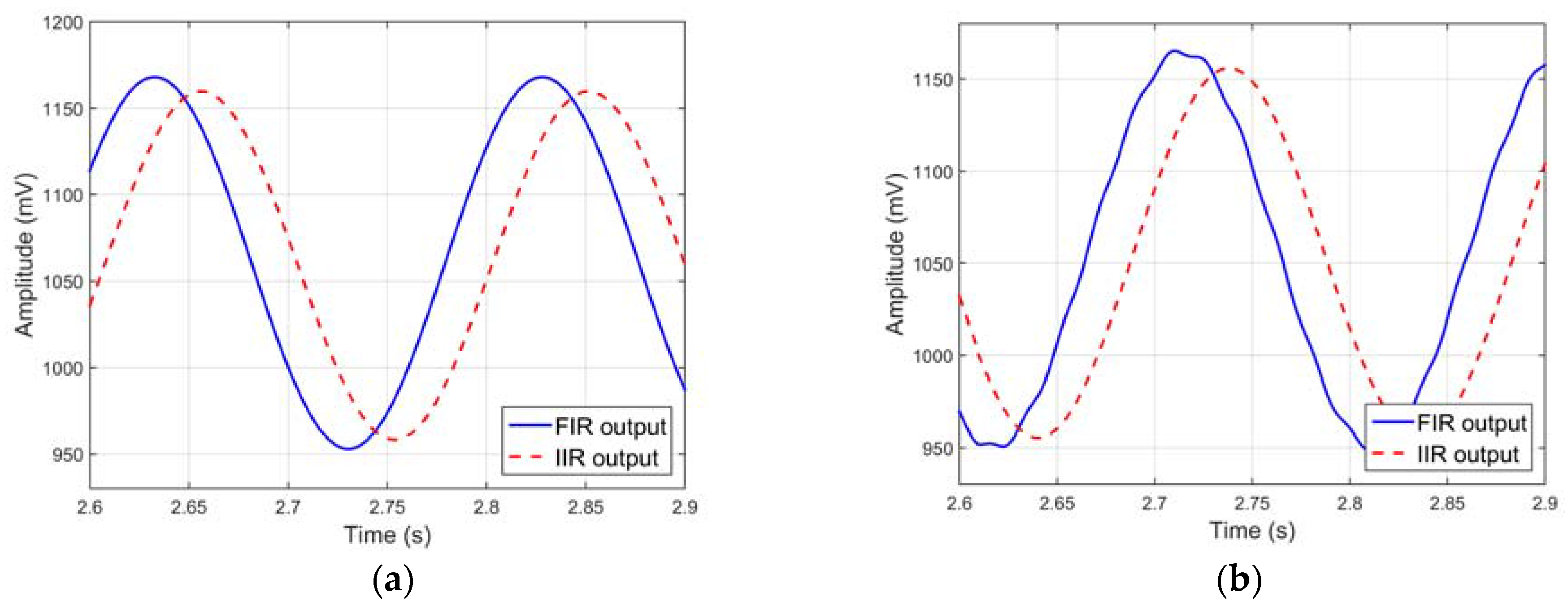
As can be seen in
Figure 5a, when the signal falls to the 0 to 10 Hz range, no appreciable distortion appears on the filters’ outputs, not considering an obvious phase change due to the different filter’s delay. With the larger spectrum
sinc(
t) (
Figure 5b), amplitude distortion of both filters is clearly visible instead. In particular, since the FIR filter achieves, in the transition band, a slope slower than the IIR, it shows less distortion and attenuation for frequencies near the pass frequency. The IIR filter, instead, shows an asymmetrical response due to the frequency variable phase delay, and a substantial shape change of the original signal is experienced.
Moreover, the signals extracted from FIR and IIR filters have specific delays and they can be evaluated at design time; in particular, for the IIR filter implementation, which has a nonlinear phase, the estimated group delay ranges from 625 up to 760 samples while, for the FIR filter, its value is constant (399 samples in this case).
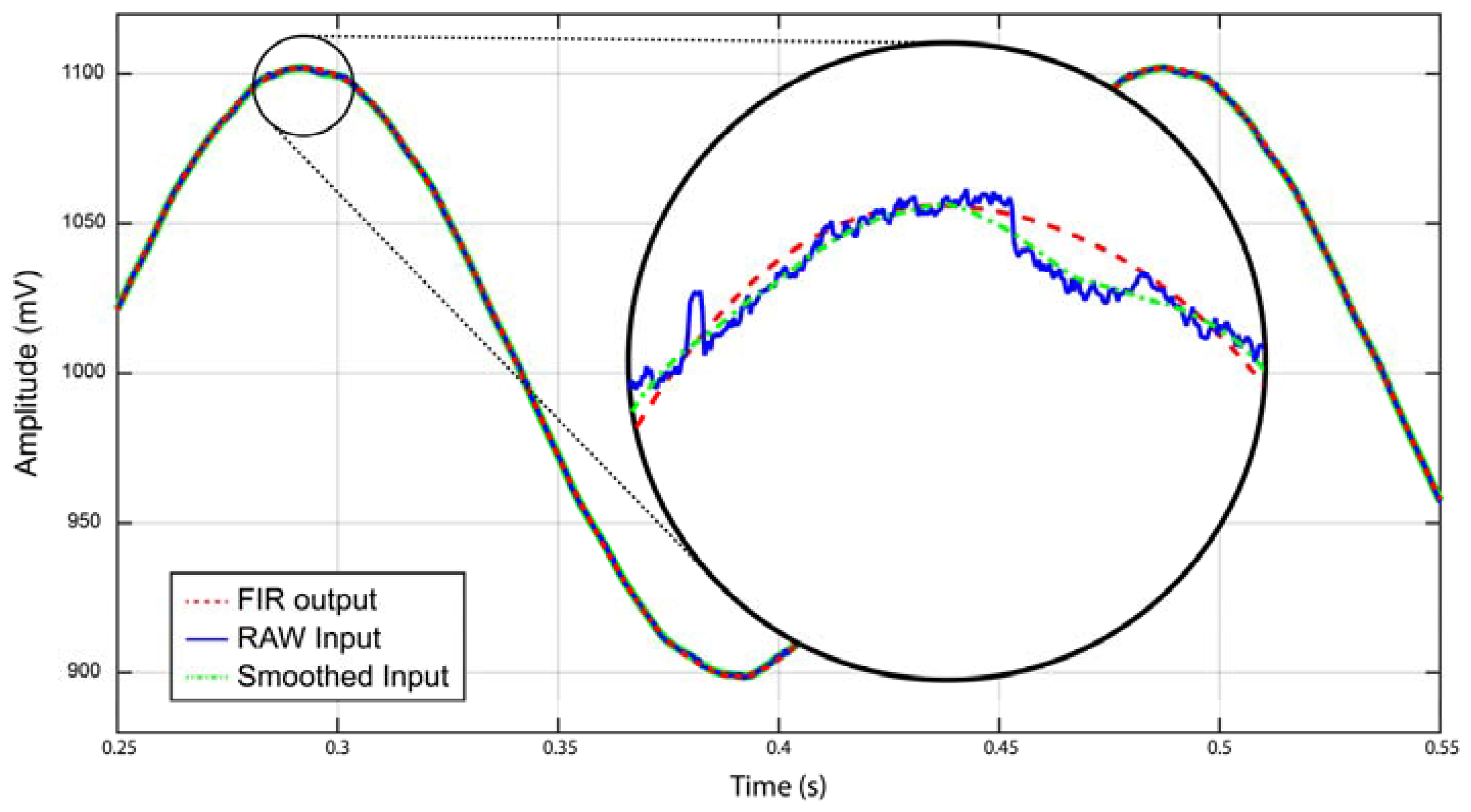
To better highlight the response of the LIA system, another comparative test has been carried out: a 100 mV sine test signal at 5 Hz has been used as a modulating signal and the raw output of the ADC has been registered together with the filters’ outputs (see
Figure 6).
As can be verified in the insert of
Figure 6, the raw input is actually a relatively noisy sine wave since it was obtained from a standard generator having a resolution of 14 bits. FIR output has been first aligned offline with the raw input data for better comparison and a smoothed input implemented with a standard 64-tap moving average filter has been also depicted. While the smoothed input suffers of the variation of the noisy raw data, the FIR output of the LIA system performs a much better reconstruction of a good 5 Hz sine wave, even showing a strong rejection of the input noise.
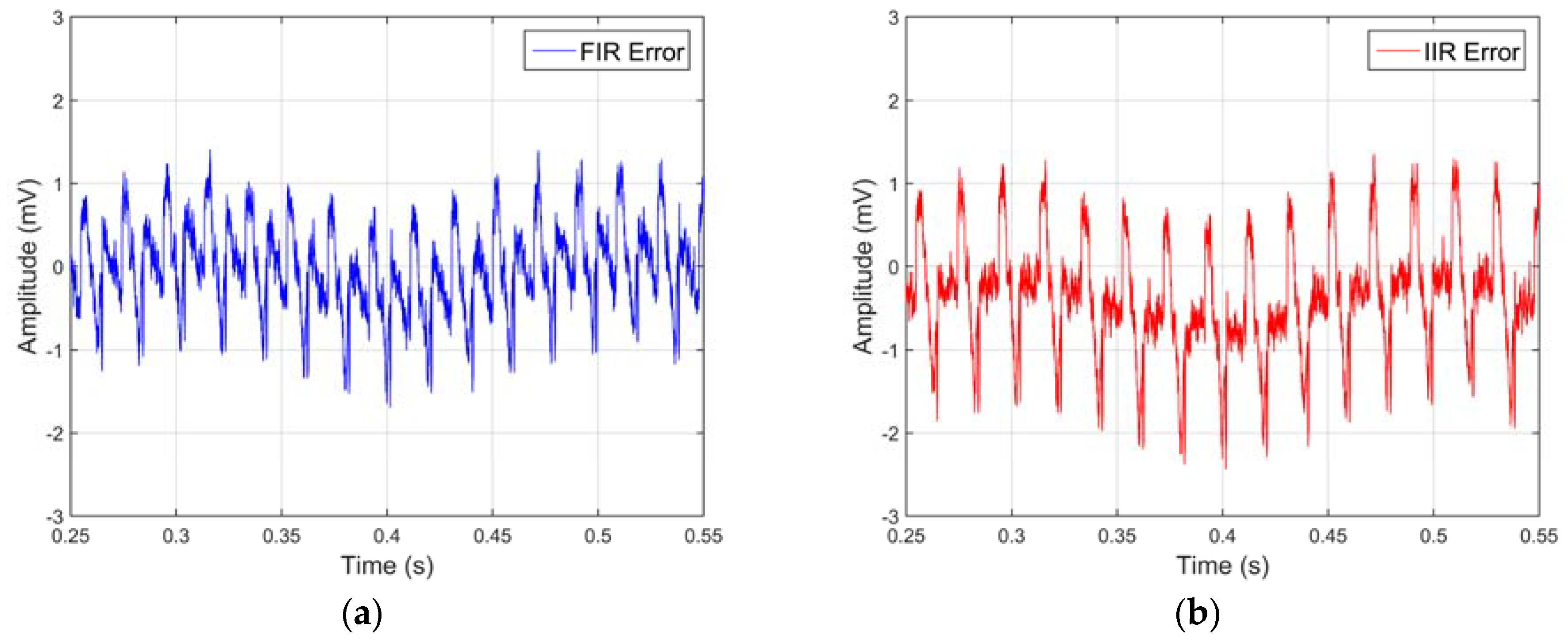
Figure 7a,b report the calculated signal difference between the raw input signal and FIR/IIR outputs for the 5 Hz sine, respectively. In both figures, small variations and offset at the modulating frequency can be observed, and they are mainly due to amplitude nonlinearity of the filters. Finally, the residual error, whose value is about ±1 mV, is largely due to the noise existing in the raw input signal and removed by the LIA action.
Table 1 shows a summary of the main hardware resource utilization within the Xilinx Zynq®-7000 and it is clear that, even if the FIR filter performs with a slightly lower signal distortion than the IIR filter, it requires fourteen times the number of lookup tables and almost thirty times the number of slice registers, hence, exhibiting a much higher power consumption.
Moreover, among the parameters, attention must be paid to the needed clock cycles per sample, since this means that IIR filters can be implemented using pipeline elaboration at least four times faster than a FIR filter with similar performance; and this can make a very large difference, especially if LIA techniques are applied in more demanding application fields.
3.2. Baseline Rejection
The baseline rejection test verifies the capability to remove DC offset and low frequency noise from the input signal. This is a typical scenario with optical sensors affected by 1/
f noise and dark current. The carrier is, again, modulated with a 3.5 Hz-band
sinc(
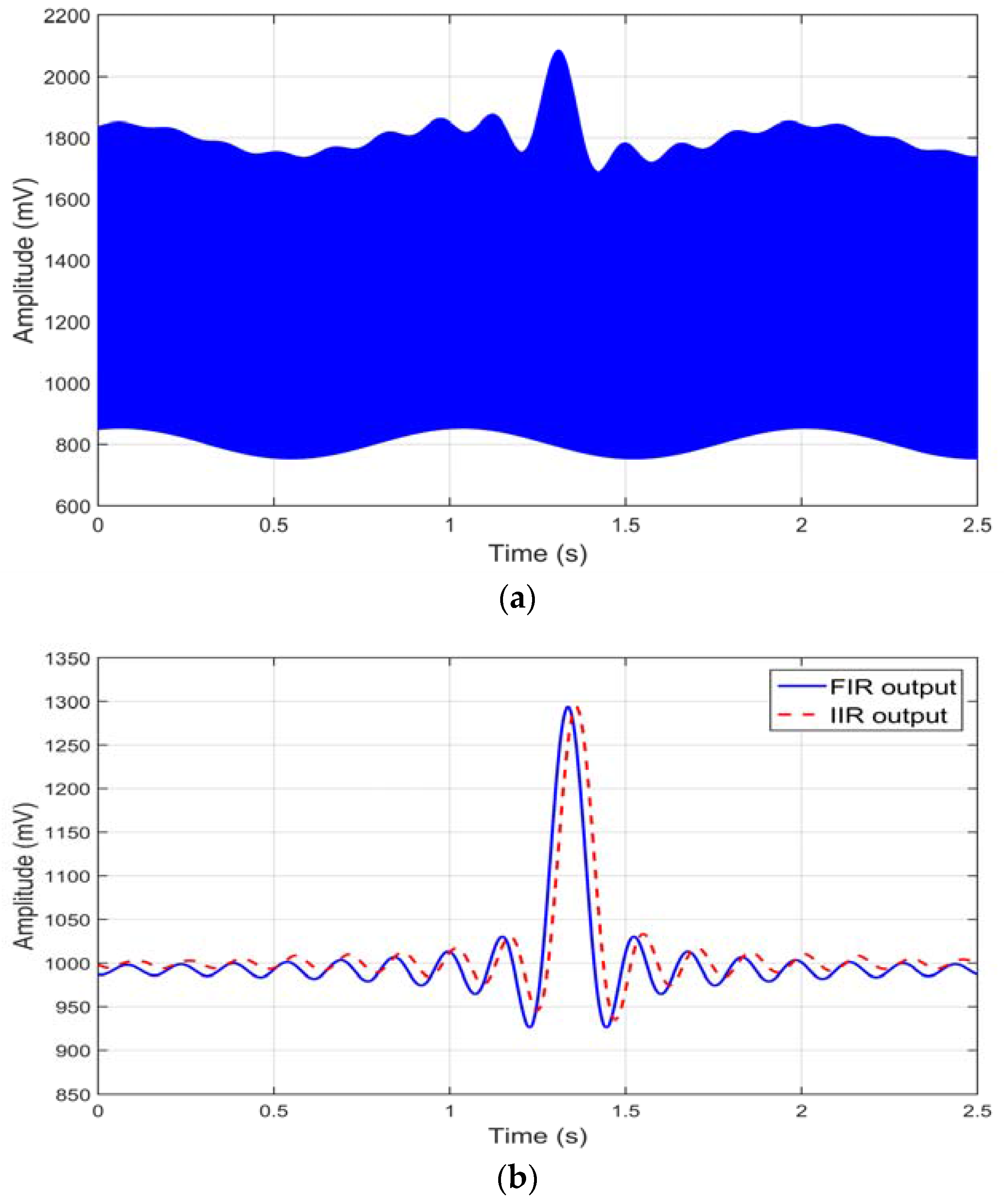
t) useful signal and a DC offset of 0.8 V is summed up with a slow 0.1 V sine signal @ 0.5 Hz, acting as superimposed noise (see
Figure 8a). The equivalent formula of signal
m(
t) is:
As can be seen in
Figure 8b, the baseline is completely removed by the lock-in chain and FIR and IIR filters give the same envelope, each one with its own delay. The baseline noise does not affect the output as long as it does not saturate the ADC input. The behavior of the system, in this case, is completely different compared to systems that simply acquire ADC values [
11] and perform some average filtering. In the latter case, in fact, since the slow baseline variation falls within the band of the wanted signal, it would thoroughly affect the output, while the LIA system completely eliminates this noise because both of the noise sources lack any component near the lock-in carrier frequency.
3.3. Noise Immunity Test
In order to check lock-in chain robustness in noise rejection, some tests have been carried out using the AWG to generate typical noise sources. In normal environments one of the most prevalent optical noise sources that can affect fNIRS measurements is the switching noise produced by neon lamps. This noise has a fundamental frequency of 100 Hz, so the experiments were carried out by adding to the useful test signal, represented by a 100 mV @ 5 Hz sine wave, a noise signal acting at 100 Hz.
The first test (see
Figure 9a) uses a sine signal with the same amplitude of the useful one and, in both filters’ outputs, a complete elimination of the 100 Hz component has been obtained. A second, more aggressive, test uses a 100 Hz square wave signal (see
Figure 9b) with the same amplitude of the first trial. In this case, while the IIR filter output shows, again, a complete elimination of the noise component, the FIR filter experiences a residual noise affecting its output.
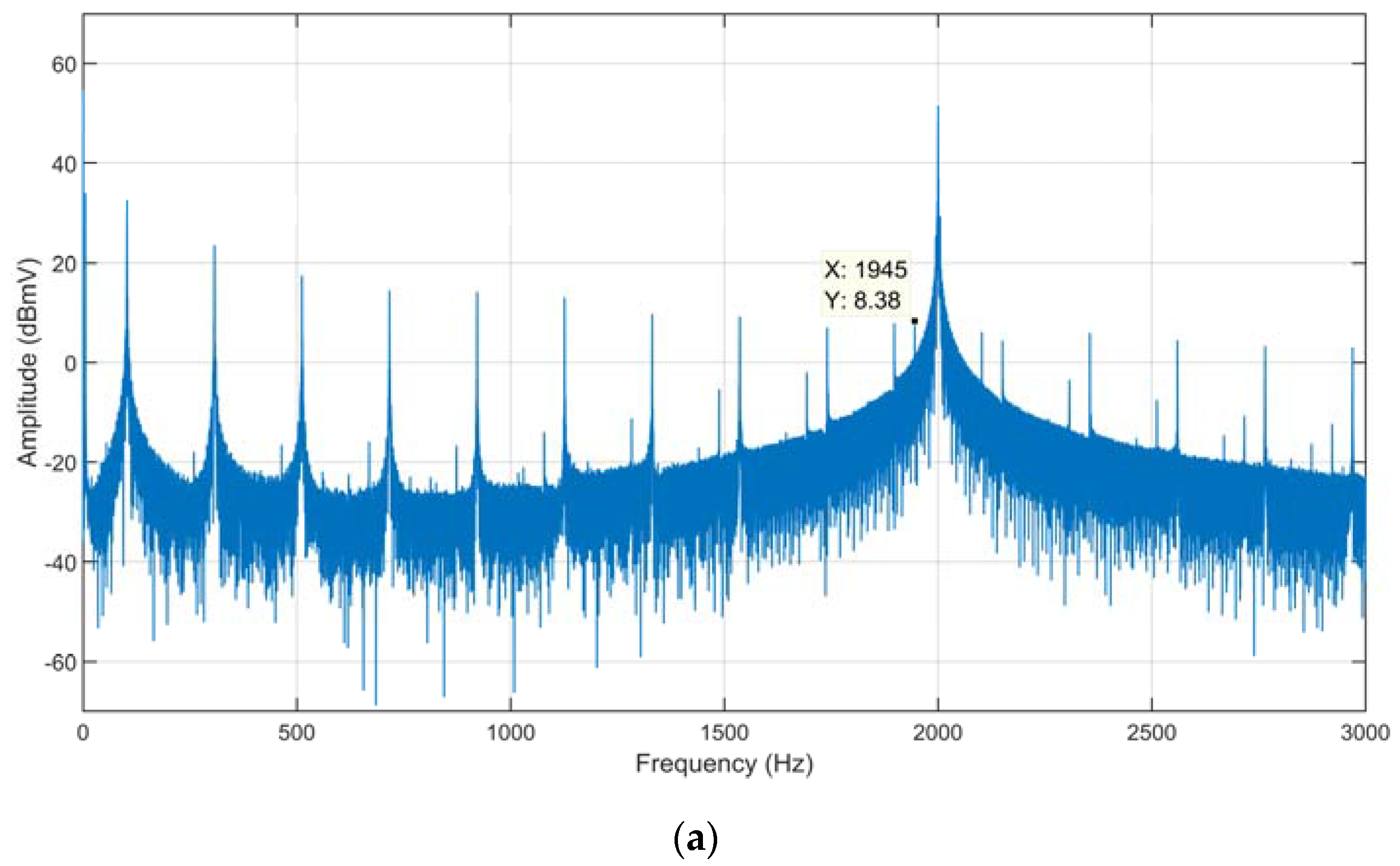
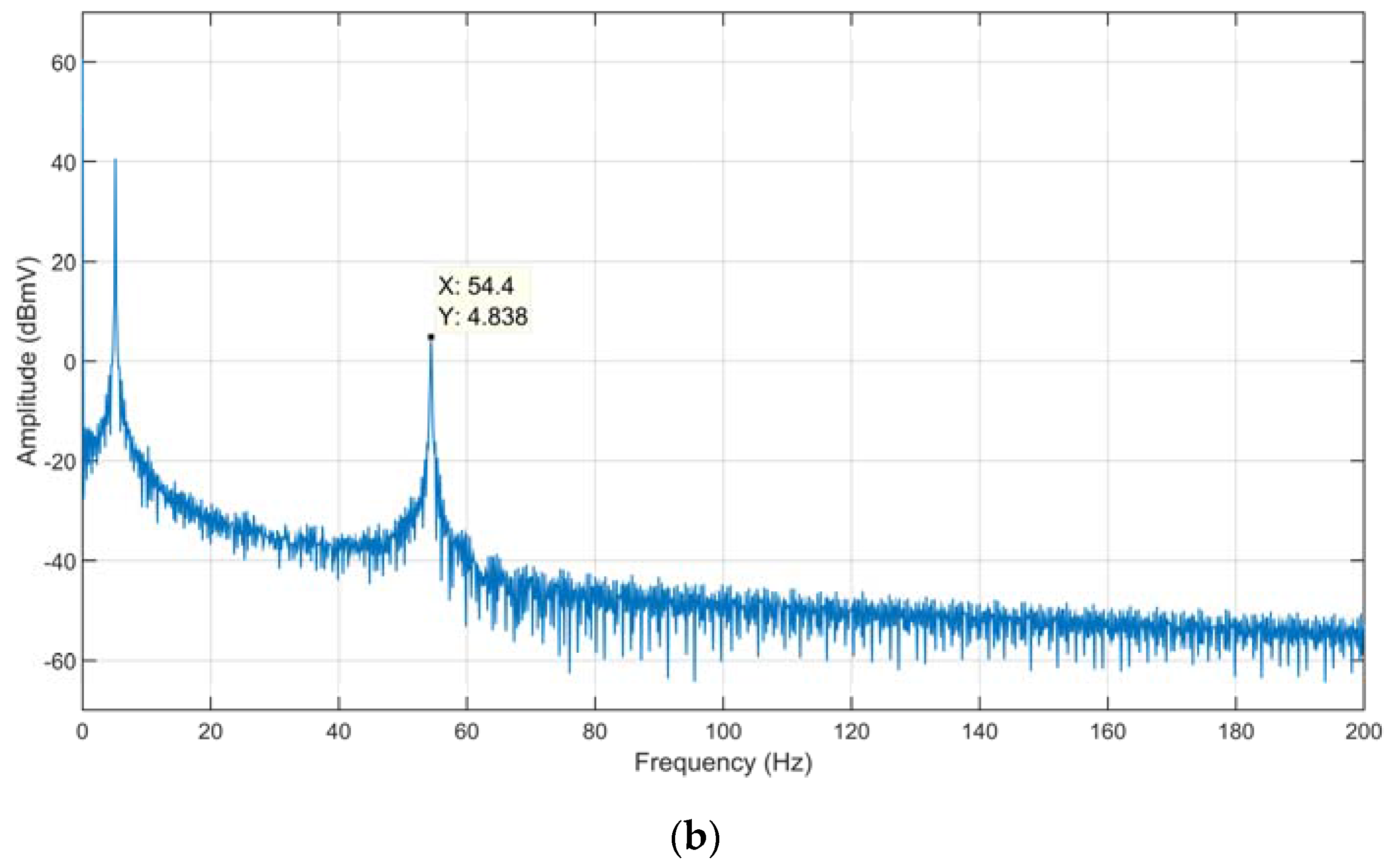
To further investigate the last experiment, a spectrum analysis of the input signal (
Figure 10a) and the corresponding FIR output (
Figure 10b) has been carried out.
In particular, it can be observed that, near the 2 KHz lock-in frequency carrier, the input signal also exhibits a small signal component at 1945 Hz, among the others generated by the square wave harmonics. This signal component, mainly due to the non-linearities of the modulating process, is shifted to the baseband, by the multiplication, at a frequency of about 55 Hz. Since the implemented FIR filter has a relatively slow slope in the transition band, part of this noise will pass through the filter with an amplitude of more than −30 dB/Hz, still above the noise floor (see
Figure 10b), while higher harmonics are completely attenuated by the FIR filter. The IIR filter, instead, has a larger slope in the transition band, hence, it completely removes the 55 Hz component below the noise floor, together with all of the other components.
4. Discussion and Conclusions
In this work an FPGA-based lock-in architecture has been designed and implemented with the aim to obtain great flexibility on key design parameters, such as sampling and lock-in frequency, together with the main characteristics of the core digital filtering action, embedded in the lock-in chain. Additionally, the design principles described in this paper may also be relevant to other research areas.
The realized system has been designed with an intrinsic level of modularity and this may ease the scale-up of the number of acquired channels without affecting the overall architecture while, for small numbers of channels, the subsequent computational effort lowering may envisage a possible implementation based on a microcontroller with suitable digital signal processing capabilities.
Extensive experimental assessments have been carried out and the obtained results show good behavior of the developed system. In particular, the action of the proposed FIR and IIR filters obtained a very strong rejection of noise affecting the baseline, particularly for signals related to fNIRS systems using SiPM as main sensors.
Moreover, some noise immunity tests exhibited a quite robust behavior against possible noise sources, such as the ones generated by neon lamps, also highlighting the better performance of IIR-based filtering, despite its less demanding resource request.
This LIA technique employs more hardware resources than the method used in [
11], based on a simple moving average filtering of a predefined number of acquired samples, but it generally leads to better results in terms of signal to noise ratio preservation, noise immunity, and low amplitude signal acquisition.
The comparison between different (FIR and IIR) filtering actions, while both show suitable results in terms of rejection performance, have a substantially different impact on FPGA resource utilization and, for some tests, on the obtained results.
The goodness of the described results encourages further investigations. The system uses a very powerful FPGA board, but in the current implementation most of the resources are not used; hence, a more suitable FPGA chip could be chosen lowering overall costs of the system and power consumption. From the comparison of the filters and considering the overall computational cost, it has been evaluated that it is plausible to implement the same method to a limited number of channels (16 seems reasonable) using IIR filters without sensible degradation of the performance, on a mainstream 32-bit microcontroller, especially if equipped with DSP functions.