Abstract
Energy efficiency is a major research focus in sustainable development and is becoming even more critical in information technology (IT) with the introduction of new technologies, such as cloud computing and big data, that attract more business users and generate more data to be processed. While many proposals have been presented to optimize power consumption at a system level, the increasing heterogeneity of current workloads requires a finer analysis in the application level to enable adaptive behaviors and in order to reduce the global energy usage. In this work, we focus on batch applications running on virtual machines in the context of data centers. We analyze the application characteristics, model their energy consumption and quantify the energy per job. The analysis focuses on evaluating the efficiency of applications in terms of performance and energy consumed per job, in particular when shared resources are used and the hosts on which the virtual machines are running are heterogeneous in terms of energy profiles, with the aim of identifying the best combinations in the use of resources.
1. Introduction
Energy efficiency in cloud computing has been increasingly studied in recent years due to the always increasing quantity of data to be processed by applications, such as data analytics and the Internet of Things, which collect and analyze large quantities of data from sensors, scientific applications, simulations and social network analysis. Such applications have a significant impact on the global amount of energy being consumed in data centers, while energy efficiency is still rather low, as shown for instance in the Data Center Maturity Model (DCMM) of the Green Grid Consortium [1], where the state of the art of average CPU usage in 2011 is stated to be around 20%, with an ideal five-year target of 60% in 2016 (the DCMM new release is expected to be published this year).
Research on energy efficiency in data centers has concentrated first on reducing the number of underused resources. Virtualization and consolidation introduced in cloud computing are efficient ways to share resources among a large number of users and thus helping to increase resource utilization. Other approaches consider the dynamic allocation of tasks and the possibility of varying the number of used resources to reduce power consumption. Another focus in this research trend has been to achieve energy proportionality as defined by [2], in order to consume energy only for executing tasks and ideally having no consumption while no task is being executed.
While the research in this area has been continuously growing in the last few years, only limited attention has been paid to the energy consumption behaviors of applications and the way computing resources are used by different application types and the consequent impact on the energy efficiency of the systems. An aspect that also needs a more careful analysis and which is analyzed in this work is that even in a virtualized environment, resources cannot be used at 100% and that, when idling and waiting for tasks to be executed, an amount of idle energy is consumed that should not be under-evaluated. In fact, once the virtual machines (VMs) are created and are in use, their power consumption depends both on the usage and on the fact that they are actually running on physical hosts. The switching between states of computing resources, i.e., idle or in use, is influenced by the operating behaviors of running applications. These behaviors can be inspected through different parameters, such as resource usage, types of applications, application workflow, and so on. Models that consider these elements in evaluating energy usage are therefore needed to better characterize the energy consumption of applications.
In this work, we model the energy consumption of a specific type of scientific high performance computing application, considering the characteristics and using monitored information from cloud telemetry systems. One of the key aspects of our proposal is that it requires a limited knowledge of the underlying infrastructure. In detail, the class of applications we consider are computing-intensive batch processing scientific computations (the batch workload), which are mainly characterized by the number of jobs to be executed and their service demands. Different configurations to execute applications are analyzed, emphasizing the impact of shared resources (e.g., storage) and of bottlenecks on energy consumption.
Although this might sound limited, many of the analysis techniques proposed here can be extended to give useful insights in more general scenarios. Moreover, we propose methods to compute the energy consumed per unit of work (the job) and use it as a driver to analyze and improve the energy consumption of applications. The ability to quantify the energy consumed per job is important, as this metric helps with enabling adaptive behaviors and ad hoc optimization techniques at the level of applications.
In the following, we confirm with a model that if we are not bound by hardware capacity (i.e., we have unlimited resources) and energy cost, the best solution for executing a given number of jobs is to use as many VMs as possible; however, if some resources cannot be parallelized (such as, for instance, shared storage), we show that while adding computing resources is not always useful for improving performance, it may result in lower energy efficiency. Therefore, in such scenarios, it is important to determine the “optimal” point where providing more resources beyond this point is no longer beneficial in terms of performance and energy efficiency. We also discuss and evaluate the impact of interference among applications in scenarios where resources are shared, and we also consider the case in which physical servers hosting the virtual machines are heterogeneous in terms of the power profile.
The proposed analytical models have been evaluated using experimental data of the ECO2Clouds (Experimental Awareness of CO2 in Federated Cloud Sourcing) European project [3], which provides a federated cloud environment with a monitoring infrastructure for studying energy efficiency and the environmental impact of federated clouds.
The paper is organized as follows. In Section 2, we discuss the state of the art and analyze it focusing on the aspects related to the main goals of this paper. In Section 3, we discuss the models adopted for evaluating energy per job. In Section 4, we discuss different execution configurations and apply the models to analyze their efficiency in terms of performance and energy usage. In Section 5, we analyze the bound of energy per job in homogeneous and heterogeneous cloud infrastructures, and we conclude the paper in Section 6.
2. Related Work
Improving energy efficiency in data centers and cloud infrastructures has been extensively considered in the literature. The surveys of [4,5,6] describe different approaches focusing on multiple aspects of energy consumption, which are not limited to the IT infrastructure, but also take into account the physical infrastructure and cooling.
A well-known principle commonly used in the area is the so-called “energy proportionality”, discussed in [2], which advocates for energy proportional computing where energy consumption is proportional to the usage. This principle has been widely applied in designing physical systems components, but its usage in distributed software architecture is still ongoing research. In order to comply with the objectives of this work, the review in this section focuses on two parts: the first part is about power models, and the second part is the discussion of improving the energy usage of applications, including also the metrics that are necessary for the assessment of energy consumption.
Concerning power usage, several models have been proposed to estimate the power consumption of systems. In data centers, two levels of investigation are being targeted: at a physical layer and at a virtualization layer. At a physical layer, one of the initial significant contributions is the work of Fan et al. [7] attempting to characterize the host’s power usage using CPU utilization. Two models are proposed, linear and non-linear. Although the non-linear model seems more accurate in many systems, the linear one gives a reasonably correct result, especially as systems nowadays are approaching the “energy proportionality” target. In [8], a classification of power consumption models is presented, including power models as a function of supplied voltage and operational frequency, or component-specific and system-level power models. For a complete system view, the power model consists of the idle power and the busy power consumed by the CPU, I/O, memory and network where the CPU is the most relevant. A different approach is taken in [9], where the power model at the host level is built based on the request arrival rate.
At a virtualization layer, several attempts have been made to derive the power consumption of virtual machines. In [10], a survey of power estimation methods for servers and virtual machines is provided. Two different directions have been adopted to estimate the consumed power of a virtual machine. The first direction uses some sort of training to obtain the power model [11,12]. The second direction analyses the consumption of resources in physical hosts and derives power consumed by the running VMs. In [13], a model considering various system components (CPU, cache, memory, disk) is proposed.
As far as energy efficiency is concerned, it is important to have adequate metrics able to assess it. In the GAMES (Green Active management of Energy in IT Service centers) European project [14], ecometrics have been classified according to different levels in which they are used (infrastructure, virtual machine, application) [15], and usage-centric metrics have been proposed as a basis for improving energy efficiency [16]. While these metrics are useful for assessing energy efficiency, they are difficult to apply in case the need of evaluating the energy consumption of an application arises, since they provide only a relative evaluation (i.e., percentage) of the consumption. To be able to assess if reserved resources for an application are being used effectively, in the ECO2Clouds project [3,17], new metrics have been introduced to evaluate energy efficiency not only at the infrastructure and data center levels, but also at the application level [18]. The proposed metrics are relative metrics that allow assessing the percentage of waste at the application level, but do not focus on directly measuring power or energy consumption. The concept of energy per job has been discussed in related work (e.g., [19]); however, a systematic method to derive it for applications and its use to assess application efficiency have not been considered so far.
Concerning the improvement of energy usage at the high level of systems, a large amount of work has been done in the literature, and existing approaches often fall into load balancing and scheduling, resources planning or consolidating categories [10,20,21], mainly at the physical resources level, and often integrating with cost optimization.
Our work does not particularly focus on those aspects, as it emphasizes analyzing the energy consumption behaviors of applications under various circumstances towards finding possible improvements. In [18], adaptive strategies are proposed for cloud applications in which applications change their execution workflow in order to exploit the dynamicity of the running environment. Although the focus of the cited work is on reducing CO emissions, a similar approach can be adopted in order to have energy-aware self-adapting applications driven by the energy consumed per job.
There are several emerging issues being considered in energy and power modeling in recent literature. A comprehensive survey in [22] examines different aspects in modeling energy consumption in data centers. The authors classify software energy models, considering different types of applications and workloads. For computing intensive applications, first they analyze regression models, then they focus on models based on the estimation of VM power consumption considering both idle and dynamic power and on models based on different components of the underlying infrastructures (CPU, I/O, memory, etc.). Models for data-intensive applications are classified into models for online and offline applications. One consideration for these cases is that the management of idle machines can have an important impact on energy efficiency.
Another aspect needing attention is the possible interferences among applications running in the same environment. One proposal is provided in [23], where the authors suggest to add a correction factor to the energy consumed by colocated applications, based on experimental evaluations. In [24], the authors study how energy efficiency can be improved considering an appropriate workload heterogeneity in task allocation selection. In the present paper, we analyze part of this issue further in detail, focusing on the impact of colocation when the running jobs share the same resources, focusing on data storage, thus allowing a precise estimation of the effects of resource sharing.
In [25], energy efficiency in cloud computing is discussed, with a focus on service providers. The difference between energy loss, i.e., energy that is “not consumed by any subsystem” or “overhead of support subsystems”, and energy waste, where energy is wasted in idle or redundant systems, is discussed. The paper illustrates the need for research focusing on server power consumption and the role of the cloud management system in reducing power consumption, considering also idle times. Among other issues, the need for more complete models, including also storage, is discussed. Reducing energy waste is particularly important, since, as discussed in [1], a number of improvement actions can be considered, and the target for CPU usage in a Level 5 data center, labeled as visionary, is 60%. This demonstrates that there are still some margins for improvement to be considered in the future.
Another aspect that needs further consideration is the fact that data centers are emerging to become more and more heterogeneous, in which several types of hosts and VMs are available ([6] analyzes different forms of heterogeneity in cloud computing in comparing techniques for energy efficiency). In addition, also in the experimental experience derived from the ECO2Clouds project on which this paper is based, the hosts of the same type can have somewhat different energy profiles [26], and therefore, it is not possible to base all analyses only on factory production data. Another factor of uncertainty that is emerging in monitored data centers is the intrinsic uncertainty in the monitoring environment itself, as for instance the imprecision of measurements under low loads [27] or the variability of cloud monitoring services [28].
We presented an initial work to study different configurations of batch job execution on VMs on a cloud platform in [29], studying energy consumption in batch applications sharing resources executed in different configurations. The main conclusion was that major differences in the deployment of applications could be noted in two main cases: sequential and parallel execution of jobs accessing a shared storage. Other cases considered in the study showed characteristics similar to one of the aforementioned two cases. An experimental analysis of the possible different configurations was studied through simulation and comparing the results in a federated cloud environment, provided within the ECO2Clouds project [17]. Within ECO2Clouds, the main focus was on deploying VMs so that CO2 emission is minimized, through adaptive scheduling algorithms based on the monitored ecometrics. Within the same project, in the paper [18], we show that an adaptive management of applications based on ecometrics can result in significant improvement, reducing the waste of resources.
In this paper, we start from the previous analysis of alternative configurations for executing jobs of batch applications, with the goal of identifying the boundaries for energy consumption of applications when they share storage resources. In the current paper, we provide an analytical formulation for the models analyzing in depth the two main deployment strategies, identifying the conditions in which no further performance improvement can be achieved adding new VMs, evaluating the energy consumption of the VMs executing the jobs and evaluating energy per job boundaries in clouds with homogeneous and heterogeneous cloud computing environments. We therefore set a basis for using application energy profiles for an evaluation of the energy consumption of the VMs performing the jobs.
3. Computing Energy per Job
This section presents the methods for computing energy per job, focusing on computing-intensive batch applications in the context of data centers. First, we present the models to estimate the power and energy consumption of applications, as the total energy consumption of an application is the basis to compute the energy per job.
3.1. Power Models
In general, the energy consumption of an application is evaluated as the integral of consumed power over its execution time (see Equation (1)):
where is the power consumed by the application at time t and E is the total energy consumption during the execution period T. In cloud infrastructures, since applications run inside virtual machines (VMs), power consumed by an application is assessed indirectly through power consumption of virtual machines; whereas the execution time T depends on the specific application configuration and deployment.
From an application viewpoint, in order to optimize the overall consumed energy, considering both power consumption and execution time is necessary as optimizing only one of them can result in unexpected outcomes. In fact, as discussed for instance in [16], a power reduction can result in longer execution times of applications and therefore in an increase of the total energy consumption. For better understanding the role of power and time in contributing to overall energy usage, we study their relation by means of evaluating the energy per job (), assessing the amount of energy spent to serve one job.
In the following, we discuss the assumptions that have been adopted in building the power models. We assume that applications are executed on virtual machines managed by the cloud infrastructure and that an underlying monitoring environment is available to provide information about typical usage metrics of running VMs (such as CPU usage). Some parameters of the physical hosts on which virtual machines are being deployed and run are also assumed to be known. In detail, the following information is required to be available:
- where is the CPU usage of the physical host, is the power consumed when the host is idle (i.e., it is on and ready to provide service, but does not perform any work) and is the power consumed when the host is fully utilized;
- the host’s capacity in terms of the number of CPU cores, ;
- for each VM, the CPU usage for the VM, .
As described more in detail in Section 3.2, we tested our models in a federated cloud infrastructure, which is able to provide the above-mentioned information and monitoring infrastructure.
As our focus in this paper is on the characterization of the application power models, we suppose that all virtual machines being considered have the same configuration, and we analyze in detail their performance and energy efficiency considering different types of access policies to shared storage, as discussed in Section 4, and in different execution environments (Section 5). However, the proposed power model has a broader applicability, and it could be exploited also in more general scenario.
First, we analyze the relationship between the total power consumed by a physical host and by the VMs running on it. In general, the power consumption of a host is composed of two components, the idle power and the busy power. We adopt the model proposed by [7] to estimate the power consumption of a physical host h:
In this formula, the power consumed by other components, such as memory and local storage, although minor, is not neglected, but included in the value of .
The power consumed by the host is distributed to the n VMs running on it. Since is reached only when all cores are simultaneously utilized, Equation (2) can be written in terms of the VMs’ utilization:
with the utilization of the i-th VM. Note that for single core VMs, is in the range . For VMs with multiple cores, the result can be extended by allowing to range from zero to the number of cores.
To attribute idle power to the VMs, we adopt a policy that attributes an equal fraction of to each running VM on the host. Equation (3) is rewritten as:
where,
The equality policy used in Equation (4) is motivated by experimental evidence collected from our cloud infrastructure, which has shown that, regardless of the number of VMs present on the host and their size, the host’s idle power does not vary or negligibly varies (see Section 3.2). Thus, it is reasonable for each VM to be responsible for an equal contribution to the total idle power. Furthermore, notice that, in general, the idle power credited to a VM will vary depending on the number of running VMs n on the host. It will have the maximum value (i.e., equal to ) when and the minimum value when , where is the maximum number of VMs that can be run on the host. Equation (4) also implies a linear relation between and that has been confirmed by our experimental data (see Section 3.2):
As a final comment, we want to stress that Equation (4) to Equation (6) are per host: all of the parameters refer to the particular host where the VMs are being executed. In the case of a heterogeneous environment, there will be different versions of such equations, each one characterized by the parameters that describe the corresponding server on which the VMs are executed.
From Equation (4), a general formula to derive the power consumption of a single VM running on a physical host is:
As in this paper, we focus on computing intensive applications, executed as batch workloads, we define now the metric assuming that a batch consists of an application run multiple times. Such applications are often characterized by long execution times for the computing part of the application. A usual scenario is a scientist setting up experiments to analyze a problem. Each experiment requires one or more runs of the application that might have the same or different sets of parameters. In this context, each run is considered as a job. The jobs in an experiment can be executed either in parallel or in sequence depending on the application configuration and on the user requirements. This application type is characterized by the number of jobs required to be executed.
Let us consider an experiment consisting of N jobs and n VMs allocated to the experiment. Note that usually in batch processing applications, VMs are acquired and released at the same time in order to simplify the resource accounting and management. The value of n can vary from one, where all jobs are executed using a single virtual machine, to N, where each job is executed in a separate virtual machine. The n VMs can be deployed on different physical hosts depending on the hosts’ capacity and their current running VMs. The power consumption of the experiment at a given time instant is:
where is computed by Equation (7). The total energy consumption of the experiment is:
and the energy per job is computed as:
3.2. Power Model Validation
In this section, we validate the power model of an experiment involving different numbers of VMs, using a real federated cloud facility. We performed the validation experiments within the ECO2Clouds European project [3]. ECO2Clouds provides a federated cloud infrastructure, based on the experimental BONFire (http://www.bonfire-project.eu/) platform, augmented with ecometrics for measuring parameters on energy and power consumption and CO2 emissions at the host, VM and application levels. The monitoring infrastructure is based on the open source platform Zabbix (http://www.zabbix.com/). A general overview of ECO2Clouds is given in [17].
It is worth mentioning that in clouds, power is measured at the host level. In our federated cloud infrastructure, PDUs (power distribution units) are used to distribute electric power to physical devices and to collect their power usage information. As a side note, currently several systems now provide software-level measuring of energy for hosts based on the monitored values at a system level, so in the future, measuring at the physical level might not be necessary anymore. In our cloud environment, based on experimental evidence measured at the PDU level, the proportional relation between host usage and its consumed power shown in Equation (2) can be considered as a good approximation in the type of host chosen for the experimental setting ( QuadCore Intel Xeon@2.83 GHz, 32 GB RAM), as shown in Figure 1. Further experimental measurements from ECO2Clouds for other types of hosts can be found in [26], and in general, a linear model provides a good approximation.
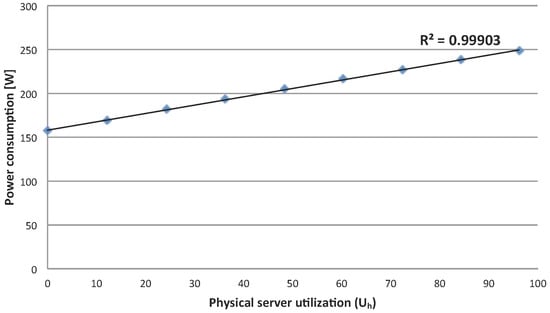
Figure 1.
Power consumption in a single host depending on usage.
To measure , we created VMs on the selected physical host without executing any applications on them. The number of VMs ranges from one to eight for the host that has eight CPU cores. For each number of VMs, power samples are collected over an idle period (15 min). The value of is computed as the average of power samples over these idle periods. We notice that regardless of the number of VMs present on the host, idle power does not change or negligibly changes (Table 1).

Table 1.
Measured values of and .
To measure , we executed a stress command (https://linux.die.net/man/1/stress) on CPU simultaneously on each VM, creating a peak period with 100% CPU load of the host. We repeated the stress command five times, each time for 15 min. The value of is computed as the average of power samples over peak periods. Table 1 shows the measured values of and for the physical hosts used in our experiments.
To validate the VM power model (Equation (8)), we created n VMs, with n ranging from one to eight, on the selected physical host, and for each value of n, we executed the CPU stress command simultaneously on the n VMs. The command is executed repeatedly five times, each time for 15 min for each value of n. The consumption of the experiment (corresponding to each value of n) is computed as an average of collected power samples. Figure 2 shows the validation results of the power model.
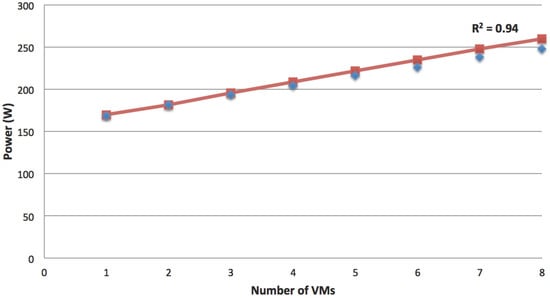
Figure 2.
Power consumption related to the number of running VMs.
4. Modeling Application Energy Efficiency
In this section, we model applications in terms of their performance and analyze the energy consumed per job, focusing in particular on the impact of shared storage resources during the execution.
One of the goals is to determine the Pareto frontier for a given number of jobs in which VMs running the applications are hosted, which will be the basis for analyzing in Section 5 the behavior of applications running on different numbers of VMs in terms of energy per job both with homogeneous and with heterogeneous hosts, characterized by different values of and .
We consider a generic batch application composed of two separated phases: the data loading phase and the computation phase. As the goal is to analyze the effect of sharing resources, and in particular, storage, we assume that it is configured such that the data storage is placed on a separated resource (named the storage) and is shared among other VMs (named the application) that perform the computation. The sharing of the storage represents a shared resources scenario that is common in data centers and often requires investigation to identify conditions that lead to a deficient use of resources.
We model the different configurations using queuing models. In the queuing models, computing resources (e.g., the VMs) are represented as a network of stations, and the number of executed jobs is presented as customers. Different types of stations are available in which the basic ones can be either the queue station (i.e., the station has a queue to store waiting jobs) or the delay station (i.e., the station has no queue). The stations are characterized by their service demands (i.e., times required to serve one job). We assume that two access policies can be used to access the storage: synchronous access, when all VMs access the storage at the same time, starting together, and asynchronous access, with no synchronization. In the model, other stations perform advanced operations, such as fork and join, to simulate synchronous/asynchronous storage access.
Given that the application has to serve N jobs, we aim to study the following objectives:
- To compute bounds on the execution time and the energy per job, as well as analyzing the effect of different access policies (asynchronous vs. synchronous) to shared resources in terms of performance and energy consumption. In order to find these bounds, we examine different configurations to execute a given number of jobs N, starting from the initial results of [29] that allow us to consider the most significant configurations. Each configuration differs in the number of used VMs and shared resource access policies (i.e., synchronous/asynchronous access). The bounds are derived from the configurations that give extreme values, i.e., one VM to execute all of the jobs and N VMs, one for each job. We perform this analysis by employing queuing theory techniques.
- To identify the bottleneck due to the presence of shared resources and the consequent impact to performance and energy consumption.
- To evaluate performance and energy consumption of configurations that use different number of VMs to execute a required number of jobs, considering both homogeneous and heterogeneous infrastructures.
4.1. Queuing Models for the Case of Asynchronous Access
For asynchronous access, the queuing models are built as shown for example in Figure 3 and Figure 4. Figure 3 is the case when the number of used VMs is minimum (named the minimum case), i.e., one VM for the application, whereas Figure 4 is when the number of used VMs is maximum (named the maximum case) with N application VMs for N jobs. Other intermediate scenarios can be modeled in a similar way as shown for example in Figure 5 when two application VMs are used and the router uses the round robin policy to schedule jobs among application VMs.
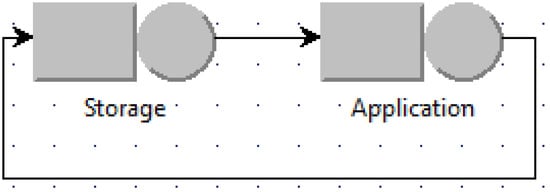
Figure 3.
Minimum number of used VMs with asynchronous access.
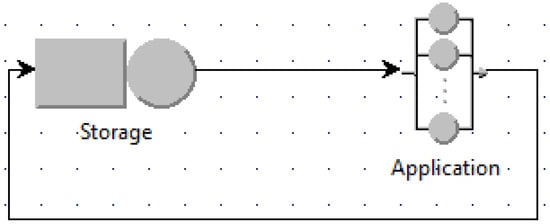
Figure 4.
Maximum number of used VMs with asynchronous access.
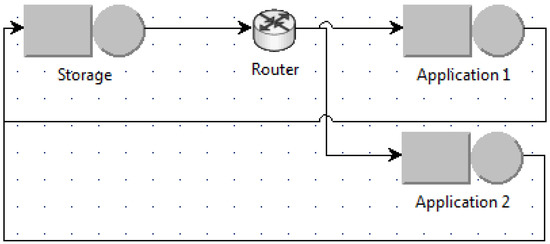
Figure 5.
Intermediate scenario: two application VMs are used (asynchronous access).
Analyzing these models shows that the two extreme cases in Figure 3 and Figure 4 indeed give the bounds on the execution time and the energy per job of the system. The minimum case provides the upper bound for the execution time and the lower bound for the energy per job, whereas the maximum case provides the lower bound for the execution time and the upper bound for the energy per job. In other cases, the execution time and the energy per job fall within this range.
We go further building the corresponding Markov chains for the queuing models of these two cases in order to obtain analytical formulas for the bounds, as shown in Figure 6 and Figure 7. In Markov chains, each node represents the system state that contains the corresponding number of jobs in the storage and in the applications; whereas, each edge represents the transition among states and is associated with a transition rate. In this specific scenario, is the rate a job finishes at the storage and moves to the application. is the rate a job is completed at the application for the minimum case, and is the rate a job is completed at the application for the maximum case. The parameter is the service demand of the storage; is the service demand of the application; and i is the number of jobs present in the application VMs.

Figure 6.
Markov chain for the minimum case with asynchronous access.

Figure 7.
Markov chain for the maximum case with asynchronous access.
By computing the steady state solution of Markov chains and by applying Little’s law, we obtain the closed-form solutions for the execution time, using standard queuing network theory [30]: the upper bound is given in Equation (11), and the lower bound is given in Equation (12).
Bounds on the average energy per job can be derived using Equation (10). Note that the power consumption of a VM depends on the number of running VMs n on the host (Equation (7)), and the value of n can be known only at runtime. In order to derive the bounds, we assume the idle power of the VM is minimum, assuming that the host is running the possible maximum number of VMs (i.e., , from the considered application or other applications). The upper bound and the lower bound are respectively given by Equations (13) and (15):
where is the average CPU utilization of the application VMs and is given by:
4.2. Queuing Models for the Case of Synchronous Access
Understanding the impact of synchronization on shared resources is important to anticipate the resource deficiencies and schedule in advance the required resources. Similarly to the asynchronous case, we build and analyze the queuing models of different synchronous scenarios, changing the number of used VMs for a given number of jobs N, as shown for example in Figure 8 and Figure 9. The fork and join stations perform the synchronization: a single customer enters the fork station, and it is immediately split into N jobs that are directed to the storage node. This models the behavior of applications that load from disk to memory their state at the beginning of their execution. The join station after the application node waits for all of the jobs to be finished, before merging them in a single customer that is immediately routed to the join node to start a new cycle with another batch of N jobs to elaborate.

Figure 8.
Minimum number of used VMs with synchronous access.
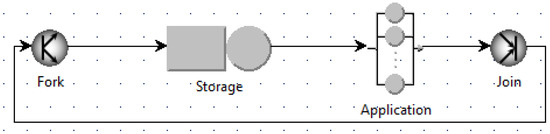
Figure 9.
Maximum number of used VMs with synchronous access.
Analyzing the queuing models provides similar results with the asynchronous case. The minimum case and maximum case provide the bounds of the execution time and the energy per job with significantly larger values of the bounds caused by the synchronization.
The corresponding Markov chains can be built to analyze these bounds analytically. However in this case, there is are no closed-form solutions for the execution time and the energy per job; thus, the numeric solutions are to be obtained by solving the Markov chains for each specific value of N.
4.3. Batch Workload Model Validation
The validation aims to verify the proposed energy model for batch workloads. The model has been evaluated under different configurations using an application experimented for batch workloads in the ECO2Clouds project. The considered application computes the trajectories followed by eel cohorts during their travel along the Atlantic Ocean [31]. The application workflow consists of two phases: it starts with a short data loading phase, followed by a much longer computing-intensive processing phase. The application is configured so that multiple executing instances can be launched in parallel, and the data storage storing eels data are shared.
The experiments are designed by considering different configurations to execute the application. A configuration refers to the variation in terms of the number of used VMs, the amount of resources allocated to each VM, the number of jobs assigned to the VMs, execution policies (i.e., parallel or sequence) and access policies to the shared resources (i.e., synchronous or asynchronous). A job in this context is the execution of an instance of the application. In this paper, we test the synchronous model using two basic configurations: (1) one VM for all: only one VM is used to execute N jobs; (2) one VM for each: one VM is dedicated to execute each job.
In order to validate Equation (9), we employ queuing theory to model the configurations and estimate their execution time T and the VM utilization . Each configuration is represented by a queuing model whose inputs include the number of jobs to be executed, the stations and their service demands. Parameters were estimated from measurements collected from the ECO2Clouds system using fitting and averaging procedures. The model outputs are the average utilization of the stations and the execution time T. We use the modeling tool JMT [32] to simulate each model to obtain the model parameters. The obtained outputs are applied to Equations (7) to (9) to estimate the average energy consumption of each configuration. We started validating the response times measured in several experiments run on the ECO2Clouds system with the one obtained from the queuing model. Figure 10 shows that model predictions are close to the running times measured on the system for both the single VM and the maximum VMs scenario. Figure 11 shows the validation results comparing the model-produced values with experimental energy consumption measured running the application on the ECO2Clouds infrastructure described in Section 3.2, confirming a good correspondence of the experiments to the proposed models ( is respectively 0.97 and 0.96 in the two cases).
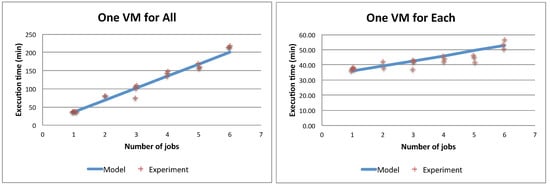
Figure 10.
Comparison of the model and experimental system response times.
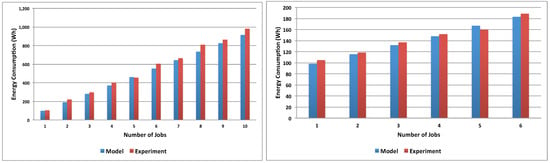
Figure 11.
Energy consumption for batch configurations one VM for all (left) and one VM for each (right).
5. Analysis of Energy Consumption and Response Times
In this section, we illustrate how the models presented in the previous sections can be used to make decisions in terms of resources allocated to applications characterized by a batch workload.
In the first place, we analyze the results of the given models comparing the cases of asynchronous and synchronous accesses, focusing on the minimum and maximum values of the two different cases. We analyze how these parameters change when the number of jobs varies. As an example, in Figure 12 and Figure 13, we visualize respectively the bounds of the two access policies with , and N in the range [1, 30] for both the response time and the energy per job. The impact of synchronous access to the shared resources can be seen by comparing these bounds together. While with the minimum case, the asynchronous and the synchronous policies do not show significant differences because the effect due to the lack of computing resources (i.e., minimal application VMs are used for the execution) dominates the effect of synchronization, the maximum case shows a significant impact caused by concurrent access to the shared storage. Both the execution time and the energy per job are more than doubled when synchronization is considered.
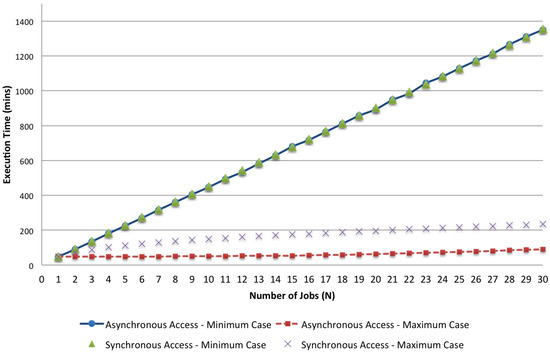
Figure 12.
Bounds on execution time.
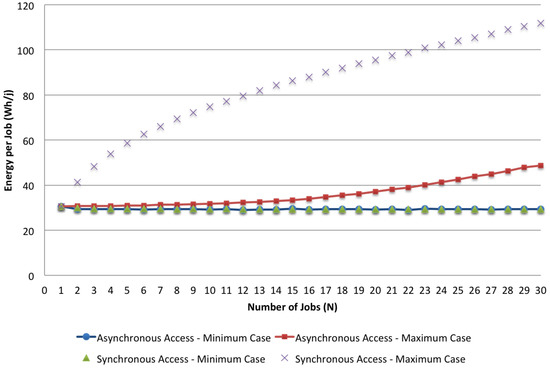
Figure 13.
Bounds on energy per job.
5.1. Varying the Number of VMs: Identification of Bottlenecks and Their Impact
A bottleneck is present in every system where one resource performs poorer compared to others, and this leads to degradation of the whole system’s performance. In the considered problem of VM deployment, we want to examine how the application’s behaviors change while varying the number of available resources and identify when the occurrence of a bottleneck is about to emerge. We start with a fixed number of jobs and varying the number of the used VMs to serve them. Queuing models are built to analyze each combination between the number of jobs and the number of used VMs for executing the application. We first analyze the case of single batch workload with . To compare different configurations, let us examine for example Figure 14 and Figure 15, which show, respectively for the asynchronous and synchronous case, the utilization of the storage and of the application VMs for two different access policies, when varying the number of used application VMs in the range of [1, 24].
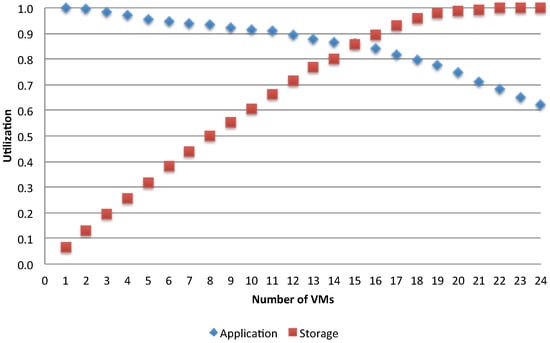
Figure 14.
Bottleneck switching with asynchronous access.
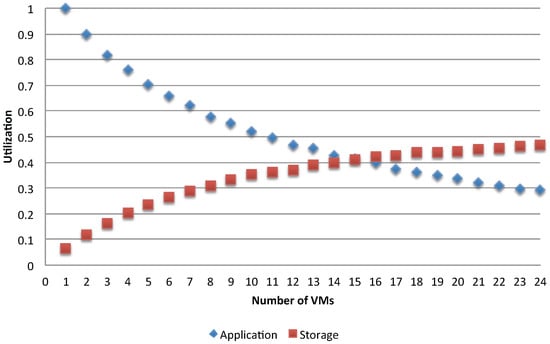
Figure 15.
Bottleneck switching with synchronous access.
The trends show a switching point in the usage of two resources. Before approaching this point, the application VMs are more utilized than the storage, while the opposite is obtained after this point. It is clear that, given a fixed N, as the number of available application VMs increases, the shared storage is increasingly overloaded and becomes the system’s bottleneck. The switching point signals when this is about to happen and it occurs when (i.e., the total demand for the storage becomes greater than the one for each parallel application run), that is when:
The impact of the bottleneck phenomenon on the application’s efficiency is further analyzed in Figure 16 and Figure 17, which show the execution time and energy per job. Before the occurrence of the bottleneck in the shared storage (), the execution time is significantly reduced by adding more VMs to serve the jobs. However, as soon as the storage becomes the bottleneck, the gain in execution time is negligible. On the other hand, adding more VMs increases the energy per job, but the rate at which this occurs changes as the storage becomes the bottleneck. This result suggests insight and improvement to be made to the application. First, there is no gain by adding more VMs to serve the jobs after the switching point . Second, in order to further improve the application’s efficiency, one can choose to replicate the storage so that loads are shared among several storage resources.
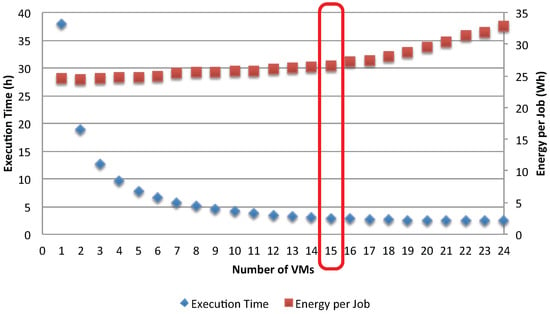
Figure 16.
Execution time and energy per job with asynchronous access.
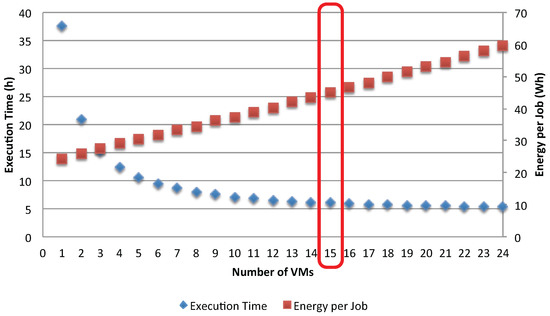
Figure 17.
Execution time and energy per job with synchronous access.
Another observation is made by comparing the impact of access policies to shared resources. The synchronization has dropped about 50% of the resources utilization (see Figure 15) compared to the asynchronous case (see Figure 14), showing the effects of interference between the execution applications. As a result, the gain in reducing the execution time is smaller while the energy per job increases faster.
Figure 18 shows a clear difference of the energy per job between synchronous and asynchronous access policies. In addition, it also shows when the bottlenecks have a significant impact on the energy per job: the advantage of adding new VMs is almost null in terms of response time after the bottleneck point is reached, while the energy per job continues to increase. As these two curves are computed considering that the minimum possible idle time is assigned to each VM, they can be used as a reference in making decisions at runtime about possible improvements in resource usage.
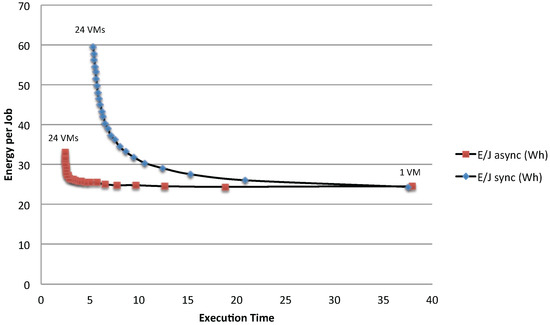
Figure 18.
Bounds for energy per job and execution time varying the number of VMs.
5.2. Total Energy Analysis for a Single Workload
In cloud infrastructures, the storage can be either managed by a specific device (i.e., a RAID connected to the physical machine through a SAN) or by dedicated VM nodes that implement some distributed file system, such as Ceph [33]. For this reason, considering the energy impact of storage cannot be trivial, and in determining the energy per job in Equation (10), we have neglected the file manager contribution. In this section, we focus on the total energy consumed by the application determined using Equation (9), with the additional hypothesis that m extra VMs handle the storage. In particular, Equation (8) becomes:
In the following, we will discuss (totally shared storage) for both the synchronous and asynchronous cases and (totally duplicated storage, with each computing VM with its own storage) for the asynchronous case. Figure 19 shows the total energy consumption of the considered application: as can be seen, for the shared storage case, the gain in execution time and total energy continuously increases until it reaches the point where the storage becomes a bottleneck. The totally parallel case has instead a constant energy consumption (since no bottleneck is present): for this type of system, the trivial solution is then to use as many VMs as possible, to produce the desired result with the minimum response time. It has to be noted, though, that full replication of data is possible only if there is no sharing of data written by the applications during the experiments; otherwise, synchronizations costs should be added.
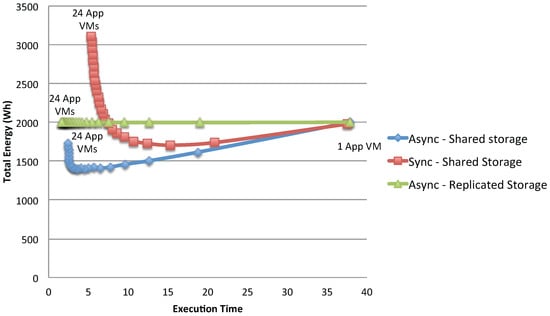
Figure 19.
Total energy consumption by varying the number of VMs.
This insight is also reflected in the analysis of the energy response time product metric (ERP; see for example [34]), which considers the trade-off between energy and time spent for a given number of jobs. Figure 20 shows that the best trade-off between execution time and total energy consumption is obtained around the optimal point where the single storage and the application resources are equally utilized. The proposed queuing network model can be used to determine the exact optimal configuration in terms of the number of VMs with a simple what-if analysis. For example, in the considered scenario, the optimal number of VMs in terms of the ERP metrics is for the asynchronous case and for the synchronous one.
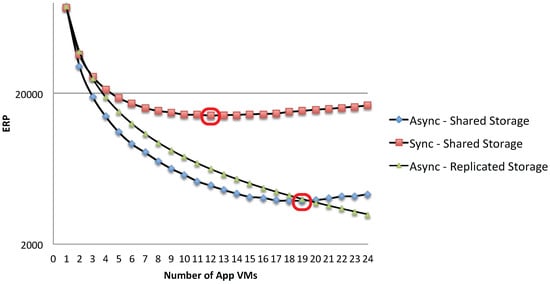
Figure 20.
Analysis of the trade-off between total energy and execution time.
In the present section, we have examined the case in which the physical machines are homogeneous in terms of energy profiles. The following section will consider the case in which heterogeneous energy profiles may be available, to further analyze the energy per job in different situations. To simplify the presentation, in the following, we will consider only the case in which the storage is totally shared ().
5.3. Execution in Heterogeneous Environments
We now suppose that the data center is equipped with two types of physical machines, the first type being the one considered in the previous examples, plus a set of newer servers that work faster, are characterized by more cores (20 instead of eight), an idle power that is of the one of the older machines and the same maximum power consumption. Let us call α the percentage of the newer machine present in the network. If we run jobs on n VMs, then we suppose that VMs (the closest integer to the product of α and n) are run on the newer hardware, and on the older machines.
Parameter still represents the number of jobs that need to be executed. We suppose that the performance of the storage, , is unaffected by the architectural change, while the application takes time units when run on the older hardware and when it is executed on the newer machines. We still consider the synchronous and asynchronous scenario, but to allow the analytical tractability of these heterogeneous scenario, we added some additional assumptions.
For the asynchronous case, we replace the round robin routing of jobs to the VMs with random routing, where all VMs can be chosen with the same probabilities. In general, this can lead to a less performant system compared to round robin, but this modification allows the models presented in Figure 3 to Figure 5 to become separable networks and be analyzed in linear time using the mean value analysis technique [30].
Figure 21 shows the results for different values of , with the number of VMs in the range . We have avoided the cases with , because we wanted and to be different integers for all of the considered values of α. As expected, the best results in terms of energy per job can be achieved when all VMs are run on newer hardware. As concerns the performance, newer machines produce better results only for configurations where the disk is not the bottleneck (). For , there is basically no gain in using faster machines: this characteristic can be exploited in the resource allocation of a data center when deciding whether a job must be assigned to a fast or to a slow machine. Fast machines should be reserved for CPU bound applications, while slower ones can be used for I/O bound applications without having an impact on the overall response time. When mixing both newer and older machines, special care should be taken when the main aspect that needs to be considered is the energy per job. Two scenarios are possible, depending on whether the number of slower machines is larger () or smaller () than the one of the faster machines. In case we have a larger amount of older machines, the addition of a newer machine should be envisaged, since it can produce a visible reduction in the energy per job. On the contrary, if we have a larger amount of newer machines, the addition of an old one should be avoided since it will produce a sensible increase in the energy consumption.
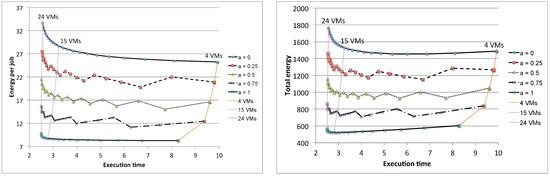
Figure 21.
Heterogeneous environment: energy per job (left) and total energy (right) with asynchronous access.
To analytically study the synchronous case, we limit our attention to round robin routing and to the deterministic service times (for both the application and the storage). In this way, each of the n VMs will start servicing the first job at time , with , and it will have to serve either or depending on its order in the round robin selection policy. We will present results where newer machines in the round robin cycle are selected first (we also have tested the case in which priority is given to slower machines and obtained basically the same behavior).
Figure 22 shows the results for and the number of VMs in the range . As a general trend, we see that there is always a noticeable performance increase, both in terms of response time and energy per job reduction, whenever the number of VMs allows terminating the N jobs in one less cycle: with jobs, this occurs with the number of VMs 1–10, . Otherwise, choosing intermediate numbers of VMs (e.g., ) produces only a degradation in the energy per job, since a larger idle power must be paid to finish all of the jobs in the same amount of time. Moreover, due to the deterministic assumptions and the synchronization, there is no influence on the number of VMs when the storage becomes the bottleneck: this however occurs for different number of VMs depending on the fact that they are of the older or newer type. Again, as expected, the best results are obtained when all of the VMs are run on newer hardware. However, due to the fact that a noticeable increase in performance can be seen only for a specific number of VMs, the curves for different values of α overlap at several points. For example, 16 slow VMs have more or less the same performance has 20 VMs with ( and ). This allows defining even more complex allocation policies, where both users and providers are involved, to choose an appropriate number of VMs depending on the availability of newer and older machines.
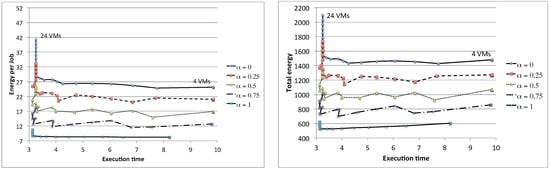
Figure 22.
Heterogeneous environment: energy per job (left) and total energy (right) with synchronous access.
The methodology proposed in this section could be easily extended to consider a larger number of classes of VMs: this however would require a more detailed description of the behavior of the infrastructure to solve issues connected to the policies used to privilege machines from one class with respect to ones of another when several choices are available.
As concerns the asynchronous case, MVA (Mean Value Analysis) could still be used, and the complexity would be where N is the total number of jobs in the system and k the number of considered classes. This happens because, thanks to the random selection assumption, each type of VM can be modeled with a different queue in the network. By exploiting the equality of the stations representing VMs of the same class, the identical queues are considered just once in the MVA procedure. When computing the total response time of the system, the number of queues is taken into account by multiplying the performance index of one queue per its multiplicity.
With a given policy to select a specific type of VM for new jobs that are starting, the proposed procedure could be extended to consider synchronous applications running on k classes of virtual machines with a complexity of , where n is the total number of machines (of all of the classes). This occurs because, thanks to the deterministic assumption and the specified policy for selection of the next VM, the exact evolution of the system can be predicted based on a simple scheduling of the start and the end times of the m jobs on the k possible different types of VMs.
In both cases, the linear complexity of the technique in the number of jobs N or VMs n and in the number of classes k allows considering very large data centers, composed of thousand of VMs and dozens of classes.
5.4. Two-Class Workload Analysis
In this section, we extend our analysis to a more general system where multiple workloads can be co-located and run together. Specifically, we study the impact of bottlenecks on the energy per job, the total energy and the execution time in a two-class workload system. Each workload is characterized by different service demands, as shown in Table 2. In the first class workload, the application is the natural bottleneck (), whereas in the second class workload, the storage is the natural bottleneck (). To analyze the co-location of two-class workloads, we fix the total number of jobs and combine different population mixes of these two classes. Then, we build the queuing models for each population mix and analyze the performance and energy usage of each combination.

Table 2.
Service demands of two considered workloads.
Figure 23 shows the energy per job of three different population mixes, (, ), (, ) and (, ), with the synchronous and asynchronous access policies. As can be seen, depending on the combination of the population mix, each combination yields a different optimal point. For example, the first combination contains 15 jobs of Class 1 and 35 jobs of Class 2, yielding the optimal number of VMs to be used for the application as ; whereas the second combination yields . While there is no exact solutions for finding optimal number in the multi-class workload system, several heuristics algorithms [35] can be used to search for a nearly optimal point.
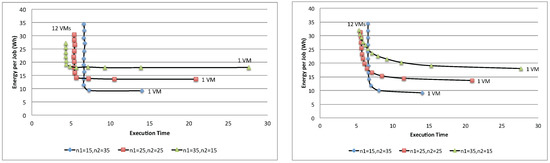
Figure 23.
Energy per job with asynchronous (left) and synchronous (right) access for two-class workloads.
Figure 24 and Figure 25 show respectively the total energy and ERP of the three population mixes. Similar to the case of a single-batch workload, each population mix yields an optimal point where it achieves the best trade-off of execution time and total energy, and adding more resources beyond this point is no longer beneficial. Furthermore, in this case, the proposed queuing network model can be used to determine such an optimal point.
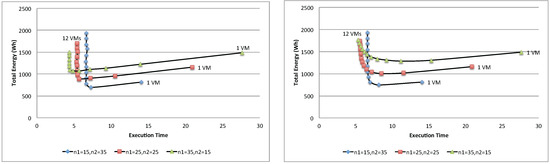
Figure 24.
Total energy with asynchronous (left) and synchronous (right) access for two-class workloads.
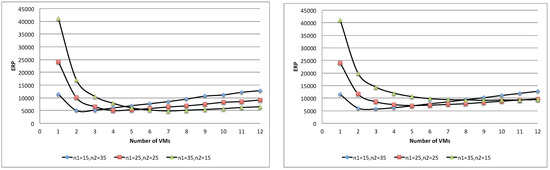
Figure 25.
Trade-off between total energy and execution time with asynchronous (left) and synchronous (right) access for two-class workloads.
5.5. Discussion
A final discussion about the proposed models concerns their usability. In particular, the underlying hypotheses in this paper are that both users and providers have some, even if limited, knowledge across layers. In fact, we assume that the monitoring infrastructure provides knowledge both about the VM characteristics and the servers on which they are deployed. Such knowledge is available within the ECO2Clouds project, but could not always be expected from other cloud infrastructures, although the trend is that monitoring systems on cloud platforms are currently providing more and more information to their users. On the other hand, we assume that providers might evaluate the energy consumption of the applications in execution having some knowledge of the parameters associated with the different application types. In the following, we discuss some of the assumptions from different user perspectives.
5.5.1. Application User Perspective
From the point of view of application users, the model requires that it is possible to evaluate the operating conditions of the host in which VMs are running. These include also some parameters directly related to the hardware characteristics of the host, such as . When these parameters are not available, an alternative is to assess them at an application level, with the only assumption that the monitoring infrastructure provides the power being consumed by the VM. Indeed, during the execution, can be easily assessed in idle times, while can be inferred from CPU usage, under the proportionality assumption. It must also be noted that these values in a complex infrastructure are inherently variable; therefore, continuous monitoring is necessary in any case. Therefore, the applicability of the proposed model is not limited to infrastructures providing information on the underlying resources, but it has a wider range of applicability. As shown in the previous sections, the users can evaluate the conditions in which applications are running. For instance, if VMs are running in homogeneous environments, the model allows the evaluation of the optimal number of VMs given the application characterizing parameters on storage and computation parts. It also allows comparing the actual monitored values to the theoretical ones, thus assessing if VMs are located in underutilized machines (which would result in higher idle time proportions in the given assumption of sharing idle times) or on machines that are consuming more than expected for other possible factors (overutilization, power profiles higher that the theoretical ones, unexpected bottlenecks). From these evaluations, the users might decide to drop underperforming VMs, or ask for alternative ones, or to vary the total used VMs.
These considerations are even more significant when a heterogeneous environment is being used. As discussed before, the quality of assigned VMs in terms of their energy profiles can vary significantly the optimal number of VMs to be used to get the best energy per job without varying response times. These analyses can therefore significantly improve, for instance, the cost of running the applications, as a lower number of machines could result in a better energy per job with the same performance for a given application.
5.5.2. Provider Perspective
From the provider perspective, the knowledge of the application characteristics is not always given, and this knowledge is important to better allocate VMs on servers. Having information collected at the application level, even if only limited to the type of application and its service demands, can result in important improvement of energy efficiency, reducing idle times in the data centers. The policies for attributing VMs to requesters could be changed on the basis of the application profiles, to avoid conflicting use of resources or to reduce idle power through consolidation. These data can be partially inferred by the usage patterns of the VMs, observing the usage behavior and comparing it to the different types of models.
6. Concluding Remarks
This paper addresses the issue of energy consumption from an application-level perspective. We propose analytical models to assess energy consumption and derive the energy per job for different configurations in data centers. The models have been validated using experimental data collected on a real cloud infrastructure executing controlled workloads. These results can be helpful for cloud consumers to evaluate the performance and energy per job of their applications running on VMs of different types and in assessing different configurations, while cloud providers can evaluate how different types of applications consume energy and, therefore, better allocate their resources to obtain maximum energy efficiency.
Starting from this work, several future directions are possible. First of all, the models can be the basis for more complex optimization studies of the energy consumption at the level of the individual applications. This can be achieved assessing the energy per job and the required response time of an application and allocating the VMs considering also the needed resources, replicating resources or changing application workflows in order to minimize energy consumption while satisfying time constraints. This evaluation can be performed dynamically, assessing the power consumption of virtual machines through the monitoring infrastructure. As the power consumption of VMs is in general variable due to changing conditions and usage of the cores, memory and disk of the hosts, this variability can be further exploited during execution, allocating the VMs where idle power is lower. More complex applications that involve other resource types, such as IO, memory and the network, are also a necessary extension.
In addition, this paper can open new scenarios for both application users and infrastructure providers to better exploit available resources negotiating the more convenient conditions on both sides. The goal in this case would be to offer to the users the best possible conditions to reduce as far as possible idle power during the computation.
Acknowledgments
This work has been partially supported by the ECO2Clouds European project (http://eco2clouds.eu/) funded by the European Commission within the 7th Framework Program and by the ACROSS (Autonomous Control for a Reliable Internet of Services) COST Action (IC1304). This work expresses the opinions of the authors and not necessarily those of the European Commission. The European Commission is not liable for any use that may be made of the information contained in this work. We would like to thank Giuseppe Serazzi for his invaluable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| utilization of a physical host | |
| utilization of a VM | |
| idle power of a physical host (W) | |
| maximum power of physical host (when the host is fully utilized) (W) | |
| power consumption of a physical host (W) | |
| power consumption of a VM (W) | |
| power consumption in an experiment | |
| energy consumption of an experiment | |
| N | number of jobs in an experiment |
| n | number of VMs used in an experiment |
| maximum number of VMs that can be deployed on a single physical host | |
| number of CPU cores in a physical host | |
| E | energy consumption (Wh) |
| S | service time (i.e., time required to serve a job) |
| D | service demand |
| T | execution time of an application |
| energy per job (Wh/j): energy consumed for serving a job |
References
- The Green Grid Consortium. Data Center Maturity Model. White Paper. 2011. Available online: http://www.thegreengrid.org/ (accessed on 6 December 2016).
- Barroso, L.A.; Hölzle, U. The Case for Energy-Proportional Computing. IEEE Comput. 2007, 40, 33–37. [Google Scholar] [CrossRef]
- ECO2Clouds Portal. 2014. Available online: http://eco2clouds.eu/ (accessed on 6 December 2016).
- Vitali, M.; Pernici, B. A Survey on Energy Efficiency in Information Systems. Int. J. Coop. Inf. Syst. 2014, 23, 1–38. [Google Scholar] [CrossRef]
- Beloglazov, A.; Buyya, R.; Lee, Y.C.; Zomaya, A. A taxonomy and survey of energy-efficient data centers and cloud computing systems. Adv. Comput. 2011, 82, 47–111. [Google Scholar]
- Kaur, T.; Chana, I. Energy Efficiency Techniques in Cloud Computing: A Survey and Taxonomy. ACM Comput. Surv. 2015, 48, 22. [Google Scholar] [CrossRef]
- Fan, X.; Weber, W.; Barroso, L.A. Power Provisioning for a Warehouse-Sized Computer. In Proceedings of the ACM International Symposium on Computer Architecture, San Diego, CA, USA, 9–11 June 2007.
- Narayan, A.; Rao, S. Power-aware cloud metering. IEEE Trans. Serv. Comput. 2014, 7, 440–451. [Google Scholar] [CrossRef]
- Zheng, X.; Cai, Y. Achieving Energy Proportionality in Server Clusters. Int. J. Comput. Netw. 2009, 1, 21–35. [Google Scholar]
- Mobius, C.; Dargie, W.; Schill, A. Power Consumption Estimation Models for Processors, Virtual Machines, and Servers. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1600–1614. [Google Scholar] [CrossRef]
- Kansal, A.; Zhao, F.; Liu, J.; Kothari, N.; Bhattacharya, A.A. Virtual machine power metering and provisioning. In Proceedings of the 1st ACM symposium on Cloud computing, Indianapolis, IN, USA, 10–11 June 2010; ACM: New York, NY, USA, 2010; pp. 39–50. [Google Scholar]
- Dhiman, G.; Mihic, K.; Rosing, T. A system for online power prediction in virtualized environments using gaussian mixture models. In Proceedings of the 2010 47th ACM/IEEE Design Automation Conference (DAC), Anaheim, CA, USA, 13–18 June 2010; ACM: New York, NY, USA, 2010; pp. 807–812. [Google Scholar]
- Bohra, A.; Chaudhary, V. VMeter: Power modelling for virtualized clouds. In Proceedings of the 2010 IEEE International Symposium on Parallel Distributed Processing, Workshops and Phd Forum (IPDPSW), Atlanta, GA, USA, 19–23 April 2010; pp. 1–8.
- GAMES: Green Active Management of Energy in IT Service Centers. 2012. Available online: http://green-datacenters.eu/ (accessed on 6 December 2016).
- Kipp, A.; Jiang, T.; Liu, J.; Fugini, M.; Vitali, M.; Pernici, B.; Salomie, I. Applying green metrics to optimise the energy consumption footprint of IT service centres. Int. J. Space-Based Situated Comput. 2012, 2, 158–174. [Google Scholar] [CrossRef]
- Chen, D.; Henis, E.; Kat, R.I.; Sotnikov, D.; Cappiello, C.; Ferreira, A.M.; Pernici, B.; Vitali, M.; Jiang, T.; Liu, J.; et al. Usage centric green performance indicators. SIGMETRICS Perform. Eval. Rev. 2011, 39, 92–96. [Google Scholar] [CrossRef]
- Wajid, U.; Cappiello, C.; Plebani, P.; Pernici, B.; Mehandjiev, N.; Vitali, M.; Gienger, M.; Kavoussanakis, K.; Margery, D.; García-Pérez, D.; et al. On Achieving Energy Efficiency and Reducing CO2 Footprint in Cloud Computing. IEEE Trans. Cloud Comput. 2016, 4, 138–151. [Google Scholar] [CrossRef]
- Cappiello, C.; Ho, T.T.N.; Pernici, B.; Plebani, P.; Vitali, M. CO2-Aware Adaptation Strategies for Cloud Applications. IEEE Trans. Cloud Comput. 2016, 4, 152–165. [Google Scholar] [CrossRef]
- Gelenbe, E.; Lent, R. Trade-offs between energy and quality of service. In Proceedings of the Sustainable Internet and ICT for Sustainability (SustainIT), Pisa, Italy, 4–5 October 2012; IEEE: New York, NY, USA, 2012; pp. 1–5. [Google Scholar]
- Paya, A.; Marinescu, D. Energy-aware Load Balancing and Application Scaling for the Cloud Ecosystem. IEEE Trans. Cloud Comput. 2015. [Google Scholar] [CrossRef]
- Adhikari, J.; Patil, S. Double threshold energy aware load balancing in cloud computing. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; IEEE: New York, NY, USA, 2013; pp. 1–6. [Google Scholar]
- Dayarathna, M.; Wen, Y.; Fan, R. Data Center Energy Consumption Modeling: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 732–794. [Google Scholar] [CrossRef]
- Pore, M.; Abbasi, Z.; Gupta, S.K.S.; Varsamopoulos, G. Energy aware colocation of workload in data centers. In Proceedings of the 2012 19th International Conference on High Performance Computing (HiPC 2012), Pune, India, 18–22 December 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 1–6. [Google Scholar]
- Moreno, I.S.; Yang, R.; Xu, J.; Wo, T. Improved energy-efficiency in cloud datacenters with interference-aware virtual machine placement. In Proceedings of the 2013 IEEE Eleventh International Symposium on Autonomous Decentralized Systems (ISADS), Mexico City, Mexico, 6–8 March 2013; pp. 1–8.
- Mastelic, T.; Brandic, I. Recent Trends in Energy-Efficient Cloud Computing. IEEE Cloud Comput. 2015, 2, 40–47. [Google Scholar] [CrossRef]
- The ECO2Clouds Team. D4.4: Results of Optimization and Adaptation of Application Deployment in Federated Cloud; Technical Report; The ECO₂Clouds Team: Barcelona, Spain, 2014. [Google Scholar]
- Tutschku, K.; Mehri, V.A.; Carlsson, A.; Chivukula, K.V.; Christenson, J. On resource description capabilities of on-board tools for resource management in cloud networking and NFV infrastructures. In Proceedings of the IEEE International Conference on Communication, ICC 2015, London, UK, 8–12 June 2015; IEEE: New York, NY, USA, 2016; pp. 442–447. [Google Scholar]
- Aceto, G.; Botta, A.; de Donato, W.; Pescapè, A. Cloud monitoring: A survey. Comput. Netw. 2013, 57, 2093–2115. [Google Scholar] [CrossRef]
- Gribaudo, M.; Ho, T.T.N.; Pernici, B.; Serazzi, G. Analysing the Influence of Application Deployment to Energy Consumption. In Proceedings of the 3rd Workshop on Energy-Efficient Data Centers (E2DC), Cambridge, UK, 10 June 2014.
- Lazowska, E.D.; Zahorjan, J.; Graham, G.S.; Sevcik, K.C. Quantitative System Performance: Computer System Analysis Using Queueing Network Models; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Melià, P.; Schiavina, M.; Gatto, M.; Bonaventura, L.; Masina, S.; Casagrande, R. Integrating field data into individual-based models of the migration of European eel larvae. Mar. Ecol. Prog. Ser. 2013, 487, 135–149. [Google Scholar] [CrossRef]
- Bertoli, M.; Casale, G.; Serazzi, G. JMT: Performance engineering tools for system modeling. ACM SIGMETRICS Perform. Eval. Rev. 2009, 36, 10–15. [Google Scholar] [CrossRef]
- Weil, S.A.; Brandt, S.A.; Miller, E.L.; Long, D.D.E.; Maltzahn, C. Ceph: A Scalable, High-performance Distributed File System. In Proceedings of the 7th Symposium on Operating Systems Design and Implementation, Seattle, WA, USA, 6–8 November 2006; USENIX Association: Berkeley, CA, USA, 2006; pp. 307–320. [Google Scholar]
- Cerotti, D.; Gribaudo, M.; Pinciroli, R.; Serazzi, G. Stochastic analysis of energy consumption in pool depletion systems. Lect. Notes Comput. Sci. 2016, 9629, 25–39. [Google Scholar]
- Balbo, G.; Serazzi, G. Asymptotic analysis of multiclass closed queueing networks: Multiple bottlenecks. Perform. Eval. 1997, 30, 115–152. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).