A Numerical Estimation of a RFID Reader Field and SAR inside a Blood Bag at UHF
Abstract
:1. Introduction
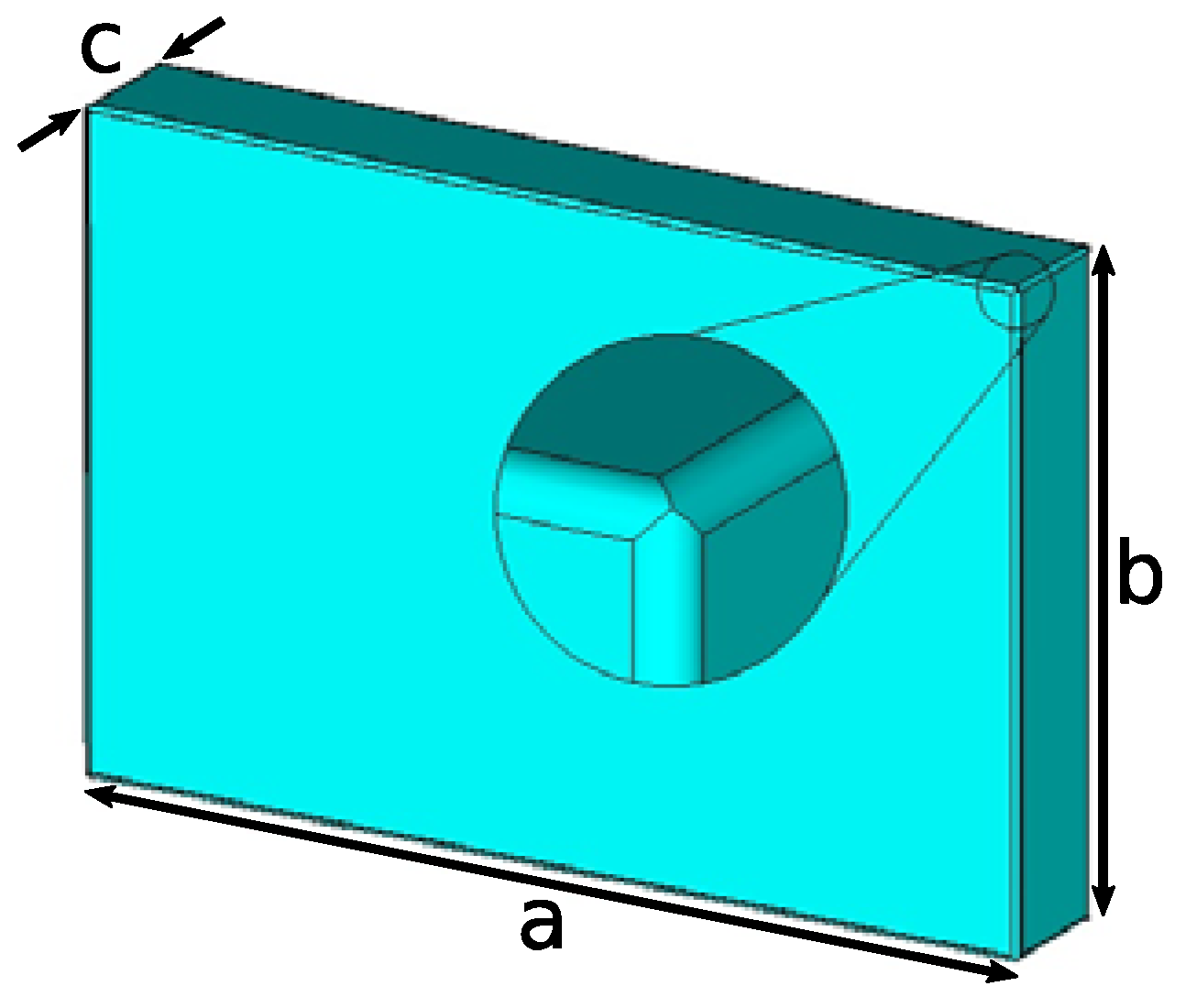
2. Materials and Methods
- field distribution along a straight line, orthogonal to the bag face, crossing the bag;
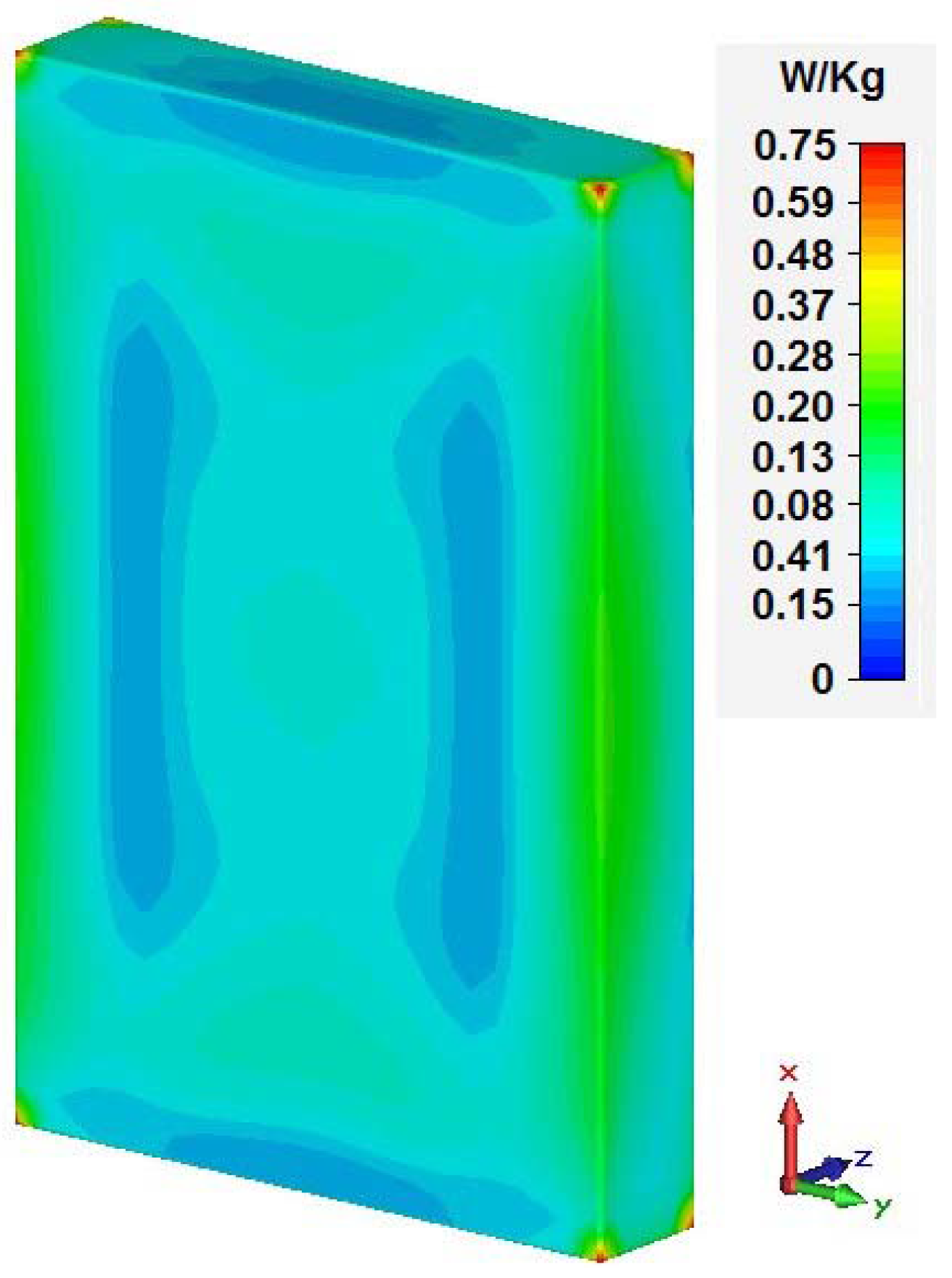
- the local SAR in the whole bag.
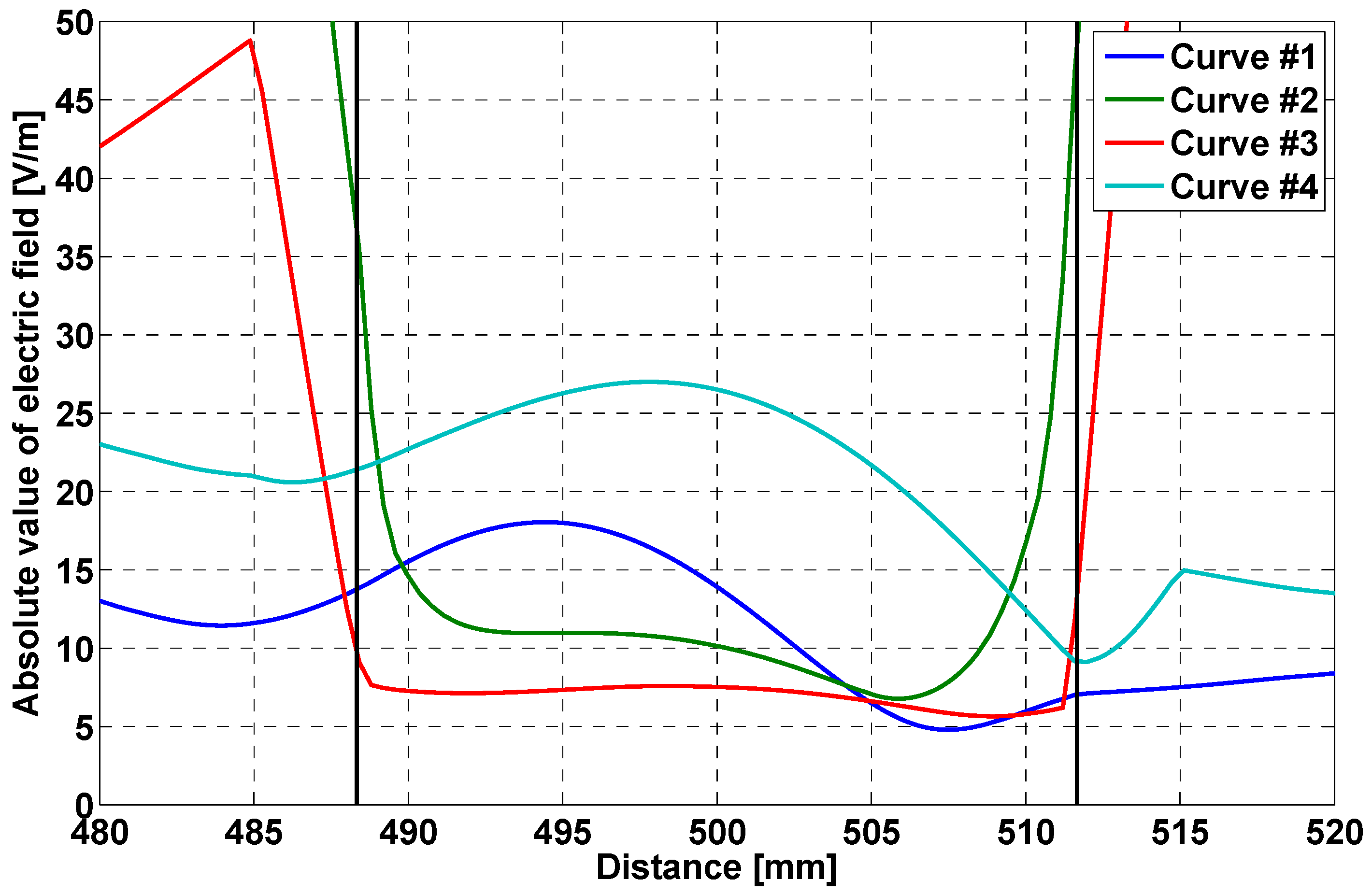
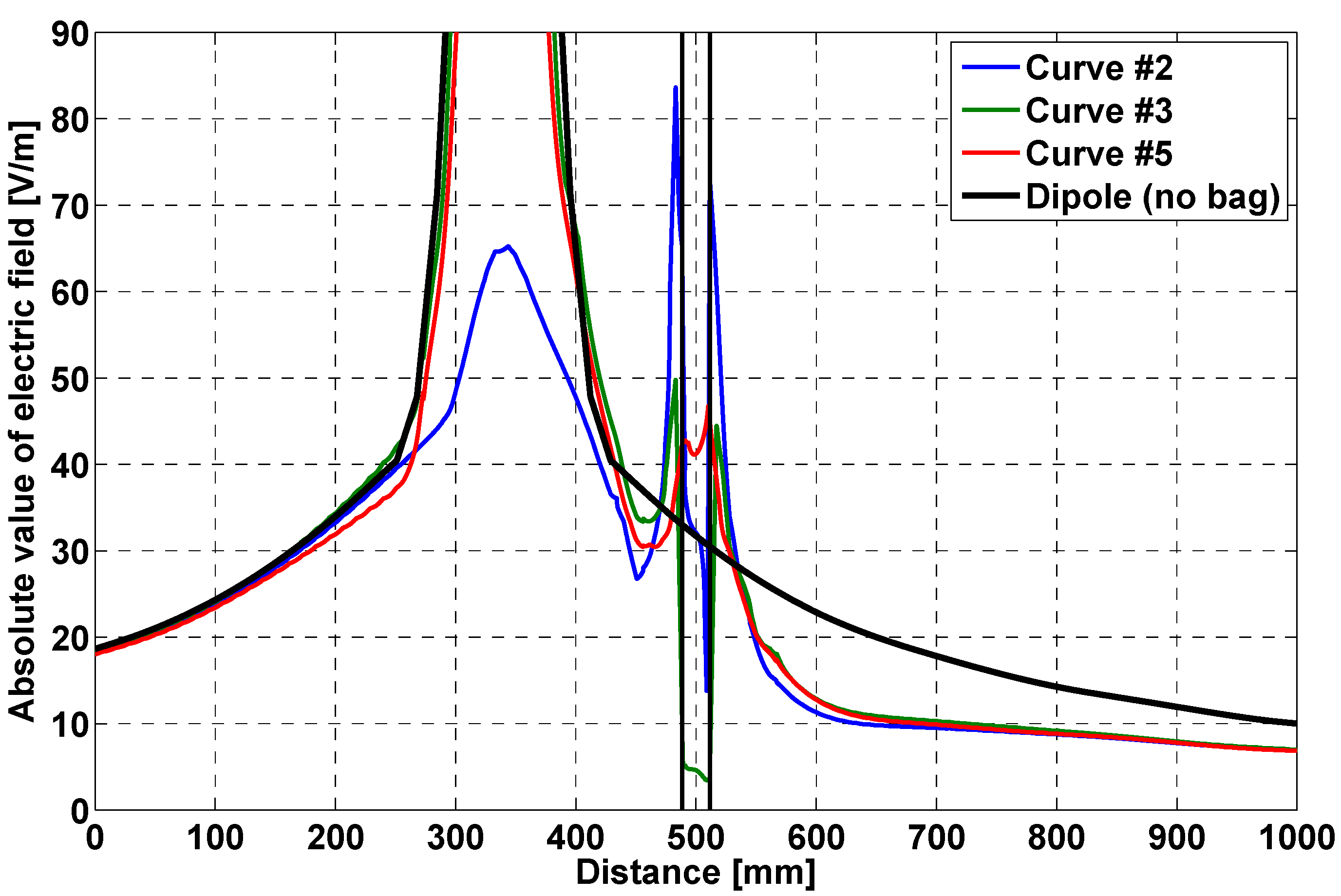
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Finkenzeller, K. RFID Handbook: Fundamentals and Applications in Contactless Smart Cards and Identification, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Dobkin, D.M. The RF in RFID: UHF RFID in Practice, 2nd ed.; Newnes: Waltham, MA, USA, 2012. [Google Scholar]
- Chiao, J.-C.; Kissinger, D. Medical Applications of RF and Microwaves—Applications and Events. IEEE Microw. Mag. 2015, 16, 14–18. [Google Scholar] [CrossRef]
- Bocan, K.N.; Ervin Sejdić, E. Adaptive Transcutaneous Power Transfer to Implantable Devices: A State of the Art Review. Sensors 2016, 16, 393. [Google Scholar] [CrossRef] [PubMed]
- Borelli, G.; Caredda, F.V.; Fanti, A.; Gatto, G.; Mazzarella, G.; Orrù, P.F.; Zedda, F. Preliminary study of RFID technologies for healthcare applications. In Proceedings of the 23rd Congress of the International Federation of Hospital Engineering (IFHE), Buenos Aires, Argentina, 13–16 October 2014.
- Borelli, G.; Caredda, F.V.; Fanti, A.; Gatto, G.; Mazzarella, G.; Montanari, R.; Orrù, P.F.; Volpi, A.; Zedda, F. Healthcare Supply Chain optimization: A comparison between two RFID-based reengineered processes. In Proceedings of the Summer School Francesco Turco, Senigallia, Italy, 9–12 September 2014; pp. 7–12.
- Davis, R.; Gottschall, J.; Gutierrez, A.; Hohberger, C.; Veeramani, D.; Holcombe, J. Absence of acute adverse in vitro effects on AS-1 RBCs and whole blood–derived platelets following prolonged exposure to 13.56 MHz radio energy. Transfusion 2010, 50, 1596–1603. [Google Scholar] [CrossRef] [PubMed]
- Knels, R.; Ashford, P.; Bidet, F.; Böcker, W.; Briggs, L.; Bruce, P.; Csöre, M.; Distler, P.; Gutierrez, A.; Henderson, I.; et al. Guidelines for the use of RFID technology in transfusion medicine. Int. J. Blood Transf. Med. 2010, 98 (Suppl. 2), 1–24. [Google Scholar]
- Davis, R.; Gottschall, J.; Gutierrez, A. Cellular and Protein Impact of RF Energy on Red Cells and Platelets; Report to the FDA; Food and Drug Administration: Silver Spring, MD, USA, 2008.
- Davis, R.; Gottschall, J.; Gutierrez, A. Temperature Impact of High RF Energy on Blood Products; Report to the FDA; Food and Drug Administration: Silver Spring, MD, USA, 2008.
- Hohberger, C.; Gottschall, J. Joule Heating of Blood Products by Intense RF Magnetic Fields; Report to the FDA; Food and Drug Administration: Silver Spring, MD, USA, 2008.
- International Organization for Standardization. ISO/IEC 18000-3:2010, Information Technology—Radio Frequency Identification for Item Management—Part 3: Parameters for Air Interface Communications at 13,56 MHz; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- Fanti, A.; Secci, R.; Boi, G.; Casu, S.; Casula, G.A.; Mazzarella, G.; Montisci, G. A polycarbonate RFID tag for blood chain tracking. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015.
- Wang, Q.-L.; Wang, X.-W.; Zhuo, H.-L.; Shao, C.-Y.; Wang, J.; Wang, H.-P. Impact on storage quality of red blood cells and platelets by ultrahigh-frequency radiofrequency identification tags. Transfusion 2011, 53, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Otin, R. Numerical study of the thermal effects induced by a RFID antenna in vials of blood plasma. Prog. Electromagn. Res. Lett. 2011, 22, 129–138. [Google Scholar]
- Casu, S.; Fanti, A.; Floris, V.; Gatto, G.; Mazzarella, G.; Migliore, M.D.; Spano, I.L. Evaluation of the effects of UHF electromagnetic fields on a blood bag. In Proceedings of the Antennas & Propagation Conference (LAPC), Loughborough, UK, 2–3 November 2015.
- Paul, C.R. Introduction to Electromagnetic Compatibility; Wiley-Interscience: Hoboken, NJ, USA, 1992. [Google Scholar]
- IEEE Antennas and Propagation Society. IEEE Standard Definitions of Terms for Antennas 145-2013; IEEE: New York, NY, USA, 2013; pp. 1–50. [Google Scholar]
- European Telecommunications Standards Institute. ETSI 302 208-1 ERM, RFID Operating in the Band 865 MHz to 868 MHz with Power Levels up to 2 W, Part 1: Technical Requirements and Methods of Measurement; ver. 1.4.1; ETSI: Sophia Antipolis, France, 2011. [Google Scholar]
- Balanis, C.A. Modern Antenna Handbook; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Promedical s.r.l. Available online: http://www.promedical.it/ (accessed on 6 November 2016).
- Ray, P.S. Broadband complex refractive indices of ice and water. Appl. Opt. 1972, 11, 1836–1844. [Google Scholar] [CrossRef] [PubMed]
- CST GmbH, CST Microwave Studio Help, CST Studio Suite version 2011.14.01. Available online: https://www.cst.com/products/csts2 (accessed on 6 November 2016).
- Weiland, M.; Clemens, T. Discrete electromagnetism with the finite integration technique. Prog. Electromagn. Res. Lett. 2001, 32, 65–87. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP), ICNIRP statement on the ‘Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz)’. Health Phys. 2009, 97, 257–258.
- Berenger, J.-P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- IFAC—Dielectric Properties of Body Tissues. Available online: http://niremf.ifac.cnr.it/tissprop/ (accessed on 6 November 2016).
- Van Bladel, J. Field singularities at metal-dielectric wedges. IEEE Trans. Antennas Propag. 1985, 33, 450–455. [Google Scholar] [CrossRef]
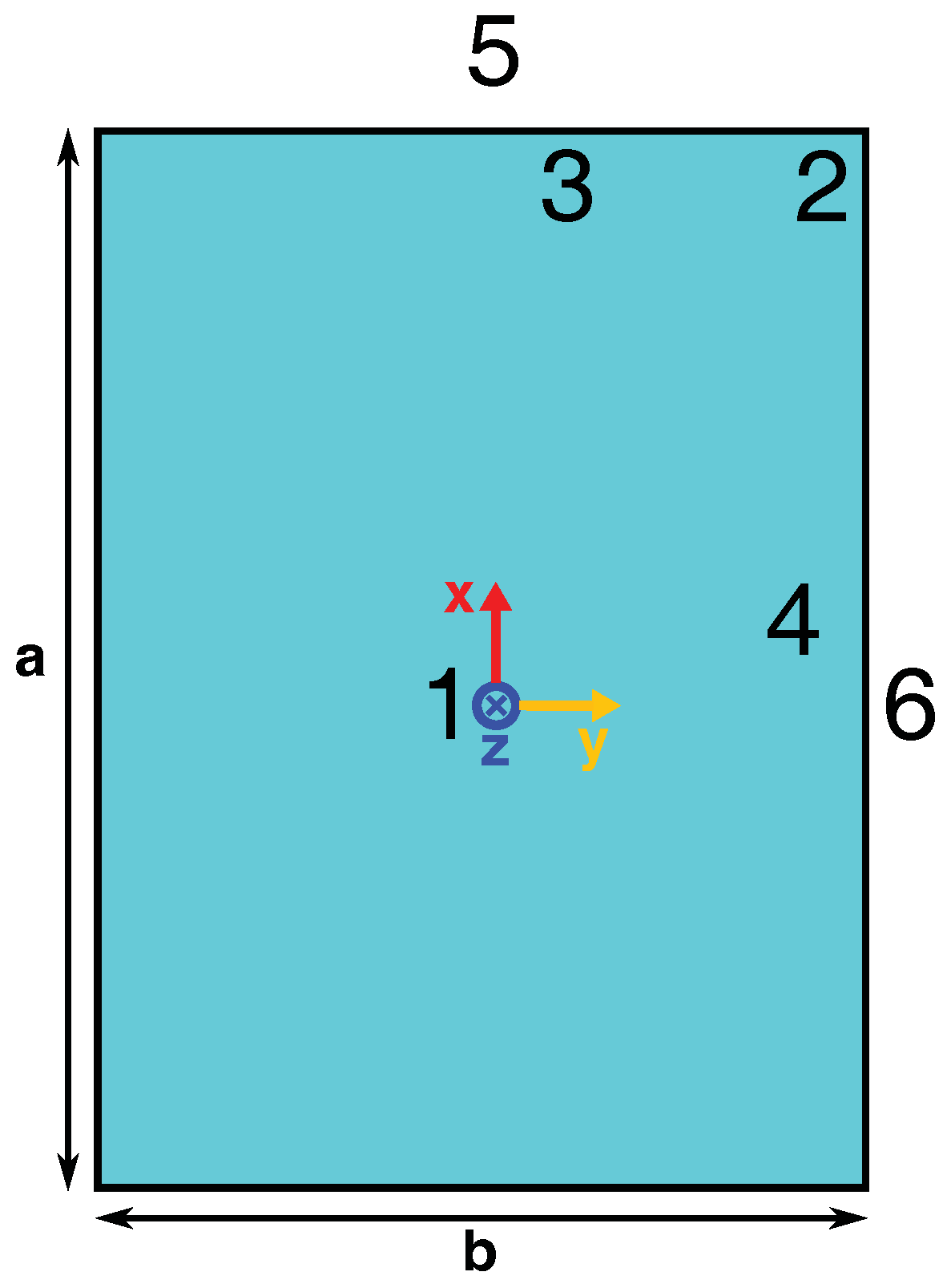
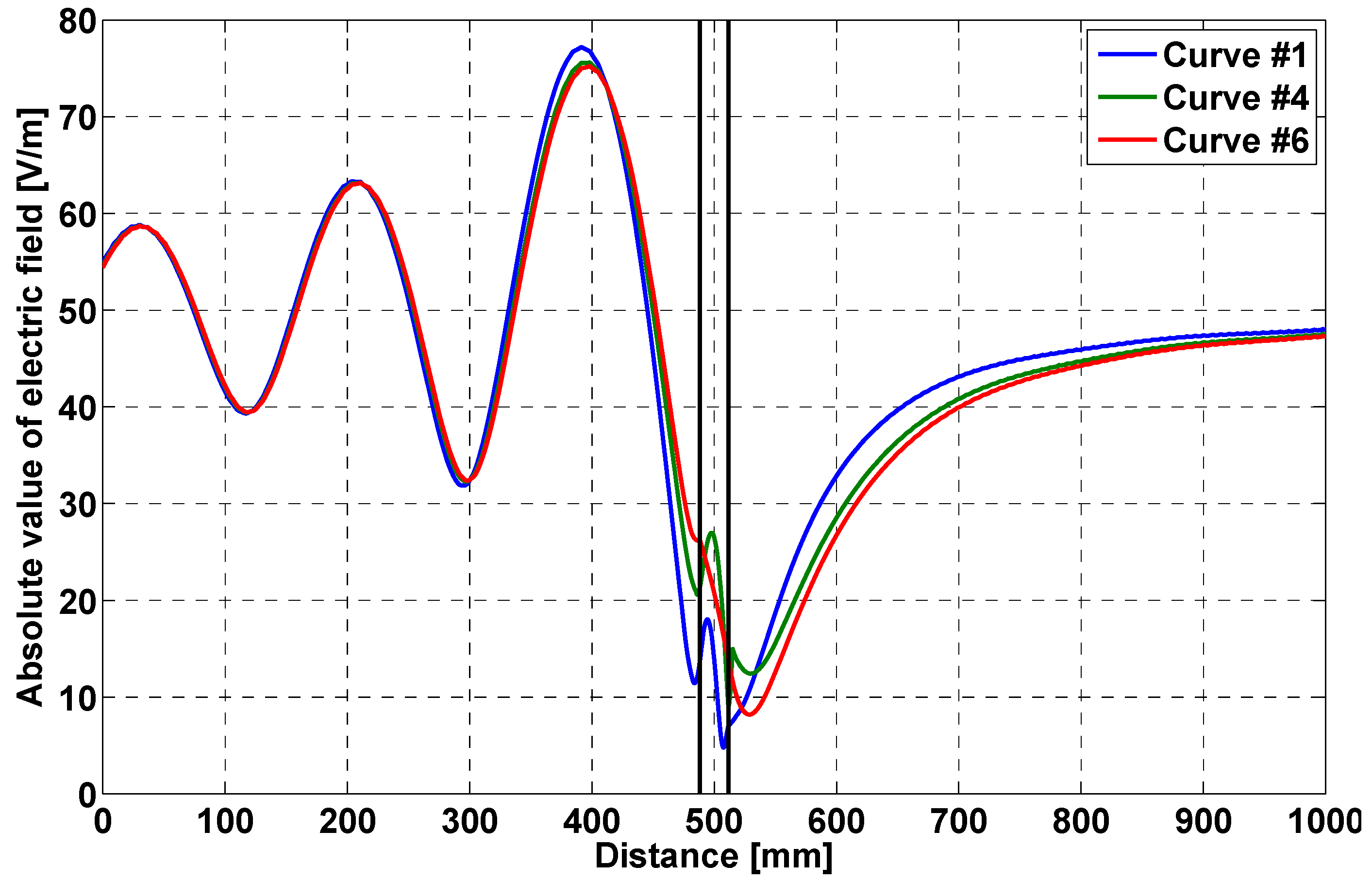
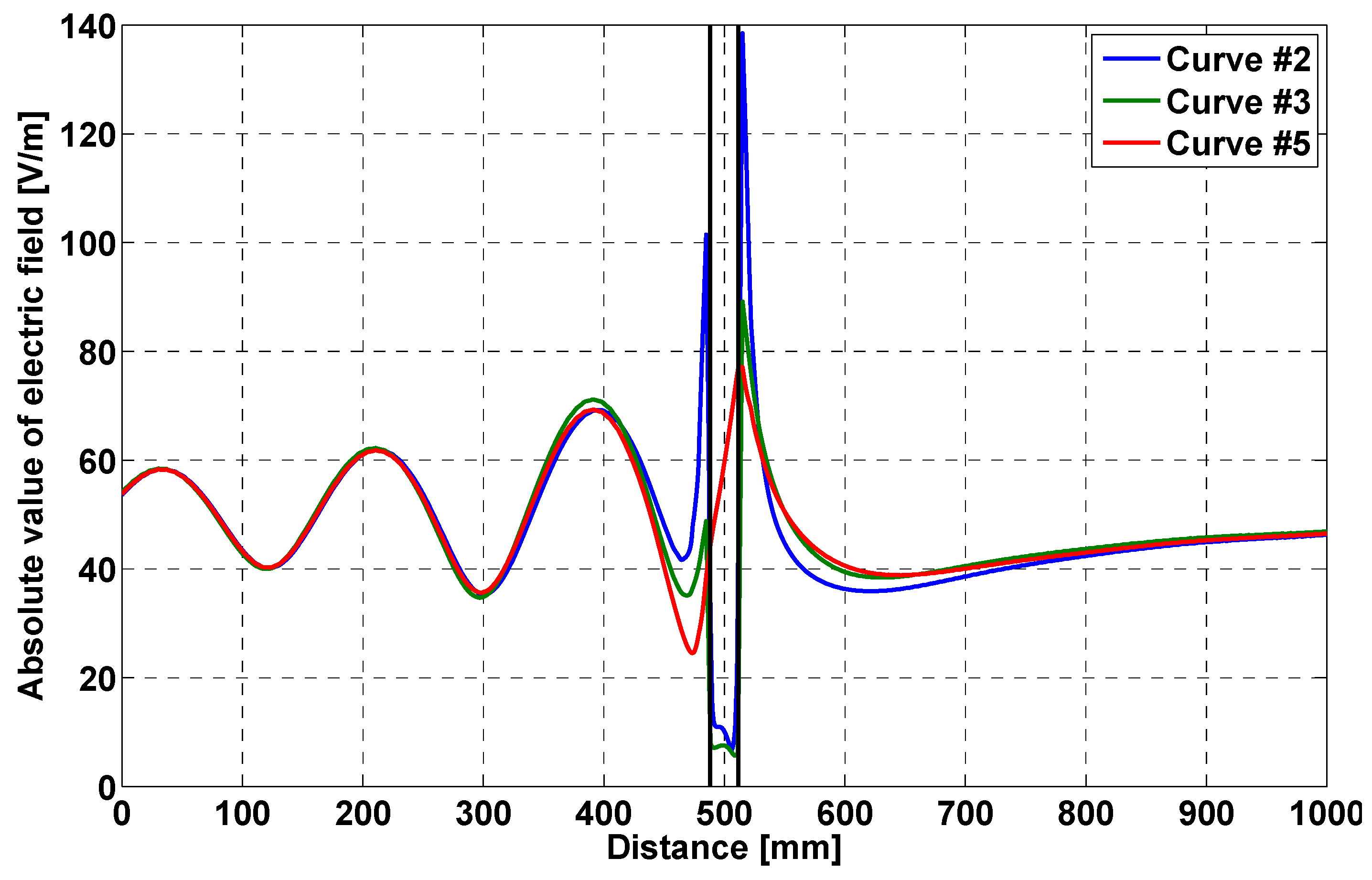



| # | X (mm) | Y (mm) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 84.11 | 55.51 |
| 3 | 80 | 10 |
| 4 | 10 | 50 |
| 5 | 95 | 0 |
| 6 | 0 | 60 |
| Distance between Blood Bag and Dipole (cm) | SAR (W/kg) | ΔT (min) for Increases the Temperature of the Blood around 0.1 °C |
|---|---|---|
| 5 | 0.44 | 16 |
| 15 | 0.11 | 62 |
| 25 | <0.01 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fanti, A.; Casu, S.; Mazzarella, G. A Numerical Estimation of a RFID Reader Field and SAR inside a Blood Bag at UHF. Electronics 2016, 5, 77. https://doi.org/10.3390/electronics5040077
Fanti A, Casu S, Mazzarella G. A Numerical Estimation of a RFID Reader Field and SAR inside a Blood Bag at UHF. Electronics. 2016; 5(4):77. https://doi.org/10.3390/electronics5040077
Chicago/Turabian StyleFanti, Alessandro, Sergio Casu, and Giuseppe Mazzarella. 2016. "A Numerical Estimation of a RFID Reader Field and SAR inside a Blood Bag at UHF" Electronics 5, no. 4: 77. https://doi.org/10.3390/electronics5040077
APA StyleFanti, A., Casu, S., & Mazzarella, G. (2016). A Numerical Estimation of a RFID Reader Field and SAR inside a Blood Bag at UHF. Electronics, 5(4), 77. https://doi.org/10.3390/electronics5040077






