Virtual Machine Replication on Achieving Energy-Efficiency in a Cloud
Abstract
:1. Introduction
2. Related Work
3. Job Execution in Cloud
3.1. System Model
3.2. Cloud Service Implementation under 1 + 1 Replication Mechanism
4. Power and Job Completion Time Modeling
4.1. Power Consumption Model
4.2. Job Completion Time Formulation
5. Job Completion Time Computation and Energy Consumption Measurement
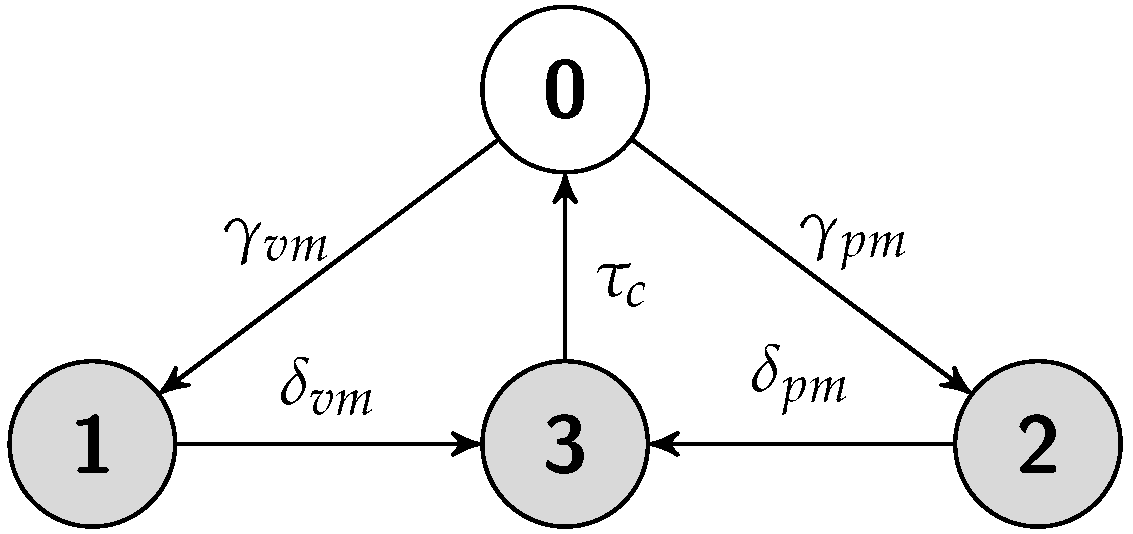
5.1. Standalone Scheme
5.1.1. Job Completion Time Computation
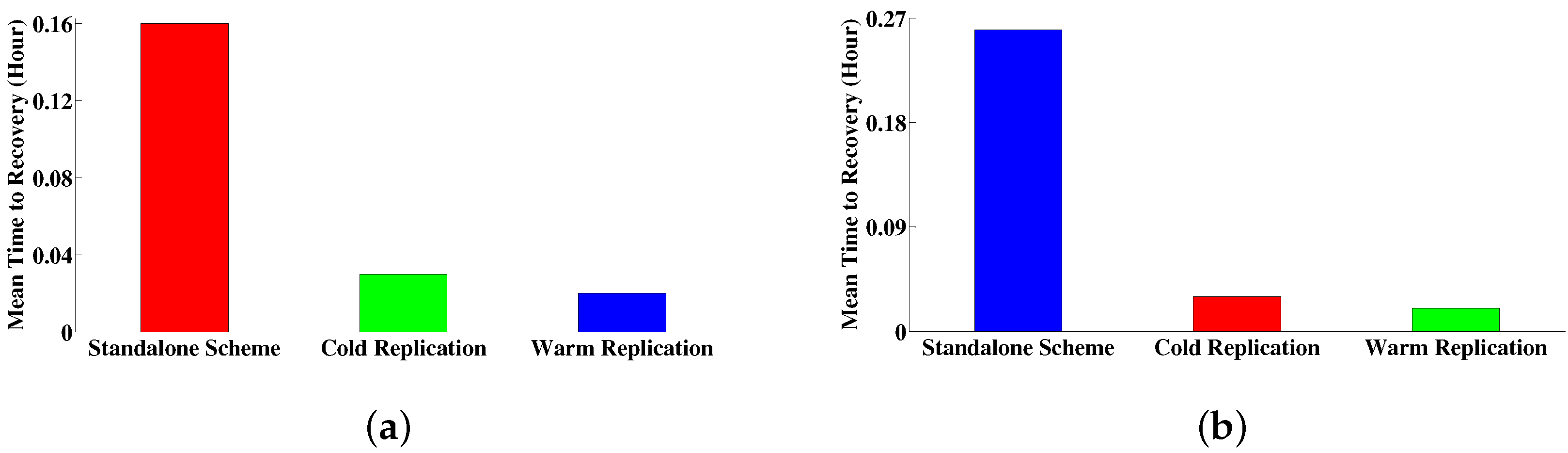
5.1.2. Failure Recovery Time
5.1.3. Energy Consumption Measurement
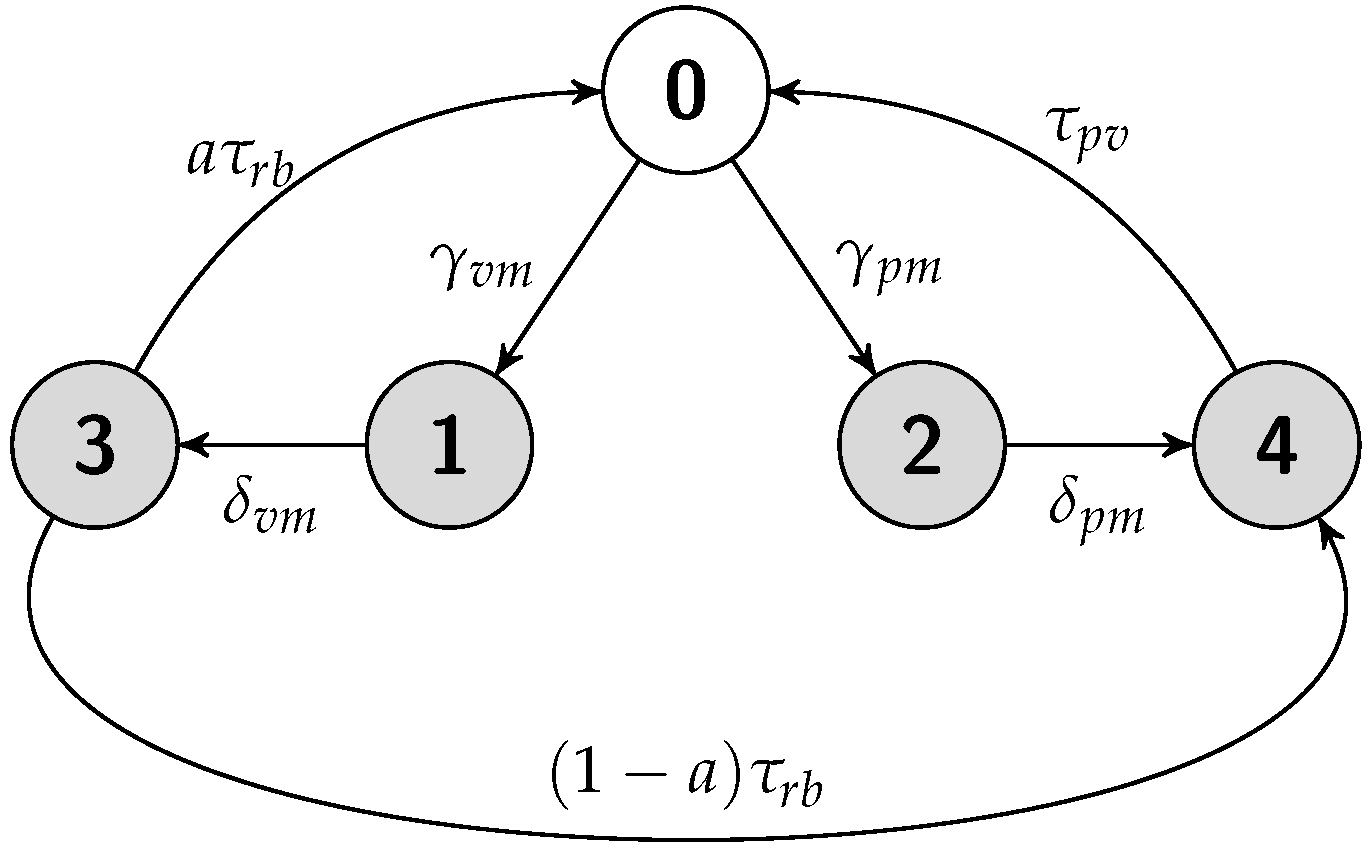
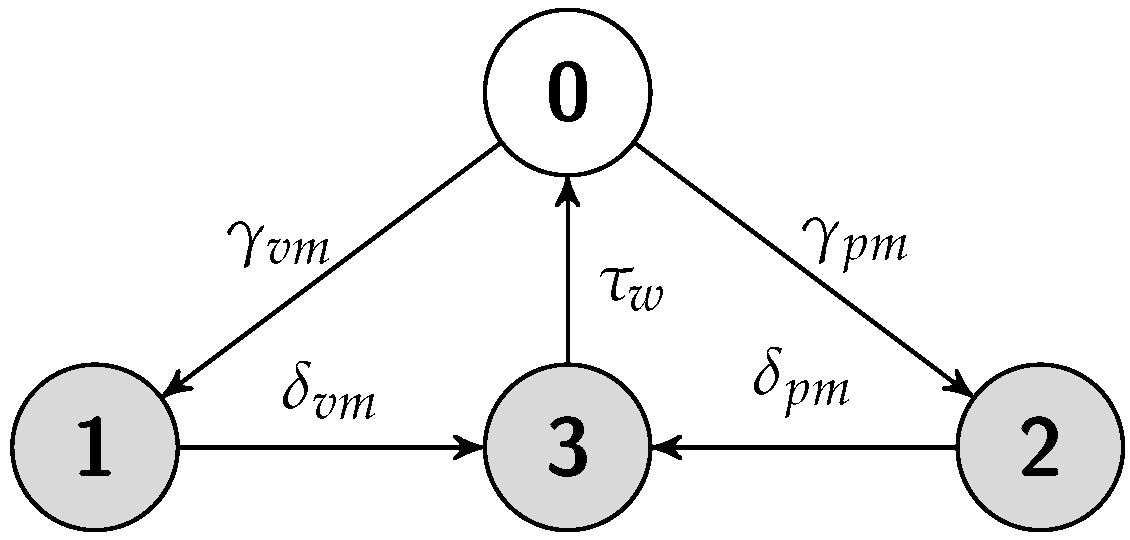
5.2. Cold Replication Scheme
5.2.1. Job Completion Time Computation
5.2.2. Failure Recovery Time
5.2.3. Energy Consumption Measurement
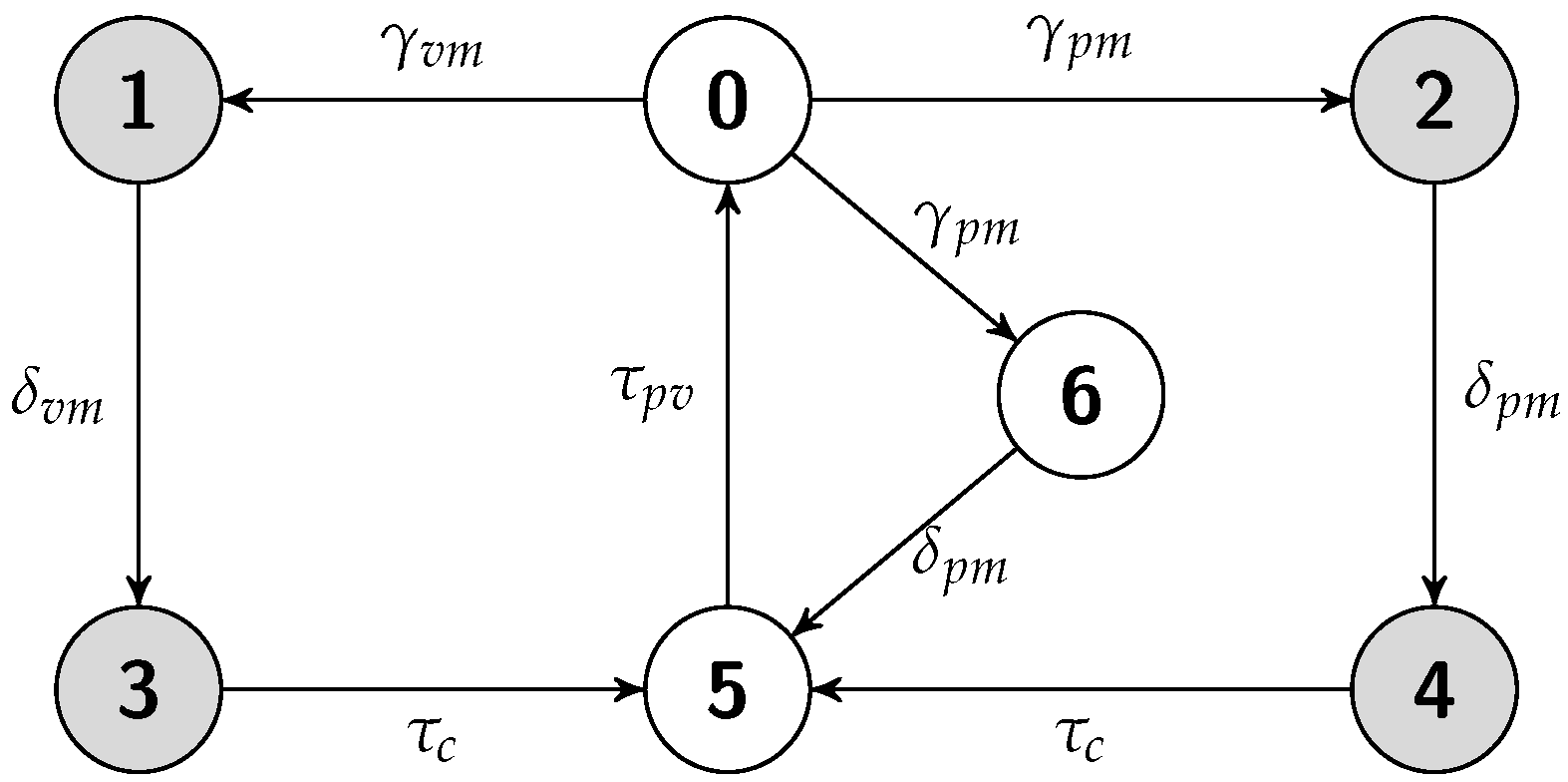
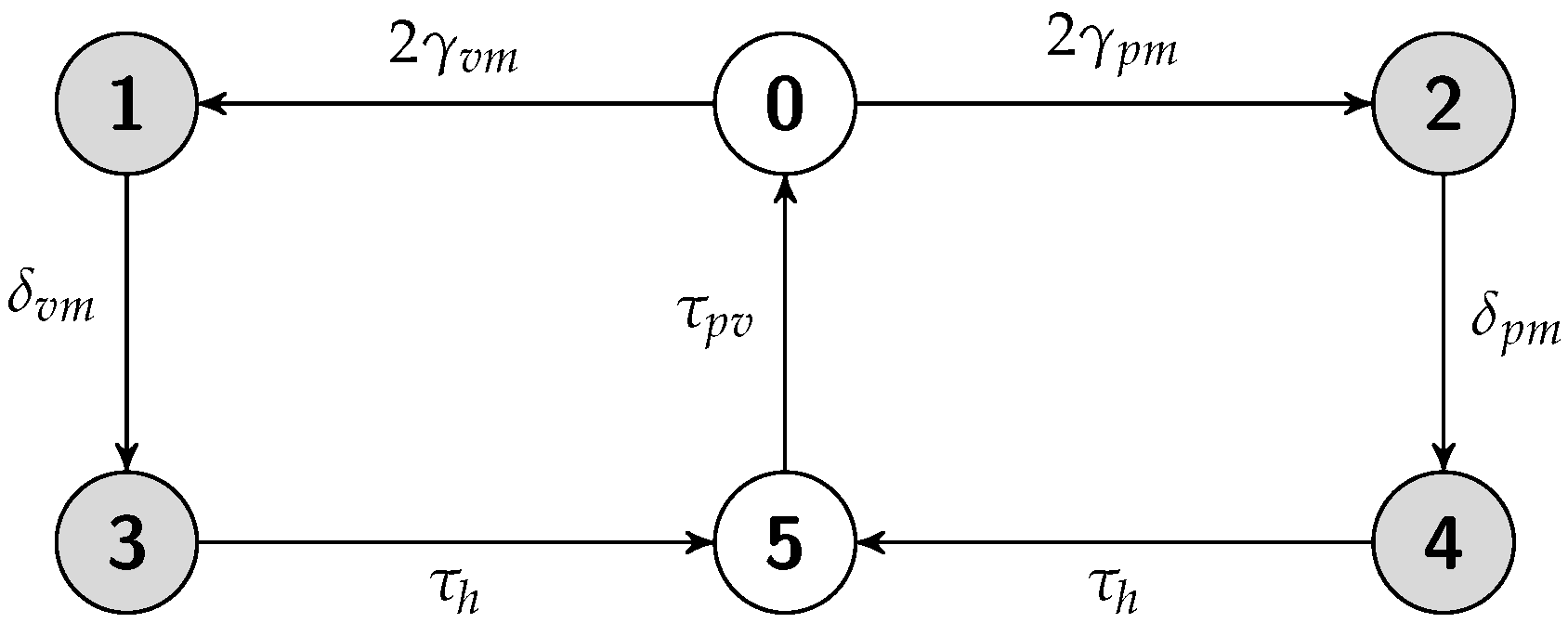
5.3. Warm Replication Scheme
5.3.1. Job Completion Time Computation
5.3.2. Failure Recovery Time
5.3.3. Energy Consumption Measurement
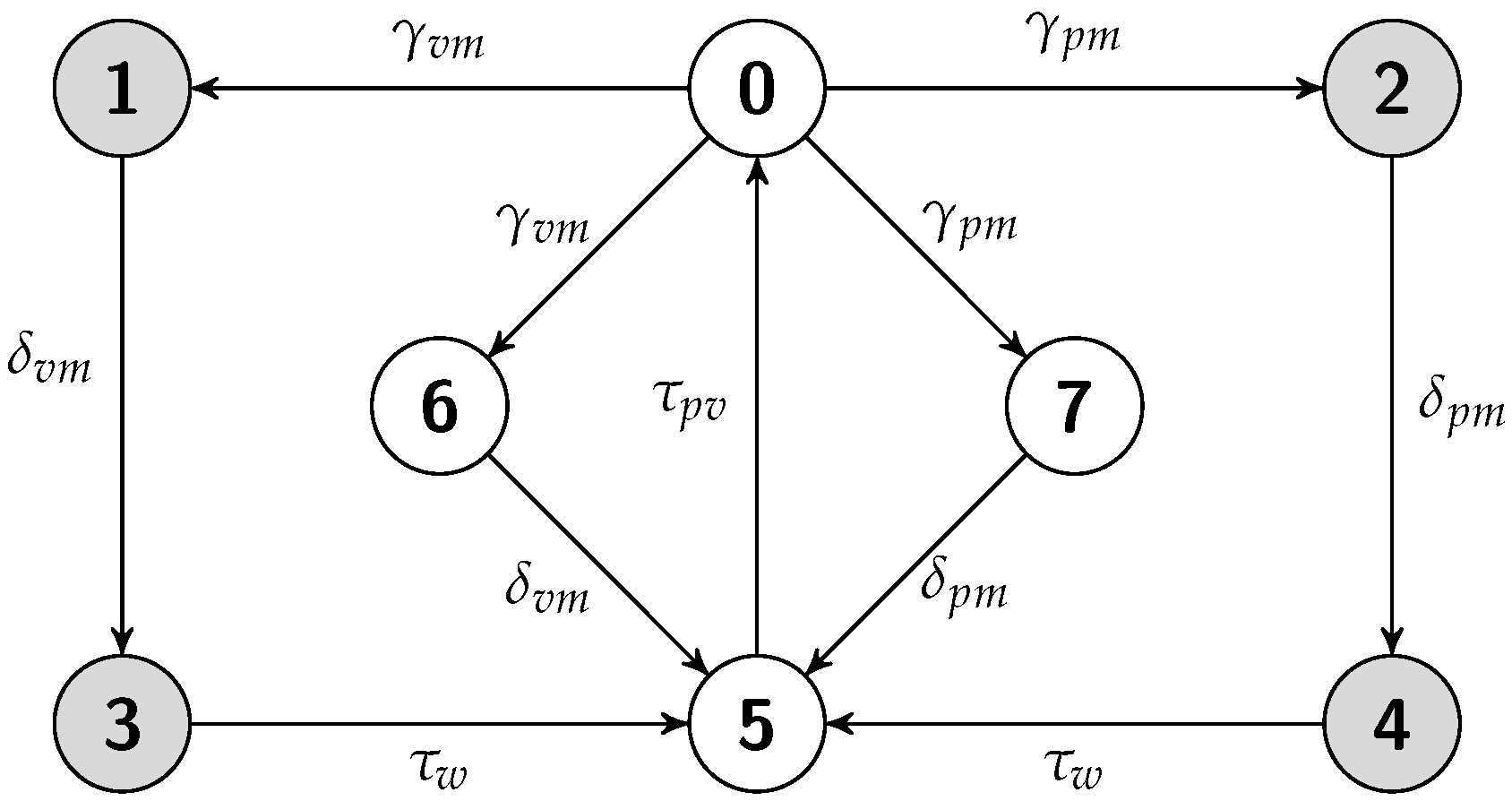
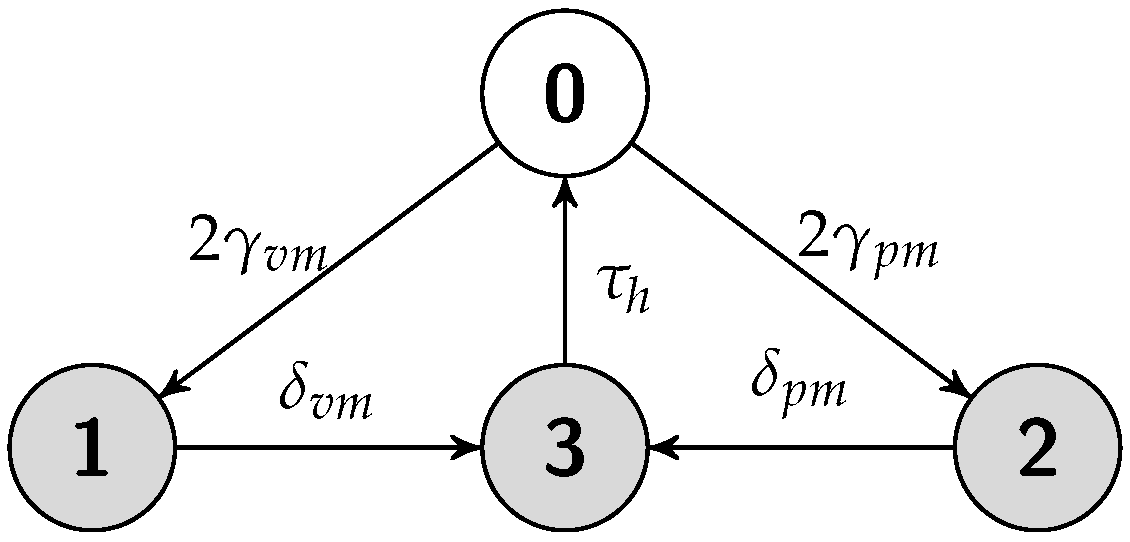
5.4. Hot Replication Scheme
5.4.1. Job Completion Time Computation
5.4.2. Failure Recovery Time
5.4.3. Energy Consumption Measurement
6. Experiments
6.1. CloudSim Extension
- A data center network is constructed to connect the host servers that can deploy more than one VM.
- VM or PM failure, failure detection, and recovery events are triggered. An event can be generated according to a specified distribution. The failure event data and the recovery event data can be saved to a file so the experiment can be repeated.
- Power consumption module and associated time event for every individual mode of resource provisioning and servicing discussed in Section 4.1 is generated.
- A checkpoint state is generated, transferred, and stored based on the preemption of structure-state process and replication scheme. This module is extensible.
- A job is resumed from a VM failure based on the saved checkpoint state and replication scheme. If there is no accessible checkpoint state, it restarts the job from the beginning.
6.2. Experimental Setup
- The miph (millions of instructions per hour) of each host server is 4,000,000, the disk size is 100 GB, the memory size is 4 GB, and the bandwidth is 4000 bps.
- The miph of each VM is 1,000,000, and the disk size is 25 GB, the memory size is 1 GB, and the bandwidth is 1000 bps.
6.3. Model Parameterization
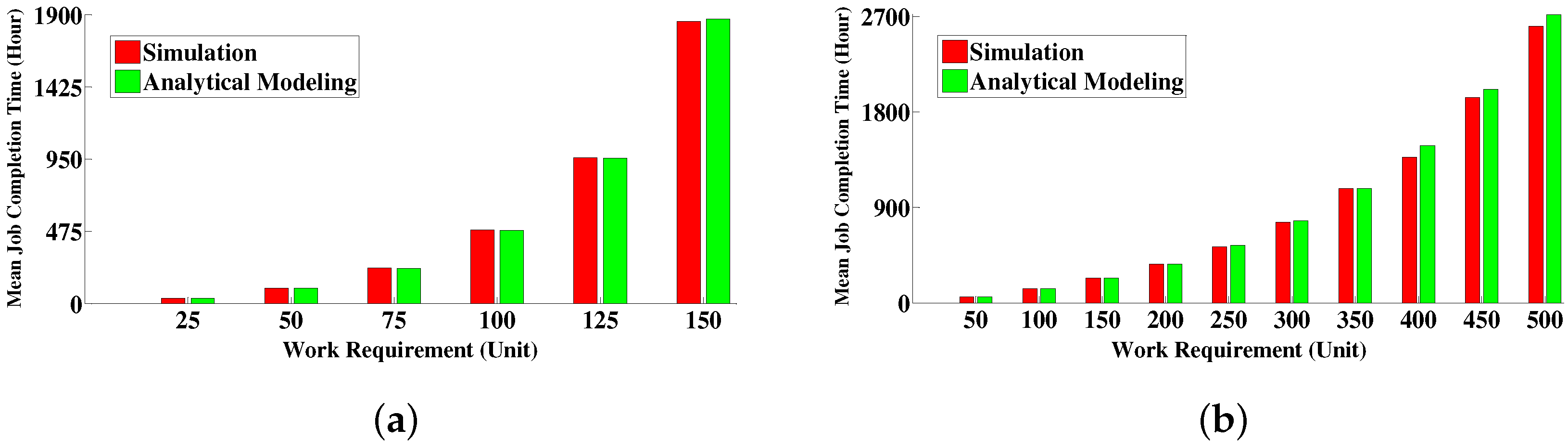
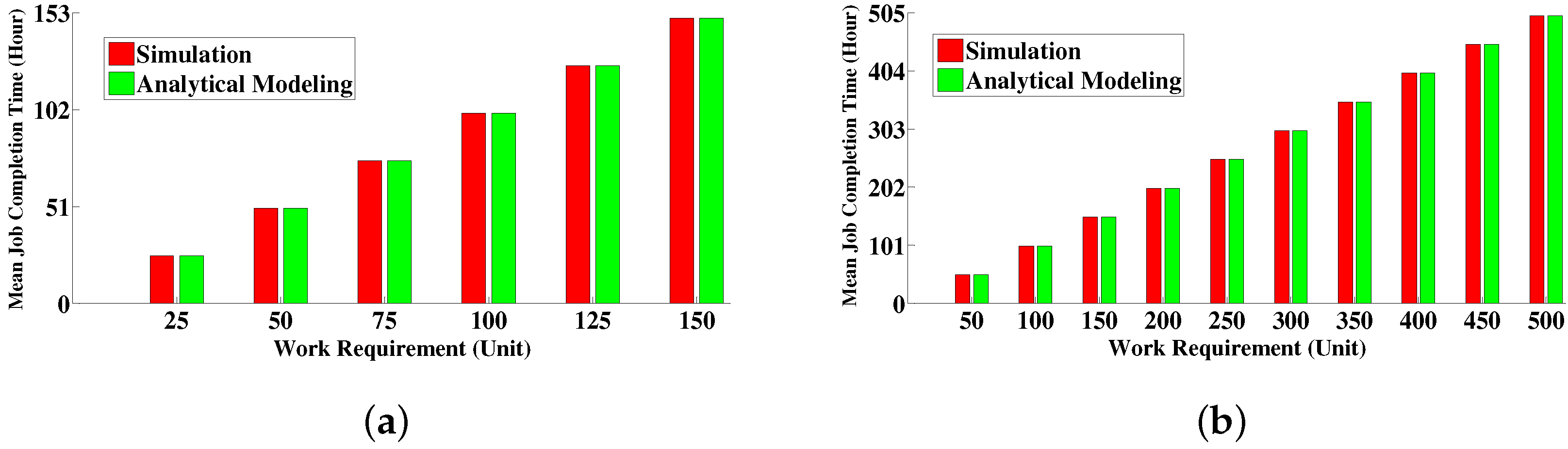
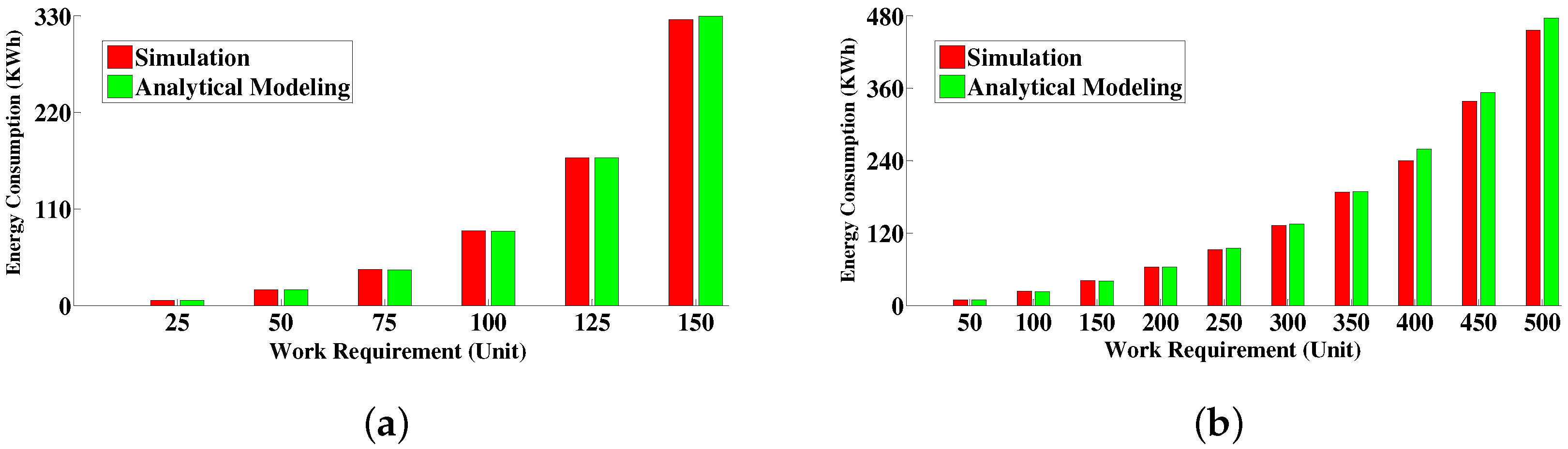
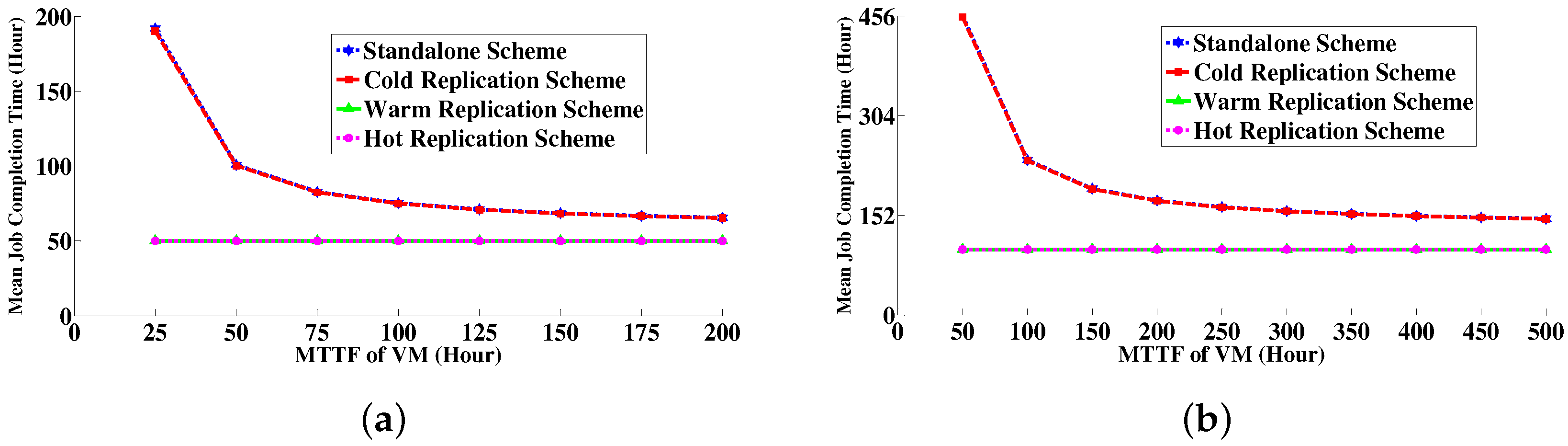
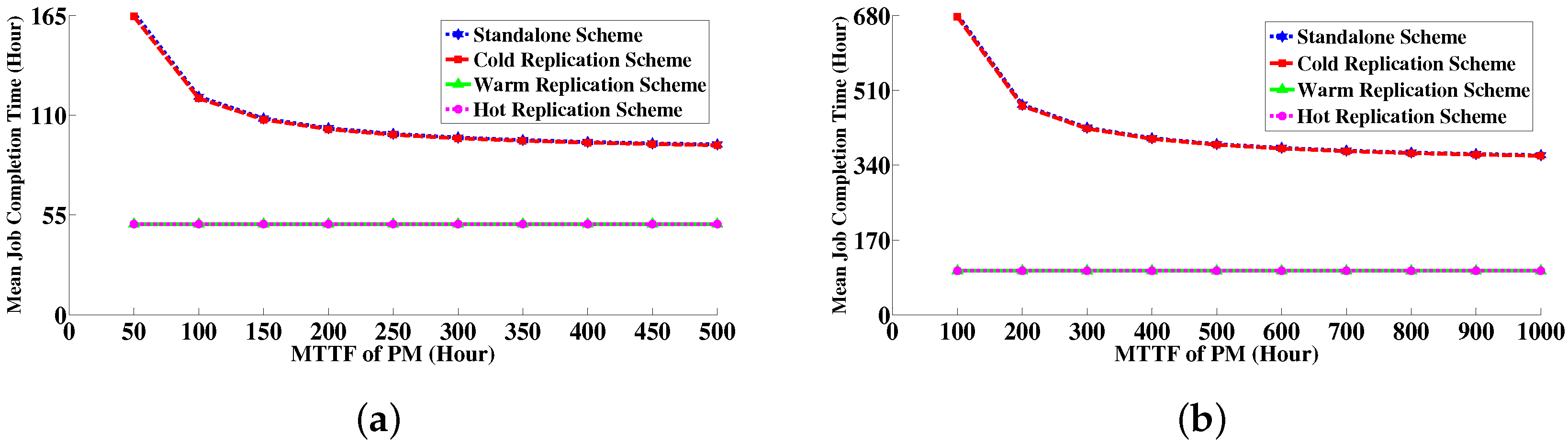
6.4. Numerical Results
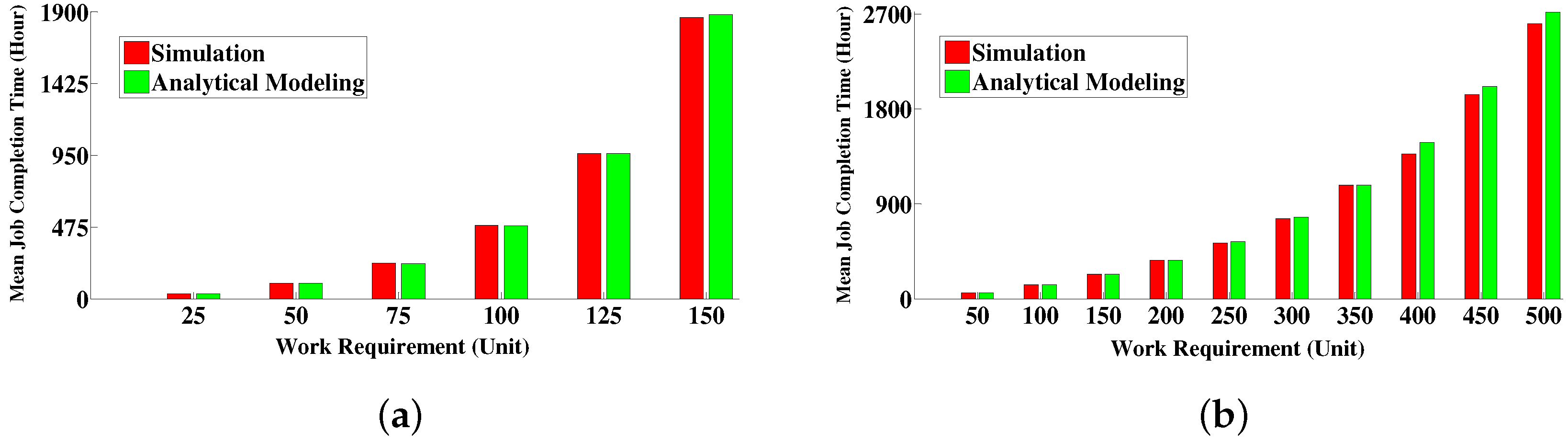
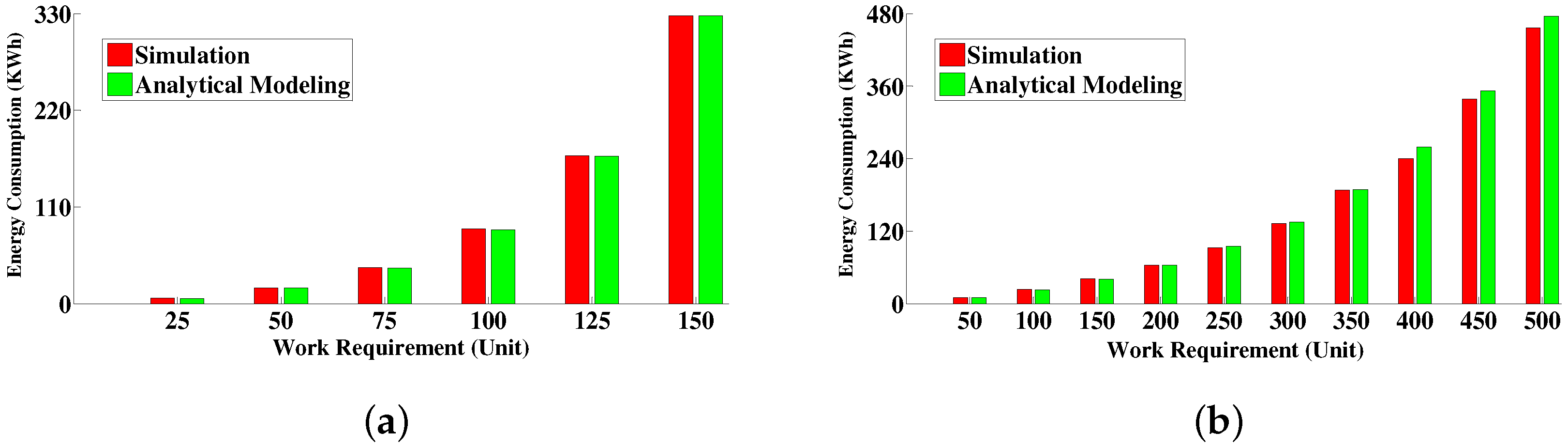
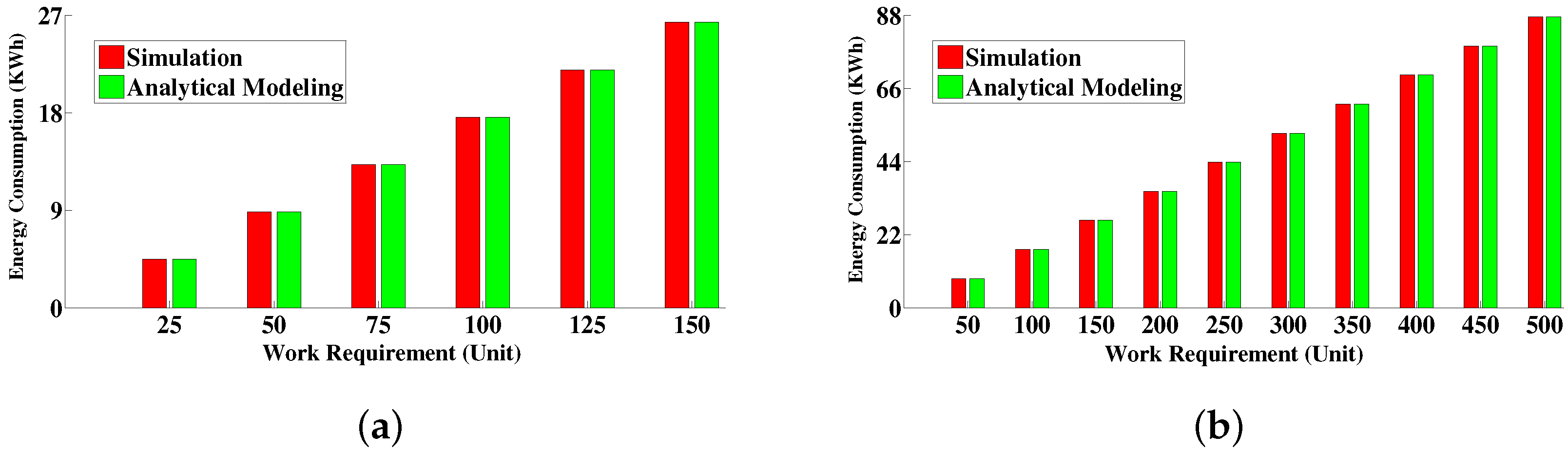
6.4.1. Comparison between Simulative Solution and Analytical Modeling Solution
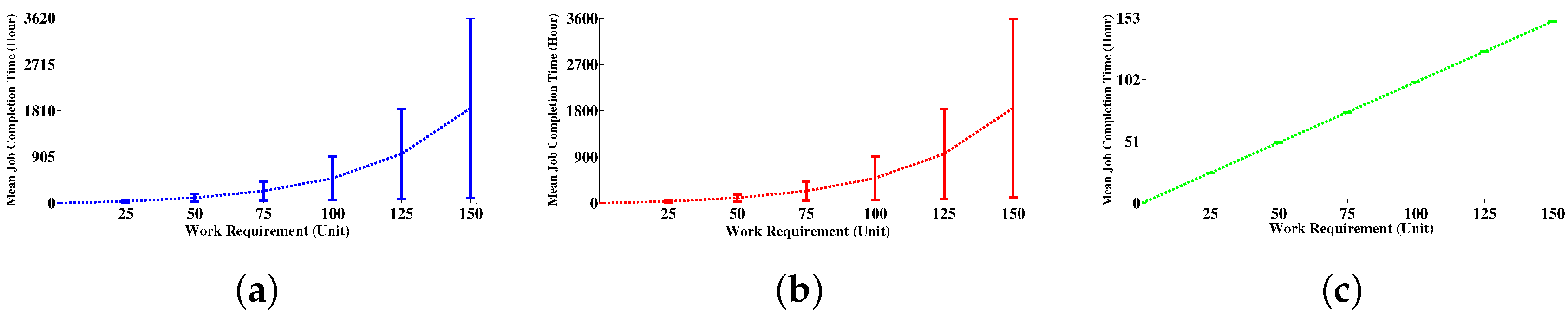
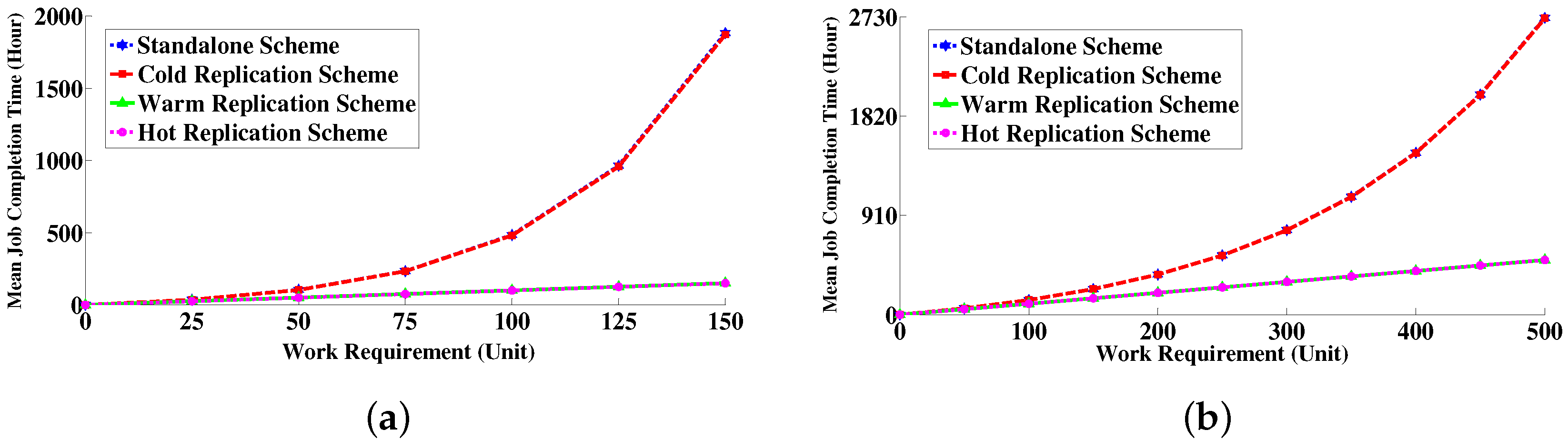
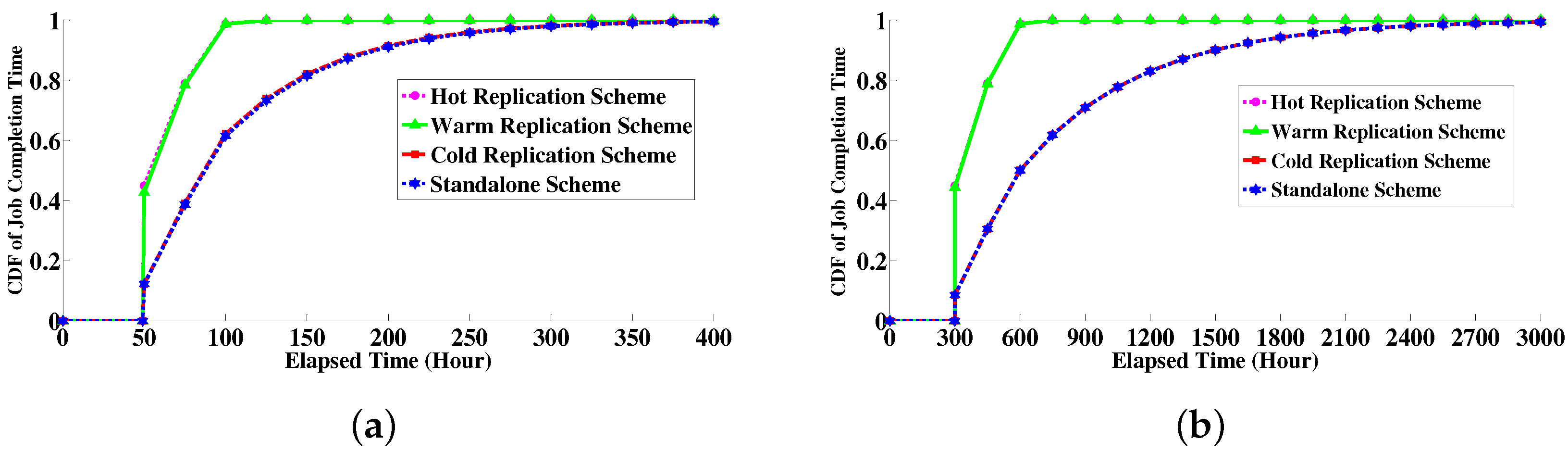
6.4.2. Job Completion Time Distribution
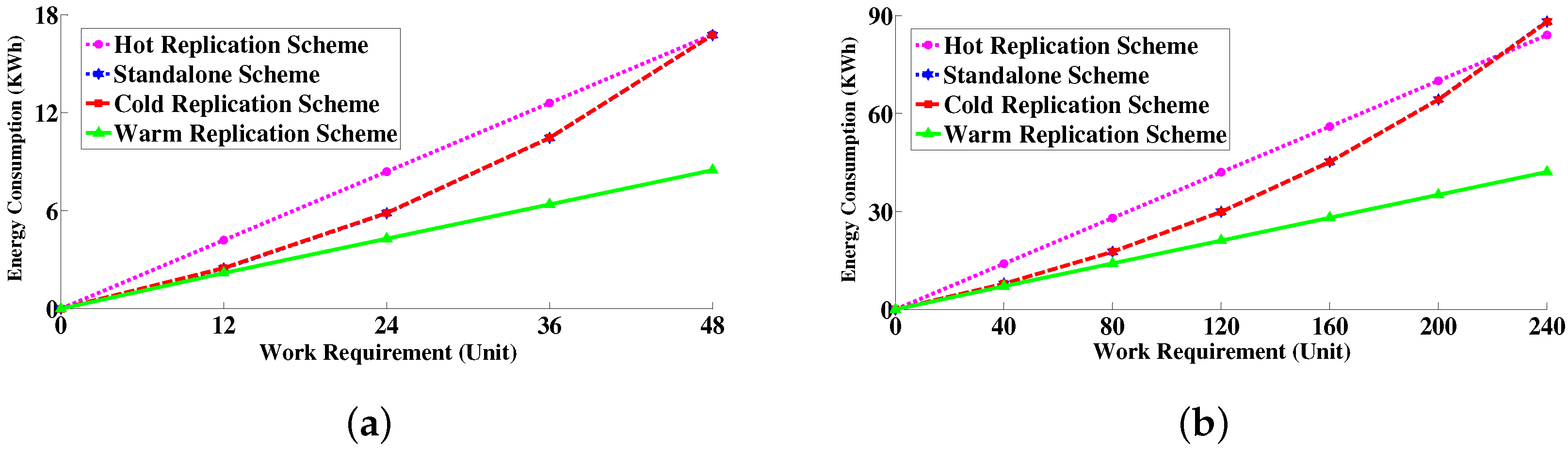
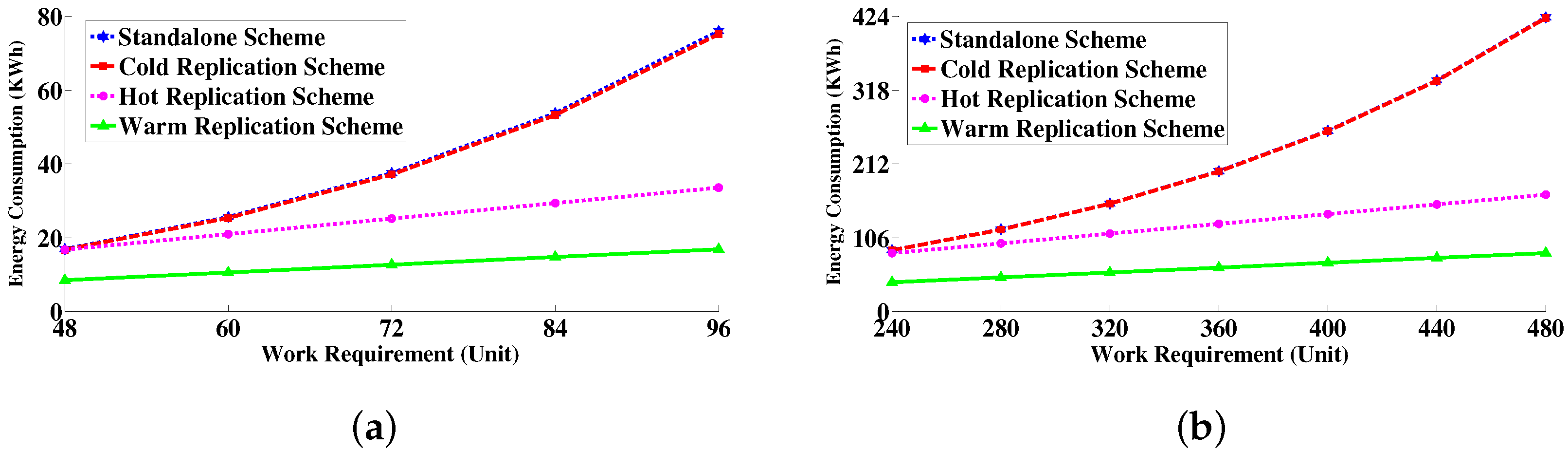
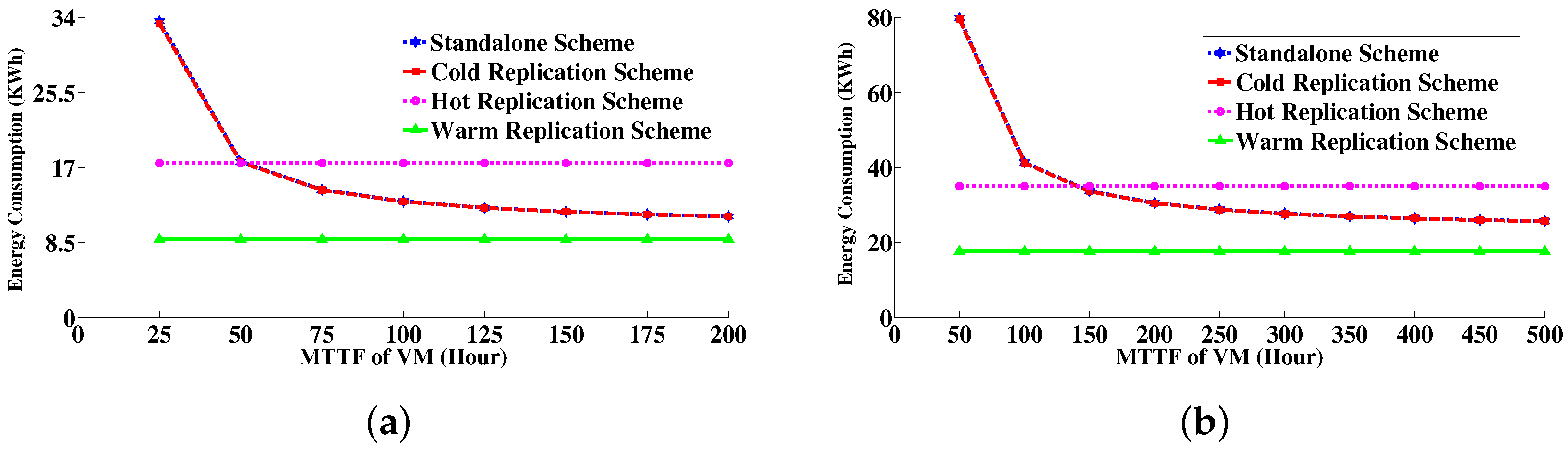
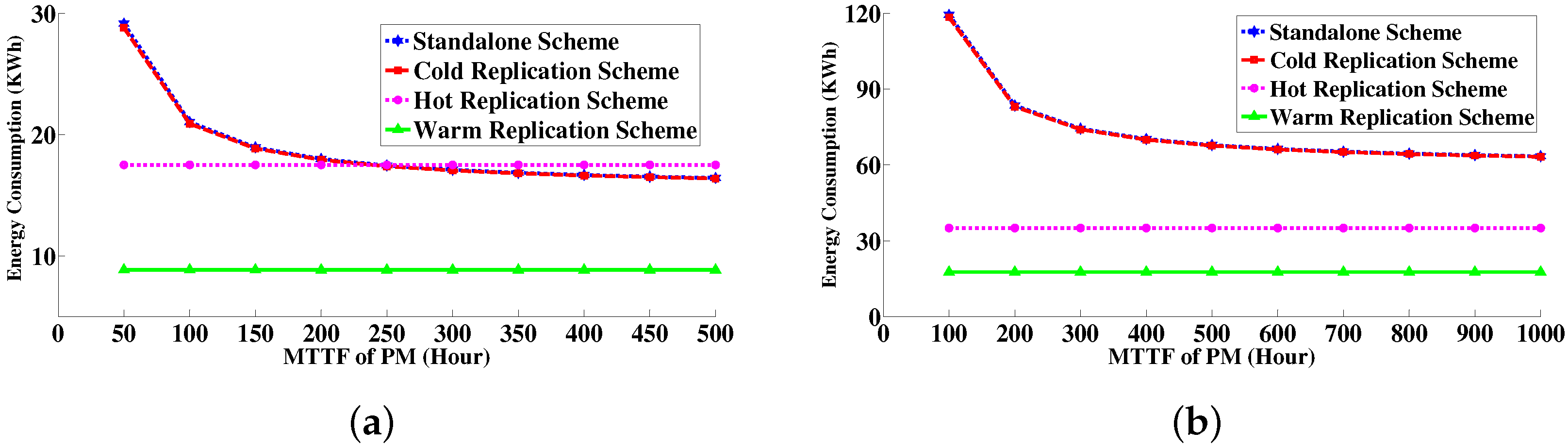
6.4.3. Energy Consumption Measurement
7. Conclusion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ghosh, R.; Longo, F.; Naik, V.K.; Trivedi, K.S. Modeling and performance analysis of large scale iaas clouds. Future Gener. Comput. Syst. 2013, 29, 1216–1234. [Google Scholar] [CrossRef]
- Khazaei, H.; Misic, J.; Misic, V. A Fine-Grained Performance Model of Cloud Computing Centers. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 2138–2147. [Google Scholar] [CrossRef]
- Mastroianni, C.; Meo, M.; Papuzzo, G. Probabilistic Consolidation of Virtual Machines in Self-Organizing Cloud Data Centers. IEEE Trans. Cloud Comput. 2013, 1, 215–228. [Google Scholar] [CrossRef]
- Beloglazov, A.; Abawajy, J.; Buyya, R. Energy-aware resource allocation heuristics for efficient management of data centers for cloud computing. Future Gener. Comput. Syst. 2012, 28, 755–768. [Google Scholar] [CrossRef]
- Mastroianni, C.; Meo, M.; Papuzzo, G. Self-economy in cloud data centers: Statistical assignment and migration of virtual machines. In Euro-Par 2011 Parallel Processing; Springer: Berlin, Germany; Heidelberg, Germany, 2011; pp. 407–418. [Google Scholar]
- Ben-Yehuda, O.; Schuster, A.; Sharov, A.; Silberstein, M.; Iosup, A. ExPERT: Pareto-Efficient Task Replication on Grids and a Cloud. In Proceedings of the IEEE 26th International Parallel Distributed Processing Symposium (IPDPS), Shanghai, China, 21–25 May 2012; pp. 167–178.
- Bauer, E.; Adams, R. Reliability and Availability of Cloud Computing; Wiley-IEEE Press: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine generals problem. ACM Trans. Program. Lang. Syst. (TOPLAS) 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Borthakur, D. The hadoop distributed file system: Architecture and design. Hadoop Proj. Website 2007, 11, 21. [Google Scholar]
- Kulkarni, V.G.; Nicola, V.F.; Trivedi, K.S. On Modeling the Performance and Reliability of Multi-mode Computer Systems. J. Syst. Softw. 1986, 6, 175–182. [Google Scholar] [CrossRef]
- Kulkarni, V.G.; Nicola, V.F.; Trivedi, K.S. The Completion Time of a Job on Multimode Systems. Adv. Appl. Probab. 1987, 19, 932–954. [Google Scholar] [CrossRef]
- Machida, F.; Nicola, V.F.; Trivedi, K.S. Job completion time on a virtualized server with software rejuvenation. ACM J. Emerg. Technol. Comput. Syst. (JETC) 2014, 10, 10. [Google Scholar] [CrossRef]
- Stedman, R. Reducing Desktop PC Power Consumption Idle and Sleep modes; Technical report; Technology Strategist, Advanced Software Technology, Dell Computer Corporation: Round Rock, TX, USA, 20 June 2005. [Google Scholar]
- Calculating Your Energy Consumption; Technical Report 4AA2-XXXXENUC; Hewlett-Packard Development Company: Palo Alto, CA, USA, December 2008.
- Kusic, D.; Kephart, J.O.; Hanson, J.E.; Kandasamy, N.; Jiang, G. Power and performance management of virtualized computing environments via lookahead control. Cluster Comput. 2009, 12, 1–15. [Google Scholar] [CrossRef]
- Chen, X.; Lu, C.D.; Pattabiraman, K. Failure Analysis of Jobs in Compute Clouds: A Google Cluster Case Study. In Proceedings of the International Symposium on Software Reliability Engineering (ISSRE), Naples, Italy, 3–6 November 2014.
- Mondal, S.K.; Machida, F.; Muppala, J.K. Service Reliability Enhancement in Cloud by Checkpointing and Replication. In Principles of Performance and Reliability Modeling and Evaluation; Springer: Berlin, Germany, 2016; pp. 425–448. [Google Scholar]
- Di, S.; Kondo, D.; Cappello, F. Characterizing Cloud Applications on a Google Data Center. In Proceedings of the 42nd International Conference on Parallel Processing (ICPP), Lyon, France, 1–4 October 2013; pp. 468–473.
- Mahesri, A.; Vardhan, V. Power consumption breakdown on a modern laptop. In Power-Aware Computer Systems; Springer: Berlin, Germany, 2005; pp. 165–180. [Google Scholar]
- Huang, S.; Huang, J.; Dai, J.; Xie, T.; Huang, B. The HiBench benchmark suite: Characterization of the MapReduce-based data analysis. In Proceedings of the 26th International Conference on IEEE Data Engineering Workshops (ICDEW), Long Beach, CA, USA, 1–6 March 2010; pp. 41–51.
- Benchmarking Hadoop & HBase on Violin; Technical report; Big Data-Violin Memory: Santa Clara, CA, USA, 2013.
- Calheiros, R.; Ranjan, R.; De Rose, C.; Buyya, R. Cloudsim: A novel framework for modeling and simulation of cloud computing infrastructures and services. Technical Report, GRIDS-TR-2009-1; Grid Computing and Distributed Systems Laboratory, The University of Melbourne: Melbourne, Australia, March 2009. [Google Scholar]
- Calheiros, R.; Ranjan, R.; Beloglazov, A.; De Rose, C.; Buyya, R. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Softw. Pract. Exp. 2011, 41, 23–50. [Google Scholar] [CrossRef]
- Mondal, S.K.; Muppala, J.K. Energy Modeling of Different Virtual Machine Replication Schemes in a Cloud Data Center. In Proceedings of the Internet of Things (iThings), 2014 IEEE International Conference on, and Green Computing and Communications (GreenCom), IEEE and Cyber, Physical and Social Computing (CPSCom), Taipei, Taiwan, 1–3 September 2014; pp. 486–493.
- Mondal, S.K.; Muppala, J.K.; Machida, F.; Trivedi, K.S. Computing Defects per Million in Cloud Caused by Virtual Machine Failures with Replication. In Proceedings of the 2014 IEEE 20th Pacific Rim International Symposium on IEEE Dependable Computing (PRDC), Singapore, 19–21 November 2014; pp. 161–168.
- Mondal, S.; Yin, X.; Muppala, J.; Alonso Lopez, J.; Trivedi, K. Defects per Million Computation in Service-Oriented Environments. IEEE Trans. Serv. Comput. 2015, 8, 32–46. [Google Scholar] [CrossRef]
- Hines, M.R.; Gopalan, K. Post-copy based live virtual machine migration using adaptive pre-paging and dynamic self-ballooning. In Proceedings of the 2009 ACM SIGPLAN/SIGOPS International Conference on Virtual Execution Environments, Washington, DC, USA, March 2009; pp. 51–60.
- Virtual Machine Migration Comparison: VMWare VSphere vs. Microsoft Hyper-V. Test Report; Principled Technologies Inc.: Durham, NC, USA, October 2011.
| Parameters | Description | Values | |
|---|---|---|---|
| Set1 | Set2 | ||
| u | Average CPU utilization of a single job | 25% | 25% |
| Mean time for PM provisioning | 3 min | 3 min | |
| Mean time for VM provisioning | 10 min | 15 min | |
| Power consumption at maximum utilization | 0.25 KW | 0.25 KW | |
| Mean time to failure of VM (MTTF_VM) | 48 h | 240 h | |
| Mean time to failure of PM (MTTF_PM) | 192 h | 720 h | |
| Mean time for failure detection of VM | 2 s | 2 s | |
| Mean time for failure detection of PM | 5 s | 5 s | |
| Mean time for VM recovery by rebooting | 5 min | 5 min | |
| Mean time for VM provisioning in a new PM | 15 min | 30 min | |
| a | Coverage factor of VM recovery by rebooting | 0.80 | 0.80 |
| Mean time for failover in cold replication | 2 min | 2 min | |
| Mean time for failover in warm replication | 1 min | 1 min | |
| Mean time for switchover in hot replication | 15 s | 30 s | |
| x | Amount of work requirements | 50 unit | 300 unit |
| Work Requirement | 95% Confidence Interval of Job Completion Time (Hour) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Standalone Scheme (Set1) | Cold Replication (Set1) | Warm Replication (Set1) | |||||||
| Lower Limit | Mean | Upper Limit | Lower Limit | Mean | Upper Limit | Lower Limit | Mean | Upper Limit | |
| 25 | 35.266 | 35.3728 | 35.4795 | 35.1995 | 35.3057 | 35.4119 | 25.0102 | 25.0103 | 25.0104 |
| 50 | 103.5778 | 104.0084 | 104.439 | 102.8789 | 103.3031 | 103.7273 | 50.0200 | 50.0201 | 50.0202 |
| 75 | 234.8593 | 236.0109 | 237.1626 | 233.8017 | 234.9451 | 236.0886 | 75.0293 | 75.0295 | 75.0296 |
| 100 | 482.0843 | 485.7264 | 487.2298 | 484.2511 | 486.8565 | 489.4619 | 100.0381 | 100.0383 | 100.0385 |
| 125 | 958.0949 | 961.1457 | 969.0413 | 956.1904 | 961.6283 | 967.0663 | 125.0462 | 125.0465 | 125.0468 |
| 150 | 1847.4 | 1855.8326 | 1869.2 | 1840.1 | 1850.9 | 1861.7 | 150.0538 | 150.0541 | 150.0545 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondal, S.K.; Muppala, J.K.; Machida, F. Virtual Machine Replication on Achieving Energy-Efficiency in a Cloud. Electronics 2016, 5, 37. https://doi.org/10.3390/electronics5030037
Mondal SK, Muppala JK, Machida F. Virtual Machine Replication on Achieving Energy-Efficiency in a Cloud. Electronics. 2016; 5(3):37. https://doi.org/10.3390/electronics5030037
Chicago/Turabian StyleMondal, Subrota K., Jogesh K. Muppala, and Fumio Machida. 2016. "Virtual Machine Replication on Achieving Energy-Efficiency in a Cloud" Electronics 5, no. 3: 37. https://doi.org/10.3390/electronics5030037
APA StyleMondal, S. K., Muppala, J. K., & Machida, F. (2016). Virtual Machine Replication on Achieving Energy-Efficiency in a Cloud. Electronics, 5(3), 37. https://doi.org/10.3390/electronics5030037








