A FPGA-Based Broadband EIT System for Complex Bioimpedance Measurements—Design and Performance Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. System Architecture
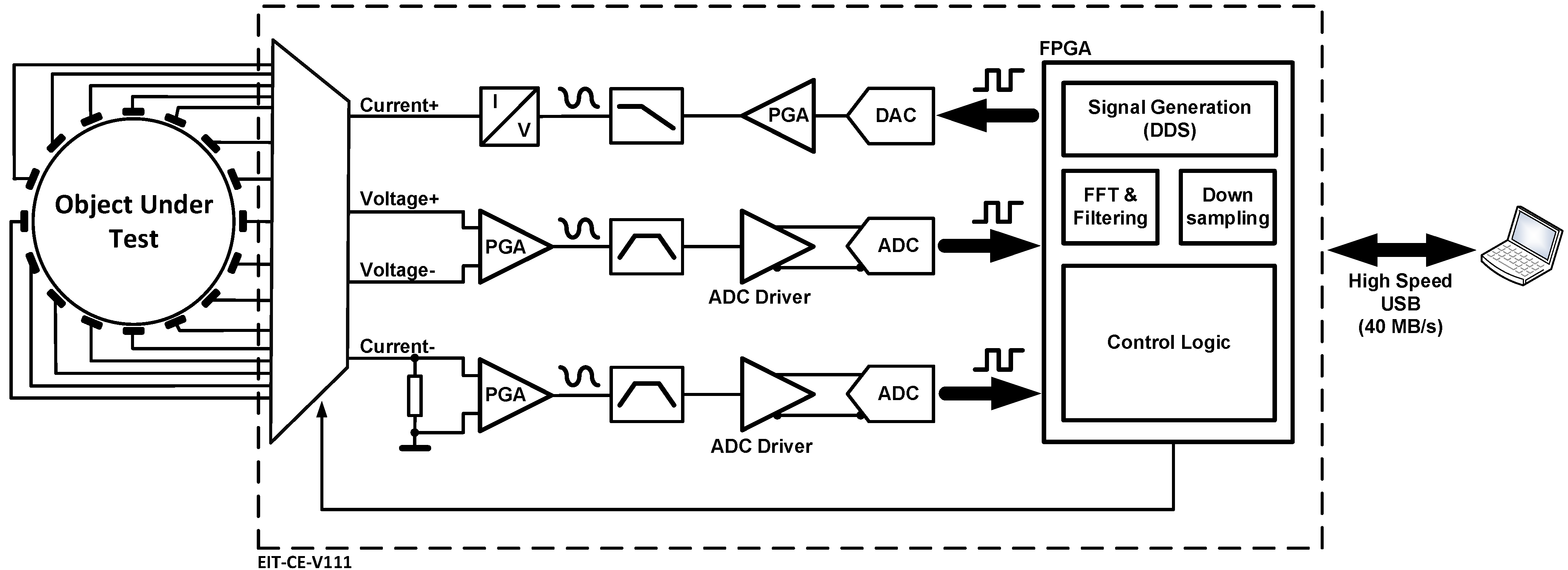

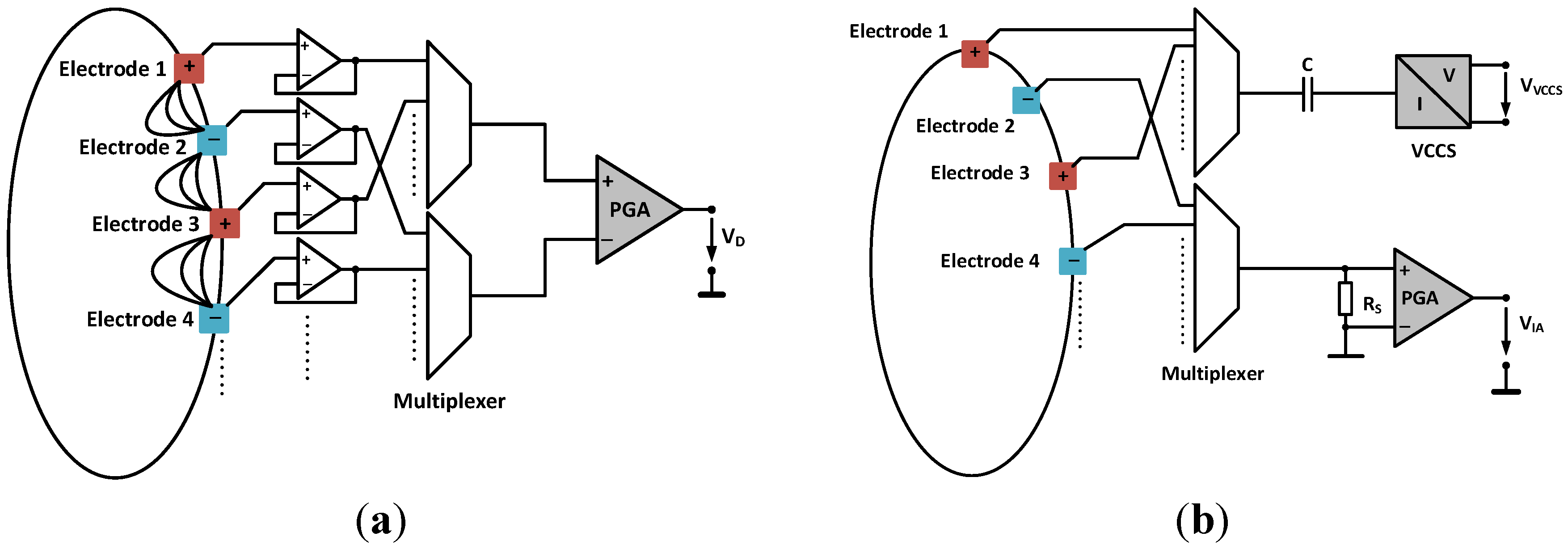
2.2. Current and Voltage Channel Multiplexing
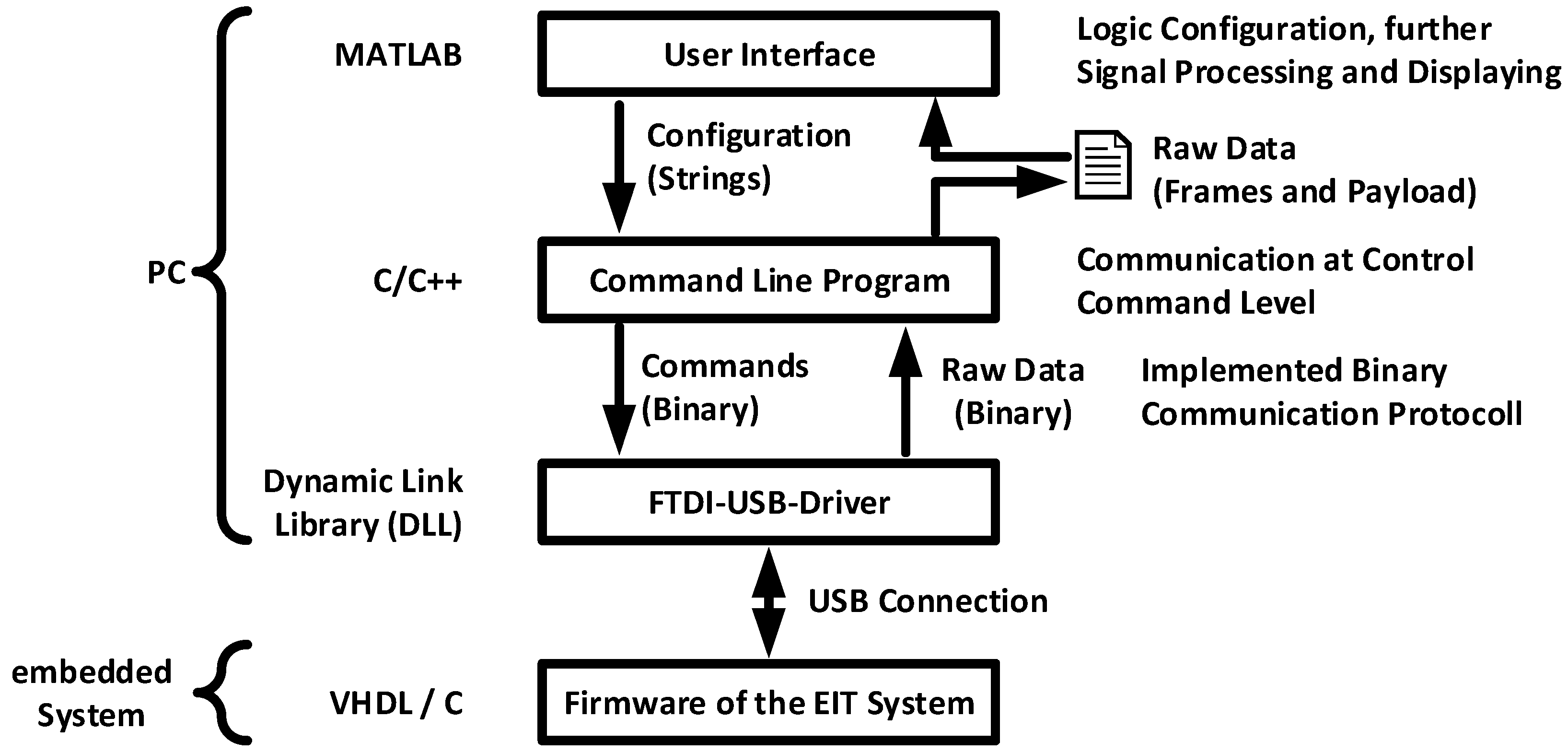
2.3. Software Architecture of the EIT System
2.4. System Performance
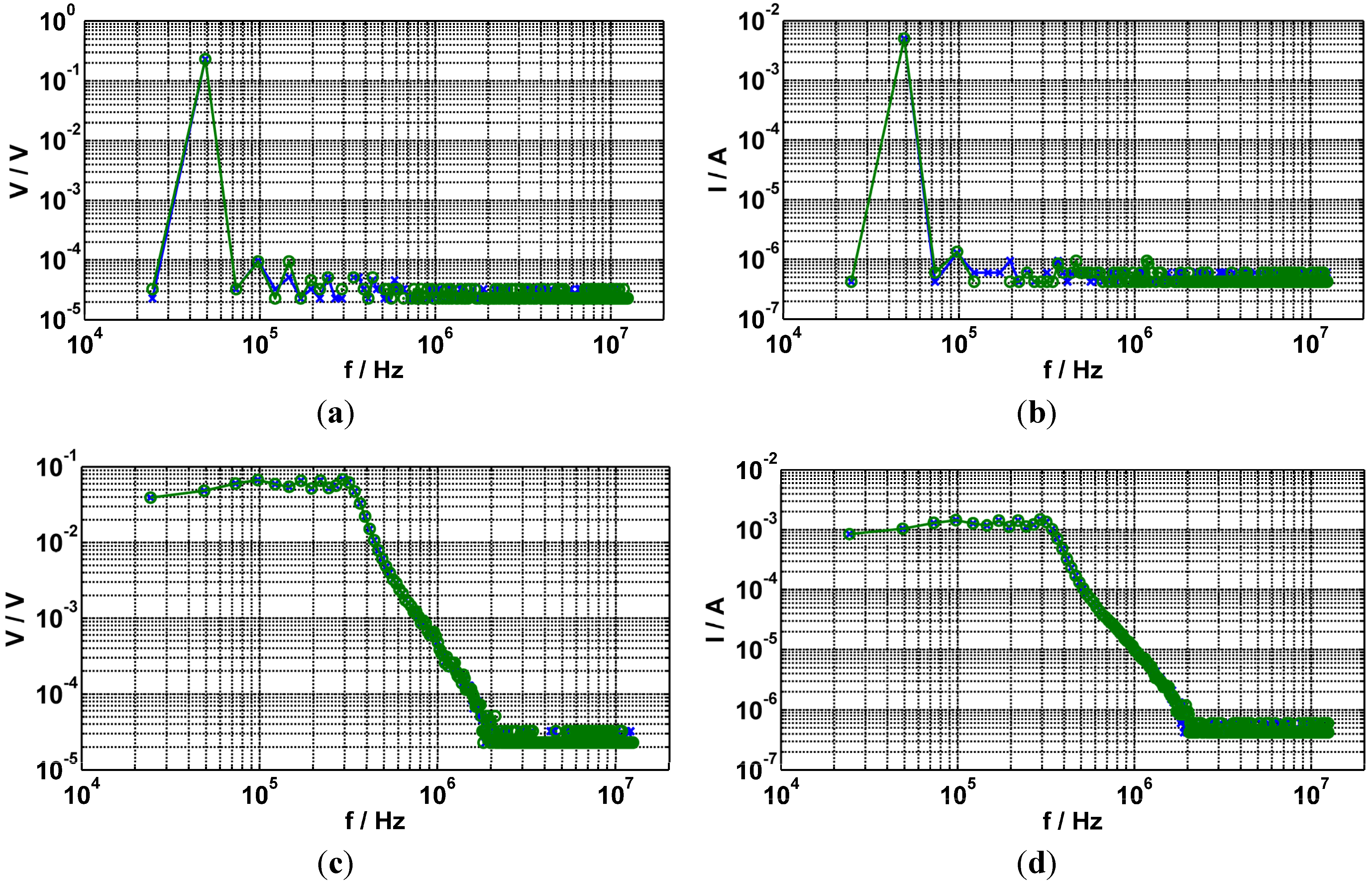
- (a)
- Voltage spectrum with sinusoidal excitation of f ≈ 48.8 kHz. The achieved SINAD is ≈89 dBFS, the ENOB is ≈14.4 bit, the SFDR is ≈67 dB and the THD+N is ≈56 dB.
- (b)
- Current spectrum with sinusoidal excitation of f ≈ 48.8 kHz. The achieved SINAD is ≈89 dBFS, ENOB is ≈14.5 bit, the SFDR is ≈69 dB and the THD+N is ≈59 dB.
- (c)
- Voltage spectrum with chirp excitation with a period of T = 40.96 µs.
- (d)
- Current spectrum with chirp excitation with a period of T = 40.96 µs.
| f | 48.8 kHz | 97.7 kHz | 195 kHz | 391 kHz |
|---|---|---|---|---|
| SINADV/dBFS | 89.0/88.6 | 87.9/88.0 | 87.5/88.1 | 87.4/86.1 |
| SINADI/dBFS | 89.5/88.7 | 87.9/87.7 | 87.9/87.6 | 86.6/86.8 |
| ENOBV/bit | 14.5/14.4 | 14.3/14.3 | 14.2/14.3 | 14.2/14.0 |
| ENOBI/bit | 14.6/14.4 | 14.3/14.3 | 14.3/14.3 | 14.2/14.1 |
| SFDRV/dB | 69.0/67.1 | 64.4/64.4 | 57.6/56.5 | 49.9/49.6 |
| SFDRI/dB | 68.5/69.0 | 64.9/63.3 | 59.1/59.7 | 54.2/54.6 |
| THDV+NV/dB | 57.4/56.6 | 57.2/57.8 | 54.2/53.6 | 48.5/48.0 |
| THDI+NI/dB | 58.9/59.0 | 59.7/59.5 | 58.1/58.1 | 53.5/53.8 |
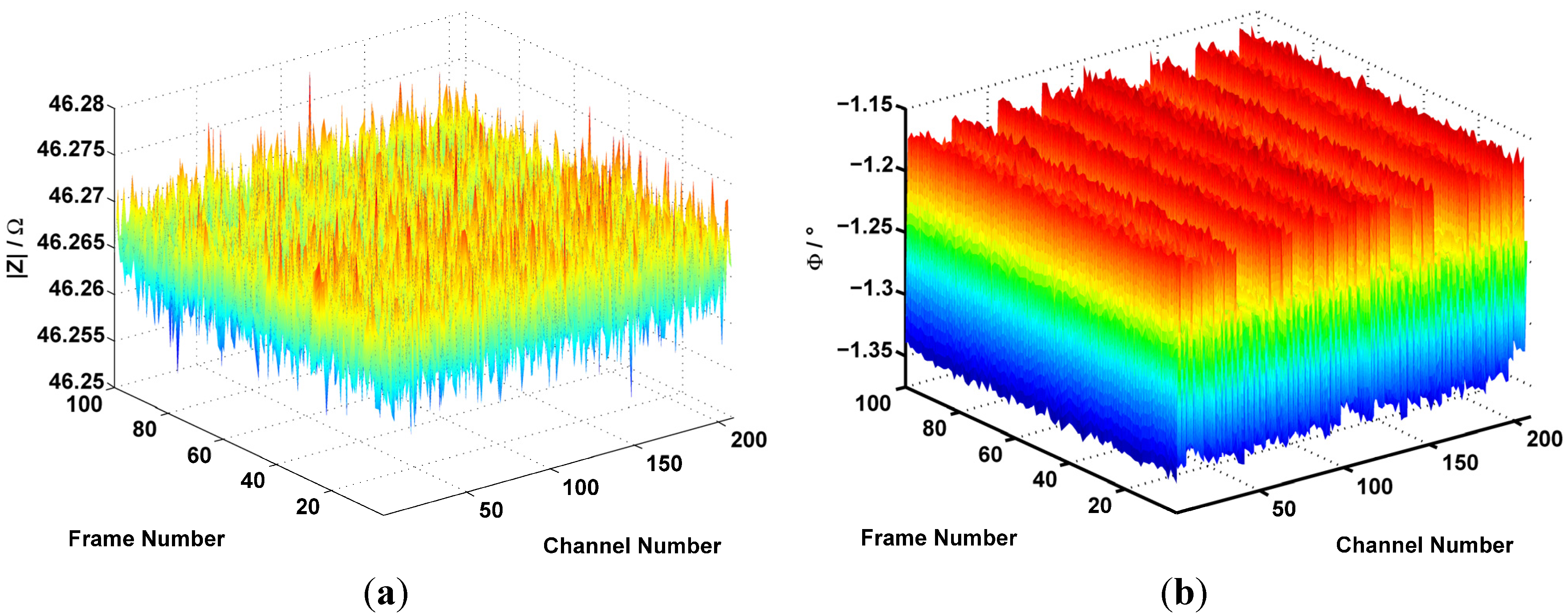
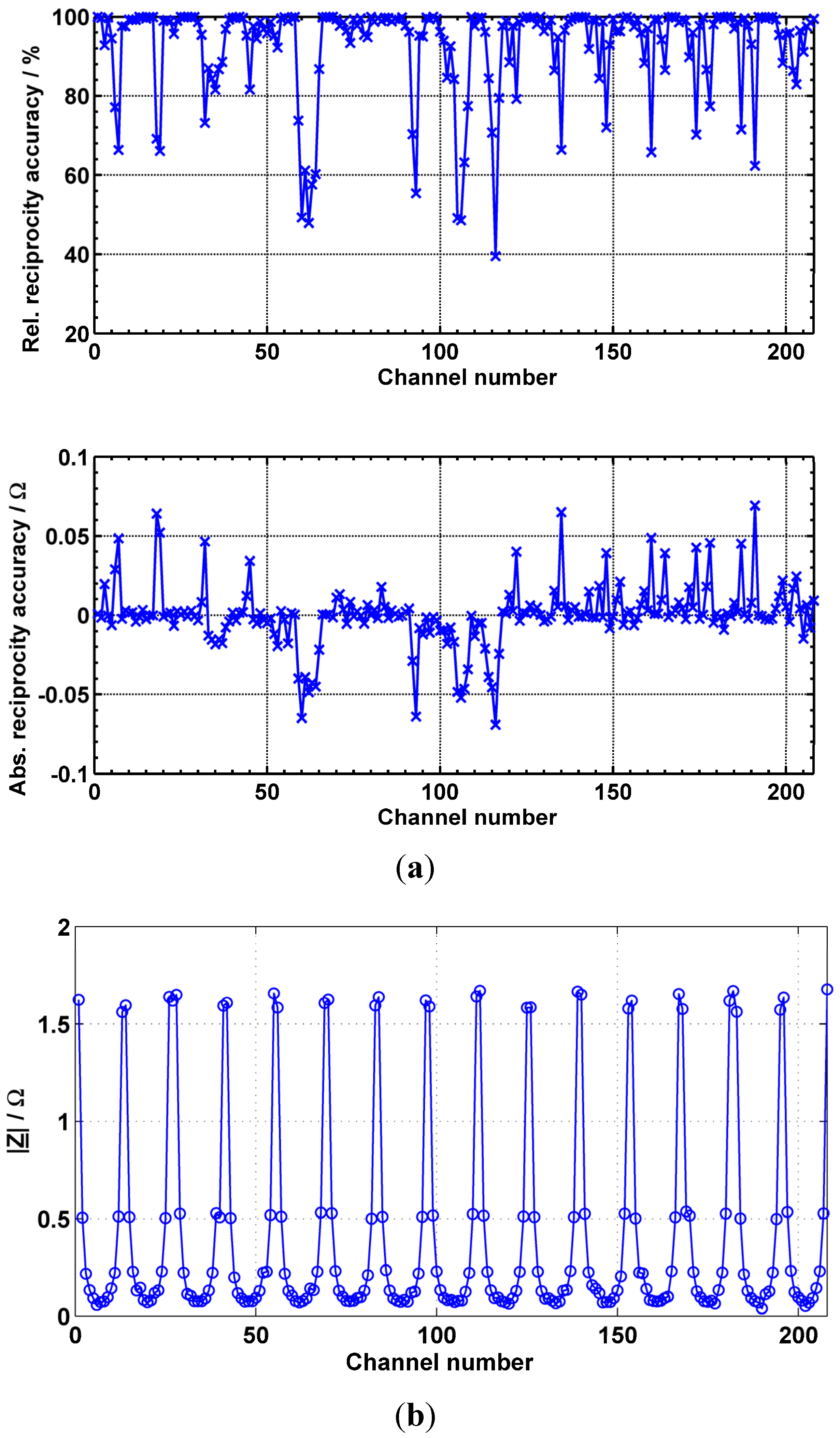
2.5. Channel-Dependent Deviations
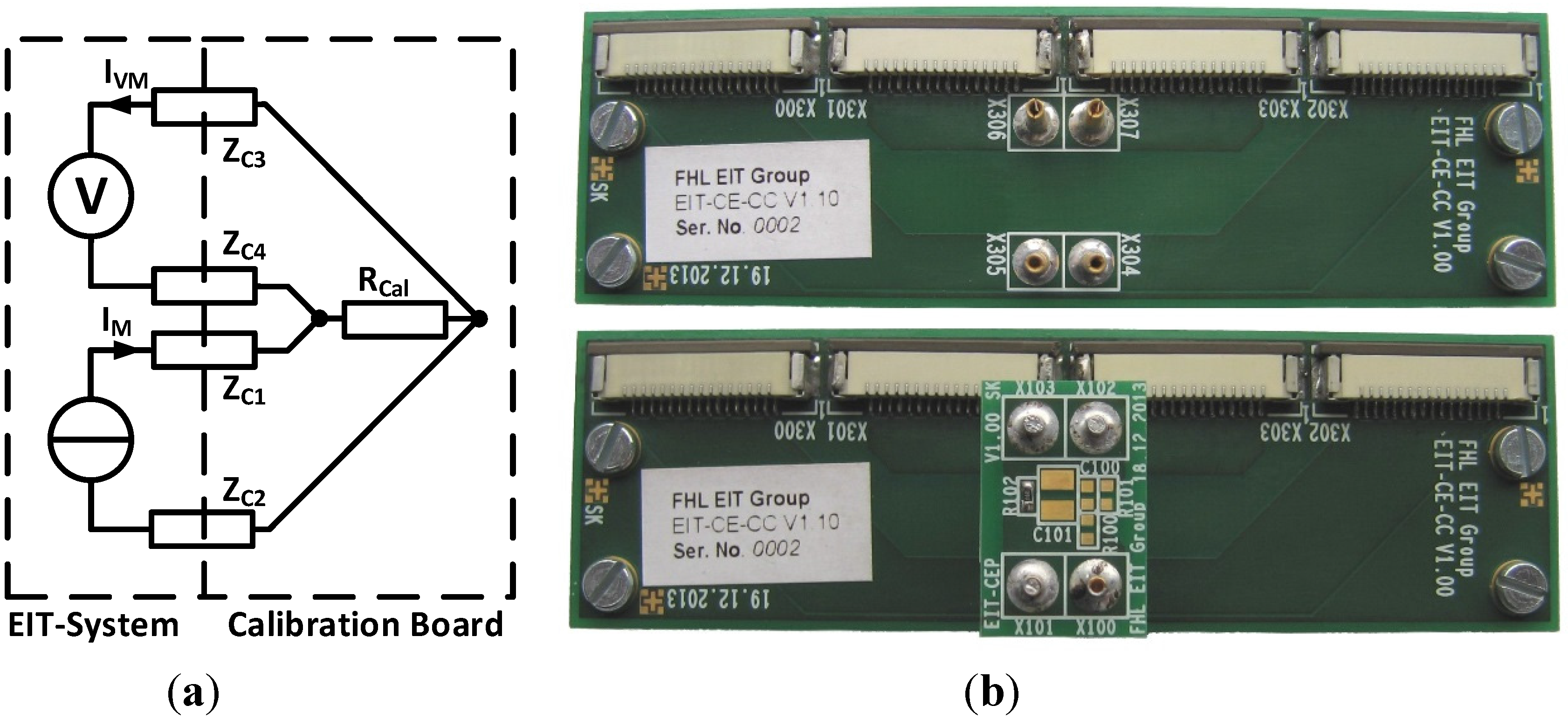
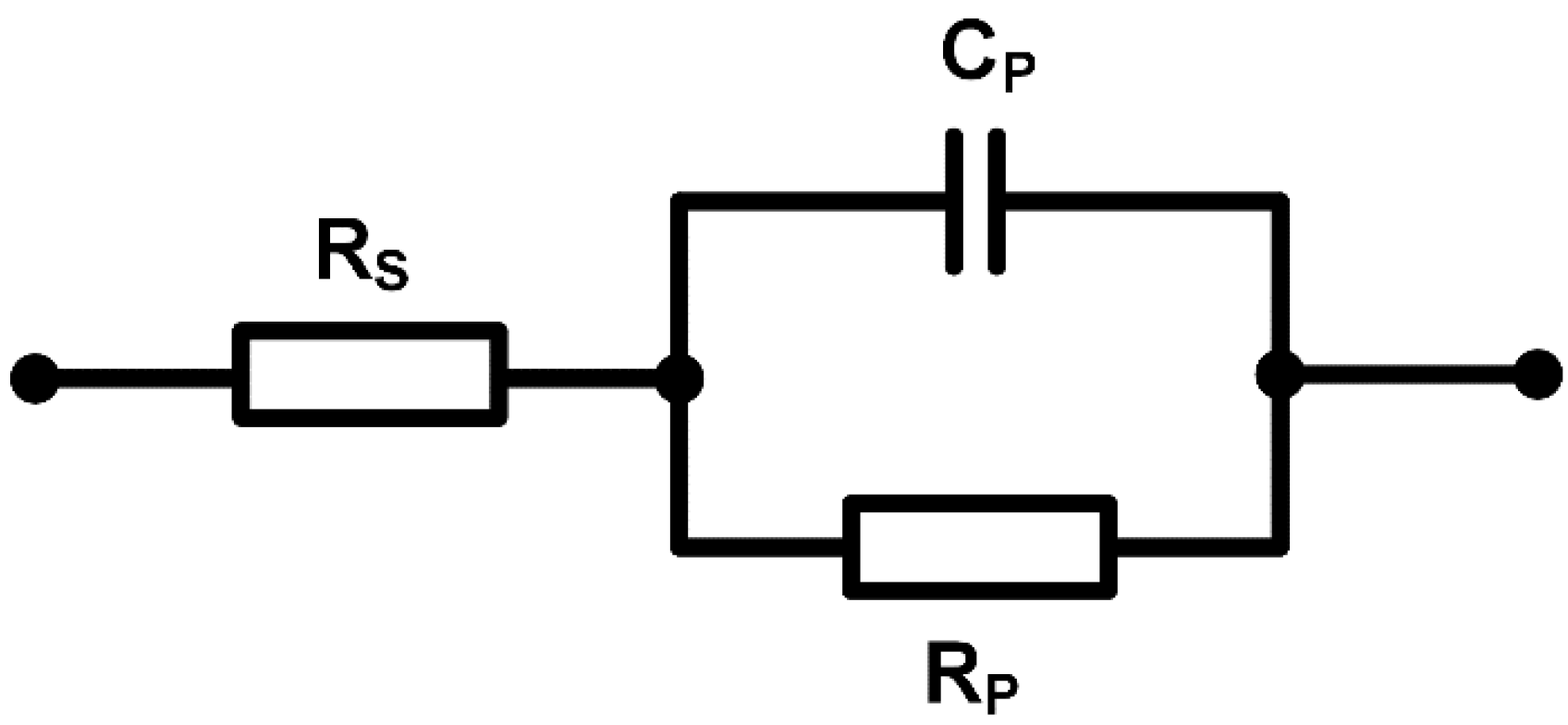
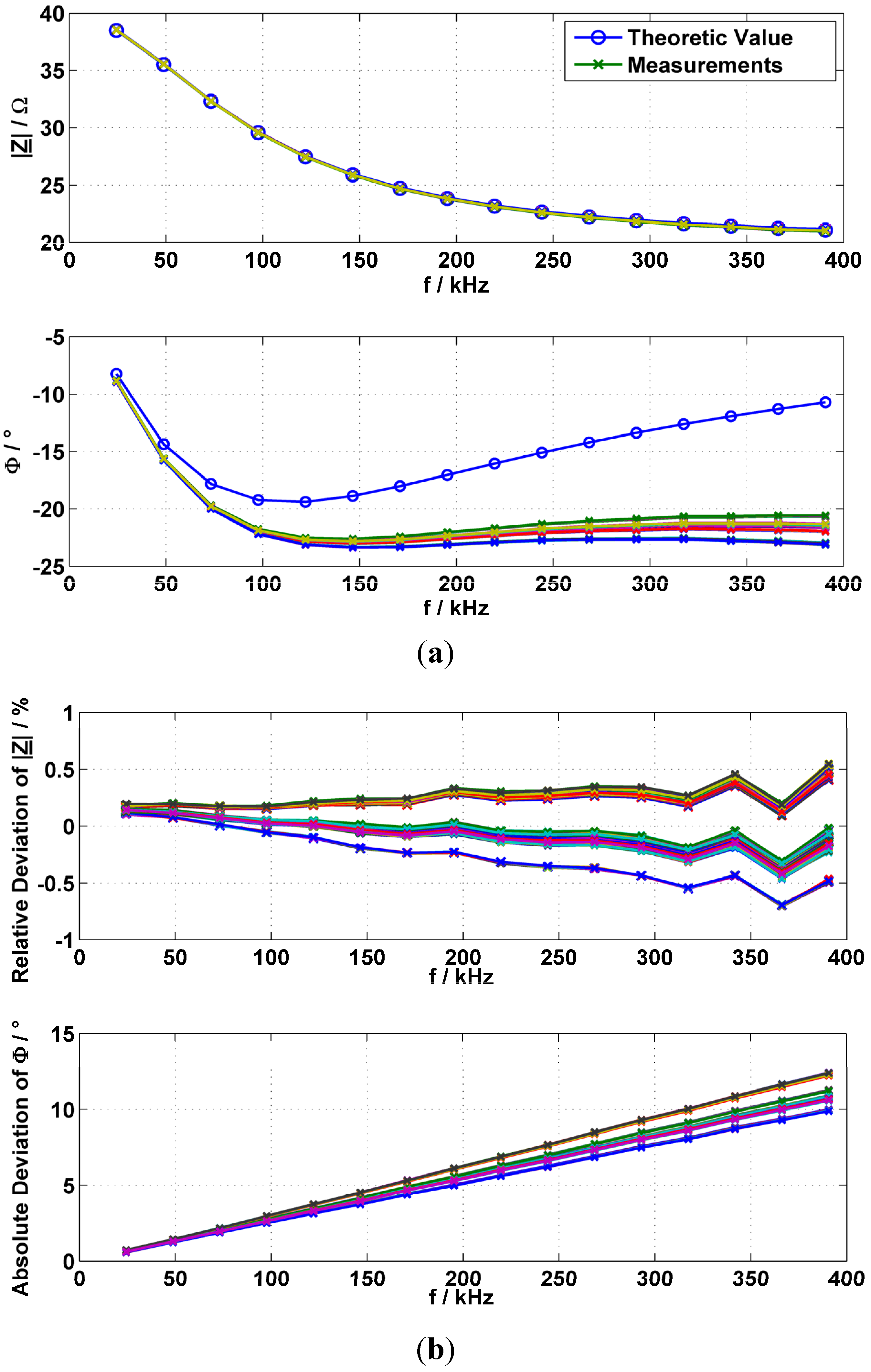
2.6. Verification with an R-R||C Phantom
3. Results
3.1. Micro-Tank Measurements
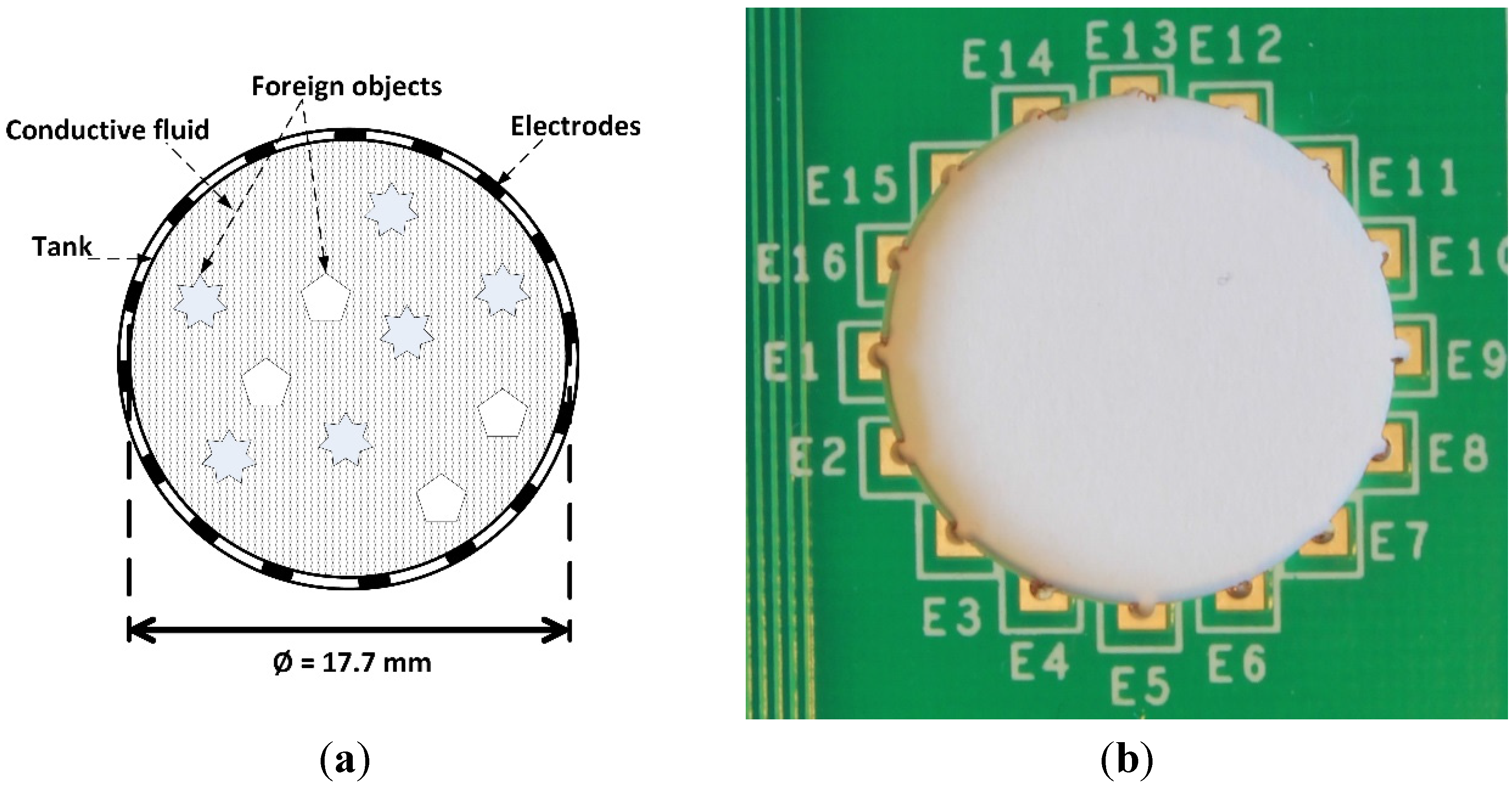
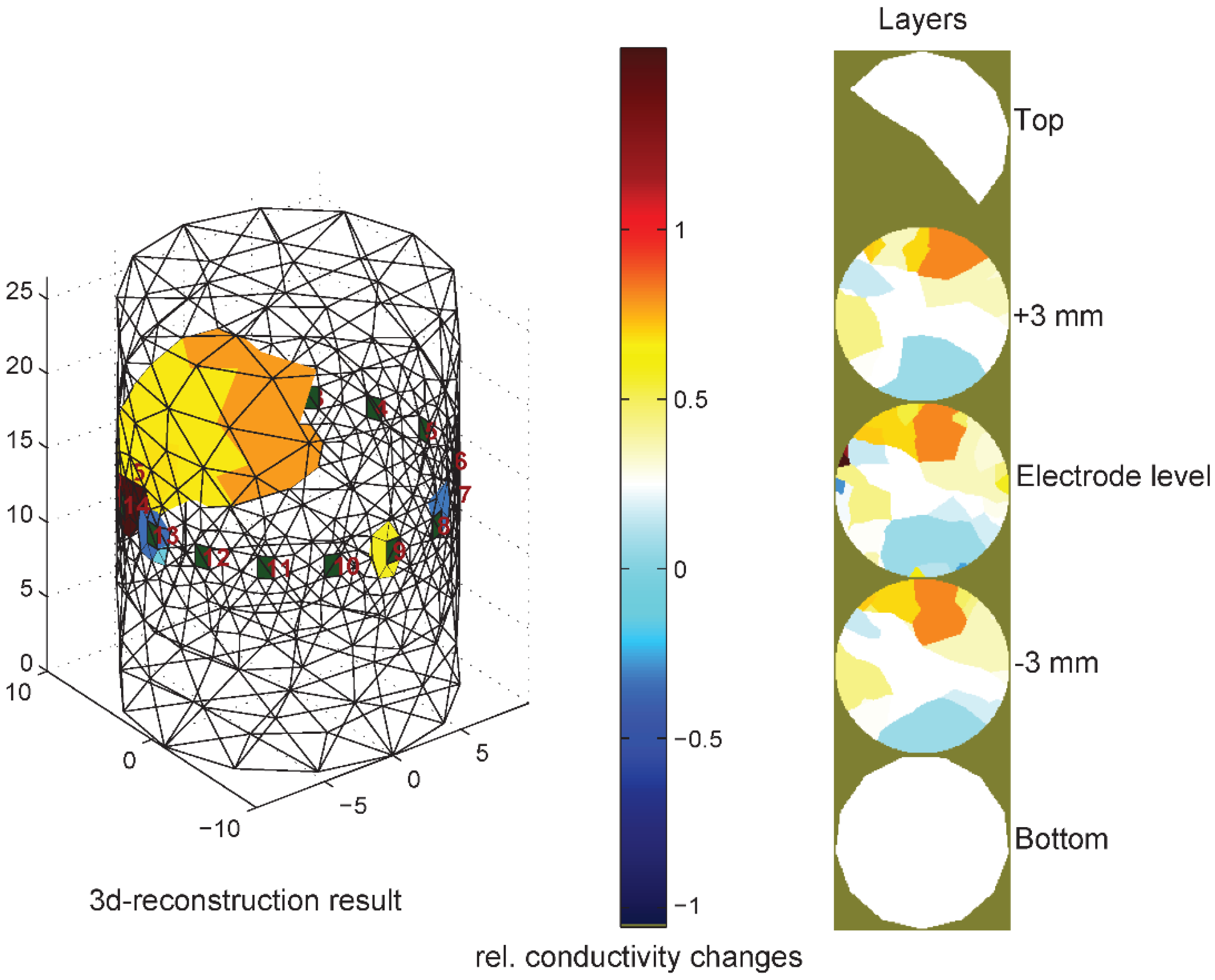
3.2. Tank Measurements
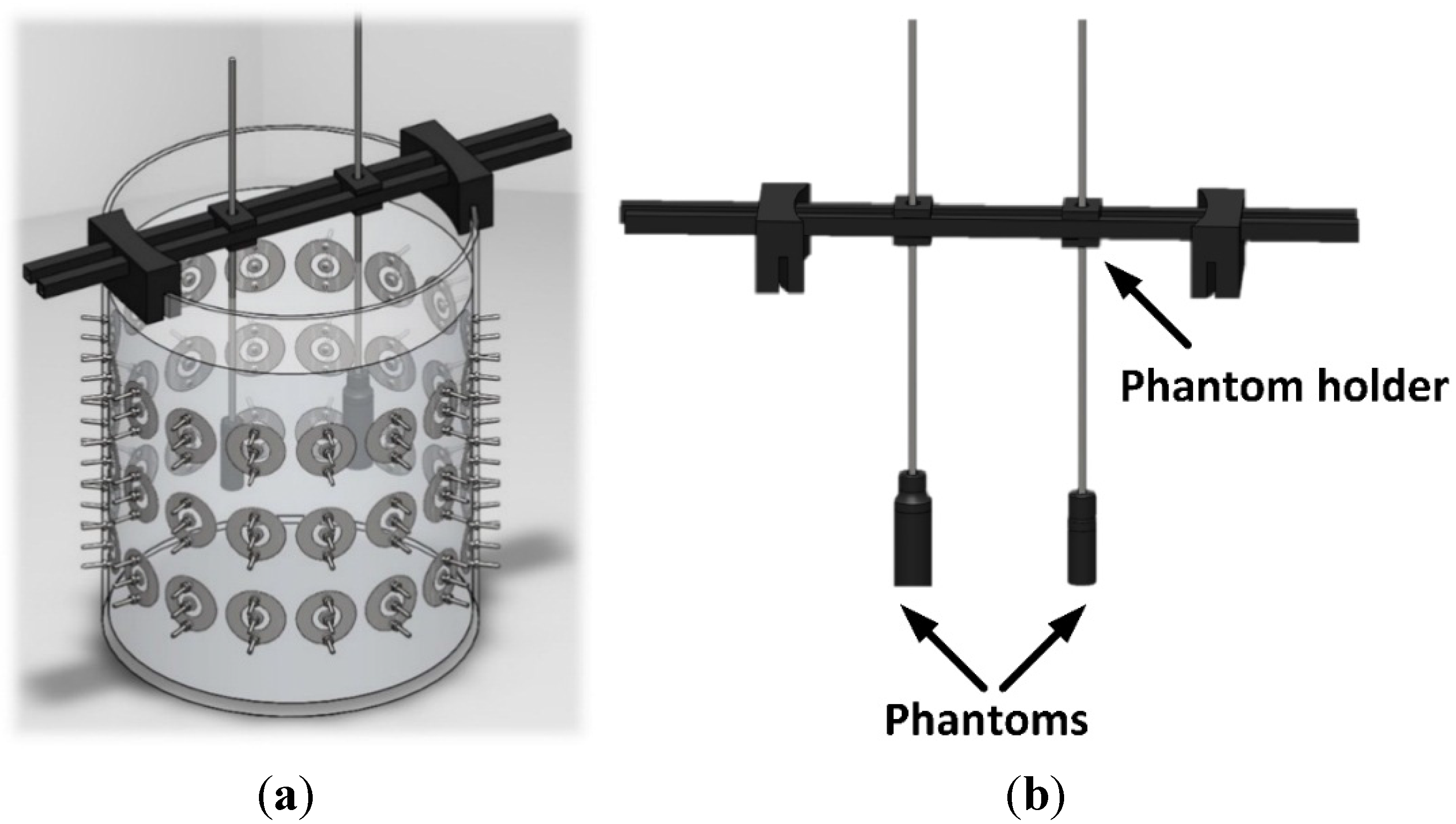

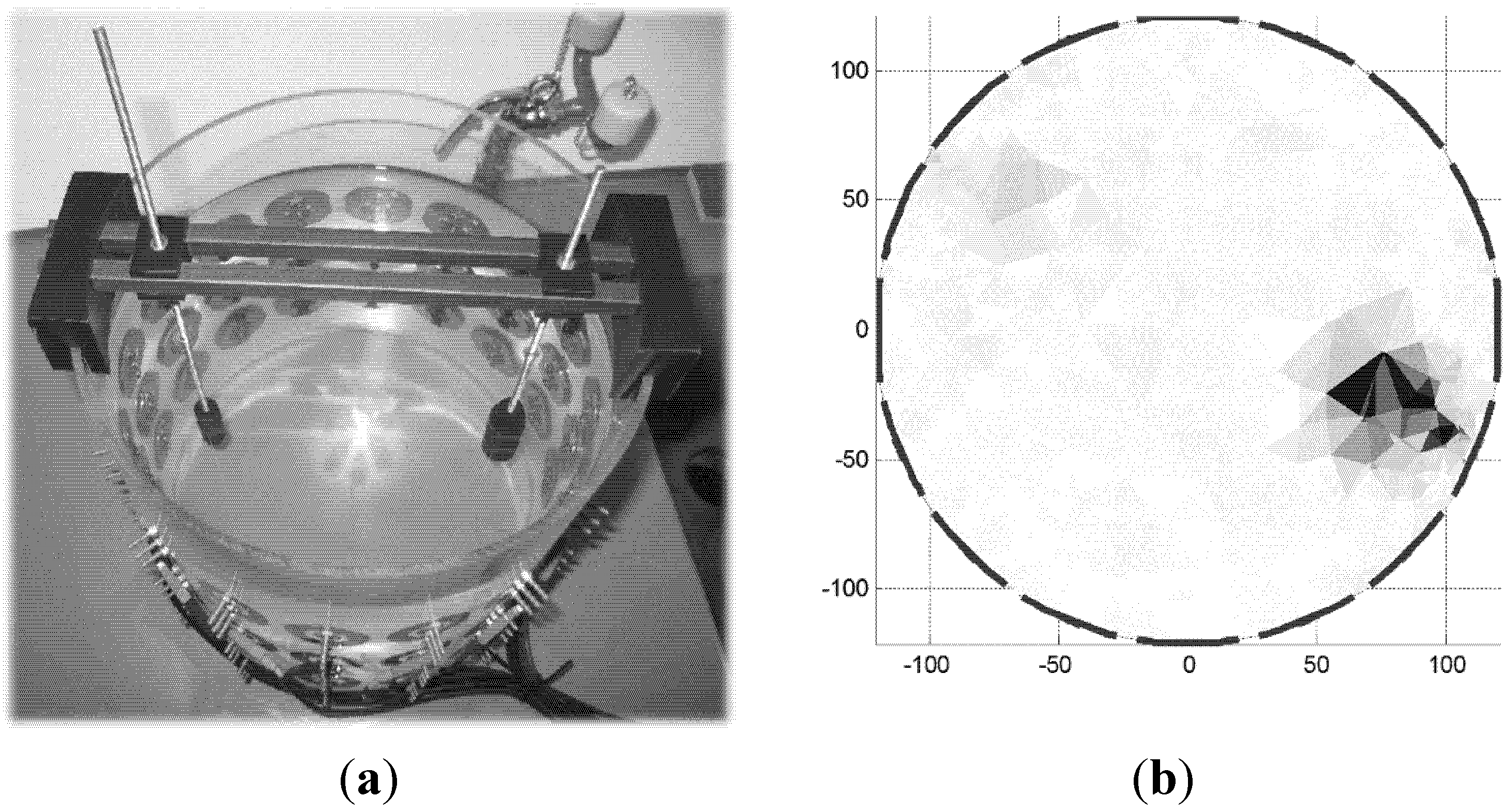
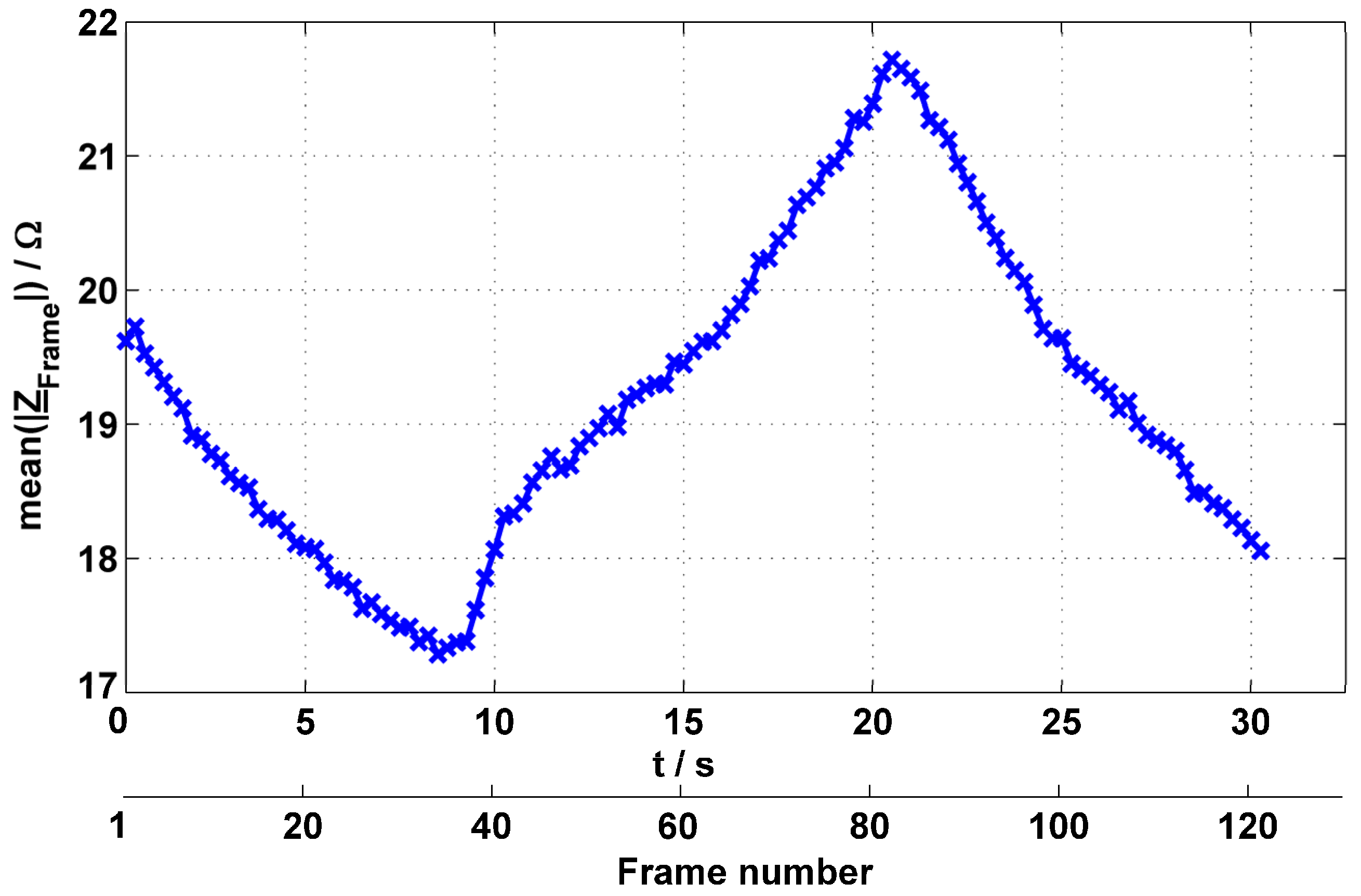
3.3. Thorax Measurements

4. Summary and Outlook
Acknowledgments

Author Contributions
Conflicts of Interest
References
- Grimnes, S.; Martinsen, O.G. Bioelectricity and Bioimpedance Basics, 2nd ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Grimnes, S.; Martinsen, O.G. Bioimpedance. In Wiley Encyclopedia of Biomedical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 438–447. [Google Scholar]
- Kaufmann, S.; Malhotra, A.; Ardelt, G.; Ryschka, M. A high accuracy broadband measurement system for time resolved complex bioimpedance measurements. Physiol. Meas. 2014, 35, 1163–1180. [Google Scholar] [CrossRef] [PubMed]
- Mello, L.A.M.; de Lima, C.R.; Amato, M.B.P.; Lima, R.G.; Silva, E.C.N. Three-Dimensional Electrical Impedance Tomography: A Topology Optimization Approach. IEEE Trans. Biomed. Eng. 2008, 55, 531–540. [Google Scholar] [CrossRef] [PubMed]
- Frerichs, I. Electrical impedance tomography (EIT) in applications related to lung and ventilation: A review of experimental and clinical activities. Physiol. Meas. 2000, 21, R1–R21. [Google Scholar] [CrossRef] [PubMed]
- Cherepenin, V.; Karpov, A.; Korjenevsky, A.; Kornienko, V.; Mazaletskaya, A.; Mazourov, D.; Meister, D. A 3D electrical impedance tomography (EIT) system for breast cancer detection. Physiol. Meas. 2001, 22, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Jossinet, J. Variability of impedivity in normal and pathological breast tissue. Med. Biol. Eng. Comput. 1996, 34, 346–350. [Google Scholar] [CrossRef] [PubMed]
- Oh, T.I.; Wi, H.; Kim, D.Y.; Yoo, P.J.; Woo, E.J. A fully parallel multi-frequency EIT system with flexible electrode configuration: KHU Mark2. Physiol. Meas. 2011, 32, 835–849. [Google Scholar] [CrossRef] [PubMed]
- Wi, H.; Sohal, H.; McEwan, A.L.; Woo, E.J.; Oh, T.I. Multi-Frequency Electrical Impedance Tomography System with Automatic Self-Calibration for Long-Term Monitoring. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 119–128. [Google Scholar] [PubMed]
- McEwan, A.; Romsauerova, A.; Yerworth, R.; Horesh, L.; Bayford, R.; Holder, D. Design and calibration of a compact multi-frequency EIT system for acute stroke imaging. Physiol. Meas. 2006, 27, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Saulnier, G.J.; Liu, N.; Tagga, C.; Xia, H.; Kao, T.J.; Newell, J.C.; Isaacson, D. An electrical impedance spectroscopy system for breast cancer detection. In Proceedings of the Annual International Conference of the IEEE EMBS, Lyon, France, 23–26 August 2007; pp. 4154–4157.
- Khan, S.; Manwaring, P.; Borsic, A.; Halter, R. FPGA-based voltage and current dual drive system for high frame rate electrical impedance tomography. IEEE Med. Imaging 2015, 34, 888–901. [Google Scholar] [CrossRef] [PubMed]
- Paavle, T.; Min, M.; Parve, T. Aspects of using chirp excitation for estimation of bioimpedance spectrum. In Fourier Transform—Signal Processing; Salih, S.M., Ed.; InTech: Rijeka, Croatia, 2012; pp. 237–256. [Google Scholar]
- Birkett, A. Bipolar current source maintains high output impedance at high frequencies. EDN Des. Ideas 2005, 12, 128–130. [Google Scholar]
- Adler, A.; Lionheart, W.R.B. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Beckmann, L.; van Riesen, D.; Leonhardt, S. Optimal electrode placement and frequency range selection for the detection of lung water using Bioimpedance Spectroscopy. In Proceedings of the Annual International Conference of the IEEE EMBS, Lyon, France, 23–26 August 2007; pp. 2685–2688.
- Kaufmann, S.; Latif, A.; Saputra, W.C.; Moray, T.; Henschel, J.; Hofmann, U.G.; Ryschka, M. Multi-frequency Electrical Impedance Tomography for Intracranial Applications. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Beijing, China, 26–31 May 2013; Volume 39, pp. 961–963.
- Gaggero, P.O. Miniaturization and Distinguishability Limits of Electrical Impedance Tomography for Biomedical Application. Ph.D. Thesis, University of Neuchtel, Neuchtel, Switzerland, 2011. [Google Scholar]
- Woo, E.J.; Hua, P.; Webster, J.; Tompkings, W.J.; Pallas-Areny, R. Skin impedance measurements using simple and compound electrodes. Med. Biol. Eng. Comput. 1992, 30, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Yasin, M.; Böhm, S.; Gaggero, P.O.; Adler, A. Evaluation of EIT system performance. Physiol. Meas. 2011, 32, 851–865. [Google Scholar] [CrossRef] [PubMed]
- Adler, A.; Gaggero, P.O.; Maimaitijiang, Y. Adjacent stimulation and measurement patterns considered harmful. Physiol. Meas. 2011, 32, 731–744. [Google Scholar] [CrossRef] [PubMed]
- Schöberl, J. NETGEN—An advancing front 2D/3D-mesh generator based on abstract rules. Comput. Vis. Sci. 1997, 1, 41–52. [Google Scholar]
- Adler, A.; Arnold, J.H.; Bayford, R.; Borsic, A.; Brown, B.; Dixon, P.; Faes, T.J.C.; Frerichs, I.; Gagnon, H.; Gärber, I.; et al. GREIT: A unified approach to 2D linear EIT reconstruction of lung images. Physiol. Meas. 2009, 30, 35–55. [Google Scholar] [CrossRef] [PubMed]
- Grychtol, B.; Lionheart, W.R.B.; Bodenstein, M.; Wolf, G.; Adler, A. Impact of Model Shape Mismatch on Reconstruction Quality in Electrical Impedance Tomography. IEEE Trans. Med. Imaging 2012, 31, 1754–1760. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusche, R.; Malhotra, A.; Ryschka, M.; Ardelt, G.; Klimach, P.; Kaufmann, S. A FPGA-Based Broadband EIT System for Complex Bioimpedance Measurements—Design and Performance Estimation. Electronics 2015, 4, 507-525. https://doi.org/10.3390/electronics4030507
Kusche R, Malhotra A, Ryschka M, Ardelt G, Klimach P, Kaufmann S. A FPGA-Based Broadband EIT System for Complex Bioimpedance Measurements—Design and Performance Estimation. Electronics. 2015; 4(3):507-525. https://doi.org/10.3390/electronics4030507
Chicago/Turabian StyleKusche, Roman, Ankit Malhotra, Martin Ryschka, Gunther Ardelt, Paula Klimach, and Steffen Kaufmann. 2015. "A FPGA-Based Broadband EIT System for Complex Bioimpedance Measurements—Design and Performance Estimation" Electronics 4, no. 3: 507-525. https://doi.org/10.3390/electronics4030507
APA StyleKusche, R., Malhotra, A., Ryschka, M., Ardelt, G., Klimach, P., & Kaufmann, S. (2015). A FPGA-Based Broadband EIT System for Complex Bioimpedance Measurements—Design and Performance Estimation. Electronics, 4(3), 507-525. https://doi.org/10.3390/electronics4030507





