Performance Analysis and Comparison of Two Deep Learning Methods for Direction-of-Arrival Estimation with Observed Data

Abstract

Direction-of-arrival (DOA) estimation is fundamental in array signal processing, yet classical algorithms suffer from significant performance degradation under low signal-to-noise ratio (SNR) conditions and require computationally intensive eigenvalue decomposition. This study presents a systematic comparative analysis of two backbone networks, a convolutional neural network (CNN) and long short-term memory (LSTM) for DOA estimation, addressing two critical research gaps: the lack of a mechanistic understanding of architecture-dependent performance under varying conditions and insufficient validation using real measured data. Both networks are trained using cross-spectral density matrices (CSDMs) from simulated uniform linear array (ULA) signals. Under baseline conditions (1° classification interval), both CNN and LSTM methods reach an accuracy (ACC) above 98%, in which the error is ±1° for CNN and ±2° for LSTM, only existing in the end-fire direction. Key findings reveal that LSTM maintains above 90% accuracy down to −20 dB SNR, demonstrating superior noise robustness, whereas CNN exhibits better angular resolution. Four performance boundaries are identified: optimal performance is achieved at half-wavelength element spacing; SNR crossover occurs at −20 dB below which accuracy drops sharply; the snapshot threshold of 32 marks the transition from snapshot-deficient to snapshot-sufficient conditions; the array size of 8 is the turning point for the performance variation rate. Comparative analysis against traditional methods demonstrates that deep learning approaches achieve superior resolution ability, batch processing efficiency, and noise robustness. Critically, models trained exclusively on single-target simulated data successfully generalize to multi-target experimental data from the Shallow Water Array Performance (SWAP) program, recovering primary target trajectories without domain adaptation. These results provide concrete engineering guidelines for architecture selection and validate the sim-to-real generalization capability of CSDM-based deep learning approaches in underwater acoustic environments.

1. Introduction

DOA estimation is a fundamental problem in array signal processing with widespread applications in radar, sonar, wireless communications, and seismology. Over the past several decades, numerous classical algorithms have been developed to address this problem, including subspace-based methods such as Multiple Signal Classification (MUSIC) [1] and Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) [2], the Capon beamformer [3], also known as minimum variance distortionless response (MVDR), and the maximum likelihood (ML) method [4].

Despite their theoretical elegance and widespread adoption, these classical algorithms suffer from three critical limitations. First, their performance degrades significantly under low SNR conditions frequently encountered in underwater acoustic environments, primarily because subspace separation becomes unreliable when noise power approaches or exceeds signal power [5]. Second, the computational burden associated with eigenvalue decomposition or matrix inversion scales cubically with array size, rendering real-time processing prohibitive for large-scale arrays [6]. Third, the computational burden associated with eigenvalue decomposition or matrix inversion scales cubically with array size, rendering real-time processing prohibitive for large-scale arrays [7,8,9].

Deep learning (DL) methods have emerged as a promising alternative that can learn robust feature representations directly from data without explicit modeling of array manifold or noise statistics [10,11]. The evolution of DL-based DOA estimation can be categorized into three main paradigms. FNN, pioneered by Xiao et al. [12], extended by Takeda and Komatani [13] and Ozanich E et al. [14], demonstrated the feasibility of learning DOA mappings from covariance matrices, though they treat the spatial structure as flattened vectors. CNNs, employed by Liu et al. [15] and Li et al. [16], preserve the matrix structure of the CSDM and extract local spatial patterns through convolutional kernels. Recurrent Neural Networks (RNNs/LSTM), employed by Wang et al. [17], Xiang et al. [18], and Xie and Wang [19], model sequential dependencies across array elements through memory mechanisms. Recent advances have also addressed practical challenges, including GNSS jamming scenarios [20], reconfigurable digital architectures for real-time angle estimation [21,22], underwater acoustics scenarios [14,23,24], and uncertainty quantification [25].

However, existing DL methods have not fully resolved the core challenges of traditional methods, and each paradigm carries inherent theoretical limitations. CNN-based methods assume spatial locality and translation invariance, extracting features through fixed-size kernels. While effective under high-SNR conditions, this local receptive field constraint limits their ability to model long-range dependencies when noise corrupts local spatial patterns [15,16]. Conversely, LSTM-based methods treat CSDM rows as sequential inputs, leveraging memory mechanisms to accumulate phase evolution information. While offering potential noise robustness, this sequential processing sacrifices explicit two-dimensional spatial correlation modeling and may compromise angular resolution [18].

Based on the above analysis, two critical research gaps can be identified. First, CNN and LSTM represent distinct feature extraction mechanisms, but existing studies have only evaluated them in isolation. Their condition-dependent performance variations and the underlying physical mechanisms remain unsystematically characterized. This gap deprives researchers of principled guidance for architecture selection, making it essential to clarify the operational conditions where each architecture outperforms and the mechanisms driving such differences. Second, the majority of DL-based DOA methods are validated exclusively through simulations, raising concerns about whether models trained on idealized signals can generalize to the real underwater acoustic environments.

This paper addresses these gaps through a systematic comparative study that bridges algorithmic understanding with practical deployment considerations. The key contributions are as follows:

(1)

Systematic investigation of distinct feature extraction paradigms. Comparative analyses are conducted to elucidate how CNN’s local spatial pattern extraction and LSTM’s sequential memory integration yield quantifiably divergent performance characteristics across varying regimes of the SNR, array element count, element spacing, and snapshot number.

(2)

Four performance boundaries are identified. Optimal performance is achieved at half-wavelength element spacing; SNR crossover occurs at −20 dB, below which accuracy drops sharply; the snapshot threshold of 32 marks the transition from snapshot-deficient to snapshot-sufficient conditions; the array size of 8 is a turning point for the performance variation rate. Based on a multidimensional analysis encompassing the SNR, array configuration, computational efficiency, and measured data performance, specific recommendations for engineering applications are provided, thereby bridging the gap between algorithmic research and practical deployment.

(3)

Validation of sim-to-real generalization capability. On the SWAP experimental dataset, it is demonstrated that models trained exclusively on single-target simulated signals can generalize to multi-target real underwater environments without domain adaptation, thus providing empirical evidence for the cross-domain applicability of CSDM-based deep learning approaches.

The remainder of this paper is organized as follows. Section 2 introduces the model of the array received signals and neural network architecture of CNN and LSTM, as well as the simulation environment, the generation of simulation data, and the information of experimental data. In Section 3, the models’ performance on simulation data and experimental data is analyzed and compared with several traditional methods. Finally, conclusions are presented in Section 4.

2. Model, Data, and Methods

2.1. Signal Model

In this paper, only ULA is discussed. As shown in Figure 1, ULA is composed of M isotropic hydrophone elements, which are arranged in a straight line with a uniform spacing of d between each element. Assuming the sound received by the array is a far-field plane wave generated from a point source, and the frequency is ${\omega }_0$, the received signal $\mathit{y}\left(t\right)$ of ULA at time $t$ can be modeled as

$$\mathit{y}\left(t\right)=\mathit{a}\left(\phi \right)\mathit{s}\left(t\right)+\mathit{n}\left(t\right)$$

(1)

where $\mathit{y}\left(t\right)={\left[y_1\left(t\right),y_2\left(t\right),\cdots ,y_M\left(t\right)\right]}^T$ is the array received vector, the observed noise vector is $\mathit{n}\left(t\right)={\left[n_1\left(t\right),n_2\left(t\right),\cdots ,n_M\left(t\right)\right]}^T$, with an additive white Gaussian noise (AWGN) model applied. $\mathit{a}\left(\phi \right)={\left[e^{-j{\omega }_0{\tau }_1\left(\phi \right)},e^{-j{\omega }_0{\tau }_2\left(\phi \right)},\cdots ,e^{-j{\omega }_0{\tau }_M\left(\phi \right)}\right]}^T$ is the steering vector when the incident angle is $\phi$, ${\tau }_m\left(\phi \right)={\displaystyle \frac{d\left(m-1\right)\cos \phi }{c}}(m=1,2,\cdots ,M)$ represents the delay in time between the m-th sensor and the reference sensor.

In underwater acoustic signal processing, the covariance matrix of the signal is also known as CSDM. Assuming that the signal and noise are uncorrelated, the CSDM of the array observed signal can be written as

$$\mathit{R}=E\left[\mathit{y}\left(t\right){\mathit{y}}^H\left(t\right)\right]=\mathit{A}{\mathit{R}}_{\mathit{s}}{\mathit{A}}^H+{\sigma }^2\mathit{I}$$

(2)

where $\mathit{A}=[\mathit{a}({\phi }_1), \mathit{a}({\phi }_2),\dots , \mathit{a}({\phi }_D)]$ is an $M\times D$ steering vector matrix (where D is the number of signal sources). ${\mathit{R}}_{\mathit{s}}$ is the covariance matrix of the sound sources and can be expressed as

$${\mathit{R}}_{\mathit{s}}=E\left[\mathit{s}\left(t\right){\mathit{s}}^H\left(t\right)\right]$$

(3)

The CSDM contains sufficient information to distinguish a sound source from different directions and is often used as the input in a DL network.

2.2. Data Information

2.2.1. The Simulation Data

For each DOA angle ${\phi }_k$ (k = 1, 2, ..., 181), corresponding to angles from 0° to 180° with 1° resolution, we generate time-series signals using Equation (1) for all M sensors. Each simulation runs for 204.8 s at a sampling rate of 1000 Hz, that is, 204,800 sample points in total for each direction. Then, the signals are segmented using sliding windows (window length $N_{\mathrm{w}}$: 4096 samples, 50% overlap) and the number of segments for each direction $N_{\mathrm{s}}$ is 159. For the l-th segment at the DOA angle ${\phi }_k$, the sample covariance matrix is computed as

$${\mathit{R}}_k^{(l)}={\displaystyle \frac{1}{N_{\mathrm{w}}}}{\displaystyle \sum _{n=1}^{N_{\mathrm{w}}}{\mathit{y}}_{\left(n\right)}^{\left(l\right)}}{\mathit{y}}_{\left(n\right)}^{\left(l\right)H}$$

(4)

where ${\mathit{y}}_{\left(n\right)}^{\left(l\right)}={\left[y_1\left(n\right),y_2\left(n\right),\cdots ,y_M\left(n\right)\right]}^T$ is the n-th snapshot in the l-th segment. This process generates a 4D tensor of covariance matrices with dimensions $\left[M \times M \times 181 \times N_{\mathrm{s}}\right]$, where 181 represents the number of DOA angles and $N_{\mathrm{s}}$ is the number of segments per angle.

Since the covariance matrices are complex-valued, we decompose each matrix into its real and imaginary components to create a suitable input format for training:

$${\mathit{R}}_k^{(l)}=\mathrm{Re}\left({\mathit{R}}_k^{(l)}\right)+j·\mathrm{Im}\left({\mathit{R}}_k^{(l)}\right)$$

(5)

The input tensor X is constructed as

$$\mathit{X}\in {ℝ}^{M\times M\times 2\times N_{\mathrm{total}}}$$

(6)

where the first channel contains Re(R), the second channel contains Im(R), and $N_{\mathrm{total}}= 181 \times N_s$ is the total number of samples. Each sample is associated with a corresponding DOA label ${\phi }_k$ ∈ {0°, 1°, ..., 180°}, which is encoded as a categorical variable for classification.

The baseline configuration is chosen as $M=32$ and $d=$ 1.5 m, which matches the geometry of the SWAP array, and the training and testing signal SNR is 20 dB with 4096 snapshots and 1° search grid spacing. Unless stated otherwise, all results reported hereafter are based on models trained and tested under the baseline configuration.

It is worth noticing that in the process of signal simulation generation, the imaginary part cannot be ignored, and a complex number model must be used. This is because complex signals can contain both amplitude and phase information at the same time, which is necessary for analyzing the frequency and phase characteristics of the signal. In array signal processing, such as DOA estimation, the signals collected by the array will produce complex samples due to differences in arrival time and phase. These samples are used to construct the CSDM, which retains the spatial characteristics of the signal. As can be seen from Figure 2, the imaginary part of the CSDM is only symmetric about one diagonal line and has the opposite sign about the other diagonal line, while the real part of the CSDM is symmetric about two diagonal lines. The real part of the CSDM for an incident angle of 170° is the same as that for an incident angle of 10°, which means that using only the real part of the data cannot distinguish between these two angles, and the theoretical upper limit of the test ACC rate is 50%.

2.2.2. The Experimental Data

The observed data was recorded by a 32-element bottom-mounted hydrophone array deployed off the Florida coast at 1 kHz frequency, as part of the SWAP program. The Universal Transverse Mercator (UTM) coordinates of the array hydrophones and the signal data are contained in files, while the targets’ information is unknown. As shown in Figure 3, it is a ULA, but the positions of the elements are offset from the standard straight line. The average spacing between the array elements is calculated to be 1.5 m. Beamforming results are calculated using both the original array shape and the ULA after correction, and the resulting pattern diagrams show minimal differences. Therefore, the ideal ULA can be used to replace the actual array shape.

Since the targets’ moving direction is unknown, the target trajectories are extracted using the CBF algorithm, and the result can be seen in Figure 4.

The left and central parts of the graph feature two continuous bright lines, corresponding to two targets; the middle of the right half of the graph has a pale blue bright straight line, corresponding to the third target; to the right of the third target, there is an inclined pale blue bright line, corresponding to the fourth target. As shown in Figure 5, the four targets are named from left to right as T1, T2, T3, and T4. T1 has a movement angle changing from 92° to 0°, T2 has a movement angle changing from 125° to 93°, T3 has an angle of 132°, and T4 has a movement angle changing from 161° to 146°.

2.3. Neural Network Architecture

In this section, the architectures of CNN and LSTM that are applied to solve the DOA estimation problem are presented in detail. The basics of these neural networks are overwhelmed since readers can find extensive descriptions in the general DL literature [26,27].

2.3.1. CNN-Based DOA Model

• Model Formulation:

For the l-th convolutional layer, the output feature map is computed as

$$Y^{(l)}=f(W^{(l)}\ast X^{(l-1)}+b^{(l)})$$

(7)

where $W^{(l)}$ is the convolutional kernel, $*$ denotes the convolution operation, $X^{(l-1)}$ is the input from the previous layer, $b^{(l)}$ is the bias term, and $f(·)$ is the activation function (ReLU).

$$\mathrm{ReLU}(z)=\max (0,z)$$

(8)

Fully Connected Layer:

$$Y_{\mathrm{FC}}=W_{\mathrm{FC}}·X_{\mathrm{FC}}+b_{\mathrm{FC}}$$

(9)

Output Layer (SoftMax):

$$\mathrm{P}\left(\mathrm{class} = i|X\right) = \exp (y_i) / {\Sigma }_j\exp (y_j)$$

(10)

Cross-Entropy Loss Function:

$$L = -{\Sigma }_i{y}_i\log ({\widehat{y}}_i)$$

(11)

where $y_i$ is the true label (one-hot encoded) and ${\widehat{y}}_i$ is the predicted probability for class i.

2.

Network Configuration

As shown in Figure 6, this CNN is composed of 3 convolution layers and 1 fully connected layer. The input layer starts with a matrix of size 32 × 32 × 2, containing two channels of inputs, corresponding to the real and imaginary parts, respectively. The activation function is ReLU, the initial learning rate is 0.0001, the learning rate optimization algorithm is Adam [28] with an initial learning rate of 0.0001, the maximum number of training epochs is 20, and the batch size is 32. An entropy loss function is used.

2.3.2. LSTM-Based DOA Model

LSTM networks are a variant of RNNs designed to capture long-term dependencies in sequential data. The LSTM architecture addresses the vanishing gradient problem through a gating mechanism that regulates information flow.

1.

Model Formulation

At each time step t, the LSTM cell computes

$$f_t=\sigma (W_f\cdots [h_{t-1}, x_t]+b_f)$$

(12)

$$i_t=\sigma (W_i\cdots [h_{t-1}, x_t]+b_i)$$

(13)

$${\tilde{C}}_t=\tanh (W_C\cdots [h_{t-1}, x_t]+b_C)$$

(14)

$$C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t$$

(15)

$$o_t=\sigma (W_i\cdots [h_{t-1}, x_t]+b_o)$$

(16)

$$h_t=o_t\odot \tanh (C_t)$$

(17)

where σ denotes the sigmoid activation function, ⊙ represents element-wise multiplication, x_t is the input vector at time t, $h_t$ is the hidden state, $C_t$ is the cell state, $f_t$, $i_t$, and $o_t$ are the forget, input, and output gates, respectively, ${\tilde{C}}_t$ is the candidate cell state, and $W$ and $b$ denote weight matrices and bias vectors with corresponding subscripts.

For bidirectional processing, forward and backward LSTM layers are employed:

$${\overrightarrow{h}}_t=\mathrm{LST}{\mathrm{M}}_{forward}(x_t,{\overrightarrow{h}}_{t-1})$$

(18)

$${\overleftarrow{h}}_t=\mathrm{LST}{\mathrm{M}}_{backward}(x_t,{\overleftarrow{h}}_{t-1})$$

(19)

$$h_t=\left[{\overrightarrow{h}}_t;{\overleftarrow{h}}_t\right]$$

(20)

where [ ; ] denotes concatenation, and ${\overrightarrow{h}}_t$ and ${\overleftarrow{h}}_t$ represent the forward and backward hidden states, respectively.

2.

Network Configuration

Define an LSTM network architecture as depicted in Figure 7. Set the input dimension to 32. If both the real and imaginary parts of the data need to be input simultaneously, the real and imaginary parts must be separated, and the imaginary part appended to the real part results in the size of each training sample $32\times 64=2048$ and the total number of samples $181\times 159=28,779$. If only the real part of the data is required, the imaginary part is removed, resulting in the size of each training sample $32\times 32=1024$ and the total number of samples $181\times 159=28,779$. Incorporate a bidirectional LSTM layer comprising 100 hidden units, and ensure the output is the final element of the sequence. Conclude with a fully connected layer of 181 units, succeeded by a SoftMax layer and a classification layer designed for 181 distinct categories.

2.3.3. Performance Metrics

Four metrics are used for performance evaluation: mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), and mean absolute percentage error (MAPE), defined as

$$E_{\mathrm{MAE}}={\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^N\left|y_i-{\widehat{y}}_i\right|}$$

(21)

$$E_{\mathrm{MSE}}={\displaystyle \frac{1}{N}}{{\displaystyle {\sum }_{i=1}^N\left(y_i-{\widehat{y}}_i\right)}}^2$$

(22)

$$E_{\mathrm{RMSE}}=\sqrt{{\displaystyle \frac{1}{N}}{{\displaystyle {\sum }_{i=1}^N\left(y_i-{\widehat{y}}_i\right)}}^2}$$

(23)

$$E_{\mathrm{MAPE}}={\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^N\frac{\left|y_i-{\widehat{y}}_i\right|}{y_i}}\times 100\%$$

(24)

where $N$ is the number of test data samples, $y$ is the true direction, and $\widehat{y}$ is the predicted direction.

2.3.4. Hyperparameter Selection

In this section, through hyperparameter experiments, the optimal CNN kernel size of 5 × 5 and LSTM hidden units of 100 are determined.

Kernel sizes ranging from 3 × 3 to 9 × 9 were evaluated by ACC and RMSE. The CNN model is retrained and tested with the specified kernel. The SNR of the training and testing data is 20 dB, consistent with the baseline configuration. As shown in Figure 8, when using a 5 × 5 kernel, the ACC is the highest and the RMSE is the lowest.

As shown in Figure 9, the performance of LSTM networks with hidden state dimensions from 32 to 200 is tested. The optimal hidden unit size of 100 outstands with the lowest RMSE and considerable ACC.

3. Results

In this section, the experimental results are presented and analyzed. Section 3.1 examines the performance of the CNN (Section 3.1.1) and LSTM (Section 3.1.2) methods on simulation data, focusing on the effects of the SNR, element spacing, and the number of array elements. Section 3.2 evaluates the trained CNN (Section 3.2.1) and LSTM (Section 3.2.2) models using experimental SWAP data and presents the corresponding DOA estimation performance. Section 3.3 compares and discusses the results of the two methods with other traditional methods under various conditions.

3.1. The Results of Simulation Data

3.1.1. The Results of the CNN Method

The test data ACC is 98.871% using CNN. To more succinctly demonstrate, a scatterplot is drawn with the actual values as the horizontal axis and the predicted values as the vertical axis. If the prediction is correct, the scatter points should be on the 45° diagonal line. There are two points that are not on the diagonal line, namely (1, 2) and (181, 180), indicating that there is an error within ±1° (Figure 10) for the prediction of the end-fire angle.

1.

SNR

The following simulation study investigates the impact of the SNR on the directional performance of the CNN algorithm.

An array configuration of ULA is set, and Gaussian white noise is added to the target signal to generate noisy signals with SNRs of −20, −15, −10, −5, 0, 5, 10, 15, and 20 dB. These noisy signals are then input into the well-trained CNN model. The changes in the CNN model’s test ACC and four error metrics (RMSE, MAE, MSE, and MAPE) are shown in Figure 11. The overall trend of the four error metrics is to decrease as the SNR increases, while the ACC increases with the increase in the SNR. During the simulation, it was found that when the SNR is below −15 dB, the ACC is below 0.95 and drops rapidly.

2.

Spacing of elements

The following simulation study investigates the impact of the spacing of elements on the directional performance of the CNN algorithm. An array configuration of ULA is set, and the array spacing is 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.05, 2.1, 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.2, 2.4, 2.6, 2.8, and 3.0 m. Since an urgent change between 2.10 and 2.2 was observed, denser test points were set within this range to explore the subtle structure (Figure 12b). As shown in Figure 12a, when the spacing is half-wavelength (2.14 m), the ACC reaches its highest point. The four-error metrics remain relatively stable when the spacing is smaller than 2.14 m, but rapidly increase between 2.14 and 2.16 m, suggesting that the model performance degrades severely.

3.

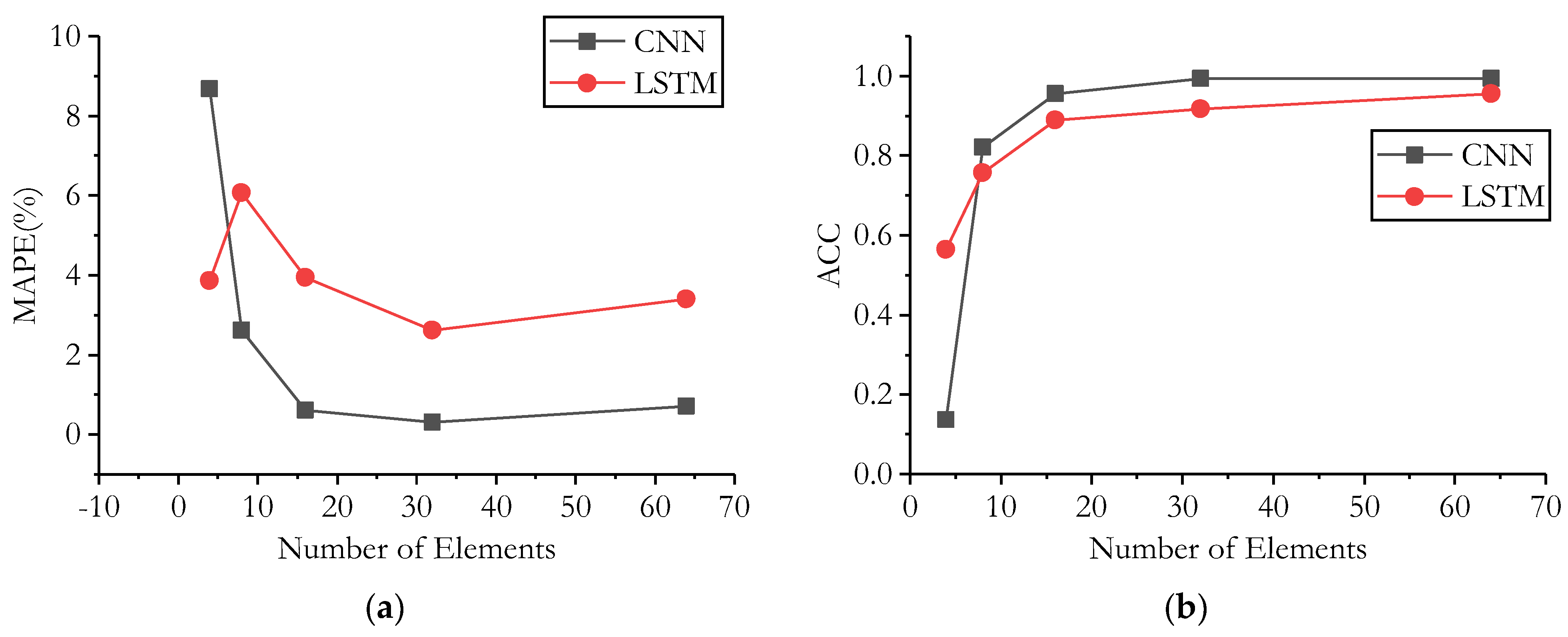
Number of elements

The following simulation studies the effect of the number of arrays on the performance of the CNN algorithm. Set the formation shape as ULA, the number of array elements as 4, 6, 8, 16, 32, 64, and 128, generate noiseless signals with a center frequency of 350 Hz, and input them into the trained CNN model. The CNN model test’s ACC and four error indicators (RMSE, MAE, MSE, and MAPE) change with the number of elements, as shown in Figure 13. The ACC rate increases with the increase in the number of elements, while the four error indicators decrease with the increase in the number of elements, and gradually become stable.

When the array element number is 4 (with the input SNR maintained at 20 dB), the DOA result is shown in Figure 14a. The scatterplot of true versus predicted angles exhibits a distinct stepped pattern, indicating that within certain angular ranges, different signal DOAs will be predicted to be the same value, which is essentially due to the reduction in angular resolution. Furthermore, as illustrated in Figure 14b, significant estimation errors frequently occur within the range of −30° to 30°, indicating a degradation in model performance under this condition.

This degradation can be explained by the relationship between the array aperture and the input feature representation. When the number of elements decreases, the size of the CSDM also decreases, the precision of the information stored by the CSDM decreases, and the CSDM generated from adjacent angles becomes more difficult to distinguish. Therefore, under the same iteration times, when the number of elements is not enough to distinguish all the wave arrival directions, the ACC decreases with the decrease in the number of elements. Conversely, when a sufficient number of array elements is used, the CSDM possesses adequate dimensions and information richness to achieve high resolution. As demonstrated in Figure 14c,d for a 64-element array (with the input SNR maintained at 20 dB), the model achieves nearly error-free prediction ACC.

3.1.2. The Results of the LSTM Method

After the training started, the training loss decreased significantly. After about 500 iterations, the test ACC began to increase markedly. Training was terminated after 10,933 iterations, with a final test ACC of 98.90%. The training results are shown in Figure 15a, with error points at (2, 1) and (180, 181). The test error is depicted in Figure 15b, within −2~2°.

1.

SNR

Gaussian white noise is added to the target signal to generate noisy signals with SNRs of −25, −20, −15, −10, −5, 0, 5, 10, 15, and 20 dB. These noisy signals are then input into the well-trained LSTM model. The test ACC of the LSTM model and the four error metrics—RMSE, MAE, MSE, and MAPE—are shown to vary with the SNR in Figure 16a. The pink area in Figure 16a with high data intensity is presented in refined Figure 16b.

The overall trend of the four-error metrics is to decrease as the SNR increases, while the ACC increases with the increase in SNR. When the SNR is below −20 dB, the directional performance of the LSTM model drops sharply.

2.

Spacing of elements

Explore the influence of matrix spacing on the performance of the LSTM algorithm below. The array was set to ULA, with an element spacing of 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.05, 2.1, 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.2, 2.4, 2.6, 2.8, 3.0 m, and a noiseless signal with a center frequency of 350 Hz was generated and input into the trained LSTM model, the LSTM model test’s ACC, and the four error indicators (RMSE, MAE, MSME, MAPE) changed with the element spacing, as shown in Figure 17.

Similarly to the rule that the performance of the CNN model is affected by the array spacing, when the spacing is 2.13 m, which is around half-wavelength (2.14 m), the ACC reaches its highest point. The four error metrics remain relatively stable when the spacing is smaller than 2.14 m, but rapidly increase between 2.14 m and 2.16 m, which suggests that the model performance degrades.

3.

Number of elements

The following simulation studies the effect of the number of arrays on the performance of the LSTM algorithm. Set the formation shape as ULA, the number of array elements as 4, 6, 8, 16, 32, 64, 128, generate noiseless signals with a center frequency of 350 Hz, and input them into the trained LSTM model. The LSTM model test’s ACC and four error indexes RMSE, MAE, MSE, and MAPE change with the number of elements, as shown in Figure 18.

Similarly to the law of the CNN model affected by the number of elements, the ACC rate increases with the increase in the number of elements, and the four error indicators decrease with the increase in the number of elements, and all indicators gradually become stable. When the array element number is 4, the DOA results are shown in Figure 19. The DOA performance is greatly affected by the end-firing direction, and different incidence angles are predicted to be the same angle within a certain range. Compared with CNN, the DOA resolution of LSTM is better when the number of elements is reduced.

3.2. The Results of Experimental Data

In this section, the SWAP data are applied to the trained CNN and LSTM classification model separately, resulting in satisfactory DOA performance. Since only one direction is predicted for each time segment, the methods mentioned above are more suitable for single-target scenario, yet they still exhibit considerable applicability in multi-target tasks such as SWAP.

To quantitatively characterize such applicability, three evaluation metrics, track recovery rate (TRR), detection rate (DR), and mean bearing error (MBE) are proposed in this paper:

$$\mathrm{TRR} = {\displaystyle \frac{1}{N_{\mathrm{T}}}}{\displaystyle {\sum }_{t=1}^{N_{\mathrm{T}}}1(\left|{\widehat{\theta }}_t-{\theta }_t^{\mathrm{GT}}\le 5^{\circ }\right|}\times 100\%$$

(25)

$$\mathrm{DR}={\displaystyle \frac{1}{N_{\mathrm{T}}}}{\displaystyle {\sum }_{t=1}^{N_{\mathrm{T}}}1(\left|{\widehat{\theta }}_t-{\theta }_t^{\mathrm{GT}}\le {10}^{\circ }\right|}\times 100\%$$

(26)

$$\mathrm{MBE}={\displaystyle \frac{1}{N_{\mathrm{valid}}}}{\displaystyle \sum _{t\in N_{\mathrm{valid}}}\left|{\widehat{\theta }}_t-{\theta }_t^{\mathrm{GT}}\right|}\times 100\%$$

(27)

where $N_{\mathrm{T}}$ denotes the total number of time segments obtained by partitioning the SWAP dataset with a sliding window of size 4096 and an overlapping ratio of 50%, ${\widehat{\theta }}_t$ represents the estimated angle output by the model for the t-th time segment, and ${\theta }_t^{\mathrm{GT}}$ denotes the corresponding true angle. Time periods where the deviation between the predicted values and the true values falls within ±10° are defined as valid prediction time periods, and the total number of valid prediction time periods is $N_{\mathrm{valid}}$. The quantitative evaluation results can be seen in

Table 1. Quantitative evaluation on SWAP experimental data.

Target	Method	Track Recovery Rate (%)	Detection Rate (%)	Mean Bearing Error (°)
T1	CNN	40.83	45.41	1.64
	LSTM	52.75	55.96	1.5
T2	CNN	4.20	26.05	6.84
	LSTM	18.49	42.86	5.00
T3	CNN	13.71	21.14	6.46
	LSTM	1.71	2.86	4.20
T4	CNN	8.54	12.80	4.05
	LSTM	4.27	6.71	4.64

.

3.2.1. The Results of the CNN Method

The target trajectories can generally be recovered as illustrated in Figure 20, with the performance for Target T1 being particularly prominent at a TRR of 40.83%. For Target T3, the DR reaches 21.14% with a mean bearing error of 6.46°, exhibiting a stable angular offset relative to the ground-truth trajectory. Target T2 is detected, yielding a detection rate of 26.05%, but has a relative large mean error of 6.84°. Target T4 is only partially detected, with a track recovery rate of merely 8.54% and a detection rate of 12.80%.

3.2.2. The Results of the LSTM Method

As shown in Figure 21, the LSTM model is essentially able to recover the target trajectory, particularly notable for Target T1 with 52.75% track recovery rate and a 1.5° mean bearing error, outperforming the CNN method in all three metrics. Target T2 prediction is basically correct with 42.86% detection rate and a 5.00° mean bearing error, also outperforming the CNN method. However, as for T3 and T4, the detection rate is only 2.86% and 6.71% separately, much lower than that for CNN of 21.14% and 12.80%.

3.3. Compare and Contrast

3.3.1. Performance Comparison of CNN and LSTM

As shown in Figure 22a, when the SNR is higher than −20 dB, the MAPE remains stable with slight turbulence; however, when the SNR is lower than −20 dB, the MAPE increases sharply, which means the DOA ability degrades when the SNR decreases. The red line is above the black line when the SNR is larger than −20 dB, which means CNN performs better than LSTM with a smaller error. But the LSTM method shows advantages in ACC under −20 dB; when the SNR is lower than −20 dB, the ACC of LSTM is higher than CNN, as shown in Figure 22b. A physical interpretation of these findings is given: Under high SNR conditions, local spatial patterns are clearly distinguishable, and the local feature extraction capability of CNN is fully effective. At a low SNR, local patterns are submerged by noise, while the statistical characteristics of global sequences remain identifiable; the memory mechanism of LSTM acts as an integration function.

As shown in Figure 23a, CNN shows lower MAPE when the spacing of elements is smaller than half-wavelength, while the MAPE of LSTM is lower when the spacing is larger than half-wavelength. Figure 23b demonstrates that the prediction ACC of CNN is slightly higher than LSTM.

Figure 24a,b present that CNN performs better when the number of elements is larger than or equal to 8, with higher ACC and smaller MAPE. When the number of elements is less than 8, LSTM maintains better performance, maintaining an ACC close to 80% with only 4–8 array elements. An array size of 8 elements serves as a critical threshold: When the number of elements is less than 8, the directional performance degrades drastically with the decrease in the element count; conversely, when the number exceeds 8, the rate of change in directional performance induced by an increase in elements diminishes significantly. It can be inferred that sufficient spatial sampling is indispensable to support the convolution operation, given that CNNs are more sensitive to the number of array elements. Conversely, the fact that LSTMs remain applicable even for miniaturized arrays suggests that sequence modeling imposes a lower requirement on spatial sampling density.

3.3.2. Performance Comparison of Other Algorithms

In this section, a systematic comparative analysis of DOA estimation performance was conducted between deep learning methods (CNN and LSTM) and conventional algorithms, CBF, MUSIC, MVDR, and ESPRIT, under a uniform array configuration (baseline configuration) and simulated signal conditions.

1.

Comparison of Algorithm Resolution

Figure 25 shows the spatial spectra obtained by different methods for a simulated signal impinging from 90° with an SNR of 20 dB under the baseline configuration (search interval of 1° for the deep-learning-based model and 1° for the traditional method). For the CNN and LSTM methods, the plotted curves correspond to the SoftMax probability spectra. In terms of main lobe width, the methods can be ranked as CBF > MVDR > LSTM > MUSIC > CNN, indicating that deep learning methods, especially CNN, show superior resolution ability compared with traditional methods.

2.

Comparison of ACC and RMSE under different SNRs

To compare the performance of CNN- and LSTM-based DOA estimation methods with traditional methods under varying SNRs, the ACC and RMSE of six methods (under the baseline configuration) across SNR levels of −25, −20, −15, −10, 0, 10, 15, and 20 dB are evaluated. Notably, for the conventional methods, the accuracy is defined as follows: a recognition result is considered correct if the angular deviation between the angle corresponding to the spectral peak and the target angle is within 0.1°.

As shown in Figure 26a, the ACC of all methods exhibits a clear upward trend with an increasing SNR. At low SNRs (e.g., −25 dB), the ACC values of traditional methods are relatively low, while the deep learning-based CNN and LSTM achieve significantly higher ACC. At high SNRs, all methods gradually approach 100% accuracy: CNN and LSTM yield slightly lower accuracy than traditional MUSIC, CBF, and MVDR but outperform the ESPRIT method. This indicates the strong noise robustness of deep learning models in DOA tasks.

Figure 26b further quantifies the error characteristics: the RMSE of all methods decreases sharply as the SNR increases. When the SNR is less than −20 dB, LSTM shows a relatively large RMSE; CNN achieves a smaller RMSE than ESPRIT and MUSIC, but a larger RMSE than MVDR and CBF. When the SNR is more than −20 dB, the RMSE of all methods drops rapidly to within 1.7°, and the differences in RMSE between methods tend to diminish as the SNR increases.

Figure 26a,b demonstrate that an SNR of −20 dB serves as a critical threshold: When the SNR is less than −20 dB, the directional performance degrades drastically with a decrease in the SNR; conversely, when the number exceeds −20 dB, the rate of change in directional performance induced by an increase in SNRs diminishes significantly. Notably, traditional methods also basically follow the same trend.

In summary, CNN- and LSTM-based DOA methods balance noise robustness (superior at low SNRs) and acceptable high-SNR accuracy, addressing the limitations of traditional methods, which perform poorly in noisy environments.

3.

Comparison of ACC and RMSE under different snapshots

To compare the performance of CNN- and LSTM-based DOA estimation methods with traditional methods under varying snapshots, the ACC and RMSE of six methods across snapshots of 1, 2, 32, 64, 128, 256, 512, 1024, 2048, 4096, and 8192 and SNRs of 20 dB are evaluated.

The choice of snapshot ranges to be tested is based on signal processing theory and underwater acoustic experience. From a signal processing perspective, these values are powers of two, ensuring computational efficiency in FFT-based processing. Additionally, for reliable covariance matrix estimation, the number of snapshots should sufficiently exceed the number of array elements. However, since single-snapshot DOA estimation has also attracted considerable research attention [23], this study includes scenarios where the number of snapshots (1, 2, 32) is fewer than the number of array elements, as well as the transition from snapshot-deficient to snapshot-sufficient conditions. From an underwater acoustic standpoint, sonar systems commonly employ time windows exceeding 1 s, and the selected range encompasses data lengths frequently adopted in the literature, such as 4096 [29].

As shown in Figure 27, the accuracy of all methods increases and the RMSE decreases as the number of snapshots increases. Snapshots of 32 constitute a critical threshold: when the number of snapshots exceeds 32 (i.e., the number of array elements), the rate of improvement gradually diminishes, and the performance differences among methods become less pronounced with increasing snapshots, except that the ACC of LSTM remains notably lower than the other methods; when the number of snapshots is fewer than the array elements, the directional performance of both conventional and deep learning-based methods degrades drastically, and LSTM and CNN outperform ESPRIT but underperform compared to CBF, MVDR, and MUSIC.

4.

Comparison of Computational Complexity and Real-Time Performance

To evaluate the real-time processing capability of each algorithm, this paper statistically analyzes the inference time and time distribution of different methods on the same hardware platform. Our experimental hardware platform consists of a workstation with an Intel Core i9-12900H CPU running at 2500 MHz and an NVIDIA GeForce RTX 3070Ti Laptop GPU with 8.6 GB of memory.

As shown in Figure 28, when processing individual samples (batch size = 1), CNN and LSTM exhibit higher computational times of approximately 1.5 ms and 2.5 ms per sample, respectively, compared to the conventional methods. This computational overhead can be attributed to the inherent architectural complexity of neural networks, which involve numerous matrix multiplications, nonlinear activation functions, and multi-layer forward propagation operations. In contrast, traditional subspace-based methods such as MUSIC (1.326 ms) and signal processing approaches like MVDR (0.480 ms) and ESPRIT (0.087 ms) demonstrate relatively stable per-sample processing times. However, a significant advantage of deep learning approaches emerges with increasing batch sizes. As the batch size increases from 1 to 128, the per-sample inference time for both CNN and LSTM decreases dramatically, ultimately falling below 0.1 ms per sample. This improvement results from the highly parallelizable nature of neural network computations, which can be efficiently accelerated through GPU-based matrix operations. At batch size 128, both CNN and LSTM achieve superior computational efficiency compared to all conventional methods except ESPRIT. Notably, the conventional algorithms, being fundamentally designed for sequential sample-by-sample processing, cannot leverage batch parallelization to improve throughput. This architectural limitation renders them less suitable for high-throughput applications where multiple signals require simultaneous processing.

The box plot in Figure 29 further illustrates the distribution of inference times across all methods at batch size = 1, confirming the higher median values and greater variability for LSTM and CNN compared to traditional approaches. The LSTM network exhibits the highest median inference time along with the largest interquartile range (IQR), indicating substantial variability in computational latency. This variability stems from the sequential nature of recurrent computations and memory access patterns inherent to LSTM architectures. The CNN demonstrates a lower median value with a narrower IQR, reflecting more consistent computational behavior due to its feed-forward structure. In contrast, the conventional methods display notably compact distributions with minimal variance, as their algorithmic operations involve deterministic matrix decompositions and fixed computational pathways. The presence of outliers (indicated by red markers) across all methods suggests occasional computational fluctuations attributable to system-level factors such as memory allocation and CPU/GPU scheduling overhead.

In summary, while deep learning methods incur higher computational costs for single-sample inference, their capacity for parallel batch processing provides substantial advantages in scenarios demanding high-throughput real-time DOA estimation.

5.

Performance Comparison in Actual Underwater Acoustic Data

The proposed model is trained on narrowband signals. To suppress broadband interference, a band-pass filter is applied when forming the covariance matrix, and only the 350 Hz component is retained. All methods are evaluated using this same filtered covariance matrix.

Since CBF, MVDR, and MUSIC are spectrum-based approaches, their results are presented in terms of power spectra, as shown in Figure 30a–c. In contrast, ESPRIT, LSTM, and CNN directly output bearing estimates; their outputs are therefore visualized as time-bearing heatmaps in Figure 30d–f.

The LSTM method produces a target bearing evolution that is broadly consistent with that of MVDR and MUSIC. Compared with MVDR, LSTM exhibits a few isolated prediction errors at certain bearings, but it still tracks the overall trajectories of targets T1 and T2. However, similar to MVDR and MUSIC, LSTM does not clearly resolve targets T3 and T4. The CNN model, on the other hand, fails to reconstruct the full trajectory of target T2, but it does capture portions of the trajectories of targets T3 and T4. This suggests that the two networks have learned complementary features and that combining their outputs could potentially recover all target tracks. ESPRIT performs worst among the tested methods and reliably resolves only target T1.

In summary, deep learning methods based on CNNs or LSTMs have not only matched but also surpassed traditional approaches on real underwater acoustic data, demonstrating strong adaptability. CBF provides the most complete set of detected targets but suffers from relatively wide beams; LSTM and CNN each have distinct advantages, with LSTM achieving performance comparable to MVDR and MUSIC, while CNN successfully highlights the T3 and T4 targets that are not well captured by LSTM, MVDR, or MUSIC. ESPRIT shows the poorest overall performance in this scenario.

4. Conclusions

This study presented a systematic comparative analysis of CNN and LSTM architectures for DOA estimation in underwater acoustic applications, addressing the mechanistic differences between local spatial feature extraction and sequential phase evolution paradigms, providing empirical evidence for sim-to-real generalization capability. The key findings are summarized as follows.

First, the two architectures exhibit complementary strengths: CNN achieves higher precision under favorable SNR conditions and efficient array size due to its ability to capture local spatial patterns, while LSTM demonstrates superior noise and array size robustness through its memory-based integration mechanism. Second, critical performance boundaries exist at half-wavelength element spacing, 8-element array size, −20 dB SNR crossover, and 32-snapshot minimum, providing actionable design guidelines. Third, systematic comparison with CBF, MVDR, MUSIC, and ESPRIT algorithms demonstrates that deep learning approaches achieve superior spatial resolution, better noise robustness, and higher computational efficiency through batch parallelization. Fourth, the successful validation on SWAP experimental data demonstrates that models trained on single-target simulations can generalize to multi-target real-world scenarios without domain adaptation, recovering primary target trajectories for up to four targets. This result validates the practical applicability of CSDM-based deep learning approaches for underwater DOA estimation.

This study is subject to several limitations that define the scope of the conclusions. First, the proposed models are trained and validated primarily on narrowband signals at a fixed frequency; performance on wideband or frequency-varying scenarios remains to be investigated. Second, the networks are formulated as single-target classifiers with 1-degree angular resolution; explicit multi-target estimation with variable source numbers and finer resolution was not addressed.

Future work will explore multi-target joint estimation, extend to wideband DOA estimation, and investigate hybrid architectures that combine CNN’s spatial precision with LSTM’s temporal robustness. Moreover, it will enhance theoretical profundity and develop physical interpretability of end-to-end learning, and employ scientific optimization strategies to mitigate the empirically driven reliance in the process of network architecture design.