Coordinated Control Strategy for Series-Parallel Connection of Low-Voltage Distribution Areas Based on Direct Power Control

Abstract

With the irregular integration of small-capacity distributed generators (DG) and single-phase loads, rural low-voltage distribution transformers are faced with issues such as three-phase imbalance, light-heavy loading, and feeder terminal voltage excursions, impacting the safe and stable operation of the system. To address this issue, a coordinated control strategy based on direct power control (DPC) for low-voltage substation series-parallel coordination is proposed. A flexible interconnection topology for multi-substation series-parallel coordination is designed to achieve coordinated optimization of alternating current–direct current (AC-DC) power quality. Addressing the three-phase imbalance, light-heavy loading, and feeder terminal voltage excursions in rural low-voltage distribution transformers, a series-parallel coordinated optimization control strategy is proposed. This strategy incorporates a DC bus voltage control strategy based on sequence-separated power compensation and a closed-loop control strategy based on phase-separated power compensation, effectively addressing three-phase imbalances and load balancing in each power distribution areas. Furthermore, a series-connected phase compensation control strategy based on DPC is proposed, efficiently mitigating feeder terminal voltage excursions. A corresponding circuit model is established using Matlab/Simulink, and simulation results validate the effectiveness of the proposed strategy.

1. Introduction

With the advancement of the “Dual Carbon” goals [1], the widespread integration of distributed new energy and the continuous growth of single-phase loads [2,3] have led to increasingly severe problems in low-voltage distribution networks. These problems mainly include three-phase unbalance and voltage over-limit at the feeder terminal [4]. Three-phase unbalance will aggravate voltage sag. In turn, the deterioration of voltage quality will worsen load asymmetry [5]. The two issues interact with each other and form a negative feedback loop [6]. Voltage over-limit at the feeder terminal not only damages sensitive equipment and reduces motor energy efficiency, but also triggers the off-grid of photovoltaic inverters. This restricts the consumption of new energy. Therefore, breaking the limitation of single-dimensional governance and establishing a coordinated governance mechanism for voltage quality and power balance is the key to improving the operational stability of the new power distribution system [7].

To address the three-phase imbalance issue in distribution areas, existing governance measures mainly include switching phase-to-phase balancing devices [8], phase-shifting switches [9], and reactive power compensation devices [10]. Traditional phase-to-phase balancing devices are low-cost. However, their discrete adjustment mechanism makes it difficult to achieve smooth power control [11,12]. Their response speed is limited by the action time of mechanical switches, failing to keep up with rapid load fluctuations. Phase-shifting switch technology can adjust the load phase sequence from the source [13,14]. But in practical engineering, large-scale and dense deployment is usually required to achieve the expected effect. This leads to a sharp increase in investment costs and difficulties in maintenance. Reactive power compensation devices connect reactive power compensation equipment in parallel. They adjust the three-phase current balance while compensating reactive power [15]. These devices are mainly divided into two categories, traditional devices and new power electronic devices. Represented by automatic compensation capacitor banks, traditional devices are based on Wang’s theorem [16]. By connecting capacitors between phases and between phase and neutral, they not only improve the power factor but also balance the active current of each phase. However, they have limitations such as slow response speed and inability to achieve continuous regulation. Therefore, new power electronic devices have become the main voltage regulation method currently [17]. They generate compensation current in real-time through power electronic converters to offset unbalanced components. Static Var Generator (SVG) based on power electronic technology has the ability of continuous reactive power regulation [18]. But restricted by its parallel topology, it cannot directly regulate the active power flow. This limits its governance effect on unbalance caused by active power. Dynamic Voltage Restorers (DVR) are widely used to handle voltage sags or fluctuations. For current harmonic and reactive power compensation, Static Synchronous Compensators (DSTATCOM) are the mainstream choice [19,20]. However, these two types of independent compensation devices have relatively single functions. They cannot simultaneously deal with the composite power quality problem of concurrent voltage and current distortion in distribution networks. To overcome this limitation, Unified Power Quality Conditioners (UPQC) realize the comprehensive governance of voltage and current issues [21]. They connect series and parallel converters through a back-to-back configuration. Although traditional UPQC perform well in single-point compensation, their topology is usually limited to the governance of a single distribution area or line [22]. They lack the ability to control power flow among multiple low-voltage distribution areas. When facing load imbalance across multiple areas or uneven power distribution of distributed generation, traditional UPQC cannot achieve inter-regional power mutual assistance and collaborative optimization [23]. This results in a situation where equipment is overloaded in some areas while capacity is idle in others.

From the perspective of control strategies, most current UPQC and related equipment adopt the voltage-current double closed-loop control based on proportional-integral (PI) regulators. This is also known as Vector Current Control (VCC) [24]. Although VCC technology is relatively mature, its inherent limitations have become increasingly prominent in complex distribution network environments. Firstly, VCC adopts a cascaded structure of inner current loop and outer voltage loop [25]. The tuning of PI parameters is cumbersome, and there is coupling between the loops. This limits the dynamic response speed of the system by the bandwidth design, making it difficult to quickly track the abrupt signals during grid faults. Secondly, the VCC strategy relies heavily on the Phase-Locked Loop (PLL) to obtain the phase and frequency synchronization signals of the grid voltage [26]. Studies have shown that under non-ideal conditions such as distortion, unbalance and sag of grid voltage, the dynamic tracking performance of traditional PLL will decrease significantly or even fail [27,28]. This leads to system orientation errors, which in turn seriously impairs the governance performance and stability of the compensation device.

In terms of governance devices and topology structures, existing solutions usually focus on addressing a single objective. To break through the limitations of the aforementioned control algorithms and topology structures, this study aims to comprehensively solve the three-phase imbalance and voltage over-limit issues in low-voltage distribution areas. This paper proposes a control strategy for series-parallel coordinated and integrated operation based on Direct Power Control (DPC). By analyzing the causes of three-phase imbalance and voltage over-limit in distribution networks, a series-parallel coordinated topology with a DC network is constructed. For the main distribution area, a phase-separated power control strategy with head-to-tail interconnection is adopted. For the secondary distribution areas, a sequence-separated compensation control strategy based on DC bus voltage is applied. The main work of this paper is as follows:

(1)

A series-parallel coordinated topology based on DPC is proposed. It is applied to the comprehensive power quality governance of low-voltage distribution areas. This method eliminates complex coordinate transformation and PI parameter tuning. Its control structure is simplified, and its dynamic response is faster. It can quickly stabilize voltage and balance current when load changes abruptly or faults occur.

(2)

A differentiated coordinated control strategy for primary and secondary distribution areas is designed. It realizes inter-area power mutual assistance and load balancing. The primary distribution area adopts phase-separated power control to govern internal imbalance. The secondary distribution areas adopt sequence-separated compensation control. They are coupled with the primary distribution area through a DC network. This enables flexible scheduling of active and reactive power, solving the problem of regional load imbalance.

(3)

A coordinated control framework for parallel-series compensation is constructed. It relies on a DC network to achieve energy exchange. It realizes the comprehensive governance of three-phase imbalance and voltage over-limit. This improves the overall power quality of the low-voltage distribution network.

2. Mechanism of Flexible Interconnected Distribution Areas Power Compensation

The equivalent circuit diagram of a low-voltage distribution network with distributed generation (DG) is shown in Figure 1. In the diagram: U_S represents the voltage at the beginning of the distribution network, and I_S is the current at the beginning of the distribution network. U_m denotes the voltage at the point of common coupling (PCC) at the end of the distribution network. R + jX stands for the line impedance. P_S and Q_S represent the active and reactive power output at the beginning of the distribution network. P_load and Q_load, respectively, indicate the active and reactive power consumed by the loads at the end of the distribution network. P_DG is the active power output of the DG. When the output power of the DG is excessive, local loads cannot fully absorb the power from the grid-connected DG, leading to the occurrence of reverse power flow in the system. This can result in the voltage at the end of the distribution network being higher than that at the beginning, potentially causing voltage violations at the P_CC. Conversely, when the output power of the DG is insufficient, due to the prevalent long supply radius in low-voltage distribution networks with line impedance R > X, the voltage drop caused by active losses may lead to the voltage at the P_CC node being lower than at the beginning. During peak electricity consumption periods, this situation can even lead to voltage undershoot.

Furthermore, due to a large number of single-phase loads and extensive PV integration into the distribution network, negative-sequence and zero-sequence currents flow through the lines and distribution network transformers. This results in uneven power output among the phases of distribution network transformers, reducing their overload capacity. In cases of transformer three-phase imbalance, the phase with lighter load will exhibit surplus capacity, leading to a decrease in the overall load on the transformer and subsequently reducing its load capacity.

To address the issues in the low-voltage distribution network mentioned above, this paper proposes a flexible interconnection topology between distribution areas. As illustrated in Figure 2, the converters are connected via low-voltage DC network lines, forming pathways for flexible energy routing. With the use of Voltage Source Converter (VSC) converters, comprehensive control of power quality aspects such as three-phase imbalance at the beginning of the distribution area and voltage violations at the end can be achieved. The direction of power transmission is shown in Figure 3.

(1)

During Operating Condition 1:

(I).

VSC1 compensates for the negative-sequence and zero-sequence power components in distribution area 1 while regulating its positive-sequence component to provide a stable and reliable DC voltage for the DC network.

(II).

VSC2 absorbs power from the DC network, compensating for the power of each phase at the beginning of distribution area 2 to maintain three-phase power balance. It adjusts its power optimization parameters and modifies the output of each transformer based on actual requirements.

(III).

VSC3 utilizes the DC network to perform phase-selective compensation at the tail end of distribution area 2, mitigating power quality issues and significantly reducing transmission losses.

(2)

Under Operating Condition 2:

(I).

VSC3 transfers excess power from the end of distribution area 2 along the DC bus to VSC1 and VSC2, significantly enhancing the integration of photovoltaics while reducing voltage violations at end users caused by excessive output power from the DG.

(II).

VSC1, by absorbing the power transmitted by VSC3, compensates to maintain three-phase balance at the beginning of distribution area 1. Additionally, it uses its positive sequence balance component to stabilize the DC bus voltage.

(III).

VSC2, by absorbing power from the DC bus, compensates the power of each phase at the beginning of distribution area 2, thereby maintaining three-phase power balance at the beginning of distribution area 1. By adjusting its power optimization parameters, the direction of power flow between distribution areas can be modified.

3. Three-Phase Imbalance and Overvoltage Suppression Mitigation Strategy

The overall strategy for mitigating three-phase imbalance and voltage suppression is as follows: VSC1 adopts a sequence-decoupled power control strategy, where the positive-sequence component maintains DC bus voltage stability, while the negative- and zero-sequence components are compensated to balance the three-phase power in distribution area 1, thereby resolving its three-phase imbalance; VSC2 employs a phase-selective power control strategy, performing phase-wise compensation for the unbalanced power from distribution area 1. By analyzing the specific conditions of each distribution area, an optimal power transfer coefficient is selected to facilitate-area power redistribution; VSC3 implements a direct power control (DPC)-based phase-selective compensation strategy, compensating for surplus or deficient power at the end-node to mitigate overvoltage suppression issues at the tail end of distribution area 1.

3.1. Direct Current Bus Voltage Control Strategy Based on Sequence Power

The three-phase imbalance current in distribution area 1 can be decomposed into positive sequence, negative sequence, and zero sequence current components using the symmetrical component method, namely:

$$\left\{\begin{array}{l}{i}_a={i_a}^{+}+{i_a}^{-}+{i_a}^0={I_a}^{+}\sin (wt+{\theta }^{+})+{I_a}^{-}\sin (wt+{\theta }^{-})+{I_a}^0\sin (wt+{\theta }^0)\\ i_b={i_b}^{+}+{i_b}^{-}+{i_b}^0={I_b}^{+}\sin (wt-{\displaystyle \frac{2\pi }{3}}+{\theta }^{+})+{I_b}^{-}\sin (wt+{\displaystyle \frac{2\pi }{3}}+{\theta }^{-})+{I_b}^0\sin (wt+{\theta }^0)\\ i_c={i_c}^{+}+{i_c}^{-}+{i_c}^0={I_c}^{+}\sin (wt+{\displaystyle \frac{2\pi }{3}}+{\theta }^{+})+{I_c}^{-}\sin (wt-{\displaystyle \frac{2\pi }{3}}+{\theta }^{-})+{I_c}^0\sin (wt+{\theta }^0)\end{array}\right.$$

(1)

where I⁺, I⁻ and I⁰ represent the amplitudes of positive sequence, negative sequence, and zero sequence currents, respectively; θ⁺, θ⁻ and θ⁰ represent the initial phases of the positive sequence, negative sequence, and zero sequence currents, respectively.

The three-phase voltage at the beginning of distribution area 1 is:

$$\left\{\begin{array}{l}{u}_a=U\sin (wt+\theta )\\ u_b=U\sin (wt-{\displaystyle \frac{2\pi }{3}}+\theta )\\ u_c=U\sin (wt+{\displaystyle \frac{2\pi }{3}}+\theta )\end{array}\right.$$

(2)

where u represents the phase voltage magnitude of distribution area 1; w represents the fundamental angular frequency, and θ represents the initial phase of the phase voltage at distribution area 1.

According to the single-phase instantaneous power theory based on orthogonal signal construction, the calculation of instantaneous power for the single-phase system is expressed as Equation (3):

$$\left\{\begin{array}{l}P={\displaystyle \frac{u_{\alpha }{i}_{\alpha }+u_{\beta }{i}_{\beta }}{2}}\\ Q={\displaystyle \frac{u_{\alpha }{i}_{\beta }-u_{\beta }{i}_{\alpha }}{2}}\end{array}\right.$$

(3)

where u_α, u_β and i_α, i_β denote the constructed orthogonal voltage and current components in the time domain. The β-axis component (a 90° lagging quadrature signal relative to the original single-phase signal) is generated by a second-order generalized integrator-based quadrature signal generator (SOGI-QSG).

From Equations (1)–(3), the three-phase unbalanced power of distribution area 1 can be expressed as the combination of sequence powers:

$$\left\{\begin{array}{l}{P}_x={\displaystyle \sum _{x=a}^c({P_x}^{+}+{P_x}^{-}+{P_x}^0)}\\ Q_x={\displaystyle \sum _{x=a}^c({Q_x}^{+}+{Q_x}^{-}+{Q_x}^0)}\end{array}\right.$$

(4)

where $P_x^{+}$, $P_x^{-}$ and $P_x^0$ represent the positive-sequence, negative-sequence, and zero-sequence active power components of phase x for distribution area 1, respectively; and $Q_x^{+}$, $Q_x^{-}$ and $Q_x^0$ represent the positive-sequence, negative-sequence, and zero-sequence reactive power components of phase x for distribution area 1, respectively.

The specific expressions are in Equations (5):

$$\left\{\begin{array}{l}{P}_{\mathrm{a}}^{+}={\displaystyle \frac{U{I}^{+}\cos {\phi }_{u-i}^{+}}{2}};P_{\mathrm{a}}^{-}={\displaystyle \frac{U{I}^{-}\cos {\phi }_{u-i}^{-}}{2}};P_{\mathrm{a}}^0={\displaystyle \frac{U{I}^0\cos {\phi }_{u-i}^0}{2}}\\ P_{\mathrm{b}}^{+}={\displaystyle \frac{U{I}^{+}\cos {\phi }_{u-i}^{+}}{2}};P_{\mathrm{b}}^{-}={\displaystyle \frac{U{I}^{-}\cos ({\phi }_{u-i}^{-}-\frac{4\mathsf{\pi }}{3})}{2}};P_{\mathrm{b}}^0={\displaystyle \frac{U{I}^0\cos ({\phi }_{u-i}^0-\frac{2\mathsf{\pi }}{3})}{2}}\\ P_{\mathrm{c}}^{+}={\displaystyle \frac{U{I}^{+}\cos {\phi }_{u-i}^{+}}{2}};P_{\mathrm{c}}^{-}={\displaystyle \frac{U{I}^{-}\cos ({\phi }_{u-i}^{-}+\frac{4\mathsf{\pi }}{3})}{2}};P_{\mathrm{c}}^0={\displaystyle \frac{U{I}^0\cos ({\phi }_{u-i}^0+\frac{2\mathsf{\pi }}{3})}{2}}\\ Q_{\mathrm{a}}^{+}={\displaystyle \frac{U{I}^{+}\sin {\phi }_{u-i}^{+}}{2}};Q_{\mathrm{a}}^{-}={\displaystyle \frac{U{I}^{-}\sin {\phi }_{u-i}^{-}}{2}};Q_{\mathrm{a}}^0={\displaystyle \frac{U{I}^0\sin {\phi }_{u-i}^0}{2}}\\ Q_{\mathrm{b}}^{+}={\displaystyle \frac{U{I}^{+}\sin {\phi }_{u-i}^{+}}{2}};Q_{\mathrm{b}}^{-}={\displaystyle \frac{U{I}^{-}\sin ({\phi }_{u-i}^{-}+\frac{4\mathsf{\pi }}{3})}{2}};Q_{\mathrm{b}}^0={\displaystyle \frac{U{I}^0\sin ({\phi }_{u-i}^0-\frac{2\mathsf{\pi }}{3})}{2}}\\ Q_{\mathrm{c}}^{+}={\displaystyle \frac{U{I}^{+}\sin {\phi }_{u-i}^{+}}{2}};Q_{\mathrm{c}}^{-}={\displaystyle \frac{U{I}^{-}\sin ({\phi }_{u-i}^{-}+\frac{4\mathsf{\pi }}{3})}{2}};Q_{\mathrm{c}}^0={\displaystyle \frac{U{I}^0\sin ({\phi }_{u-i}^0+\frac{2\mathsf{\pi }}{3})}{2}}\end{array}\right.$$

(5)

As indicated by Equations (4) and (5), the positive-sequence active and reactive power components for each phase in distribution area 1 are identical, whereas the negative- and zero-sequence components are not. Therefore, it can be deduced that the three-phase power imbalance in the distribution area is attributable to the negative- and zero-sequence power components. According to the mathematical model of the three-phase four-leg converter in the dq0 coordinate system, the DC component on the d-axis of the positive-sequence component corresponds to the active component of the output current. Therefore, a DC value can be given on the d-axis of the positive-sequence component to control the capacitor voltage and ensure the stability of the DC network.

Based on the theoretical analysis above, the block diagram of the designed DC-bus voltage control strategy based on sequence power is shown in Figure 4.

The three-phase currents are filtered and separated using a SOGI-QSG to obtain the negative- and zero-sequence currents at node 0. Concurrently, the phase angle of the positive-sequence current θ⁺ is determined by a Synchronous Reference Frame Phase-Locked Loop (SRF-PLL). The DC-bus voltage U_dc is regulated via a closed-loop PI controller, the output of which serves as the reference value for the d-axis component of the positive-sequence current. This reference, along with the phase angle obtained from the PLL, undergoes a coordinate transformation to generate the three-phase positive-sequence current reference components. Subsequently, these positive-sequence components are superimposed with the separated negative- and zero-sequence components to yield the final unbalanced current compensation reference for the converter. This methodology addresses the three-phase unbalance within the distribution area caused by asymmetrical loads, thereby achieving load balancing among the phases in distribution area 1. The inner current loop, implemented using Model Predictive Control (MPC), tracks the command signal from the outer voltage loop as well as the reference signals for positive-sequence reactive power, negative-sequence, and zero-sequence components, thus compensating for each sequence component within the transformer area.

3.2. Closed-Loop Control Strategy Based on Phase-Separated Power Compensation

From Equation (3), the three-phase load power of distribution area 2 can be calculated as:

$$S_y=P_y+j{Q}_y$$

(6)

where P_y and Q_y are the active and reactive loads, respectively, of phase y in distribution area 2.

Then, the total three-phase power output of distribution area 2 is:

$$S_{\mathrm{total}}={\displaystyle \sum _{y=a}^c\left(P_y+j{Q}_y\right)}$$

(7)

To ensure three-phase load balancing, the unbalanced load must be compensated to achieve system power balance. Let the balanced three-phase power output of distribution area 2 be given by the following equation:

$$\left\{\begin{array}{l}{P}_{sa}=P_{sb}=P_{sc}=\eta \left({\displaystyle \frac{P_a+P_b+P_c}{3}}\right)\\ Q_{sa}=Q_{sb}=Q_{sc}=\gamma \left({\displaystyle \frac{Q_a+Q_b+Q_c}{3}}\right)\end{array}\right.$$

(8)

where η is the active power sharing coefficient and γ is the reactive power sharing coefficient.

Therefore, the three-phase unbalanced power compensation reference for the converter is:

$$\left\{\begin{array}{l}{P}_{yref}=P_y-\eta \left({\displaystyle \frac{P_a+P_b+P_c}{3}}\right)\\ Q_{yref}=Q_y-\gamma \left({\displaystyle \frac{Q_a+Q_b+Q_c}{3}}\right)\end{array}\right.$$

(9)

where P_yref and Q_yref are the active and reactive power output references, respectively, for each phase of the converter.

The values of η and γ must be determined based on constraints such as the converter and transformer capacities. These coefficients are selected to achieve power sharing between distribution areas and load balancing, all while operating within the permissible power transfer limits.

(1)

Transformer Capacity Constraint:

$$\sqrt{{P_s}^2+{Q_s}^2}\le S_N$$

(10)

where P_s is the sum of the three-phase active power output of the distribution area, and Q_s is the sum of the three-phase reactive power output.

(2)

VSC Capacity Constraint:

$$\sqrt{{P_{vsc}}^2+{Q_{vsc}}^2}\le S_{vscN}$$

(11)

where P_vsc and Q_vsc are the sum of the three-phase active and reactive power outputs of the converter, respectively.

Since direct per-phase current control suffers from drawbacks such as poor disturbance rejection capability, a dual closed-loop control strategy incorporating both power and current loops is employed. This approach not only overcomes the shortcomings of single-loop current control but also enhances the steady-state accuracy of the system. The block diagram of the designed closed-loop control strategy, which is based on phase-separated power compensation, is presented in Figure 5. It is composed of three primary components:

(1)

Unbalanced Compensation Power Calculation: The first segment calculates the required compensation power for unbalance conditions.

(2)

Outer Power Loop Control: The second segment encompasses the outer power loop, which ensures the stable tracking of the converter’s output power against the phase-separated power reference commands. Subsequently, it generates reference signals for the inner loop via coordinate transformation.

(3)

MPC Inner Current Loop Control: The third segment refers to the inner current loop built on Model Predictive Control (MPC). This loop is tasked with tracking the current reference commands transmitted by the outer power loop and outputting the corresponding switching signals.

Figure 5. Block diagram of the phase-separated power control.

Figure 5. Block diagram of the phase-separated power control.

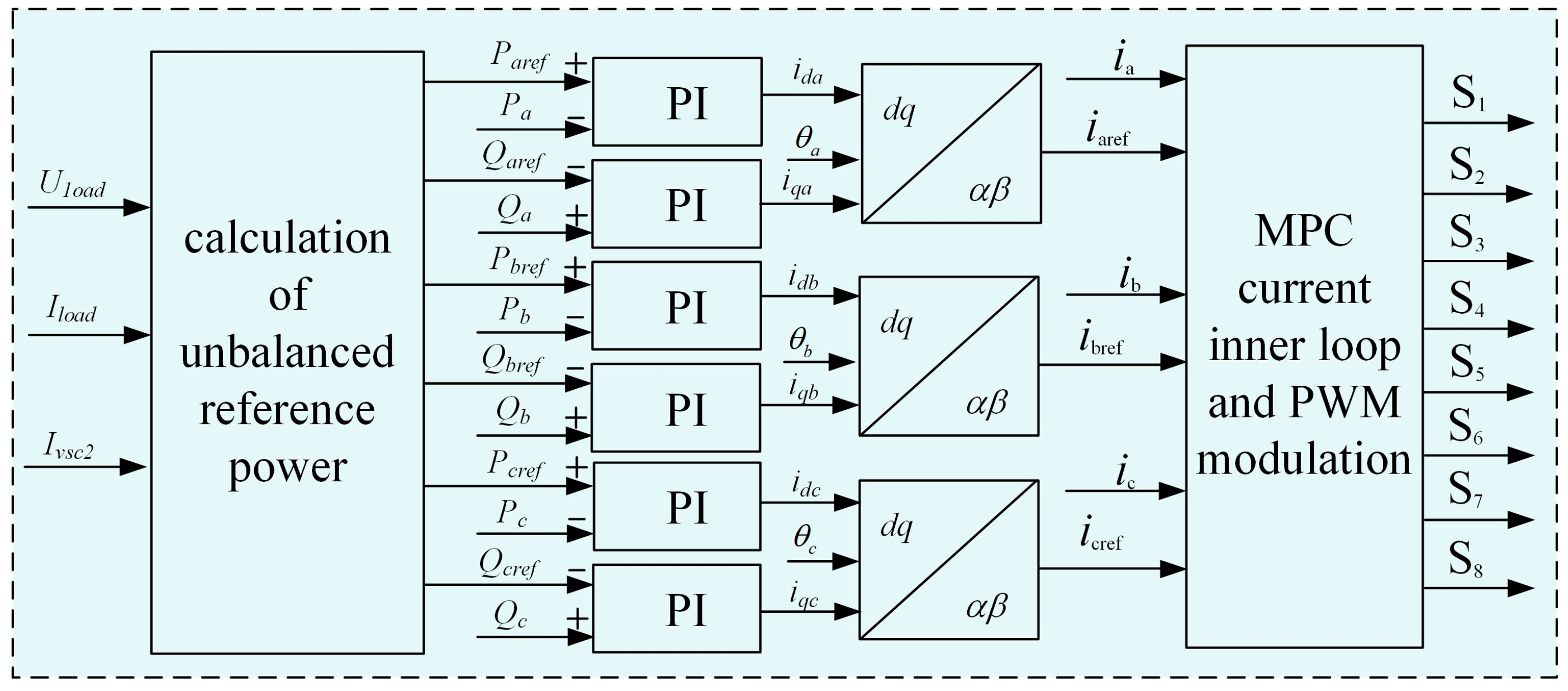
3.3. Phase-Separated Power Compensation Control Strategy Based on DPC

The principle of series compensation is shown in Figure 6.

In Figure 6., U_Aref, U_Bref, and U_Cref represent the phase voltage reference vectors of the three-phase system. The magnitudes of these three reference voltages are equal and denoted as U_r. U_Aref is the reference vector of the system, with a phase of 0, hence means the phase angles of U_Bref and U_Cref are −2π/3 and 2π/3, respectively. U_As, U_Bs, and U_Cs are the three-phase voltage phasors at the series connection point at the end of the distribution area, where φ_As, φ_Bs, and φ_Cs are the phases of the three-phase voltages at the distribution area end relative to the reference voltage vectors U_Aref, U_Bref, and U_Cref. Additionally, φ_A, φ_B, and φ_C represent the phase differences between the three-phase currents I_As, I_Bs, and I_Cc and the three-phase voltages U_As, U_Bs, and U_Cs at the serial connection point, respectively, yielding the three-phase compensation voltage vectors.

From Figure 6., the three-phase powers at this moment can be calculated as:

$$\left\{\begin{array}{l}{P}_{As}=U_{AS}\times I_{As}\times \mathrm{c}\mathrm{o}\mathrm{s}\left({\phi }_A\right)\\ Q_{As}=U_{AS}\times I_{As}\times \mathrm{s}\mathrm{i}\mathrm{n}\left({\phi }_A\right)\\ P_{Bs}=U_{Bs}\times I_{Bs}\times \mathrm{c}\mathrm{o}\mathrm{s}\left({\phi }_B\right)\\ Q_{Bs}=U_{Bs}\times I_{Bs}\times \mathrm{s}\mathrm{i}\mathrm{n}\left({\phi }_B\right)\\ P_{Cs}=U_{Cs}\times I_{Cs}\times \mathrm{c}\mathrm{o}\mathrm{s}\left({\phi }_C\right)\\ Q_{Cs}=U_{Cs}\times I_{Cs}\times \mathrm{s}\mathrm{i}\mathrm{n}\left({\phi }_C\right)\end{array}\right.$$

(12)

where U_As, U_Bs, and U_Cs are the magnitudes of the three-phase voltages at the series connection point, I_As, I_Bs, and I_Cs are the magnitudes of the three-phase currents, and φ_A, φ_B, and φ_C represent the phase differences between the respective voltages and currents.

By multiplying the three-phase reference voltages U_Aref, U_Bref, and U_Cref with the three-phase currents I_A, I_B, and IC, the resulting three-phase power values at the terminal under balanced voltage conditions are given as follows:

$$\left\{\begin{array}{l}{P}_{Aref}=U_{Aref}\times I_{As}\times \cos ({\phi }_A\pm {\phi }_{As})\\ Q_{Aref}=U_{Aref}\times I_{As}\times \sin ({\phi }_A\pm {\phi }_{As})\\ P_{Bref}=U_{Bref}\times I_{Bs}\times \cos ({\phi }_B\pm {\phi }_{Bs})\\ Q_{Bref}=U_{Bref}\times I_{Bs}\times \sin ({\phi }_B\pm {\phi }_{Bs})\\ P_{Cref}=U_{Cref}\times I_{Cs}\times \cos ({\phi }_C\pm {\phi }_{Bs})\\ Q_{Cref}=U_{Cref}\times I_{Cs}\times \sin ({\phi }_C\pm {\phi }_{Bs})\end{array}\right.$$

(13)

where U_Aref, U_Bref, and U_Cref are the magnitudes of the three-phase reference voltages; I_As, I_Bs, and I_Cc are the magnitudes of the three-phase currents at the series connection point; φ_As, φ_Bs, and φ_Cs are the phase differences between the actual three-phase voltages and their respective reference voltages. The phase difference φ is defined as negative when the actual voltage leads the reference voltage, and positive when it lags.

The active and reactive compensation command values for each phase of the controller are:

$$\left\{\begin{array}{l}{P}_{aref}=P_{Aref}-P_{As}\\ Q_{aref}=Q_{Aref}-Q_{As}\\ P_{bref}=P_{Bref}-P_{Bs}\\ Q_{bref}=Q_{Bref}-Q_{Bs}\\ P_{cref}=P_{Cref}-P_{Cs}\\ Q_{cref}=Q_{Cref}-Q_{Cs}\end{array}\right.$$

(14)

When P_xref > 0 and Q_xref > 0 (for x = a, b, c), this indicates an undervoltage condition at the transformer area terminal. In this case, the series compensator injects active and reactive power according to these compensation commands to raise the voltage at the connection point from its sagged state to the rated level. Conversely, when P_xref > 0 and Q_xref > 0, this signifies an overvoltage condition. The series compensator then absorbs power based on the commands to reduce the voltage from its swollen state down to the rated level.

Through the above analysis, the designed direct power control phase compensation strategy is illustrated in Figure 7. It is primarily divided into three parts. Firstly, by capturing the effective values of the three-phase unbalanced voltage at the series connection point and the output voltage of compensator, the phase difference angle between the three-phase unbalanced voltage and the reference voltage is calculated. Secondly, by utilizing the SRF-PLL to determine the phase of the three-phase unbalanced voltage, the phase differences are combined to construct the three-phase voltage reference. The three-phase reference vectors are then compared with the acquired three-phase voltages through power calculations to obtain the power compensation command values for each phase. Finally, the power compensation reference values are input into the power control loops of each phase, and ultimately, the switch control signals of the compensator are output through 3D-Space Vector Pulse Width Modulation (3D-SVPWM).

4. Simulation

To evaluate the effectiveness of the unbalance compensation in the distribution area, the three-phase current unbalance factor is calculated using the following formula:

$${\lambda }_I={\displaystyle \frac{\left(I_{\mathrm{m}\mathrm{a}\mathrm{x}}−I_{av}\right)}{I_{av}}}\times 100\%$$

(15)

$$\beta ={\displaystyle \frac{S}{S_n}}\times 100\%$$

(16)

where λ_I is the three-phase current imbalance, I_max is the maximum value in the ABC phase current, I_av is the effective value mean of phase currents. β represents the distribution transformer load rate, S is the transformer active power used, and S_n is the transformer apparent power.

4.1. Experimental Setup

To validate the effectiveness of the proposed control strategy, a simulation model was constructed in MATLAB/Simulink software based on the actual topology of a specific distribution area. The simulation software employed was MATLAB 2024b, utilizing the ode1 (Euler) solver with a simulation step size of 1 × 10⁻⁶ s and a sampling frequency of 10 kHz. The distribution area topologies are illustrated in Figure 8.

To address the three-phase imbalance at the output side of the low-voltage distribution substation transformer, power sharing, and voltage issues at the end of the distribution network, the parallel compensation converters VSC1 and VSC2 within the coordinated optimization flexible interconnection device are embedded at nodes 0 of Substation 1 and Substation 2, respectively. The series compensation converter VSC3 is embedded at node 26 of Substation 2. The length of the DC line is 0.4 km. The DC line resistance parameter is set to 0.46 Ω/km, and the line equivalent impedance is set to 0.276 Ω. Combined with the original substation analysis, the parallel compensator converters VSC1 and VSC2 have a capacity of 100 kVA each, and the series compensator converter VSC3 has a capacity of 50 kVA. The LC filter has an inductance L of 3 mH and a capacitance C of 8 μF. The neutral inductance Ln is set to 3 mH, the DC network voltage regulation capacitance C_dc is set to 3 mF, and the converter switch frequency is 10 kHz.

The system control parameters are shown in

Table 1. System control parameter.

Parameter	Value
Relevant parameters of distribution transformer 1	SN1 = 200 kVA, UN1 = 380 V, Z1ep = 0.00388 + j0.0014 Ω
Relevant parameters of distribution transformer 2	SN2 = 200 kVA, UN2 = 380 V, Z2ep = 0.0958 + j0.0324 Ω
Inverter VSC1 control parameters	KP = 8, KI = 50
Inverter VSC2 control parameters	KP = 0.002, KI = 1.1
Inverter VSC3 control parameters	KPP = 0.001, KIP = 2, KPU = 1.5, KIU = 50 KPI = 50, KII = 100

. The loads and PV connections at each node of distribution areas 1 and distribution areas 2 are shown in Appendix A,

Table A1. Three-phase load and photovoltaic integration data of power distribution areas 1 (typical day 12/18 h).

Node	Load (kW)			PV (kW)
	A Phase	B Phase	C Phase	A Phase	B Phase	C Phase
1	1.8/3	1.8/3	1.8/3	2.925	0	0
2	0	0	1.8/3	0	2.925	0
3	1.8/3	1.8/3	0	0	0	2.925
4	0	1.8/3	0	2.925	0	0
5	1.8/3	0	0	0	0	2.925
6	1.8/3	1.8/3	1.8/3	0	0	0
7	0	0	0	2.925	0	0
8	1.8/3	1.8/3	1.8/3	2.925	2.925	0
9	0	0	0	0	0	0
10	1.8/3	1.8/3	0	2.925	2.925	2.925
11	0	0	1.8/3	0	0	0
12	1.8/3	1.8/3	0	0	0	0
13	0	0	1.8/3	2.925	2.925	0
14	1.8/3	1.8/3	0	0	0	2.925
15	0	0	1.8/3	2.925	0	0
16	0	0	0	0	2.925	0
17	0	1.8/3	0	0	0	0
18	1.8/3	0	0	0	0	0
19	0	0	0	0	0	0
20	0	0	0	0	0	0

and

Table A2. Three-phase load and photovoltaic integration data of power distribution areas 2 (typical day 12/18 h).

Node	Load (kW)			PV (kW)
	A Phase	B Phase	C Phase	A Phase	B Phase	C Phase
1	1.8/3	1.8/3	1.8/3	0	0	0
2	1.8/3	0	0	0	2.925	0
3	1.8/3	1.8/3	1.8/3	0	0	0
4	1.8/3	0	1.8/3	2.925	0	0
5	0	1.8/3	0	0	0	0
6	1.8/3	1.8/3	0	0	0	0
7	1.8/3	0	1.8/3	0	0	2.925
8	1.8/3	1.8/3	1.8/3	0	0	0
9	0	1.8/3	0	0	0	0
10	1.8/3	0	0	0	0	0
11	1.8/3	0	0	2.925	0	0
12	0	1.8/3	1.8/3	0	2.925	2.925
13	1.8/3	1.8/3	0	0	0	0
14	1.8/3	0	0	0	0	0
15	0	1.8/3	0	0	0	0
16	1.8/3	0	1.8/3	0	0	0
17	1.8/3	1.8/3	1.8/3	0	0	2.925
18	0	0	0	2.925	2.925	0
19	1.8/3	1.8/3	0	0	0	0
20	1.8/3	0	1.8/3	0	0	0
21	1.8/3	1.8/3	1.8/3	0	0	0
22	0	1.8/3	0	0	2.925	0
23	1.8/3	0	1.8/3	2.925	0	0
24	1.8/3	1.8/3	0	0	0	0
25	0	0	1.8/3	0	0	0
26	1.8/3	1.8/3	0	2.925	2.925	0
27	1.8/3	1.8/3	1.8/3	0	0	2.925
28	1.8/3	1.8/3	0	2.925	2.925	0
29	1.8/3	0	1.8/3	0	0	2.925
30	1.8/3	1.8/3	0	2.925	2.925	0
31	1.8/3	1.8/3	1.8/3	2.925	2.925	2.925
32	1.8/3	1.8/3	1.8/3	2.925	0	0

.

For analytical purposes, the following operating conditions have been established (load power factor of 0.9).

Operating Condition 1: Select the PV and load data at 18:00 in the afternoon to represent a scenario with a high proportion of load and a low proportion of photovoltaics.

Operating Condition 2: Select the PV and load data at 12:00 noon to represent a scenario with a high proportion of photovoltaics and a low proportion of load.

Boundary conditions: The interconnected transformer areas are all three-phase four-wire low-voltage distribution networks, with the effective value of the line voltage on the secondary side of the transformer being 380 V ± 10% and the frequency being 50 Hz. The reference value of the DC bus voltage is 750 V.

Load scenarios of Operating Condition 1: Distribution Area 1 is a short-line and light-load area with a low transformer load rate, while distribution Area 2 is a long-line and heavy-load area with an excessively high transformer load rate and an excessively low voltage at the end of its distribution network.

Load scenarios of Operating Condition 2: Distribution Area 1 is a short-line area with low photovoltaic (PV) penetration, while distribution Area 2 is a long-line area with high PV penetration, and the PV output at its end is much higher than the power consumed by end users.

In this simulation validation, VSC1 is selected to control the DC bus voltage. The coordinated optimization flexible interconnection device is activated when the system operates for 1 s. In Operating Condition 1, there is a sudden increase in the load at the end of distribution area 2 at 1.5 s, while in Operating Condition 2, there is a sudden decrease in the load at the end of distribution area 2 at 1.5 s.

4.2. Simulation Analysis

4.2.1. Operating Condition 1

The simulation waveforms for each distribution area under Operating Condition 1 are as Figure 9 and Figure 10. The simulation process for Operating Condition 1 can be divided into three stages, with the analysis data from the simulation results presented in

Table 2. Detailed steady-state electrical parameters for Case 1 simulation stages.

Stage	Location	Phase	P (kW)	Q (kvar)	I (A)	U (V)
Stage 1	node 0 of DA 1	A/B/C	22.65/18.52/14.21	9.68/8.09/6.37	158.1/129.4/99.5	-
	node 0 of DA 2	A/B/C	67.15/54.81/40.92	30.96/25.46/19.23	477.6/389.5/288.8	-
	node 26 of DA 2	A/B/C	13.16/13.22/9.63	6.34/6.39/4.66	-	277.8/266.1/252.1
Stage 2	node 0 of DA 1	A/B/C	30.72/39.65/39.55	16.83/16.82/17.05	275.5/275.1/276.0	-
	node 0 of DA 2	A/B/C	39.72/39.71/39.68	27.26/27.23/27.28	310.2/311.1/309.6	-
	node 26 of DA 2	A/B/C	20.15/18.10/12.11	9.68/8.76/5.86	-	311.8/311.6/311.4
Stage 3	node 0 of DA 1	A/B/C	45.42/45.34/45.22	19.46/19.43/19.65	316.2/318.1/316.4	-
	node 0 of DA 2	A/B/C	40.05/40.01/40.02	29.15/29.18/29.20	318.2/318.3/318.4	-
	node 26 of DA 2	A/B/C	25.18/22.10/15.13	12.08/10.70/7.32	-	310.8/310.9/310.9

and

Table 3. Evolution of key system performance indices in Case 1.

Index	Parameter Symbol	Stage 1	Stage 2	Stage 3	Governance Outcomes
Current imbalance	λI1	22.56%	0.17%	0.26%	Maintain a high degree of equilibrium
	λI2	23.96%	0.26%	0.03%
Load factor of distribution transformers	β1	30.21% (Light load)	64.60%	73.99%	Proactively assume additional load
	β2	89.78% (Heavy load)	72.21%	74.26%	Maintain the load factor within a reasonable range.
Terminal voltage	Unode26	252.1~277.8 V	311 V	311 V	Voltage has recovered from a severe over-limit condition to its rated value

.

Based on the above data analysis, there are distinct operational characteristics and improvements of the power distribution system in different stages regarding the interconnected compensator. Prior to the activation of the interconnected compensator, several critical issues plagued the system: both distribution area 1 and distribution area 2 faced severe three-phase unbalance at node 0; the two areas had disparate loading conditions, with the distribution transformer in area 1 running under light load while that in area 2 was heavily loaded; most critically, node 26 of distribution area 2 suffered a severe voltage limit violation, with the voltage dropping over 10% below the nominal value, and prolonged operation under such circumstances would pose a huge risk of equipment damage and lead to substantial economic losses. After installing the interconnection compensation device, notable improvements were achieved: the three-phase current imbalance at node 0 of distribution area 1 and 2 dropped drastically from 22.56% and 23.96% to 0.17% and 0.26%, respectively; the load factor of the transformer in distribution area 1 rose from 30.21% to 64.6%, while that of distribution area 2 declined from 89.78% to 72.21%; the low voltage at node 26 of distribution area 2 increased from the original 277.8 V, 266.1 V, and 252.1 V to around 311 V, effectively resolving the problems of three-phase imbalance and voltage limit violations at substation terminals. Additionally, when a sudden load surge occurred at node 26 of distribution area 2, given that distribution area 1 still had spare capacity, most of the energy needed for the sudden load increase was directly supplied by distribution area 1 through the DC network, which not only boosted the utilization rate of distribution area 1 but also lowered the load rate of distribution area 2. The power transmitted by each converter in Operating Condition 1 is shown in Figure 11.

4.2.2. Operating Condition 2

The simulation waveforms for each distribution area under operating condition 2 are as Figure 12 and Figure 13. The simulation process for operating condition 2 can be divided into three stages, with the analysis data from the simulation results presented in

Table 4. Detailed steady-state electrical parameters for Case 2 simulation stages.

Stage	Location	Phase	P (kW)	Q (kvar)	I (A)	U (V)
Stage 1	node 0 of DA 1	A/B/C	2.74/1.75/0.40	8.52/6.56/5.17	57.5/43.6/33.3	-
	node 0 of DA 2	A/B/C	29.01/22.22/16.38	28.03/22.58/15.99	260.7/204.8/147.3	-
	node 26 of DA 2	A/B/C	27.89/23.45/15.23	12.97/11.03/7.21	-	365.2/352.4/345.5
Stage 2	node 0 of DA 1	A/B/C	2.64/2.58/2.65	10.95/10.85/10.91	73.1/72.5/72.2	-
	node 0 of DA 2	A/B/C	16.50/16.49/16.49	27.56/27.54/27.55	207.4/207.3/207.2	-
	node 26 of DA 2	A/B/C	20.17/18.21/12.32	9.38/8.56/5.82	-	310.8/310.2/310.8
Stage 3	node 0 of DA 1	A/B/C	1.62/1.60/1.63	6.55/6.50/6.40	43.9/43.5/42.5	-
	node 0 of DA 2	A/B/C	13.06/13.05/13.05	24.24/24.23/24.24	177.3/177.6/177.7	-
	node 26 of DA 2	A/B/C	13.63/12.28/8.27	6.42/5.83/3.94	-	310.2/310.8/310.8

and

Table 5. Evolution of key system performance indices in Case 2.

Index	Parameter Symbol	Stage 1	Stage 2	Stage 3	Governance Outcomes
Current imbalance	λI1	28.35%	0.68%	1.38%	Maintain a high degree of equilibrium
	λI2	27.63%	0.04%	0.11%
Load factor of distribution transformers	β1	10.42%	16.80%	10.02%	Photovoltaic power is being fed back into the grid, whilst the load factor remains at a low level
	β2	47.45%	48.18%	41.30%	Maintain the load factor within a reasonable range
Terminal voltage	Unode26	345.5~365.2 V	310 V	310 V	Severe overvoltage has been suppressed to normal levels.

.

Based on the above data analysis, it is evident that before the interconnection compensation device is activated, the irregular connection of single-phase photovoltaics can to some extent lower the load rate of the distribution transformer, yet a severe three-phase imbalance problem persists at node 0 of both distribution area 1 and distribution area 2; additionally, the PV output at the end of distribution area 2 far surpasses the local end users’ consumption capacity, resulting in a serious voltage violation at node 26 of distribution area 2. Upon the activation of the interconnection compensation device, the three-phase current imbalance at node 0 of distribution area 1 and distribution area 2 drops drastically from 28.35% and 27.63% to 0.68% and 0.04% respectively; meanwhile, the excess PV output at the end of distribution area 2 is transmitted to the start of each distribution area via the DC network, which reduces the active output of each transformer, brings the overvoltage at node 26 of distribution area 2 down from around 365.2 V, 352.4 V, and 345.5 V to approximately 311 V, and enhances PV absorption capacity, thus resolving both the three-phase imbalance and the end-of-substation voltage violation issues. Furthermore, when there is a sudden load drop at node 26 of distribution area 2, end users there would theoretically encounter a more severe overvoltage problem, but the application of the series compensator to transfer surplus power to the beginning of each distribution area not only mitigates the overvoltage risk but also leads to a notable reduction in the load rate of distribution transformers in each substation. The power transfer of each converter in operating condition 2 is depicted in Figure 14.

Through the simulation verification of the above two operating conditions, the integrated operation control strategy based on series-parallel coordinated operation proposed in this paper has been effectively demonstrated to address the three-phase imbalance and end-of-substation voltage violation issues, thereby achieving power sharing between distribution areas.

5. Conclusions

To address the power quality issues such as three-phase imbalance at the beginning of a low-voltage distribution network and overvoltage at the end, this paper proposes a control strategy based on series-parallel coordinated operation. The following conclusions are drawn from the MATLAB simulation analysis:

(1)

A low-voltage substation series-parallel coordinated control strategy considering direct power control is proposed in this study, comprehensively addressing the issues of three-phase imbalance at the substation and end-of-substation voltage violations.

(2)

Interconnecting substations through VSCs allows for balancing transformer output power by scheduling active power and compensating reactive power. This can reduce overall system losses and significantly enhance the economic efficiency of interconnected substations.

(3)

The proposed topology can upgrade traditional distribution networks into topologically flexible, controllable AC/DC hybrid distribution networks, aligning with the development trends of modern distribution systems.

During the simulation process of this paper, all compensation devices cooperated well; they possess high dynamic response capability. However, practical application is confronted with challenges of measurement delay and converter capacity limitation. A reasonably designed protection scheme can respond quickly when the system fails. It effectively ensures the safe and stable operation of the power system.